A Novel Method for Estimating State of Power of Lithium-Ion Batteries Considering Core Temperature
Abstract
1. Introduction
- (1)
- A battery electro-thermal model is developed which accounts for battery core temperature. The parameters of this electrical and thermal model are coupled with each other to accurately characterize the electro-thermal properties of the battery, which are identified by MLM and AGA, respectively. The thermal model also contains the core and surface temperatures of the battery. UKF is used to estimate model results, which ensures that the model is highly accurate.
- (2)
- Multi-constrained SOP estimation with core temperature is included. A multi-parameter coupled method for estimating SOP is proposed based on the above electro-thermal model. This method is capable of accurately estimating the SOP under multiple constraints throughout the battery charging and discharging process. Constraining core temperature improves battery safety at high temperatures.
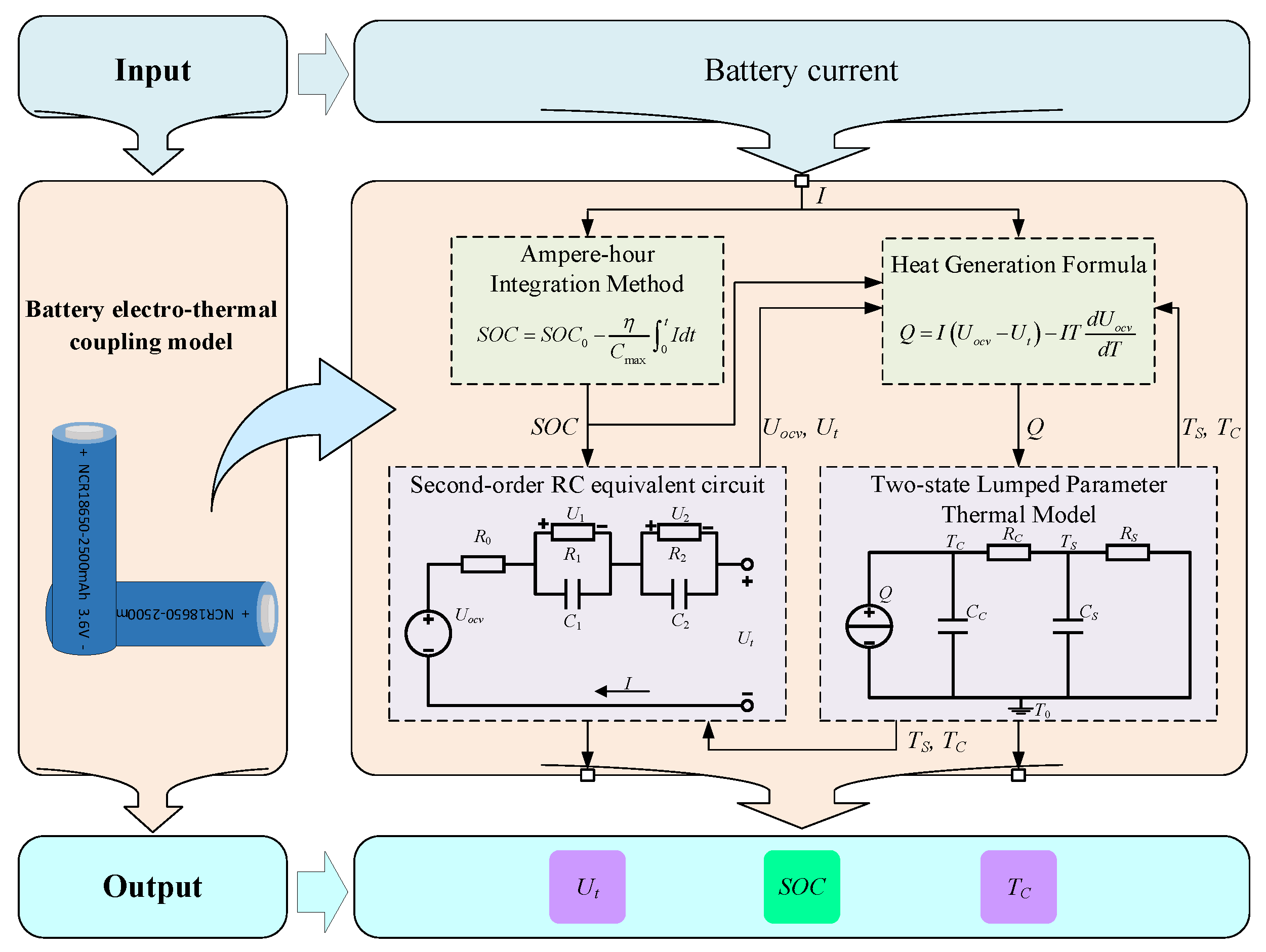
2. Battery Electro-Thermal Model
2.1. Model Structure
2.2. Experiment
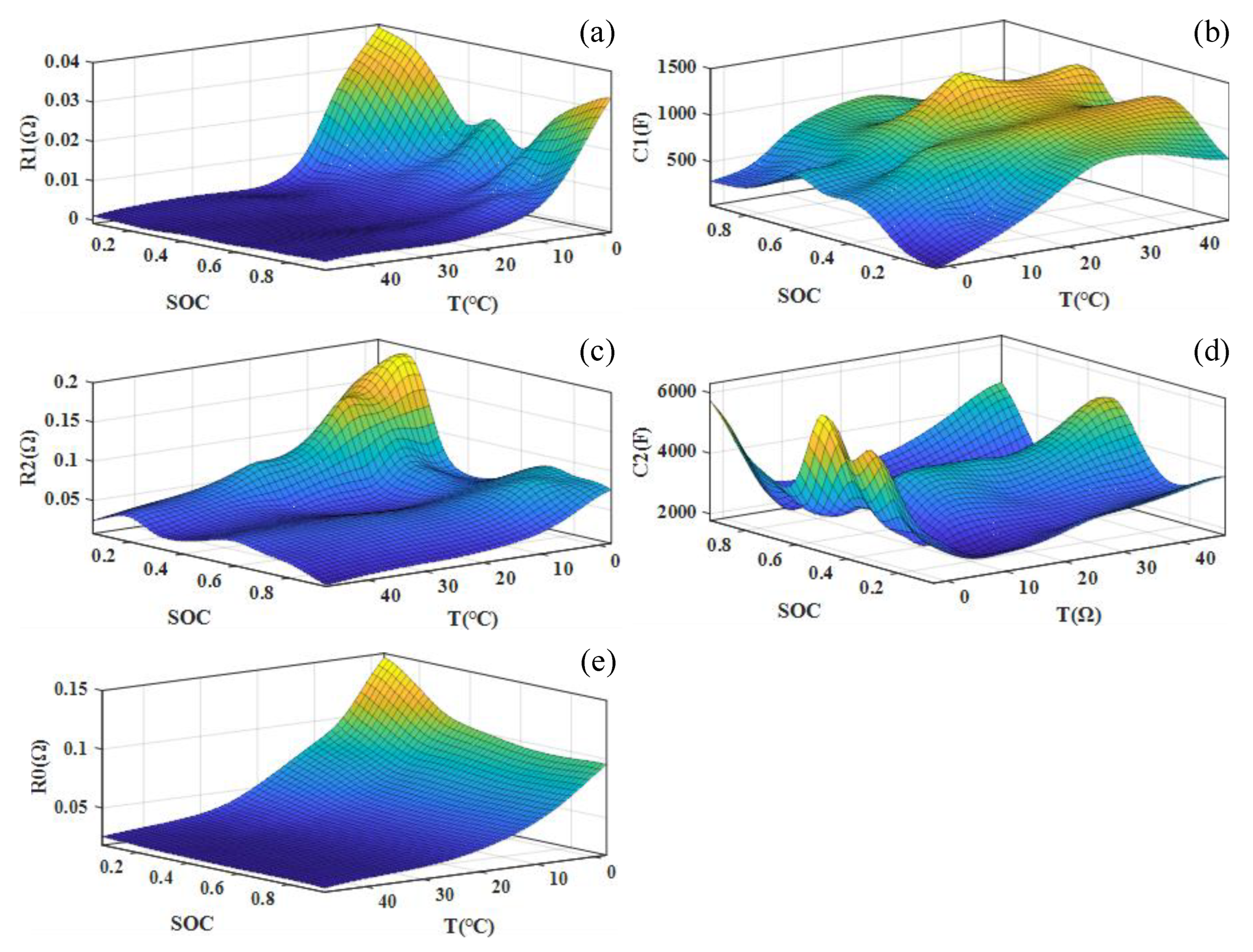
2.3. Parameter Identification
2.3.1. Parameter Identification of Electrical Model
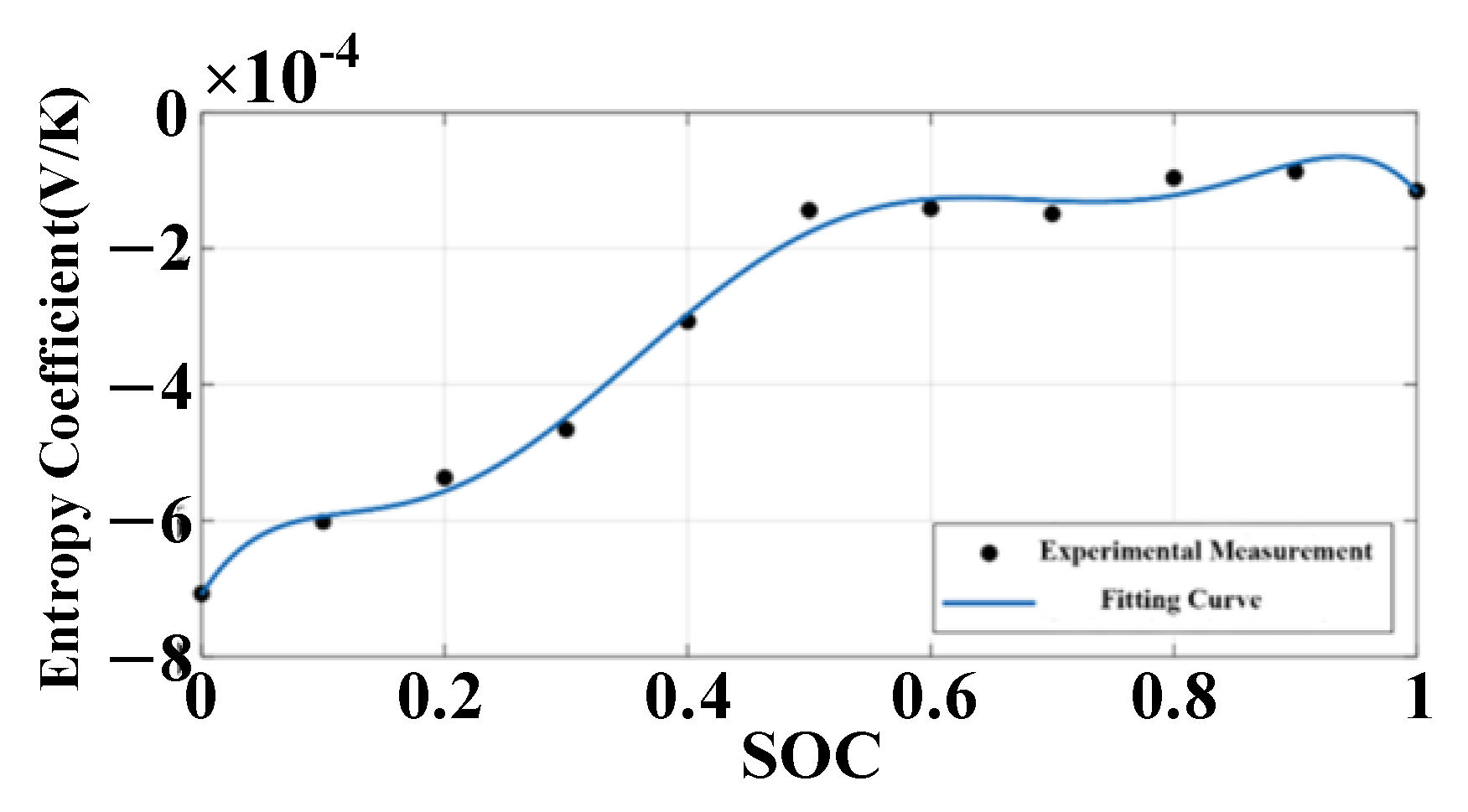
2.3.2. Parameter Identification of Thermal Model
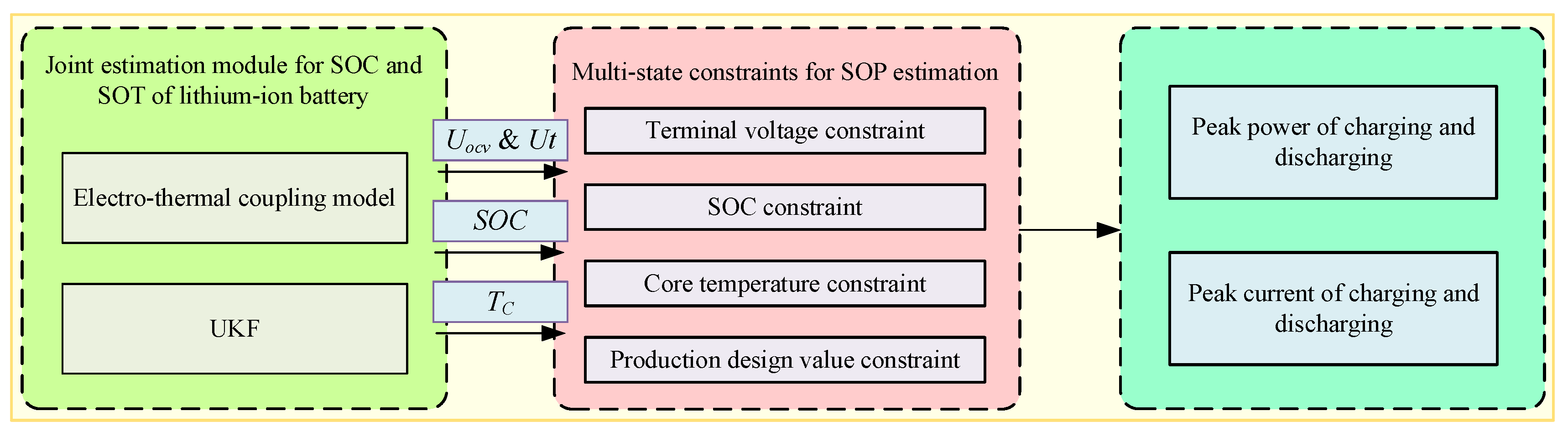
3. Joint Estimate of SOC and SOT
3.1. Joint Estimation Algorithm Based on UKF
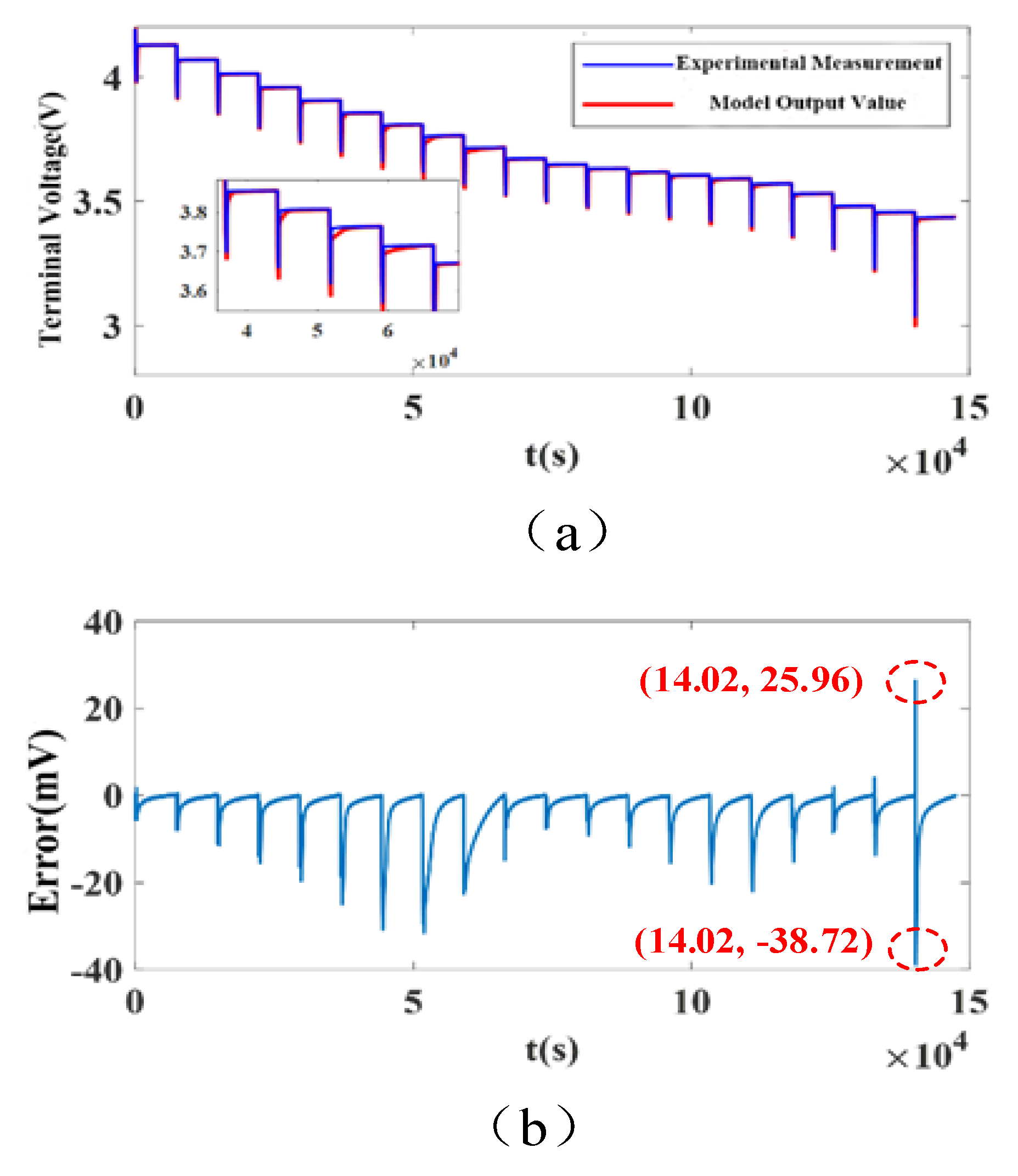
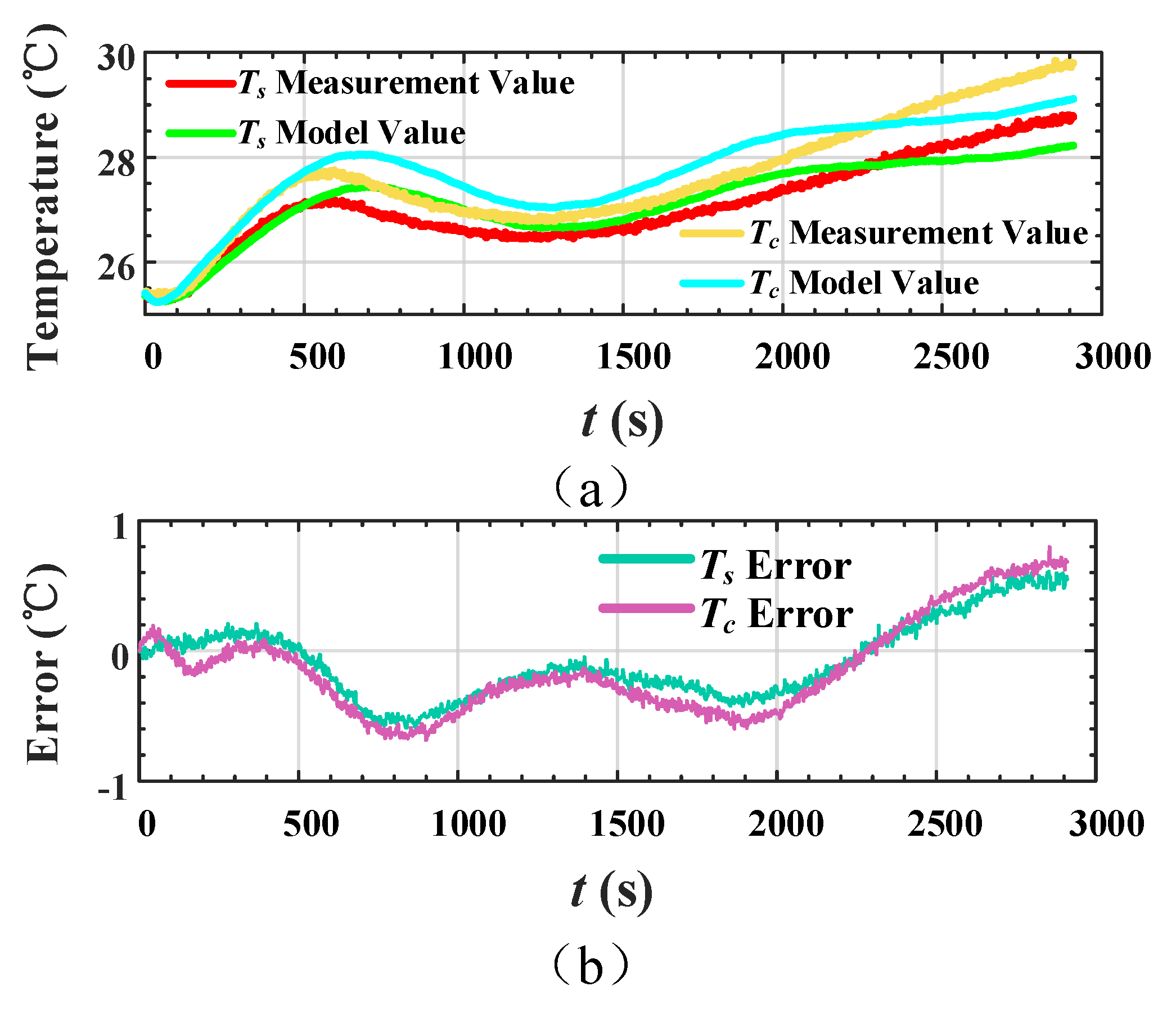
3.2. Results of Estimation for SOC and SOTC
4. SOP Estimation with Multi-State Constraints
4.1. SOC Constraint
4.2. Terminal Voltage Constraint
4.3. Core Temperature Constraints
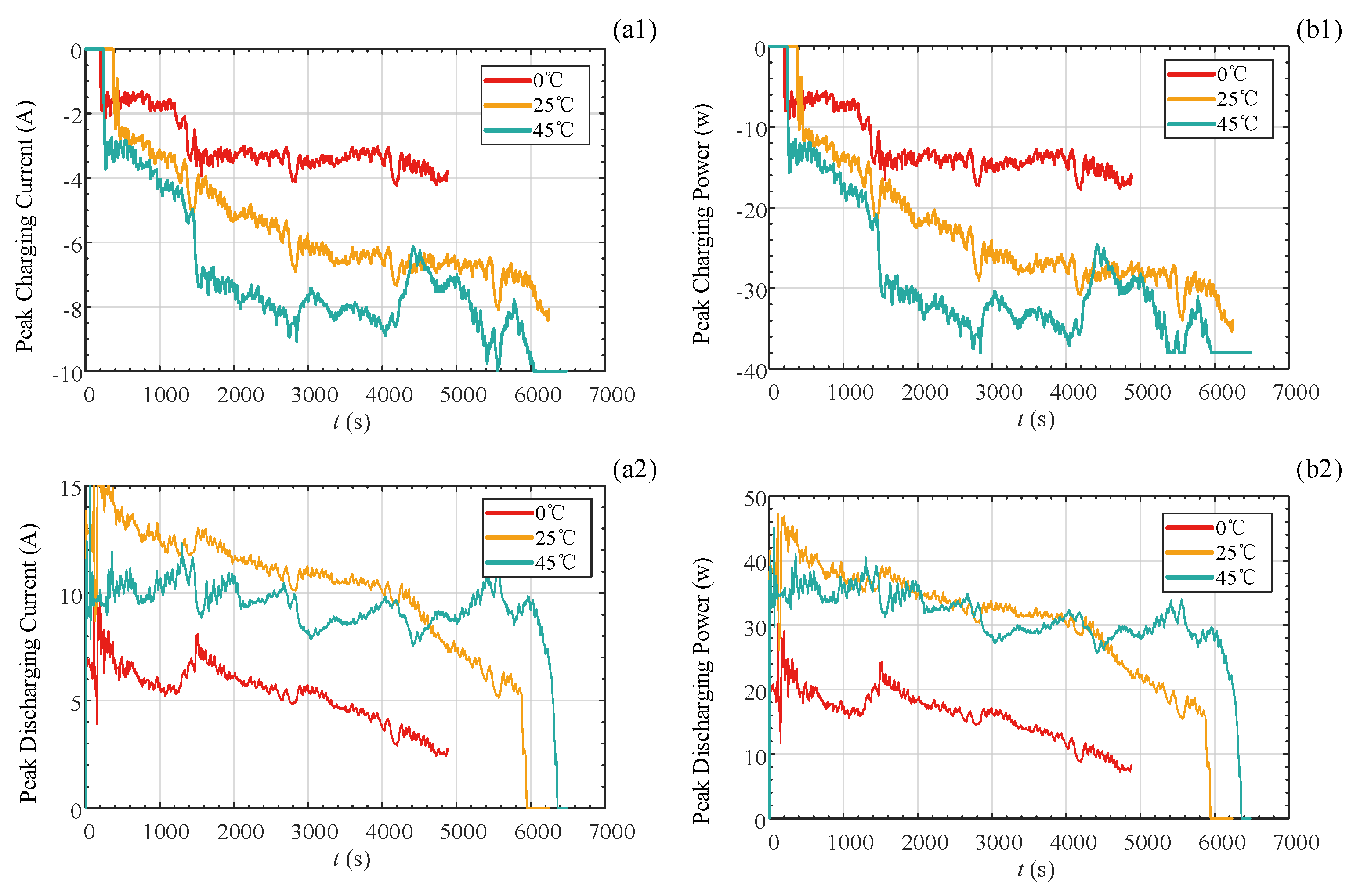
4.4. Results and Analysis of SOP Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, L.; Zhang, S.; Huang, H.; Liu, R.; Cai, M.; Bian, Y.; Chang, L.; Du, H. Artificial intelligence-driven rechargeable batteries in multiple fields of development and application towards energy storage. J. Energy Storage 2023, 73, 108926. [Google Scholar] [CrossRef]
- Duffner, F.; Kronemeyer, N.; Tübke, J.; Leker, J.; Winter, M.; Schmuch, R. Post-lithium-ion battery cell production and its compatibility with lithium-ion cell production infrastructure. Nat. Energy 2021, 6, 123–134. [Google Scholar] [CrossRef]
- Li, M.; Mo, R.; Ding, A.; Zhang, K.; Guo, F.; Xiao, C. Electrochemical technology to drive spent lithium-ion batteries (LIBs) recycling: Recent progress, and prospects. Energy Mater. 2024, 4, 400070. [Google Scholar] [CrossRef]
- Guo, F.; Wu, X.; Liu, L.; Ye, J.; Wang, T.; Fu, L.; Wu, Y. Prediction of remaining useful life and state of health of lithium batteries based on time series feature and Savitzky-Golay filter combined with gated recurrent unit neural network. Energy 2023, 270, 126880. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.L.; Tian, J.P. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Chakraborty, B. Battery management strategies: An essential review for battery state of health monitoring techniques. J. Energy Storage 2022, 51, 104427. [Google Scholar] [CrossRef]
- Farmann, A.; Sauer, D.U. A comprehensive review of on-board State-of-Available-Power prediction techniques for lithium-ion batteries in electric vehicles. J. Power Sources 2016, 329, 123–137. [Google Scholar] [CrossRef]
- Han, W.; Altaf, F.; Zou, C.; Wik, T. Sensitivity Analysis of the Battery System State of Power. IEEE Trans. Transp. Electrif. 2022, 8, 976–989. [Google Scholar] [CrossRef]
- Liu, F.; Shao, C.; Su, W.; Liu, Y. Online joint estimator of key states for battery based on a new equivalent circuit model. J. Energy Storage 2022, 52, 104780. [Google Scholar] [CrossRef]
- Shrivastava, P.; Naidu, P.A.; Sharma, S.; Panigrahi, B.K.; Garg, A. Review on technological advancement of lithium-ion battery states estimation methods for electric vehicle applications. J. Energy Storage 2023, 64, 107159. [Google Scholar] [CrossRef]
- Tong Poh, W.Q.; Xu, Y.; Poh Tan, R.T. A Review of Machine Learning Applications for Li-Ion Battery State Estimation in Electric Vehicles. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 1–5 November 2022; pp. 265–269. [Google Scholar]
- Liu, X.; He, Y.; Zeng, G.; Zhang, J.; Zheng, X. State-of-Power Estimation of Li-Ion Batteries Considering the Battery Surface Temperature. Energy Technol. 2018, 6, 1352–1360. [Google Scholar] [CrossRef]
- Guo, R.; Shen, W. Lithium-Ion Battery State of Charge and State of Power Estimation Based on a Partial-Adaptive Fractional-Order Model in Electric Vehicles. IEEE Trans. Ind. Electron. 2023, 70, 10123–10133. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Liu, X.; Liu, Z. Model-based state of charge and peak power capability joint estimation of lithium-ion battery in plug-in hybrid electric vehicles. J. Power Sources 2013, 229, 159–169. [Google Scholar] [CrossRef]
- Guo, R.; Shen, W. A Model Fusion Method for Online State of Charge and State of Power Co-Estimation of Lithium-Ion Batteries in Electric Vehicles. IEEE Trans. Veh. Technol. 2022, 71, 11515–11525. [Google Scholar] [CrossRef]
- Fu, S.; Lv, T.; Xie, J.; Wu, L.; Luo, C. A Multiple Time-Scales Based Multi-state Co-estimation Method for Lithium-ion Battery. In Proceedings of the 2021 11th International Conference on Power and Energy Systems (ICPES), Virtual, 18–20 December 2021; pp. 183–189. [Google Scholar]
- Zhang, T.; Guo, N.; Sun, X.; Fan, J.; Yang, N.; Song, J.; Zou, Y. A Systematic Framework for State of Charge, State of Health and State of Power Co-Estimation of Lithium-Ion Battery in Electric Vehicles. Sustainability 2021, 13, 5166. [Google Scholar] [CrossRef]
- Han, W.; Altaf, F.; Zou, C.; Wik, T. State of Power Prediction for Battery Systems with Parallel-Connected Units. IEEE Trans. Transp. Electrif. 2022, 8, 925–935. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.; Liu, C.; Chang, C.; Li, X. A novel Co-estimation framework of state-of-charge, state-of-power and capacity for lithium-ion batteries using multi-parameters fusion method. Energy 2023, 269, 126820. [Google Scholar] [CrossRef]
- Wang, Y. Online estimation of battery power state based on improved equivalent circuit model. IOP Conf. Ser. Earth Environ. Sci. 2021, 651, 022080. [Google Scholar] [CrossRef]
- Guo, R.; Shen, W. An enhanced multi-constraint state of power estimation algorithm for lithium-ion batteries in electric vehicles. J. Energy Storage 2022, 50, 104628. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H.; Li, W.; Aussems JE, E. Model-based dynamic multi-parameter method for peak power estimation of lithium–ion batteries. Appl. Energy 2012, 96, 378–386. [Google Scholar] [CrossRef]
- Li, X.Y.; Sun, J.L.; Hu, Z.H.; Lu, R.G.; Zhu, C.B.; Wu, G.L. A New Method of State of Peak Power Capability Prediction for Li-ion Battery. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (Vppc), Montreal, QC, Canada, 19–22 October 2015. [Google Scholar]
- Li, B.; Wang, S.; Fernandez, C.; Yu, C.; Xia, L.; Fan, Y. A linear recursive state of power estimation method based on fusion model of voltage and state of charge limitations. J. Energy Storage 2021, 40, 10258. [Google Scholar] [CrossRef]
- Guo, R.; Shen, W. A Review of Equivalent Circuit Model Based Online State of Power Estimation for Lithium-Ion Batteries in Electric Vehicles. Vehicles 2021, 4, 1–31. [Google Scholar] [CrossRef]
- Li, W.; Fan, Y.; Ringbeck, F.; Jöst, D.; Sauer, D.U. Unlocking electrochemical model-based online power prediction for lithium-ion batteries via Gaussian process regression. Appl. Energy 2022, 306, 11811. [Google Scholar] [CrossRef]
- Lei, X.; Zhao, X.; Wang, G.; Liu, W. A Novel Temperature–Hysteresis Model for Power Battery of Electric Vehicles with an Adaptive Joint Estimator on State of Charge and Power. Energies 2019, 12, 362. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Yu, C.; Li, B.; He, M. An Online Method for Power State Estimation of Lithium-Ion Batteries under the Constraints of the Fusion Model Considering Temperature Effect. Int. J. Electrochem. Sci. 2022, 17, 220764. [Google Scholar] [CrossRef]
- Xin, Q.; Xiao, J.; Yang, T.; Zhang, H.; Long, X. Thermal management of lithium-ion batteries under high ambient temperature and rapid discharging using composite PCM and liquid cooling. Appl. Therm. Eng. 2022, 210, 118230. [Google Scholar] [CrossRef]
- Lukic, S.M.; Cao, J.; Bansal, R.C.; Rodriguez, F.; Emadi, A. Energy storage systems for automotive applications. IEEE Trans. Ind. Electron. 2008, 55, 2258–2267. [Google Scholar] [CrossRef]
- Forgez, C.; Do, D.V.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal modeling of a cylindrical LiFePO4 graphite lithium-ion battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
- Lyu, D.Z.; Niu, G.X.; Liu, E.H.; Yang, T.; Chen, G.; Zhang, B. Uncertainty Management and Differential Model Decomposition for Fault Diagnosis and Prognosis. IEEE Trans. Ind. Electron. 2022, 69, 5235–5246. [Google Scholar] [CrossRef]
- Hua, Y.; Liu, X.; Zhou, S.; Huang, Y.; Ling, H.; Yang, S. Toward Sustainable Reuse of Retired Lithium-ion Batteries from Electric Vehicles. Resour. Conserv. Recycl. 2021, 168, 105249. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| Nominal capacity | 2.5 Ah |
| Anode | Graphite |
| Cathode | Li(NiCoMn)O2 |
| Nominal voltage | 3.6 V |
| Max. charge voltage | 4.2 ± 0.05 V |
| Min. discharge voltage | 3.0 V |
| 2.85 | 9.74 | 41.75 | 12.87 |
| Estimate Type | Thermal Sensor Accuracy | Temperature/°C | RMSE | MAE |
|---|---|---|---|---|
| SOTC | ±0.2 °C | 0 | 0.42 °C | 0.25 °C |
| 25 | 0.52 °C | 0.23 °C | ||
| 45 | 0.62 °C | 0.41 °C | ||
| SOC | / | 0 | 2.06% | 1.19% |
| 25 | 1.15% | 0.64% | ||
| 45 | 0.88% | 0.51% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Wang, K.; Yu, Z.; Zhao, G. A Novel Method for Estimating State of Power of Lithium-Ion Batteries Considering Core Temperature. Batteries 2024, 10, 409. https://doi.org/10.3390/batteries10120409
Zhang R, Wang K, Yu Z, Zhao G. A Novel Method for Estimating State of Power of Lithium-Ion Batteries Considering Core Temperature. Batteries. 2024; 10(12):409. https://doi.org/10.3390/batteries10120409
Chicago/Turabian StyleZhang, Ruixue, Keyi Wang, Zhilong Yu, and Gang Zhao. 2024. "A Novel Method for Estimating State of Power of Lithium-Ion Batteries Considering Core Temperature" Batteries 10, no. 12: 409. https://doi.org/10.3390/batteries10120409
APA StyleZhang, R., Wang, K., Yu, Z., & Zhao, G. (2024). A Novel Method for Estimating State of Power of Lithium-Ion Batteries Considering Core Temperature. Batteries, 10(12), 409. https://doi.org/10.3390/batteries10120409





