A Data-Driven Online Prediction Model for Battery Charging Efficiency Accounting for Entropic Heat
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Contributions and Innovation Points
1.3. Section Arrangement
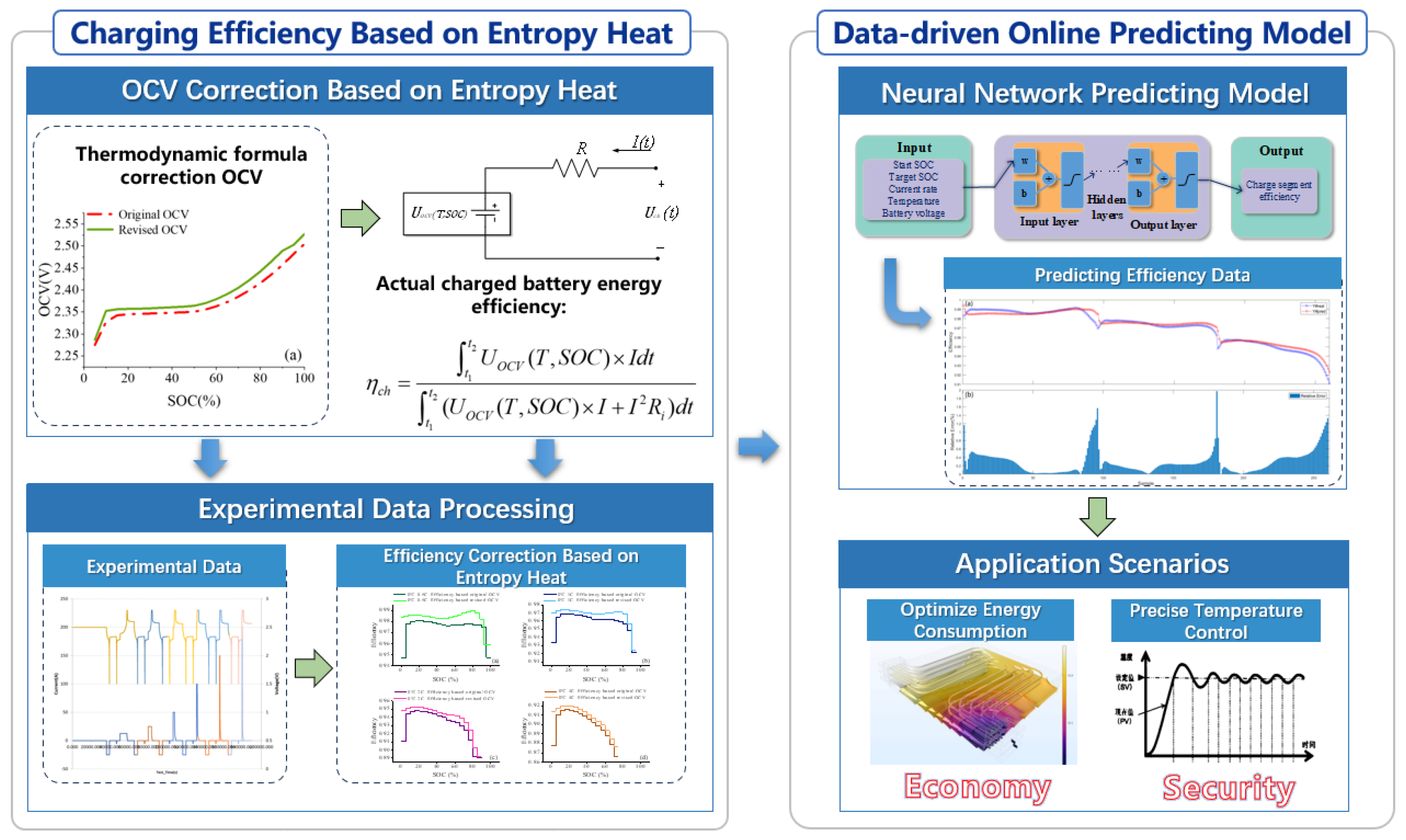
2. A Battery Internal Resistance Model Incorporating Entropic Heat Effects
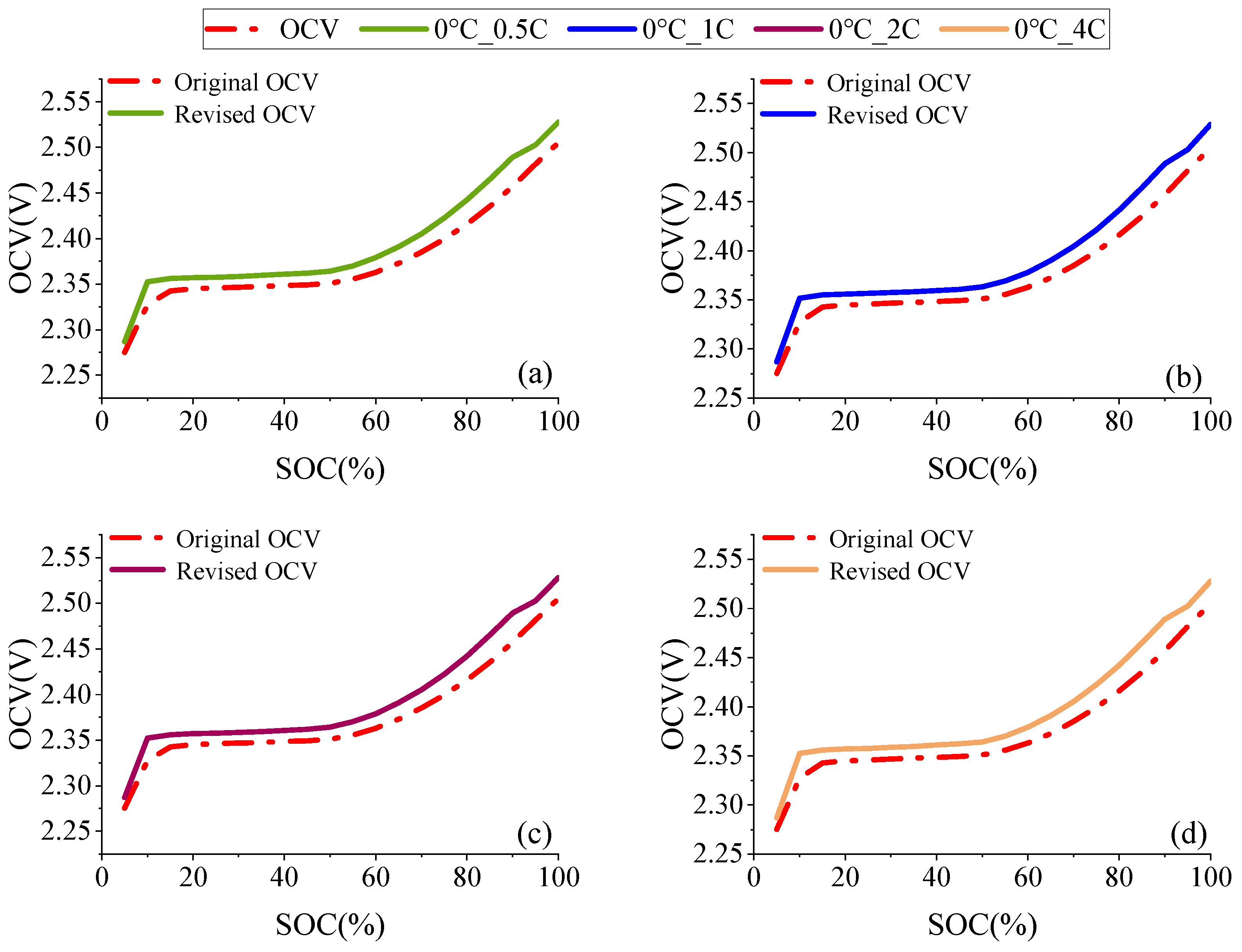
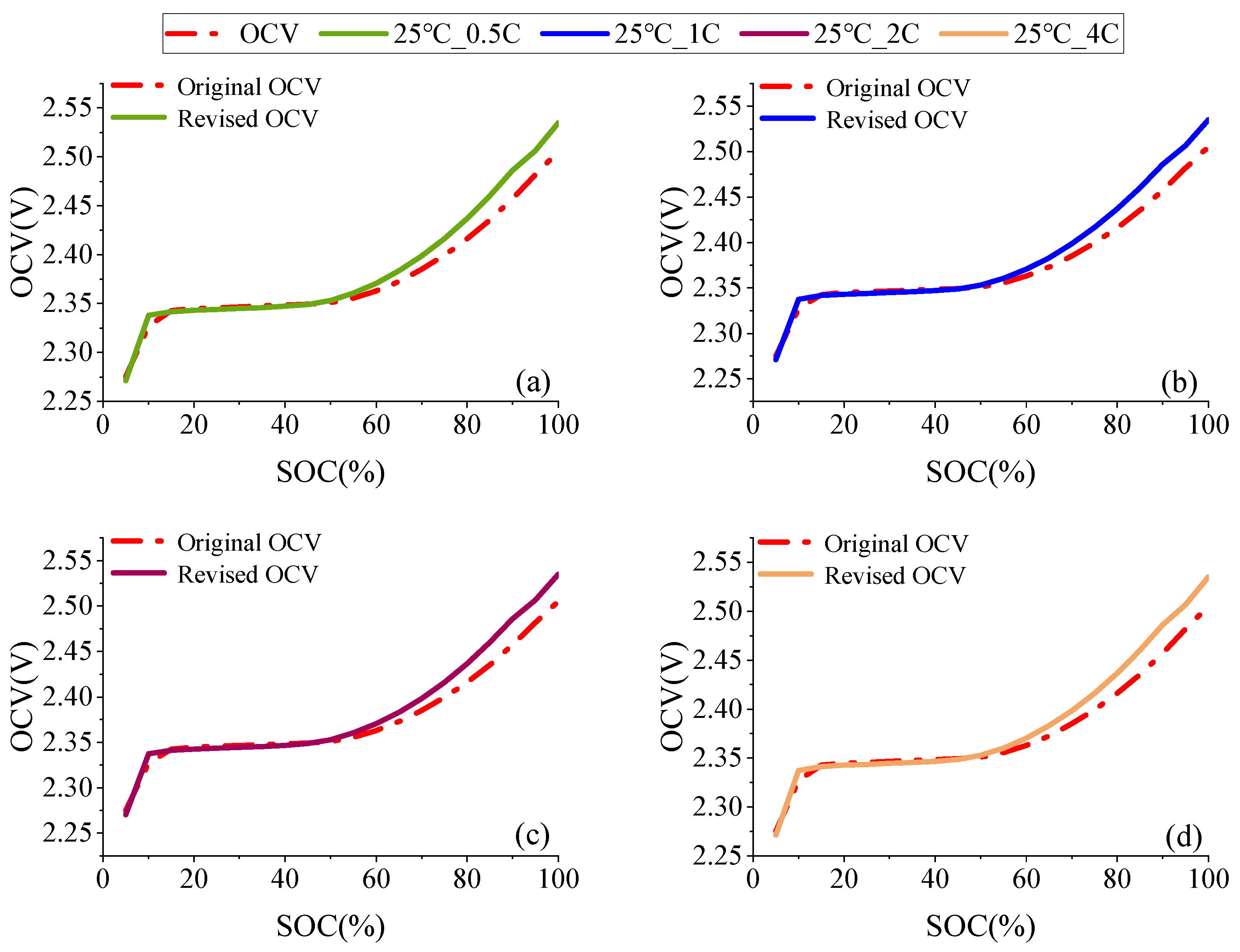
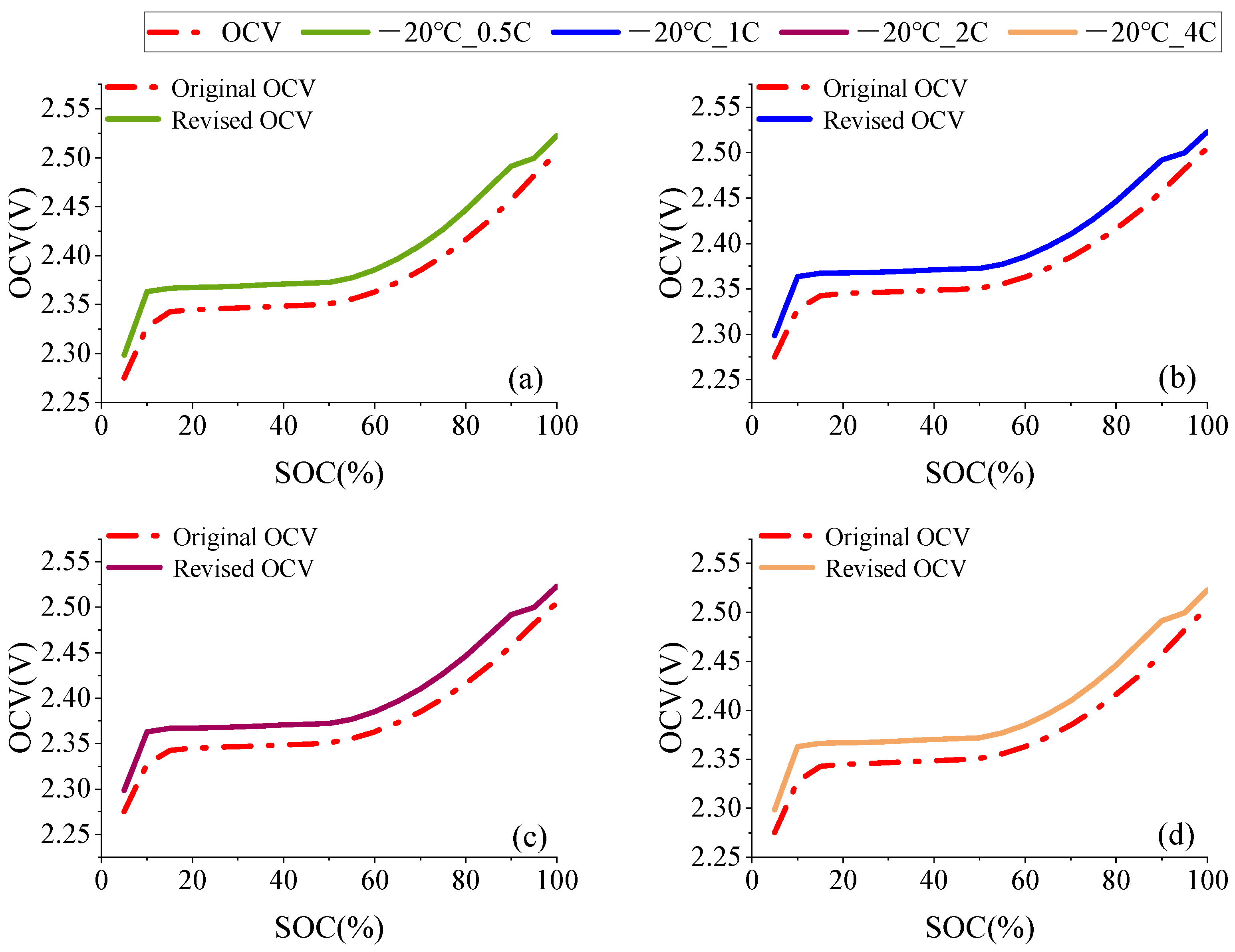
2.1. OCV Correction Based on Entropic Heat
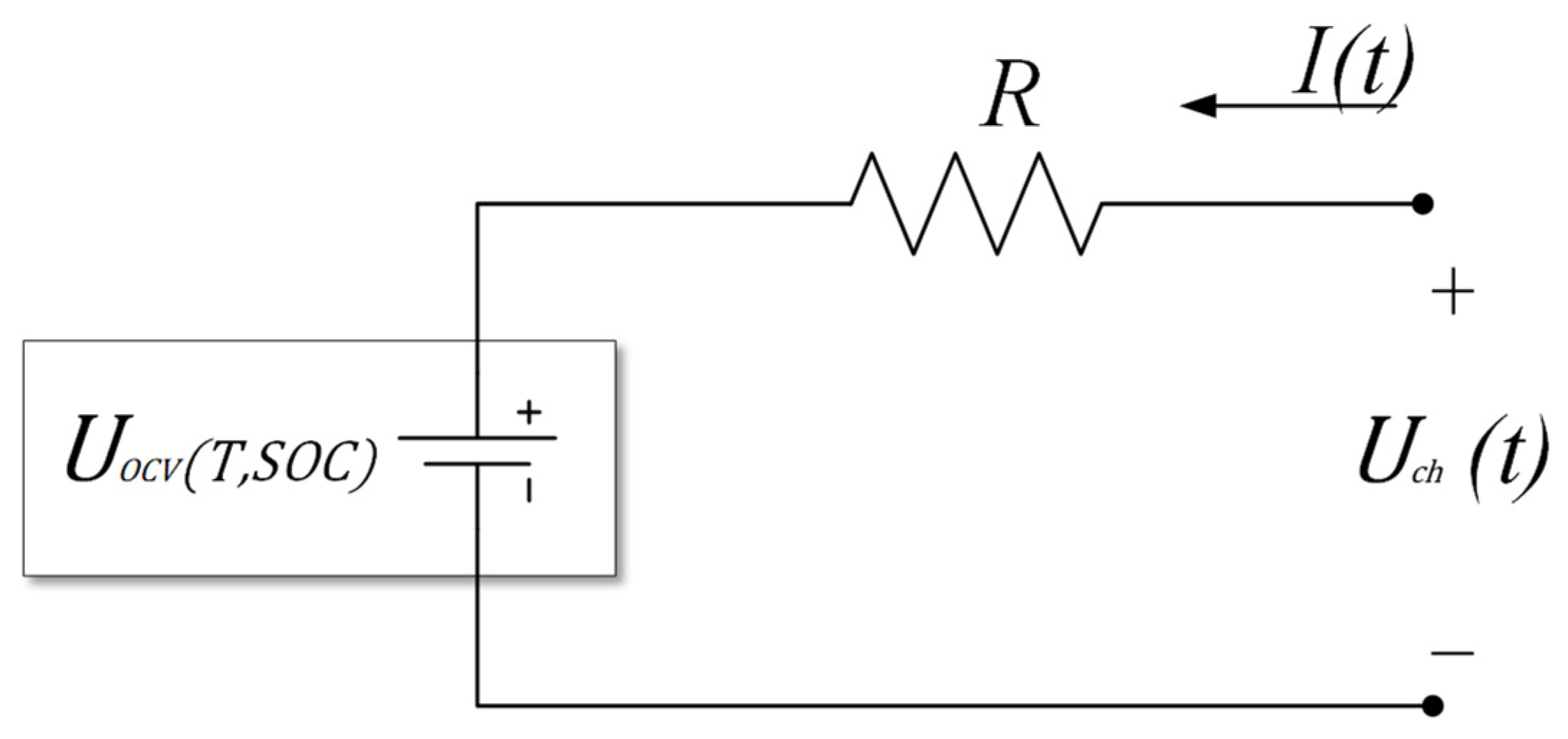
2.2. Improved Internal Resistance Model for Lithium-Ion Batteries
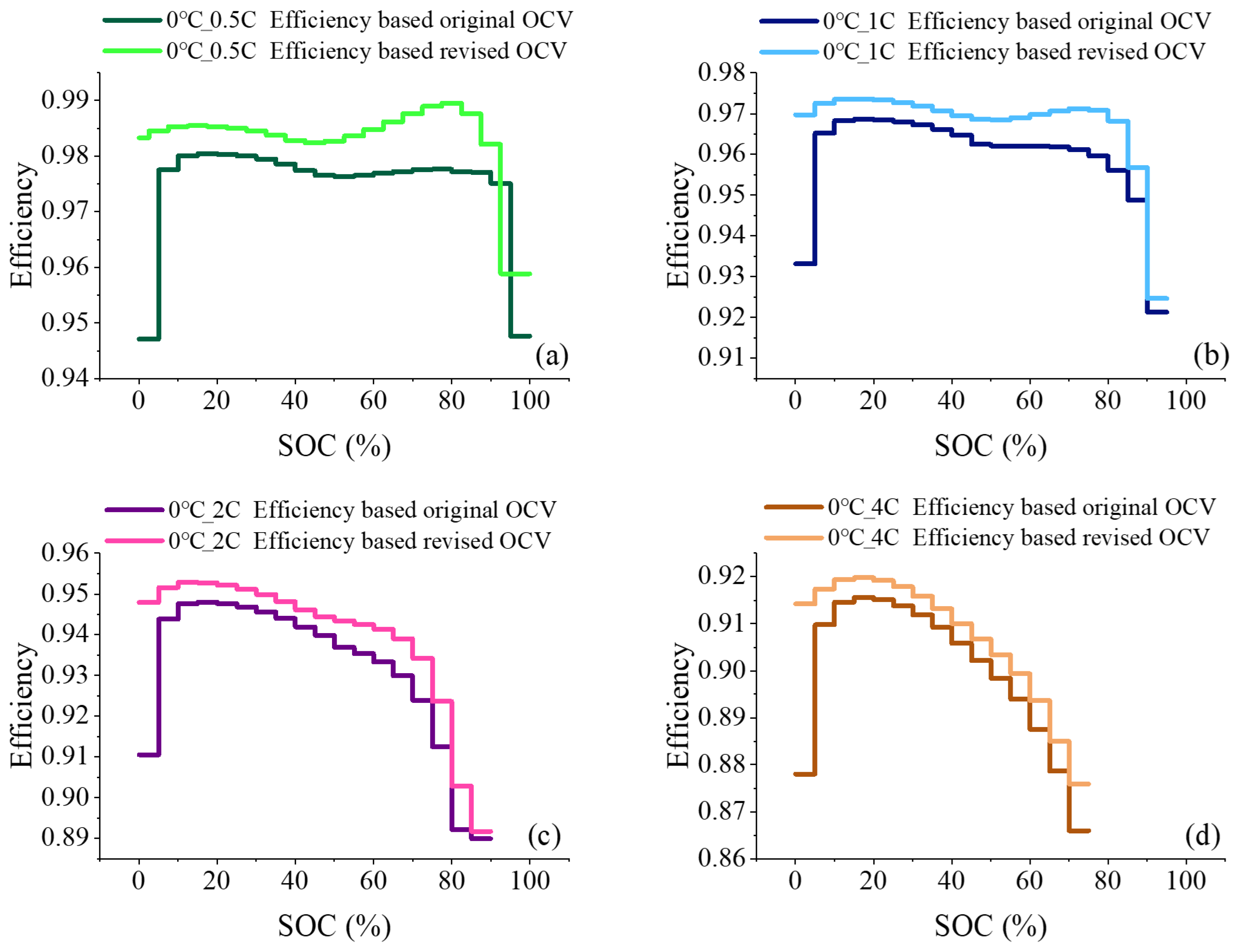
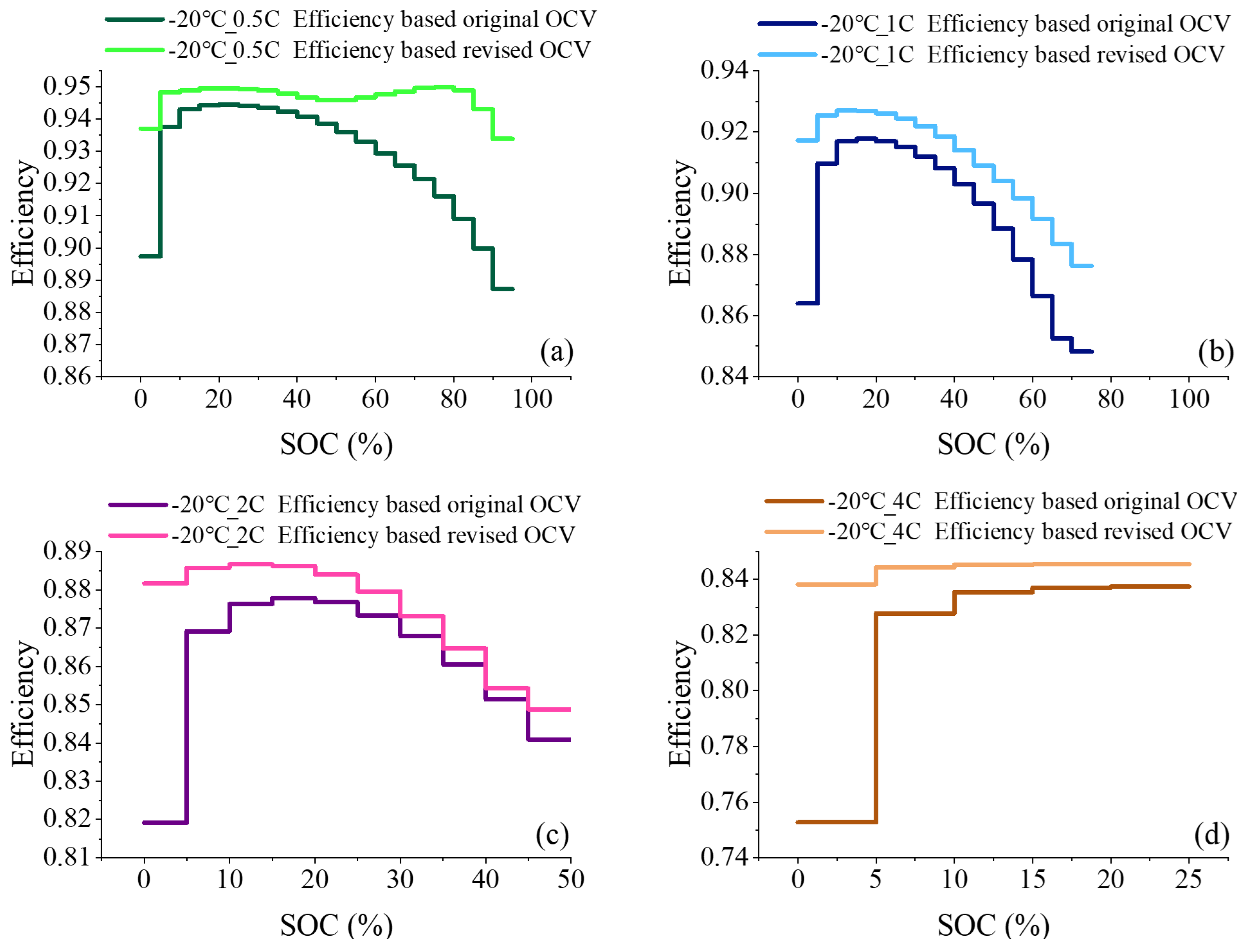
2.3. Derivation of Charging Efficiency Considering Entropic Heat
3. Data-Driven Charging Efficiency Prediction Method
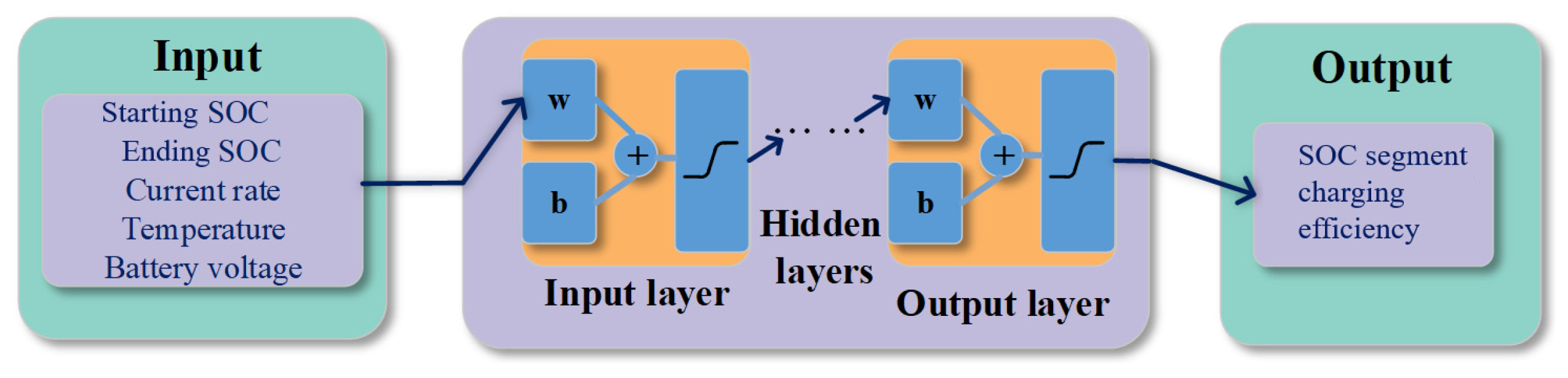
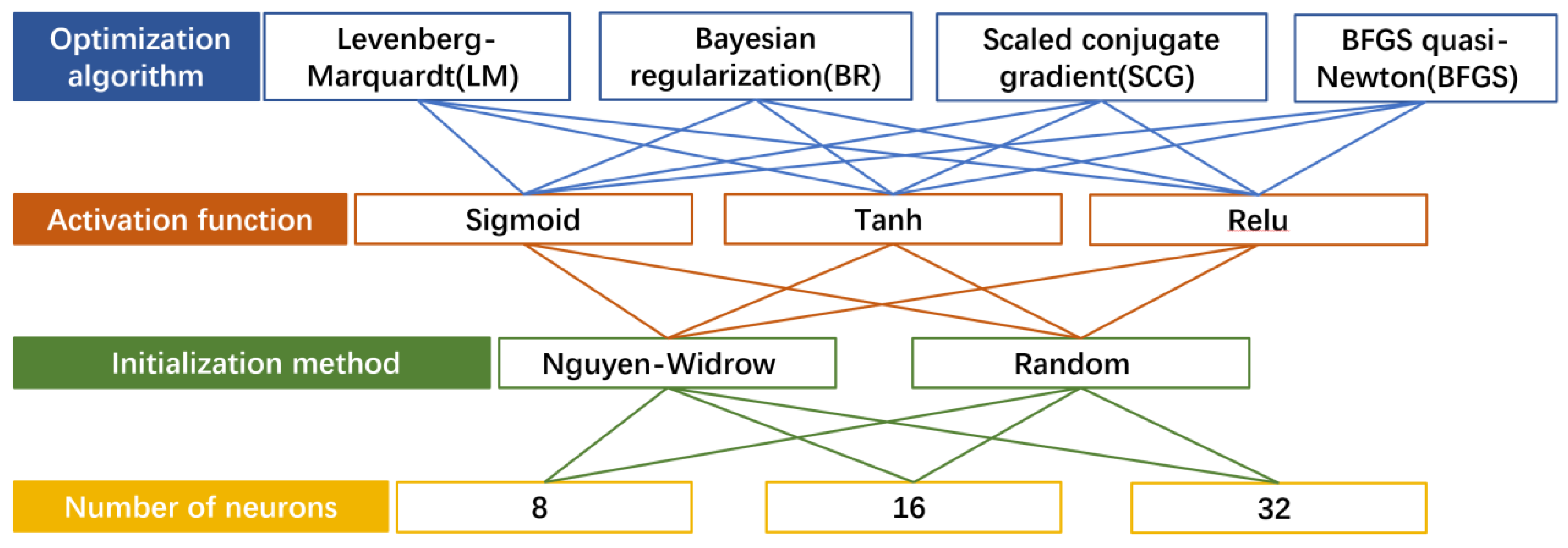
3.1. Model Development and Training Setting
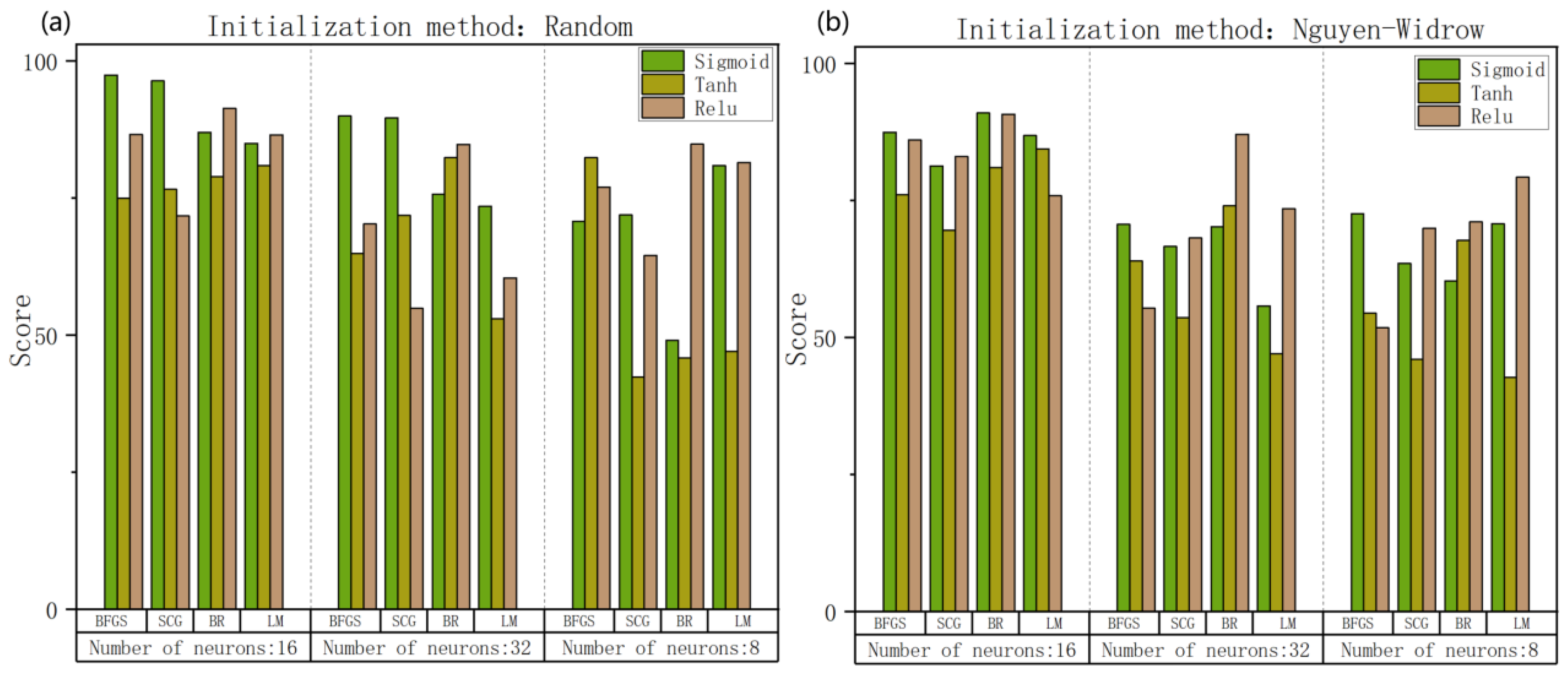
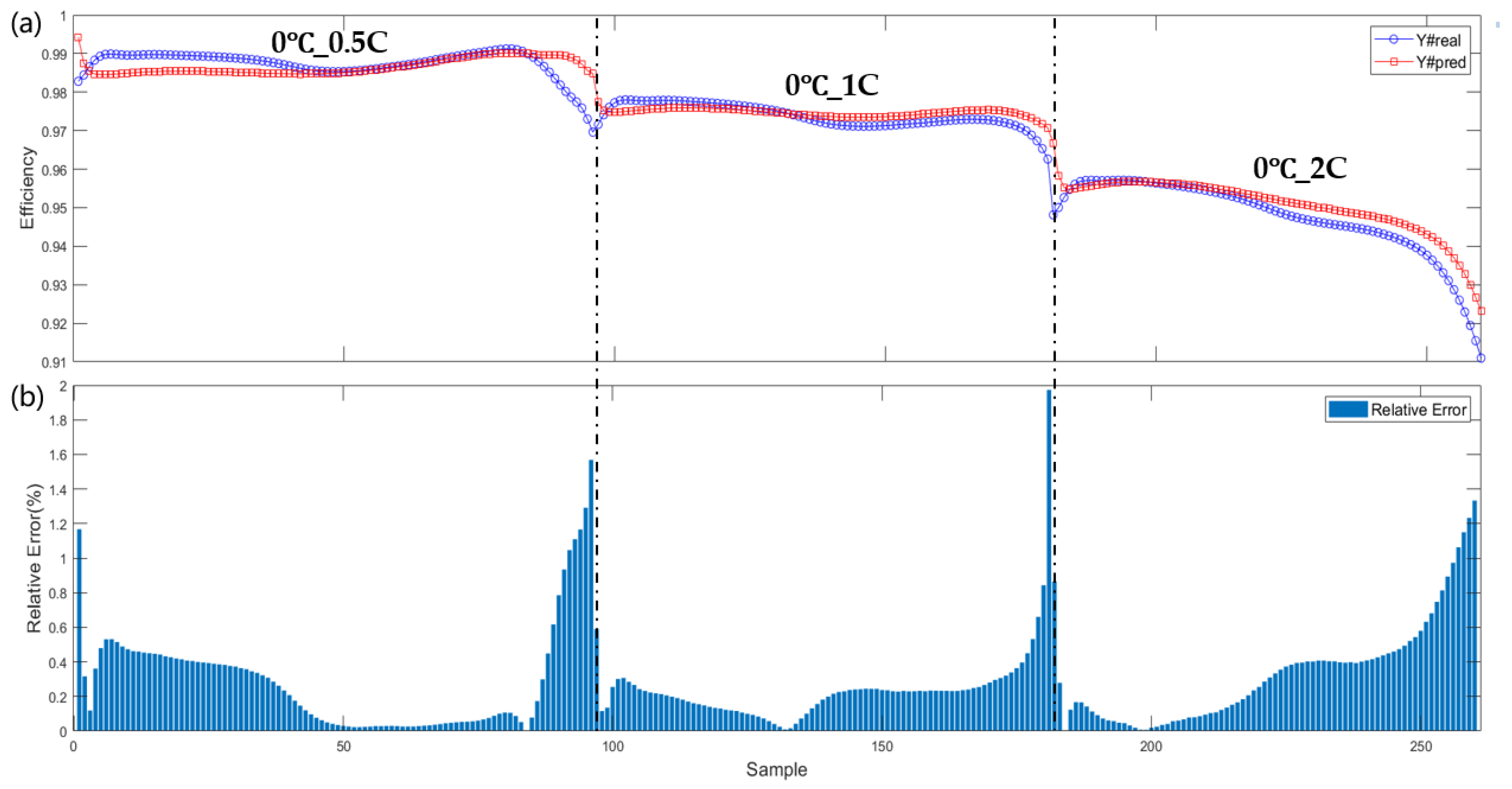
3.2. Comparison of Efficiency Prediction Results
4. Conclusions and Final Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, L.; Aziz, J.; Kong, P.; Idris, N.; Alsofyani, I. Modeling of lithium titanate battery for charger design. In Proceedings of the 2014 Australasian Universities Power Engineering Conference (AUPEC), Perth, WA, Australia, 28 September–1 October 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Yue, Y. Study on Fast Charging Method of Lithium Titanate Battery. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 549–553. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, X.; Zhang, W.; Sun, B.; Shi, J.; Huang, Q. Parameter sensitivity analysis and parameter identifiability analysis of electrochemical model under wide discharge rate. J. Energy Storage 2023, 68, 107788. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Z.; Zhang, W.; Sun, B.; Su, X.; Shi, J.; Huang, Q. Construction of simplified impedance model based on electrochemical mechanism and identification of mechanism parameters. J. Energy Storage 2024, 76, 109673. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, J.; Shi, W.; Ma, Z.; Wang, L.; Guo, H. Butler–volmer-equation-based electrical model for high-power lithium titanate batteries used in electric vehicles. IEEE T. Ind. Electron. 2015, 62, 7557–7568. [Google Scholar] [CrossRef]
- Ahmadi, L.; Fowler, M.; Young, S.; Fraser, R.; Gaffney, B.; Walker, S. Energy efficiency of Li-ion battery packs re-used in stationary power applications. Sustain. Energy Technol. 2014, 8, 9–17. [Google Scholar] [CrossRef]
- Xiao, J.; Li, Q.; Bi, Y.; Cai, M.; Dunn, B.; Glossmann, T.; Liu, J.; Osaka, T.; Sugiura, R.; Wu, B.; et al. Understanding and applying coulombic efficiency in lithium metal batteries. Nat. Energy 2020, 5, 561–568. [Google Scholar] [CrossRef]
- Lin, Z.; Li, D.; Zou, Y. Energy efficiency of lithium-ion batteries: Influential factors and long-term degradation. J. Energy Storage 2023, 74, 109386. [Google Scholar] [CrossRef]
- Yang, F.; Wang, D.; Zhao, Y.; Tsui, K.; Bae, S. A study of the relationship between coulombic efficiency and capacity degradation of commercial lithium-ion batteries. Energy 2018, 145, 486–495. [Google Scholar] [CrossRef]
- Zhu, W.; Zhu, Y.; Davis, Z.; Tatarchuk, B. Energy efficiency and capacity retention of Ni–MH batteries for storage applications. Appl. Energy 2013, 106, 307–313. [Google Scholar] [CrossRef]
- Liu, C.; Wang, S.; Zhang, C.; Fu, H.; Nan, X.; Yang, Y.; Cao, G. High power high safety battery with electrospun Li3V2(PO4)3 cathode and Li4Ti5O12 anode with 95% energy efficiency. Energy Stor. 2016, 5, 93–102. [Google Scholar] [CrossRef]
- Li, K.; Tseng, K. Energy efficiency of lithium-ion battery used as energy storage devices in micro-grid. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 005235–005240. [Google Scholar]
- Lai, X.; Zhou, L.; Zhu, Z.; Zheng, Y.; Sun, T.; Shen, K. Experimental investigation on the characteristics of coulombic efficiency of lithium-ion batteries considering different influencing factors. Energy 2023, 274, 127408. [Google Scholar] [CrossRef]
- Kang, J.; Yan, F.; Zhang, P.; Du, C. Comparison of comprehensive properties of Ni-MH (nickel-Metal Hydride) and Li-ion (lithium-ion) batteries in terms of energy efficiency. Energy 2014, 70, 618–625. [Google Scholar] [CrossRef]
- Wang, S. Entropy and heat generation of lithium cells/batteries. Chin. Phys. B 2016, 25, 010509. [Google Scholar] [CrossRef]
- Jalkanen, K.; Aho, T.; Vuorilehto, K. Entropy change effects on the thermal behavior of a LiFePO4/graphite lithium-ion cell at different states of charge. J. Power Sources 2013, 243, 354–360. [Google Scholar] [CrossRef]
- Doh, H.; Ha, Y.; Eom, S. Entropy measurement of a large format lithium ion battery and its application to calculate heat generation. Electrochim. Acta 2019, 309, 382–391. [Google Scholar] [CrossRef]
- Lai, Y.; Du, S.; Ai, L.; Ai, L.; Cheng, Y.; Tang, Y.; Jia, M. Insight into heat generation of lithium ion batteries based on the electrochemical-thermal model at high discharge rates. Int. J. Hydrogen Energy 2015, 40, 13039–13049. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, W.; Bao, Y.; Gao, D.; Wang, Z. Load Forecasting of Electric Vehicle Charging Stations: Attention Based Spatiotemporal Multi-Graph Convolutional Networks. IEEE Trans. Smart Grid 2023, 15, 3016–3027. [Google Scholar] [CrossRef]
- Nascimento, R.; Corbetta, M.; Kulkarni, C.; Viana, F. Hybrid physics-informed neural networks for lithium-ion battery modeling and prognosis. J. Power Sources 2021, 513, 230526. [Google Scholar] [CrossRef]
- Wang, F.; Zhi, Q.; Zhao, Z.; Zhai, Z.; Liu, Y.; Xi, H.; Wang, S.; Chen, X. Inherently Interpretable Physics-Informed Neural Network for Battery Modeling and Prognosis. IEEE Trans. Neural Netw. Learn. Syst. 2023, 1–15. [Google Scholar] [CrossRef]
- Dong, C.; Wang, G. Estimation of power battery SOC based on improved BP neural network. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 2022–2027. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Li, C.; Yu, Y.; Zhou, G.; Wang, C.; Zhao, W. Temperature prediction of lithium-ion battery based on artificial neural network model. Appl. Therm. Eng. 2023, 228, 120482. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Jiang, J.; Wei, S.; Liu, S.; Zhang, W. A Data-Driven Learning-Based Continuous-Time Estimation and Simulation Method for Energy Efficiency and Coulombic Efficiency of Lithium Ion Batteries. Energies 2017, 10, 597. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical review on the battery state of charge estimation methods for electric vehicles. IEEE Access 2017, 6, 1832–1843. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, G.; Zhu, H.; Sun, X. An open circuit voltage and internal resistance estimation method of lithium-ion batteries with constant current tests. Trans. China Electrotech. Soc. 2018, 33, 3976–3988. [Google Scholar]
- Liu, X.; Chen, Z.; Zhang, C.; Wu, J. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation. Appl. Energy 2014, 123, 263–272. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, M.; Ding, T.; Wu, S.; Li, Y.; Liang, G.; Li, H.; Pan, H. Estimation the internal resistance of lithium-ion-battery using a multi-factor dynamic internal resistance model with an error compensation strategy. Energy Rep. 2021, 7, 3050–3059. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman filtering for battery management systems of Li PB-based HEV battery packs, Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Z. Study on SOC Estimation of Lithium Battery Based on Improved BP Neural Network. In Proceedings of the 2019 8th International Symposium on Next Generation Electronics (ISNE), Zhengzhou, China, 9–10 October 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Shrestha, A.; Mahmood, A. Review of Deep Learning Algorithms and Architectures. IEEE Access 2019, 7, 53040–53065. [Google Scholar] [CrossRef]
- Sheng, L.; Zhang, Z.; Su, L.; Zhang, H.; Zhang, H.; Li, K.; Fang, Y.; Ye, W. Experimental and numerical approach for analyzing thermal behaviors of a prismatic hard-cased lithium-ion battery. J. Energy Storage 2021, 35, 102313. [Google Scholar] [CrossRef]
- Foresee, F.; Hagan, M. Gauss-Newton approximation to Bayesian learning. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 9–12 June 1997; Volume 3, pp. 1930–1935. [Google Scholar]

| Training Set | Test Set |
|---|---|
| −20 °C_0.5 C, −20 °C_1 C, −20 °C_2 C, 0 °C_4 C, 25 °C_0.5 C, 25 °C_1 C, 25 °C_2 C, 25 °C_4 C | 0 °C_0.5 C, 0 °C_1 C, 0 °C_2 C |
| Optimal Structure of Neural Network | |
|---|---|
| Optimization algorithm | Scaled conjugate gradient |
| Activation function | Sigmoid |
| Initialization method | Random |
| Number of neurons | 8 |
| Neural network structure | Feedforward neural network |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Zhang, W.; Yuan, C.; Ge, C.; Bao, Y.; An, Z.; Liu, Q.; Wang, Z.; Shi, J.; Wang, Z. A Data-Driven Online Prediction Model for Battery Charging Efficiency Accounting for Entropic Heat. Batteries 2024, 10, 350. https://doi.org/10.3390/batteries10100350
Ding X, Zhang W, Yuan C, Ge C, Bao Y, An Z, Liu Q, Wang Z, Shi J, Wang Z. A Data-Driven Online Prediction Model for Battery Charging Efficiency Accounting for Entropic Heat. Batteries. 2024; 10(10):350. https://doi.org/10.3390/batteries10100350
Chicago/Turabian StyleDing, Xiaowei, Weige Zhang, Chenyang Yuan, Chang Ge, Yan Bao, Zhenjia An, Qiang Liu, Zhenpo Wang, Jinkai Shi, and Zhihao Wang. 2024. "A Data-Driven Online Prediction Model for Battery Charging Efficiency Accounting for Entropic Heat" Batteries 10, no. 10: 350. https://doi.org/10.3390/batteries10100350
APA StyleDing, X., Zhang, W., Yuan, C., Ge, C., Bao, Y., An, Z., Liu, Q., Wang, Z., Shi, J., & Wang, Z. (2024). A Data-Driven Online Prediction Model for Battery Charging Efficiency Accounting for Entropic Heat. Batteries, 10(10), 350. https://doi.org/10.3390/batteries10100350








