Abstract
Lithium-ion batteries have revolutionized the portable and stationary energy industry and are finding widespread application in sectors such as automotive, consumer electronics, renewable energy, and many others. However, their efficiency and longevity are closely tied to accurately measuring their SOC and state of health (SOH). The need for precise algorithms to estimate SOC and SOH has become increasingly critical in light of the widespread adoption of lithium-ion batteries in industrial and automotive applications. While the benefits of lithium-ion batteries are undeniable, the challenges related to their efficient and safe management cannot be overlooked. Accurate estimation of SOC and SOH is crucial for ensuring optimal battery management, maximizing battery lifespan, optimizing performance, and preventing sudden failures. Consequently, research and development of reliable algorithms for estimating SOC and SOH have become an area of growing interest for the scientific and industrial community. This review article aims to provide an in-depth analysis of the state-of-the-art in SOC and SOH estimation algorithms for lithium-ion batteries. The most recent and promising theoretical and practical techniques used to address the challenges of accurate SOC and SOH estimation will be examined and evaluated. Additionally, critical evaluation of different approaches will be highlighted: emphasizing the advantages, limitations, and potential areas for improvement. The goal is to provide a clear view of the current landscape and to identify possible future directions for research and development in this crucial field for technological innovation.
1. Introduction
The application of advanced mathematical models emerges as a key pillar in power electronics for vehicles, robotics, and mechatronic systems. This approach proves to be essential for meeting competitive challenges and optimizing operational efficiency [1,2]. The use of mathematical models enables more accurate and predictive design of devices. Through advanced simulation, potential issues can be anticipated and resolved, significantly reducing development time and costs [3,4]. Detailed simulation of dynamic behaviors provides a solid foundation for the development of highly efficient control and monitoring systems. This methodology makes it possible to optimize control algorithms, improve monitoring accuracy, and ensure rapid and reliable responses to changes in operating conditions [5,6,7,8]. The integration of mathematical models is synonymous with technological innovation. Leading companies in the industry take this approach to overcome the limitations of existing technologies in order to position themselves at the forefront of the market. Virtual simulation makes it possible to identify and solve inefficiencies and design problems before the production phase. This results in significant resource optimization, which reduces associated costs and improves business sustainability [9,10]. Early identification of critical issues during the design ensures the production of reliable and safe products. In addition, the adoption of mathematical models gives agility and adaptability to companies, enabling them to remain competitive in an ever-changing market.
The strategic application of mathematical models is a distinctive and indispensable element for companies engaged in power electronics and mechatronic systems and offers competitive advantages and contributes significantly to success in the modern industrial environment [11,12,13,14]. The accurate estimation of the SOC and state of health (SOH) of batteries holds paramount significance in modern battery management systems and is primarily driven by the increasing demand for robust, efficient, and reliable energy storage solutions. Recent research endeavors have been dedicated to the development of advanced algorithms for SOC/SOH estimation owing to several critical factors:
- Energy Management Optimization: In various battery-powered systems, precise SOC estimation is indispensable for efficient energy management [15,16,17]. By accurately gauging the available charge, these algorithms enable optimal utilization of the battery capacity, thus preventing potentially detrimental conditions such as overcharging or over-discharging [18,19,20]. Avoiding these extremes is vital as they can lead to irreversible damage to the battery’s internal chemistry and structure, significantly compromising its overall lifespan and performance [21,22,23]. Implementing accurate SOC estimation techniques facilitates intelligent energy utilization strategies, which ensure prolonged battery life and sustained system performance over extended operational periods [24,25,26].
- Enhanced Safety Measures: The accuracy of SOC estimation is directly linked to ensuring the safety and integrity of battery-powered systems [27,28,29]. Inaccurate SOC determination can lead to scenarios of overcharging or over-discharging, exacerbating the risk of critical safety hazards such as thermal runaway [30,31,32]. Uncontrolled thermal runaway has the potential to trigger severe consequences, including battery failure, fire hazards, and even catastrophic explosions, thereby posing serious threats to both the equipment and personnel associated with the system [33,34,35]. Hence, the development of precise and reliable SOC estimation algorithms plays a pivotal role in enhancing the overall safety and risk management strategies within battery-dependent applications [36,37,38].
- Proactive Battery Health Monitoring: Accurate estimation of SOH is instrumental to effective battery health monitoring and enables the timely detection of degradation and performance decline [39,40,41]. These algorithms facilitate the assessment of critical battery parameters, such as capacity fade, impedance changes, and chemical degradation, to provide insight into the battery’s remaining useful life (RUL) [42,43,44]. By implementing proactive SOH estimation methodologies, operators can anticipate potential battery failures, initiate timely maintenance interventions, and prevent costly downtime and unplanned disruptions in industrial and automotive operations [45,46,47]. The ability to predict the RUL allows for informed decision-making regarding battery replacement or reconditioning, thereby optimizing maintenance costs and ensuring continuous system reliability [48,49,50].
The continuous evolution and refinement of SOC/SOH estimation algorithms hold the promise of significant improvements in the accuracy and reliability of battery management systems. Leveraging these advanced algorithms facilitates optimized energy utilization, extended battery lifespans, enhanced operational safety, and streamlined maintenance practices, thereby fostering increased efficiency, reduced operational costs, and improved overall performance in a diverse range of industrial and automotive applications. Considering the diverse array of available algorithms, such as coulomb counting, the voltage method, the Kalman filter method, neural network algorithms, and hybrid algorithms, the selection of a specific estimation technique is dependent on various factors, including the battery’s electro–chemical characteristics, the operational requirements of the specific application, and the desired level of estimation accuracy. There are several algorithms used for the estimation of SOC and state of health (SOH) of batteries, each with its own advantages and limitations. Understanding these algorithms is crucial for efficient battery management and to ensure optimal performance in various applications. Here is a more comprehensive overview of the most commonly used methods for SOC/SOH estimation:
- Coulomb Counting Method: This widely used method estimates SOC by integrating the current flowing in and out of the battery over time. Despite its simplicity and ease of implementation, the Coulomb counting method is susceptible to cumulative errors arising from measurement inaccuracies, parasitic currents, and changes to the battery capacity caused by aging and temperature fluctuations [51,52]. Calibration and frequent updates are often necessary to mitigate the impact of these factors on the accuracy of SOC estimation, especially over the long term [53,54].
- Voltage Method: The voltage method estimates SOC by measuring the battery’s open-circuit voltage (OCV) and comparing it to a lookup table or a mathematical model. While being noninvasive and relatively simple, this method is affected by temperature variations and the dynamic nature of battery aging [55,56,57], leading to potential inaccuracies in SOC estimation. Moreover, the nonlinear relationship between SOC and OCV necessitates careful calibration and temperature compensation to improve the accuracy of the estimation, particularly in real-world applications where temperature variations are common [58,59,60].
- Kalman Filter Method: This approach leverages a recursive filter algorithm, such as the Kalman filter, in combination with a detailed mathematical model of the battery. The Kalman filter method provides a more accurate estimation of SOC compared to simpler methods such as Coulomb counting and voltage estimation [61,62]. However, its efficacy heavily relies on the accuracy of the underlying battery model, which requires precise knowledge of the battery’s characteristics and behavior under varying operating conditions. Additionally, the implementation of the Kalman filter method demands significant computational resources, limiting its practicality in resource-constrained applications, particularly in the automotive and industrial sectors where real-time performance is critical [63,64,65].
- Neural Network Algorithm: This method involves training a neural network using a dataset of battery measurements to establish a relationship between input parameters (e.g., current, voltage, and temperature) and SOC. The trained neural network is then utilized to predict the SOC based on real-time or historical battery data [66,67]. The neural network algorithm offers enhanced accuracy compared to traditional methods, especially in complex scenarios where the relationships between input parameters and SOC are nonlinear and are challenging to model analytically. Nevertheless, the successful implementation of this algorithm relies heavily on the availability of a substantial and diverse dataset for training the neural network along with significant computational resources for training and inference, which could pose practical challenges in resource-limited applications [68,69].
- Hybrid Algorithm: As the name suggests, a hybrid algorithm combines the strengths of two or more estimation methods to improve the overall accuracy of SOC estimation. For instance, a hybrid algorithm may integrate the coulomb counting method with the Kalman filter technique to compensate for their respective limitations and enhance the accuracy and robustness of SOC estimation [70,71]. By leveraging the complementary strengths of multiple algorithms, the hybrid approach aims to mitigate the impact of individual weaknesses, leading to more reliable SOC estimation in diverse operating conditions and environments [72,73,74].
In the context of industrial and automotive applications, the choice of a specific SOC/SOH estimation algorithm is determined by a multitude of factors, including the type of battery chemistry, the targeted application requirements, the desired accuracy level, and the available computational resources. Accurate estimation of SOC/SOH is paramount for effective battery management systems as it not only optimizes the performance and reliability of the entire energy storage system but also extends the overall lifespan of the battery, thereby minimizing operational costs and maximizing the return on investment for various industrial and automotive applications.
2. Overview of Battery Systems
Battery energy storage systems (BESSs) include batteries, power converter systems, control electronics, and other parts for system protection, as has been noted in the literature [75]. Batteries are essential because they are made up of stacks of cells that transform chemical energy into electrical energy [76]. Tailored qualities are made possible by a variety of cell topologies and chemistry, including series and parallel connections. The dynamism of BESS is highlighted by the ongoing large investments and research in this subject [77]. Selecting a particular chemistry for a given application requires careful study since every chemistry has unique benefits and downsides [78]. This calls for a comprehensive evaluation of the benefits and drawbacks of different cell shape and chemistry trade-offs [79]. We concentrate on the chemistry’s general characteristics in our examination [80].
Nowadays, lithium-ion (Li-ion) batteries are the most popular option, particularly for commercial use, because of how quickly they can be charged [81]. Although they have a wide operating window, it is advisable to exercise caution when approaching maximum and minimum charge states for extended periods of time because doing so might increase the danger of explosions and fires [82]. The focus of lithium battery research is on uses like automation that need big battery packs [79]. LiNiO2 is an example of a nickel–cobalt–aluminum (NCA) battery, which is a more affordable option than lithium-ion batteries. Even though cobalt is less expensive than nickel, aluminum reduces volumetric fluctuations and ensures a longer lifespan that is appropriate for automation applications. But because of the cathode’s instability and vulnerability to thermal runaway, safety issues surface [83].
LiNixCoyMnzO2 composition in nickel–manganese–cobalt (NMC) batteries allows for customization while resolving safety problems associated with NCA batteries (see Figure 1). It is expected that NMC batteries would offer high capacity, strong C-rate capability, and performance metrics comparable to NCA batteries since manganese improves safety and nickel enhances cycle life. Battery management systems (BMSs) with balancing systems are required due to ongoing safety and cost issues [84,85]. A more contemporary and affordable cathode material that exhibits stability at higher temperatures is lithium–iron–phosphate (LFP). Its SOC function curve is LFP flat, which makes it appropriate for motor applications even if its volumetric energy density is lower than that of NMC. However, safety issues necessitate a BMS [86,87].

Figure 1.
Qualitative comparison in terms of specific chemistry.
Although nickel batteries are not as energy efficient as Li-ion batteries under normal circumstances, they are suitable at high current rates, which eliminates the need for balancing devices and lowers the cost of control electronics. Metal hydride (Ni-MH) cells provide a respectably high energy density and C rates. The negative electrode of these cells is made of hydrogen alloys. They have fewer chances of overheating and internal short circuiting, which makes them a good substitute for lead–acid batteries in some situations [88,89]. Nickel–cadmium (Ni-Cd) batteries are utilized in sealed, maintenance-free cells with a high cycle life since they are well-known for their good safety and dependability. Calendar aging is well supported by Ni-Cd batteries despite their lower energy density compared to Li-ion batteries [90,91]. Because sodium is abundant in the Earth’s crust, sodium electrode batteries provide a financially viable solution to the lack of active materials. Despite being inexpensive, sodium–sulfur (Na-S) batteries present a safety risk due to their high operating temperature. The development of room-temperature Na-S batteries is still underway and offers a promising solution to the problem of aging. Reduction batteries, sometimes referred to as metal–air batteries, produce energy by a redox reaction with atmospheric oxygen. A higher energy density is facilitated by their open-air cell form [92]. In summary, solid-state batteries are a possible successor to lithium-ion batteries, which are now the industry standard for energy storage systems in cars and other consumer products. However, the landscape is changing. A battery management system (BMS) is necessary for overall system dependability, safety, efficiency, and performance monitoring regardless of the chemistry used (see Table 1). A battery energy storage system comprises various logical and physical levels, each necessitating a dedicated control system.

Table 1.
Summary of the pros and cons of each type of battery.
These levels are intricately connected to ensure the safe and efficient operation of the entire system. Let us delve into a more detailed discussion of these key levels:
- Battery Packs and Cells: The foundational level of the BESS consists of multiple battery packs, each containing interconnected batteries.This arrangement is designed to achieve the desired values of current and voltage. The batteries are organized to collectively contribute to the overall energy storage capacity [93,94].
- Battery Management System (BMS): Operating at the cellular level, the battery management system (BMS) is responsible for overseeing the individual cells’ performance. It ensures that each cell operates within safe voltage, current, and temperature ranges, which promotes both the safety of the system and the optimal functioning of the batteries. The BMS also undertakes the critical tasks of calibrating and equalizing the SOC across all cells, which promotes uniform performance [95].
- Power Conversion System (PCS): The battery system interfaces with inverters through a specific power electronic level known as the power conversion system (PCS). Typically organized into a conversion unit, the PCS handles the conversion of stored energy into AC power. Additionally, it integrates auxiliary services necessary for comprehensive monitoring and controlling the BESS [96,97].
- Energy Management System (EMS): At a higher level, the energy management system (EMS) takes charge of monitoring and controlling the energy flow within the BESS. This system ensures that the power flow aligns with specific applications and operational requirements. It plays a pivotal role in optimizing the utilization of stored energy based on real-time demands and conditions [98,99].
- Supervisory Control and Data Acquisition (SCADA) System: The broader monitoring and control aspects are often encapsulated within the supervisory control and data acquisition (SCADA) system. This system provides a comprehensive overview of the entire BESS, including its various components and their performance. It acts as the centralized control hub for monitoring the overall health and status of the system [100].
- Transformer Connections: Finally, the BESS interfaces with transformers to manage the voltage levels. Depending on the system’s size, there are connections with medium-voltage/low-voltage transformers and, in larger systems, high-voltage/medium-voltage transformers located in dedicated substations. These transformers facilitate the integration of the BESS with the broader electrical infrastructure [101,102].
In essence, the BESS operates as a multi-tiered system, with each level playing a crucial role in ensuring the reliability, safety, and efficiency of the overall energy storage and distribution process.
Modeling electric batteries is a crucial aspect in designing battery management systems (BMSs) and energy management systems in automotive systems for several reasons.
- Performance Optimization: An accurate battery model allows the BMS to monitor and control battery performance efficiently. With a precise model, it is possible to optimize the battery’s charging and discharging, which maximizes its lifespan and ensures safe and reliable operation [103].
- Planning and Thermal Control: Modeling helps with monitoring the battery temperature, which is a critical parameter for safety and durability. Thermal models enable the BMS to predict and control temperature variations in order to avoid overheating situations that could damage the battery [104].
- Wear Management: Battery models help estimate wear over time, which assists the BMS with efficiently managing the battery’s lifespan. This is particularly important in automotive systems, where the battery must operate under varying conditions and last for an extended period [105].
Regarding the generality and scalability of mathematical battery models, there are several reasons:
- Similarities in Basic Behaviors: Even though batteries may use different chemical technologies (e.g., lithium, lead–acid, and nickel–metal hybrid), there are similarities in basic behaviors such as charging, discharging, temperature, and internal resistance.
- General Parameters: Mathematical models rely on general parameters like internal resistance, capacity, and open-circuit voltage that are commonly present in all batteries. These parameters can be measured or experimentally derived to fit specific batteries [106].
- Physical–Mathematical Approach: Models often rely on physical and mathematical equations reflecting fundamental principles of battery operation. These principles are applicable to many different technologies and allow for some universality in models [107].
- Adaptability through Configurable Parameters: Models can be configured and adapted using technology-specific parameters. This allows BMS designers to customize models to fit the specific characteristics of the battery they are managing [108].
In summary, battery modeling is essential for optimizing performance, ensuring safety, and extending battery lifespan in automotive energy management systems. The generality and scalability of models is possible due to similarities in basic principles and parameter adaptability.
3. Overview of Modeling Approaches
3.1. Empirical Modeling
Empirical models are valuable tools in battery research and management due to their ability to efficiently represent the behavior of batteries based on experimental data. They offer a practical approach for predicting battery performance and aging, which enables researchers and engineers to make informed decisions about battery design and management strategies. Here is an elaboration on the types of empirical models for Li-ion batteries as mentioned in the description:
- Semi-empirical model: A semi-empirical approach combines elements of theoretical understanding with empirical data, which allows for a more accurate representation of the electrochemical processes within Li-ion batteries [109,110]. By incorporating both theoretical and experimental components, this model can provide insights into the battery’s performance over its lifetime and aid with the prediction of degradation and capacity loss [111,112].
- Empirical data hybrid driven approach: This approach combines empirical data with other predictive methods to assess the remaining useful life of Li-ion batteries. By considering capacity diving, this model offers insights into the battery’s degradation patterns and remaining performance, which is crucial for implementing effective battery management strategies and prolonging the battery’s lifespan [113,114].
- Empirical aging model: An empirical aging model is specifically designed to evaluate the impact of different operating strategies, such as vehicle-to-grid (V2G) approaches, on the lifespan of Li-ion batteries. By simulating the effects of various usage scenarios, this model helps with understanding how different operational conditions can affect the long-term performance and aging of the battery and enables the development of effective management protocols [115,116,117].
Empirical models, with their simplified structures and fast computational capabilities, play a vital role in battery management systems (BMSs) by facilitating efficient monitoring and control of battery performance. When appropriately calibrated, these models serve as powerful tools for optimizing battery designs and management strategies: ultimately contributing to the advancement and widespread adoption of Li-ion batteries in various applications. In the generic empirical method, the objective is to provide an “instantaneous” estimate based on a limited amount of information and on instantaneous direct measurements.
A typical formulation consists of representing the SOC as an explicit function of time, of the rough estimate of the initial conditions, and of an empirical factor that expresses the weight that the charge lost/accumulated due to the passage of current as time passes and also as a function of temperature.
where the term represents the rudimentary estimate of the initial SOC, while the term represents the fraction of charge lost or accumulated due to the passage of current for a certain number N of samples measured over a time horizon of length . The term is the time and temperature function, which must take into account the battery characteristics, usage time, and (measured) temperature. From a computational complexity point of view, it is certainly the most efficient method. From the point of view of accuracy, it is certainly among the methods that can be improved, and it can be said that it serves to give an approximate view of the state of the battery based on the direct measurements available and connected to each other in a physically coherent way.
The Shepherd model [118,119,120,121], widely used in the realm of Li-ion battery analysis, serves as an empirical representation of the open-circuit voltage (). Its foundation lies in a polynomial equation that correlates the OCV with the SOC () of the battery. The mathematical formulation of the Shepherd model is outlined as follows: Consideration of the battery cell model within the Shepherd model includes an internal resistance (R) and the open-circuit voltage (). The relationship between the voltage () and the current () for a constant-current discharge is articulated by the following equations:
where represents the initial voltage, K denotes a constant, Q signifies the battery capacity, and t represents time. The polynomial equation is often modified to illuminate the battery’s exponential behavior in more detail. Notably, the Shepherd model, functioning as a voltage-dependent model, effectively characterizes the Li-ion voltage behavior for different scenarios. Its parameters are typically derived from the manufacturer’s data-sheets. Moreover, the Shepherd model is implemented in MATLAB/Simulink for testing the accuracies for and traits of diverse cell types. The Shepherd model proves to be a valuable tool for predicting the of a Li-ion battery based on its . With precise calibration, this model can swiftly and accurately predict real battery performance and thereby help with finding practical applications for optimizing battery management strategies and estimating the remaining useful life of the battery.
The Nernst equation, a cornerstone in electrochemistry, offers an essential understanding of the potential difference and concentration gradient of ions across a membrane. In battery modeling, the Nernst equation finds application in describing the open-circuit voltage (OCV) as a function of the battery’s SOC and temperature. Here are the elaborated mathematical formulations for the Nernst model in batteries:
The Nernst model for batteries, derived from the Nernst equation, is defined as:
where symbolizes the open-circuit voltage, denotes the standard potential, R represents the gas constant, T signifies the temperature, n signifies the number of electrons transferred in the reaction, F is the Faraday constant, and a represents the activity of ions in the electrolyte.
The Nernst model is often expanded to incorporate additional parameters to account for temperature and aging effects on the battery’s performance. Combining the Nernst model with other battery models such as the equivalent circuit model and the Shepherd model enhances the accuracy of the representation of the battery’s behavior. The Nernst model [122,123,124,125] serves as a valuable tool for predicting the OCV of a battery based on its SOC and temperature. When appropriately calibrated, this model can swiftly and accurately predict real battery performance and help with finding applications for optimizing battery management strategies and estimating the remaining useful life of a battery.
3.2. Equivalent Circuit Modeling
Equivalent circuit modeling (ECM) is certainly the most complete approach with regard to the description of the behavior of a single cell, and being “modular”, it also describes the electro–thermal dynamics (also starting from chemical considerations) of the entire battery. Many methods for estimating SOC/SOH are in fact “model-based”; therefore, concrete and exhaustive formal modeling is certainly a fundamental requirement for what concerns the design of efficient and reliable estimation algorithms. In the case of ECM, the main objective of using a dynamic model is the description of the response of the cells to a variation in the input current (or load current). The combination of simulations and real data acquired directly from tests on the battery is used to estimate some essential parameters to make the model reliable for the design of SOC/SOH estimation algorithms. Below, we propose an “incremental” description starting from the basic idea and showing which types of details it makes sense to add in a dynamic model for the study of cell/battery charge/discharge transients in order to finally arrive at the formalization of the structure of the ECM most used in today’s literature [126,127]. Let us start with the ideal model depicted in Figure 2(left). This model is called an “Ideal Voltage Source” and is based on the obviously far-fetched hypothesis that the battery voltage is independent of the current absorbed/delivered by the battery, independent of past operating conditions, and constant over time. In this model, therefore, would result, where OCV is denominated as “Open-Circuit Voltage”. Although it is an unrealistic model, it serves to establish some fundamental concepts: (i) the battery imposes voltage on the load; (ii) when not connected to a load, the open-circuit voltage is easily predictable; and (iii) even sophisticated models include the ideal voltage source.
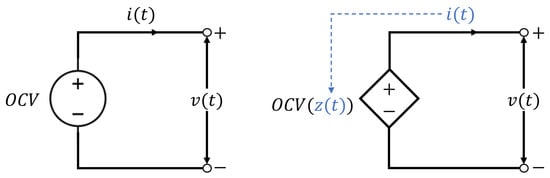
Figure 2.
Ideal circuit with constant OCV (left) and with OCV dependent on SOC (right).
The first enrichment of details is based on the experimental evidence that when the cell/battery is fully charged, its is higher than when it is in a discharged condition. Therefore, the dependence of the on the can be introduced into the model, which, by convention, is named the time variable . It is assumed that for a fully charged battery and for a fully discharged battery. We also call Q the total amount of charge that is removed from the cells during the transition from charged to discharged conditions, which is normally provided by the manufacturer (or is measurable) in . As shown in Figure 2(right), the voltage source is driven with respect to the charge: .
Knowing that decreases if (discharge condition) and, vice versa, increases if (recharge condition), it is possible to associate the following differential equation to describe the variation to SOC as a function of current [128].
From experimental evidence, we have that not all the charge moved by the current is actually used in the charge/discharge process due to the fact that a certain quantity of charge is dispersed in some regions of the electrodes; therefore, we introduce as a further level of detail the so-called “Coulomb efficiency” . Note that in general this efficiency is a function of time in order to take into account the use of the battery (or its aging). Efficiency in the classical sense is relative to the input/output energy flow ; therefore, in general, . In particular, for lithium-ion batteries, experimentally, we have values of the type: and .
An evolution of the above model is the so-called “ model”, in which the presence of a series resistor (shown in Figure 3) is included to account for energy losses due to heating, which obviously do not result in charge losses. The important phenomenon that through is (at least partially) included in the modeling is “polarization”, which is understood as the voltage drop across the battery terminals with respect to , such as the intrinsic voltage drop due to the connection with the load. Of course, serious resistance alone represents a level of abstraction sufficient only for simple electronic system design but certainly not enough for BMS design and advanced estimation algorithms in HV/EV applications [129,130].
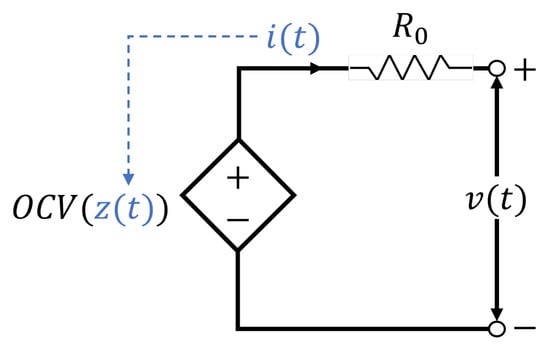
Figure 3.
Equivalent circuit model taking into account internal resistance.
In the case of the model, the circuit equilibrium can be expressed as , which shows that in the discharge phase, ; conversely, in the charging phase. The limitation of this model is that the dynamic response with respect to a change in turns out to be instantaneous (because of the term), whereas experimentally, there is a settling transient due to internal electrochemical processes.
The realistic cell/battery response is shown in Figure 4, where at , a pulse of positive current is applied (thus bringing the cell to a discharged condition) until the instant . It can be seen that during the time window for which the current is constant, the voltage tends to drop transiently, and when the current returns to zero, the voltage slowly rises again to a steady-state value, which, however, is less than the starting value. This phenomenon is called “diffusion voltage”: meaning that can never be instantaneous but is always characterized by settling transients. To represent even this degree of detail, circuit components for which the fundamental V-I relationship is integral–differential must be included in the circuit and, in particular, through parallel RC branches as, for example, shown in Figure 5, which is called the RC–Thevenin model [131,132].
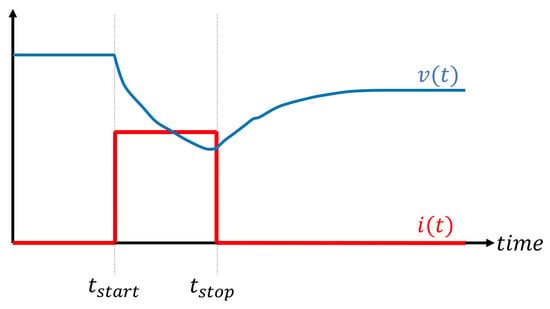
Figure 4.
Schematic representation of the current pulse response of a “realistic” cell/battery model.
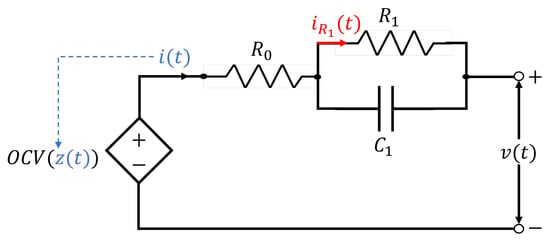
Figure 5.
RC–Thevenin model.
In this case, the dynamic electric equilibrium is represented by the set of algebraic–differential equations shown in Equation (5).
Typically, the model is integrated on a microcontroller-based embedded platform, so a key step in the implementation of model-based SOC/SOH estimation systems is the discretization technique so that an efficient and numerically accurate SW task can be defined. In Equation (6) are given the recursive (or finite difference) equations that are obtained by applying the ZOH (zero-order-holder) numerical approximation; we denote by the appropriate numerical integration step (or sampling time).
In the end, it is possible to use this model efficiently to describe cell/battery behavior by correlating experimental evidence with the choice of parameters through a systematic procedure. The basic steps for deriving the parameters of the RC–Thevenin model are described below:
- -
- For estimating the total charge Q, a simple and effective method is to bring the cell/battery to the maximum rated voltage (corresponding to the maximum level of ), apply a load, and directly measure , i.e., directly monitor the “amperes per hour” , up to the minimum rated voltage (corresponding to the minimum level of ).
- -
- For estimating the efficiency , by opposite procedure, one starts from the full discharge condition of the battery and slowly brings it up to the maximum nominal voltage level () from the minimum (); one directly monitors . This results in an estimated .
- -
- Estimation of the circuit parameters is done during the “Pulse Current Test” analysis and by applying some simple concepts of linear dynamic systems analysis to the graphical meaning of the step response. In particular, reference is made to the situation depicted in Figure 6. As can be seen, at , the voltage has a rising transient characterized by a “vertical” stretch, which can be associated with the term , so from the direct voltage measurement it is possible to derive the value and consequently to obtain an estimate of the parameter. Similarly, one can associate the steady-state value of the voltage with the series of resistors to procedurally derive as well. As for the value of , we can consider the pseudo-empirical relationship between the settling time and characteristic constant.
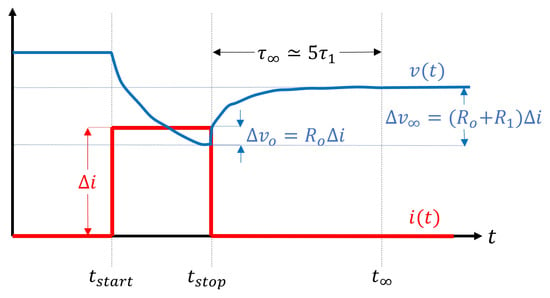 Figure 6. Schematic representation of dynamic response to current pulse, with meanings of the model parameter contributions highlighted.
Figure 6. Schematic representation of dynamic response to current pulse, with meanings of the model parameter contributions highlighted.
Further refinements are achieved by increasing the number of RC blocks put in series, which results in a model that is essentially linear but of such an order that it can approximate even more complex phenomena, such as the effect of Warberg impedance or the effect of cell hysteresis. For an “nRC–Thevenin” model (as in Figure 7), the set of recursive equations to be implemented has the form given in Equation (7).
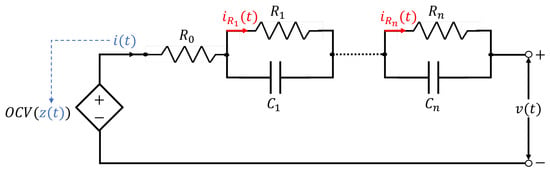
Figure 7.
Thevenin equivalent model with nRC branches.
3.3. Other Models
The Partnership for a New Generation of Vehicles (PNGV) battery equivalent model is used for accurate description and SOC estimation of lithium batteries, particularly for electric vehicles. It is based on the existing charging state estimation method and the Davidson’s battery model. The model is established using the Kalman filtering algorithm and a state space expression. It includes parameters related to environmental temperature, battery charge and discharge, and SOC. The PNGV model is suitable for modeling monomers and modules of lithium iron phosphate batteries, and it has been shown to have higher modeling accuracy, especially when electric vehicles are running in a city. The PNGV model is a conventional battery equivalent circuit model (ECM) [133,134]. The PNGV model for batteries offers several advantages and some limitations.
Advantages:
- Accurate Description: The PNGV model provides an accurate description of the discharge behavior of lithium batteries.
- SOC Estimation: It enables precise SOC estimation for Li-ion batteries based on multi-model switching.
- Suitability for Electric Vehicles: The model is suitable for modeling the monomers and modules of lithium–iron–phosphate batteries with higher accuracy, especially when electric vehicles are running in a city.
Disadvantages:
- Complexity: The model may involve a relatively complex equivalent circuit and state space expression, which may require computational resources and expertise to implement effectively.
- Parameter Sensitivity: Some parameters of the model are related to environmental factors and battery charge and discharge, which may introduce sensitivity and require careful calibration.
In summary, the PNGV model offers an accurate description and SOC estimation for lithium batteries and is particularly suitable for electric vehicles. However, its complexity and parameter sensitivity are aspects that need to be carefully considered during implementation.
The dual polarization (DP) model is an equivalent circuit model used for the characterization of lithium batteries, particularly in the context of battery management systems and SOC estimation. This model is known for its dynamic performance and accurate SOC estimation, which makes it a valuable tool for optimizing charging profiles and understanding the transient response during power transfer to and from the battery. The DP model represents the open-circuit voltage of the battery as a function of the SOC. It is considered one of the most flexible methods for battery management systems. The model is based on the polarization characteristics of the battery and is used to simulate and understand the behavior of lithium batteries under different operating conditions [135,136]. As with the other models, the DP model has some advantages and some limitations.
Advantages:
- Dynamic Performance: The DP model is known for its excellent dynamic performance, which makes it valuable for understanding the transient response during power transfer to and from the battery.
- Accurate SOC Estimation: It provides the most accurate SOC estimation compared to other models, which is crucial for effective battery management systems and electric vehicles.
- Flexibility: The DP model is considered one of the most flexible methods for battery management systems as it allows for optimized charging profiles based on proper battery models.
Disadvantages:
- Complexity: The model’s dynamic performance and accuracy may come with increased complexity, which may require a sophisticated implementation and computational resources.
- Parameter Sensitivity: Like many battery models, the DP model may exhibit sensitivity to different SOC initial values, which could impact its robustness in practical applications.
In summary, the DP model offers excellent dynamic performance, accurate SOC estimation, and flexibility for battery management systems. However, its complexity and potential parameter sensitivity are aspects that need to be carefully considered during practical implementation.
The Warburg impedance concept is an important element in battery modeling, particularly in the context of electrochemical impedance spectroscopy (EIS) and equivalent circuit models. It represents the diffusion process of ions in the electrodes and the electrolyte of a battery and is used to capture the battery’s dynamic behavior at low frequencies. The Warburg impedance is integrated into battery models, such as the dynamic battery model, to accurately represent the diffusion processes occurring within the battery during charging and discharging [137]. This integration allows for a more comprehensive and accurate representation of the battery’s electrochemical behavior, especially at different operating conditions and charging modes, making it a valuable tool for understanding and optimizing battery performance. The Warburg impedance is often used in conjunction with other elements, such as RC pairs, in equivalent circuit models to provide a more detailed representation of the battery’s electrochemical processes [138]. This comprehensive modeling approach, which includes the Warburg impedance, enables better understanding of the battery’s dynamic behavior and facilitates the development of advanced battery management systems and charging strategies. In summary, the Warburg impedance concept is integrated into battery models to capture the diffusion processes within the battery, especially at low frequencies, and is a valuable tool for understanding and optimizing battery performance, making it an essential element in the development of advanced battery management systems and charging strategies [139].
Pros of integrating Warburg impedance in battery models:
- Modeling Slow Dynamic Processes: The Warburg impedance allows for the modeling of slow dynamic processes happening inside the battery, such as diffusion processes, to provide a more comprehensive representation of the battery’s behavior.
- Accurate Representation of Battery Response: By integrating the Warburg impedance, battery models can accurately represent the response of the battery at low frequencies, which is essential for understanding the battery’s behavior during different operating conditions and charging modes.
- Improved Dynamic Model Performance: The integration of the Warburg impedance has been shown to improve the performance of dynamic battery models, making them more effective for various charging modes, including those intended for electric vehicle charging.
Cons of integrating Warburg impedance in battery models:
- Increased Model Complexity: The integration of the Warburg impedance may lead to increased model complexity, which may require additional computational resources and expertise for implementation.
- Effect on Low-Frequency Response: The Warburg impedance primarily affects the response at low frequencies, and its integration may introduce challenges related to parameter adjustment and the transformation of visual information obtained from impedance measurements into evolving parameters.
In summary, integrating the Warburg impedance in battery models offers the advantage of modeling slow dynamic processes, accurately representing the battery’s response, and improving dynamic model performance. However, it may also lead to increased model complexity and pose challenges related to the low-frequency response and parameter adjustment.
As can be observed from simulation scenario in Figure 8 and Figure 9, the model achieves a minimal SOC error during the first 2020 s because of the exact starting SOC and Ah counting approach. However, because of the model’s inferior precision, an accumulation error arises and a maximum SOC error is acquired at the conclusion of the computation.
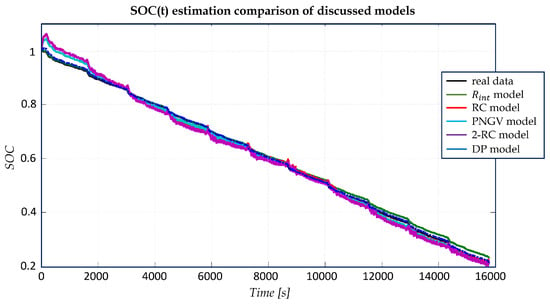
Figure 8.
Simulation of SOC estimation of the discussed models.
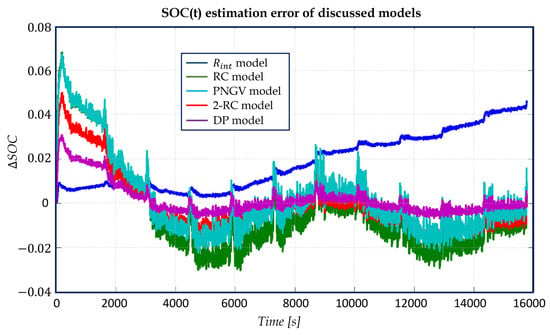
Figure 9.
SOC estimation error obtained within proposed simulation.
Similar variations and trends are seen for the other four models that take into account the polarization features. This indicates that the SOC error is highest during the first stage of the calculation process and then rapidly decreases toward the correct SOC, albeit with varying degrees of precision. The maximum SOC error for the DP, RC, Thevenin, and PNGV models appears at the first stage, whereas it appears at the final stage for the Rint model. This indicates that the Rint model is not appropriate for long-term use in SOC estimation, with the exception of timely revision of the initial SOC, while the other four models perform well at SOC estimation, particularly for extended periods of time. In contrast, the DP model’s SOC error consistently remains low, with the exception being the initial 2020 s; this further confirms that the DP model has the best accuracy for SOC estimate.
4. Main SOC/SOH Estimation Algorithms
4.1. Coulomb Counting Method
The estimation of the SOC of a battery is critical for its efficient and reliable utilization across a wide array of applications. The coulomb counting method represents a fundamental approach to SOC estimation that relies on the measurement of the current flowing in and out of the battery and its integration over time to estimate the transferred charge amount. The associated mathematical equation for the coulomb counting method can be expressed as follows:
We denote as the initial SOC at time ; represents the battery current; represents the current consumed by loss reactions; and represents the nominal capacity of the battery. While the coulomb counting method is straightforward to implement, it presents several sources of error, including the accuracy of the initial SOC, current measurement accuracy, current integration error, uncertainty of battery capacity, and timing error. Furthermore, the method provides a relative change to SOC rather than an absolute SOC and thus requires calibration to enhance its accuracy. This approach is suitable for applications that demand low computational load and moderate precision, such as mobile phones and laptops. However, it may not be suitable for applications requiring high precision and real-time performance, such as electric vehicles and grid storage systems. Given the significance of accurate SOC estimation, various research studies have proposed enhancements to the coulomb counting method to augment its accuracy, including the implementation of a piecewise SOC-OCV relationship, the use of a Kalman filter, or a neural network algorithm. However, careful consideration of the battery type, application context, and required precision is crucial for selecting the most suitable SOC estimation algorithm. The selection or adaptation of a specific algorithm must account for the specific application requirements and battery characteristics to ensure efficient and reliable battery management across a wide range of operational settings. The coulomb counting method, a foundational technique for estimating the SOC in batteries, has recently been augmented by the introduction of the enhanced coulomb counting algorithm. This enhanced approach was developed to address the limitations inherent in the traditional coulomb counting method and to significantly improve its accuracy for estimating both the SOC and state of health (SOH) parameters in lithium-ion batteries. The enhanced coulomb counting algorithm incorporates several key elements to refine the SOC estimation process. It derives the initial SOC from the loaded voltages during charging and discharging or from the open-circuit voltages. Moreover, it factors in the losses incurred during these processes by considering the charging and discharging efficiencies. This algorithm dynamically re-calibrates the maximum releasable capacity of the battery during operation, thereby allowing for the concurrent evaluation of the battery’s SOH. Consequently, this approach contributes to a more precise estimation of the SOC and enhances the overall accuracy and reliability of the estimation process.
The algorithm’s technical principle is rooted in the concept of the releasable capacity, denoted as , which represents the released capacity when the battery is fully discharged. As a result, the SOC is defined as the percentage of the releasable capacity relative to the battery’s rated capacity as provided by the manufacturer. Additionally, the algorithm accounts for the varying maximal releasable capacity , which can deviate from the rated capacity and tends to decline over time. This characteristic is instrumental for evaluating the battery’s state of health (SOH) and assessing its aging pattern during operation.
Furthermore, the algorithm involves comprehensive considerations of the battery’s depth of discharge (DOD) and the operating efficiency during the charging and discharging stages. The integration of these parameters refines the calculation of the DOD: thereby enabling a more accurate estimation of the SOC. This nuanced approach enhances the precision of the estimation process, leading to an improved understanding of the battery’s performance characteristics and health status over its operational cycle.
The practical implementation of the enhanced coulomb counting algorithm is facilitated by its straightforward computational framework and its minimal hardware requirements. This user-friendly and efficient algorithm has the potential for widespread integration across various portable devices and electric vehicles. Its notable feature of reducing the estimation error to as low as during the operating cycle highlights its capacity to enhance the overall performance and reliability of battery management systems and underscores its significance for advancing the realm of battery technology and energy management applications. See Figure 10 for a schematic representation of the enhanced coulomb counting method implementation.
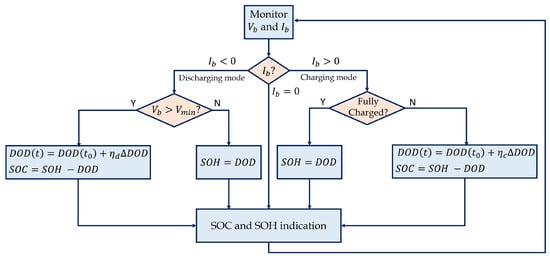
Figure 10.
Schematic illustration of the main operation in CCM.
4.2. Open-Circuit Voltage Method
To model the relationship between the open-circuit voltage (OCV) and the state of charge (SOC) of a battery, commonly used mathematical functions are the sigmoid and polynomial functions.
The objective is to obtain the parameters of the function through a regression process based on data collection measuring the OCV during different charging and discharging cycles and iterating the fitting process until obtaining functions useful for estimating the SOC. The operational limit of this methodology is that the coefficients of the chosen function may not make physical sense; therefore, it then becomes difficult to evaluate the state of health of the battery. Furthermore, this method is valid only and exclusively for the type and operational range experimentally acquired. The calibration procedure involves collecting data, whereby the open-circuit voltage and known state of charge are measured. Through the regression process, the parameters are adjusted to best fit the experimental data. It is important to emphasize that the choice of this function depends on the specific chemistry of the battery and its response to voltage variations. The sigmoid function is a common choice, but other mathematical functions may be used based on the battery type and specific system characteristics. Once the model is calibrated, during the normal operation of the battery, by measuring the open-circuit voltage, this function can be used to estimate the corresponding state of charge. Proper temperature compensation and periodic model revision are important to maintain the accuracy of SOC estimates over time [140,141,142,143].
4.3. Kalman-Filter-Based Method
The Kalman filter is an estimation algorithm that combines measurements with a system prediction to obtain a more accurate estimation of the system state. It is widely used in various fields, including navigation, electronic engineering, and robotics, to obtain accurate estimates of a system’s state in the presence of noise or data uncertainty. In the context of estimating the SOC and SOH for lithium batteries, the Kalman filter plays a crucial role in providing accurate and reliable estimates of these key parameters. The SOC represents the amount of remaining energy available in a battery at a given instant, while the SOH is a measure of the overall integrity and capacity of a battery over time. This algorithm works in two main phases—the prediction phase and the correction phase—using a mathematical model that takes into account the specific characteristics of the battery and the dynamics of the charging and discharging process. The state model for a lithium battery can be represented by a set of differential equations that describe the charging and discharging processes along with factors such as battery age, residual capacity, and internal resistance. In the following, we report the essential formal aspects.
We denote as the internal system state at time k; F is the state transition matrix that represents the system dynamics; B is the control matrix that represents the influence of input on the state; and is the zero-mean process noise. The observation model relates to the actual measurements of SOC and SOH of the lithium battery. The relationship between the state and the observation can be described as following:
where is the actual measurement at time k; H is the observation matrix that projects the state into the measurement space; and is the zero-mean measurement noise.
In the following, we report the fundamental aspect for integration of the classic Kalman filter to linear time-invariant system models.
- 1
- Prediction Phase:
- 1.a
- State prediction:
- 1.b
- Covariance prediction:where is the a priori estimate of the state at time k; is the a priori covariance of the estimation error; Q represents the process noise.
- 2
- Correction Phase:
- 2.a
- Kalman gain calculation:
- 2.b
- Corrected state estimation:
- 2.c
- Covariance update:where is the Kalman gain at time k; R represents the measurement noise covariance matrix.
The precise implementation of these equations requires a detailed understanding of the specific parameters of the battery and the dynamic models involved in the charging and discharging process. The choice of a suitable set of input data and the sampling frequency is crucial to ensure reliable and accurate estimation of the SOC and SOH over time. The Kalman filter offers a powerful and versatile approach to improve the accuracy of SOC and SOH estimates for lithium batteries, which allows for more precise monitoring of battery performance and better management of the overall system. See Figure 11 for a schematic representation of the prediction and correction loop in the classic linear KF.
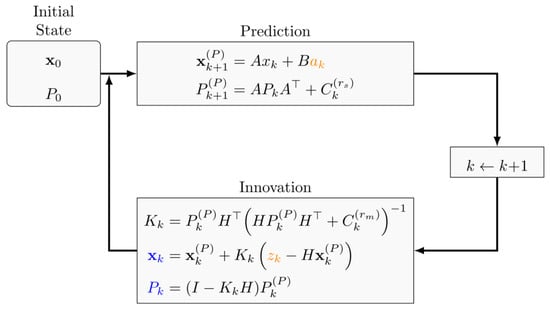
Figure 11.
Schematic illustration of the KF recursive steps.
Alongside the traditional Kalman filter, the extended Kalman filter (EKF) and unscented Kalman filter (UKF) are commonly employed for more complex nonlinear systems, such as those often encountered in battery state estimation. The extended Kalman filter is an adaptation designed for nonlinear systems.
In UKF, the model is linearized around the current mean and covariance: effectively applying the standard Kalman filter to the linearized system. This allows the EKF to handle some non-linearities, but it has limitations, particularly for systems with high non-linearities, where linearization may introduce significant errors. The EKF extends the basic Kalman filter to nonlinear systems. It approximates the system using a first-order Taylor expansion around the current mean and covariance estimates (see Figure 12 for a schematic representation of the EKF phases).
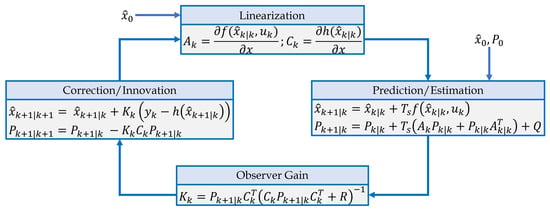
Figure 12.
Schematic illustration of the EKF recursive steps.
- 1
- Prediction Step:
- 1.a
- State prediction:
- 1.b
- Error covariance prediction:
- 2
- Correction Step:
- 2.a
- Compute the Kalman gain:
- 2.b
- Update the state estimate:
- 2.c
- Update the error covariance:
These formulations highlight the nonlinear extensions of the standard Kalman filter to showcase the additional complexity and computational demands of the EKF and UKF.
Careful consideration of these complexities is vital when integrating them into embedded systems for battery SOC/SOH estimation, particularly concerning computational resources and real-time performance requirements. On the other hand, the unscented Kalman filter provides an improved solution to the limitations of the EKF.
It operates by approximating the mean and covariance of the probability distribution through a set of carefully chosen points, known as sigma points, propagated through the nonlinear functions. This technique better captures the nonlinearities without the need for linearization, thus providing more accurate estimations for highly nonlinear systems compared to the EKF. The UKF avoids linearization by utilizing a set of carefully chosen sigma points that capture the mean and covariance of the estimated distribution in order to preserve moments up to the third order.
- 1
- Prediction Step:
- 1.a
- Generate sigma points:
- 1.b
- Propagate sigma points through the nonlinear process model:
- 1.c
- Compute predicted state and covariance:
- 2
- Correction Step:
- 2.a
- Propagate sigma points through the observation model:
- 2.b
- Compute the predicted measurement mean and covariance:
- 2.c
- Compute the cross-covariance matrix:
- 2.d
- Compute the Kalman gain:
- 2.e
- Update the state estimate:
- 2.f
- Update the error covariance:
In Figure 13 is reported a schematic representation of the recursive phases required for UKF algorithm integration.
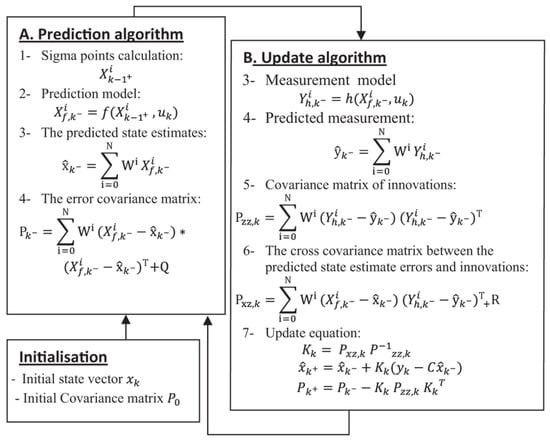
Figure 13.
Schematic illustration of the UKF recursive steps.
While the EKF and UKF offer better adaptability to nonlinear systems compared to the traditional Kalman filter, they are computationally more intensive due to the increased number of calculations involved to handle the nonlinearities. This can pose challenges for embedded systems, especially in real-time applications where computational resources are limited.
Moreover, the complexity of implementation and the need for careful tuning of parameters can increase the development effort and time. When integrating these filters into embedded systems for Li-ion battery SOC/SOH estimation, it is crucial to consider the trade-off between computational complexity and estimation accuracy. In resource-constrained environments, simplifying the model or adopting a less computationally intensive method might be necessary. However, for applications where high accuracy is critical, the EKF or UKF might be preferred, with optimization efforts focused on efficient implementation and utilization of available hardware resources. Furthermore, the integration of any of these filters into embedded systems demands meticulous consideration of memory usage, processing power, and real-time performance requirements. Efficient algorithm optimization, careful selection of hardware components, and algorithmic simplifications tailored to the specific application can aid with the successful integration of these advanced filters for Li-ion battery SOC/SOH estimation in embedded systems.
4.4. AI-Based Methods
4.4.1. Bayesian Neural Network
A Bayesian neural network (BNN) is a variant of a neural network that incorporates Bayesian concepts, which allows the capture of the uncertainty associated with SOC estimates. In a battery SOC estimation context, the BNN can be formulated to model the probability distribution of the estimated SOC to provide a probabilistic rather than a deterministic estimate [144,145,146,147,148,149,150,151]. Let us consider a simple BNN with a single hidden layer. The output of the BNN will be a probability distribution for the estimated SOC. The weights of the neural network, traditionally denoted by W, become random variables. In a BNN, we represent the probability distribution of the weights as .
Using Bayes’ theorem, the goal is to obtain the posterior distribution , where D represents the training dataset.
where is the likelihood (the probability of the data given the weights), and is the prior (the a priori knowledge about the weights). The output of the BNN given an input X is a probability distribution for the estimated SOC .
The integration takes into account the uncertainty associated with the weights. During training, we maximize the likelihood function , which measures how well the weights explain the observed data.
The loss function can be formulated as the Kullback–Leibler divergence between the prior distribution and the posterior distribution of the weights.
where represents the parameters of the BNN. Training involves minimizing the Bayesian loss function using Bayesian optimization techniques such as Bayes optimization through Gaussian processes. The BNN captures the uncertainty associated with SOC estimates, which is essential for critical applications. It provides a natural extension to probabilistic prediction and provides more detailed information than a deterministic estimate. In exploring computational complexity, the BNN emerges as a model that may require a more considerable amount of resources, mainly due to Bayesian inference. When compared to support vector machines (SVMs), BNN is on a higher scale in terms of computational intensity but is comparable to traditional neural networks. By analyzing the complexity of the software (SW) and hardware (HW) tools necessary for training, the BNN presents itself as a model that requires significant resources: in line with the needs of traditional neural networks and superior to those of SVMs. In the context of busy memory, the BNN may be more expensive due to the probability distributions associated with the weights. In this aspect, it surpasses SVM and confirms itself in line with the greater resource demand of traditional neural networks. When evaluating the possibility of implementation on embedded systems, the BNN may present additional challenges due to its computational complexity and required memory. When compared to traditional neural networks, BNN may appear less suitable for implementation on embedded systems, although it is more efficient than more complex neural networks. Finally, regarding the possibility of real-time implementation, BNN shows similar flexibility to traditional neural networks, but the speed of implementation depends on the complexity of the model and the available computing power. In summary, while BNN offers more accurate management of uncertainty in SOC estimates, its implementation requires significant computational and memory resources, which influences implementation choices in real-time and on embedded systems. The decision between AI models depends on the specific needs of the application and the available resources.
4.4.2. Support Vector Machines
Support vector machines (SVMs) are supervised learning algorithms used for classification and regression. For estimating the SOC of batteries, SVMs can be adopted to model the relationship between the input variables and the SOC [152,153]. We consider a linear SVM model for SOC estimation.
where represents the decision function, w is the weight vector, x are the input variables, and b is the bias term. The goal of SVMs is to maximize the margin between classes. The margin is the distance between the closest point of each class and the decision plane.
where is the class label of . The margin condition ensures that points are correctly classified outside the margin. The loss function, also called the cost function, penalizes classification errors.
where the parameter C regulates the trade-off between maximizing the margin and minimizing errors. SVMs can use the “kernel trick” to handle nonlinearly separable data without having to explicitly transform them into a feature space.
where is the kernel function that computes the similarity between and x, and are the Lagrange multipliers. Training of SVMs involves optimizing the parameters w and b in order to maximize the margin and minimize classification errors. The computational complexity of SVMs mainly depends on the size of the dataset and the type of kernel used. The linear case is more efficient than complex kernels. The memory occupied depends on the number of support vectors, i.e., the most relevant data points for defining the margin. SVMs stand out for their ability to generalize excellently, even when faced with complex data and noise. This feature makes them reliable when dealing with real scenarios and challenges typical of battery SOC estimation applications [154,155,156]. Another strength of SVMs is their versatility at managing input variables. They can successfully navigate between both continuous and categorical variables, which offers flexibility that adapts to different application contexts [157,158]. SVMs, despite their power, present a certain sensitivity to parameter configuration. Carefully choosing key factors such as the regularization parameter C and the kernel type can significantly influence the model’s performance in SOC estimation. This requires special attention during the configuration phase [159,160]. Another important consideration is the handling of complex kernels. While these can offer greater modeling flexibility, their implementation can require large amounts of data to prevent overfitting. This aspect underlines the importance of a robust data collection strategy adapted to the peculiarities of SVMs when dealing with more complex models. SVMs offer a robust approach for estimating battery SOC: providing good generalization and effectively handling complex data. However, choosing appropriate parameters and handling large datasets are crucial considerations during implementation.
4.4.3. Long Short-Term Memory
Recurrent neural networks (RNNs)—in particular, long short-term memory (LSTM)—are used to model complex relationships in the context of estimating the SOC of batteries. LSTMs are particularly well suited to managing temporal sequences and capturing long-term dependencies [161,162]. The long-term memory or cell state is a key component of LSTMs and is updated using the formula:
where is the forgetting gate, is the input gate, and is the new candidate information. The hidden state , which represents the information to pass to the next step, is calculated as:
where is the output value. The decision gates govern the updating and output of the LSTM cell. The equations for the doors are given by:
where are weight matrices, are the biases, is the sigmoid function, and tanh is the hyperbolic tangent function. Training LSTMs involves using the back-propagation through time (BPTT) algorithm to optimize weights and biases. The computational complexity of LSTMs depends on the length of the time sequence and the size of the hidden layers. The use of mini-batches during training contributes to computational efficiency. The occupied memory is influenced by the size of the hidden layers and the number of network parameters. Training LSTMs involves back-propagation through time (BPTT), a key process for optimizing model weights and biases. BPTT is a variant of traditional back-propagation adapted to recurrent neural networks. Referring to Figure 14, the learning procedure for LSTM-type networks is explained in detail below.
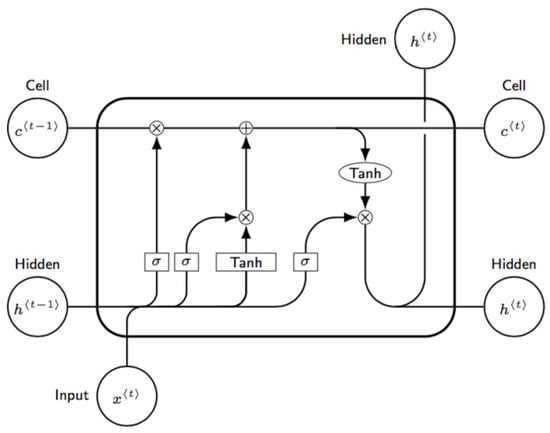
Figure 14.
Schematic illustration of the learning process in LSTM models.
The error at time t is calculated based on the difference between the desired output and the actual output :
The error is propagated backwards through the state cell using the hyperbolic tangent tanh:
The error propagates through the decision gates:
The error propagates in the hidden state:
The weights and biases are updated using the calculated error:
The hidden state weights and biases are updated considering the error in the hidden state:
The parameter represents the learning rate. The BPTT process is iteratively repeated to optimize the weights and biases of the LSTM network. Long short-term memory (LSTM) emerges as a powerful tool in the context of SOC estimation of batteries by offering a number of significant advantages. One of the distinguishing characteristics of LSTMs is their ability to capture long-term dependencies. This property is of particular relevance when it comes to modeling the dynamic behavior of the SOC over time [163,164]. The recurrent structure of LSTMs gives them a natural adaptability to temporal sequences. This peculiarity makes them particularly suitable for dealing with data from battery systems, for which changes to SOC over time must be modeled accurately [165,166]. However, it is also essential to consider the limitations associated with the use of LSTMs for SOC estimation. First, model complexity can be a challenge. Complex LSTM models, although capable of capturing intricate relationships, may require longer training times. In addition, model complexity can make them prone to overfitting, whereby the model overfits the training data, which compromises its ability to generalize [167,168]. Another critical consideration concerns the need for sufficient data to ensure the effectiveness of LSTMs. These models depend on the availability of a representative and large training dataset to capture the inherent complexity of the system.
In the absence of sufficient data, LSTMs may not be able to learn optimally and, consequently, may compromise performance at accurately estimating the SOC [169,170,171]. In summary, while offering significant advantages for capturing long-term relationships and dealing with sequential data, the implementation of LSTMs for SOC estimation requires a careful balance between model complexity and the availability of training data.
4.5. Method Comparison Discussion
In the intricate landscape of SOC estimation for batteries, diverse models and algorithms have emerged to address the complex dynamics of energy storage systems. This section aims to compare three prominent approaches: support vector machines (SVMs), long short-term memory (LSTM) networks, and Bayesian neural networks (BNNs). Batteries, as intricate electrochemical systems, demand accurate SOC estimation for optimal operation. From traditional support vector machines (SVMs) to sophisticated LSTM networks and probabilistic Bayesian neural networks (BNNs), various models and algorithms have been proposed. SVMs employ mathematical formulations that optimize the margin between data points, making them effective at capturing intricate relationships. However, their adaptability to battery dynamics and temporal sequences may be limited compared to other methods. LSTMs, a type of recurrent neural network, excel at capturing long-term dependencies within sequential data. Widely adopted for their ability to adapt to temporal sequences and handle complex, nonlinear relationships, LSTMs prove effective at modeling the dynamic behavior of batteries over time. Introducing a probabilistic approach, BNNs incorporate uncertainty into neural networks. This is advantageous in scenarios for which uncertainty in predictions is critical, such as battery SOC estimation. Offering a balance between complexity and efficiency, BNNs present an intriguing option. In Table 2, we comprehensively compare SVM, LSTM, and BNN based on criteria such as mathematical formulation, computational complexity, memory usage, implementation considerations, and adaptability to temporal sequences. This comparative analysis aims to guide the selection of the most suitable method based on specific application requirements.

Table 2.
Comparison between SVM, LSTM, and BNN.
This comparative analysis provides valuable insights for researchers and practitioners navigating the strengths and limitations of each method in the context of SOC estimation for battery systems. In the complex challenge of estimating the state of charge (SOC) of batteries, several methods are employed, each with unique approaches and specific challenges (see Table 3). The coulomb counting method is based on measuring the current flowing into and out of the battery over time. Its conceptual simplicity and economical implementation make it attractive, but it is subject to the accumulation of errors over time due to phenomena such as current measurement drift. This method may be particularly susceptible to inaccurate results in the presence of batteries that exhibit nonlinear behavior or variations in efficiency under different operating conditions. The open-circuit voltage (OCV) method, on the other hand, is based on the open-circuit voltage of the battery. It is a nonintrusive approach and is relatively simple to implement. However, its accuracy is closely tied to correct calibration, and it can be less accurate during rapid charge and discharge transitions. The Kalman filter, a more advanced method, offers adaptability to changes to the operating conditions. This method is capable of integrating multiple data to reduce uncertainty, but its implementation requires in-depth knowledge of the system and a careful choice of parameters. Artificial intelligence techniques, such as neural networks, present a flexible approach that can adapt to complex models. However, they require a large amount of data for training, can be sensitive to the quality and representativeness of the data, and can require significant computational resources. In summary, the choice of SOC estimation method depends on various factors, such as the required accuracy, the complexity of the system, and the availability of accurate calibration data. A combined approach that leverages the advantages of multiple methods could be the ideal solution to address the specific challenges that each SOC estimation application presents.

Table 3.
Comparison of SOC estimation methods for batteries.
5. Conclusions and Future Work
In conclusion, this state-of-the-art analysis has outlined a detailed and in-depth picture of current methodologies and algorithms for SOC estimation in batteries and emphasized the crucial importance of such approaches in power electronics for vehicles and mechatronic systems.
The survey went beyond the limitations of conventional research to provide a level of detail that is currently lacking in the literature. Examination of the methodologies, such as Coulomb counting, the voltage method, Kalman filters, neural network algorithms, and hybrid algorithms, highlighted the strengths and limitations of each approach. This in-depth understanding is crucial for the practical implementation of advanced energy management solutions, which can ensure optimal battery utilization and enhanced operational safety. The detailed comparison of SOC estimation algorithms identified the operational situations in which each method excels in order to help provide practical guidelines for selecting the most suitable algorithm based on the specific needs of the electric vehicle or mechatronic system. This study stands out for its depth of analysis and detail and fills a gap in the existing literature. The information gathered provides a vital resource for researchers, engineers, and practitioners interested in optimizing energy management strategies. Looking ahead, promising insights emerge for further research and development in the field of power electronics for vehicles and mechatronic systems: The integration of cybersecurity into power electronics systems is a key research direction. With the expansion of electric and hybrid vehicles, protection from potential cyber attacks becomes crucial to ensure the integrity and safety of the vehicle and its occupants. Developing SOC estimation algorithms that are resilient to cyber threats will become a critical aspect of future design. Exploration of multi-objective optimization approaches for SOC estimation algorithms that balance estimation accuracy with computational complexity is necessary. This could lead to more energy- and computationally efficient solutions. As storage technologies, such as solid-state batteries, evolve, future research should focus on how SOC estimation algorithms can adapt to and benefit from these new solutions to help further improve battery efficiency and lifetime. In conclusion, this study has not only expanded the current understanding of SOC estimation methodologies but also outlined a road map for future investigations to address emerging challenges in the field of power electronics for vehicles and mechatronic systems. Further investigation of these issues will not only ensure significant advances in energy management but will also help make electric vehicles safer and more reliable in a rapidly changing environment.
Author Contributions
Conceptualization, P.D. and S.S.; methodology, P.D. and S.S.; software, P.D.; validation, P.D., S.S. and A.C.; formal analysis, P.D. and S.S.; investigation, P.D. and S.S.; resources, P.D.; data curation, P.D., S.S. and A.C.; writing—original draft preparation, P.D., S.S. and A.C.; writing—review and editing, P.D., S.S. and A.C.; visualization, P.D., S.S. and A.C.; supervision, P.D., S.S. and A.C.; project administration, P.D., S.S. and A.C.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially funded by: MIUR FoReLab Project “Dipartimenti di Eccellenza”; the PNRR project “CN1 Big Data, HPC and Quantum Computing in Spoke 6 Multiscale Modeling and Engineering Applications”; and by the ECSEL JU project Hiefficient n. 101007281 (EU ECSEL-2020-2-RIA call).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, P.D., upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dini, P.; Saponara, S. Cogging torque reduction in brushless motors by a nonlinear control technique. Energies 2019, 12, 2224. [Google Scholar]
- Dini, P.; Saponara, S.; Colicelli, A. Overview on Battery Charging Systems for Electric Vehicles. Electronics 2023, 12, 4295. [Google Scholar] [CrossRef]
- Pacini, F.; Matteo, S.D.; Dini, P.; Fanucci, L.; Bucchi, F. Innovative Plug-and-Play System for Electrification of Wheel-Chairs. IEEE Access 2023, 11, 89038–89051. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Processor-in-the-loop validation of a gradient descent-based model predictive control for assisted driving and obstacles avoidance applications. IEEE Access 2022, 10, 67958–67975. [Google Scholar]
- Dini, P.; Saponara, S.; Chakraborty, S.; Hosseinabadi, F.; Hegazy, O. Experimental Characterization and Electro-Thermal Modeling of Double Side Cooled SiC MOSFETs for Accurate and Rapid Power Converter Simulations. IEEE Access 2023, 11, 79120–79143. [Google Scholar] [CrossRef]
- Pierpaolo, D.; Saponara, S. Control system design for cogging torque reduction based on sensor-less architecture. In Proceedings of the Applications in Electronics Pervading Industry, Environment and Society, Pisa, Italy, 11–13 September 2019; pp. 309–321. [Google Scholar]
- Dini, P.; Saponara, S. Design of adaptive controller exploiting learning concepts applied to a BLDC-based drive system. Energies 2020, 13, 2512. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Electro-thermal model-based design of bidirectional on-board chargers in hybrid and full electric vehicles. Electronics 2021, 11, 112. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Review on model based design of advanced control algorithms for cogging torque reduction in power drive systems. Energies 2022, 15, 8990. [Google Scholar]
- Dini, P.; Ariaudo, G.; Botto, G.; Greca, F.L.; Saponara, S. Real-time electro-thermal modelling & predictive control design of resonant power converter in full electric vehicle applications. IET Power Electron. 2023, 16, 2045–2064. [Google Scholar]
- Bernardeschi, C.; Dini, P.; Domenici, A.; Saponara, S. Co-simulation and Verification of a Non-linear Control System for Cogging Torque Reduction in Brushless Motors. In Proceedings of the Software Engineering and Formal Methods: SEFM 2019 Collocated Workshops: CoSim-CPS, ASYDE, CIFMA, and FOCLASA, Oslo, Norway, 16–20 September 2019; Revised Selected Papers 17. Springer: Berlin/Heidelberg, Germany, 2020; pp. 3–19. [Google Scholar]
- Cosimi, F.; Dini, P.; Giannetti, S.; Petrelli, M.; Saponara, S. Analysis and design of a non-linear MPC algorithm for vehicle trajectory tracking and obstacle avoidance. In Proceedings of the Applications in Electronics Pervading Industry, Environment and Society, APPLEPIES 2020, Berlin, Germany, 19–20 November 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 229–234. [Google Scholar]
- Dini, P.; Saponara, S. Model-based design of an improved electric drive controller for high-precision applications based on feedback linearization technique. Electronics 2021, 10, 2954. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Design of an observer-based architecture and non-linear control algorithm for cogging torque reduction in synchronous motors. Energies 2020, 13, 2077. [Google Scholar]
- Wang, Y.; Zhang, Y.; Zhang, C.; Zhou, J.; Hu, D.; Yi, F.; Fan, Z.; Zeng, T. Genetic algorithm-based fuzzy optimization of energy management strategy for fuel cell vehicles considering driving cycles recognition. Energy 2023, 263, 126112. [Google Scholar]
- Geng, W.; Lou, D.; Wang, C.; Zhang, T. A cascaded energy management optimization method of multimode power-split hybrid electric vehicles. Energy 2020, 199, 117224. [Google Scholar] [CrossRef]
- Dong, X.; Li, X.; Cheng, S. Energy Management Optimization of Microgrid Cluster Based on Multi-Agent-System and Hierarchical Stackelberg Game Theory. IEEE Access 2020, 8, 206183–206197. [Google Scholar] [CrossRef]
- Teng, T.; Zhang, X.; Dong, H.; Xue, Q. A comprehensive review of energy management optimization strategies for fuel cell passenger vehicle. Int. J. Hydrogen Energy 2020, 45, 20293–20303. [Google Scholar]
- Xing, X.; Xie, L.; Meng, H. Cooperative energy management optimization based on distributed MPC in grid-connected microgrids community. Int. J. Electr. Power Energy Syst. 2019, 107, 186–199. [Google Scholar] [CrossRef]
- Mellouk, L.; Ghazi, M.; Aaroud, A.; Boulmalf, M.; Benhaddou, D.; Zine-Dine, K. Design and energy management optimization for hybrid renewable energy system-case study: Laayoune region. Renew. Energy 2019, 139, 621–634. [Google Scholar]
- Hou, X.; Wang, J.; Huang, T.; Wang, T.; Wang, P. Smart Home Energy Management Optimization Method Considering Energy Storage and Electric Vehicle. IEEE Access 2019, 7, 144010–144020. [Google Scholar] [CrossRef]
- Khayyam, S.; Berr, N.; Razik, L.; Fleck, M.; Ponci, F.; Monti, A. Railway System Energy Management Optimization Demonstrated at Offline and Online Case Studies. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3570–3583. [Google Scholar] [CrossRef]
- Qi, J.; Lai, C.; Xu, B.; Sun, Y.; Leung, K.S. Collaborative Energy Management Optimization Toward a Green Energy Local Area Network. IEEE Trans. Ind. Inform. 2018, 14, 5410–5418. [Google Scholar] [CrossRef]
- EI-Bidairi, K.S.; Duc Nguyen, H.; Jayasinghe, S.D.G.; Mahmoud, T.S. Multiobjective Intelligent Energy Management Optimization for Grid-Connected Microgrids. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- He, H.; Niu, Z.; Wang, Y.; Huang, R.; Shou, Y. Energy management optimization for connected hybrid electric vehicle using offline reinforcement learning. J. Energy Storage 2023, 72, 108517. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, S.; Shen, S.; Liu, Y.; Guo, F.; Zhang, Y. Co-optimization of velocity planning and energy management for autonomous plug-in hybrid electric vehicles in urban driving scenarios. Energy 2023, 263, 126060. [Google Scholar] [CrossRef]
- Zhu, Y.; Dong, Z.; Cheng, Z.; Huang, X.; Dong, Y.; Zhang, Z. Neural network extended state-observer for energy system monitoring. Energy 2023, 263, 125736. [Google Scholar]
- Amini, F.; Ghassemzadeh, S.; Rostami, N.; Tabar, V.S. Electrical energy systems resilience: A comprehensive review on definitions, challenges, enhancements and future proceedings. IET Renew. Power Gener. 2023, 17, 1835–1858. [Google Scholar] [CrossRef]
- Barykina, Y.; Chernykh, A. Ensuring of reliability and security of energy systems in the Russian Federation. IOP Conf. Ser. Earth Environ. Sci. 2022, 990, 012001. [Google Scholar]
- Pong, P.W.; Annaswamy, A.M.; Kroposki, B.; Zhang, Y.; Rajagopal, R.; Zussman, G.; Poor, H.V. Cyber-enabled grids: Shaping future energy systems. Adv. Appl. Energy 2021, 1, 100003. [Google Scholar] [CrossRef]
- Zografopoulos, I.; Ospina, J.; Liu, X.; Konstantinou, C. Cyber-Physical Energy Systems Security: Threat Modeling, Risk Assessment, Resources, Metrics, and Case Studies. IEEE Access 2021, 9, 29775–29818. [Google Scholar] [CrossRef]
- Choo, B.L.; Go, Y.I. Energy storage for large scale/utility renewable energy system-An enhanced safety model and risk assessment. Renew. Energy Focus 2022, 42, 79–96. [Google Scholar] [CrossRef]
- O’Dwyer, E.; Pan, I.; Acha, S.; Shah, N. Smart energy systems for sustainable smart cities: Current developments, trends and future directions. Appl. Energy 2019, 237, 581–597. [Google Scholar]
- Liu, L.; Wang, D.; Hou, K.; Jia, H.J.; Li, S.Y. Region model and application of regional integrated energy system security analysis. Appl. Energy 2020, 260, 114268. [Google Scholar] [CrossRef]
- Mohan, A.M.; Meskin, N.; Mehrjerdi, H. A comprehensive review of the cyber-attacks and cyber-security on load frequency control of power systems. Energies 2020, 13, 3860. [Google Scholar]
- Azzuni, A.; Aghahosseini, A.; Ram, M.; Bogdanov, D.; Caldera, U.; Breyer, C. Energy security analysis for a 100% renewable energy transition in Jordan by 2050. Sustainability 2020, 12, 4921. [Google Scholar] [CrossRef]
- Lisin, E.; Strielkowski, W.; Chernova, V.; Fomina, A. Assessment of the territorial energy security in the context of energy systems integration. Energies 2018, 11, 3284. [Google Scholar] [CrossRef]
- Martišauskas, L.; Augutis, J.; Krikštolaitis, R. Methodology for energy security assessment considering energy system resilience to disruptions. Energy Strategy Rev. 2018, 22, 106–118. [Google Scholar]
- Li, X.; Yuan, C.; Wang, Z.; He, J.; Yu, S. Lithium battery state-of-health estimation and remaining useful lifetime prediction based on non-parametric aging model and particle filter algorithm. Etransportation 2022, 11, 100156. [Google Scholar] [CrossRef]
- Lao, D.; Shen, Y.; Ren, S.; Lin, S.; Zhang, F. Battery Health Monitoring using Guided Wave Signal Features. In Proceedings of the 50th Annual Review of Progress in Quantitative Nondestructive Evaluation. American Society of Mechanical Engineers, Austin, TX, USA, 23–27 July 2023; Volume 87202, p. V001T09A008. [Google Scholar]
- Semeraro, C.; Caggiano, M.; Olabi, A.G.; Dassisti, M. Battery monitoring and prognostics optimization techniques: Challenges and opportunities. Energy 2022, 255, 124538. [Google Scholar] [CrossRef]
- Lupan, O.; Krüger, H.; Siebert, L.; Ababii, N.; Kohlmann, N.; Buzdugan, A.; Bodduluri, M.T.; Magariu, N.; Terasa, M.I.; Strunskus, T.; et al. Additive manufacturing as a means of gas sensor development for battery health monitoring. Chemosensors 2021, 9, 252. [Google Scholar] [CrossRef]
- Chen, M.; Ma, G.; Liu, W.; Zeng, N.; Luo, X. An overview of data-driven battery health estimation technology for battery management system. Neurocomputing 2023, 532, 152–169. [Google Scholar]
- Liu, F.; Liu, X.; Su, W.; Lin, H.; Chen, H.; He, M. An online state of health estimation method based on battery management system monitoring data. Int. J. Energy Res. 2020, 44, 6338–6349. [Google Scholar] [CrossRef]
- Begni, A.; Dini, P.; Saponara, S. Design and Test of an LSTM-Based Algorithm for Li-Ion Batteries Remaining Useful Life Estimation. In Proceedings of the International Conference on Applications in Electronics Pervading Industry, Environment and Society, Genoa, Italy, 26–27 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 373–379. [Google Scholar]
- Dini, P.; Begni, A.; Ciavarella, S.; De Paoli, E.; Fiorelli, G.; Silvestro, C.; Saponara, S. Design and Testing Novel One-Class Classifier Based on Polynomial Interpolation with Application to Networking Security. IEEE Access 2022, 10, 67910–67924. [Google Scholar] [CrossRef]
- Khaleghi, S.; Firouz, Y.; Van Mierlo, J.; Van Den Bossche, P. Developing a real-time data-driven battery health diagnosis method, using time and frequency domain condition indicators. Appl. Energy 2019, 255, 113813. [Google Scholar] [CrossRef]
- Sheikh, S.S.; Anjum, M.; Khan, M.A.; Hassan, S.A.; Khalid, H.A.; Gastli, A.; Ben-Brahim, L. A battery health monitoring method using machine learning: A data-driven approach. Energies 2020, 13, 3658. [Google Scholar] [CrossRef]
- Shah, F.A.; Shahzad Sheikh, S.; Mir, U.I.; Owais Athar, S. Battery Health Monitoring for Commercialized Electric Vehicle Batteries: Lithium-Ion. In Proceedings of the 2019 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Istanbul, Turkey, 26–27 August 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Babu, S.; Udayasankaran, J.G.; Krishnan, B.; Reddy Tamanampudi, A.S.; Prem Shaji, S.; Vishwanatham, A.; Raja, P.; Sai Sanagapati, S.S. Smart telemetry kit for proactive health monitoring in rural India: The journey so far and the road ahead. In Proceedings of the 2018 IEEE 20th International Conference on e-Health Networking, Applications and Services (Healthcom), Ostrava, Czech Republic, 17–20 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Xie, J.; Ma, J.; Bai, K. Enhanced coulomb counting method for state-of-charge estimation of lithium-ion batteries based on peukert’s law and coulombic efficiency. J. Power Electron. 2018, 18, 910–922. [Google Scholar]
- Zhao, L.; Lin, M.; Chen, Y. Least-squares based coulomb counting method and its application for state-of-charge (SOC) estimation in electric vehicles. Int. J. Energy Res. 2016, 40, 1389–1399. [Google Scholar] [CrossRef]
- Zine, B.; Marouani, K.; Becherif, M.; Yahmedi, S. Estimation of battery SOC for hybrid electric vehicle using coulomb counting method. Int. J. Emerg. Electr. Power Syst. 2018, 19, 20170181. [Google Scholar]
- Baccouche, I.; Jemmali, S.; Mlayah, A.; Manai, B.; Amara, N.E.B. Implementation of an improved Coulomb-counting algorithm based on a piecewise SOC-OCV relationship for SOC estimation of li-IonBattery. arXiv 2018, arXiv:1803.10654. [Google Scholar]
- Dong, G.; Wei, J.; Zhang, C.; Chen, Z. Online state of charge estimation and open circuit voltage hysteresis modeling of LiFePO4 battery using invariant imbedding method. Appl. Energy 2016, 162, 163–171. [Google Scholar]
- Lavigne, L.; Sabatier, J.; Francisco, J.M.; Guillemard, F.; Noury, A. Lithium-ion Open Circuit Voltage (OCV) curve modelling and its ageing adjustment. J. Power Sources 2016, 324, 694–703. [Google Scholar] [CrossRef]
- Baroi, S.; Sarker, P.C.; Baroi, S. An Improved MPPT Technique – Alternative to Fractional Open Circuit Voltage Method. In Proceedings of the 2017 2nd International Conference on Electrical & Electronic Engineering (ICEEE), Rajshahi, Bangladesh, 27–29 December 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, X.; Lei, H.; Xiong, R.; Shen, W.; Yang, R. A novel approach to reconstruct open circuit voltage for state of charge estimation of lithium ion batteries in electric vehicles. Appl. Energy 2019, 255, 113758. [Google Scholar] [CrossRef]
- Yang, J.; Huang, W.; Xia, B.; Mi, C. The improved open-circuit voltage characterization test using active polarization voltage reduction method. Appl. Energy 2019, 237, 682–694. [Google Scholar]
- Das, P. Maximum power tracking based open circuit voltage method for PV system. Energy Procedia 2016, 90, 2–13. [Google Scholar]
- Lim, K.; Bastawrous, H.A.; Duong, V.H.; See, K.W.; Zhang, P.; Dou, S.X. Fading Kalman filter-based real-time state of charge estimation in LiFePO4 battery-powered electric vehicles. Appl. Energy 2016, 169, 40–48. [Google Scholar]
- Topan, P.A.; Ramadan, M.N.; Fathoni, G.; Cahyadi, A.I.; Wahyunggoro, O. State of Charge (SOC) and State of Health (SOH) estimation on lithium polymer battery via Kalman filter. In Proceedings of the 2016 2nd International Conference on Science and Technology-Computer (ICST), Yogyakarta, Indonesia, 27–28 October 2016; pp. 93–96. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar]
- Zhang, S.; Xie, C.; Zeng, C.; Quan, S. SOC estimation optimization method based on parameter modified particle Kalman Filter algorithm. Clust. Comput. 2019, 22, 6009–6018. [Google Scholar]
- Schacht-Rodriguez, R.; Ortiz-Torres, G.; García-Beltrán, C.; Astorga-Zaragoza, C.; Ponsart, J.; Theilliol, D. SoC estimation using an Extended Kalman filter for UAV applications. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 179–187. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, Z.; Huang, L. SoC estimation of Lithium battery based on improved BP neural network. Energy Procedia 2017, 105, 4153–4158. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Xu, K.; Wu, X.; Jiang, H.; Sun, H. Open-circuit voltage-based state of charge estimation of lithium-ion battery using dual neural network fusion battery model. Electrochim. Acta 2016, 188, 356–366. [Google Scholar] [CrossRef]
- Yan, Q.; Wang, Y. Predicting for power battery SOC based on neural network. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 4140–4143. [Google Scholar] [CrossRef]
- Tong, S.; Lacap, J.H.; Park, J.W. Battery state of charge estimation using a load-classifying neural network. J. Energy Storage 2016, 7, 236–243. [Google Scholar]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Chang, W.Y. The state of charge estimating methods for battery: A review. Int. Sch. Res. Not. 2013, 2013, 953792. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, Z.; Tang, G.; Chen, Z.; Zhang, N. Estimation method of state-of-charge for lithium-ion battery used in hybrid electric vehicles based on variable structure extended kalman filter. Chin. J. Mech. Eng. 2016, 29, 717–726. [Google Scholar] [CrossRef]
- Mukherjee, N.; De, D. A New State-of-Charge Control Derivation Method for Hybrid Battery Type Integration. IEEE Trans. Energy Convers. 2017, 32, 866–875. [Google Scholar] [CrossRef]
- Chang, Y.; Fang, H.; Zhang, Y. A new hybrid method for the prediction of the remaining useful life of a lithium-ion battery. Appl. Energy 2017, 206, 1564–1578. [Google Scholar] [CrossRef]
- Chen, C.; Shang, F.; Salameh, M.; Krishnamurthy, M. Challenges and Advancements in Fast Charging Solutions for EVs: A Technological Review. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; pp. 695–701. [Google Scholar] [CrossRef]
- Lithium-ion battery manufacturing for electric vehicles: A contemporary overview. In Advances in Battery Manufacturing, Service, and Management Systems; Wiley: Hoboken, NJ, USA, 2017; pp. 1–28. [CrossRef]
- Ansean, D.; Gonzalez, M.; Blanco, C.; Viera, J.C.; Fernandez, Y.; Garcia, V.M. Lithium-ion battery degradation indicators via incremental capacity analysis. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Y.; Ye, Q.; Tung, L.J.; Greenleaf, M.; Li, H. Integrated Size and Energy Management Design of Battery Storage to Enhance Grid Integration of Large-Scale PV Power Plants. IEEE Trans. Ind. Electron. 2018, 65, 394–402. [Google Scholar] [CrossRef]
- Ma, C.; Yao, R.; Li, C.; Qu, X. A Family of IPT Battery Chargers with Small Clamp Coil for Configurable and Self-Sustained Battery Charging Profile. IEEE Trans. Power Electron. 2023, 38, 7910–7919. [Google Scholar] [CrossRef]
- Tariq, M.; Maswood, A.I.; Gajanayake, C.J.; Gupta, A.K. Modeling and Integration of a Lithium-Ion Battery Energy Storage System with the More Electric Aircraft 270 V DC Power Distribution Architecture. IEEE Access 2018, 6, 41785–41802. [Google Scholar] [CrossRef]
- Soares dos Santos, G.; José Grandinetti, F.; Augusto Rocha Alves, R.; de Queiróz Lamas, W. Design and Simulation of an Energy Storage System with Batteries Lead Acid and Lithium-Ion for an Electric Vehicle: Battery vs. Conduction Cycle Efficiency Analysis. IEEE Lat. Am. Trans. 2020, 18, 1345–1352. [Google Scholar] [CrossRef]
- Jiao, S.; Zhang, G.; Zhou, M.; Li, G. A Comprehensive Review of Research Hotspots on Battery Management Systems for UAVs. IEEE Access 2023, 11, 84636–84650. [Google Scholar] [CrossRef]
- Karneddi, H.; Ronanki, D. Reconfigurable Battery Charger with a Wide Voltage Range for Universal Electric Vehicle Charging Applications. IEEE Trans. Power Electron. 2023, 38, 10606–10610. [Google Scholar] [CrossRef]
- Amini, M.; Nazari, M.H.; Hosseinian, S.H. Optimal Scheduling and Cost-Benefit Analysis of Lithium-Ion Batteries Based on Battery State of Health. IEEE Access 2023, 11, 1359–1371. [Google Scholar] [CrossRef]
- Jafari, M.; Gauchia, A.; Zhao, S.; Zhang, K.; Gauchia, L. Electric Vehicle Battery Cycle Aging Evaluation in Real-World Daily Driving and Vehicle-to-Grid Services. IEEE Trans. Transp. Electrif. 2018, 4, 122–134. [Google Scholar] [CrossRef]
- Alramlawi, M.; Li, P. Design Optimization of a Residential PV-Battery Microgrid with a Detailed Battery Lifetime Estimation Model. IEEE Trans. Ind. Appl. 2020, 56, 2020–2030. [Google Scholar] [CrossRef]
- Bai, Y.; Li, J.; He, H.; Santos, R.C.D.; Yang, Q. Optimal Design of a Hybrid Energy Storage System in a Plug-In Hybrid Electric Vehicle for Battery Lifetime Improvement. IEEE Access 2020, 8, 142148–142158. [Google Scholar] [CrossRef]
- Masrur, M.A.; Skowronska, A.G.; Hancock, J.; Kolhoff, S.W.; McGrew, D.Z.; Vandiver, J.C.; Gatherer, J. Military-Based Vehicle-to-Grid and Vehicle-to-Vehicle Microgrid—System Architecture and Implementation. IEEE Trans. Transp. Electrif. 2018, 4, 157–171. [Google Scholar] [CrossRef]
- Li, S.; Zhao, P.; Gu, C.; Li, J.; Huo, D.; Cheng, S. Aging Mitigation for Battery Energy Storage System in Electric Vehicles. IEEE Trans. Smart Grid 2023, 14, 2152–2163. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Zhang, L.; Liu, P.; Zhang, Z. A Novel Consistency Evaluation Method for Series-Connected Battery Systems Based on Real-World Operation Data. IEEE Trans. Transp. Electrif. 2021, 7, 437–451. [Google Scholar] [CrossRef]
- Kumar, R.R.; Bharatiraja, C.; Udhayakumar, K.; Devakirubakaran, S.; Sekar, K.S.; Mihet-Popa, L. Advances in Batteries, Battery Modeling, Battery Management System, Battery Thermal Management, SOC, SOH, and Charge/Discharge Characteristics in EV Applications. IEEE Access 2023, 11, 105761–105809. [Google Scholar] [CrossRef]
- Singh, S.; More, V.; Batheri, R. Driving Electric Vehicles into the Future with Battery Management Systems. IEEE Eng. Manag. Rev. 2022, 50, 157–161. [Google Scholar] [CrossRef]
- Zhang, E.; Xu, C.; Wang, S.; Shi, Q.; Zhang, Y.; Li, H.; Wang, K.; Jiang, K. Effects of cell-to-cell variations on series-connected liquid metal battery pack capacity. J. Energy Storage 2023, 73, 109148. [Google Scholar] [CrossRef]
- Shen, K.; Sun, J.; Zheng, Y.; Xu, C.; Wang, H.; Wang, S.; Chen, S.; Feng, X. A comprehensive analysis and experimental investigation for the thermal management of cell-to-pack battery system. Appl. Therm. Eng. 2022, 211, 118422. [Google Scholar]
- BS, S.; Hampannavar, S.; Bairwa, B. Applications of battery management system (bms) in sustainable transportation: A comprehensive approach from battery modeling to battery integration to the power grid. World Electr. Veh. J. 2022, 13, 80. [Google Scholar]
- Famà, F.R.; Loreti, G.; Calabrò, G.; Ubertini, S.; Volpe, F.A.; Facci, A.L. An optimized power conversion system for a stellarator-based nuclear fusion power plant. Energy Convers. Manag. 2023, 276, 116572. [Google Scholar]
- Haque, M.M.; Wolfs, P.J.; Alahakoon, S.; Islam, M.A.; Nadarajah, M.; Zare, F.; Farrok, O. Three-Port Converters for Energy Conversion of PV-BES Integrated Systems—A Review. IEEE Access 2023, 11, 6551–6573. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Nandi, C. Advanced Energy Management System (A-EMS) Design of a Grid-Integrated Hybrid System. Iran. J. Sci. Technol. Trans. Electr. Eng. 2023, 47, 1021–1044. [Google Scholar] [CrossRef]
- Ahmadifar, A.; Ginocchi, M.; Golla, M.S.; Ponci, F.; Monti, A. Development of an Energy Management System for a Renewable Energy Community and Performance Analysis via Global Sensitivity Analysis. IEEE Access 2023, 11, 4131–4154. [Google Scholar] [CrossRef]
- Zeng, H.; Dai, J.; Zuo, C.; Chen, H.; Li, M.; Zhang, F. Correlation investigation of wind turbine multiple operating parameters based on SCADA data. Energies 2022, 15, 5280. [Google Scholar] [CrossRef]
- Cervero, D.; Fotopoulou, M.; Muñoz-Cruzado, J.; Rakopoulos, D.; Stergiopoulos, F.; Nikolopoulos, N.; Voutetakis, S.; Sanz, J.F. Solid State Transformers: A Critical Review of Projects with Relevant Prototypes and Demonstrators. Electronics 2023, 12, 931. [Google Scholar]
- Mollik, M.S.; Hannan, M.A.; Reza, M.S.; Abd Rahman, M.S.; Lipu, M.S.H.; Ker, P.J.; Mansor, M.; Muttaqi, K.M. The Advancement of Solid-State Transformer Technology and Its Operation and Control with Power Grids: A Review. Electronics 2022, 11, 2648. [Google Scholar] [CrossRef]
- Viswanathan, V.; Palaniswamy, L.N.; Leelavinodhan, P.B. Optimization techniques of battery packs using re-configurability: A review. J. Energy Storage 2019, 23, 404–415. [Google Scholar] [CrossRef]
- Abronzini, U.; Di Monaco, M.; Porpora, F.; Tomasso, G.; D’Arpino, M.; Attaianese, C. Thermal Management Optimization of a Passive BMS for Automotive Applications. In Proceedings of the 2019 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Turin, Italy, 2–4 July 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Cârstoiu, G.; Micea, M.V.; Ungurean, L.; Marcu, M. Novel battery wear leveling method for large-scale reconfigurable battery packs. Int. J. Energy Res. 2021, 45, 1932–1947. [Google Scholar] [CrossRef]
- Miniguano, H.; Barrado, A.; Lázaro, A.; Zumel, P.; Fernández, C. General Parameter Identification Procedure and Comparative Study of Li-Ion Battery Models. IEEE Trans. Veh. Technol. 2020, 69, 235–245. [Google Scholar] [CrossRef]
- Al-Refai, A.; Alkhateeb, A.; Dalala, Z.M. Enhancing the LCO 18,650 Battery Charging/Discharging Using Temperature and Electrical Based Model. Batteries 2022, 8, 199. [Google Scholar]
- Wu, X.; Li, S.; Gan, S.; Hou, C. An adaptive energy optimization method of hybrid battery-supercapacitor storage system for uncertain demand. Energies 2022, 15, 1765. [Google Scholar] [CrossRef]
- Gao, Y.; Lei, H. Semi-Empirical Ageing Model Development of Traction Battery; Chalmers University of Technology: Gothenburg, Sweden, 2023. [Google Scholar]
- Xu, W.; Cao, H.; Lin, X.; Shu, F.; Du, J.; Wang, J.; Tang, J. Data-Driven Semi-Empirical Model Approximation Method for Capacity Degradation of Retired Lithium-Ion Battery Considering SOC Range. Appl. Sci. 2023, 13, 11943. [Google Scholar] [CrossRef]
- Qingwei, Z.; Xiaoli, Y.; Qichao, W.; Yidan, X.; Fenfang, C. Semi-empirical degradation model of lithium-ion battery with high energy density. Energy Storage Sci. Technol. 2022, 11, 2324. [Google Scholar]
- Singh, P.; Chen, C.; Tan, C.M.; Huang, S.C. Semi-Empirical capacity fading model for SoH estimation of Li-Ion batteries. Appl. Sci. 2019, 9, 3012. [Google Scholar]
- Chen, D.; Meng, J.; Huang, H.; Wu, J.; Liu, P.; Lu, J.; Liu, T. An Empirical-Data Hybrid Driven Approach for Remaining Useful Life prediction of lithium-ion batteries considering capacity diving. Energy 2022, 245, 123222. [Google Scholar]
- Cui, F.; Li, Z.; Liu, C.; Shi, Y. A Data-Driven Hybrid Approach for Capacity Estimation on Lithium-ion Battery. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 5895–5898. [Google Scholar] [CrossRef]
- Ganesh, S.V.; D’Arpino, M. Critical Comparison of Li-Ion Aging Models for Second Life Battery Applications. Energies 2023, 16, 3023. [Google Scholar] [CrossRef]
- Naumann, M.; Schimpe, M.; Keil, P.; Hesse, H.C.; Jossen, A. Analysis and modeling of calendar aging of a commercial LiFePO4/graphite cell. J. Energy Storage 2018, 17, 153–169. [Google Scholar] [CrossRef]
- Hahn, S.L.; Storch, M.; Swaminathan, R.; Obry, B.; Bandlow, J.; Birke, K.P. Quantitative validation of calendar aging models for lithium-ion batteries. J. Power Sources 2018, 400, 402–414. [Google Scholar] [CrossRef]
- Hemi, H.; M’Sirdi, N.K.; Naamane, A. A new proposed shepherd model of a li-ion open circuit battery based on data fitting. In Proceedings of the IMAACA 2019, Lisbonne, Portugal, 18–20 September 2019. [Google Scholar]
- Campagna, N.; Castiglia, V.; Miceli, R.; Mastromauro, R.A.; Spataro, C.; Trapanese, M.; Viola, F. Battery models for battery powered applications: A comparative study. Energies 2020, 13, 4085. [Google Scholar]
- Raszmann, E.; Baker, K.; Shi, Y.; Christensen, D. Modeling stationary lithium-ion batteries for optimization and predictive control. In Proceedings of the 2017 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 23–24 February 2017; pp. 1–7. [Google Scholar]
- Moussa, S.; Ben Ghorbal, M.J. Shepherd Battery Model Parametrization for Battery Emulation in EV Charging Application. In Proceedings of the 2022 IEEE International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 26–28 October 2022; Volume 4, pp. 1–6. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, J.; Zheng, L. An Effective Method for Estimating State of Charge of Lithium-Ion Batteries Based on an Electrochemical Model and Nernst Equation. IEEE Access 2020, 8, 211738–211749. [Google Scholar] [CrossRef]
- Liu, X.T.; Qin, S.X.; He, Y.; Zheng, X.X.; Cao, C.R. SOC estimation of the lithium-ion battery with the temperature-based Nernst model. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1419–1422. [Google Scholar] [CrossRef]
- Liu, D.; Wang, X.; Zhang, M.; Gong, M. SOC Estimation of Lithium Battery Based on N-2RC Model in Electric Vehicle. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 2916–2921. [Google Scholar] [CrossRef]
- Chang, F.; Zheng, Z. An SOC estimation method based on sliding mode observer and the Nernst Equation. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 6187–6190. [Google Scholar] [CrossRef]
- Haeverbeke, M.V.; Stock, M.; De Baets, B. Equivalent Electrical Circuits and Their Use Across Electrochemical Impedance Spectroscopy Application Domains. IEEE Access 2022, 10, 51363–51379. [Google Scholar] [CrossRef]
- Ates, M.; Chebil, A. Supercapacitor and battery performances of multi-component nanocomposites: Real circuit and equivalent circuit model analysis. J. Energy Storage 2022, 53, 105093. [Google Scholar]
- Guo, R.; Shen, W. A review of equivalent circuit model based online state of power estimation for lithium-ion batteries in electric vehicles. Vehicles 2021, 4, 1–29. [Google Scholar]
- Dierickx, S.; Weber, A.; Ivers-Tiffée, E. How the distribution of relaxation times enhances complex equivalent circuit models for fuel cells. Electrochim. Acta 2020, 355, 136764. [Google Scholar] [CrossRef]
- Chaibi, Y.; Allouhi, A.; Malvoni, M.; Salhi, M.; Saadani, R. Solar irradiance and temperature influence on the photovoltaic cell equivalent-circuit models. Sol. Energy 2019, 188, 1102–1110. [Google Scholar] [CrossRef]
- Khayamy, M.; Nasiri, A.; Okoye, O. Development of an Equivalent Circuit for Batteries Based on a Distributed Impedance Network. IEEE Trans. Veh. Technol. 2020, 69, 6119–6128. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef]
- Liu, X.; Li, W.; Zhou, A. PNGV equivalent circuit model and SOC estimation algorithm for lithium battery pack adopted in AGV vehicle. IEEE Access 2018, 6, 23639–23647. [Google Scholar]
- Geng, Y.; Pang, H.; Liu, X. State-of-charge estimation for lithium-ion battery based on PNGV model and particle filter algorithm. J. Power Electron. 2022, 22, 1154–1164. [Google Scholar]
- Xia, B.; Ye, B.; Cao, J. Polarization Voltage Characterization of Lithium-Ion Batteries Based on a Lumped Diffusion Model and Joint Parameter Estimation Algorithm. Energies 2022, 15, 1150. [Google Scholar] [CrossRef]
- Xie, S.; Zhang, X.; Bai, W.; Guo, A.; Li, W.; Wang, R. State-of-Charge Estimation of Lithium-Ion Battery Based on an Improved Dual-Polarization Model. Energy Technol. 2023, 11, 2201364. [Google Scholar] [CrossRef]
- Barcellona, S.; Colnago, S.; Codecasa, L.; Piegari, L. Unified model of lithium-ion battery and electrochemical storage system. J. Energy Storage 2023, 73, 109202. [Google Scholar] [CrossRef]
- Cruz-Manzo, S.; Martínez-Zárate, I. Analytical transfer function for the simulation of the frequency-domain and time-domain responses of the blocked-diffusion Warburg impedance. J. Energy Storage 2023, 72, 108676. [Google Scholar] [CrossRef]
- Choudhury, B.; Jangale, A.; Suthar, B. Warburg Conductivity for Binary Electrolyte for Enabling Electrolyte Screening and Efficient Battery Operations. J. Electrochem. Soc. 2023, 170, 070519. [Google Scholar] [CrossRef]
- Xianrong, J.; Duan, X.; Jiang, W.; Wang, Y.; Zou, Y.; Lei, W.; Sun, L.; Ma, Z. Structural design of a composite board/heat pipe based on the coupled electro-chemical-thermal model in battery thermal management system. Energy 2021, 216, 119234. [Google Scholar]
- Duan, X.; Jiang, W.; Zou, Y.; Lei, W.; Ma, Z. A coupled electrochemical–thermal–mechanical model for spiral-wound Li-ion batteries. J. Mater. Sci. 2018, 53, 10987–11001. [Google Scholar] [CrossRef]
- Jin, X.; Duan, X. Investigate Thermodynamic and Kinetic Degradation of Lithium-Ion Batteries through a Combined Experimental and Modeling Approach. ECS Meet. Abstr. 2021, 239, 268. [Google Scholar] [CrossRef]
- Jin, X.; Duan, X. (Invited) Parameter Identification and Degradation Estimation of Li-Ion Batteries: Physics-Based Model and EIS Experimental Coupling. ECS Meeting Abstr. 2023, 243, 1648. [Google Scholar]
- Nascimento, R.G.; Viana, F.A.; Corbetta, M.; Kulkarni, C.S. A framework for Li-ion battery prognosis based on hybrid Bayesian physics-informed neural networks. Sci. Rep. 2023, 13, 13856. [Google Scholar] [CrossRef]
- Pugalenthi, K.; Park, H.; Hussain, S.; Raghavan, N. Remaining useful life prediction of lithium-ion batteries using neural networks with adaptive bayesian learning. Sensors 2022, 22, 3803. [Google Scholar]
- Zhang, S.; Liu, Z.; Su, H. A Bayesian Mixture Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2022, 8, 4708–4721. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Y.; Zhan, Y. Lithium battery state-of-charge estimation based on a Bayesian optimization bidirectional long short-term memory neural network. Energies 2022, 15, 4670. [Google Scholar] [CrossRef]
- Lin, Y.H.; Li, G.H. A Bayesian Deep Learning Framework for RUL Prediction Incorporating Uncertainty Quantification and Calibration. IEEE Trans. Ind. Inform. 2022, 18, 7274–7284. [Google Scholar] [CrossRef]
- Pei, H.; Si, X.S.; Hu, C.; Li, T.; He, C.; Pang, Z. Bayesian Deep-Learning-Based Prognostic Model for Equipment without Label Data Related to Lifetime. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 504–517. [Google Scholar] [CrossRef]
- Kim, M.; Han, S. Novel Data-Efficient Mechanism-Agnostic Capacity Fade Model for Li-Ion Batteries. IEEE Trans. Ind. Electron. 2021, 68, 6267–6275. [Google Scholar] [CrossRef]
- Pugalenthi, K.; Park, H.; Hussain, S.; Raghavan, N. Hybrid Particle Filter Trained Neural Network for Prognosis of Lithium-Ion Batteries. IEEE Access 2021, 9, 135132–135143. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, S.; Li, C.; Wu, L.; Wang, Y. A Data-Driven Method with Mode Decomposition Mechanism for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Power Electron. 2022, 37, 13684–13695. [Google Scholar] [CrossRef]
- Shateri, N.; Shi, Z.; Auger, D.J.; Fotouhi, A. Lithium-Sulfur Cell State of Charge Estimation Using a Classification Technique. IEEE Trans. Veh. Technol. 2021, 70, 212–224. [Google Scholar] [CrossRef]
- Cao, M.; Zhang, T.; Yu, B.; Liu, Y. A Method for Interval Prediction of Satellite Battery State of Health Based on Sample Entropy. IEEE Access 2019, 7, 141549–141561. [Google Scholar] [CrossRef]
- Zhu, J.; Tan, T.; Wu, L.; Yuan, H. RUL Prediction of Lithium-Ion Battery Based on Improved DGWO-ELM Method in a Random Discharge Rates Environment. IEEE Access 2019, 7, 125176–125187. [Google Scholar] [CrossRef]
- Crocioni, G.; Pau, D.; Delorme, J.M.; Gruosso, G. Li-Ion Batteries Parameter Estimation with Tiny Neural Networks Embedded on Intelligent IoT Microcontrollers. IEEE Access 2020, 8, 122135–122146. [Google Scholar] [CrossRef]
- Xiong, W.; Mo, Y.; Yan, C. Online State-of-Health Estimation for Second-Use Lithium-Ion Batteries Based on Weighted Least Squares Support Vector Machine. IEEE Access 2021, 9, 1870–1881. [Google Scholar] [CrossRef]
- Li, R.; Xu, S.; Li, S.; Zhou, Y.; Zhou, K.; Liu, X.; Yao, J. State of Charge Prediction Algorithm of Lithium-Ion Battery Based on PSO-SVR Cross Validation. IEEE Access 2020, 8, 10234–10242. [Google Scholar] [CrossRef]
- Vidal, C.; Malysz, P.; Kollmeyer, P.; Emadi, A. Machine Learning Applied to Electrified Vehicle Battery State of Charge and State of Health Estimation: State-of-the-Art. IEEE Access 2020, 8, 52796–52814. [Google Scholar] [CrossRef]
- Zhang, L.; Li, K.; Du, D.; Guo, Y.; Fei, M.; Yang, Z. A Sparse Learning Machine for Real-Time SOC Estimation of Li-ion Batteries. IEEE Access 2020, 8, 156165–156176. [Google Scholar] [CrossRef]
- Xue, K.; Yang, J.; Yang, M.; Wang, D. An Improved Generic Hybrid Prognostic Method for RUL Prediction Based on PF-LSTM Learning. IEEE Trans. Instrum. Meas. 2023, 72, 1–21. [Google Scholar] [CrossRef]
- Lai, C.M.; Kuo, T.J. Available Capacity Computation Model Based on Long Short-Term Memory Recurrent Neural Network for Gelled-Electrolyte Batteries in Golf Carts. IEEE Access 2022, 10, 54433–54444. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, G.; Xu, J.; Liu, Z.; Yan, X.; McCann, J.A. A Simplified Historical-Information-Based SOC Prediction Method for Supercapacitors. IEEE Trans. Ind. Electron. 2022, 69, 13090–13098. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Zhou, D.; Chen, M. State-of-Charge Estimation for Lead-Acid Battery Using Isolation Forest Algorithm and Long Short Term Memory Network with Attention Mechanism. IEEE Access 2023, 11, 49193–49204. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Lipu, M.S.H.; Ker, P.J.; Mansor, M.; Sahari, K.S.M.; Muttaqi, K.M. SOC Estimation Using Deep Bidirectional Gated Recurrent Units with Tree Parzen Estimator Hyperparameter Optimization. IEEE Trans. Ind. Appl. 2022, 58, 6629–6638. [Google Scholar] [CrossRef]
- Wang, X.; Hao, Z.; Chen, Z.; Zhang, J. Joint Prediction of Li-ion Battery State of Charge and State of Health Based on the DRSN-CW-LSTM Model. IEEE Access 2023, 11, 70263–70273. [Google Scholar] [CrossRef]
- Qin, Y.; Adams, S.; Yuen, C. Transfer Learning-Based State of Charge Estimation for Lithium-Ion Battery at Varying Ambient Temperatures. IEEE Trans. Ind. Inform. 2021, 17, 7304–7315. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Cao, Y.; Jiang, L.; Wan, J.; Rehtanz, C. An RNN with Small Sequence Trained by Multi-Level Optimization for SOC Estimation in Li-Ion Battery Applications. IEEE Trans. Veh. Technol. 2023, 72, 11469–11481. [Google Scholar] [CrossRef]
- Caliwag, A.C.; Lim, W. Hybrid VARMA and LSTM Method for Lithium-ion Battery State-of-Charge and Output Voltage Forecasting in Electric Motorcycle Applications. IEEE Access 2019, 7, 59680–59689. [Google Scholar] [CrossRef]
- Wei, M.; Ye, M.; Li, J.B.; Wang, Q.; Xu, X. State of Charge Estimation of Lithium-Ion Batteries Using LSTM and NARX Neural Networks. IEEE Access 2020, 8, 189236–189245. [Google Scholar] [CrossRef]
- Song, X.; Yang, F.; Wang, D.; Tsui, K.L. Combined CNN-LSTM Network for State-of-Charge Estimation of Lithium-Ion Batteries. IEEE Access 2019, 7, 88894–88902. [Google Scholar] [CrossRef]
- Ray, S. An analysis of computational complexity and accuracy of two supervised machine learning algorithms—K-nearest neighbor and support vector machine. In Proceedings of the Data Management, Analytics and Innovation: Proceedings of ICDMAI 2020, New Delhi, India, 17–19 January 2020; Springer: Berlin/Heidelberg, Germany, 2021; Volume 1, pp. 335–347. [Google Scholar]
- Chauhan, V.K.; Dahiya, K.; Sharma, A. Problem formulations and solvers in linear SVM: A review. Artif. Intell. Rev. 2019, 52, 803–855. [Google Scholar] [CrossRef]
- Li, J.; Ye, M.; Meng, W.; Xu, X.; Jiao, S. A Novel State of Charge Approach of Lithium Ion Battery Using Least Squares Support Vector Machine. IEEE Access 2020, 8, 195398–195410. [Google Scholar] [CrossRef]
- Bajaj, N.; Chiu, G.T.C.; Allebach, J.P. Reduction of memory footprint and computation time for embedded Support Vector Machine (SVM) by kernel expansion and consolidation. In Proceedings of the 2014 IEEE International Workshop on Machine Learning for Signal Processing (MLSP), Reims, France, 21–24 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Shi, D.; Zhao, J.; Wang, Z.; Zhao, H.; Eze, C.; Wang, J.; Lian, Y.; Burke, A.F. Cloud-Based Deep Learning for Co-Estimation of Battery State of Charge and State of Health. Energies 2023, 16, 3855. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wu, J.; Cheng, W.; Zhu, Q. SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output. Energy 2023, 262, 125375. [Google Scholar] [CrossRef]
- Shen, L.; Li, J.; Meng, L.; Zhu, L.; Shen, H.T. Transfer Learning-based State of Charge and State of Health Estimation for Li-ion Batteries: A Review. IEEE Trans. Transp. Electrif. 2023, 1. [Google Scholar] [CrossRef]
- Gao, Y.; Ji, W.; Zhao, X. SOC Estimation of E-Cell Combining BP Neural Network and EKF Algorithm. Processes 2022, 10, 1721. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, J.; Wang, Z.; Jiang, Y. Joint SOH-SOC estimation model for lithium-ion batteries based on GWO-BP neural network. Energies 2022, 16, 132. [Google Scholar] [CrossRef]
- Eleftheriadis, P.; Leva, S.; Ogliari, E. Bayesian hyperparameter optimization of stacked bidirectional long short-term memory neural network for the state of charge estimation. Sustain. Energy Grids Netw. 2023, 36, 101160. [Google Scholar] [CrossRef]
- Eleftheriadis, P.; Hegde, M.; Sohal, H.S.; Leva, S. Hyperband Optimization of Stacked Bidirectional Long Short-Term Memory Neural Network for the State of Charge Estimation. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Mohammadi, F. Lithium-ion battery State-of-Charge estimation based on an improved Coulomb-Counting algorithm and uncertainty evaluation. J. Energy Storage 2022, 48, 104061. [Google Scholar] [CrossRef]
- Huang, H.; Meng, J.; Wang, Y.; Feng, F.; Cai, L.; Peng, J.; Liu, T. A comprehensively optimized lithium-ion battery state-of-health estimator based on Local Coulomb Counting Curve. Appl. Energy 2022, 322, 119469. [Google Scholar] [CrossRef]
- Lee, J.; Won, J. Enhanced Coulomb Counting Method for SoC and SoH Estimation Based on Coulombic Efficiency. IEEE Access 2023, 11, 15449–15459. [Google Scholar] [CrossRef]
- Xiong, R.; Duan, Y.; Zhang, K.; Lin, D.; Tian, J.; Chen, C. State-of-charge estimation for onboard LiFePO4 batteries with adaptive state update in specific open-circuit-voltage ranges. Appl. Energy 2023, 349, 121581. [Google Scholar] [CrossRef]
- Sesidhar, D.; Badachi, C.; Green, R.C., II. A review on data-driven SOC estimation with Li-Ion batteries: Implementation methods & future aspirations. J. Energy Storage 2023, 72, 108420. [Google Scholar]
- Rey, S.O.; Romero, J.A.; Romero, L.T.; Martínez, À.F.; Roger, X.S.; Qamar, M.A.; Domínguez-García, J.L.; Gevorkov, L. Powering the future: A comprehensive review of battery energy storage systems. Energies 2023, 16, 6344. [Google Scholar]
- Zhou, Z.; Zhang, C. An Extended Kalman Filter Design for State-of-Charge Estimation Based on Variational Approach. Batteries 2023, 9, 583. [Google Scholar] [CrossRef]
- Liu, X.; Li, Q.; Wang, L.; Lin, M.; Wu, J. Data-Driven State of Charge Estimation for Power Battery with Improved Extended Kalman Filter. IEEE Trans. Instrum. Meas. 2023, 72, 1500910. [Google Scholar] [CrossRef]
- Lin, Q.; Li, X.; Tu, B.; Cao, J.; Zhang, M.; Xiang, J. Stable and Accurate Estimation of SOC Using eXogenous Kalman Filter for Lithium-Ion Batteries. Sensors 2023, 23, 467. [Google Scholar] [CrossRef]
- Shi, D.; Zhao, J.; Eze, C.; Wang, Z.; Wang, J.; Lian, Y.; Burke, A.F. Cloud-Based Artificial Intelligence Framework for Battery Management System. Energies 2023, 16, 4403. [Google Scholar] [CrossRef]
- Marques, T.M.B.; dos Santos, J.L.F.; Castanho, D.S.; Ferreira, M.B.; Stevan, S.L., Jr.; Illa Font, C.H.; Antonini Alves, T.; Piekarski, C.M.; Siqueira, H.V.; Corrêa, F.C. An Overview of Methods and Technologies for Estimating Battery State of Charge in Electric Vehicles. Energies 2023, 16, 5050. [Google Scholar]
- Tian, J.; Chen, C.; Shen, W.; Sun, F.; Xiong, R. Deep learning framework for lithium-ion battery state of charge estimation: Recent advances and future perspectives. Energy Storage Mater. 2023, 61, 102883. [Google Scholar]
- Yang, F.; Shi, D.; Mao, Q.; Lam, K.H. Scientometric research and critical analysis of battery state-of-charge estimation. J. Energy Storage 2023, 58, 106283. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).