Evaluating the Aging-Induced Voltage Slippery as Cause for Float Currents of Lithium-ion Cells
Abstract
:1. Introduction
2. Materials and Methods
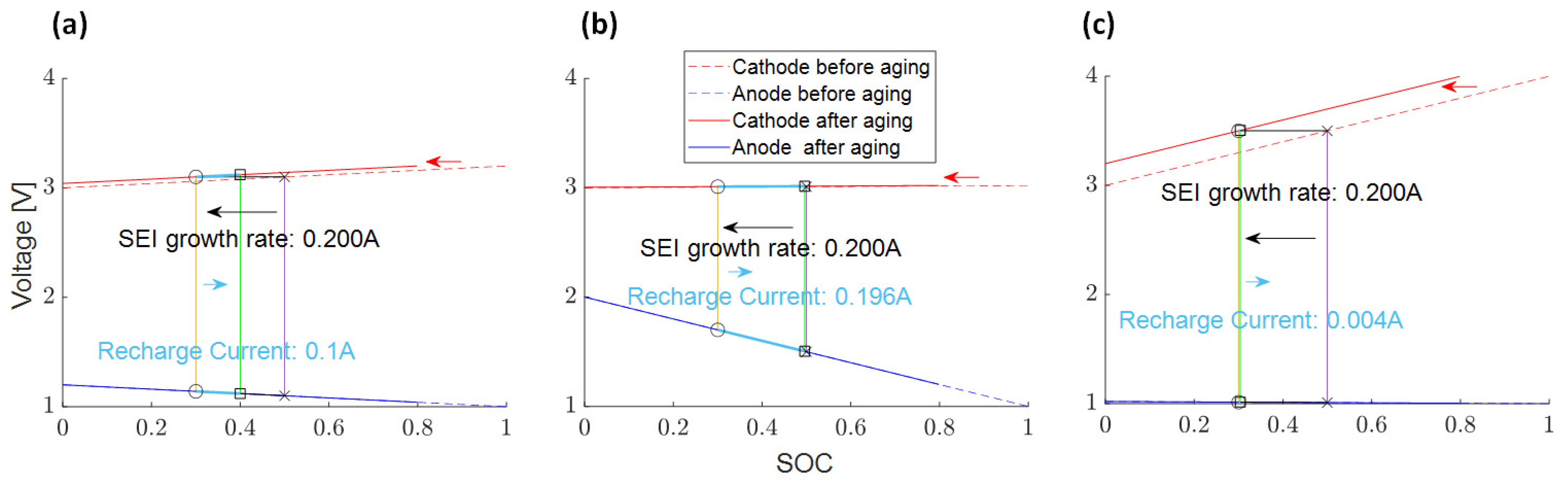
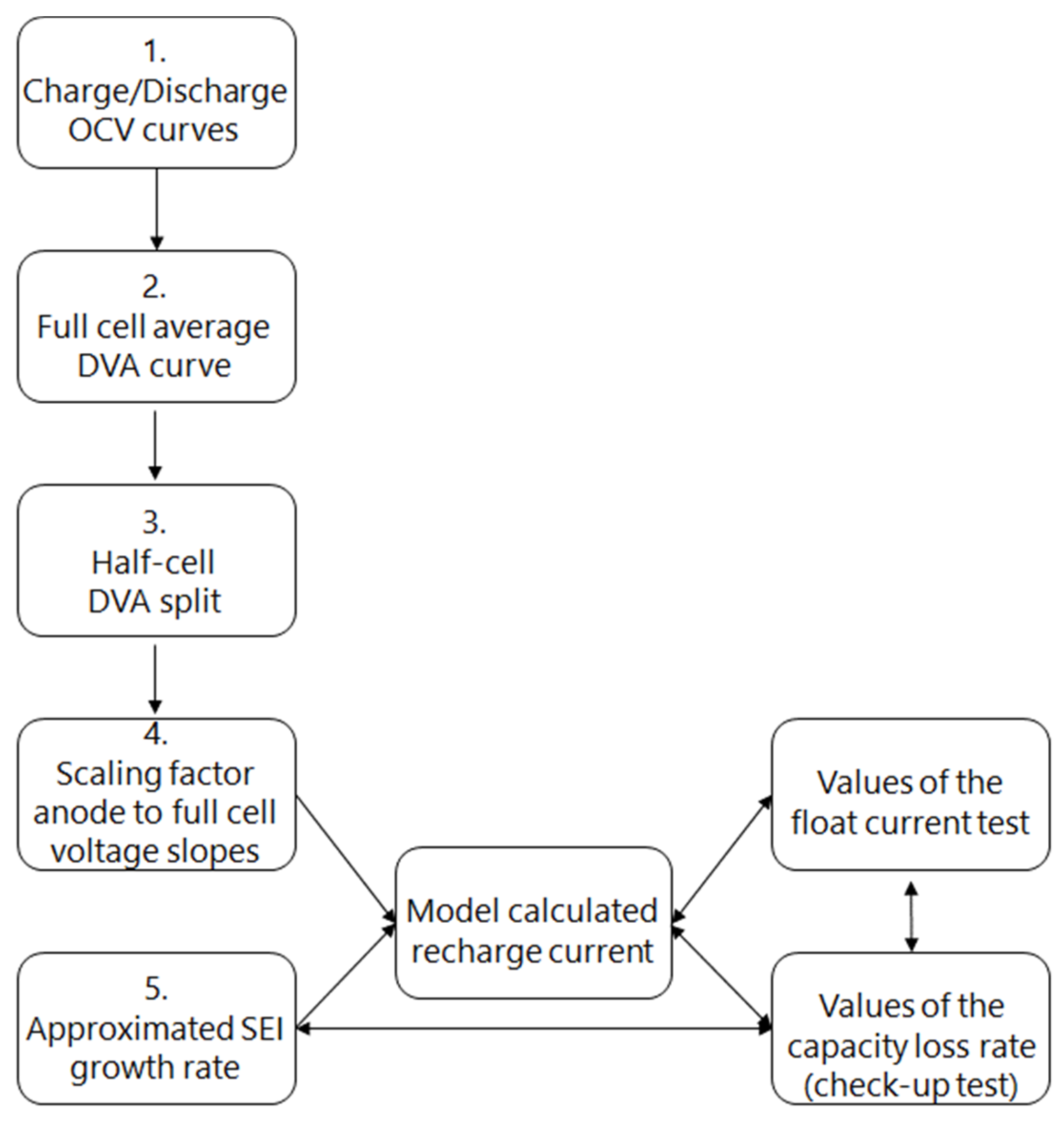
Recharge Current Induced by Voltage Slippery and SEI Growth
3. Results and Discussion
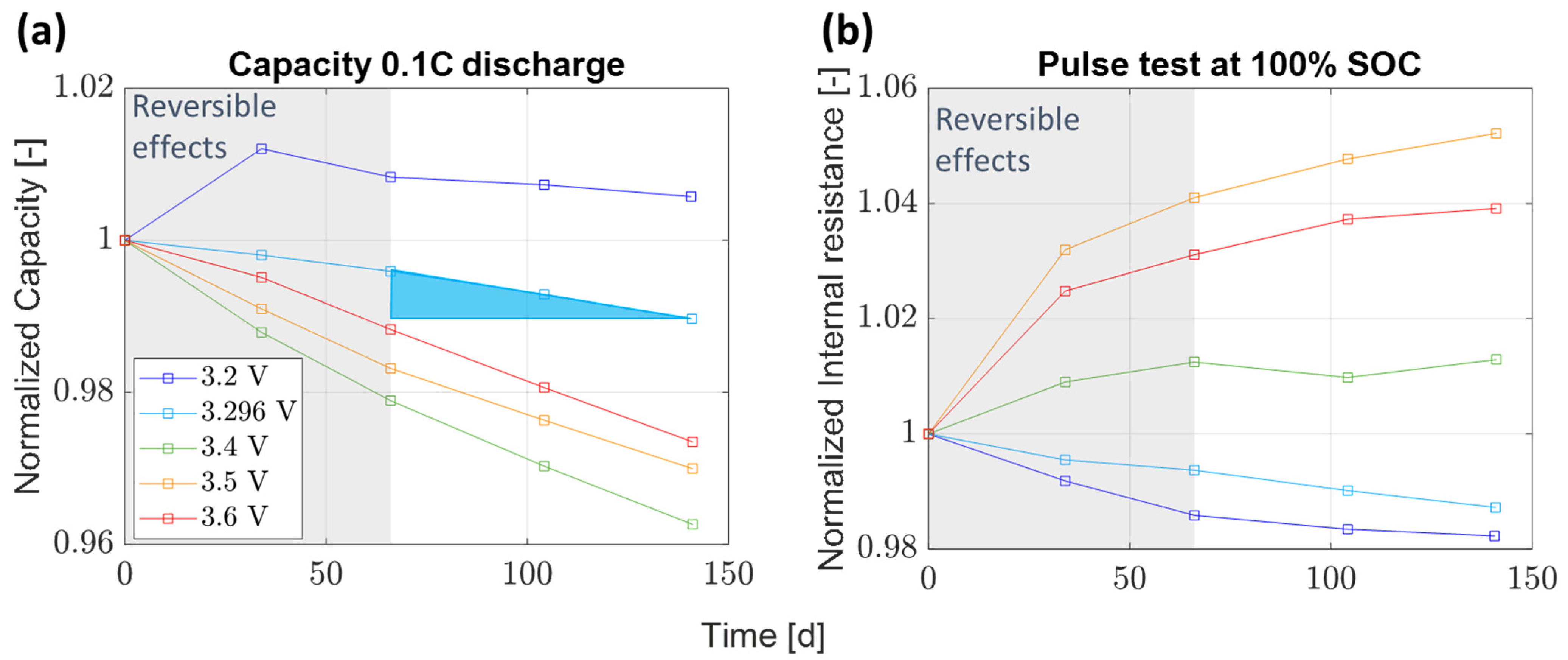
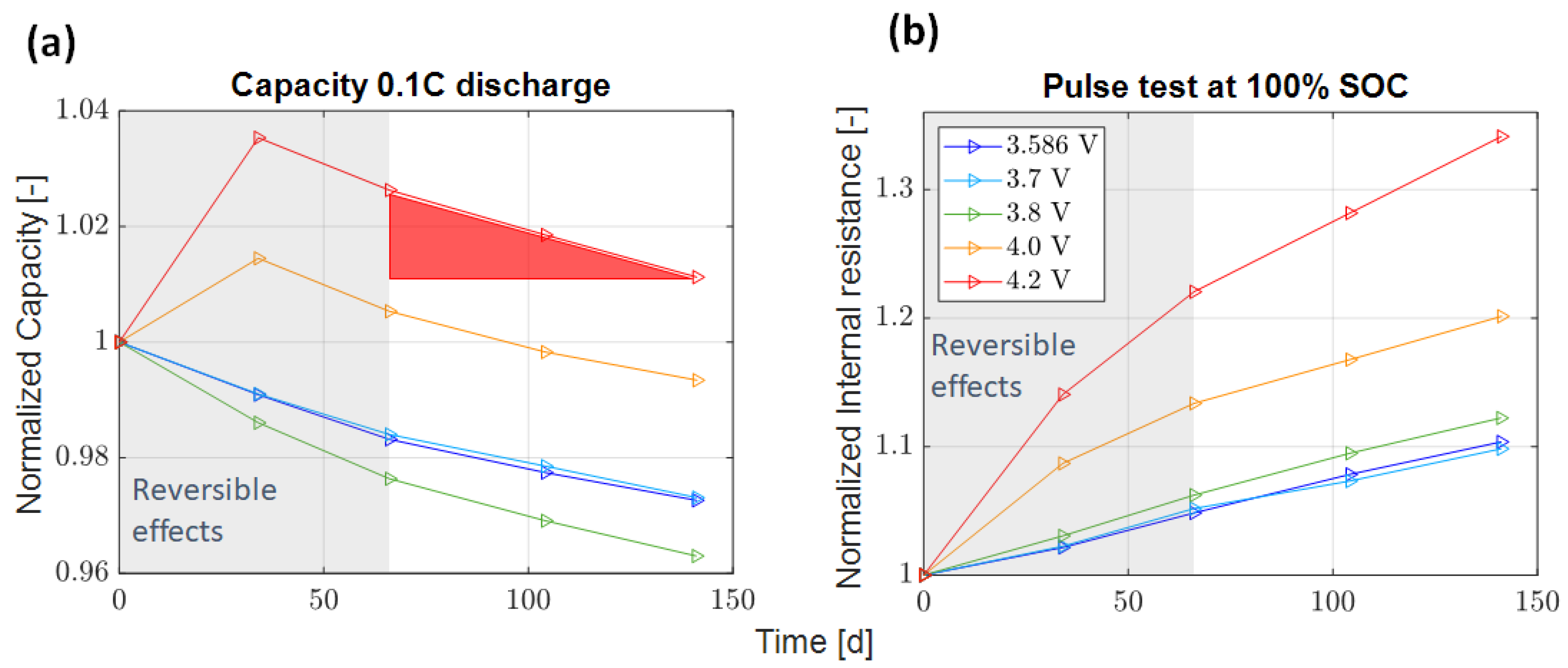
3.1. Capacity Loss Rate and Pulse Resistance
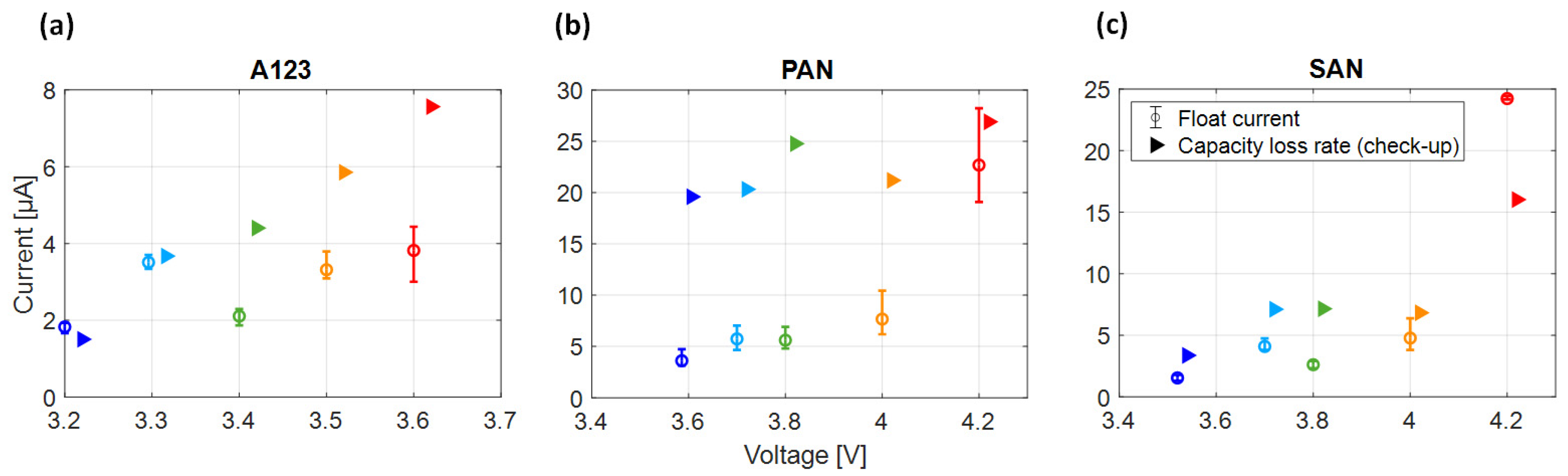
3.2. Correlation between Float Current and the Capacity Loss Rate in Check-Ups
3.3. SEI Growth as the Main Calendar Aging Mechanism
3.4. Model Development for the Voltage Slippery Application
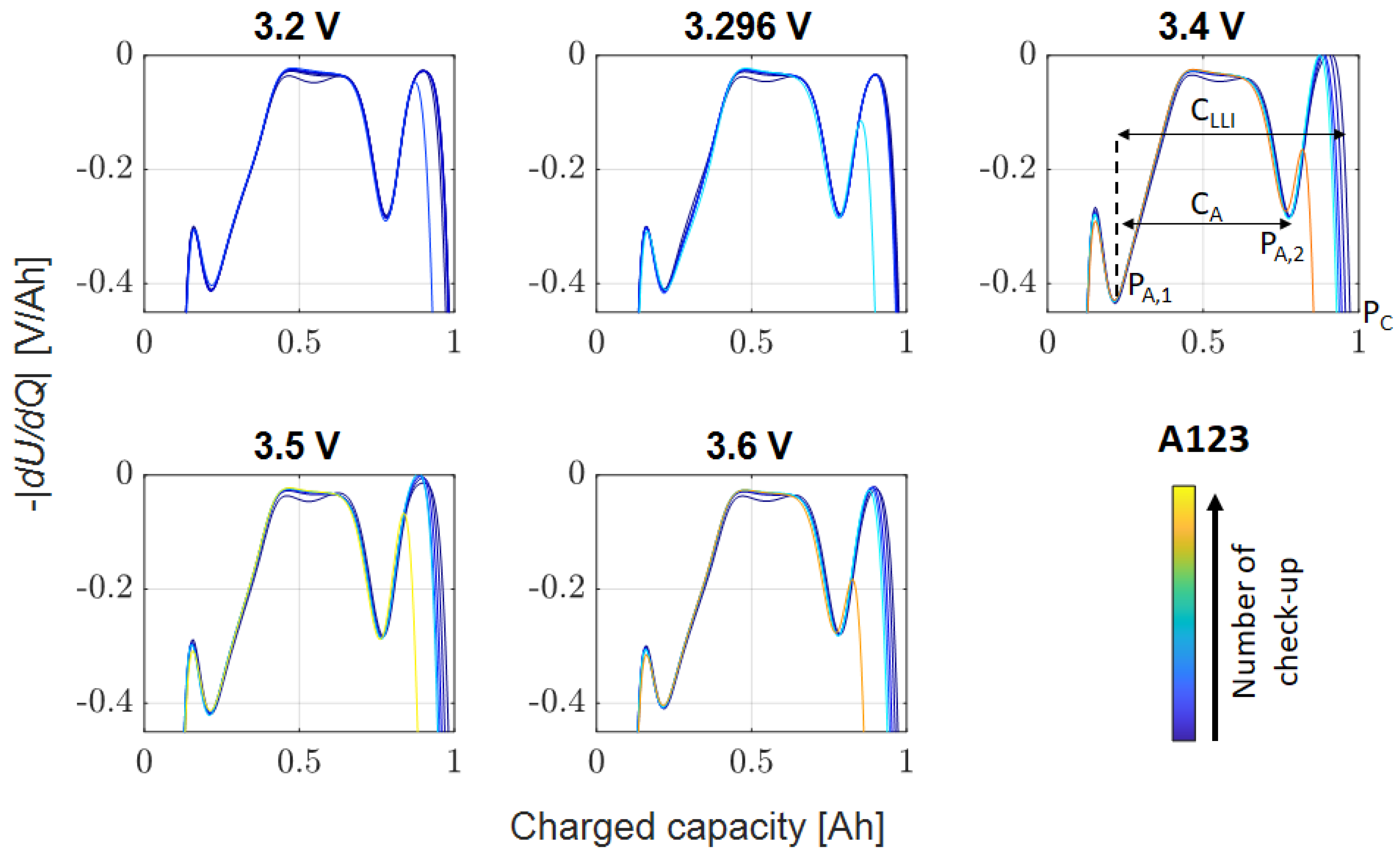
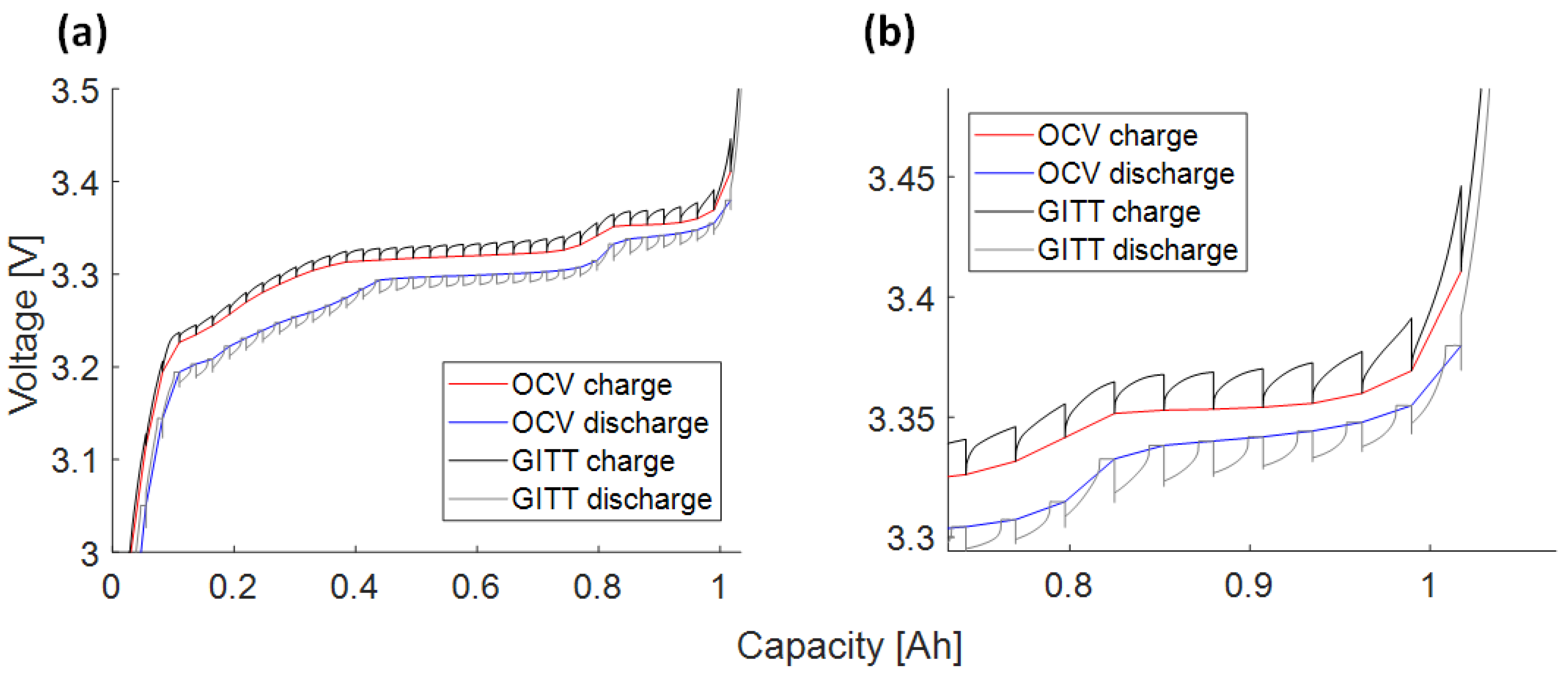
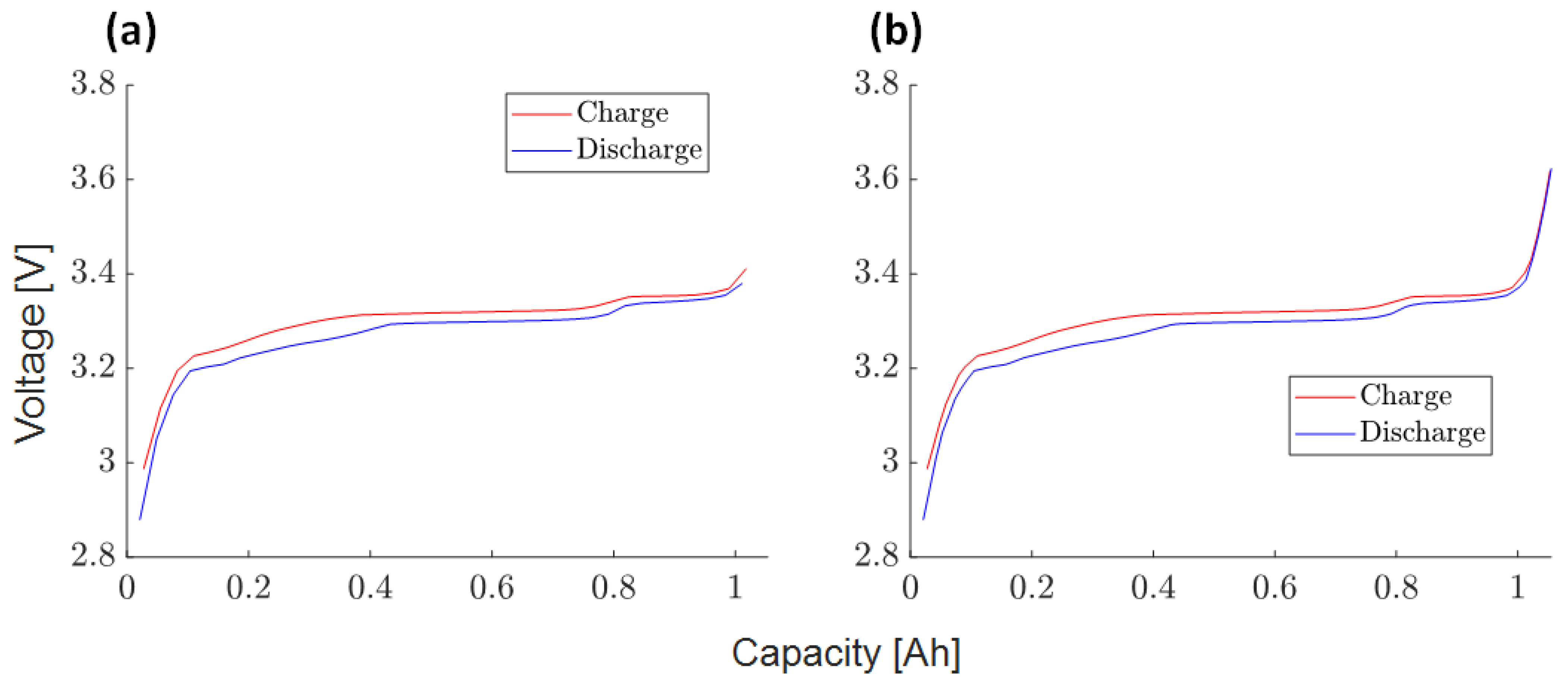
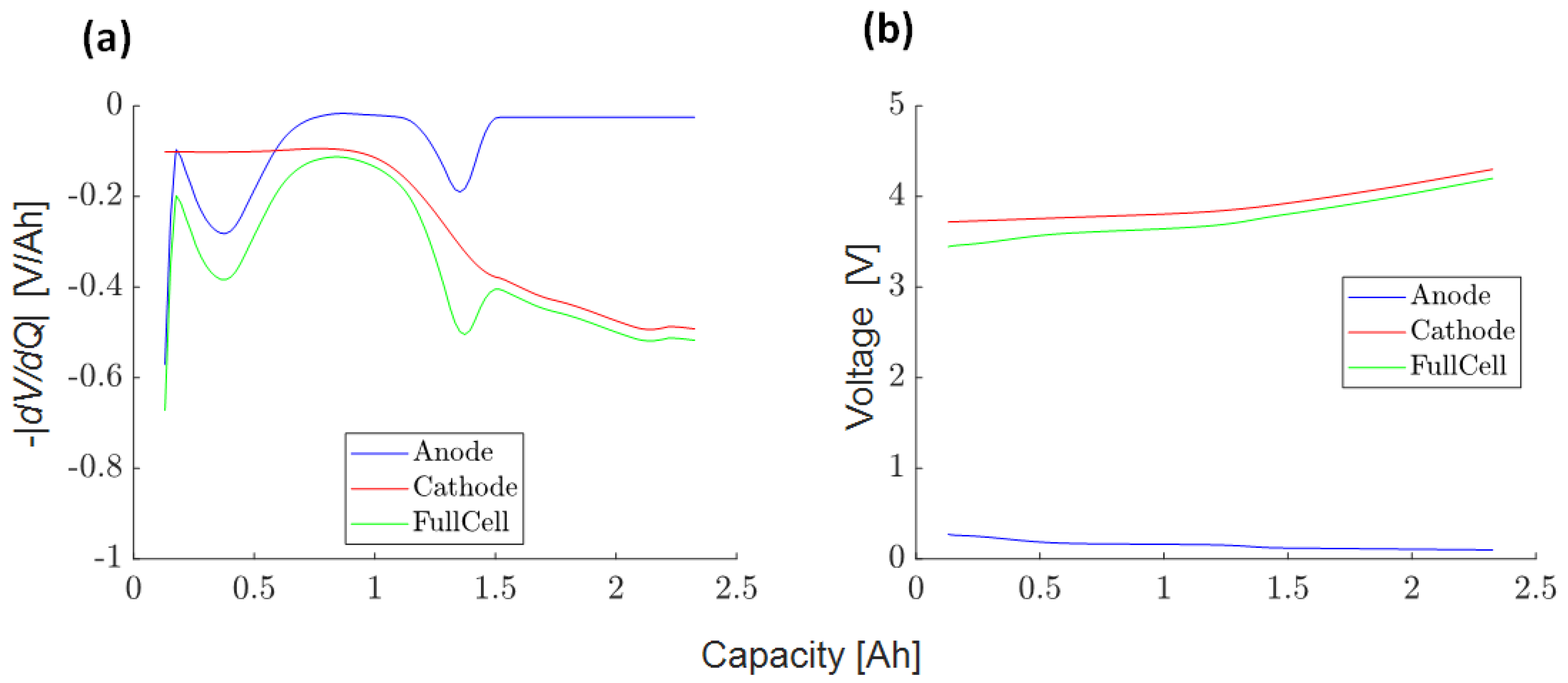
3.4.1. Charge/Discharge OCV Curves (1)
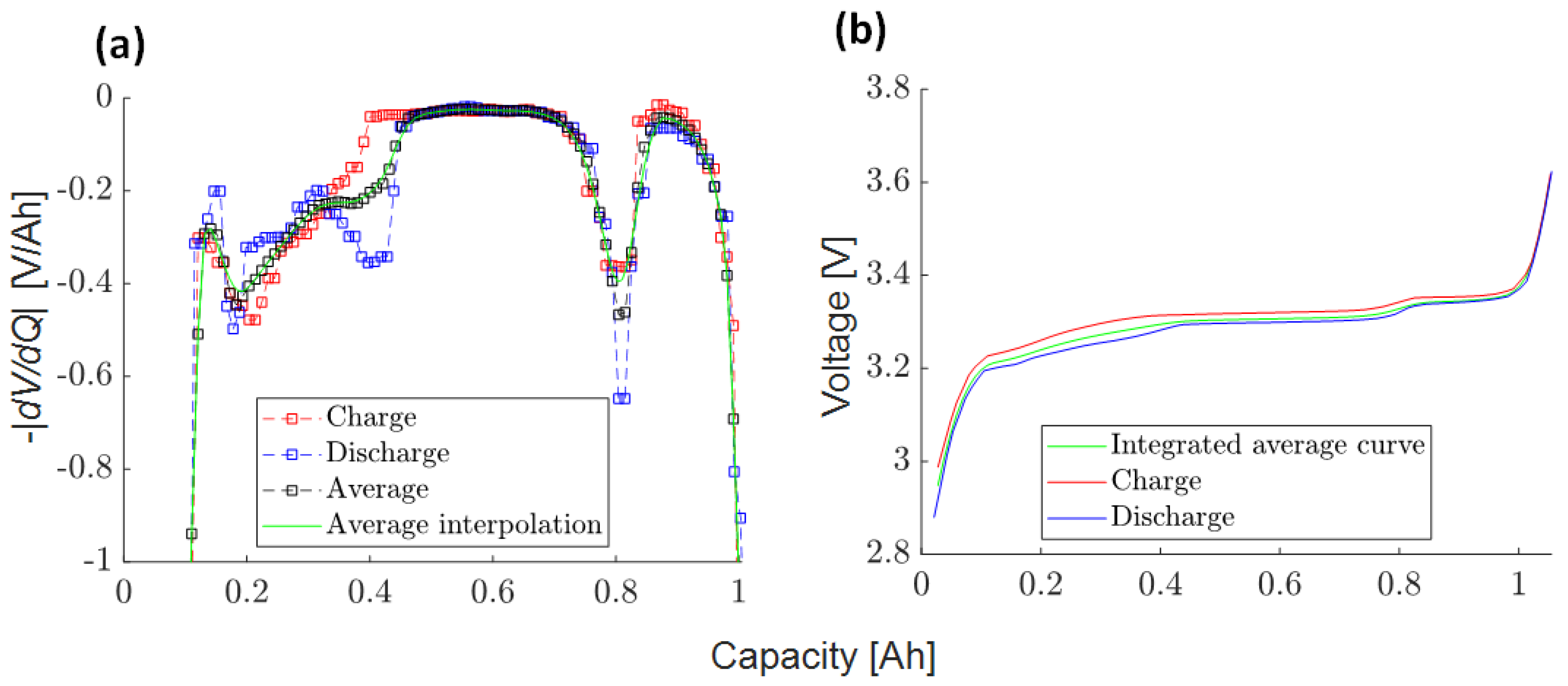
3.4.2. Full Cell Average DVA Curve (2)
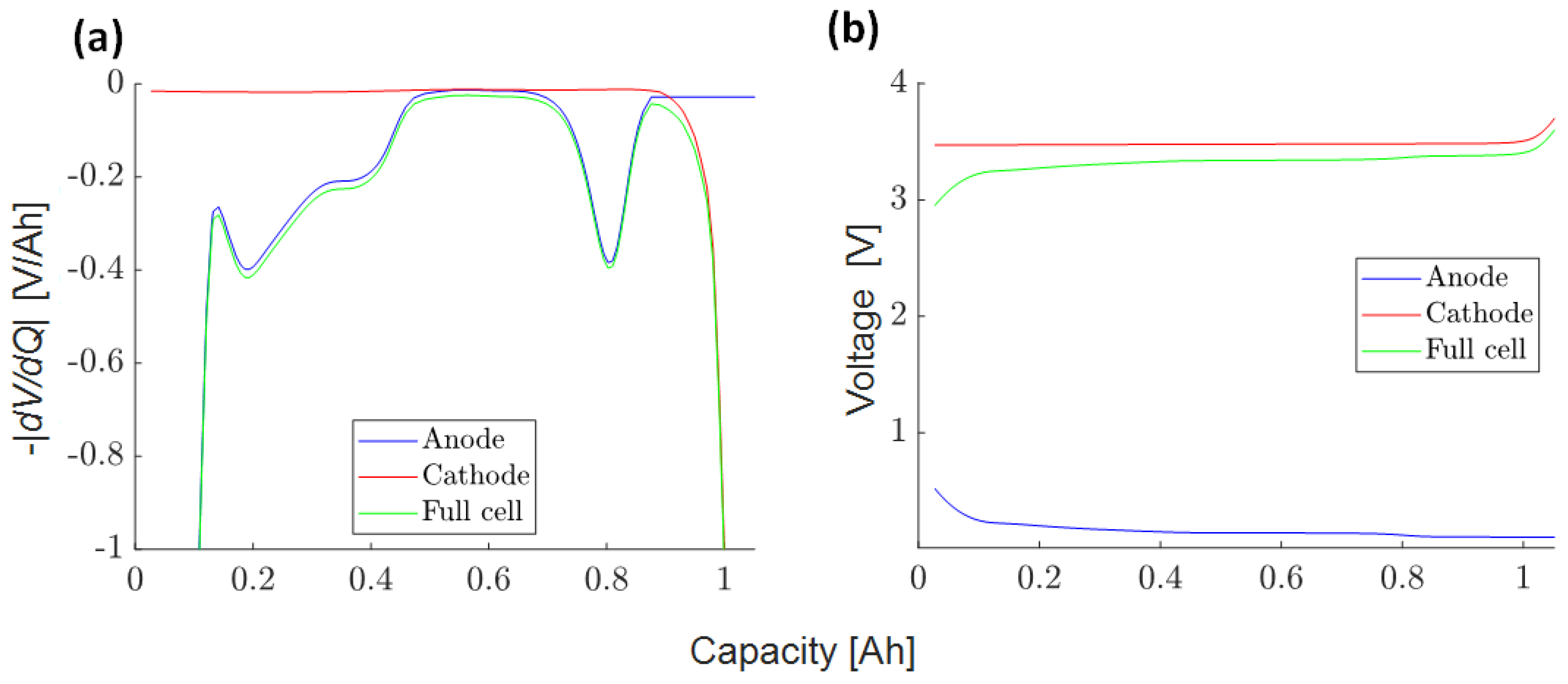
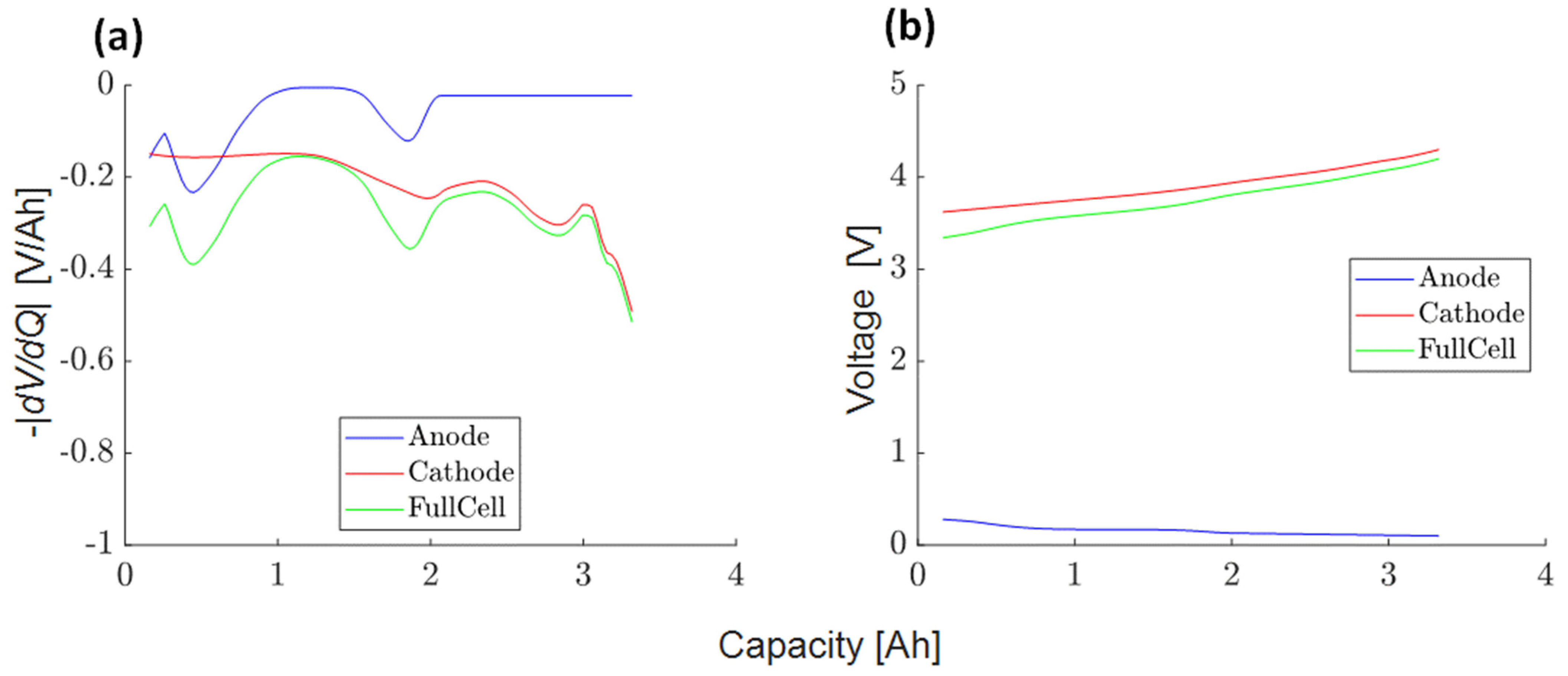
3.4.3. Half-Cell DVA Split (3)
3.4.4. Scaling Factor Anode to Full-Cell Voltage Slopes (4)
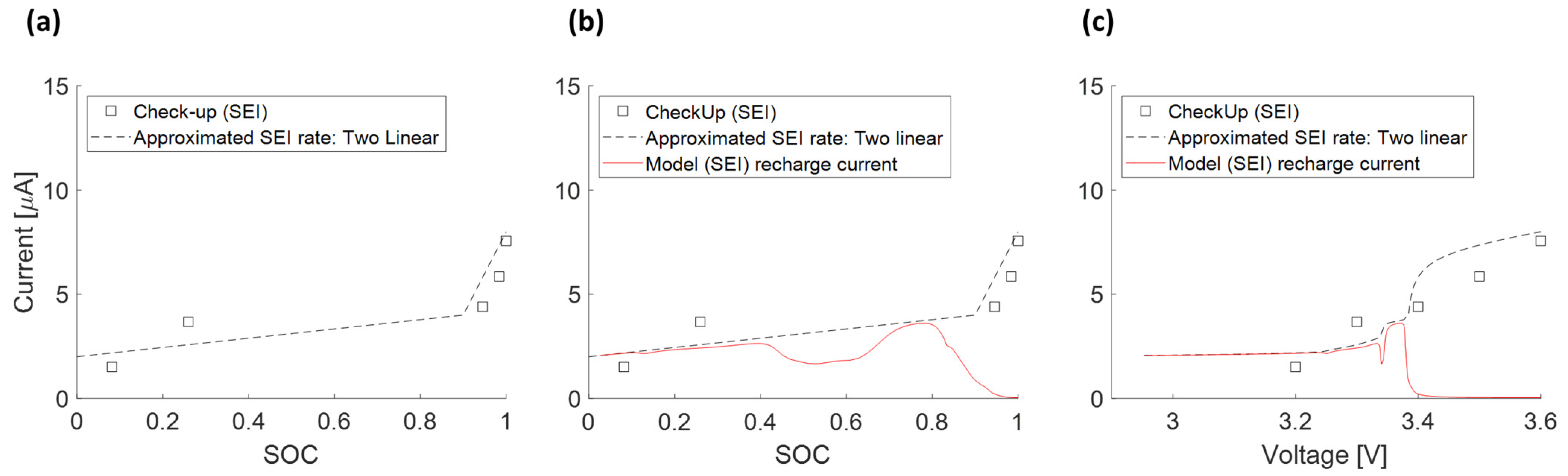
3.4.5. Approximated SEI Growth Rate (5)
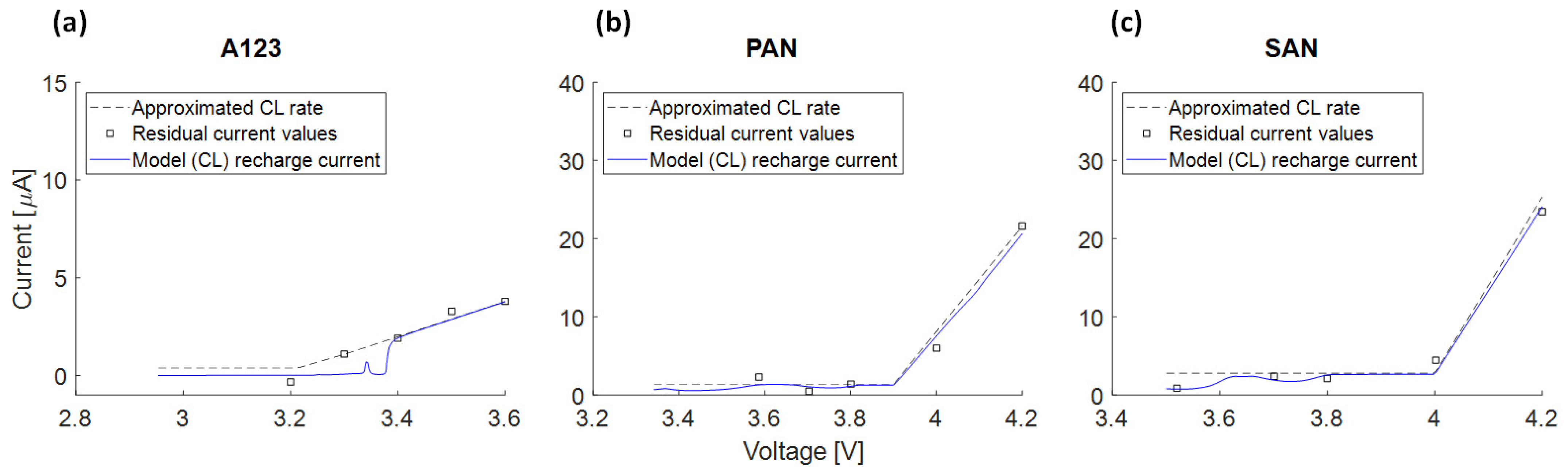
3.4.6. Recharge Current due to SEI Growth and Measured Float Current
3.5. Float Currents Trends over Temperature Steps
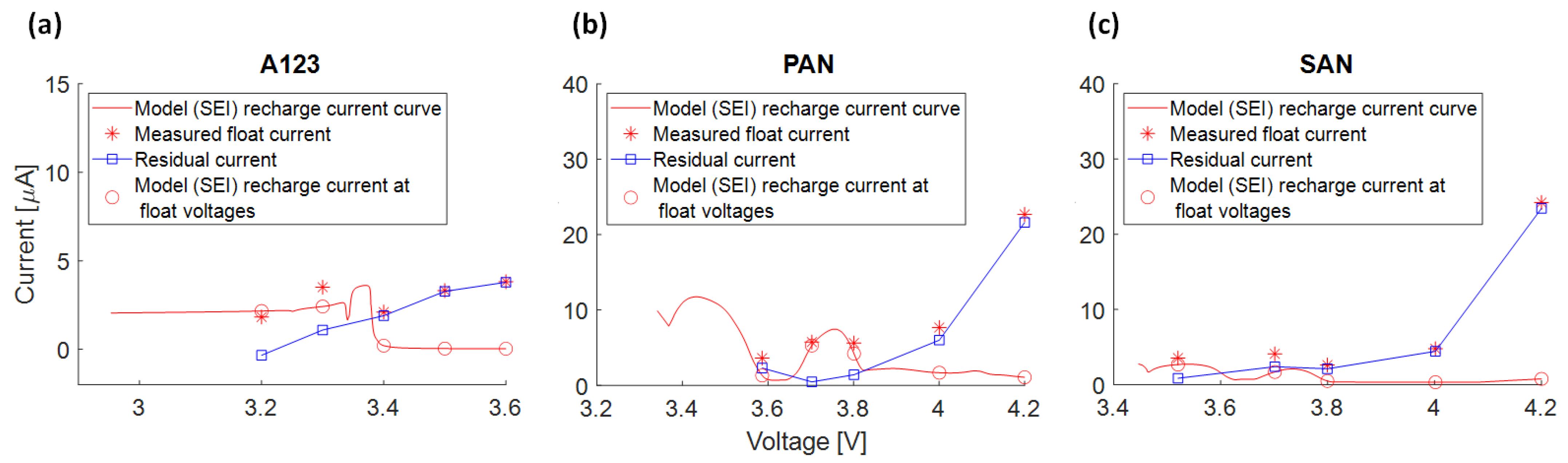
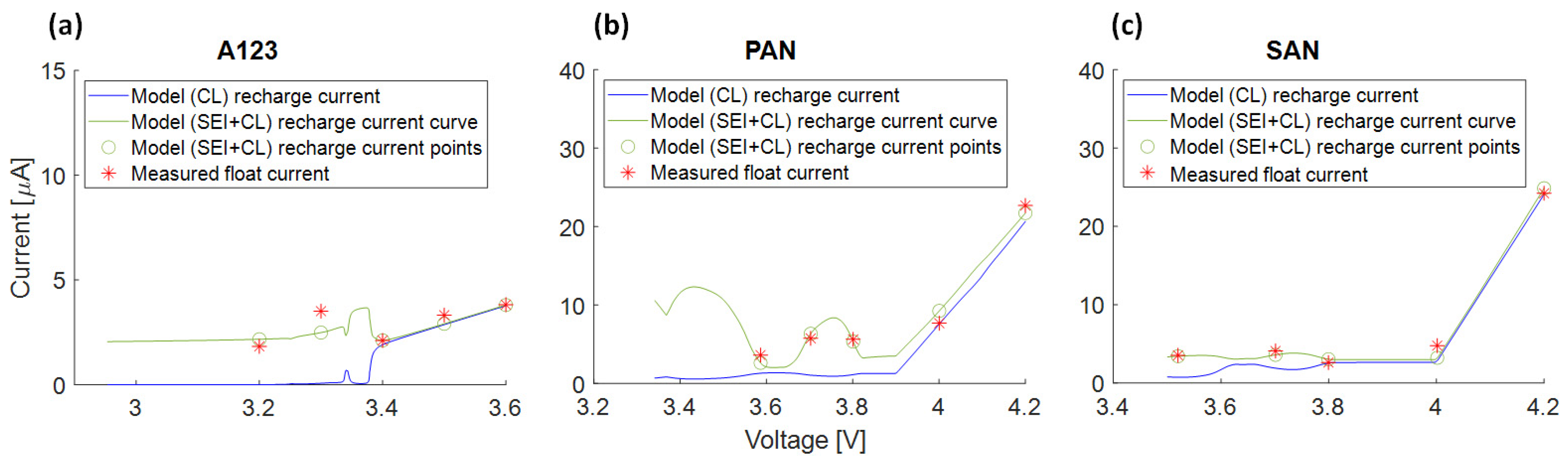
3.6. Interpretation Approach of Additional Effects Explaining the Residual Current
- Float currents and capacity loss rates align for specific voltages and cell types, with float current values consistently equal to or lower than the capacity loss rate (except for SAN at 4.2 V).
- The voltage slippery model, triggered by SEI loss current, cannot fully explain float currents, especially at higher cell voltages. This is due to the low anode voltage slope compared to the full cell.
- The higher capacities observed at high voltages during the 1st and 2nd check-up suggest an effect leading to increased capacities at higher cell voltages.
- General float current trends are comparable at 30 °C and 60 °C, indicating similar underlying effects.
Integration of Cathode Lithiation in the Voltage Slippery Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix
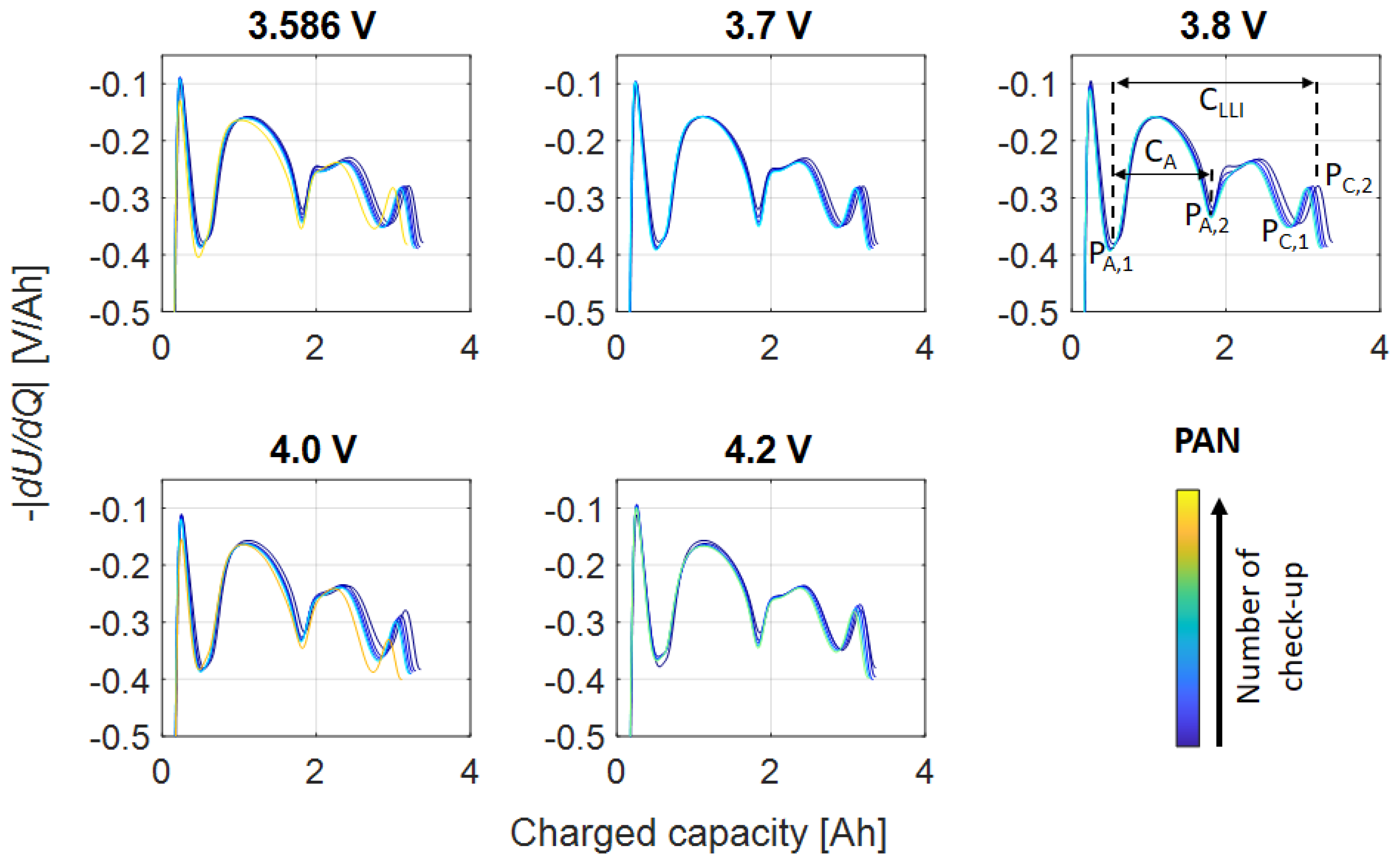
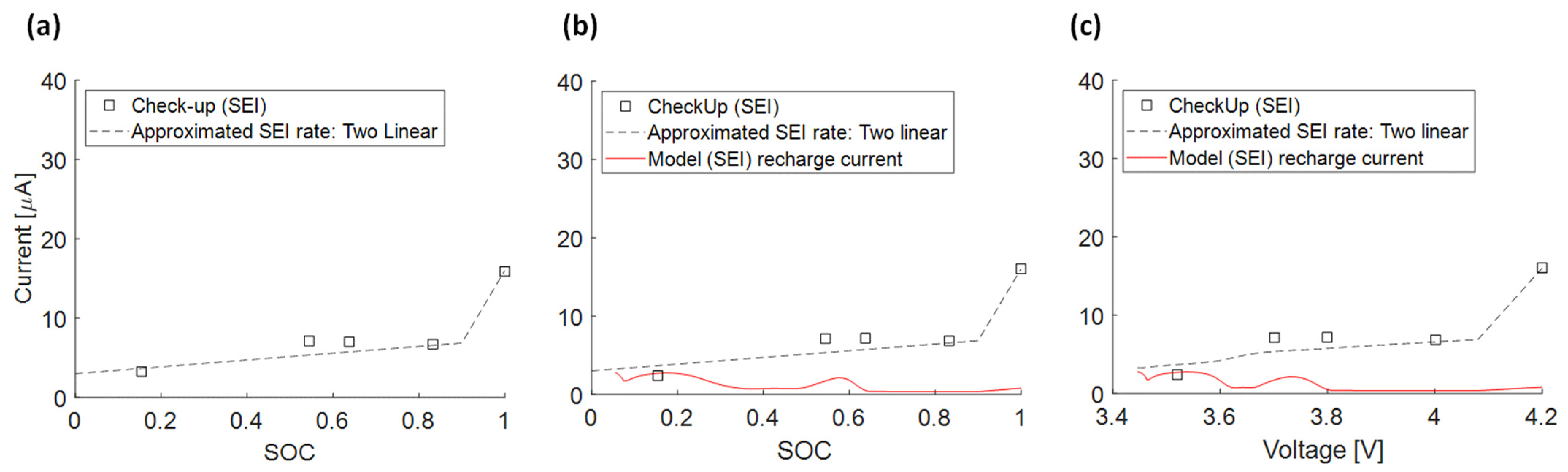
Appendix A.1. PAN

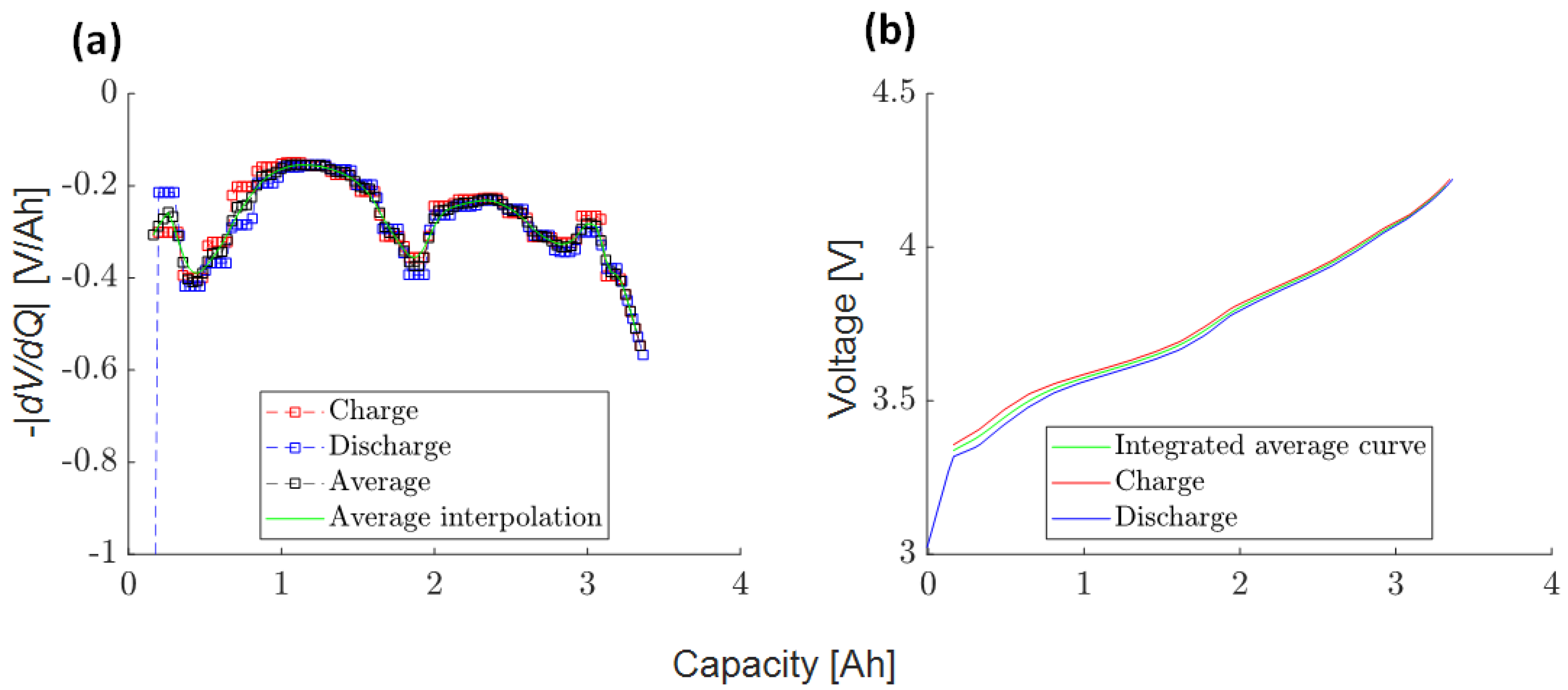
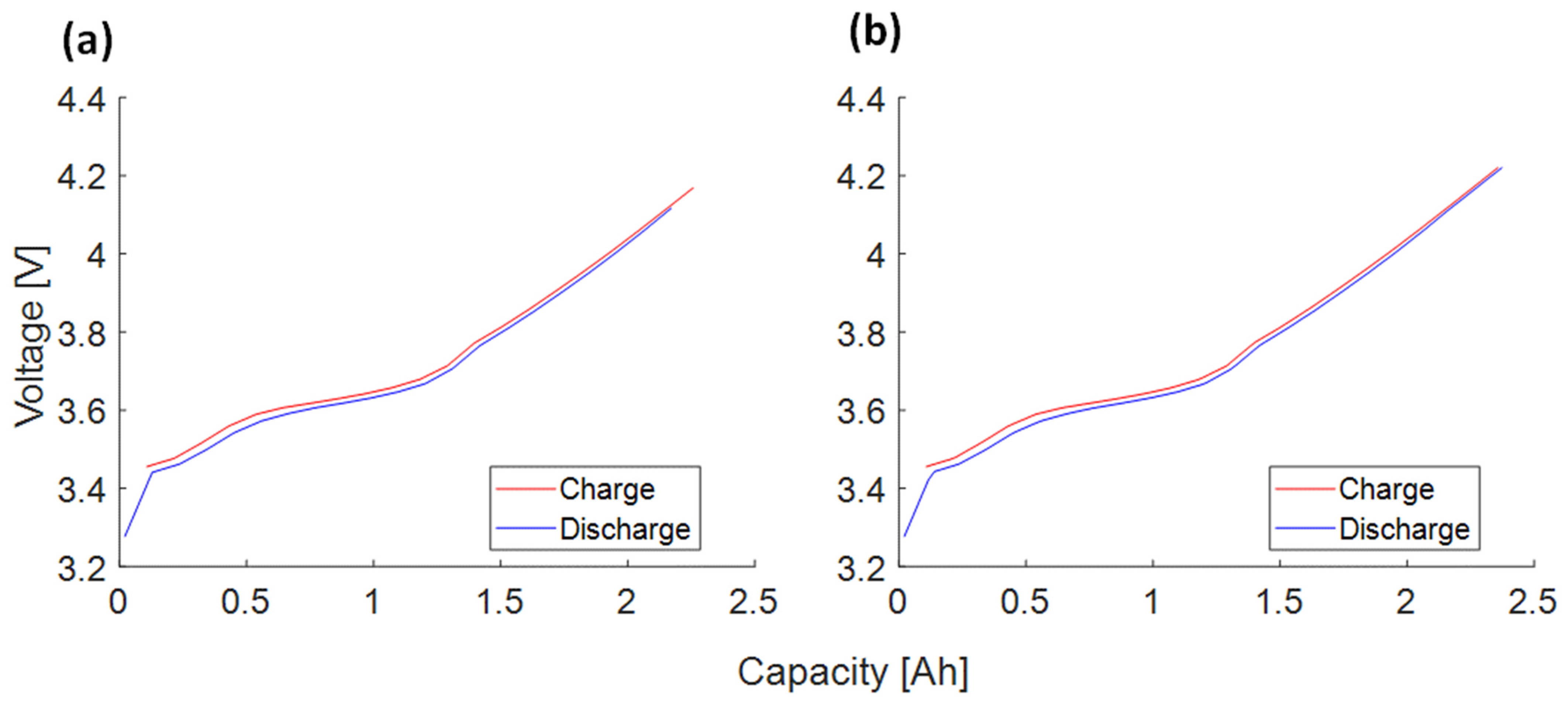
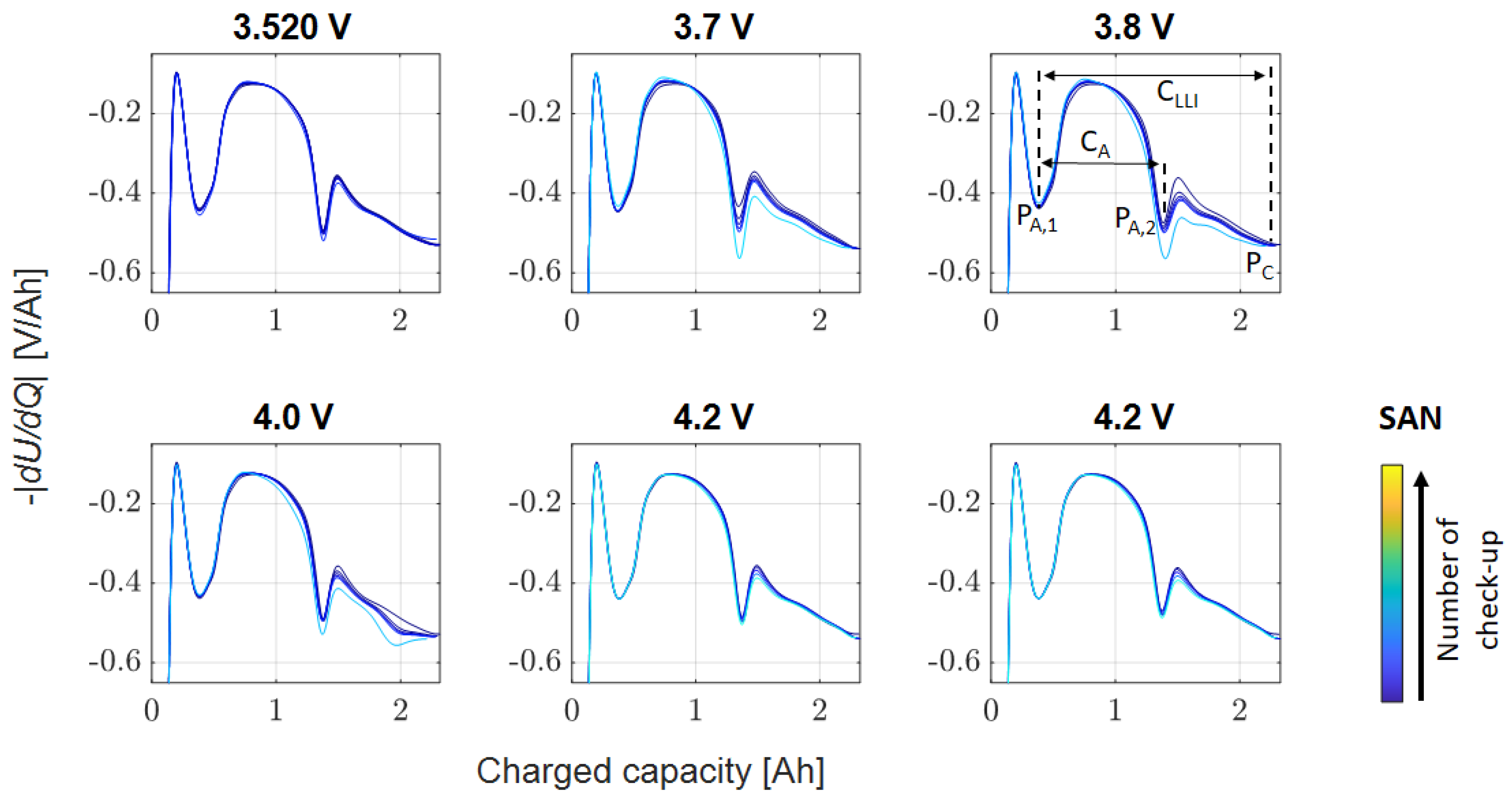
Appendix A.2. SAN
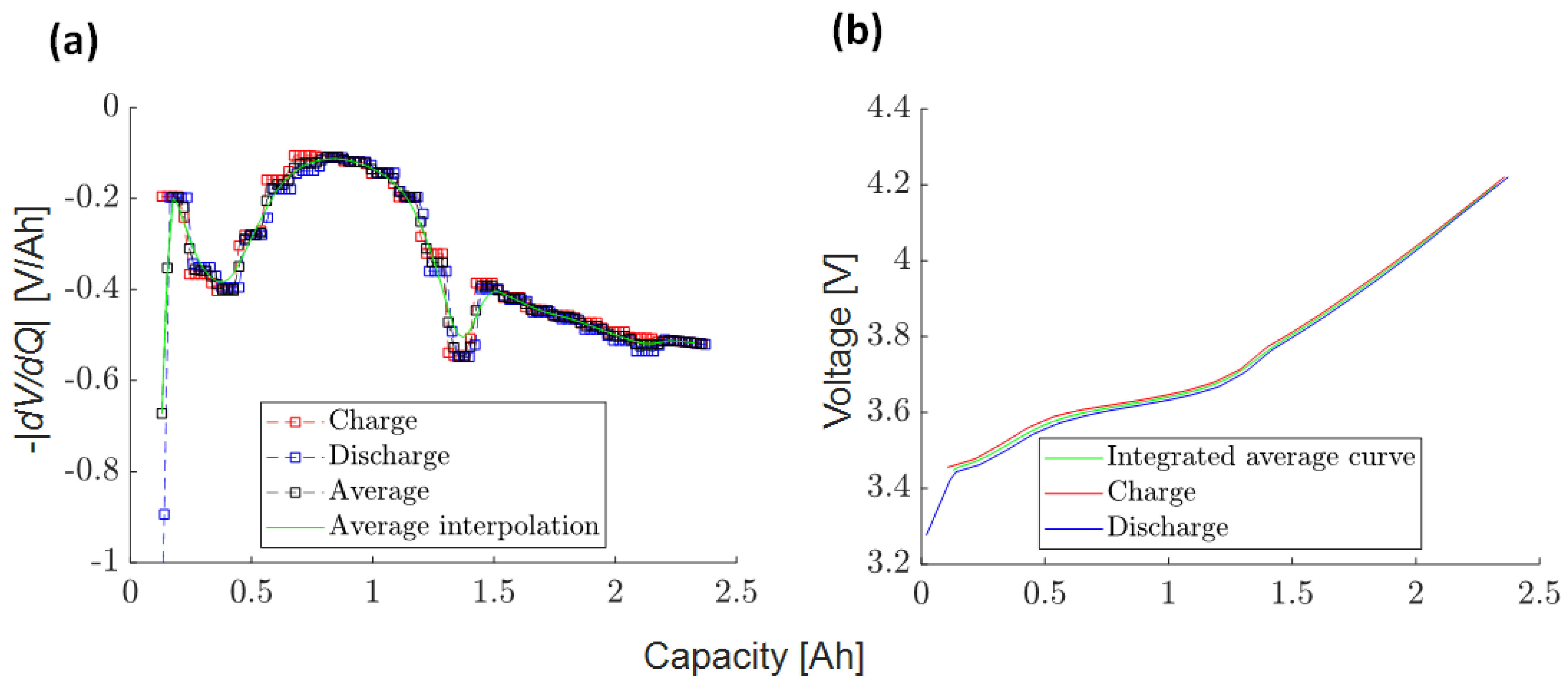
References
- Johnen, M.; Pitzen, S.; Kamps, U.; Kateri, M.; Dechent, P.; Sauer, D.U. Modeling long-term capacity degradation of lithium-ion batteries. J. Energy Storage 2021, 34, 102011. [Google Scholar] [CrossRef]
- Marquis, S.G. Long-Term Degration of Lithium-Ion Batteries. Ph.D. Thesis, St Anne’s College, University of Oxford, Oxford, UK, 2020. [Google Scholar]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Kassem, M.; Delacourt, C. Postmortem analysis of calendar-aged graphite/LiFePO4 cells. J. Power Sources 2013, 235, 159–171. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Naumann, M.; Schimpe, M.; Keil, P.; Hesse, H.C.; Jossen, A. Analysis and modeling of calendar aging of a commercial LiFePO4/graphite cell. J. Energy Storage 2018, 17, 153–169. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Sources 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Mingant, R.; Bernard, J.; Sauvant Moynot, V.; Delaille, A.; Mailley, S.; Hognon, J.-L.; Huet, F. EIS Measurements for Determining the SoC and SoH of Li-Ion Batteries. ECS Trans. 2011, 33, 41–53. [Google Scholar] [CrossRef]
- Keil, P.; Schuter, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Katl, R.C.; Jossen, A. Calendar Aging of Lithium-Ion Batteries: I. Impact of the Graphite Anode on Capacity Fade. J. Electrochem. Soc. 2016, 163, A1872–A1880. [Google Scholar] [CrossRef]
- Jalkanen, K.; Karppinen, J.; Skogström, L.; Laurila, T.; Nisula, M.; Vuorilehto, K. Cycle aging of commercial NMC/graphite pouch cells at different temperatures. Appl. Energy 2015, 154, 160–172. [Google Scholar] [CrossRef]
- Guan, T.; Sun, S.; Gao, Y.; Du, C.; Zuo, P.; Cui, Y.; Zhang, L.; Yin, G. The effect of elevated temperature on the accelerated aging of LiCoO2/mesocarbon microbeads batteries. Appl. Energy 2016, 177, 1–10. [Google Scholar] [CrossRef]
- Lewerenz, M.; Käbitz, S.; Knips, M.; Münnix, J.; Schmalstieg, J.; Warnecke, A.; Sauer, D.U. New method evaluating currents keeping the voltage constant for fast and highly resolved measurement of Arrhenius relation and capacity fade. J. Power Sources 2017, 353, 144–151. [Google Scholar] [CrossRef]
- Theiler, M.; Endisch, C.; Lewerenz, M. Float Current Analysis for Fast Calendar Aging Assessment of 18650 Li(NiCoAl)O2/Graphite Cells. Batteries 2021, 7, 22. [Google Scholar] [CrossRef]
- Käbitz, S.; Gerschler, J.B.; Ecker, M.; Yurdagel, Y.; Emmermacher, B.; André, D.; Mitsch, T.; Sauer, D.U. Cycle and calendar life study of a graphite|LiNi1/3Mn1/3Co1/3O2 Li-ion high energy system. Part A: Full cell characterization. J. Power Sources 2013, 239, 572–583. [Google Scholar] [CrossRef]
- Streck, L.; Roth, T.; Keil, P.; Strehle, B.; Ludmann, S.; Jossen, A. A Comparison of Voltage Hold and Voltage Decay Methods for Side Reactions Characterization. J. Electrochem. Soc. 2023, 170, 40520. [Google Scholar] [CrossRef]
- Belov, D.; Yang, M.-H. Failure mechanism of Li-ion battery at overcharge conditions. J. Solid State Electrochem. 2008, 12, 885–894. [Google Scholar] [CrossRef]
- Azzam, M.; Ehrensberger, M.; Scheuer, R.; Endisch, C.; Lewerenz, M. Long-Term Self-Discharge Measurements and Modelling for Various Cell Types and Cell Potentials. Energies 2023, 16, 3889. [Google Scholar] [CrossRef]
- Gyenes, B.; Stevens, D.A.; Chevrier, V.L.; Dahn, J.R. Understanding Anomalous Behavior in Coulombic Efficiency Measurements on Li-Ion Batteries. J. Electrochem. Soc. 2015, 162, A278–A283. [Google Scholar] [CrossRef]
- Zilberman, I.; Sturm, J.; Jossen, A. Reversible self-discharge and calendar aging of 18650 nickel-rich, silicon-graphite lithium-ion cells. J. Power Sources 2019, 425, 217–226. [Google Scholar] [CrossRef]
- Lewerenz, M.; Münnix, J.; Schmalstieg, J.; Käbitz, S.; Knips, M.; Sauer, D.U. Systematic aging of commercial LiFePO4|Graphite cylindrical cells including a theory explaining rise of capacity during aging. J. Power Sources 2017, 345, 254–263. [Google Scholar] [CrossRef]
- Roth, T.; Streck, L.; Graule, A.; Niehoff, P.; Jossen, A. Relaxation Effects in Self-Discharge Measurements of Lithium-Ion Batteries. J. Electrochem. Soc. 2023, 170, 20502. [Google Scholar] [CrossRef]
- Schulze, M.C.; Rodrigues, M.-T.F.; McBrayer, J.D.; Abraham, D.P.; Apblett, C.A.; Bloom, I.; Chen, Z.; Colclasure, A.M.; Dunlop, A.R.; Fang, C.; et al. Critical Evaluation of Potentiostatic Holds as Accelerated Predictors of Capacity Fade during Calendar Aging. J. Electrochem. Soc. 2022, 169, 50531. [Google Scholar] [CrossRef]
- Deutschen, T.; Gasser, S.; Schaller, M.; Siehr, J. Modeling the self-discharge by voltage decay of a NMC/graphite lithium-ion cell. J. Energy Storage 2018, 19, 113–119. [Google Scholar] [CrossRef]
- Jannesari, H.; Emami, M.D.; Ziegler, C. Effect of electrolyte transport properties and variations in the morphological parameters on the variation of side reaction rate across the anode electrode and the aging of lithium ion batteries. J. Power Sources 2011, 196, 9654–9664. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Rodriguez-Martinez, L.M.; Villarreal, I. Calendar ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions. J. Power Sources 2014, 272, 45–57. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Martinez-Laserna, E.; Berecibar, M.; Gandiaga, I.; Rodriguez-Martinez, L.M.; Villarreal, I. Realistic lifetime prediction approach for Li-ion batteries. Appl. Energy 2016, 162, 839–852. [Google Scholar] [CrossRef]
- Vermeer, W.; Chandra Mouli, G.R.; Bauer, P. A Comprehensive Review on the Characteristics and Modeling of Lithium-Ion Battery Aging. IEEE Trans. Transp. Electrific. 2022, 8, 2205–2232. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef]
- German, F.; Hintennach, A.; LaCroix, A.; Thiemig, D.; Oswald, S.; Scheiba, F.; Hoffmann, M.J.; Ehrenberg, H. Influence of temperature and upper cut-off voltage on the formation of lithium-ion cells. J. Power Sources 2014, 264, 100–107. [Google Scholar] [CrossRef]
- Weppner, W.; Huggins, R.A. Electrochemical Methods for Determining Kinetic Properties of Solids. Annu. Rev. Mater. Sci. 1978, 8, 269–311. [Google Scholar] [CrossRef]
- Knap, V.; Stroe, D.-I. Effects of open-circuit voltage tests and models on state-of-charge estimation for batteries in highly variable temperature environments: Study case nano-satellites. J. Power Sources 2021, 498, 229913. [Google Scholar] [CrossRef]
- Barai, A.; Widanage, W.D.; Marco, J.; McGordon, A.; Jennings, P. A study of the open circuit voltage characterization technique and hysteresis assessment of lithium-ion cells. J. Power Sources 2015, 295, 99–107. [Google Scholar] [CrossRef]
- Marongiu, A.; Nußbaum, F.G.W.; Waag, W.; Garmendia, M.; Sauer, D.U. Comprehensive study of the influence of aging on the hysteresis behavior of a lithium iron phosphate cathode-based lithium ion battery—An experimental investigation of the hysteresis. Appl. Energy 2016, 171, 629–645. [Google Scholar] [CrossRef]
- Roscher, M.A.; Bohlen, O.; Vetter, J. OCV Hysteresis in Li-Ion Batteries including Two-Phase Transition Materials. Int. J. Electrochem. 2011, 2011, 984320. [Google Scholar] [CrossRef]
- Simolka, M.; Heger, J.-F.; Traub, N.; Kaess, H.; Friedrich, K.A. Influence of Cycling Profile, Depth of Discharge and Temperature on Commercial LFP/C Cell Ageing: Cell Level Analysis with ICA, DVA and OCV Measurements. J. Electrochem. Soc. 2020, 167, 110502. [Google Scholar] [CrossRef]
- Safari, M.; Delacourt, C. Aging of a Commercial Graphite/LiFePO4 Cell. J. Electrochem. Soc. 2011, 158, A1123. [Google Scholar] [CrossRef]
- Ando, K.; Matsuda, T.; Imamura, D. Degradation diagnosis of lithium-ion batteries with a LiNi0.5Co0.2Mn0.3O2 and LiMn2O4 blended cathode using dV/dQ curve analysis. J. Power Sources 2018, 390, 278–285. [Google Scholar] [CrossRef]
- Fath, J.P.; Dragicevic, D.; Bittel, L.; Nuhic, A.; Sieg, J.; Hahn, S.; Alsheimer, L.; Spier, B.; Wetzel, T. Quantification of aging mechanisms and inhomogeneity in cycled lithium-ion cells by differential voltage analysis. J. Energy Storage 2019, 25, 100813. [Google Scholar] [CrossRef]
- Yoon, T.; Milien, M.S.; Parimalam, B.S.; Lucht, B.L. Thermal Decomposition of the Solid Electrolyte Interphase (SEI) on Silicon Electrodes for Lithium Ion Batteries. Chem. Mater. 2017, 29, 3237–3245. [Google Scholar] [CrossRef]
- Sahore, R.; O’Hanlon, D.C.; Tornheim, A.; Lee, C.-W.; Garcia, J.C.; Iddir, H.; Balasubramanian, M.; Bloom, I. Revisiting the Mechanism Behind Transition-Metal Dissolution from Delithiated LiNixMnyCozO2 (NMC) Cathodes. J. Electrochem. Soc. 2020, 167, 20513. [Google Scholar] [CrossRef]
- Eldesoky, A.; Logan, E.R.; Johnson, M.B.; McFarlane, C.R.M.; Dahn, J.R. Scanning Micro X-ray Fluorescence (μXRF) as an Effective Tool in Quantifying Fe Dissolution in LiFePO4 Cells: Towards a Mechanistic Understanding of Fe Dissolution. J. Electrochem. Soc. 2020, 167, 130539. [Google Scholar] [CrossRef]
- Ruff, Z.; Xu, C.; Grey, C.P. Transition Metal Dissolution and Degradation in NMC811-Graphite Electrochemical Cells. J. Electrochem. Soc. 2021, 168, 60518. [Google Scholar] [CrossRef]
- Wen, J.; Yu, Y.; Chen, C. A Review on Lithium-Ion Batteries Safety Issues: Existing Problems and Possible Solutions. Mater. Express 2012, 2, 197–212. [Google Scholar] [CrossRef]
- Boetticher, T.; Adamson, A.; Buechele, S.; Alter, E.D.; Metzger, M. Understanding the Self-Discharge Redox Shuttle Mechanism of Dimethyl Terephthalate in Lithium-Ion Batteries. J. Electrochem. Soc. 2023, 170, 60507. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Calendar Aging of NCA Lithium-Ion Batteries Investigated by Differential Voltage Analysis and Coulomb Trackin. J. Electrochem. Soc. 2017, 164, A6066–A6074. [Google Scholar] [CrossRef]






| Short Name | A123 | PAN | SAN |
| Producer | A123 | Panasonic | Sanyo |
| Cell type | APR18650M-A1 | NCR18650B | UR18650AAN |
| Cathode | LFP: LiFePO4 | NCA: Li(Ni0.81Co0.16Al0.03)O2 | NMC: Li(NixMnyCoz)O2 |
| Anode | Graphite | Graphite | Graphite |
| Nom. capacity | 1.1 Ah | 3.2 Ah | 2.15 Ah |
| Nom. voltage | 3.3 V | 3.6 V | 3.6 V |
| Storage voltage (SOC) before test | 3.296 V (26%) | 3.586 V (28%) | 3.520 V (14%) |
| Examined float voltages | 3.2 V, 3.296 V, 3.4 V, 3.5 V, 3.6 V | 3.586 V, 3.7 V, 3.8 V, 4.0 V, 4.2 V | 3.520 V, 3.7 V 3.8 V, 4.0 V, 4.2 V, 4.2 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azzam, M.; Endisch, C.; Lewerenz, M. Evaluating the Aging-Induced Voltage Slippery as Cause for Float Currents of Lithium-ion Cells. Batteries 2024, 10, 3. https://doi.org/10.3390/batteries10010003
Azzam M, Endisch C, Lewerenz M. Evaluating the Aging-Induced Voltage Slippery as Cause for Float Currents of Lithium-ion Cells. Batteries. 2024; 10(1):3. https://doi.org/10.3390/batteries10010003
Chicago/Turabian StyleAzzam, Mohamed, Christian Endisch, and Meinert Lewerenz. 2024. "Evaluating the Aging-Induced Voltage Slippery as Cause for Float Currents of Lithium-ion Cells" Batteries 10, no. 1: 3. https://doi.org/10.3390/batteries10010003
APA StyleAzzam, M., Endisch, C., & Lewerenz, M. (2024). Evaluating the Aging-Induced Voltage Slippery as Cause for Float Currents of Lithium-ion Cells. Batteries, 10(1), 3. https://doi.org/10.3390/batteries10010003







