Abstract
We investigate the gap symmetry of the topological superconductor candidate HfRuP, which crystallizes in a noncentrosymmetric hexagonal crystal structure, using muon spin rotation/relaxation (SR) measurements in transverse-field (TF) geometry. The temperature and magnetic field dependencies of the superconducting relaxation rate derived from the TF-SR spectra can be well described by an isotropic s-wave gap. The superconducting carrier density = 1.41(1) × 10 m and the magnetic penetration depth, (0) = 603(2) nm, were calculated from the TF-SR data. Interestingly, the ratio between the superconducting transition temperature and the superfluid density, /(0) ∼ 3.3, is very close to those of unconventional superconductors. Further, our zero-field (ZF) SR results do not show any considerable change in the muon spin relaxation above and below the superconducting transition temperature, suggesting that time-reversal symmetry is preserved in the superconducting state of this superconductor.
1. Introduction
Research on topological superconductors has attracted tremendous attention due to its potential application in quantum computers [1,2,3,4,5,6,7,8]. In the search for new topological superconductors, the ternary transition metal pnictides ( Ca, Zr, and Hf; Ir, Ru, Ag, and Os; P, As, and Si) offer considerable promise, as many members of this series exhibit interesting topological properties and some undergo a superconducting transition [9,10,11,12,13,14,15,16]. The observation of relatively high transition temperatures, , in ZrRuAs ( = 13.0 K) and HfRuP ( K) [9,10] motivated the research community to explore related compounds.
HfRuP crystallizes in a hexagonal FeP-type structure without any inversion symmetry in the crystal structure [9,11,17]. Recent ARPES studies on this compound show that HfRuP has 12 pairs of type-II Weyl points [17]. Thus, it is very important to understand the superconducting gap structure of this interesting superconductor. Further, the noncentrosymmetric structure of this compound, containing heavy elements with strong spin–orbit interactions, sparks the possibility of mixed spin-singlet and spin-triplet pairing [18,19,20], which breaks the time-reversal symmetry. Tempted by these intriguing aspects, we carried out detailed muon spin rotation/relaxation (SR) measurements on HfRuP.
In the case of a type-II superconductor, a vortex state creates an inhomogeneous spatial distribution of local magnetic fields. Such a field distribution influences the muon spin depolarization rate in the superconducting state. From the superconducting state depolarization rate, we can directly calculate the magnetic penetration depth . The temperature dependence of is related to the superconducting gap structure. Further, zero-field SR is a well-established experimental technique to check if the time-reversal symmetry is broken in the superconducting state [21]. Here, we demonstrate that HfRuP contains a single s-wave pairing gap and the time-reversal symmetry is preserved in the superconducting sate of this compound.
2. Experimental Details
A polycrystalline sample of HfRuP was prepared by pulverizing single crystals grown using the Cu-P flux method. To grow the single crystals, high-purity Hf, Ru, P, and Cu elements were combined in a 1:1:5.6:16.8 molar ratio in an alumina crucible within a glove box. The crucible was then sealed inside a tantalum ampule under an argon atmosphere and subsequently sealed in an evacuated quartz tube. The quartz tube was heated to 1170 °C for 15 h and then left for 5 h. Then, the tube was slowly cooled down to 1100 °C and immediately quenched into ice water to form HfRuP with a hexagonal structure. Finally, needle-like single crystals were yielded after dissolving the Cu-As fluxes in nitric acid. Primary characterization data have been published elsewhere [17]. Transverse-field (TF)- and zero-field (ZF)-SR experiments were carried out at the Paul Scherrer Institute (Villigen, Switzerland). The temperature-dependent TF and ZF experiments were performed on the DOLLY spectrometer and field-dependent TF experiments at 1.6 K were carried out on a GPS spectrometer. We first ground the sample of HfRuP to a powder, which was in the form of small single crystals, and pressed it into a 9 mm diameter pellet, using a hydraulic press, that was then mounted on a Cu holder using GE varnish. It was then placed in the appropriate spectrometer cryostat. DOLLY and GPS spectrometers are equipped with a standard veto setup [22] which allows a low-background SR signal. For the TF experiments, a field was first applied above , followed by cooling the sample. The SR time spectra were analyzed using the MUSRFIT software package [23].
3. Results and Discussion
3.1. Crystal Structure and Magnetization
The Rietveld refinement of the XRD pattern of HfRuP presented in Figure 1a reveals the single phase nature of the polycrystalline sample with an Fe2P-type hexagonal structure with space group (No. 189, Z = 3). The obtained lattice parameters and atomic position parameters are in good agreement with the values reported previously in the literature [9,24]. Figure 1b,c show the layered hexagonal structure of HfRuP. Each layer in the hexagonal lattice is occupied by either Hf and P atoms or Ru and P atoms. The triangular clusters of three Ru atoms are formed in the ab-plane, while the corner-sharing triangular lattice is formed by Hf atoms. Furthermore, the Hf ions are arranged in a geometrically frustrated quasikagome network in the hexagonal basal plane. The Fe2P-type hexagonal structure does not have a center of inversion and hence the crystal structure of HfRuP is noncentrosymmetric. The structure has two kinds of mirror symmetries, and , which are vital to define the mirror Chern numbers. Figure 1d shows the temperature dependence of the zero-field-cooled (ZFC) and field-cooled (FC) dc magnetic susceptibility in an applied magnetic field of 20 Oe. A clear diamagnetic signal is observed in both the ZFC and FC curves, with an onset superconducting critical temperature = 9 K. Further, the values of ZFC magnetic susceptibility below reveal a 100% superconducting volume fraction in HfRuP.
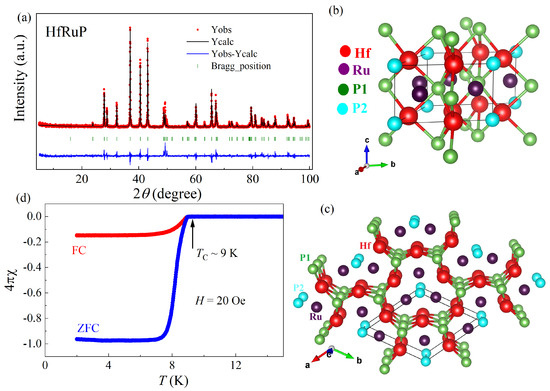
Figure 1.
(a) Room temperature Rietveld-fitted XRD pattern of HfRuP powder sample. (b,c) The hexagonal crystal structure of HfRuP. The red, purple, green, and cyan colored atoms are Hf, Ru, and the two types of P environment. (d) Temperature dependence of dc magnetic susceptibility, collected under ZFC and FCC conditions.
3.2. TF-SR Measurements
In Figure 2a, we present TF-SR asymmetry spectra for HfRuP at temperatures above (20 K) and below (0.27 K) . Temperature-dependent TF-SR measurements were performed in an applied magnetic field of 30 mT, which is higher than the lower critical field, (0) = 6.05 mT, and lower than the upper critical field, (0) = 13.4 T. The TF-SR spectra above show a very small relaxation due to the presence of random local fields associated with the nuclear magnetic moments. For a type-II superconductor, in the mixed state, due to the formation of the flux line lattice (FLL), the relaxation rate of the SR signal is enhanced. Thus, we observe a rapidly relaxing signal below for HfRuP. Assuming a Gaussian field distribution, the observed TF-SR asymmetry spectra can be described using
where refers to the initial asymmetry, MHz/T is the muon gyromagnetic ratio, is the initial phase of the muon spin ensemble, corresponds to the internal magnetic field at the muon site, and is the total relaxation rate. is related to the superconducting relaxation rate, , via the relation , where is the nuclear contribution which is assumed to be temperature independent. We considered the value of obtained from fitting TF spectra above and kept it fixed. The fits to the observed spectra with Equation (1) are shown in solid lines in Figure 2a. Figure 2b shows the Fourier transform amplitudes of the TF-SR asymmetry spectra recorded at 20 K and 0.27 K (Figure 2a). We observed a sharp peak in the Fourier amplitude around 30 mT (external applied field) at 20 K, confirming homogeneous field distribution throughout the sample. In contrast, a fairly broad signal, with a peak position slightly shifted to a lower value (diamagnetic shift), was observed at 0.27 K, confirming that the sample is in the superconducting mixed state. The formation of FLL results in such broadening of the line shape.
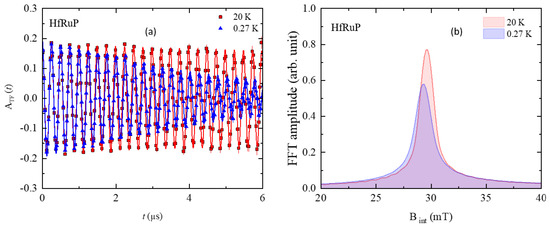
Figure 2.
(a) Transverse-field (TF)-SR time spectra obtained above (20 K—red) and below (0.27 K—blue) for HfRuP (after field cooling the sample from above ) in 30 mT. (b) Fourier transform of the SR time spectra from panel (a) at 20 K (red) and 0.27 K (blue).
Considering a perfect triangular vortex lattice, the muon spin depolarization rate can be related to the London magnetic penetration depth by [25,26]:
where = 2.068 × 10 Wb is the magnetic flux quantum. Equation (2) is only valid when the separation between the vortices is smaller than , which is presumed to be field independent in this model [25]. Figure 3a shows the temperature dependence of derived from using Equation (2). The inset of Figure 3a shows the temperature evolution of the relative change in the internal field (i.e., change in field normalized to the applied field), . As expected for type-II superconductors, we observe that below the internal field values in the superconducting state are lower than the applied field due to a diamagnetic shift.
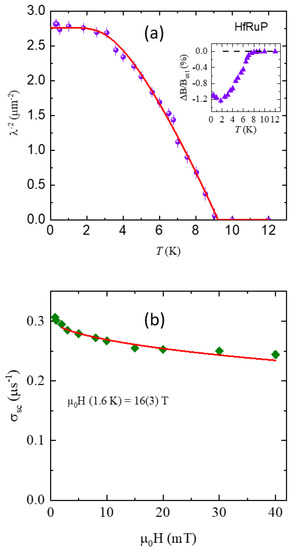
Figure 3.
(a) Temperature dependence of inverse squared London penetration depth () for HfRuP, measured in an applied field mT. The solid line corresponds to the fitting of the experimental data using an isotropic single s-wave gap model. (b) Field dependence of the superconducting muon spin depolarization rate at 1.6 K. The solid red line represents fitting with an isotropic single s-wave gap model.
To comprehend the superconducting gap structure and, further, to extract quantitative information of different superconducting parameters of HfRuP, we analyzed the temperature dependence of the magnetic penetration depth, , which is directly associated with the superconducting gap. Within the London approximation (), can be correlated with the superconducting gap of an s-wave superconductor using: [23,27,28]
here, is the Fermi function and . is the maximum gap value at K. The temperature dependence of the gap is expressed as [29]. As seen from Figure 3a, the experimentally obtained can be well described by a momentum-independent single-gap s-wave model (red solid line) with a gap value of = 1.34(1) meV and = 9.22(6) K.
We note that the of our sample is very similar to that reported for the single crystal of HfRuP ( K) by Qian et al. [17], however, lower than the K reported by Meisner et al. [9,10]. Interestingly, the crystal structure of the samples investigated remains the same. This discrepancy is most likely due to the difference in the sample preparation methods followed. Qian et al. [17] argued that the difference in annealing temperatures is accountable for the discrepancy in ’s. Thus, we also anticipate that the lower in the HfRuP sample used in the present study is because of a different heat treatment procedure. Furthermore, the ratio of the superconducting gap to was estimated to be (2/)∼ 3.38(4), which is slightly smaller than the BCS value of 3.53. Our conclusion of the gap symmetry from the SR study is in agreement with the temperature dependence of the magnetic penetration depth measurement using the tunnel-diode oscillator (TDO) method, which also found an s-wave superconductivity in HfRuP [30]. We obtained an absolute value of the penetration depth = 603(2) nm, which is slightly higher than that obtained from the TDO experiments [30]. It is to be noted that the SR method is more accurate than the TDO measurements in measuring the absolute value of the penetration depth. In Table 1, we have compared various superconducting parameters of different superconductors belonging to the family.
In London theory [31], the penetration depth, , is related to different superconducting parameters such as the effective mass, , and the superconducting carrier density, , via the relation =. Here, can be determined using the relation , where is the electron–phonon coupling constant and is the rest electron mass.
Using McMillan’s relation, it is also possible to determine the electron–phonon coupling constant () [32]:
where is the repulsive screened Coulomb parameter, usually assigned as = 0.13, and is the Debye temperature. As the value of for HfRuP is not available in the literature, we have used the = 345 K of ZrRuP [33,34], and using the scaling relation given in ref. [35] we have estimated the = 294.6 K for HfRuP, and using Equation (4) we have estimated = 1.799m, where m is the mass of the free electron for HfRuP. Using this value of m, we estimated the value of = 1.41 carriers/m. This value of is comparable to that observed in other X members such as ZrRuAs ( m) [36], HfIrSi ( m) [37], and ZrIrSi ( m) [38]. Notably, this value of is of the same order of magnitude as reported in some other TSCs, e.g., NbBiSe (m) [39] and -MoTe (m) [40]. It is worth highlighting that the relatively high value of and low value of in HfRuP evinces possible unconventional superconductivity in this compound. The ratio is often considered as a crucial parameter to qualitatively address any unconventional origin of the superconductivity. For HfRuP, the ratio is estimated to be ∼3.3, which resides between the values observed for electron-doped () and hole-doped () cuprates [41,42,43]. This is indicative of a possible unconventional mechanism of superconductivity in HfRuP.
The presence of a single s-wave gap is further corroborated by field-dependent TF measurements at 1.6 K. During these measurements, for each field point we field cooled the sample from 15 K (above ) to 1.6 K. The field dependence of the relaxation rate is presented in Figure 3b. The observed can be described using the Brandt formula (for an s-wave superconductor) [26],
Thus, we obtained an upper critical field of T, which is very similar to that obtained from the electrical resistivity measurements [17].

Table 1.
Superconducting parameters of some superconductors belonging to the family.
Table 1.
Superconducting parameters of some superconductors belonging to the family.
| Compound | (K) | (nm) | ( m) | Ref. | |
|---|---|---|---|---|---|
| ZrIrSi | 1.7 | 5.1 | 254 (3) | 6.9 (1) | [38] |
| HfIrSi | 3.6 (1) | 3.34 | 259 (4) | 6.6 (1) | [37] |
| ZrRuAs | 7.93 (2) | 3.34 | 471 (3) | 2.11 (1) | [36] |
| HfRuP | 9.22 (6) | 3.38 (4) | 603 (2) | 1.41 (1) | This work |
3.3. ZF-SR Measurements
We also performed ZF-SR experiments at temperatures above and below , to test whether the time-reversal symmetry is preserved or broken in HfRuP. As seen from Figure 4, the ZF-SR spectra can be well described by a damped Gaussian Kubo–Toyabe depolarization function [44] , where is the initial asymmetry, is the Gaussian Kubo–Toyabe (KT) function [44] representing the contribution from an isotropic Gaussian distribution of randomly oriented static (or quasistatic) local fields at the muon sites, and is the exponential relaxation rate. We do not observe any noticeable difference in the spectra collected at 10 K and at 0.27 K, suggesting the absence of any spontaneous field in the superconducting state and, hence, the time-reversal symmetry is preserved in the superconducting state of HfRuP.
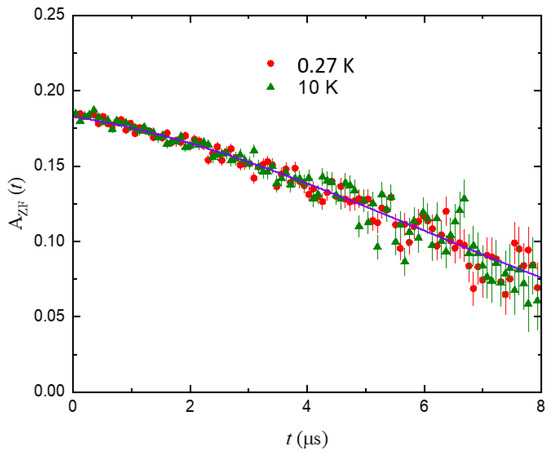
Figure 4.
ZF-SR asymmetry spectra recorded at 0.27 and 10 K for HfRuP.
4. Summary
The temperature dependence of the magnetic penetration depth determined using TF-SR experiments confirm a single s-wave gap structure in HfRuP. The gap to ratio, /, is slightly smaller than that expected for a BCS superconductor. The results from field-dependent TF measurements also confirm single-gap s-wave superconductivity. The ZF-SR results suggest that time-reversal symmetry is preserved in the superconducting state of HfRuP. Although the admixture of spin-singlet and spin-triplet pairing states is allowed in the noncentrosymmetry crystal structure of HfRuP, our TF-SR study, and also TDO measurements [30], do not suggest the presence of a node or spin-triplet pairing. Similar conclusions on the s-wave gap symmetry and preservation of the TRS have been reported in the noncentrosymmetric topological superconductor ZrRuAs [36]. The results of the present study will be important to understand the superconductivity in other topological superconductors.
Author Contributions
Conceptualization, D.D. and D.A.; methodology, D.D., D.A., R.T., Z.W., D.Y., H.L. (Hubertus Luetkens) and Y.S.; validation, D.D., D.A., R.T., Z.G., H.L. (Hubertus Luetkens), Z.W., D.Y., H.L. (Huiqian Luo) and Y.S.; formal analysis, D.D. and D.A.; investigation, D.D., D.A., R.T., Z.G., F.H., H.L. (Hubertus Luetkens), Z.W., D.Y., H.L. (Huiqian Luo) and Y.S.; resources, D.D., D.A. and Y.S.; data curation, D.D. and D.A.; writing—original draft preparation, D.D. and D.A.; writing—review and editing, D.D., D.A., R.T., Z.G., F.H., H.L. (Hubertus Luetkens), D.Y., H.L. (Huiqian Luo) and Y.S.; visualization, D.D., D.A. and R.T.; supervision, D.D. and D.A.; project administration, D.D. and D.A.; funding acquisition, D.D. and D.A. All authors have read and agreed to the published version of the manuscript.
Funding
D.A. would like to thank the Royal Society of London for International Exchange funding between the UK and Japan, Newton Advanced Fellowship funding between UK and China, and EPSRC UK for the funding (Grant No. EP/W00562X/1). Huiqian Luo acknowledges Newton Advanced Fellowship funding between UK and China, the National Key Research and Development Program of China (Grant No. 2018YFA0704200), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grants No. XDB25000000). R.T. acknowledges the support of the Indian Nanomission for a postdoctoral fellowship. Y.S. acknowledges funding from the Strategic Priority Research Program of the Chinese Academy of Sciences (Grants No. XDB33030000) and the Informatization Plan of the Chinese Academy of Sciences (CAS-WX2021SF-0102).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Acknowledgments
We thank Martin Lees and Amitava Bhattacharyya for interesting discussions. The muon spectroscopy studies were performed at the Swiss Muon Source (SS), Paul Scherrer Insitute, Villigen, Switzerland.
Conflicts of Interest
The authors declare that they do not have any known conflict of interest.
References
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Ando, Y.; Fu, L. Topological crystalline insulators and topological superconductors: From concepts to materials. Annu. Rev. Condens. Matter Phys. 2015, 6, 361. [Google Scholar] [CrossRef]
- Tanaka, Y.; Sato, M.; Nagaosa, N. Symmetry and topology in superconductors-odd-frequency pairing and edge states. J. Phys. Soc. Jpn. 2012, 81, 011013. [Google Scholar] [CrossRef]
- Sato, M.; Ando, Y. Topological superconductors: A review. Rep. Prog. Phys. 2017, 80, 076501. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Physics-Uspekhi 2001, 44, 131. [Google Scholar] [CrossRef]
- Wilczek, F. Majorana returns. Nat. Phys. 2009, 5, 614. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter Phys. 2013, 4, 113. [Google Scholar] [CrossRef]
- Barz, H.; Ku, H.; Meisner, G.; Fisk, Z.; Matthias, B. Ternary transition metal phosphides: High-temperature superconductors. Proc. Natl. Acad. Sci. USA 1980, 77, 3132. [Google Scholar] [CrossRef]
- Meisner, G.P. Superconductivity and structural transformation in HfRuAs. Phys. Lett. A 1983, 96, 483. [Google Scholar] [CrossRef]
- Meisner, G.P.; Ku, H.C. The superconductivity and structure of equiatomic ternary transition metal pnictides. Appl. Phys. A 1983, 31, 201. [Google Scholar] [CrossRef]
- Meisner, G.P.; Ku, H.C.; Barz, H. Superconducting equiatomic ternary transition metal arsenides. Mat. Res. Bull. 1983, 18, 983. [Google Scholar] [CrossRef]
- Shirotani, I.; Tachi, K.; Konno, Y.; Todo, S.; Yagi, T. Superconductivity of the ternary ruthenium compounds HfRuP and ZrRuX (X = P, As, Si or Ge) prepared at a high pressure. Phil. Mag. B 1999, 79, 767. [Google Scholar] [CrossRef]
- Shirotani, I.; Tachi, K.; Takeda, K.; Todo, S.; Yagi, T.; Kanoda, K. Superconductivity of ZrRuSi prepared at high pressure. Phys. Rev. B 1995, 52, 6197. [Google Scholar] [CrossRef]
- Ivanov, V.; Savrasov, S.Y. Monopole mining method for high-throughput screening for Weyl semimetals. Phys. Rev. B 2019, 99, 125124. [Google Scholar] [CrossRef]
- Yamakage, A.; Yamakawa, Y.; Tanaka, Y.; Okamoto, Y.J. Line-Node Dirac Semimetal and Topological Insulating Phase in Noncentrosymmetric Pnictides CaAgX (X = P, As). Phys. Soc. Jpn. 2016, 85, 013708. [Google Scholar] [CrossRef]
- Qian, Y.; Nie, S.; Yi, C.; Kong, L.; Fang, C.; Qian, T.; Ding, H.; Shi, Y.; Wang, Z.; Weng, H.; et al. Topological electronic states in HfRuP family superconductors. NPJ Comput. Mater. 2019, 5, 121. [Google Scholar] [CrossRef]
- Bauer, E.; Hilscher, G.; Michor, H.; Paul, C.; Scheidt, E.W.; Gribanov, A.; Seropegin, Y.; Noël, H.; Sigrist, M.; Rogl, P. Heavy fermion superconductivity and magnetic order in noncentrosymmetric CePt3Si. Phys. Rev. Lett. 2004, 92, 027003. [Google Scholar] [CrossRef]
- Bauer, E.; Sigrist, M. (Eds.) Non-Centrosymmetric Superconductors: Introduction and Overview; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Tanaka, Y.; Mizuno, Y.; Yokoyama, T.; Yada, K.; Sato, M. Anomalous Andreev bound state in noncentrosymmetric superconductors. Phys. Rev. Lett. 2010, 105, 097002. [Google Scholar] [CrossRef]
- Yaouanc, A.; de Réotier, P.D. Muon Spin Rotation, Relaxation, and Resonance Applications to Condensed Matter; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Amato, A.; Luetkens, H.; Sedlak, K.; Stoykov, A.; Scheuermann, R.; Elender, M.; Raselli, A.; Graf, D. The new versatile general purpose surface-muon instrument (GPS) based on silicon photomultipliers for μSR measurements on a continuous-wave beam. Rev. Sci. Instrum. 2017, 88, 093301. [Google Scholar] [CrossRef]
- Suter, A.; Wojek, B. Musrfit: A free platform-independent framework for μSR data analysis. Phys. Procedia 2012, 30, 69. [Google Scholar] [CrossRef]
- Shirotani, I.; Ichihashi, N.; Nozawa, K.; Kinshirta, M.; Yagi, T.; Suzuki, K.; Enoki, T. In Proceedings of the 9th International Conference Ternary and Multinary Compounds, Yokohama, Japan, 8–12 August 1993. Jpn. J. Appl. Phys. 1993, 32, 695–697. [Google Scholar] [CrossRef]
- Brandt, E.H. Flux distribution and penetration depth measured by muon spin rotation in high TC superconductors. Phys. Rev. B 1988, 37, 2349. [Google Scholar] [CrossRef] [PubMed]
- Brandt, E.H. Properties of the ideal Ginzburg-Landau vortex lattice. Phys. Rev. B 2003, 68, 054506. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; Dover: Mineola, NY, USA, 1996. [Google Scholar]
- Prozorov, R.; Giannetta, R.W. Magnetic penetration depth in unconventional superconductors. Supercond. Sci. Technol. 2006, 19, R41. [Google Scholar] [CrossRef]
- Carrington, A.; Manzano, F. Magnetic penetration depth of MgB2. Phys. C 2003, 385, 205. [Google Scholar] [CrossRef]
- Duan, W.; Nie, Z.; Yan, D.; Su, H.; Chen, Y.; Chen, Y.; Shi, Y.; Song, Y.; Yuan, H. Nodeless superconductivity in topologically nontrivial materials HfRuP and ZrRuAs. J. Phys. Condens. Matter 2022, 34, 455601. [Google Scholar] [CrossRef]
- Sonier, J.E.; Brewer, J.H.; Kiefl, R.F. μSR studies of the vortex state in type-II superconductors. Rev. Mod. Phys. 2000, 72, 769. [Google Scholar] [CrossRef]
- McMillan, W. Transition temperature of strong-coupled superconductors. Phys. Rev. 1968, 167, 331. [Google Scholar] [CrossRef]
- Stewart, G.R.; Meisner, G.P.; Ku, H.C. Superconductivity in d- and f-Band Metal; Buckel, W., Weber, W., Eds.; Kernforschungszentrum: Karlsruhe, Germany, 1982; p. 331. [Google Scholar]
- Keiber, H.; Wuhl, H.; Meisner, G.P.; Stewart, G.R. Phonon anomalies in ZrRuP. Low. Temp. Phys. 1984, 55, 11. [Google Scholar] [CrossRef]
- Anand, V.; Tennant, D.; Lake, B.J. Investigations of the effect of nonmagnetic Ca substitution for magnetic Dy on spin-freezing in Dy2Ti2O7. Phys. Condens. Matter 2015, 27, 436001. [Google Scholar] [CrossRef]
- Das, D.; Adroja, D.T.; Lees, M.R.; Taylor, R.W.; Bishnoi, Z.S.; Anand, V.K.; Bhattacharyya, A.; Guguchia, Z.; Baines, C.; Luetkens, H.; et al. Probing the superconducting gap structure in the noncentrosymmetric topological superconductor ZrRuAs. Phys. Rev. B 2021, 103, 144516. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Panda, K.; Adroja, D.T.; Kase, N.; Biswas, P.K.; Saha, S.; Das, T.; Lees, M.R.; Hillier, A.D. Investigation of superconducting gap structure in HfIrSi using muon spin relaxation/rotation. J. Phys. Condens. Matter 2020, 32, 085601. [Google Scholar] [CrossRef]
- Panda, K.; Bhattacharyya, A.; Adroja, D.T.; Kase, N.; Biswas, P.K.; Saha, S.; Das, T.; Lees, M.R.; Hillier, A.D. Probing the superconducting ground state of ZrIrSi: A muon spin rotation and relaxation study. Phys. Rev. B. 2019, 99, 174513. [Google Scholar] [CrossRef]
- Das, D.; Kobayashi, K.; Smylie, M.P.; Mielke, C., III; Takahashi, T.; Willa, K.; Yin, J.-X.; Welp, U.; Hasan, M.Z.; Amato, A.; et al. Time-reversal invariant and fully gapped unconventional superconducting state in the bulk of the topological compound Nb0.25Bi2Se3. Phys. Rev. B 2020, 102, 134514. [Google Scholar] [CrossRef]
- Guguchia, Z.; von Rohr, F.; Shermadini, Z.; Lee, A.T.; Banerjee, S.; Wieteska, A.R.; Marianetti, C.A.; Frandsen, B.A.; Luetkens, H.; Gong, Z.; et al. Signatures of the topological s+− superconducting order parameter in the type-II Weyl semimetal Td-MoTe2. Nat. Commun. 2017, 8, 1082. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.N.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R.; et al. Universal Correlations between TC and (Carrier Density over Effective Mass) in High-TC Cuprate Superconductors. Phys. Rev. Lett. 1989, 62, 2317. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Keren, A.; Le, L.P.; Luke, G.M.; Sternlieb, B.J.; Wu, W.D.; Brewer, J.H.; Whetten, R.L.; Huang, S.M.; Lin, S.; et al. Magnetic-field penetration depth in K3C60 measured by muon spin relaxation. Nature 1991, 352, 605. [Google Scholar] [CrossRef]
- Shengelaya, A.; Khasanov, R.; Eshchenko, D.G.; Castro, D.D.; Savić, I.M.; Park, M.S.; Kim, K.H.; Lee, S.; Müller, K.A.; Keller, H. Muon-Spin-Rotation Measurements of the Penetration Depth of the Infinite-Layer Electron-Doped Sr0.9La0.1CuO2 Cuprate Superconductor. Phys. Rev. Lett. 2005, 94, 127001. [Google Scholar] [CrossRef]
- Kubo, R.; Toyabe, T. Magnetic Resonance and Relaxation; Blinc, R., Ed.; North-Holland: Amsterdam, The Netherlands, 1967; p. 810. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).