Magneto-Optical Faraday Effect in Quasicrystalline and Aperiodic Microresonator Structures
Abstract
1. Introduction
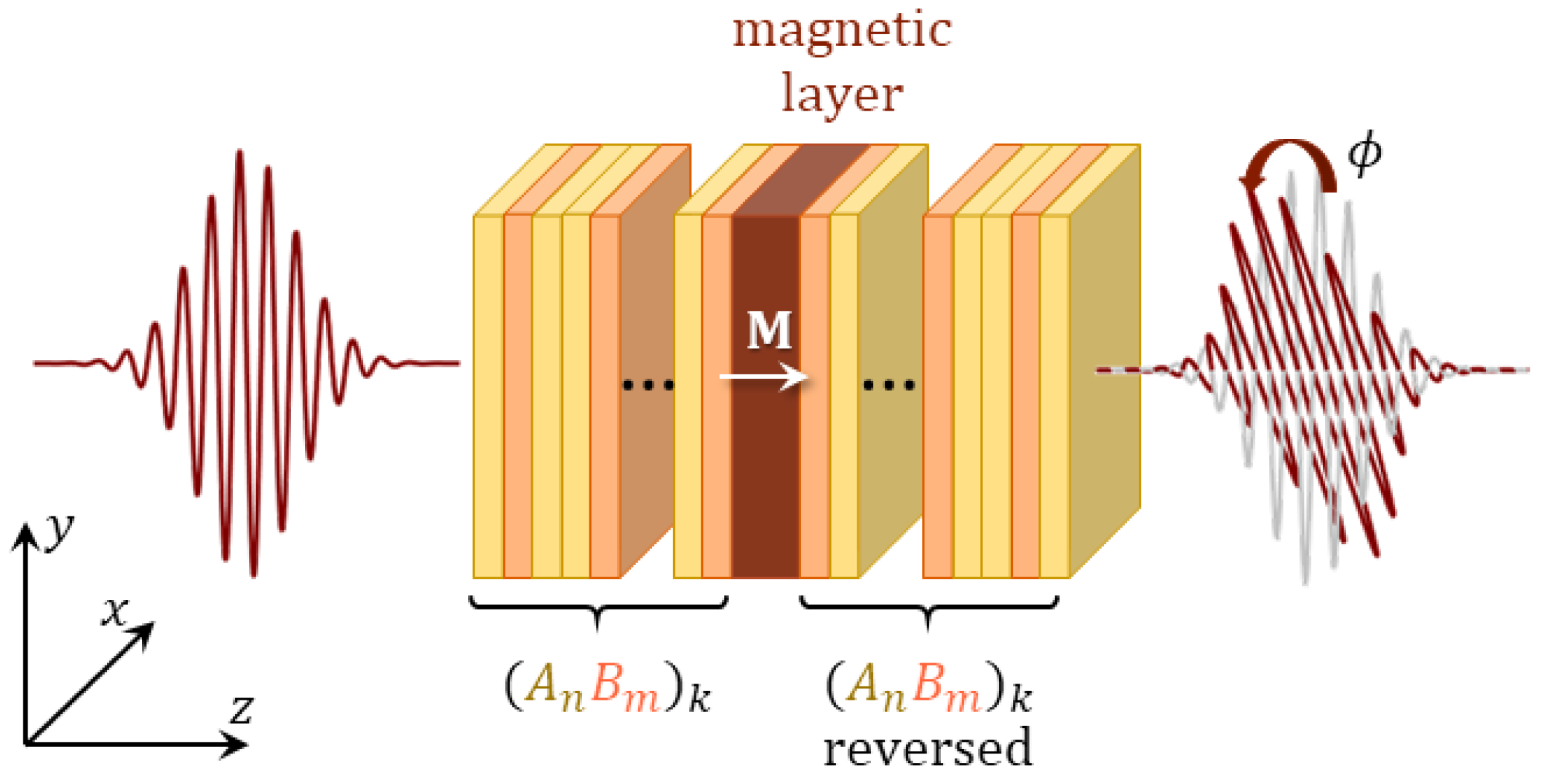
2. Materials and Methods
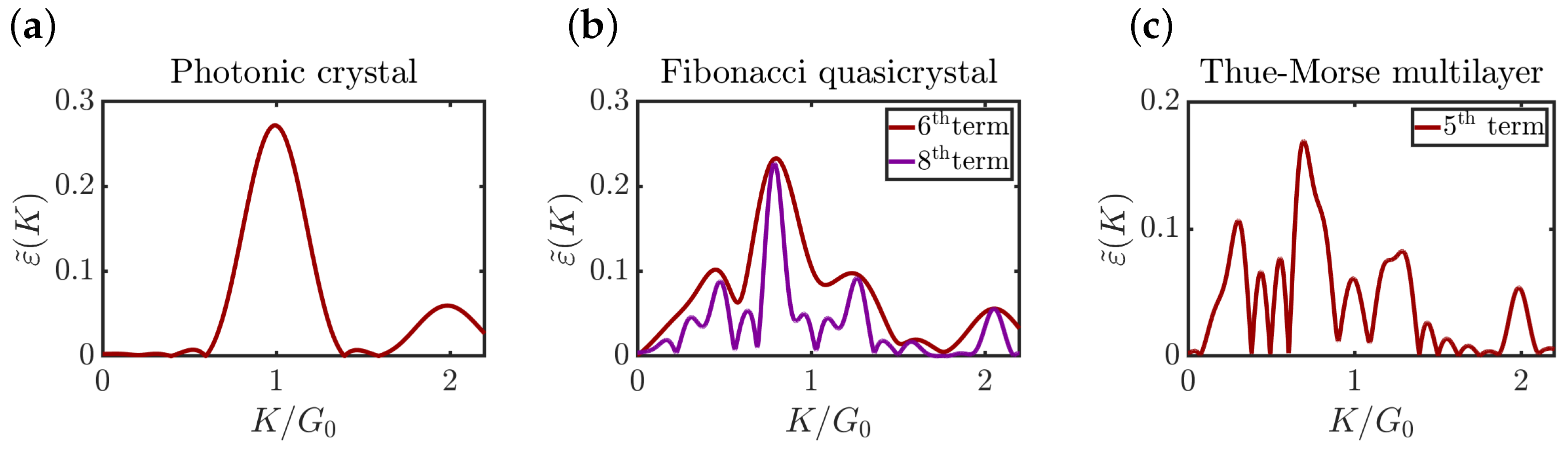
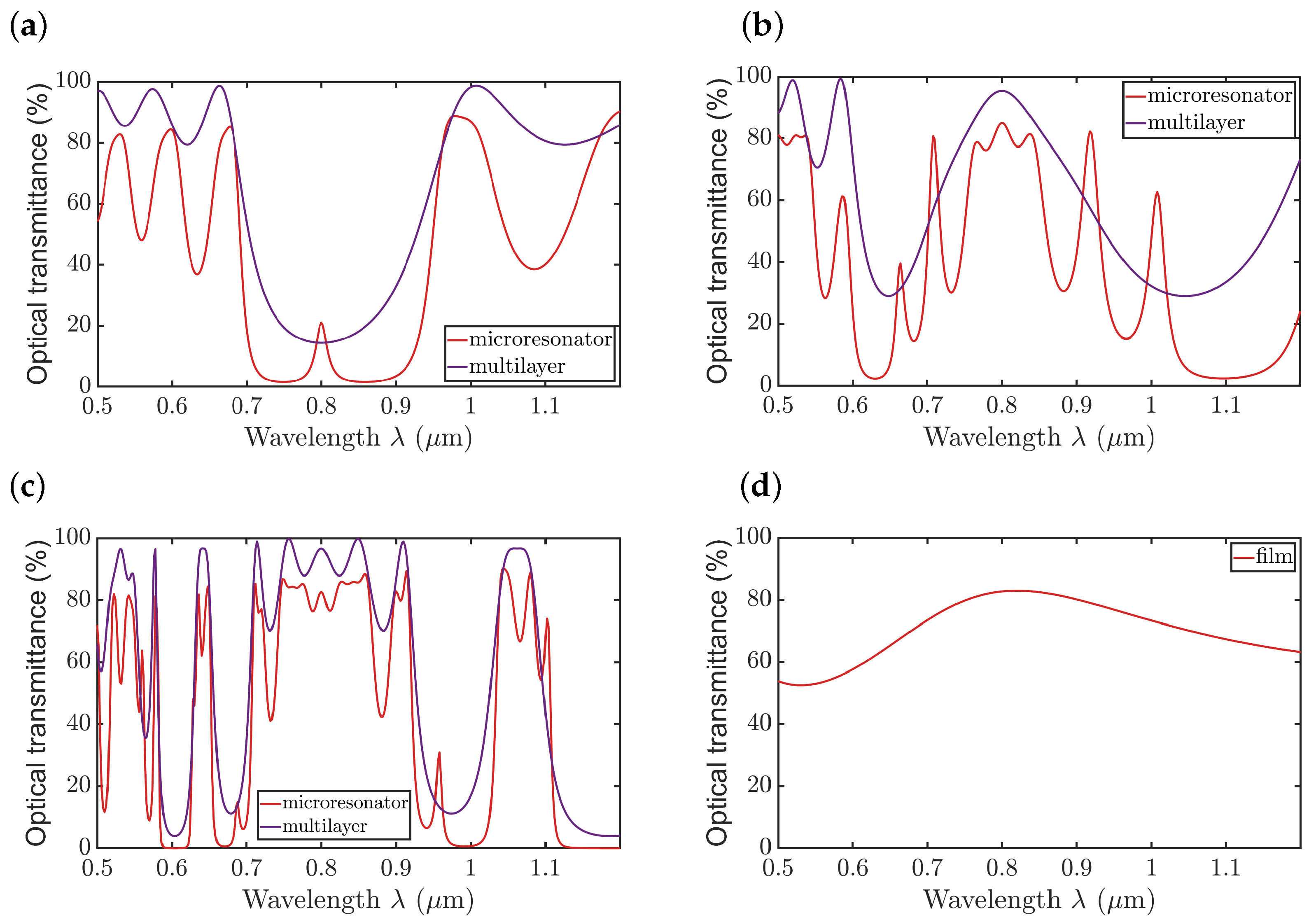
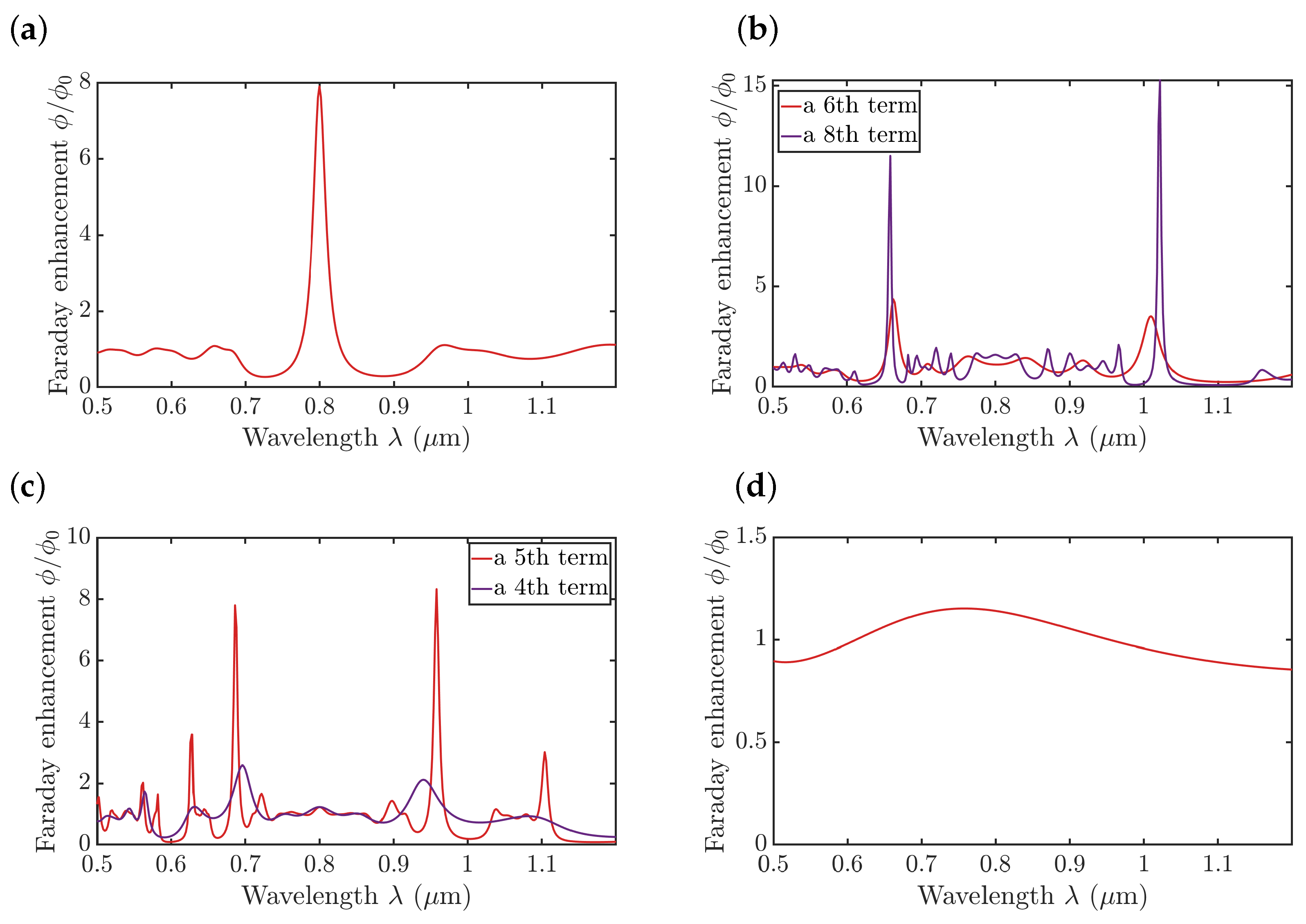
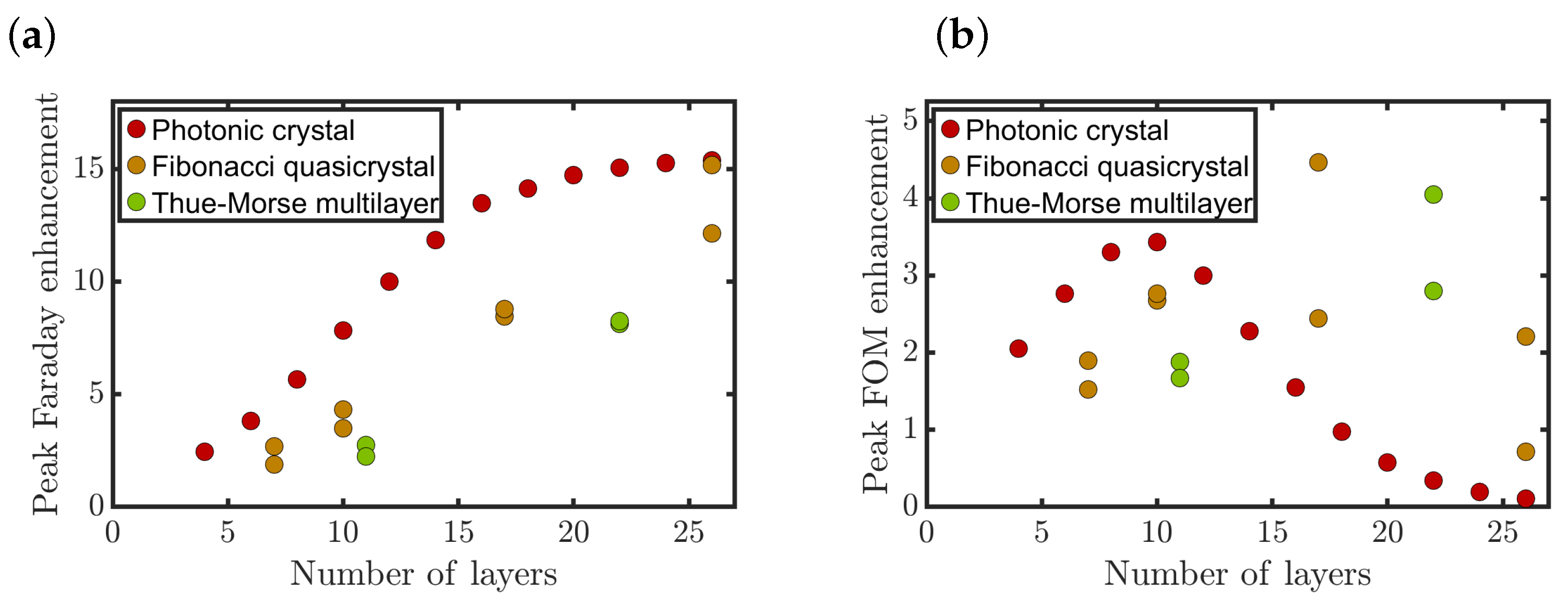
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faraday, M. On the magnetization of light and the illumination of magnetic lines of force. Philos. Trans. R. Soc. Lond. 1846, 136, 1–20. [Google Scholar]
- Kimel, A.; Zvezdin, A.; Sharma, S.; Shallcross, S.; De Sousa, N.; García-Martín, A.; Salvan, G.; Hamrle, J.; Stejskal, O.; McCord, J.; et al. The 2022 magneto-optics roadmap. J. Phys. Appl. Phys. 2022, 55, 463003. [Google Scholar] [CrossRef]
- Karki, D.; El-Ganainy, R.; Levy, M. Toward high-performing topological edge-state optical isolators. Phys. Rev. Appl. 2019, 11, 034045. [Google Scholar] [CrossRef]
- Silva, C.; Guedes, M.; Pereira, N.; Alvarenga, A. Assembly of a Faraday modulator for polarimetric measurements. In Proceedings of the Journal of Physics: Conference Series, Brasilia, Brazil, 23–27 June 2015; IOP Publishing: Bristol, UK, 2015; Volume 575, p. 012019. [Google Scholar]
- Ho, K.S.; Im, S.J.; Pae, J.S.; Ri, C.S.; Han, Y.H.; Herrmann, J. Switchable plasmonic routers controlled by external magnetic fields by using magneto-plasmonic waveguides. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Maccaferri, N.; E Gregorczyk, K.; De Oliveira, T.V.; Kataja, M.; Van Dijken, S.; Pirzadeh, Z.; Dmitriev, A.; Åkerman, J.; Knez, M.; Vavassori, P. Ultrasensitive and label-free molecular-level detection enabled by light phase control in magnetoplasmonic nanoantennas. Nat. Commun. 2015, 6, 1–9. [Google Scholar]
- Rizal, C.; Manera, M.G.; Ignatyeva, D.O.; Mejía-Salazar, J.R.; Rella, R.; Belotelov, V.I.; Pineider, F.; Maccaferri, N. Magnetophotonics for sensing and magnetometry toward industrial applications. J. Appl. Phys. 2021, 130, 230901. [Google Scholar] [CrossRef]
- Fujikawa, R.; Tanizaki, K.; Baryshev, A.; Lim, P.B.; Shin, K.H.; Uchida, H.; Inoue, M. Magnetic field sensors using magnetophotonic crystals. In Proceedings of the Photonic Crystals and Photonic Crystal Fibers for Sensing Applications II, SPIE, 2006, Boston, MA, USA, 1–4 October 2006; Volume 6369, pp. 85–92. [Google Scholar]
- Ignatyeva, D.O.; Knyazev, G.A.; Kalish, A.N.; Chernov, A.I.; Belotelov, V.I. Vector magneto-optical magnetometer based on resonant all-dielectric gratings with highly anisotropic iron garnet films. J. Phys. Appl. Phys. 2021, 54, 295001. [Google Scholar] [CrossRef]
- Lodewijks, K.; Maccaferri, N.; Pakizeh, T.; Dumas, R.K.; Zubritskaya, I.; Åkerman, J.; Vavassori, P.; Dmitriev, A. Magnetoplasmonic design rules for active magneto-optics. Nano Lett. 2014, 14, 7207–7214. [Google Scholar] [CrossRef]
- Belotelov, V.; Zvezdin, A. Magnetooptics and extraordinary transmission of the perforated metallic films magnetized in polar geometry. J. Magn. Magn. Mater. 2006, 300, e260–e263. [Google Scholar] [CrossRef]
- Lyubchanskii, I.; Dadoenkova, N.; Lyubchanskii, M.; Shapovalov, E.; Rasing, T. Magnetic photonic crystals. J. Phys. Appl. Phys. 2003, 36, R277. [Google Scholar] [CrossRef]
- Inoue, M.; Baryshev, A.; Goto, T.; Baek, S.; Mito, S.; Takagi, H.; Lim, P. Magnetophotonic crystals: Experimental realization and applications. Magnetophotonics 2013, Vol. 178, 163–190. [Google Scholar]
- Sakoda, K. Optical Properties of Photonic Crystals; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; Volume 80. [Google Scholar]
- Inoue, M.; Yamamoto, T.; Isamoto, K.; Fujii, T. Effect of structural irregularity on propagation properties of optical waves in discontinuous magneto-optical media with one-dimensional quasirandom aray structures. J. Appl. Phys. 1996, 79, 5988–5990. [Google Scholar] [CrossRef]
- Steel, M.; Levy, M.; Osgood, R. High transmission enhanced Faraday rotation in one-dimensional photonic crystals with defects. IEEE Photonics Technol. Lett. 2000, 12, 1171–1173. [Google Scholar] [CrossRef]
- Koerdt, C.; Rikken, G.; Petrov, E. Faraday effect of photonic crystals. Appl. Phys. Lett. 2003, 82, 1538–1540. [Google Scholar] [CrossRef]
- Inoue, M.; Arai, K.; Fujii, T.; Abe, M. Magneto-optical properties of one-dimensional photonic crystals composed of magnetic and dielectric layers. J. Appl. Phys. 1998, 83, 6768–6770. [Google Scholar] [CrossRef]
- Inoue, M.; Fujikawa, R.; Baryshev, A.; Khanikaev, A.; Lim, P.; Uchida, H.; Aktsipetrov, O.; Fedyanin, A.; Murzina, T.; Granovsky, A. Magnetophotonic crystals. J. Phys. Appl. Phys. 2006, 39, R151. [Google Scholar] [CrossRef]
- Kahl, S.; Grishin, A.M. Enhanced Faraday rotation in all-garnet magneto-optical photonic crystal. Appl. Phys. Lett. 2004, 84, 1438–1440. [Google Scholar] [CrossRef]
- Dermeche, N.; Bouras, M.; Abdi-Ghaleh, R.; Kahlouche, A.; Hocini, A. Existence of high Faraday rotation and transmittance in magneto photonic crystals made by silica matrix doped with magnetic nanoparticles. Optik 2019, 198, 163225. [Google Scholar] [CrossRef]
- Lyubchanskii, I.; Dadoenkova, N.; Lyubchanskii, M.; Shapovalov, E.; Zabolotin, A.; Lee, Y.; Rasing, T. Response of two-defect magnetic photonic crystals to oblique incidence of light: Effect of defect layer variation. J. Appl. Phys. 2006, 100, 096110. [Google Scholar] [CrossRef]
- Pankin, P.S.; Vetrov, S.Y.; Timofeev, I.V. Tunable hybrid Tamm-microcavity states. JOSA B 2017, 34, 2633–2639. [Google Scholar] [CrossRef]
- Goto, T.; Dorofeenko, A.; Merzlikin, A.; Baryshev, A.; Vinogradov, A.; Inoue, M.; Lisyansky, A.; Granovsky, A. Optical Tamm states in one-dimensional magnetophotonic structures. Phys. Rev. Lett. 2008, 101, 113902. [Google Scholar] [CrossRef] [PubMed]
- Goto, T.; Baryshev, A.; Inoue, M.; Dorofeenko, A.; Merzlikin, A.; Vinogradov, A.; Lisyansky, A.; Granovsky, A. Tailoring surfaces of one-dimensional magnetophotonic crystals: Optical Tamm state and Faraday rotation. Phys. Rev. B 2009, 79, 125103. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Baryshev, A.V.; Inoue, M.; Kivshar, Y.S. One-way electromagnetic Tamm states in magnetophotonic structures. Appl. Phys. Lett. 2009, 95, 011101. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals: A new class of ordered structures. Phys. Rev. Lett. 1984, 53, 2477. [Google Scholar] [CrossRef]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951. [Google Scholar] [CrossRef]
- Vardeny, Z.V.; Nahata, A.; Agrawal, A. Optics of photonic quasicrystals. Nat. Photonics 2013, 7, 177–187. [Google Scholar] [CrossRef]
- Fu, X.; Liu, Y.; Zhou, P.; Sritrakool, W. Perfect self-similarity of energy spectra and gap-labeling properties in one-dimensional Fibonacci-class quasilattices. Phys. Rev. B 1997, 55, 2882. [Google Scholar] [CrossRef]
- Beck, M.; Geoghegan, R. The Art of Proof: Basic Training for Deeper Mathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Xu, P.; Tian, H.; Ji, Y. One-dimensional fractal photonic crystal and its characteristics. JOSA B 2010, 27, 640–647. [Google Scholar] [CrossRef]
- Segovia-Chaves, F.; Vinck-Posada, H. Transmittance spectrum in a 1D photonic crystal with a Fibonacci sequence composed of polymer materials. Optik 2019, 196, 163141. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, X.; Wang, L.; Lu, H.; Wang, G. Multiple responses of TPP-assisted near-perfect absorption in metal/Fibonacci quasiperiodic photonic crystal. Opt. Express 2011, 19, 9759–9769. [Google Scholar] [CrossRef]
- Lin, Z.; Kubo, H.; Goda, M. Self-similarity and scaling of wave function for binary quasiperiodic chains associated with quadratic irrationals. Z. Für Phys. B Condens. Matter 1995, 98, 111–118. [Google Scholar] [CrossRef]
- Liu, N.h. Propagation of light waves in Thue-Morse dielectric multilayers. Phys. Rev. B 1997, 55, 3543. [Google Scholar] [CrossRef]
- Liviotti, E. A study of the structure factor of Thue-Morse and period-doubling chains by wavelet analysis. J. Phys. Condens. Matter 1996, 8, 5007. [Google Scholar] [CrossRef]
- Steurer, W.; Sutter-Widmer, D. Photonic and phononic quasicrystals. J. Phys. D Appl. Phys. 2007, 40, R229. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Alipour-Banaei, H. Bandgap management in two-dimensional photonic crystal thue-morse structures. J. Opt. Commun. 2013, 34, 61–65. [Google Scholar] [CrossRef]
- Moretti, L.; Mocella, V. Two-dimensional photonic aperiodic crystals based on Thue-Morse sequence. Opt. Express 2007, 15, 15314–15323. [Google Scholar] [CrossRef]
- Loiko, V.; Miskevich, A. Optical properties of structures composed of periodic, quasi-periodic, and aperiodic sequences of particulate monolayers. Opt. Spectrosc. 2017, 122, 16–24. [Google Scholar] [CrossRef]
- Xavier, J.; Probst, J.; Becker, C. Deterministic composite nanophotonic lattices in large area for broadband applications. Sci. Rep. 2016, 6, 1–12. [Google Scholar] [CrossRef]
- Kasture, S.; Ravishankar, A.P.; Yallapragada, V.; Patil, R.; Valappil, N.V.; Mulay, G.; Achanta, V.G. Plasmonic quasicrystals with broadband transmission enhancement. Sci. Rep. 2014, 4, 1–6. [Google Scholar] [CrossRef]
- Ghorbani-Oranj, F.; Abdi-Ghaleh, R.; Roumi, B.; Jamshidi-Ghaleh, K.; Madani, A.; Zhou, Y. Comparative study of Faraday rotation spectra of periodic and Fibonacci multilayer structures containing graphene sheets. Phys. B Condens. Matter 2022, 636, 413835. [Google Scholar] [CrossRef]
- da Silva, R.; Zanetti, F.; Lyra, M.; de Oliveira, I. Polarization rotation of localized modes in magneto-photonic Fibonacci structures containing nematic layers. Mol. Cryst. Liq. Cryst. 2017, 657, 11–20. [Google Scholar] [CrossRef]
- Zamani, M.; Amanollahi, M.; Taraz, M. Octonacci magnetophotonic quasi-crystals. Opt. Mater. 2019, 88, 187–194. [Google Scholar] [CrossRef]
- Guo, S.J.; Hu, C.X.; Zhang, H.F. A reconfigurable device based on the one-dimensional magnetized plasma photonic crystals nested with the Pell and Thue–Morse sequences. Opt. Quantum Electron. 2020, 52, 1–18. [Google Scholar] [CrossRef]
- Kalish, A.N.; Komarov, R.S.; Kozhaev, M.A.; Achanta, V.G.; Dagesyan, S.A.; Shaposhnikov, A.N.; Prokopov, A.R.; Berzhansky, V.N.; Zvezdin, A.K.; Belotelov, V.I. Magnetoplasmonic quasicrystals: An approach for multiband magneto-optical response. Optica 2018, 5, 617–623. [Google Scholar] [CrossRef]
- Dotsenko, A.A.; Kalish, A.N.; Kozhaev, M.A.; Ignatyeva, D.O.; Achanta, V.G.; Zvezdin, A.K.; Belotelov, V.I. Magneto-optical effects in 2D plasmonic gratings with various types of ordering. AIP Conf. Proc. 2020, 2300, 020026. [Google Scholar]
- Wu, J.; Wang, Z.; Wu, B.; Shi, Z.; Wu, X. The giant enhancement of nonreciprocal radiation in Thue-morse aperiodic structures. Opt. Laser Technol. 2022, 152, 108138. [Google Scholar] [CrossRef]
- Guo, S.; Hu, C.; Zhang, H. Ultra-wide unidirectional infrared absorber based on 1D gyromagnetic photonic crystals concatenated with general Fibonacci quasi-periodic structure in transverse magnetization. J. Opt. 2020, 22, 105101. [Google Scholar] [CrossRef]
- Guo, S.; Mao, M.; Zhou, Z.; Zhang, D.; Zhang, H. The wide-angle broadband absorption and polarization separation in the one-dimensional magnetized ferrite photonic crystals arranged by the Dodecanacci sequence under the transverse magnetization configuration. J. Phys. D Appl. Phys. 2020, 54, 015004. [Google Scholar] [CrossRef]
- Wang, H.; Yu, B.; Cai, D.; Chen, K. Magneto-Optical Goos- Hänchen Displacement in Quasiperiodic Gradient 1D Photonic Crystal. Phys. Status Solidi 2022, 259, 2100624. [Google Scholar] [CrossRef]
- Moharam, M.; Grann, E.B.; Pommet, D.A.; Gaylord, T. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. JOSA A 1995, 12, 1068–1076. [Google Scholar] [CrossRef]
- Li, L. Fourier modal method for crossed anisotropic gratings with arbitrary permittivity and permeability tensors. J. Opt. A Pure Appl. Opt. 2003, 5, 345. [Google Scholar] [CrossRef]
- Zvezdin, A.K.; Kotov, V.A. Modern Magnetooptics and Magnetooptical Materials; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Ignatyeva, D.; Kapralov, P.; Knyazev, G.; Sekatskii, S.; Dietler, G.; Vasiliev, M.; Alameh, K.; Belotelov, V. High-Q surface modes in photonic crystal/iron garnet film heterostructures for sensor applications. JETP Lett. 2016, 104, 679–684. [Google Scholar] [CrossRef]
- Ignatyeva, D.O.; Karki, D.; Voronov, A.A.; Kozhaev, M.A.; Krichevsky, D.M.; Chernov, A.I.; Levy, M.; Belotelov, V.I. All-dielectric magnetic metasurface for advanced light control in dual polarizations combined with high-Q resonances. Nat. Commun. 2020, 11, 1–8. [Google Scholar] [CrossRef]
- Voronov, A.A.; Karki, D.; Ignatyeva, D.O.; Kozhaev, M.A.; Levy, M.; Belotelov, V.I. Magneto-optics of subwavelength all-dielectric gratings. Opt. Express 2020, 28, 17988–17996. [Google Scholar] [CrossRef] [PubMed]
- Levy, M.; Borovkova, O.V.; Sheidler, C.; Blasiola, B.; Karki, D.; Jomard, F.; Kozhaev, M.A.; Popova, E.; Keller, N.; Belotelov, V.I. Faraday rotation in iron garnet films beyond elemental substitutions. Optica 2019, 6, 642–646. [Google Scholar] [CrossRef]
- Belotelov, V.I.; Kalish, A.N.; Zvezdin, A.K.; Gopal, A.V.; Vengurlekar, A.S. Fabry–Perot plasmonic structures for nanophotonics. JOSA B 2012, 29, 294–299. [Google Scholar] [CrossRef]
- Poddubny, A.; Pilozzi, L.; Voronov, M.; Ivchenko, E. Exciton-polaritonic quasicrystalline and aperiodic structures. Phys. Rev. B 2009, 80, 115314. [Google Scholar] [CrossRef]
- Poddubny, A.; Ivchenko, E. Photonic quasicrystalline and aperiodic structures. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 42, 1871–1895. [Google Scholar] [CrossRef]

| Type | Multilayer Composition |
|---|---|
| Photonic crystal | A B A B A B A B A B |
| Quasicrystal | A B A A B A B A A B A A B |
| Thue–Morse sequence | A B B A B A A B B A A B A B B A B A A B A B B A A B B A B A A B |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ignatyeva, D.O.; Golovko, P.V.; Belotelov, V.I. Magneto-Optical Faraday Effect in Quasicrystalline and Aperiodic Microresonator Structures. Magnetochemistry 2023, 9, 54. https://doi.org/10.3390/magnetochemistry9020054
Ignatyeva DO, Golovko PV, Belotelov VI. Magneto-Optical Faraday Effect in Quasicrystalline and Aperiodic Microresonator Structures. Magnetochemistry. 2023; 9(2):54. https://doi.org/10.3390/magnetochemistry9020054
Chicago/Turabian StyleIgnatyeva, Daria O., Polina V. Golovko, and Vladimir I. Belotelov. 2023. "Magneto-Optical Faraday Effect in Quasicrystalline and Aperiodic Microresonator Structures" Magnetochemistry 9, no. 2: 54. https://doi.org/10.3390/magnetochemistry9020054
APA StyleIgnatyeva, D. O., Golovko, P. V., & Belotelov, V. I. (2023). Magneto-Optical Faraday Effect in Quasicrystalline and Aperiodic Microresonator Structures. Magnetochemistry, 9(2), 54. https://doi.org/10.3390/magnetochemistry9020054







