Critical Behavior of La0.8Ca0.2Mn1−xCoxO3 Perovskite (0.1 ≤ x ≤ 0.3)
Abstract
:1. Introduction
2. Experimental Details
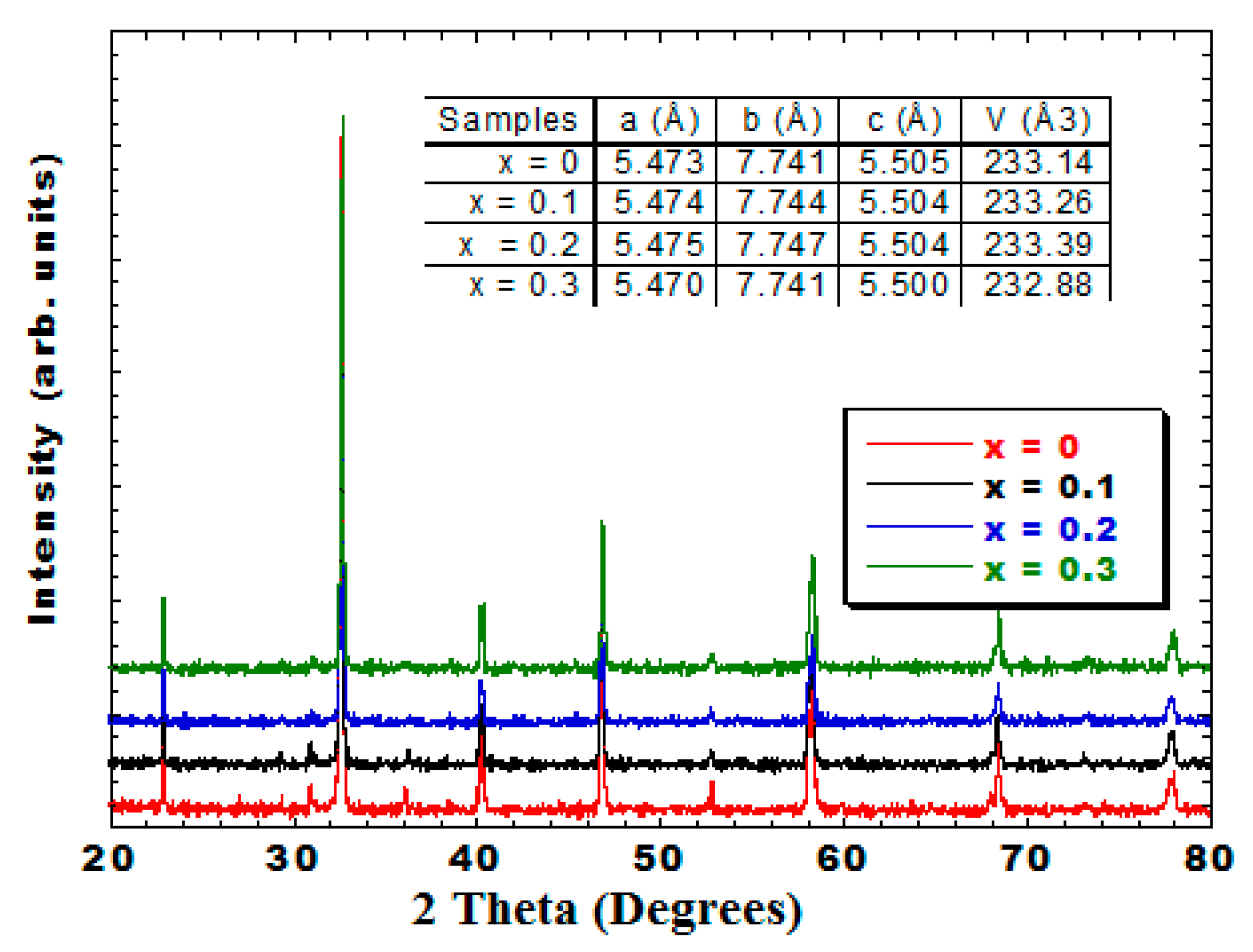
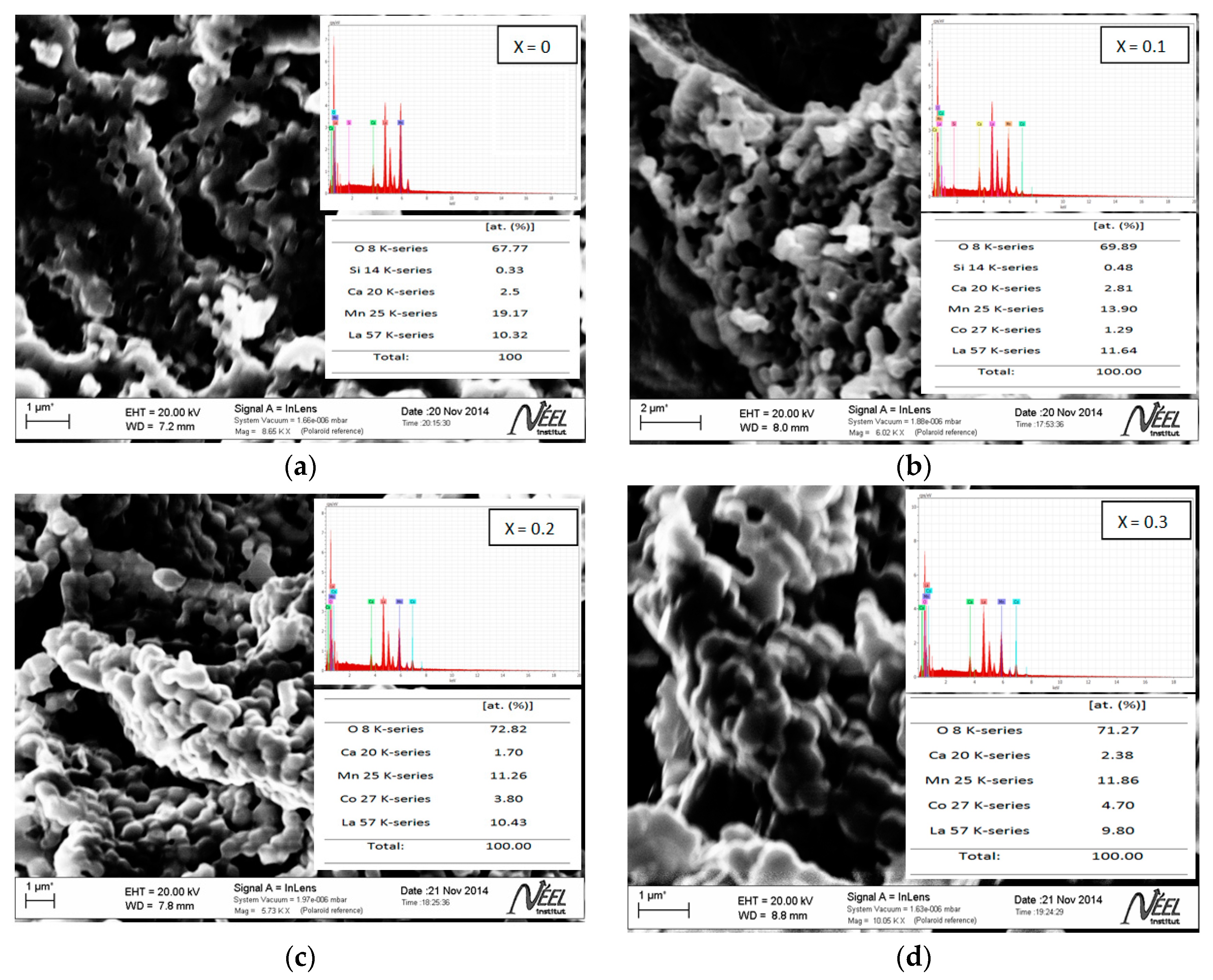
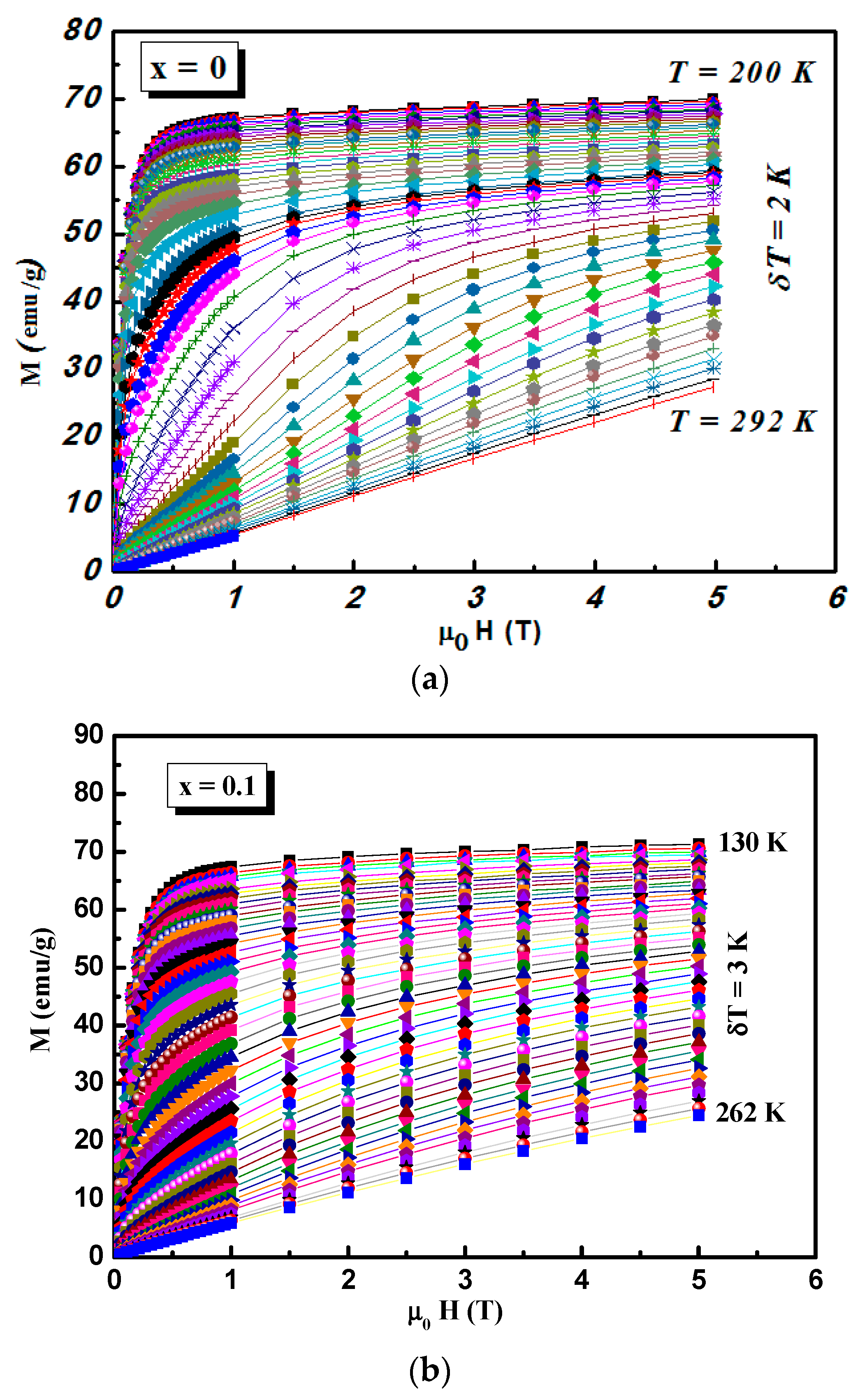
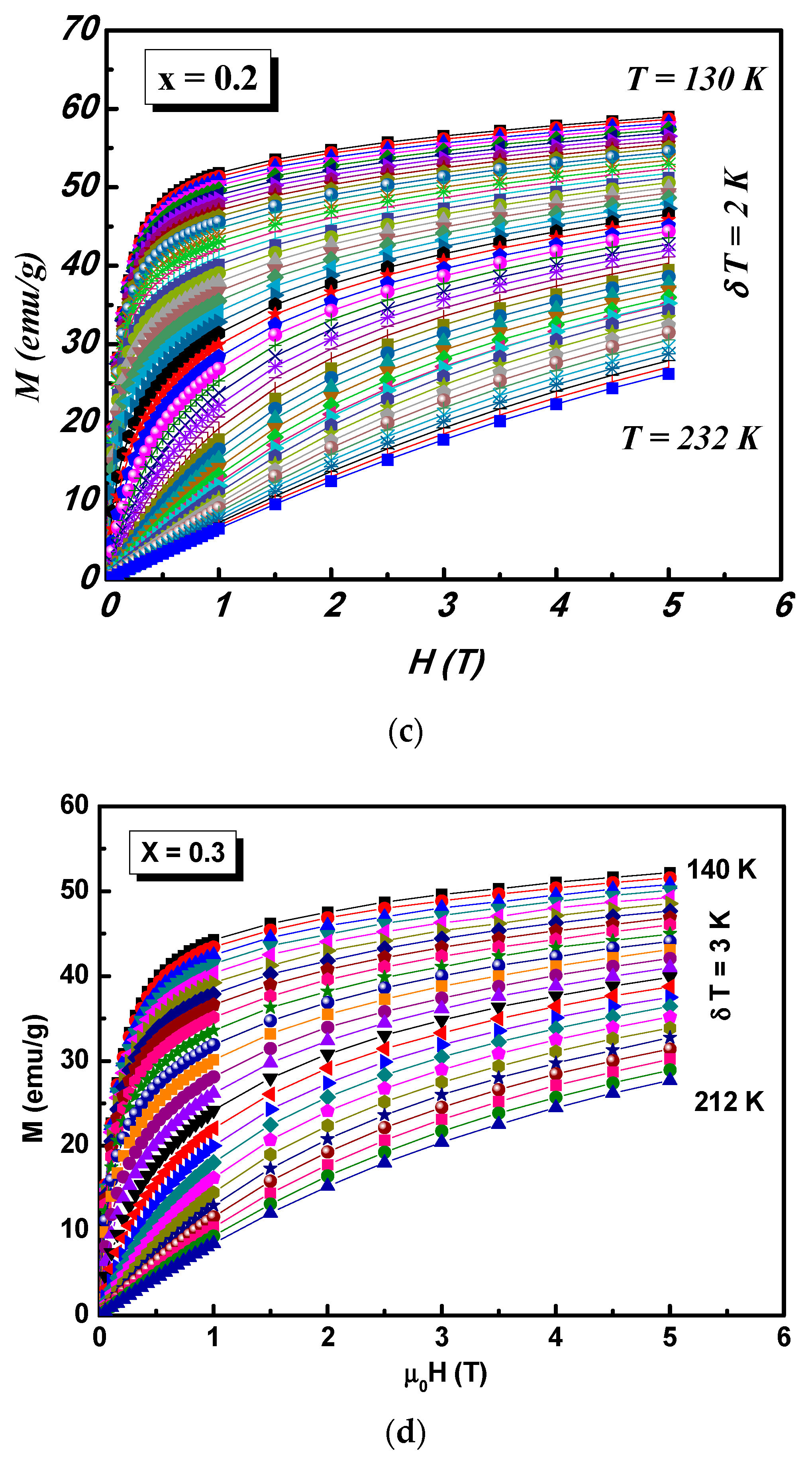
3. Results and Discussion
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Abdelkhalek, S.B.; Kallel, N.; Kallel, S.; Pena, O.; Oumezzine, M. Critical behavior and magnetic entropy change in the La0.6Sr0.4Mn0.8Fe0.1Cr0.1O3 perovskite. J. Magn. Magn. Mater. 2012, 324, 3615–3619. [Google Scholar] [CrossRef]
- Nasri, M.; Triki, M.; Dhahri, E.; Hlil, E.K. Critical behavior in Sr-doped manganites La0.6Ca0.4−xSrxMnO3. J. Magn. Magn. Mater. 2013, 324, 806. [Google Scholar] [CrossRef]
- Chen, L.; He, J.H.; Mei, Y.; Cao, Y.Z.; Xia, W.W.; Xu, H.F.; Zhu, Z.W.; Xu, Z. Critical behavior of Mo-doping La0.67Sr0.33Mn1−xMoxO3 perovskite system. Phys. B Condens. Matter 2009, 404, 1879–1882. [Google Scholar] [CrossRef]
- Oumezzine, M.; Pena, O.; Kallel, S.; Oumezzine, M. Crossover of the magnetocaloric effect and its importance on the determination of the critical behaviour in the La0.67Ba0.33Mn0.9Cr0.1O3 perovskite manganite. J. Alloys Compd. 2012, 539, 116–123. [Google Scholar] [CrossRef]
- Zener, C. Interaction between the d-Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure. Phys. Rev. 1951, 82, 403. [Google Scholar] [CrossRef]
- Anderson, P.W.; Hasegawa, H. Considerations on Double Exchange. Phys. Rev. 1955, 100, 675. [Google Scholar] [CrossRef]
- Burgy, J.; Dagotto, E.; Mayr, M. Percolative transitions with first-order characteristics in the context of colossal magnetoresistance manganites. Phys. Rev. B 2003, 67, 014410. [Google Scholar] [CrossRef]
- Millis, A.J.; Littlewood, P.B.; Shraiman, B.I. Double Exchange Alone Does Not Explain the Resistivity of La1−xSrxMnO3. Phys. Rev. Lett. 1995, 74, 5144. [Google Scholar] [CrossRef] [PubMed]
- Millis, A.J.; Shraiman, B.I.; Mueller, R. Dynamic Jahn-Teller Effect and Colossal Magnetoresistance in La1−xSrxMnO3. Phys. Rev. Lett. 1996, 77, 175. [Google Scholar] [CrossRef] [PubMed]
- Salamon, M.B.; Lin, P.; Chun, S.H. Colossal Magnetoresistance is a Griffiths Singularity. Phys. Rev. Lett. 2002, 88, 197203. [Google Scholar] [CrossRef] [PubMed]
- Phan, T.-L.; Thanh, T.D.; Yu, S.C. Influence of Co doping on the critical behavior of La0.7Sr0.3Mn1−xCoxO3. J. Alloys Compd. 2014, 615, S247–S251. [Google Scholar] [CrossRef]
- Triki, M.; Dhahri, E.; Hlil, E.K. Unconventional critical magnetic behavior in the Griffiths ferromagnet La0.4Ca0.6MnO2.8∆0.2oxide. J. Solid State Chem. 2013, 201, 63–67. [Google Scholar] [CrossRef]
- Gdaiem, M.A.; Abassi, M.; Dhahri, J.; Hlil, E.K. Structural, magnetic, magnetocaloric properties and the formation of nano-size Griffiths-like clusters in La0.8Ba0.1Ca0.1Mn0.8Co0.2O3 manganites. J. Alloys Compd. 2015, 646, 1068–1074. [Google Scholar] [CrossRef]
- Mira, J.; Rivsa, J.; Rivadulla, F.; Vazquez, C.V.; Quintela, M.A.L. Change from first- to second-order magnetic phase transition in La2/3(Ca,Sr)1/3MnO3 perovskites. Phys. Rev. B 1999, 60, 2998. [Google Scholar]
- Zhang, P.; Lampen, P.; Phan, T.L.; Yu, S.C.; Thanh, T.D.; Dan, N.H.; Lam, V.D.; Srikanth, H.; Phan, M.H. Influence of magneticfield on critical behavior near afirst order transition in optimally doped manganites: The case of La1−xCaxMnO3 (0.2 < x < 0.4). J. Magn. Magn. Mater. 2013, 348, 146–153. [Google Scholar]
- Phan, M.H.; Franco, V.; Bingham, N.S.; Srikanth, H.; Hur, N.H.; Yu, S.C. Tricritical point and critical exponents of La0.7Ca0.3−xSrxMnO3 (x = 0, 0.05, 0.1, 0.2, 0.25) single crystals. J. Alloys Compd. 2010, 508, 238–244. [Google Scholar] [CrossRef]
- Phan, T.-L.; Tran, Q.T.; Thanh, P.Q.; Yen, P.D.H.; Thanh, T.D.; Yu, S.C. Critical behavior of La0.7Ca0.3Mn1−xNixO3 manganites exhibiting the crossover of first-and second-order phase transitions. Solid State Commun. 2014, 184, 40–46. [Google Scholar] [CrossRef]
- Seeger, M.; Kaul, S.N.; Kronmuller, H.; Reisser, R. Asymptotic critical behavior of Ni. Phys. Rev. B 1995, 51, 12585. [Google Scholar] [CrossRef]
- Kubo, K.; Ohata, N. A Quantum Theory of Double Exchange. J. Phys. Soc. Jpn. 1972, 33, 21–32. [Google Scholar] [CrossRef]
- Motome, Y.; Furulawa, N. Critical Temperature of Ferromagnetic Transition in Three-Dimensional Double-Exchange Models. J. Phys. Soc. Jpn. 2000, 69, 3785–3788. [Google Scholar] [CrossRef]
- Motome, Y.; Furulawa, N. Critical Phenomena of Ferromagnetic Transition in Double-Exchange Systems. J. Phys. Soc. Jpn. 2001, 70, 1487–1490. [Google Scholar] [CrossRef]
- Xi, S.B.; Lu, W.; Sun, Y. Magnetic properties and magnetocaloric effect of La0.8Ca0.2MnO3 nanoparticles tuned by particle size. J. Appl. Phys. 2012, 111, 063922. [Google Scholar]
- Khlifi, M.; Tozri, A.; Bejar, M.; Dhahri, E.; Hlil, E.K. Effect of calcium deficiency on the critical behavior near the paramagnetic to ferromagnetic phase transition temperature in La0.8Ca0.2MnO3 oxides. J. Magn. Magn. Mater. 2012, 324, 2142–2146. [Google Scholar] [CrossRef]
- Oesterreicher, H.; Parker, F.T. Magnetic cooling near Curie temperatures above 300 KJ. Appl. Phys. 1984, 55, 4334–4338. [Google Scholar] [CrossRef]
- Franco, V.; Blazquez, J.S.; Conde, A. The magnetocaloric effect in soft magnetic amorphous alloys. Appl. Phys. Lett. 2006, 89, 222512. [Google Scholar] [CrossRef]
- Turki, D.; Cherif, R.; Hlil, E.K.; Ellouze, M.; Elhalouani, F. The effect of Co doping on structural, magnetic and magnetocaloricproperties of La0.8Ca0.2Mn1−xCoxO3 perovskites (0 ≤ x ≤ 0.3). Int. J. Mod. Phys. B 2014, 28, 1450230. [Google Scholar] [CrossRef]
- Turki, D.; Remenyi, G.; Mahmood, S.H.; Hlil, E.K.; Ellouze, M.; Halouani, F. Magnetic contributions to the specific heat of La0.8Ca0.2Mn1−xCoxO3 Perovskite. Mater. Res. Bull. 2016, 84, 245–253. [Google Scholar] [CrossRef]
- Banerjee, S.K. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
- Khlifi, M.; Bejar, M.; Dhahri, E.; Hlil, E.K. Preparation of New Composite Magnetocaloric Compounds by Modifying the Annealing Temperature of La0.8Ca0.2−x∆xMnO3 Perovskite. J. Supercond. Nov. Magn. 2012, 25, 1151–1157. [Google Scholar] [CrossRef]
- Lynn, J.W.; Erwin, R.W.; Borchers, J.A.; Huang, Q.; Santoro, A.; Peng, J.-L.; Li, Z.Y. Unconventional Ferromagnetic Transition in La1−xCaxMnO3. Phys. Rev. Lett. 1996, 76, 4046. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.; Chun, S.H.; Salamon, M.B.; Tomioka, Y.; Tokura, Y. Magnetic heat capacity in lanthanum manganite single crystals. J. Appl. Phys. 2000, 87, 5825–5827. [Google Scholar] [CrossRef]
- Bonilla, C.M.; Albillos, J.H.; Bartolomé, F.; García, L.M.; Parra-Borderías, M.; Franco, V. Universal behavior for magnetic entropy change in magnetocaloric materials: An analysis on the nature of phase transitions. Phys. Rev. B 2010, 81, 224424. [Google Scholar] [CrossRef]
- Kim, D.; Revaz, B.; Zink, B.L.; Hellman, F.; Rhyme, J.J.; Mitchell, J.F. Tricritical Point and the Doping Dependence of the Order of the Ferromagnetic Phase Transition of La1−xCaxMnO3. Phys. Rev. Lett. 2002, 89, 227202. [Google Scholar] [CrossRef] [PubMed]
- Arrot, A.; Noakes, J.E. Approximate Equation of State For Nickel Near its Critical Temperature. Phys. Rev. Lett. 1967, 19, 786. [Google Scholar] [CrossRef]
- Fan, J.; Ling, L.; Hong, B.; Zhang, L.; Pi, L.; Zhang, Y. Critical properties of the perovskite manganite La0.1Nd0.6Sr0.3MnO3. Phys. Rev. B 2010, 81, 144426. [Google Scholar] [CrossRef]
- Kouvel, J.S.; Fisher, M.E. Detailed magnetic behavior of nickel near its curie point. Phys. Rev. 1964, 43, A1626. [Google Scholar] [CrossRef]
- Zhang, L.; Fang, J.; Fan, J.; Ge, M.; Ling, L.; Zhang, C.; Pi, L.; Tan, S.; Zhang, Y. Critical behavior of the half-doped perovskite Pr0.5Sr0.5CoO3−∆. J. Alloys Compd. 2014, 588, 294–299. [Google Scholar] [CrossRef]
- Ghosh, K.; Lobb, C.J.; Greene, R.L.; Karabashev, S.G.; Shulyatev, D.A.; Arsenov, A.A.; Mukovskii, Y. Critical Phenomena in the Double-Exchange Ferromagnet La0.7Sr0.3MnO3. Phys. Rev. Lett. 1998, 81, 4740. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, X.Z.; Williams, G.; Mukovskii, Y.; Privezentsev, R. The evolution of Griffiths-phase-like features and colossal magnetoresistance in La(1−x)Ca(x)MnO(3) (0.18 ≤ x ≤ 0.27) across the compositional metal-insulator boundary. J. Phys. Condens. Matter 2009, 21, 415603. [Google Scholar] [CrossRef] [PubMed]
- Thanh, T.D.; Linh, D.C.; Manh, T.V.; Ho, T.A.; Phan, T.; Yu, S.C. Coexistence of short- and long-range ferromagnetic order in La0.7Sr0.3Mn1−xCoxO3 compounds. J. Appl. Phys. 2015, 117, 17C101. [Google Scholar] [CrossRef]
- Phan, T.-L.; Ho, T.A.; Thang, P.D.; Tran, Q.T.; Thanh, T.D.; Phuc, N.X.; Phan, M.H.; Huy, B.T.; Yu, S.C. Critical behavior of Y-doped Nd0.7Sr0.3MnO3 manganites exhibiting the tricritical point and large magnetocaloric effect. J. Alloys Compd. 2014, 615, 937–945. [Google Scholar]
- Ho, T.A.; Phan, T.L.; Thang, P.D.; Yu, S.C. Influence of Pb doping on the Magnetocaloric Effect and Critical Behavior of (La0.9Dy0.1)0.8Pb0.2MnO3. J. Electron. Mater. 2016, 45, 2328–2333. [Google Scholar] [CrossRef]
- Won, C.; Wu, Y.Z.; Arenholz, E.; Choi, J.; Wu, J.; Qiu, Z.Q. Symmetry-breaking induced exchange bias in ferromagnetics Ni-Cu-Co and Ni-Fe-Co sandwiches grown on vicinal Co (001) surface. Phys. Rev. Lett. 2007, 99, 77203. [Google Scholar] [CrossRef] [PubMed]
- Widom, B. Surface Tension and Molecular Correlations near the Critical Point. J. Chem. Phys. 1964, 41, 163. [Google Scholar] [CrossRef]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: London, UK, 1971. [Google Scholar]
- Khelifi, J.; Tozri, A.; Dhahri, E.; Hlil, E.K. Influence of Pr-doped manganite on critical behavior of La0.7−xPrxBa0.3MnO3 (x = 0.00, 0.1, 0.2). J. Magn. Magn. Mater. 2014, 349, 149–155. [Google Scholar] [CrossRef]
- Phan, T.L.; Min, S.G.; Yu, S.C.; Oh, S.K. Critical exponents of La0.9Pb0.1MnO3 perovskite. J. Magn. Magn. Mater 2006, 304, e778–e780. [Google Scholar] [CrossRef]
- Akahoshi, D.; Uchida, M.; Tomioka, Y.; Arima, T.; Matsui, Y.; Tokura, Y. Random Potential Effect near the Bicritical Region in Perovskite Manganites as Revealed by Comparison with the Ordered Perovskite Analogs. Phys. Rev. Lett. 2003, 90, 177203. [Google Scholar] [CrossRef] [PubMed]
- Franco, V.; Conde, A. Magnetic refrigerants with continuous phase transitions: Amorphous and nanostructured materials. Sci. Mater. 2012, 67, 594–599. [Google Scholar] [CrossRef]
- Franco, V.; Conde, A. Scaling laws for the magnetocaloric effect in second order phase transitions: From physics to applications for the characterization of materials, Lois d’échelle gouvernant l’effet magnétocalorique des transitions de phase de seconde ordre: De la physique aux applications permettant de caractériser les matériaux. Int. J. Refriger. 2010, 33, 465–473. [Google Scholar]
- Caballero-Flores, R.; Franco, V.; Conde, A.; Dong, Q.Y.; Zhang, H.W. Study of the field dependence of the magnetocaloric effect in Nd1.25Fe11Ti: A multiphase magnetic system. J. Magn. Mang. Mater. 2010, 322, 804–807. [Google Scholar]
- Nasri, M.; Triki, M.; Dhahri, E.; Hlil, E.K. Electrical transport and magnetoresistance properties of (1−x) La0.6Sr0.4MnO3/x(Sb2O3) composites. J. Alloys Compd. 2013, 576, 404–408. [Google Scholar] [CrossRef]
- Victorino, F.G.; Clara Francisca, C.A.; Javier Sebastián, B.G.; Alejandro, C.A.; Švec, P.; Janičkovič, D.; Kiss, F.L. A constant magnetocaloric response in FeMoCuB amorphous alloys with different FeB ratios. J. Appl. Phys. 2007, 101, 093903. [Google Scholar]
- Prida, V.M.; Franco, V.; Vega, V.; S-Llamazares, J.L.; Sunol, J.J.; Conde, A.; Hernando, B. Magnetocaloric effect in melt-spun FePd ribbon alloy with second order phase transition. J. Alloys Compd. 2011, 509, 190–194. [Google Scholar] [CrossRef]
- Shen, T.D.; Schwarz, R.B.; Coulter, J.Y.; Thompson, J.D. Magnetocaloric effect in bulk amorphous Pd40Ni22.5Fe17.5P20Pd40Ni22.5Fe17.5P20 alloy. J. Appl. Phys. 2002, 91, 5240–5245. [Google Scholar] [CrossRef]
- Caballero-Flores, R.; Bingham, N.S.; Phan, M.H.; Torija, M.A.; Leighton, C.; Franco, V.; Conde, A.; L-Phan, T.; Yu, S.C.; Srikanth, H. Magnetocaloric effect and critical behavior in Pr0.5Sr0.5MnO3: An analysis of the validity of the Maxwell relation and the nature of the phase transitions. J. Phys. Condens. Matter 2014, 26, 286001. [Google Scholar] [CrossRef] [PubMed]
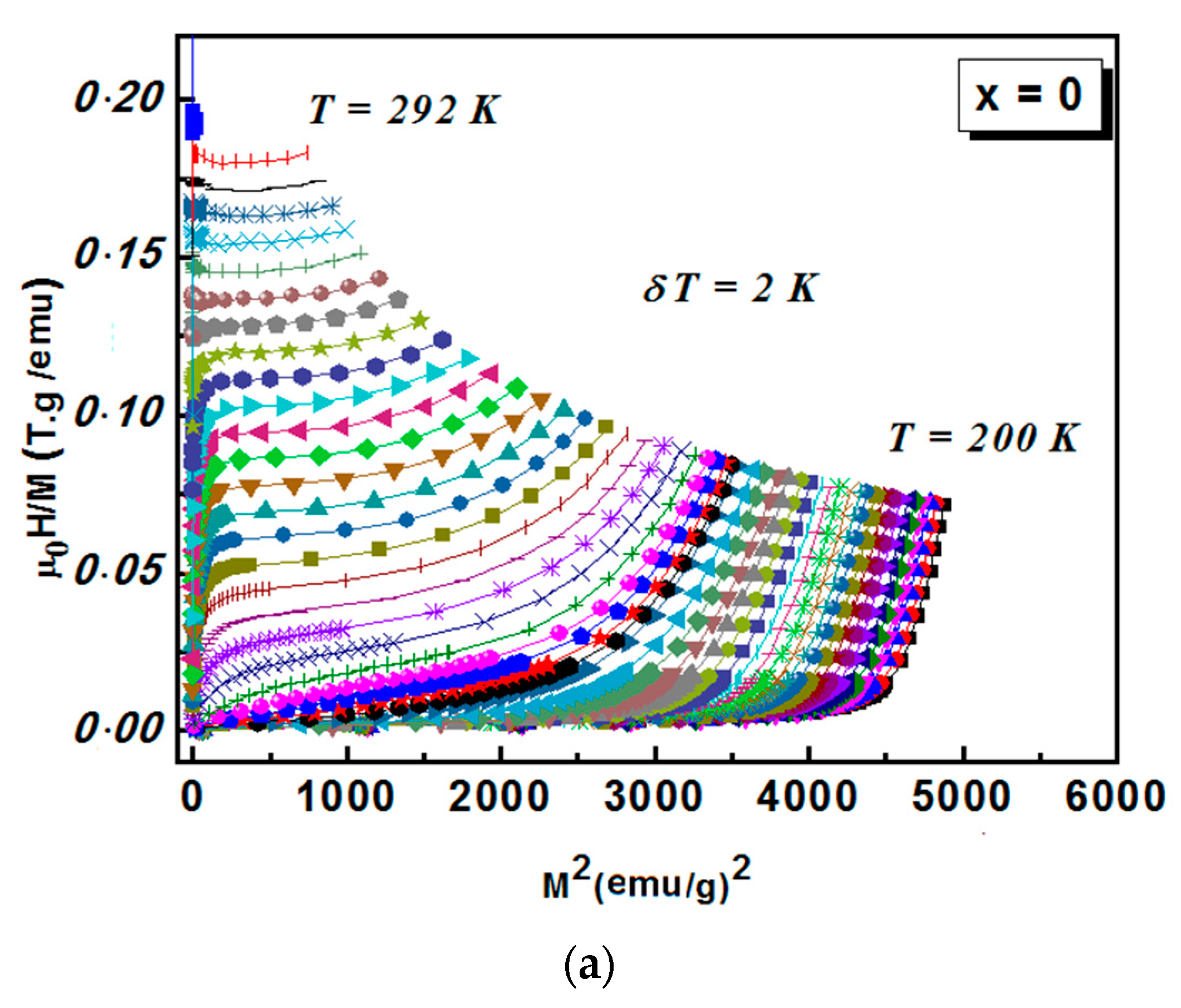
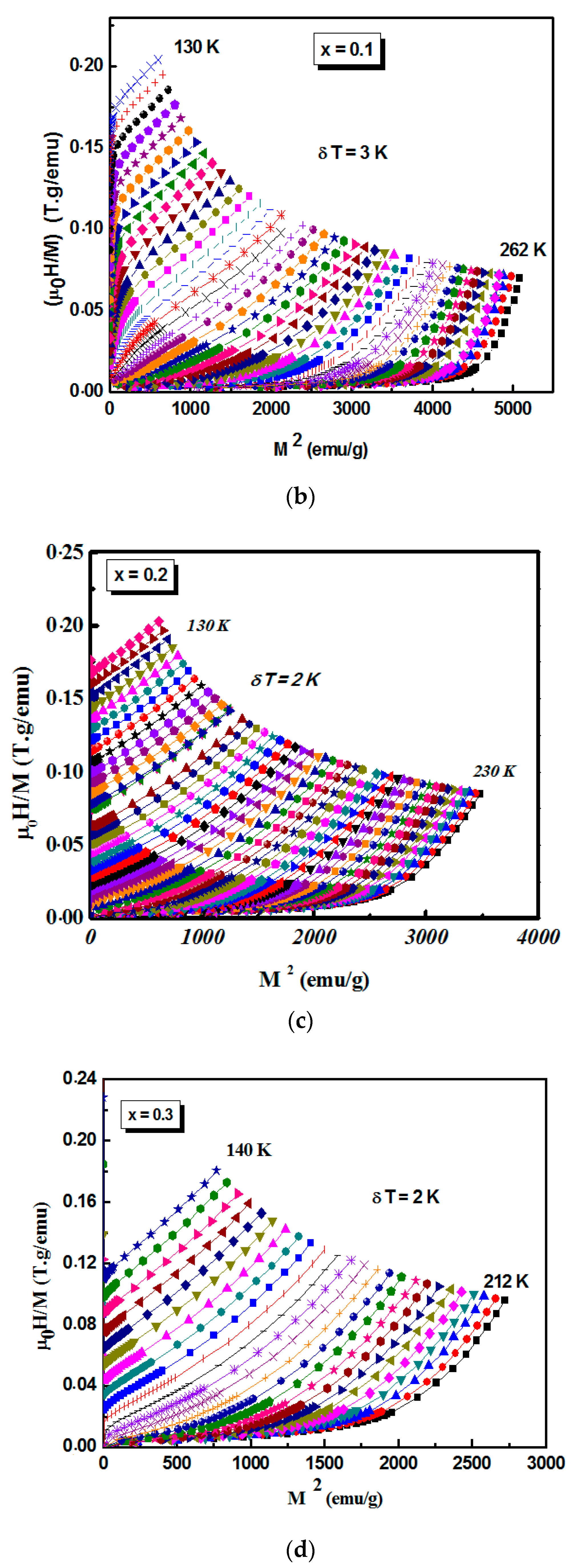

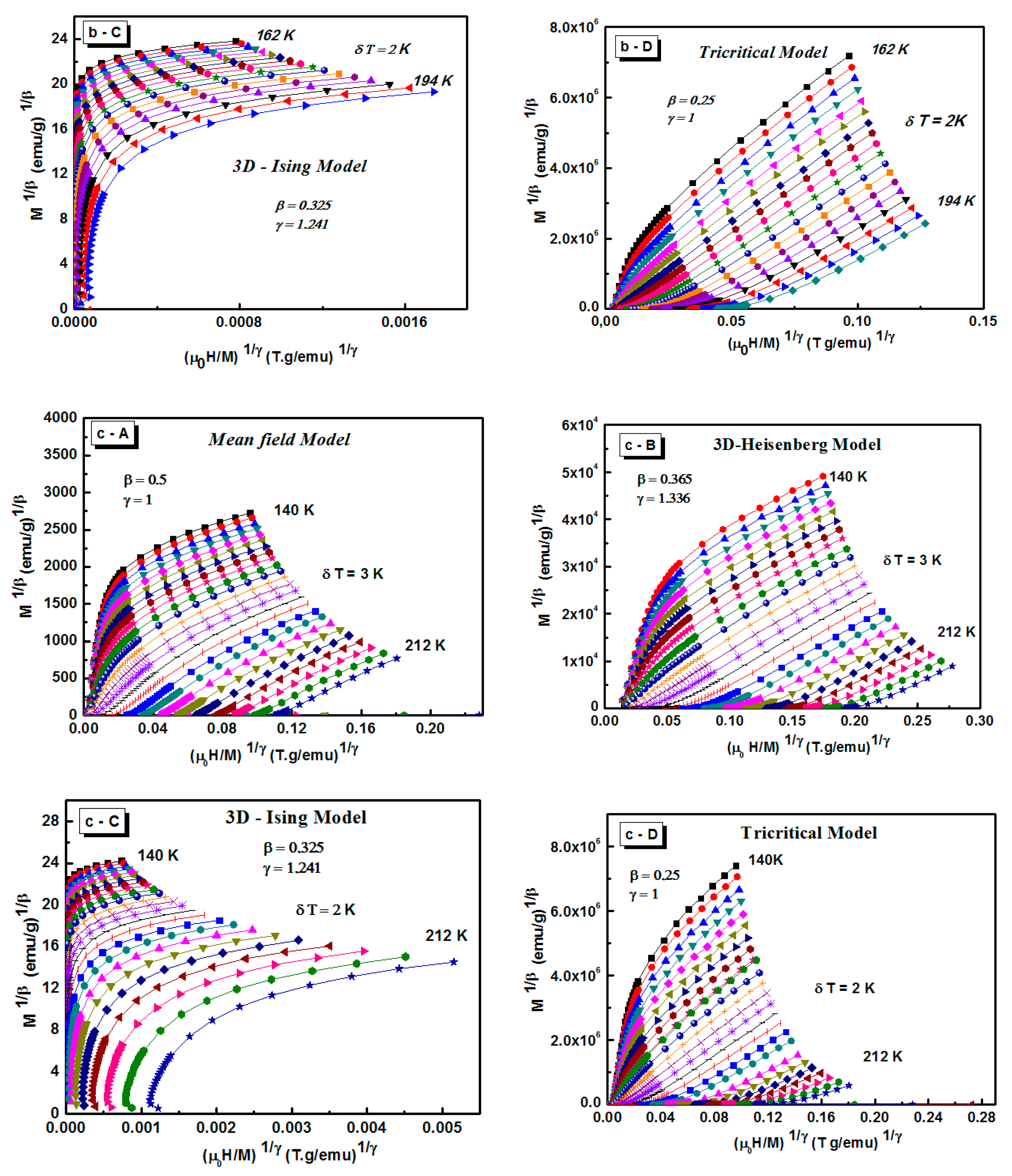
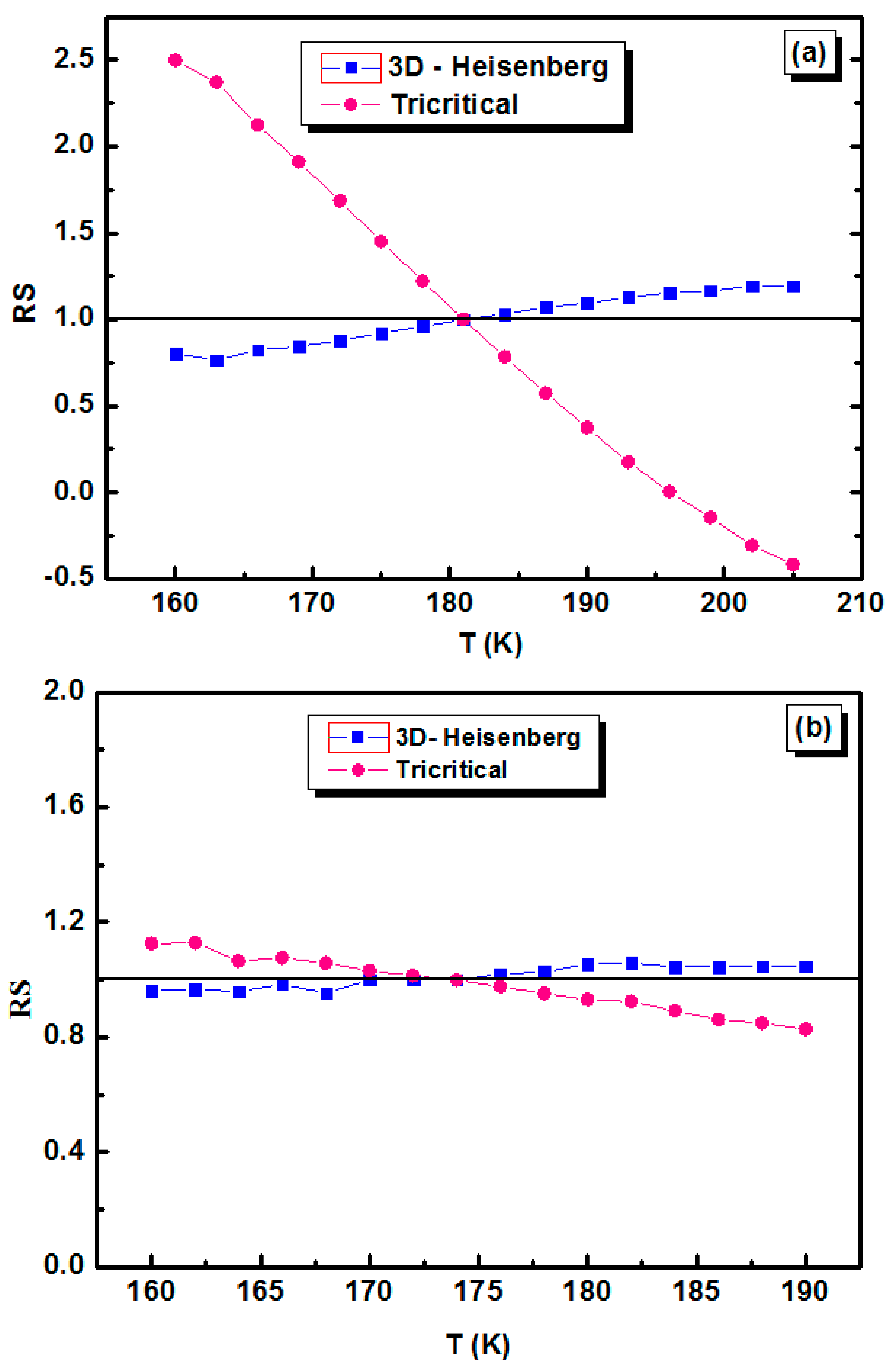

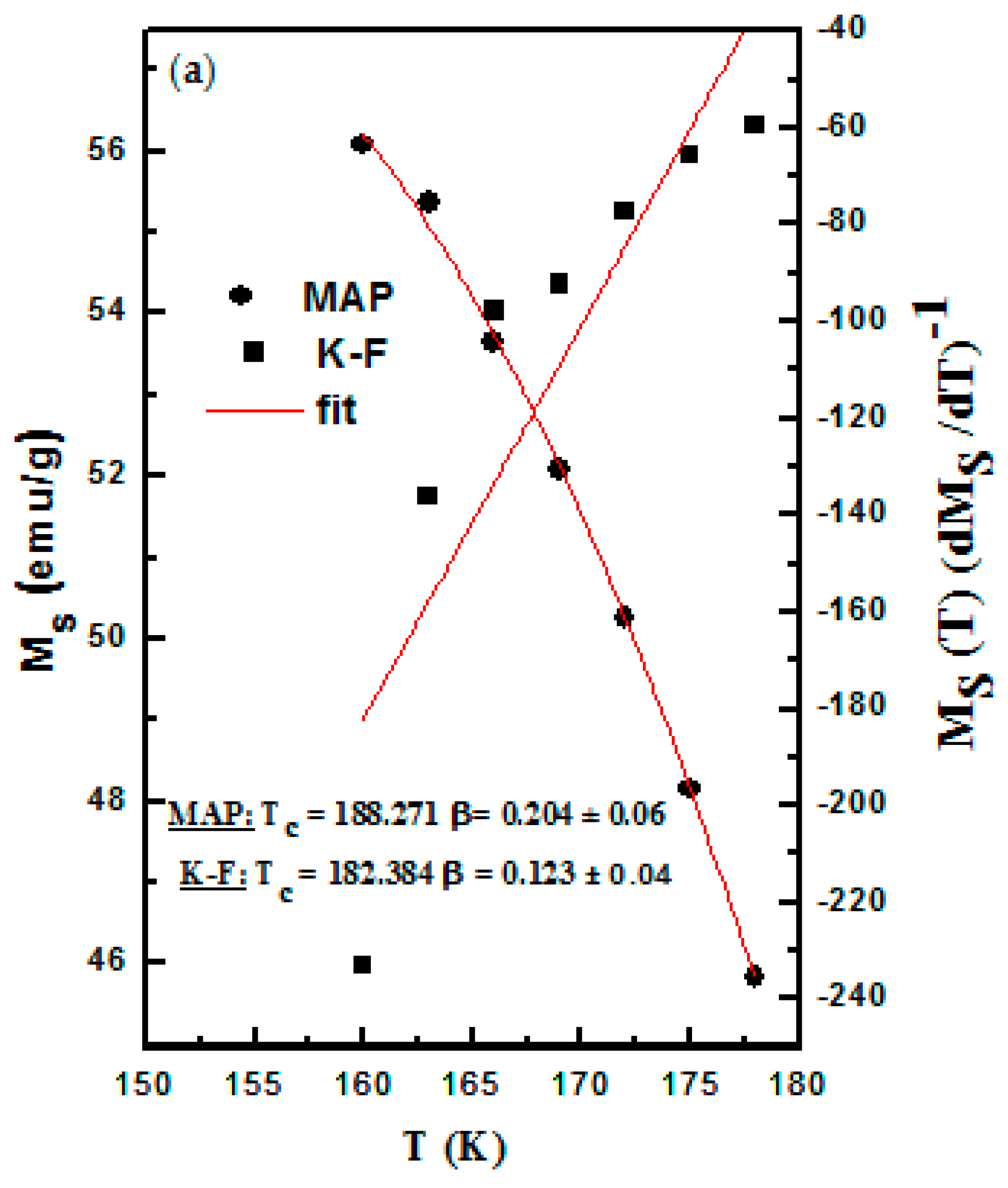
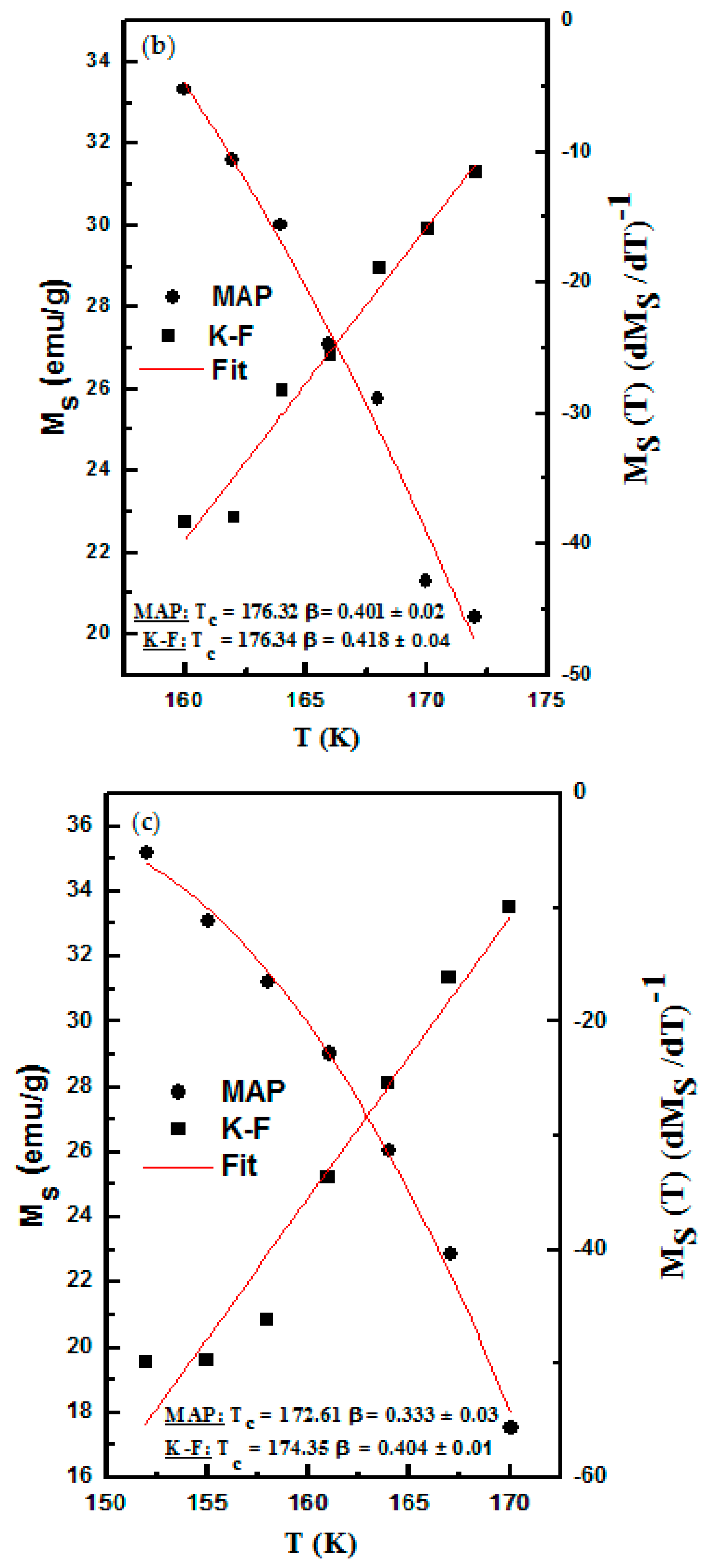
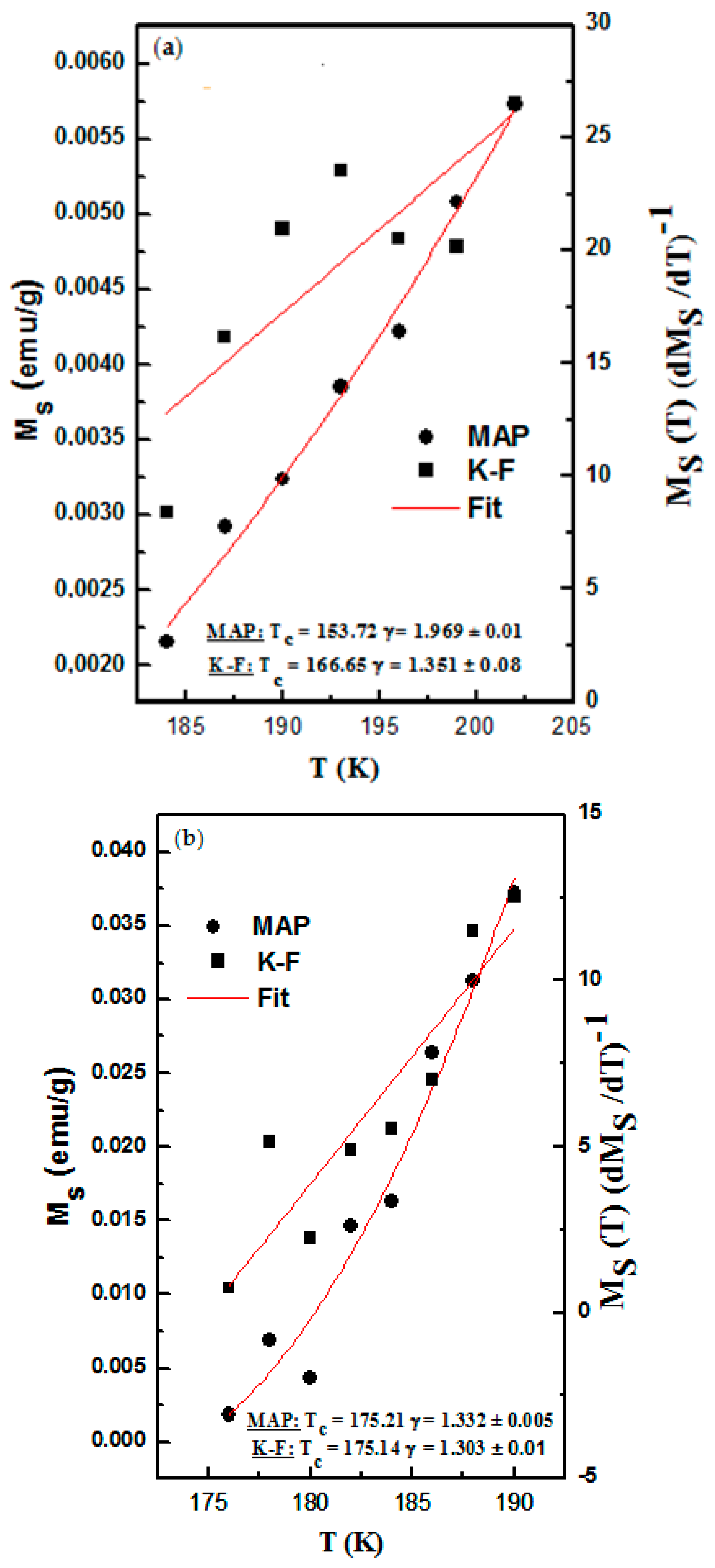

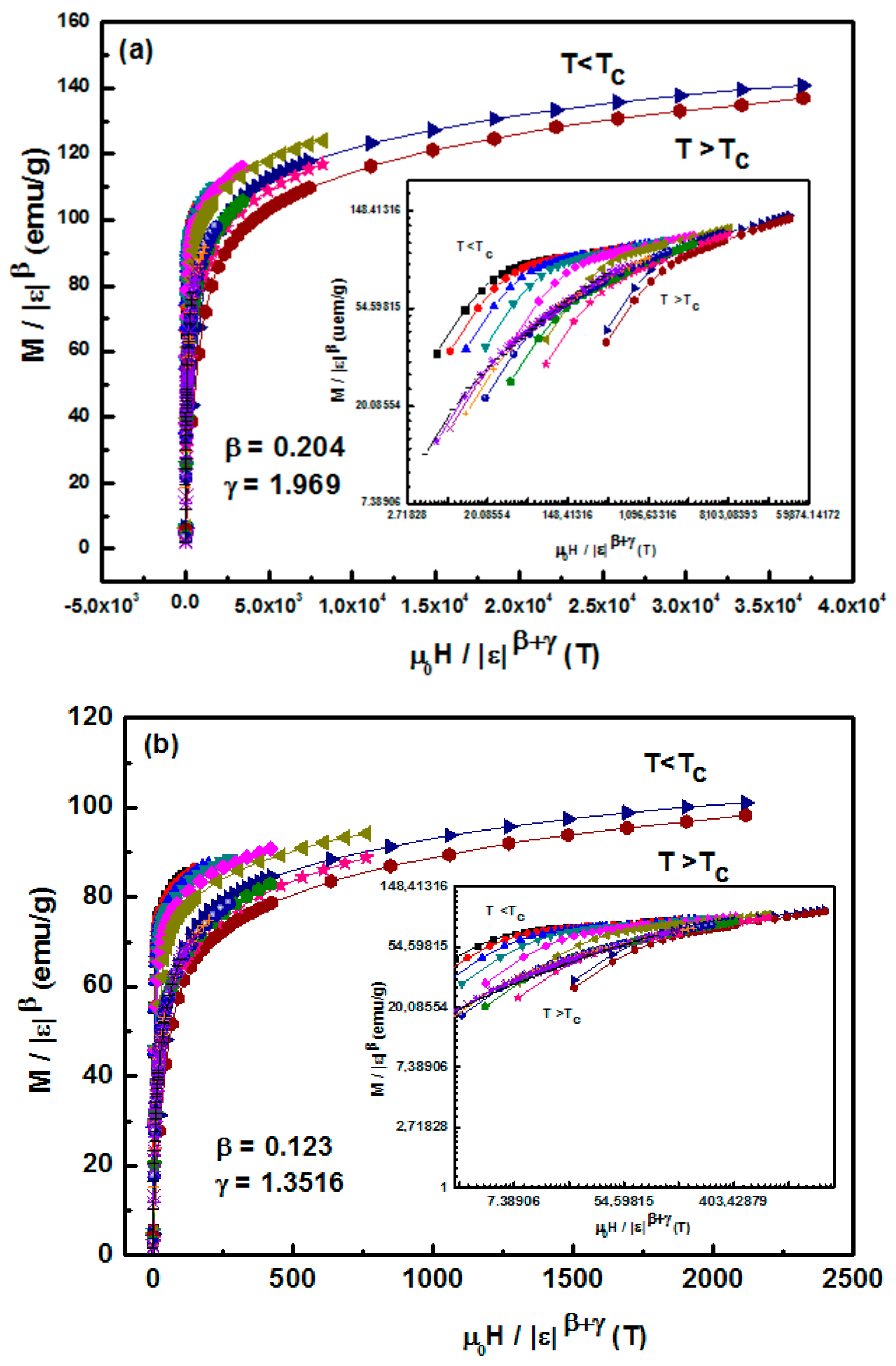
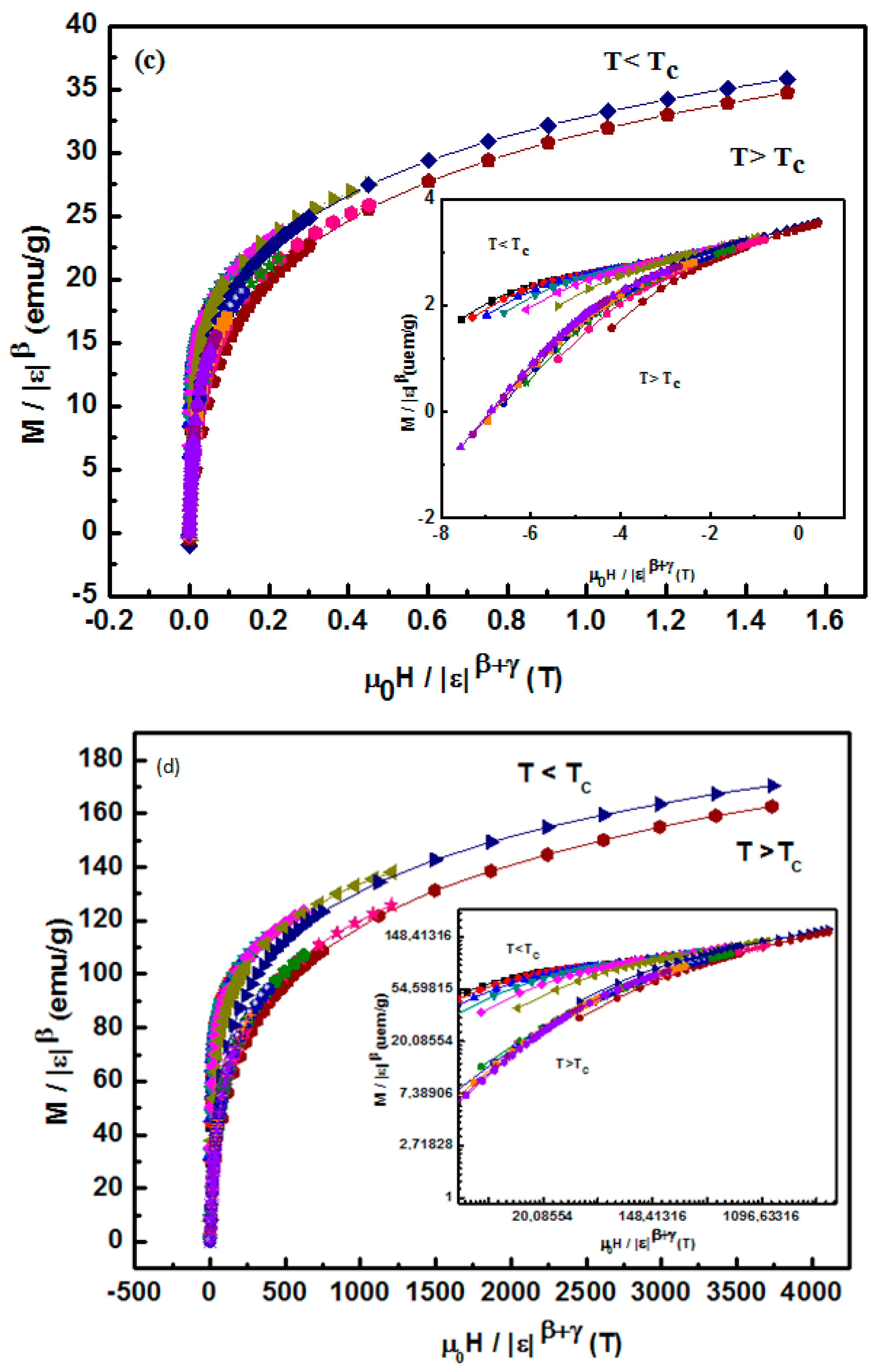
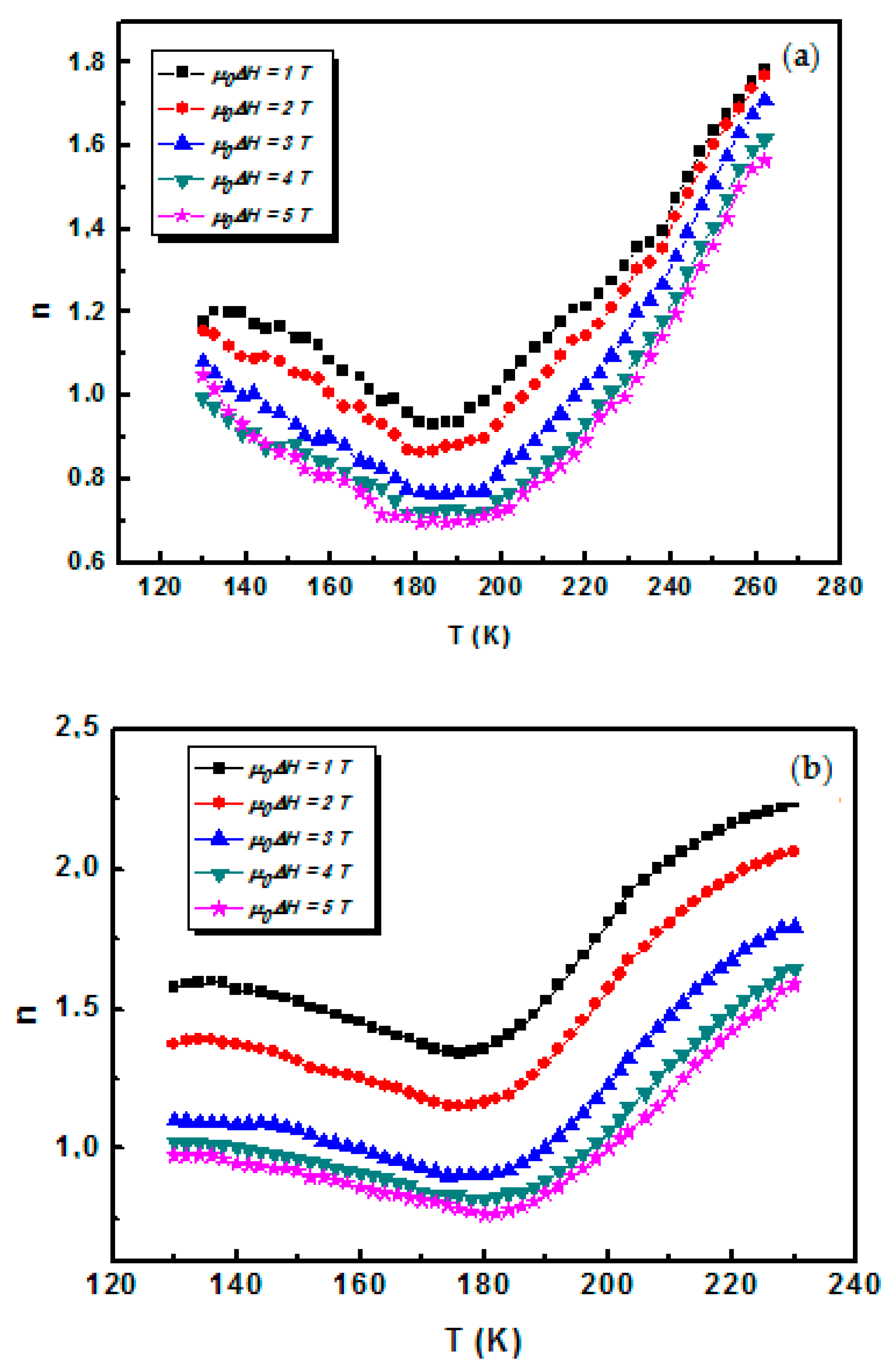
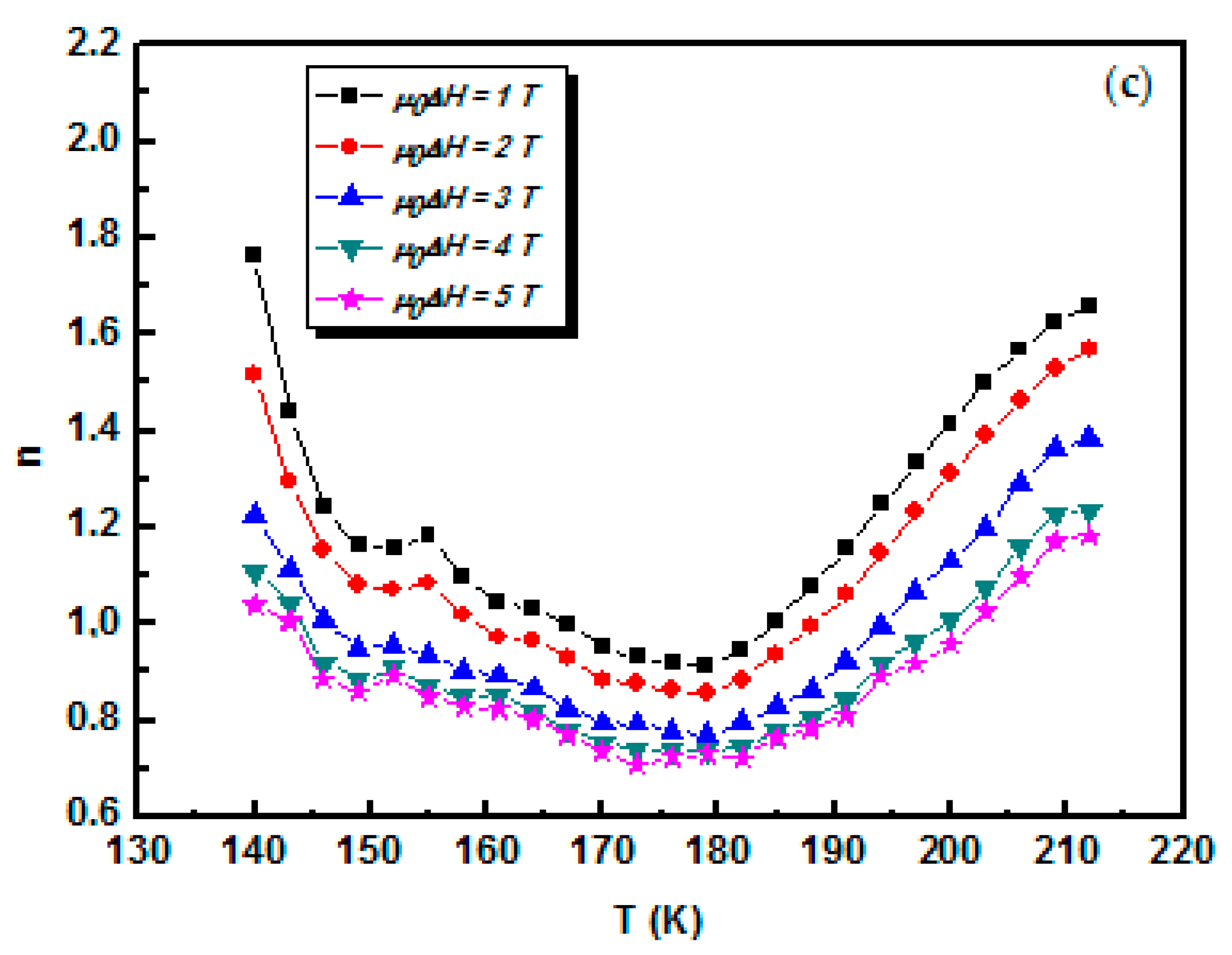
| Compositions | Model | TC(K) | β | γ | δ | Ref. |
|---|---|---|---|---|---|---|
| Mean-field model | Theory | - | 0.5 | 1 | 3 | [28] |
| 3D-Heisenberg model | Theory | - | 0.365 ± 0.003 | 1.386 ± 0.004 | 4.8 | [28] |
| 3D-Ising model | Theory | - | 0.325 ± 0.003 | 1.241 ± 0.002 | 4.82 | [28] |
| Tricritical mean field model | Theory | - | 0.25 | 1 | 5 | [28] |
| La0.8Ca0.2Mn0.9Co0.1O3 | MAP | 188.3 | 0.204 ± 0.06 | 1.969 ± 0.01 | 11.983 | This Work |
| KF method | 182.4 | 0.123 ± 0.04 | 1.351 ± 0.08 | |||
| CI (exp) | 181 | - | - | 7.51 | ||
| La0.8Ca0.2Mn0.8Co0.2O3 | MAP | 176.3 | 0.401 ± 0.02 | 1.332 ± 0.05 | 4.321 | This Work |
| KF method | 176.3 | 0.418 ± 0.04 | 1.303 ± 0.01 | |||
| CI (exp) | 176 | - | - | 4.081 | ||
| La0.8Ca0.2Mn0.7Co0.3O3 | MAP | 172.6 | 0.333 ± 0.03 | 1.298 ± 0.02 | 4.897 | This Work |
| KF method | 174.3 | 0.404 ± 0.01 | 1.27 ± 0.04 | |||
| CI (exp) | 173 | - | - | 4.629 | ||
| La0.8Ca0.2MnO3 (0–1T) | - | 185.6 | 0.349 ± 0.013 | 1.231 ± 0.03 | 4.524 | [15] |
| La0.8Ca0.2MnO3 (1–2T) | - | 188.5 | 0.316 ± 0.007 | 1.081 ± 0.036 | 4.421 | |
| La0.8Ca0.2MnO3 (2–3T) | - | 190.4 | 0.281 ± 0.009 | 0.992 ± 0.036 | 4.534 | |
| La0.8Ca0.2MnO3 (3–4T) | - | 194.0 | 0.272 ± 0.006 | 0.910 ± 0.021 | 4.341 | |
| La0.8Ca0.2MnO3 (4–5T) | - | 195.3 | 0.259 ± 0.004 | 0.918 ± 0.036 | 4.552 | |
| La0.8Ca0.2MnO3 | MAP | 181.375 | 0.328 | 1.193 | - | [23] |
| KF method | 181.676 | 0.325 | 1.180 | - | ||
| CI (exp) | - | - | - | 4.826 | ||
| CI (cal) | - | - | - | 4.630 | ||
| Pr0.73Ca0.27MnO3 | - | 127 | 0.36 | 1.36 | 4.81 | [37] |
| La0.9Te0.1MnO3 | - | 240 | 0.201 | 1.27 | 7.14 | [38] |
| La0.77Ca0.23MnO3 | - | 185 | 0.43 | 1.35 | 5.5 | [39] |
| La0.75Ca0.25MnO3 | - | 189 | 0.51 | 1.15 | 15 | |
| La0.7Sr0.3MnO3 | KF | 360 | 0.3776 ± 0.004 | 1.1686 ± 0.006 | 4.106 ± 0.01 | [40] |
| La0.7Sr0.3Mn0.95Co0.05O3 | KF | 320 | 0.4036 ± 0.005 | 1.1596 ± 0.007 | 3.886 ± 0.01 | |
| La0.7Sr0.3Mn0.9Co0.1O3 | KF | 281 | 0.4576 ± 0.007 | 1.1146 ± 0.005 | 3.446 ± 0.01 | |
| La0.7Sr0.3Mn0.85Co0.15O3 | KF | 274 | 0.4186 ± 0.004 | 1.1876 ± 0.006 | 3.846 ± 0.01 | |
| La0.7Sr0.3CoO3 | KF | 224 | 0.4146 ± 0.007 | 1.2086 ± 0.008 | 3.926 ± 0.01 | |
| La0.7Sr0.3Mn0.95Co0.05O3 | - | 360 | 0.387 ± 0.008 | 1.166 ± 0.01 | 4 4.01 | [11] |
| La0.7Sr0.3Mn0.94Co0.06O3 | - | 311 | 0.478 ± 0.013 | 1.165 ± 0.027 | 3.44 | |
| La0.7Sr0.3Mn0.92Co0.08O3 | - | 297 | 0.483 ± 0.018 | 1.112 ± 0.028 | 3.30 | |
| La0.7Sr0.3Mn0.9Co0.1O3 | - | 281 | 0.487 ± 0.016 | 1.109 ± 0.063 | 3.28 | |
| Nd0.7Sr0.3MnO3 | - | 240 | 0.271 | 0.922 | - | [41] |
| (Nd0.93Y0.07)0.7Sr0.3MnO3 | - | 175 | 0.234–0.236 | 1.044–1.063 | - | |
| (La0.9Dy0.1)0.8Pb0.2MnO3 | - | 248.4 | 0.484 ± 0.02 | 0.961 ± 0.012 | 2.90 ± 0.01 | [42] |
| La0.79Ca0.21MnO3 | - | 182 | 0.09 | 1.71 | 20 | [43] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turki, D.; Ghouri, Z.K.; Al-Meer, S.; Elsaid, K.; Ahmad, M.I.; Easa, A.; Remenyi, G.; Mahmood, S.; Hlil, E.K.; Ellouze, M.; et al. Critical Behavior of La0.8Ca0.2Mn1−xCoxO3 Perovskite (0.1 ≤ x ≤ 0.3). Magnetochemistry 2017, 3, 28. https://doi.org/10.3390/magnetochemistry3030028
Turki D, Ghouri ZK, Al-Meer S, Elsaid K, Ahmad MI, Easa A, Remenyi G, Mahmood S, Hlil EK, Ellouze M, et al. Critical Behavior of La0.8Ca0.2Mn1−xCoxO3 Perovskite (0.1 ≤ x ≤ 0.3). Magnetochemistry. 2017; 3(3):28. https://doi.org/10.3390/magnetochemistry3030028
Chicago/Turabian StyleTurki, Dorra, Zafar Khan Ghouri, Saeed Al-Meer, Khaled Elsaid, M. I. Ahmad, Ahmed Easa, Gyorgy Remenyi, Sami Mahmood, El Kebir Hlil, Mohamed Ellouze, and et al. 2017. "Critical Behavior of La0.8Ca0.2Mn1−xCoxO3 Perovskite (0.1 ≤ x ≤ 0.3)" Magnetochemistry 3, no. 3: 28. https://doi.org/10.3390/magnetochemistry3030028
APA StyleTurki, D., Ghouri, Z. K., Al-Meer, S., Elsaid, K., Ahmad, M. I., Easa, A., Remenyi, G., Mahmood, S., Hlil, E. K., Ellouze, M., & Elhalouani, F. (2017). Critical Behavior of La0.8Ca0.2Mn1−xCoxO3 Perovskite (0.1 ≤ x ≤ 0.3). Magnetochemistry, 3(3), 28. https://doi.org/10.3390/magnetochemistry3030028







