Effect of Twisting and Stretching on Magneto Resistance and Spin Filtration in CNTs
Abstract
:1. Introduction
2. Simulation Method and Setup
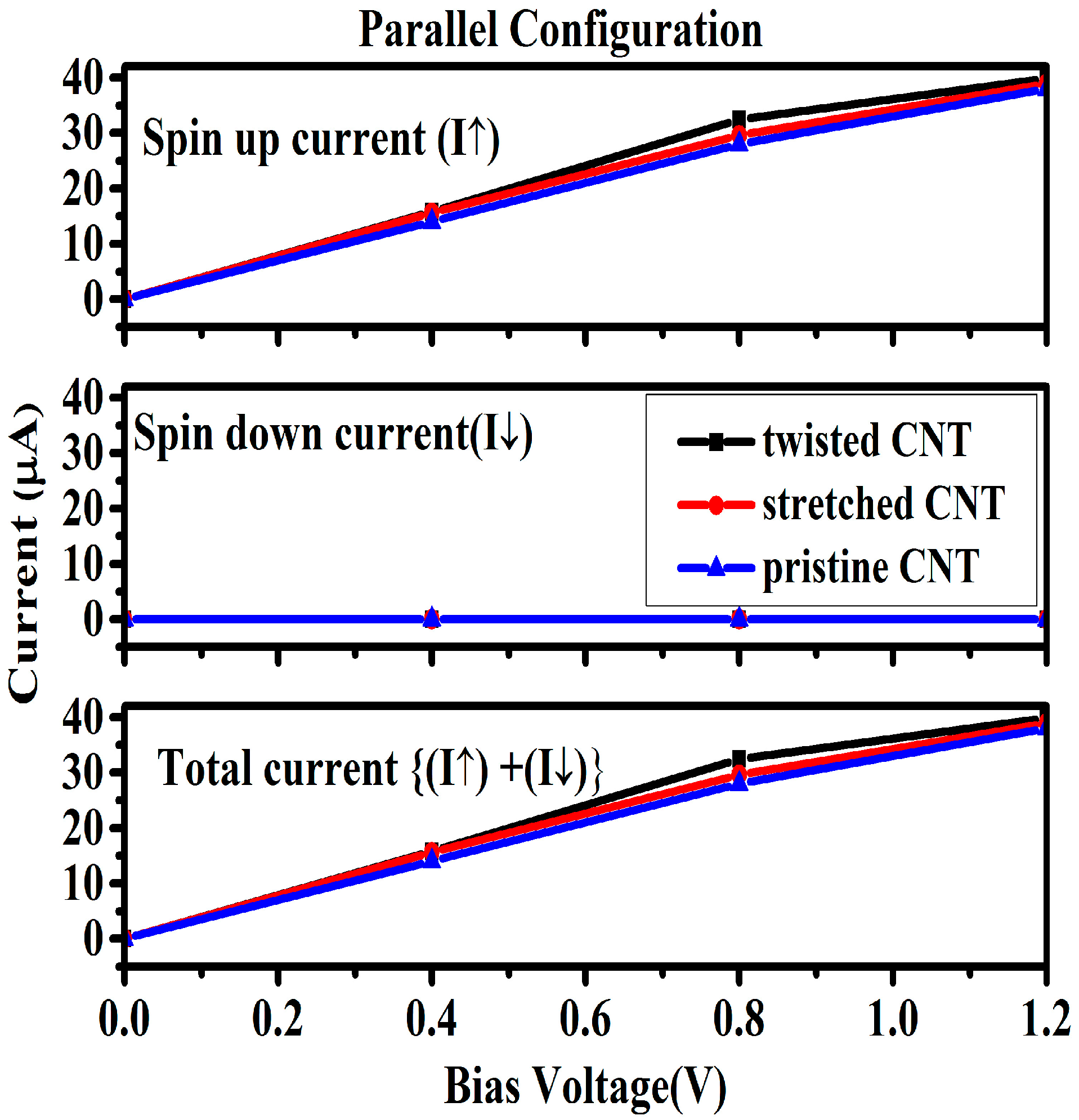
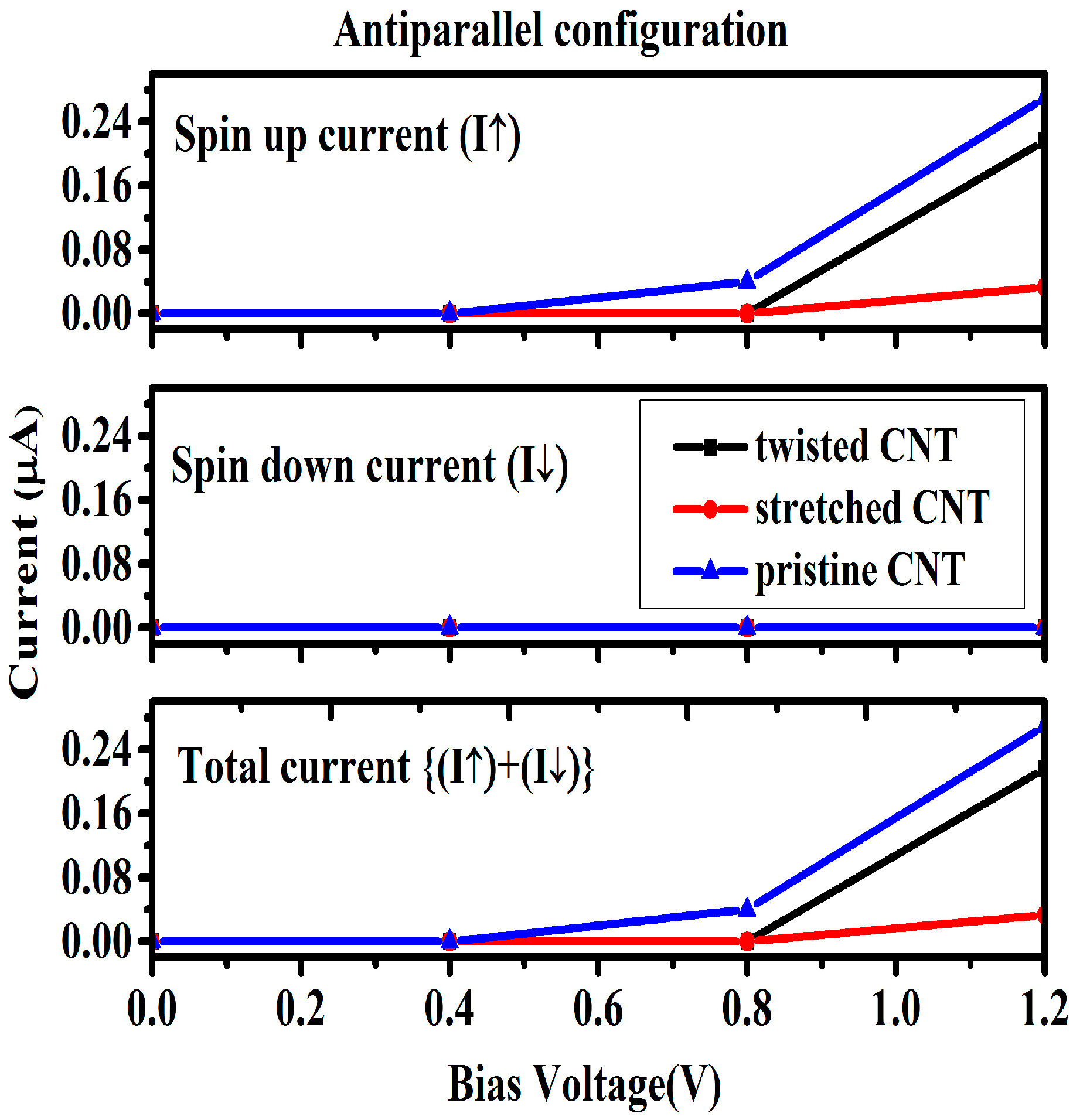
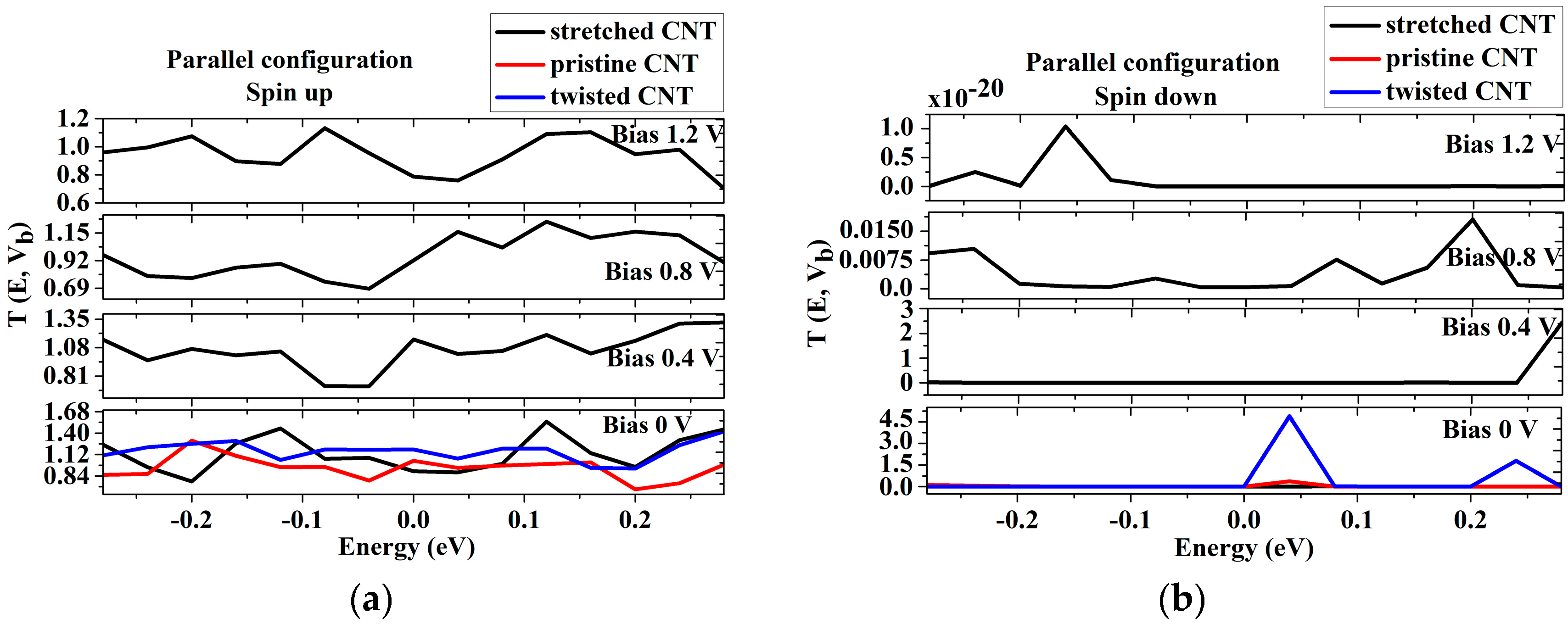
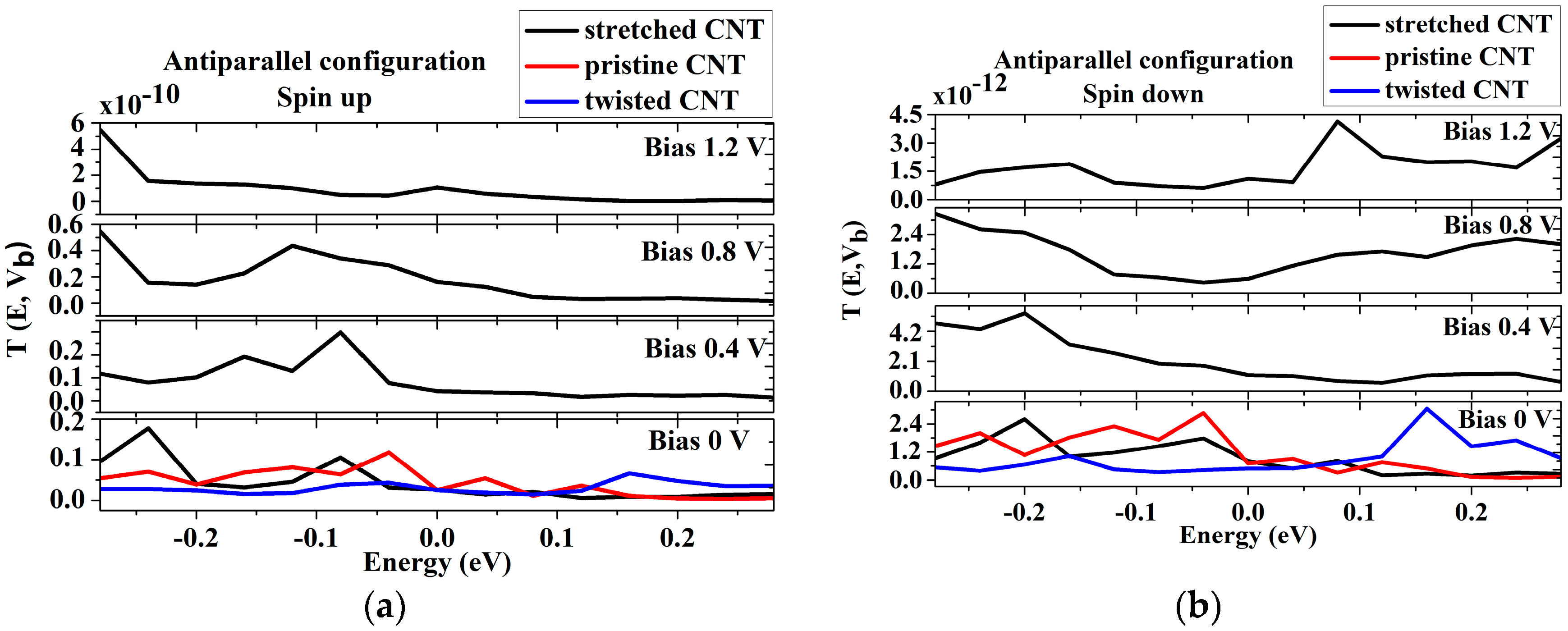
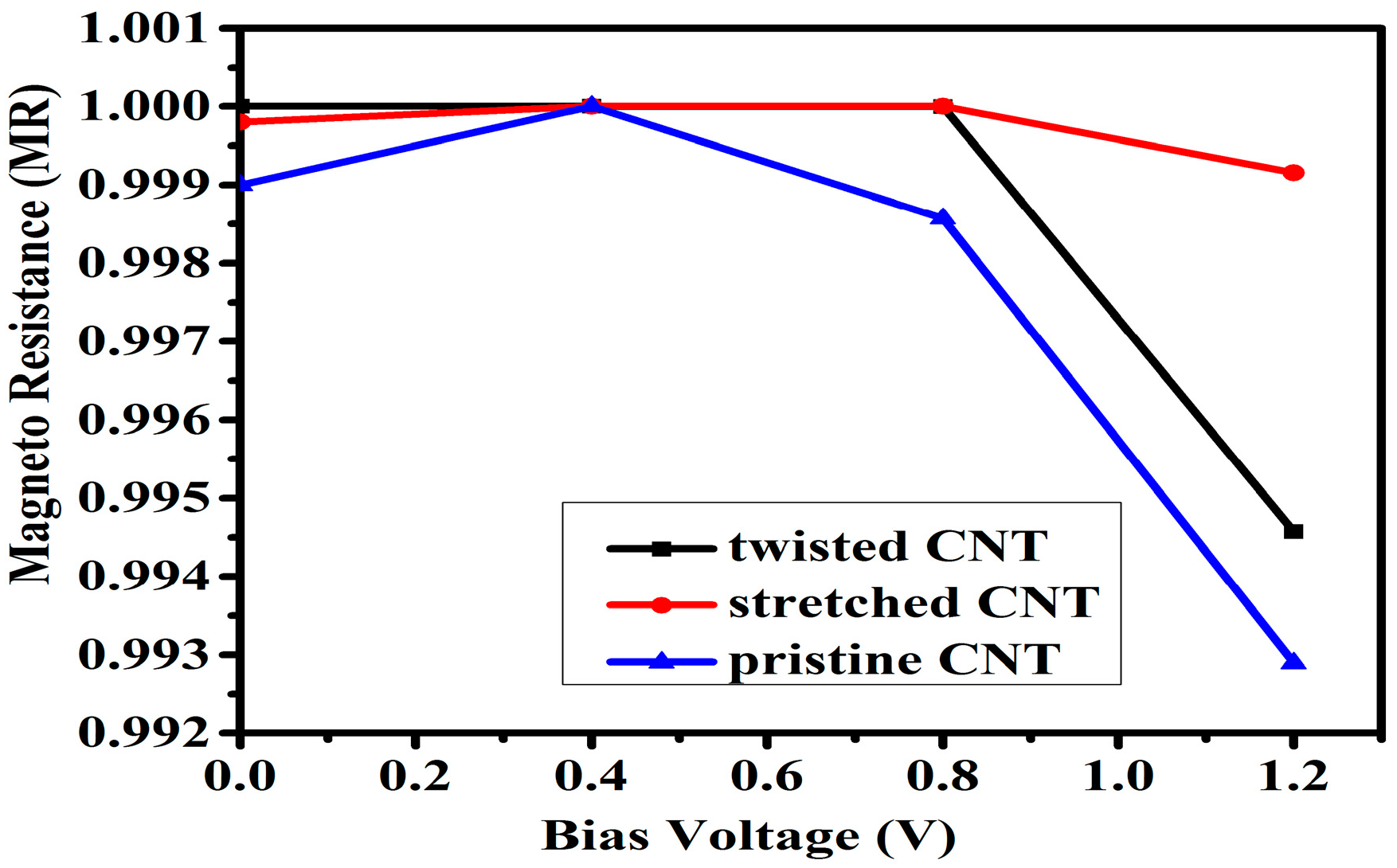
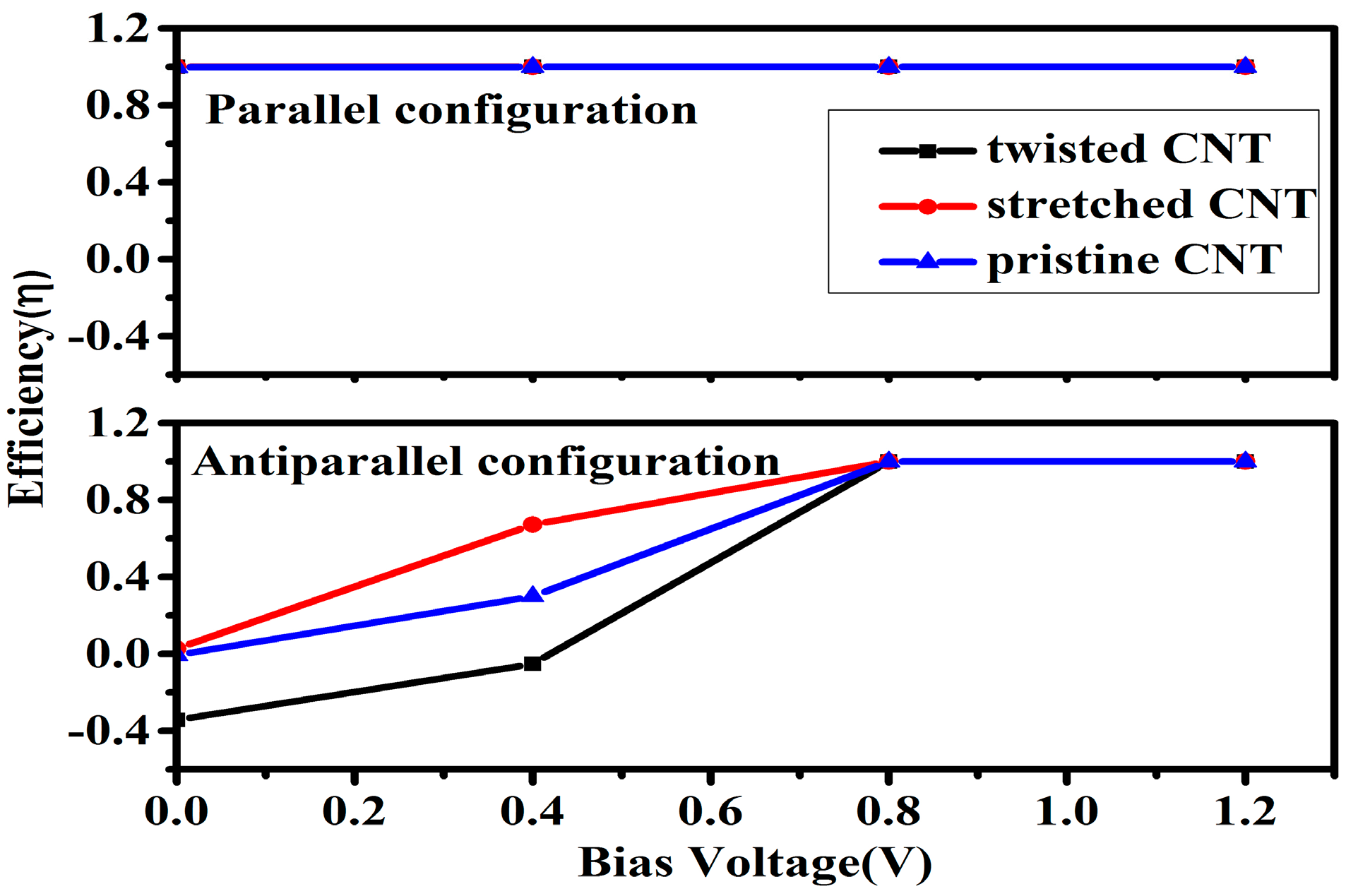
3. Results and Discussion
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Yao, K.L.; Min, Y.; Liu, Z.L.; Cheng, H.G.; Zhu, S.C.; Gao, G.Y. First-principles study of transport of V doped boron nitride nanotube. Phys. Lett. A 2008, 372, 5609–5613. [Google Scholar] [CrossRef]
- Titus, E.; Krishna, R.; Grácio, J.; Singh, M.; Ferreira, A.L.; Dias, R.G. Carbon nanotube based magnetic tunnel junctions (MTJs) for spintronics application, Electronic Properties of Carbon Nanotube. InTech 2011. [Google Scholar] [CrossRef]
- Bratkovsky, A.M. Tunneling of electrons in conventional and half-metallic systems towards very large magnetoresistance. Phys. Rev. B 1997, 56, 2344. [Google Scholar] [CrossRef]
- Anguelouch, A.; Gupta, A.; Xiao, G.; Abraham, D.W.; Ji, Y.; Ingvarsson, S.; Chien, C.L. Near-complete spin polarization in atomically-smooth chromium-dioxide epitaxial films prepared using a CVD liquid precursor. Phys. Rev. B 2001, 64, 180408. [Google Scholar] [CrossRef]
- Miao, G.X.; LeClair, P.; Gupta, A.; Xiao, G.; Varela, M.; Pennycook, S. Magnetic tunnel junctions based on CrO2/SnO2 epitaxial bilayers. Appl. Phys. Lett. 2006, 89, 022511. [Google Scholar] [CrossRef]
- Fu, Q.F.; Hao, D.P.; Yan, X.M.; He, D.W.; Chen, Z.S.; Wang, L.G.; Terence, K.S. Electronics properties of Single-walled Twisted carbon nanotubes. In Proceedings of the 2011 IEEE Fourth International Conference on Information and Computing (ICIC), Phuket Island, Thailand, 25–27 April 2011. [Google Scholar]
- Mintmire, J.W.; Dunlap, B.I.; White, C.T. Are fullerene tubes metallic. Phys. Rev. Lett. 1992, 68, 631–634. [Google Scholar] [CrossRef] [PubMed]
- Hamada, N.; Sawada, S.; Oshiyama, A. New one-dimensional conductors: Graphitic microtubules. Phys. Rev. Lett. 1992, 68, 1579–1581. [Google Scholar] [CrossRef] [PubMed]
- Saito, R.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Electronic structure of chiral graphene tubules. Appl. Phys. Lett. 1992, 60, 2204–2206. [Google Scholar] [CrossRef]
- Saito, R.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Electronic structure of graphene tubules based on C60. Phys. Rev. B 1992, 46, 1804–1811. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, Y.; Ren, W.; Wang, J.; Guo, H. Spin-dependent transport in Fe-doped carbon nanotubes. Phys. Rev. B 2007, 75, 235415. [Google Scholar] [CrossRef]
- Zhao, B.; Monch, I.; Vinzelberg, H.; Muhl, T.; Schneider, C.M. Spin-coherent transport in ferromagnetically contacted carbon nanotubes. Appl. Phys. Lett. 2002, 80, 3144. [Google Scholar] [CrossRef]
- Choudhary, S.; Varshney, M. First-Principles Study of Spin Transport in CrO2–CNT–CrO2 Magnetic Tunnel Junction. J. Superconduct. Novel Magn. 2015, 28, 3141–3145. [Google Scholar] [CrossRef]
- Atomistix, QuantumWise A/S. Available online: www.quantumwise.com (accessed on 1 April 2011).
- Brandbyge, M.; Mozos, J.L.; Ordejón, P.; Taylor, J.; Stokbro, K. Density-functional method for nonequilibriun electron transport. Phys. Rev. B 2002, 65, 165401. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.; Guo, H.; Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 2001, 63, 245407. [Google Scholar] [CrossRef] [Green Version]
- José, M.; Emilio Artacho, S.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar]
- Engel, E.; Vosko, S.H. Exact exchange-only potentials and the virial relation as microscopic criteria for generalized gradient approximations. Phys. Rev. B 1993, 47, 13164. [Google Scholar] [CrossRef]
- Lee, I.-H.; Martin, R.M. Applications of the generalized-gradient approximation to atoms, clusters, and solids. Phys. Rev. B 1997, 56, 7197. [Google Scholar] [CrossRef]
- Wang, W.G.; Li, M.; Hageman, S.; Chien, C.L. Electric-field-assisted switching in magnetic tunnel junctions. Nat. Mater. 2012, 11, 64. [Google Scholar] [CrossRef] [PubMed]
- Nowak, J.; Rauluszkiewicz, J. Spin dependent electron tunneling between ferromagnetic films. J. Magn. Magn. Mater. 1992, 109, 79–90. [Google Scholar] [CrossRef]
- Choudhary, S.; Qureshi, S. Theoretical study on transport properties of a BN co-doped SiC nanotube. Phys. Lett. A 2011, 375, 3382–3385. [Google Scholar] [CrossRef]
- Poklonski, N.A.; Ratkevich, S.V.; Vyrko, S.A.; Kislyakov, E.F.; Bubel, O.N.; Popov, A.M.; Lozovik, Y.E.; Hieu, N.N.; Viet, N.A. Structural phase transition and bandgap of uniaxiallydeformed (6, 0) carbon nanotube. Chem. Phys. Lett. 2012, 545, 71–77. [Google Scholar] [CrossRef]
- Chakraverty, M.; Kittur, H.M.; Arun Kumar, P. First principle simulations of various magnetic tunnel junctions for applications in magnetoresistive random access memories. IEEE Trans. Nanotechnol. 2013, 6, 12. [Google Scholar]
- Kiran, V.; Cohen, S.R.; Naaman, R. Structure dependent spin selectivity in electron transport through oligopeptides. J. Chem. Phys. 2017, 146, 092302. [Google Scholar] [CrossRef]



© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, A.K.; Choudhary, S. Effect of Twisting and Stretching on Magneto Resistance and Spin Filtration in CNTs. Magnetochemistry 2017, 3, 27. https://doi.org/10.3390/magnetochemistry3030027
Singh AK, Choudhary S. Effect of Twisting and Stretching on Magneto Resistance and Spin Filtration in CNTs. Magnetochemistry. 2017; 3(3):27. https://doi.org/10.3390/magnetochemistry3030027
Chicago/Turabian StyleSingh, Anil Kumar, and Sudhanshu Choudhary. 2017. "Effect of Twisting and Stretching on Magneto Resistance and Spin Filtration in CNTs" Magnetochemistry 3, no. 3: 27. https://doi.org/10.3390/magnetochemistry3030027
APA StyleSingh, A. K., & Choudhary, S. (2017). Effect of Twisting and Stretching on Magneto Resistance and Spin Filtration in CNTs. Magnetochemistry, 3(3), 27. https://doi.org/10.3390/magnetochemistry3030027




