Abstract
This mini-review describes electrical conductivity, magnetic properties, and magnetotransport properties of one-dimensional partially oxidized salts composed of axially ligated phthalocyanines, TPP[M(Pc)(CN)2]2 (TPP = tetraphenylphosphonium, Pc = phthalocyaninato), with M of Fe (d5, S = 1/2) and Cr (d3, S = 3/2). These salts are isomorphous, and π–π interactions in the crystal, that becomes the origin of the charge carriers, are nearly the same. Both the Fe and Cr salts show carrier localization and charge disproportionation which is enhanced by the interaction between local magnetic moments and conduction π-electrons (π–d interaction). However, the magnetic properties are slightly different between them. M = Fe has been found to show unique anisotropic magnetic properties and antiferromagnetic short-range magnetic order between the d-spins. On the other hand, for M = Cr, its magnetic moment is isotropic. Temperature dependence of the magnetic susceptibility shows typical Curie–Weiss behavior with negative Weiss temperature, but the exchange interaction is complicated. Both M = Fe and M = Cr show large negative magnetoresistance, reflecting the difference in the anisotropy. The magnetoresistance ratio (MR) is larger in the Fe system than in the Cr system in the low magnetic field range, but MR in the Cr system exceeds that in the Fe system when the magnetic field becomes higher than 15 T. We discuss the mechanism of the giant negative magnetoresistance with reference to the d–d, π–d, and π–π interactions.
1. Introduction
As well as the planar phthalocyanines, M(Pc) (Figure 1a), axially ligated phthalocyanine anions, [M(Pc)L2]− (Figure 1b), give electrically conducting partially oxidized salts by electrolysis [1]. So far, the anionic complexes with M of Co [2], Fe [3], Cr [4], Mn [5], and Ru [6] and L of CN, Cl, and Br [7] have been synthesized. The d orbitals in M show ligand-field splitting by the coordination of Pc2− and L, and take low-spin d electron configuration. In this situation, CoIII (d6) becomes non-magnetic, but the other metals have unpaired electrons, introducing local magnetic moments in the conduction paths. In this mini-review, we describe the magnetic, transport, and magnetotransport properties of the conductors of M = Fe (d5, S = 1/2) and Cr (d3, S = 3/2) with the cationic component of TPP (tetraphenylphosphonium) and L = CN. Before starting to describe the properties of these magnetic conductors, we briefly survey the structure and properties of the system with M = Co.
Figure 1.
(a) Planar M(Pc) and (b) axially ligated [M(Pc)L2]−.
For M = Co and L = CN, a partially oxidized salt of TPP[Co(Pc)(CN)2]2 was obtained when the TPP salt (TPP[Co(Pc)(CN)2]) was electrochemically oxidized. If the cationic part was exchanged, a series of conducting crystals with various dimensionality of the π–π interactions were obtained [8,9]. In this mini-review, we will focus on the TPP salts.
In TPP[Co(Pc)(CN)2]2, the Pc units form a one-dimensional (1D) π–π stacking chain with negligible interchain interactions (Figure 2a) [2]. The π–π stacking is uniform. Since each Pc ring is oxidized by 1/2e (TPP+[Co3+(Pc1.5−)(CN−)2]2), the HOMO (highest occupied molecular orbital of the Pc π-system) band becomes three-quarters-filled (metallic band). However, the temperature dependence of the resistivity showed thermally activated behavior (Figure 2b). The 59Co-NQR experiments revealed that the ground state was a charge disproportionation phase (Figure 2c) [10]. This results from the fact that the π system is susceptible to the electron correlation effect due to the narrow conduction band. Indeed, the band width of the slipped π–π stacking system was estimated to be about 0.5 eV from the thermoelectric power measurements, which is much smaller compared with those of the typical face-to-face stacked systems, e.g., 0.88 eV for Ni(Pc)I [1].
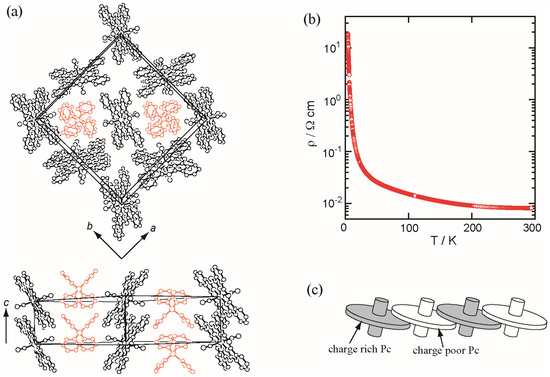
Figure 2.
(a) Crystal structure of TPP[Co(Pc)(CN)2]2 (TPP = tetraphenylphosphonium); (b) temperature dependence of the single-crystal resistivity (along the c-axis) of TPP[Co(Pc)(CN)2]2; and (c) schematic picture of the charge disproportionation in TPP[Co(Pc)(CN)2]2.
We were interested in how the physical properties would be altered by exchanging non-magnetic CoIII (d6, S = 0) with magnetic FeIII (d5, S = 1/2) in this TPP salt [3]. Fortunately, introduction of FeIII negligibly affected the molecular structure of the Pc unit and the crystal structure in the TPP salt. This is because the ion size of Fe3+ is almost the same as that of Co3+ (ionic radius r(Fe3+) = 0.64 Å and r(Co3+) = 0.63 Å). Thus, the geometry of the Pc unit was not affected and the crystal of TPP[Fe(Pc)(CN)2]2 was isomorphous with TPP[Co(Pc)(CN)2]2 (Table 1). In addition, the difference in π–π interaction between these two crystals was found to be negligible (overlap integral between the Pc π-HOMOs; 0.0085 in the Co system and 0.0087 in the Fe system) [3]. Therefore, one can see that the Co compound can be a good reference of the pure π-system when one discusses the effect of the local magnetic moments on the physical properties in the Fe compound.

Table 1.
Crystal Data of TPP[M(Pc)(CN)2]2.
Similarly, replacement by CrIII (d3, S = 3/2) gave negligible effects on the molecular geometry, crystal structure (Table 1), and π–π interaction (overlap integral between the Pc π-HOMOs = 0.0091) because of almost the same ion size (r(Cr3+) = 0.63 Å) [4]. The Cr system is expected to have an isotropic magnetization because of the d3 configuration under the axially deformed octahedral ligand field (Figure 3a). On the other hand, the Fe system is expected to have an anisotropic magnetization by the spin-orbit interaction, because the degenerate dxz and dyz orbitals accommodate the unpaired electron under the D4h symmetry of low-spin d5 (Figure 3b). Thus, the difference between the Fe and Cr systems lies in the presence of the anisotropy in addition to the absolute value of the magnetic moment.
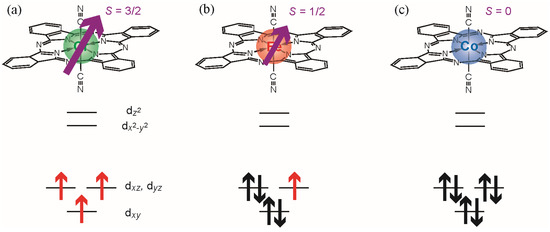
Figure 3.
Schematic picture of the energy levels of d-orbitals in the (a) CrIII(Pc)(CN)2; (b) FeIII(Pc)(CN)2, and (c) CoIII(Pc)(CN)2 units.
As described above, the replacement of M = Co by M = Fe and Cr in TPP[M(Pc)(CN)2]2 gives a good opportunity to discuss the π–d interactions by the various magnetic moments in the systems with common π–π interactions. Especially, we would like to emphasize that the Pc system is advantageous because the magnetic moment is introduced in the center of the π-ligand with fixed geometry. This situation is expected to yield larger π–d interactions compared with the other two-component systems with indirect π–d interactions between the individual π-conduction assemblies and counter ions with the local moment.
2. TPP[Fe(Pc)(CN)2]2 Magnetic Conductor
Since the discovery of the fascinating property of TPP[Fe(Pc)(CN)2]2, giant negative magnetoresistance [11], the magnetic exchange interactions between the π-spin and d-spin, including whether they are ferromagnetic or antiferromagnetic and how large they are, have been subjected to discussion. The experimental evidence was recently provided [12]. In conclusion, significantly strong ferromagnetic exchange interaction was found to exist between the Pc π-spin and Fe d-spin (Jπd/kB > 500 K). This confirms the unique feature expected for the Pc system, namely, strong intramolecular π–d exchange interaction should work in the single Pc unit. It should be noted that the magnitude of Jπd is extremely large compared with that estimated for the systems with π–d interactions between the individual π-conduction assemblies and counter ions with the local moment (order of ca. 10 K [13]).
With this feature in mind, the physical properties of TPP[Fe(Pc)(CN)2]2 are introduced. Firstly, its electrical conductivity is compared with that of the Co system [3]. The room-temperature resistivity (about 10−1 Ω cm) is one order of magnitude higher than that of the Co system, whereas the increase of the resistivity by lowering the temperature is rather steep. The value at 20 K is, thus, more than six orders of magnitude larger than that of the Co system (Figure 4a). This feature is considered to result from the development of charge disproportionation owing to the interaction between the local magnetic moment and π conduction electrons [14], and is consistent with the large Jπd.
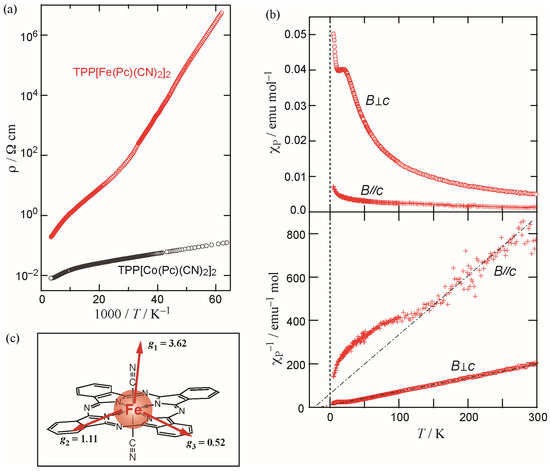
Figure 4.
(a) Temperature dependence of the resistivity (along the c axis) of TPP[Fe(Pc)(CN)2]2 and TPP[Co(Pc)(CN)2]2; (b) [upper panel] χp vs. T plot of the magnetic susceptibility of TPP[Fe(Pc)(CN)2]2 measured in the magnetic field (1 T) perpendicular and parallel to the c-axis. [lower panel] 1/χp vs. T plot for the same susceptibility data; (c) g-tensor anisotropy determined from the angular dependence of ESR of PNP[Fe(Pc)(CN)2] single crystal (PNP = bis(triphenylphosphine)iminium).
Secondly, its magnetic properties are described. Figure 4b shows the temperature dependence of the magnetic susceptibility (χP) of the oriented crystals. Large anisotropy is a prominent feature [11]. In B ⊥ c, the susceptibility shows an anomaly at 20–25 K, indicating the occurrence of the antiferromagnetic magnetic order. However, the susceptibility for B//c is significantly smaller and changes monotonically. The lower panel of Figure 4b shows a plot of 1/χP vs. T. For both B ⊥ c and B//c, the susceptibility reveals the Curie–Weiss-like behavior with similar Weiss temperature (–20 K < θ < –10 K) in the temperature range of 120–300 K.
The magnetic anisotropy was found to result from the large anisotropy of the g-tensor (Figure 4c) from the angular dependence of the ESR spectra of [Fe(Pc)(CN)2]− [15]. The origin of this anisotropy was considered to arise from the spin-orbit interaction under the situation in which the degenerate dxz and dyz orbitals accommodate the unpaired electron under the D4h symmetry (Figure 3b) [15]. However, the quantum chemistry calculation revealed that the Jahn–Teller effect lowers the symmetry to D2h, inducing splitting of dxz and dyz orbitals [7]. Even in this case, the energy difference between the ground state (dxz)2(dyz)1 and the excited state (dxz)1(dyz)2 configurations is very small (0.01–0.02 eV), and this situation suggests that the strong spin-orbit interaction plays an essential role in this system.
The numerical simulation based on the anisotropic Heisenberg model in one dimension was performed to explain the anomaly observed at 25 K for the susceptibility with B ⊥ c and the large anisotropy [16]. The results indicate that the anomaly at 25 K is due to antiferromagnetic short range order formation of the d electrons and that the π-electrons fall into an antiferromagnetic state at the lower temperatures. By combining the simulation results for the other one-dimensional system (PTMA0.5[Fe(Pc)(CN)2]·CH3CN, PTMA = phenyltrimethylammonium [17]), a model of charge-ordered ferrimagnetism was proposed for the spontaneous magnetization at low temperatures [18].
The most fascinating feature of this system is its magnetotransport properties, and the above-mentioned magnetic state is important to elucidate the origin of them. The negative magnetoresistance effect appears regardless of the direction of the magnetic field (Figure 5a). However, the magnitude of this effect precisely reflects the anisotropy of the magnetic susceptibility, namely, the effect is enhanced for B ⊥ c while it is reduced for B//c [11].
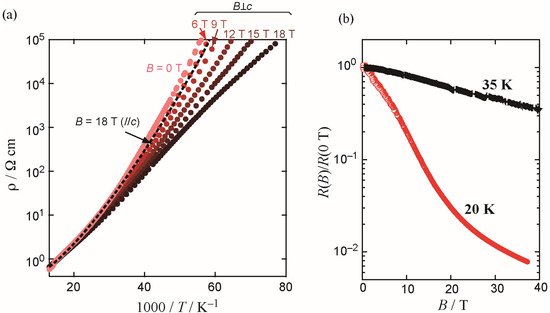
Figure 5.
(a) Temperature dependence of the resistivity of TPP[Fe(Pc)(CN)2]2 measured along the c axis in magnetic fields (0–18 T) perpendicular to the c axis and that in a magnetic field of 18 T parallel to the c axis (dashed curve); (b) Field dependence (B ⊥ c) of the magnetoresistance at 20 and 35 K.
Figure 5b shows the field dependence of the magnetoresistance up to 37 T at 20 K [19] and at 35 K. The resistance decreases smoothly, indicating that the giant negative magnetoresistance effect is not due to a magnetic field-induced first order phase transition. Though the magnetoresistance is still decreasing in 37 T, even at this stage, the magnetoresistance ratio (MR = {[R(B) − R(0 T)]/R(0 T)} × 100 (%)) is as large as −99.5%. The MR at 35 K is relatively small, about −65%, indicating less development of the charge disproportionation at this temperature (vide infra).
Now, let us discuss the mechanism of the appearance of the giant negative magnetoresistance in TPP[Fe(Pc)(CN)2]2. At zero magnetic field, the charge disproportionation state in π-electrons is caused by the intersite Coulomb interaction V, as observed for the Co salt. At low temperatures, a short-range antiferromagnetic order between the localized d-spins appears (|Jdd|/kB ~ 32 K). The d–d interaction is assumed to be through a superexchange mechanism, since the interaction rapidly decreases when the d-spin concentration is diluted below 50% [20]. The π-electron interacts with the localized magnetic moment by the strong π–d interaction (|Jπd|/kB >500 K). As a result, the charge disproportionation is enhanced (charge-ordered ferrimagnetism: middle panel in Figure 6). If the π-electron hops to the neighboring site whilst keeping the spin state, the spin becomes antiparallel to the localized d-spin. This situation increases the energy of the electronic system by Jπd. Therefore, Jπd effectively enhances the Coulomb effect of V.
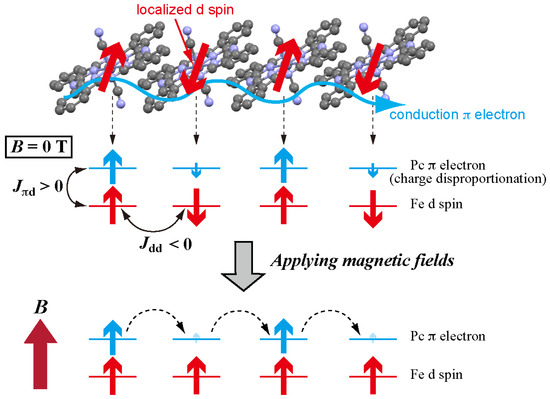
Figure 6.
One-dimensional chain of [Fe(Pc)(CN)2]1/2− (upper panel). Middle and lower panels show the schematic diagrams of the magnetic interactions at low temperature. At B = 0 T, Fe d-spins tend to form the antiferromagnetic short-range order that makes Pc π-electrons localized due to strong π–d interaction. In magnetic fields, breakage of the antiferromagnetic order of Fe d-spins allows Pc π-electrons to transfer to the neighboring site when the field is applied perpendicular to the c axis (1D chain direction).
Next, we consider the state in magnetic fields. At high temperature, there is an antiferromagnetic fluctuation enhancing the charge disproportionation. The resistivity may be increased only in this fluctuation region. Negative magnetoresistance is considered to be achieved by reducing this fluctuation region with applying magnetic fields. At low temperatures where weak ferromagnetism is observed, the antiferromagnetic order may grow considerably along the one-dimensional direction. As can be seen from the magnetization, high magnetic fields are required to destroy the short-range antiferromagnetic order of Fe d-spins. From the detailed magnetoresistance measurements of TPP[FexCo1-x(Pc)(CN)2]2, it was revealed that the charge disproportionation was rather developed in intermediate magnetic fields [20]. This is because the energy in the electronic system can decrease owing to the Zeeman effect when the π-electrons are localized. When the field becomes much higher, the short-range antiferromagnetic order of Fe d-spins is destroyed. At this stage, the local moment in the Pc unit becomes parallel to those in the neighboring units, and π-electrons can hop to the neighboring sites, leading to the reduction of the electrical resistance (lower panel in Figure 6) [21].
3. TPP[Cr(Pc)(CN)2]2 Magnetic Conductor
As shown in Figure 3a, CrIII in TPP[Cr(Pc)(CN)2]2 has S = 3/2, resulting in a larger magnetic moment than that of FeIII. In addition, even under D4h symmetry, all degenerate t3g orbitals accommodate an unpaired electron in the high spin state, thus the magnetization moment becomes almost isotropic, because the contribution from the spin-orbit momentum to the magnetism is quenched. Indeed, angular dependent ESR [4] and multifrequency ESR [22] experiments gave nearly isotropic g-value (g = 1.995 ± 0.005). The temperature dependence of the static magnetic susceptibility was found to follow the Curie–Weiss law above 50 K (Figure 7a) with the Curie constant C = 4.16 emu K mol−1 (expected value for S = 3/2; 3.75 emu K mol−1 (the formula unit contains two Cr(Pc)(CN)2 units)) and the Weiss temperature θ = −20 K (|J|/kB = 8.2 K from θ = zJS(S + 1)/3kB, where z (coordination number) = 2 for the 1-D system) [22]. Below 15 K, the observed susceptibility data is larger than that expected from the Curie–Weiss law. This may be due to contribution from the charge-order ferrimagnetism as observed for the Fe system. In the magnetization experiments under high magnetic fields, since the saturation of the magnetization was not observed even in 53 T within the measured temperature range, magnetic exchange interaction was estimated to be |Jdd|/kB >11.9 K [22].
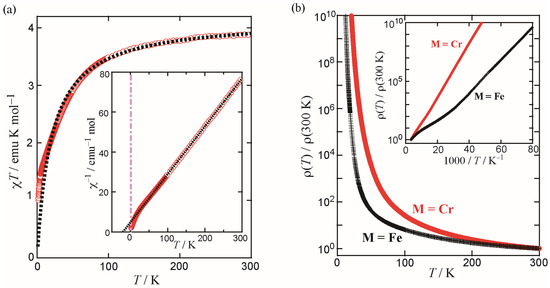
Figure 7.
(a) Temperature dependence of the product of magnetic susceptibility and temperature (χT) in 1 T of TPP[Cr(Pc)(CN)2]2. The dotted line represents a best fit by the Curie–Weiss law for the data above 50 K. Inset: Temperature dependence of the inverse susceptibility; (b) Temperature dependence of the resistivity normalized by the value at 300 K (ρ(T)/ρ(300 K)) of TPP[M(Pc)(CN)2]2 with M = Fe and Cr. Inset: Arrhenius plot of the normalized resistivity.
Figure 7b shows the temperature dependence of the resistivity of TPP[Cr(Pc)(CN)2]2. Though the room-temperature resistivity is almost the same as the Fe system (10−1~100 Ω cm), the activation energy of the conduction is higher compared with the Fe system, suggesting that the charge disproportionation is more developed in the Cr system. Indeed, the current density–electric field plot of TPP[Cr(Pc)(CN)2]2 showed negative differential resistance (NDR) below 60 K [4]; the temperature at which NDR appeared was significantly higher than that in the Fe system (NDR appeared below 30 K [23]). These facts strongly support that the charge localization in the Cr system occurs at higher temperature compared with the Fe system.
Since the charge disproportionation was suggested to be more developed in the Cr system, it was expected to show larger magnetoresistance effects. The first report up to the field strength of 9 T at 20 K indicated that the effect is only 25% of that observed for the Fe system [4]. However, the measurements at higher magnetic fields indicated that the magnetoresistance effect of the Cr system at 35 K near 50 T was 1.3 times larger than that observed for the Fe system (Figure 8). It can be seen from Figure 8 that the non-magnetic Co system shows normal positive magnetoresistance.
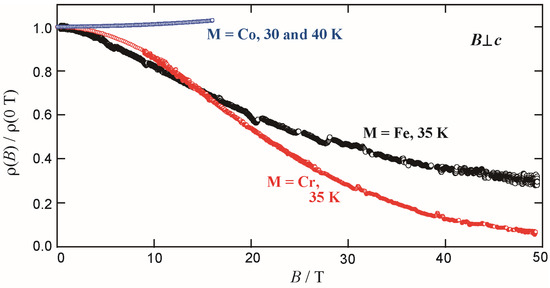
Figure 8.
Magnetic-field dependence of normalized resistivity [ρ(B)/ρ(0 T)] of TPP[M(Pc)(CN)2]2 for M = Fe (35 K), Cr (35 K) and Co (30 and 40 K) in magnetic fields perpendicular to the c axis.
Now, let us consider the difference between the Fe and Cr systems. For the saturation of the magnetization, higher magnetic fields are required in the Cr system than in the Fe system. This suggests that the antiferromagnetic interaction between the d-spins is larger in the Cr system than in the Fe system. This stronger interaction in the Cr system makes the charge disproportionation of the π-electrons more developed. As a result, when the d-spins are aligned parallel by the external magnetic fields, the charge disproportionation is attenuated by a larger degree, making the magnetoresistance effect more pronounced in the Cr system. When the magnetic field strength is insufficient to align the d-spins parallel, the charge disproportionation is affected by a much smaller degree, resulting in a smaller magnetoresistance effect compared with the Fe system.
At the present stage, there is no quantitative evaluation of the field strength required to align the d local moments. For the Fe system, the field dependence of the magnetoresistance seems to approach the point of saturation at this temperature. However, it is suggested that much higher field strength is required for the saturation of the magnetoresistance as well as magnetization in the Cr system than in the Fe system.
So far, the magnetic moment of the π-electron has not been included in the discussion. In the system without local magnetic moment, TPP[Co(Pc)(CN)2]2, the susceptibility shows nearly constant small values in the high-temperature region (~5 × 10−4 emu mol−1), because π-electrons can hop to the neighboring sites with the aid of finite t (transfer integral), resulting in the Pauli-like behavior [24]. However, at low temperatures, the susceptibility increases gradually where the line width of the ESR signal shows gradual broadening. This indicates that the π-electrons bear localized character along with the antiferromagnetic fluctuation [10], suggesting the growth of charge disproportionation.
This situation seems to be drastically changed by introducing a local magnetic moment (this accompanies large ferromagnetic π–d interaction). In the high-temperature region where the charge disproportionation is not fully developed, the susceptibility of the π-electrons is considered to become as small as that observed for the Co system (π-electrons can hop to the neighboring sites with certain probability due to the thermal fluctuation). At the present stage, we have not succeeded in estimating the contribution of the π-electrons from the observed susceptibility containing the large value of the localized magnetic moment. In the Fe system, there is a steep rise of the susceptibility in the low-temperature region. The magnetic torque experiments [16,18] suggested that the susceptibility of the π-electrons contributes to this steep rise. The π-electrons show an antiferromagnetic state below 13 K, and it is explained that this order leads to the charge-order ferrimagnetism (middle panel of Figure 6). In the Cr system, a steep rise of magnetization was also observed at low temperatures. However, there are different aspects in the magnetic behavior, suggesting more complicated magnetic interactions in the Cr system.
Though the magnetic order state of spins originating from the π-electrons can be observable only at low temperatures, traces of the order state may remain up to higher temperatures, as is the case for the d-spins (in the temperature range in which the charge disproportionation is observable). As shown in Figure 8, the negative magnetoresistance is indeed observed at 35 K. At this temperature, the charge disproportionation is considered to develop, though the ordering of the π-spins was not observed. The spins originating from the π-electrons also respond to the magnetic field through the strong π–d interactions. The detailed magnetic structure of the π-electrons in the Cr system may be different from that in the Fe system. However, it can be assumed that, in both the systems at 35 K, the π-electrons are released from the localized state in the charge disproportionation by destroying small domains of antiferromagnetic order of d-spins by applying external magnetic fields.
4. Conclusions
This mini-review describes the series of isostructural Pc conductors of TPP[M(Pc)(CN)2]2 that shows giant negative magnetoresistance with M = Fe and Cr. After the discovery of giant negative magnetoresistance of the Fe system in 2000, many studies have been conducted. The detailed aspects of the charge disproportionation, π–d interactions, d–d interactions, and π–π interactions have been disclosed by comparison with the non-magnetic Co system, by theoretical studies, and by the elaborate magnetic and magnetotransport measurements. At zero magnetic field, short-range antiferromagnetic order of d-spins follows the development of charge disproportionation. From the above experimental results, a model of charge-ordered ferrimagnetism was proposed. In magnetic fields, the following mechanism was proposed. The antiferromagnetic order of the d-spins is destroyed by the magnetic field, which leads to destabilization of the charge disproportionation state of the π-electrons. This causes the decrease of the resistance from the value at zero field.
On the other hand, studies on the system with a larger magnetic moment, M = Cr, have recently been conducted. In contrast to the anisotropic moment of the Fe system, the Cr system showed an almost isotropic moment. The charge disproportionation was suggested to be more developed in the Cr system. The magnetic measurements at high fields have suggested that there are rather robust antiferromagnetic interactions in the Cr system, supporting more developed charge disproportionation. As a result, the field dependence of the magnetoresistance of the Cr system crosses that of the Fe system, resulting in a larger negative magnetoresistance effect of the Cr system at higher magnetic fields.
Magnetic properties at high fields suggested that the mechanism of the negative magnetoresistance in the Cr system might contain some different aspects compared with the Fe system. Nevertheless, there seems to be a common feature in these systems: breakage of magnetic interactions between the d-spins follows destabilization of the charge disproportionation of the π-electrons that leads to the reduction of the resistance.
The occurrence of π–d interactions is ensured when magnetic ions of M are introduced into M(Pc)L2 units composing the molecular conductors. This is a valuable system that realizes unique magnetotransport properties. Though the M(Pc)L2 unit is flexible toward substitution of the components, the structural framework is rather robust. Therefore, this is a useful building block for the design of functional π–d systems.
Acknowledgments
The authors acknowledge all the researchers who collaborated this study. The authors especially thank to the following co-workers for their great contribution: Hiroyuki Tajima at University of Hyogo, Masaki Matsuda at Kumamoto University, Hiroshi Murakawa and Mitsuo Ikeda at Osaka University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Inabe, T.; Tajima, H. PhthalocyaninesVersatile components of molecular conductors. Chem. Rev. 2004, 104, 5503–5533. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, H.; Naito, T.; Inabe, T.; Akutagawa, T.; Nakamura, T. A highly conducting partially oxidized salt of axially substituted phthalocyanine. Structure and physical properties of TPP[Co(Pc)(CN)2]2 {TPP = tetraphenylphosphonium, [Co(Pc)(CN)2] = dicyano(phthalocyaninato)cobalt(III)}. J. Mater. Chem. 1998, 8, 1567–1570. [Google Scholar] [CrossRef]
- Matsuda, M.; Naito, T.; Inabe, T.; Hanasaki, N.; Tajima, H.; Otsuka, T.; Awaga, K.; Narymbetov, B.; Kobayashi, H. A one-dimensional macrocyclic π-ligand conductor carrying a magnetic center. Structure and electrical, optical and magnetic properties of TPP[Fe(Pc)(CN)2]2 {TPP = tetraphenylphosphonium, [Fe(Pc)(CN)2] = dicyano(phthalocyaninato)iron(III)}. J. Mater. Chem. 2000, 10, 631–636. [Google Scholar] [CrossRef]
- Takita, Y.; Hasegawa, H.; Takahashi, Y.; Harada, J.; Kanda, A.; Hanasaki, N.; Inabe, T. One-dimensional phthalocyanine-based conductor with S = 3/2 isotropic magnetic centers. J. Porphyr. Phthalocyanines 2014, 18, 814–823. [Google Scholar] [CrossRef]
- Matsuda, M.; Yamaura, J.; Tajima, H.; Inabe, T. Structure and magnetic properties of a low-spin manganese(III) phthalocyanine dycyanide complex. Chem. Lett. 2005, 34, 1524–1525. [Google Scholar] [CrossRef]
- Yu, D.E.; Kikuchi, A.; Taketsugu, T.; Inabe, T. Crystal structure of ruthenium phthalocyanine with diaxial monoatomic ligand: Bis(triphenylphosphine)iminium dichloro(phthalocyaninato(2-))ruthenium(III). J. Chem. 2013, 2013, 486318. [Google Scholar] [CrossRef]
- Yu, D.E.C.; Matsuda, M.; Tajima, H.; Kikuchi, A.; Taketsugu, T.; Hanasaki, N.; Naito, T.; Inabe, T. Variable magnetotransport properties in the TPP[Fe(Pc)L2]2 system (TPP = tetraphenylphosphonium, Pc = phthalocyaninato, L = CN, Cl, and Br). J. Mater. Chem. 2009, 19, 718–723. [Google Scholar] [CrossRef]
- Asari, T.; Naito, T.; Inabe, T.; Matsuda, M.; Tajima, H. Novel phthalocyanine conductor containing two-dimensional Pc stacks, [PXX]2[Co(Pc)(CN)2] (PXX = peri-xanthenoxanthene, Co(Pc)(CN)2 = dicyano(phthalocyaninato)cobalt(III)). Chem. Lett. 2004, 33, 128–129. [Google Scholar] [CrossRef]
- Asari, T.; Ishikawa, M.; Naito, T.; Matsuda, M.; Tajima, H.; Inabe, T. Nearly isotropic two-dimensional sheets in a partially oxidized Co(Pc)(CN)2 salt (Pc = phthalocyaninato). Chem. Lett. 2005, 34, 936–937. [Google Scholar] [CrossRef]
- Hanasaki, N.; Masuda, K.; Kodama, K.; Matsuda, M.; Tajima, H.; Yamazaki, J.; Takigawa, M.; Yamaura, J.; Ohmichi, E.; Osada, T.; et al. Charge disproportionation in highly one-dimensional molecular conductor TPP[Co(Pc)(CN)2]2. J. Phys. Soc. Jpn. 2006, 75, 104713. [Google Scholar] [CrossRef]
- Hanasaki, N.; Tajima, H.; Matsuda, M.; Naito, T.; Inabe, T. Giant negative magnetoresistance in quasi-one-dimensional conductor TPP[Fe(Pc)(CN)2]2: Interplay between local moments and one-dimensional conduction electrons. Phys. Rev. B 2000, 62, 5839–5842. [Google Scholar] [CrossRef]
- Murakawa, K.; Kanda, A.; Ikeda, M.; Matsuda, M.; Hanasaki, N. Giant ferromagnetic π-d interaction in a phthalocyanine molecule. Phys. Rev. B 2015, 92, 054429. [Google Scholar] [CrossRef]
- Mori, T.; Katsuhara, M. Estimation of πd-interactions in organic conductors including magnetic anions. J. Phys. Soc. Jpn. 2002, 71, 826–844. [Google Scholar] [CrossRef]
- Hotta, C.; Ogata, M.; Fukuyama, H. Interaction of the ground state of quarter-filled one-dimensional strongly correlated electronic system with localized spins. Phys. Rev. Lett. 2005, 95, 216402. [Google Scholar] [CrossRef] [PubMed]
- Hanasaki, N.; Matsuda, M.; Tajima, H.; Naito, T.; Inabe, T. Contribution of degenerate molecular orbitals to molecular orbital angular momentum in molecular magnet Fe(Pc)(CN)2. J. Phys. Soc. Jpn. 2003, 72, 3226–3230. [Google Scholar] [CrossRef]
- Tajima, H.; Yoshida, G.; Matsuda, M.; Nara, K.; Kajita, K.; Nishio, Y.; Hanasaki, N.; Naito, T.; Inabe, T. Magnetic torque and heat capacity measurements on TPP[Fe(Pc)(CN)2]2. Phys. Rev. B 2008, 78, 064424. [Google Scholar] [CrossRef]
- Matsuda, M.; Naito, T.; Inabe, T.; Hanasaki, N.; Tajima, H. Structure and electrical and magnetic properties of (PTMA)x[M(Pc)(CN)2]·y(solvent) (PTMA = phenyltrimethylammonium and [M(Pc)(CN)2] = dicyano(phthalocyaninato)MIII with M = Co and Fe). Partial oxidation by partial solvent occupation of the cationic site. J. Mater. Chem. 2001, 11, 2493–2497. [Google Scholar] [CrossRef]
- Tajima, H.; Yoshida, G.; Matsuda, M.; Yamaura, J.; Hanasaki, N.; Naito, T.; Inabe, T. Magnetic torque and ac and dc magnetic susceptibility measurements on PTMA0.5[Fe(Pc)(CN)2]·CH3CN: Origin of spontaneous magnetization in [Fe(Pc)(CN)2] molecular conductors. Phys. Rev. B 2009, 80, 024424. [Google Scholar] [CrossRef]
- Hanasaki, N.; Matsuda, M.; Tajima, H.; Ohmichi, E.; Osada, T.; Naito, T.; Inabe, T. Giant negative magnetoresistance reflecting molecular symmetry in dicyano(phthalocyaninato)iron compounds. J. Phys. Soc. Jpn. 2006, 75, 033703. [Google Scholar] [CrossRef]
- Ikeda, M.; Kanda, A.; Murakawa, H.; Matsuda, M.; Inabe, T.; Tajima, H.; Hanasaki, N. Effect of localized spin concentration on giant magnetoresistance in molecular conductor TPP[FexCo1-x(Pc)(CN)2]2. J. Phys. Soc. Jpn. 2016, 85, 024713. [Google Scholar] [CrossRef]
- Hanasaki, N.; Tateishi, T.; Tajima, H.; Kimata, M.; Tokunaga, M.; Matsuda, M.; Kanda, A.; Murakawa, H.; Naito, T.; Inabe, T. Metamagentic transition and its related magnetocapacitance effect in phthalocyanine-molecular conductor exhibiting giant magnetoresistance. J. Phys. Soc. Jpn. 2013, 82, 094713. [Google Scholar] [CrossRef]
- Ikeda, M.; Kida, T.; Tahara, T.; Murakawa, H.; Nishi, M.; Matsuda, M.; Hagiwara, M.; Inabe, T.; Hanasaki, N. High magnetic field study on giant negative magnetoresistance in the molecular conductor TPP[Cr(Pc)(CN)2]2. J. Phys. Soc. Jpn. 2016, 85, 064713. [Google Scholar] [CrossRef]
- Ishikawa, M.; Yamashita, S.; Naito, T.; Matsuda, M.; Tajima, H.; Hanasaki, N.; Akutagawa, T.; Nakamura, T.; Inabe, T. Nonlinear transport phenomena in highly one-dimsnsional MIII(Pc)(CN)2 chains with π–d interaction (M = Co and Fe and Pc = phthalocyaninnato). J. Phys. Soc. Jpn. 2009, 78, 104709. [Google Scholar] [CrossRef]
- Yamashita, S.; Naito, T.; Inabe, T. Purity effects on the charge-transport propertoes in one-dimensional TPP[CoIII(Pc)(CN)2]2 (TPP = tetraphenylphosphonium and Pc = phthalocyaninato) conductors. Bull. Chem. Soc. Jpn. 2009, 82, 692–694. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).