Molecular Spins in the Context of Quantum Technologies
Abstract
:1. Introduction
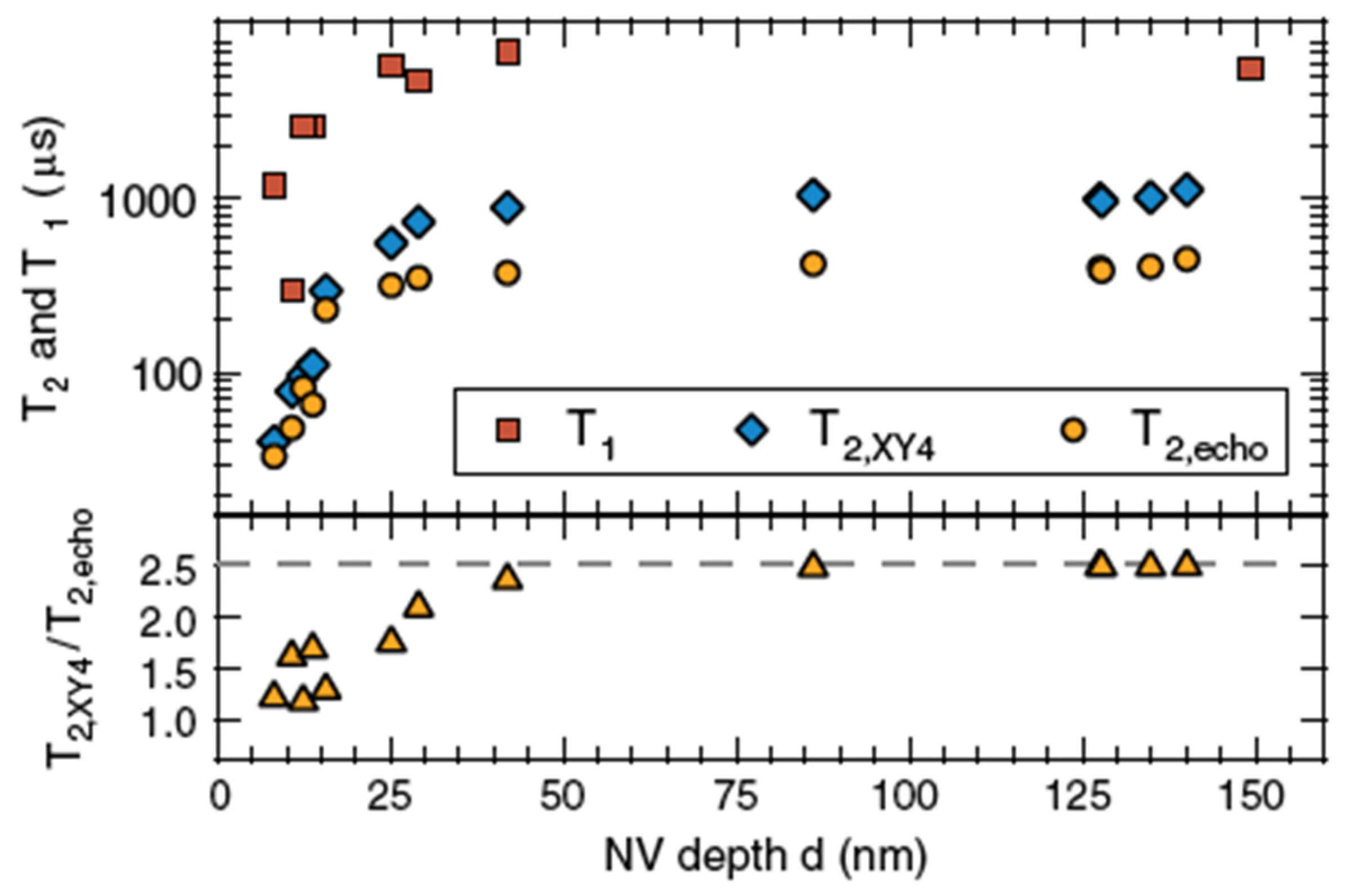
2. Coherent Spin Dynamics of Spin Ensembles
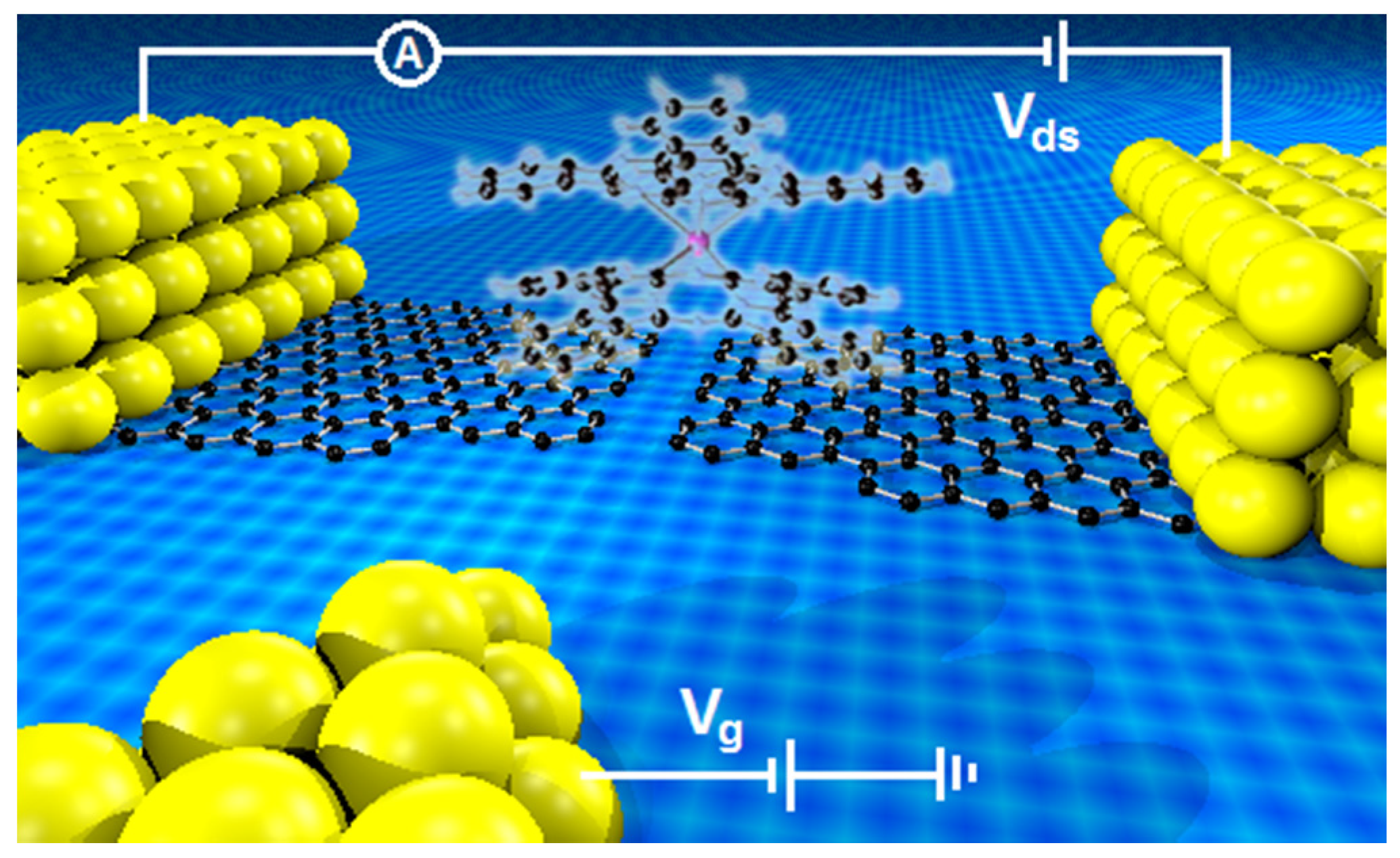
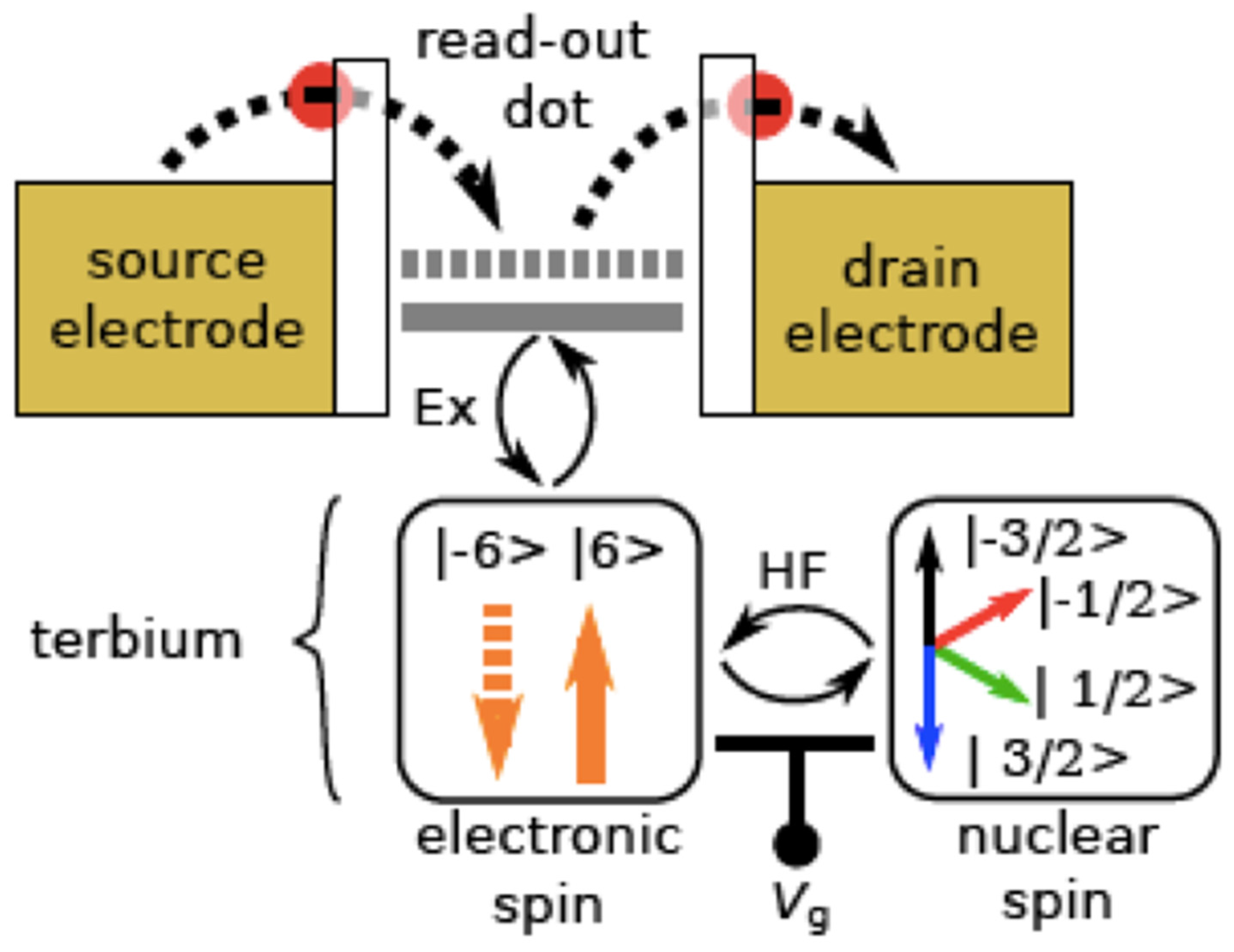
3. Molecular Quantum Spintronics
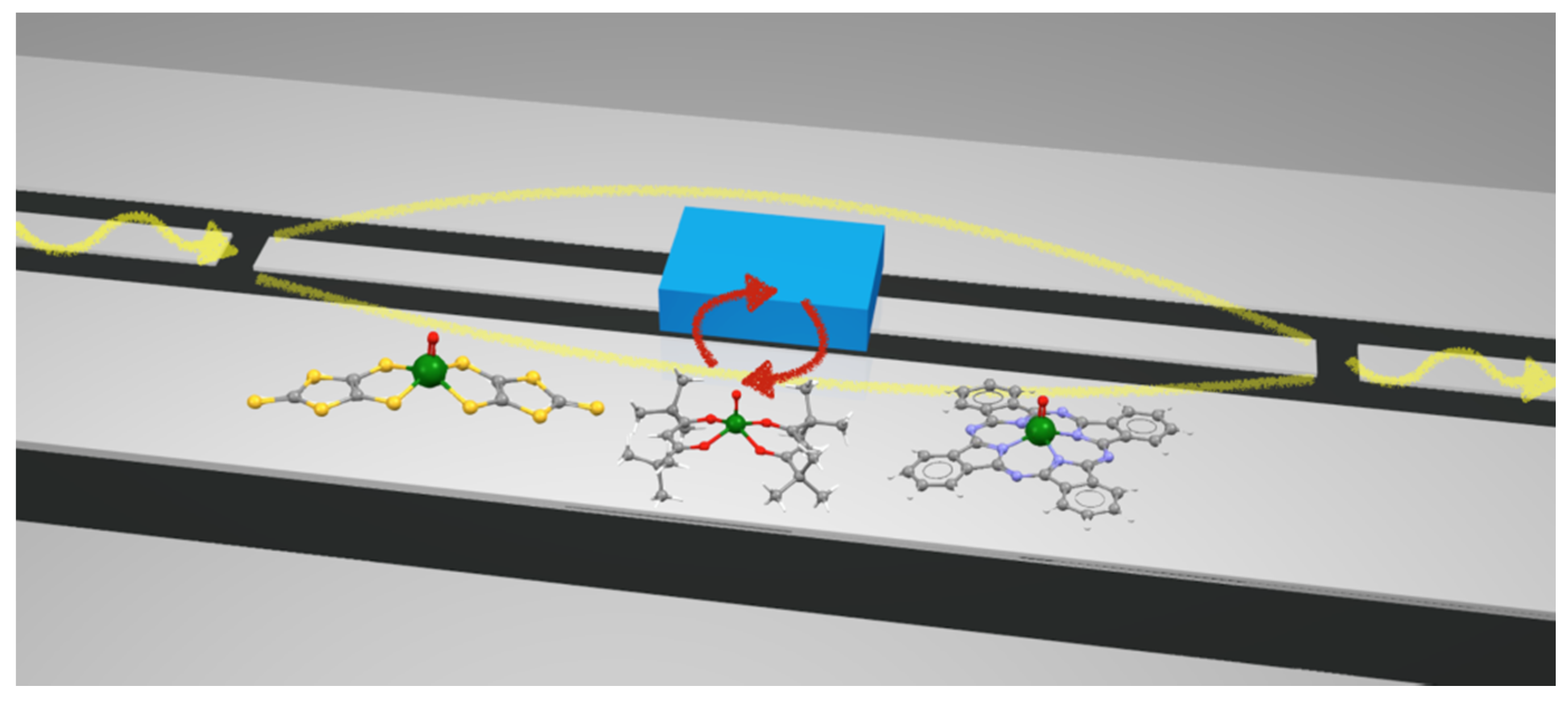
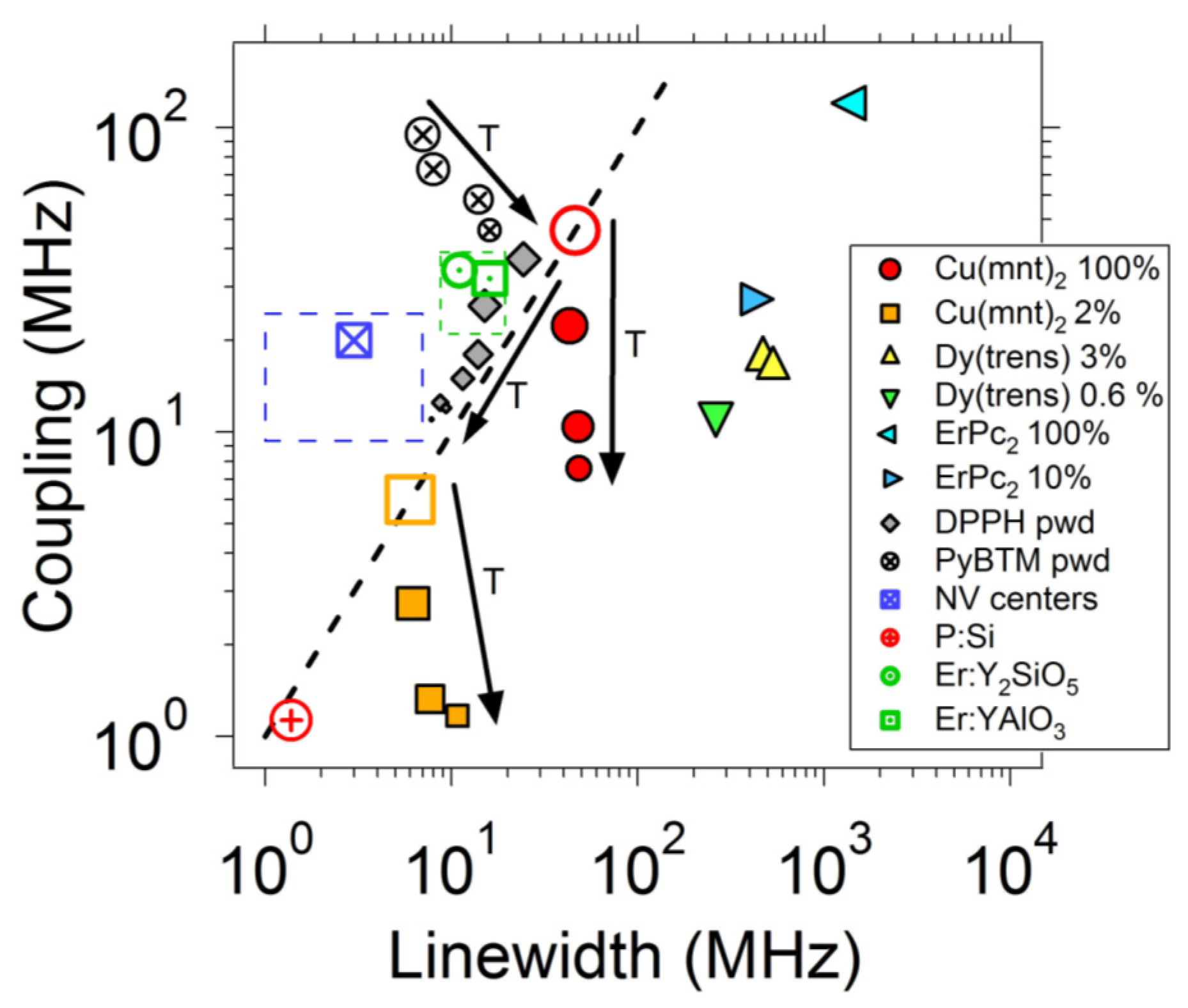
4. Molecular Spins in Hybrid Quantum Architectures
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Quantum technology. Available online: https://en.wikipedia.org/wiki/Quantum_technology (accessed on 24 February 2017).
- Dutt, M.V.; Childress, L.; Jiang, L.; Togan, E.; Maze, J.; Jelezko, F.; Zibrov, A.S.; Hemmer, P.R.; Lukin, M.D. Quantum Register Based on Individual Electronic and Nuclear Spin Qubits in Diamond. Science 2007, 316, 1312–1316. [Google Scholar] [CrossRef] [PubMed]
- Morton, J.J.; McCamey, D.R.; Eriksson, M.A.; Lyon, S.A. Embracing the quantum limit in silicon computing. Nature 2011, 479, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Troiani, F.; Ghirri, A.; Affronte, M.; Carretta, S.; Santini, P.; Amoretti, G.; Piligkos, S.; Timco, G.; Winpenny, R.E.P. Molecular Engineering of antiferromagnetic rings for quantum computation. Phys. Rev. Lett. 2005, 94, 207208. [Google Scholar] [CrossRef] [PubMed]
- Troiani, F.; Affronte, M. Molecular Spins for Quantum Information Technologies. Chem. Soc. Rev. 2011, 40, 3119–3129. [Google Scholar] [CrossRef] [PubMed]
- Ghirri, A.; Troiani, F.; Affronte, M. Quantum Computation with Molecular Nanomagnets: achivements, challenges and new trends. In Molecular Nanomagnets and Related Phenomena—Structure and Bonding; Gao, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 164, pp. 383–430. [Google Scholar]
- J. Mater. Chem. 2009, whole issue 19. Available online: http://pubs.rsc.org/en/journals/journalissues/jm?e=1#!issueid=jm019019&type=archive&issnprint=0959-9428 (accessed on 24 February 2017).
- Bartolomé, j.; Luis, F.; Fernandez, J.F. Molecular magnets Physics and Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Coronado, E.; Yamashita, M. Molecular Spintronics: The role of Coordination Chemistry. Dalton Trans. 2016, 45, 16553–16555. [Google Scholar] [CrossRef] [PubMed]
- Ardavan, A.; Rival, O.; Morton, J.J.L.; Blundell, S.J.; Tyryshkin, A.M.; Timco, G.A.; Winpenny, R.E.P. Will Spin-Relaxation Times in Molecular Magnets Permit Quantum Information Processing? Phys. Rev. Lett. 2007, 98, 057201. [Google Scholar] [CrossRef] [PubMed]
- Bertaina, S.; Gambarelli, S.; Mitra, T.; Tsukerblat, B.; Müller, A.; Barbara, B. Quantum oscillations in a molecular magnet. Nature 2008, 453, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Warner, M.; Din, S.; Tupitsyn, I.S.; Morley, G.W.; Marshall Stoneham, A.; Gardener, J.A.; Wu, Z.; Fisher, A.J.; Heutz, S.; Kay, C.W.M.; et al. Potential for spin-based information processing in a thin-film molecular semiconductor. Nature 2013, 503, 504–508. [Google Scholar] [CrossRef] [PubMed]
- Bader, K.; Dengler, D.; Lenz, S.; Endeward, B.; Jiang, S.-D.; Neugebauer, P.; van Slageren, J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. [Google Scholar] [CrossRef] [PubMed]
- Graham, M.J.; Zadrozny, J.M.; Shiddiq, M.; Anderson, J.S.; Fataftah, M.S.; Hill, S.; Freedman, D.E. Influence of Electronic Spin and Spin-Orbit Coupling on Decoherence in Mononuclear Transition Metal Complexes. J. Am. Chem. Soc. 2014, 136, 7623–7626. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Niklas, J.; Poluektov, O.G.; Freedman, D.E. Multiple Quantum Coherences from Hyperfine Transitions in a Vanadium(IV) Complex. J. Am. Chem. Soc. 2014, 136, 15841–15844. [Google Scholar] [CrossRef] [PubMed]
- Atzori, M.; Tesi, L.; Morra, E.; Chiesa, M.; Sorace, L.; Sessoli, R. Room Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016, 138, 2154–2157. [Google Scholar] [CrossRef] [PubMed]
- Myers, B.A.; Das, A.; Dartiailh, M.C.; Ohno, K.; Awschalom, D.D.; Bleszynski Jayich, A.C. Probing Surface Noise with Depth-Calibrated Spins in Diamond. Phys. Rev. Lett. 2014, 113, 027602. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Mamin, H.J.; Sherwood, M.H.; Ohno, K.; Awschalom, D.D.; Rugar, D. Decoherence of Near-Surface Nitrogen-Vacancy Centers Due to Electric Field Noise. Phys. Rev. Lett. 2015, 115, 087602. [Google Scholar] [CrossRef] [PubMed]
- Wedge, C.J.; Timco, G.A.; Spielberg, E.T.; George, R.E.; Tuna, F.; Rigby, S.; McInnes, E.J.L.; Winpenny, R.E.P.; Blundell, S.J.; Ardavan, A. Chemical Engineering of Molecular Qubits. Phys. Rev. Lett. 2012, 108, 107204. [Google Scholar] [CrossRef] [PubMed]
- Cornia, A.; Taham, D.; Affronte, M. Thin Layers of Molecular Nanomagnets Chapter in Book Molecular Magnetic Materials. Concepts and Applications; Sieklucka, B., Pinkowicz, D., Eds.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ding, Y.-S.; Deng, Y.-F.; Zheng, Y.-Z. The Rise of Single-Ion Magnets as Spin Qubits. Magnetochemistry 2016, 2, 40. [Google Scholar] [CrossRef]
- Troiani, F.; Bellini, V.; Candini, A.; Lorusso, G.; Affronte, M. Spin Entanglement in supramolecular structures. Nanotechnology 2010, 21, 274009. [Google Scholar] [CrossRef] [PubMed]
- Timco, G.A.; Carretta, S.; Troiani, F.; Tuna, F.; Pritchard, R.J.; McInnes, E.J.L.; Ghirri, A.; Candini, A.; Santini, P.; Amoretti, G.; et al. Engineering coupling between molecular spin qubits by coordination chemistry. Nat. Nanotechnol. 2009, 4, 173–178. [Google Scholar] [CrossRef] [PubMed]
- Candini, A.; Lorusso, G.; Troiani, F.; Ghirri, A.; Carretta, S.; Santini, P.; Amoretti, G.; Muryn, C.; Tuna, F.; Timco, G.; et al. Entanglement in supramolecular spin systems of two weakly coupled antiferromagnetic rings (purple Cr7Ni). Phys. Rev. Lett. 2010, 104, 037203. [Google Scholar] [CrossRef] [PubMed]
- Troiani, F.; Affronte, M.; Carretta, S.; Santini, P.; Amoretti, G. Proposal for Quantum-gate in permanently coupled AF spin rings, without need of local fields. Phys. Rev. Lett. 2005, 94, 190501. [Google Scholar] [CrossRef] [PubMed]
- Chiesa, A.; Whitehead, G.F.S.; Carretta, S.; Carthy, L.; Timco, G.A.; Teat, S.J.; Amoretti, G.; Pavarini, E.; Winpenny, R.E.P.; Santini, P. Molecular nanomagnets with switchable coupling for quantum simulation. Sci. Rep. 2014, 4, 7423. [Google Scholar] [CrossRef] [PubMed]
- Toyli, D.M.; Weis, C.D.; Fuchs, G.D.; Schenkel, T.; Awschalom, D.D. Chip-scale nanofabrication of single spins and spin arrays in diamond. Nano Lett. 2010, 10, 3168–3172. [Google Scholar] [CrossRef] [PubMed]
- Dolde, F.; Bergholm, V.; Wang, Y.; Jakobi, I.; Naydenov, B.; Pezzagna, S.; Meijer, J.; Jelezko, F.; Neumann, P.; Schulte-Herbruggen, T.; et al. High-fidelity spin entanglement using optimal control. Nat. Commun. 2014, 5, 3371. [Google Scholar] [CrossRef] [PubMed]
- Aguila, D.; Barrios, L.A.; Velasco, V.; Roubeau, O.; Repollés, A.; Alonso, P.J.; Sesé, J.; Teat, S.J.; Luis, F.; Aromí, G. Heterodimetallic [LnLn′] Lanthanide Complexes: Toward a Chemical Design of Two-Qubit Molecular Spin Quantum Gates. J. Am. Chem. Soc. 2014, 136, 14215–14222. [Google Scholar] [CrossRef] [PubMed]
- Nakazawa, S.; Nishida, S.; Ise, T.; Yoshino, T.; Mori, N.; Rahimi, R.D.; Sato, K.; Morita, Y.; Toyota, K.; Shiomi, D.; et al. A Synthetic Two-Spin Quantum Bit: G-Engineered Exchange-Coupled Biradical Designed for Controlled-NOT Gate Operations. Angew. Chem. Int. Ed. 2012, 51, 9860–9864. [Google Scholar] [CrossRef] [PubMed]
- Ferrando-Soria, J.; Pineda, E.M.; Chiesa, A.; Fernandez, A.; Magee, S.A.; Carretta, S.; Santini, P.; Vitorica-Yrezabal, I.J.; Tuna, F.; Timco, G.A.; et al. A modular design of molecular qubits to implement universal quantum gates. Nat. Commun. 2016, 7, 11377. [Google Scholar] [CrossRef] [PubMed]
- Baker, M.L.; Blundell, S.J.; Domingo, N.; Hill, S. Spectroscopy Methods for Molecular Nanomagnets. In Molecular Nanomagnets and Related Phenomena; Gao, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Du, J.; Rong, X.; Zhao, N.; Wang, Y.; Yang, J.; Liu, J.R.B. Preserving electron spin coherence in solids by optimal dynamical decoupling. Nature 2009, 461, 1265–1268. [Google Scholar] [CrossRef] [PubMed]
- Sato, K.; Nakazawa, S.; Rahimi, R.; Ise, T.; Nishida, S.; Yoshino, T.; Mori, N.; Toyota, K.; Shiomi, D.; Yakiyama, Y.; et al. Molecular electron-spin quantum computers and quantum information processing: pulse-based electron magnetic resonance spin technology applied to matter spin-qubits. Mater. Chem. 2009, 19, 3739–3754. [Google Scholar] [CrossRef]
- Santini, P.; Carretta, S.; Troiani, F.; Amoretti, G. Molecular Nanomagnets as Quantum Simulators. Phys. Rev. Lett. 2011, 107, 230502. [Google Scholar] [CrossRef] [PubMed]
- Chiesa, A.; Santini, P.; Carretta, S. Supramolecular Complexes for Quantum Simulation. Magnetochemistry 2016, 2, 37. [Google Scholar] [CrossRef]
- Cleuziou, J.-P.; Wernsdorfer, W.; Bouchiat, V.; Ondarcuhu, T.; Monthioux, M. Carbon nanotube superconducting quantum interference device. Nat. Nanotechnol. 2006, 1, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Brede, J.; Chilian, B.; Khajetoorians, A.A.; Wiebe, J.; Wiesendanger, R. Atomic-Scale Spintronics. In Handbook of Spintronics; Xu, Y., Awschalom, D., Nitta, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Komeda, T.; Isshiki, H.; Liu, J.; Zhang, Y.-F.; Lorente, N.; Katoh, K.; Breedlove, B.K.; Yamashita, M. Observation and electric current control of a local spin in a single-molecule magnet. Nat. Commun. 2011, 2, 217. [Google Scholar] [CrossRef] [PubMed]
- Müllegger, S.; Tebi, S.; Das, A.K.; Schöfberger, W.; Faschinger, F.; Koch, R. Radio Frequency Scanning Tunneling Spectroscopy for Single-Molecule Spin Resonance. Phys. Rev. Lett. 2014, 113, 133001. [Google Scholar] [CrossRef] [PubMed]
- Baumann, S.; Paul, W.; Choi, T.; Lutz, K.P.; Ardavan, A.; Heinrich, A.J. Electron paramagnetic resonance of individual atoms on a surface. Science 2015, 350, 417. [Google Scholar] [CrossRef] [PubMed]
- Zyazin, A.S.; van den Berg, J.W.G.; Osorio, E.A.; van der Zant, H.S.J.; Konstantinidis, N.P.; Leijnse, M.; Wegewijs, M.R.; May, F.; Hofstetter, W.; Danieli, C.; et al. Electric Field Controlled Magnetic Anisotropy in a Single Molecule. Nano Lett. 2010, 10, 3307–3311. [Google Scholar] [CrossRef] [PubMed]
- Burgess, J.A.J.; Malavolti, L.; Lanzilotto, V.; Mannini, M.; Yan, S.; Ninova, S.; Totti, F.; Rolf-Pissarczyk, S.; Cornia, A.; Sessoli, R.; et al. Magnetic fingerprint of individual Fe4 molecular magnets under compression by a scanning tunnelling microscope. Nat. Commun. 2015, 6, 8216. [Google Scholar] [CrossRef] [PubMed]
- Vincent, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Balestro, F. Electronic read-out of a single nuclear spin using a molecular spin transistor. Nature 2012, 488, 357–360. [Google Scholar] [CrossRef] [PubMed]
- Gaudenzi, R.; Burzurí, E.; Reta, D.; de P.R. Moreira, I.; Bromley, S.T.; Rovira, C.; Veciana, J.; van der Zant, H.S.J. Exchange Coupling Inversion in a High-Spin Organic Triradical Molecule. Nano Lett. 2016, 16, 2066–2071. [Google Scholar] [CrossRef] [PubMed]
- Urdampilleta, M.; Klyatskaya, S.; Cleuziou, J.P.; Ruben, M.; Wernsdorfer, W. Supramolecular spin valves. Nat. Mater. 2011, 10, 502–506. [Google Scholar] [CrossRef] [PubMed]
- Candini, A.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Affronte, M. Graphene Spintronic Devices with Molecular Nanomagnets. Nano Lett. 2011, 11, 2634–2639. [Google Scholar] [CrossRef] [PubMed]
- Urdampilleta, M.; Klayatskaya, S.; Ruben, M.; Wernsdorfer, W. Magnetic Interaction between a Radical Spin and a Single-Molecule Magnet in a Molecular Spin-Valve. ACS Nano 2015, 9, 4458–4464. [Google Scholar] [CrossRef] [PubMed]
- Lumetti, S.; Candini, A.; Godfrin, C.; Balestro, F.; Wernsdorfer, W.; Klyatskaya, S.; Ruben, M.; Affronte, M. Single-molecule devices with graphene electrodes. Dalton Trans. 2016, 45, 16570–16574. [Google Scholar] [CrossRef] [PubMed]
- Thiele, S.; Vincent, R.; Holzmann, M.; Klyatskaya, S.; Ruben, M.; Balestro, F.; Wernsdorfer, W. Electrical Readout of Individual Nuclear Spin Trajectories in a Single-Molecule Magnet Spin Transistor. Phys. Rev. Lett. 2013, 111, 037203. [Google Scholar] [CrossRef] [PubMed]
- Thiele, S.; Balestro, F.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W. Electrically driven nuclear spin resonance in single-molecule magnets. Science 2014, 344, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Pla, J.J.; Tan, K.Y.; Dehollain, J.P.; Lim, W.H.; Morton, J.J.L.; Jamieson, D.N.; Dzurak, A.S.; Morello, A. A single-atom electron spin qubit in silicon. Nature 2012, 489, 541–545. [Google Scholar] [CrossRef] [PubMed]
- Veldhorst, M.; Yang, C.H.; Hwang, J.C.C.; Huang, W.; Dehollain, J.P.; Muhonen, J.T.; Simmons, S.; Laucht, A.; Hudson, F.E.; Itoh, K.M.; et al. A two-qubit logic gate in silicon. Nature 2015, 526, 410–414. [Google Scholar] [CrossRef] [PubMed]
- Jelezko, F.; Gaebel, T.; Popa, I.; Domhan, M.; Gruber, A.; Wrachtrup, J. Observation of Coherent Oscillation of a Single Nuclear Spin and Realization of a Two-Qubit Conditional Quantum Gate. Phys. Rev. Lett. 2004, 93, 130501. [Google Scholar] [CrossRef] [PubMed]
- Waldherr, G.; Wang, Y.; Zaiser, S.; Jamali, M.; Schulte-Herbrüggen, T.; Abe, H.; Ohshima, T.; Isoya, J.; Du, J.F.; Neumann, P.; et al. Quantum error correction in a solid-state hybrid spin register. Nature 2014, 506, 204–207. [Google Scholar] [CrossRef] [PubMed]
- Leuenberger, M.N.; Loss, D. Quantum Computing in Molecular Nanomagnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Kubo, Y.; Ong, F.R.; Bertet, P.; Vion, D.; Jacques, V.; Zheng, D.; Dreau, A.; Roch, J.F.; Auffeves, A.; Jelezko, F.; et al. Strong Coupling of a Spin Ensemble to a Superconducting Resonator. Phys. Rev. Lett. 2010, 105, 140502. [Google Scholar] [CrossRef] [PubMed]
- Probst, S.; Rotzinger, H.; Wunsch, S.; Jung, P.; Jerger, M.; Siegel, M.; Ustinov, A.V.; Bushev, P.A. Anisotropic Rare-Earth Spin Ensemble Strongly Coupled to a Superconducting Resonator. Phys. Rev. Lett. 2013, 110, 157001. [Google Scholar] [CrossRef] [PubMed]
- Ghirri, A.; Bonizzoni, C.; Gerace, D.; Sanna, S.; Cassinese, A.; Affronte, M. YBCO microwave resonators for strong collective coupling with spin ensemble. Appl. Phys. Lett. 2015, 106, 184101. [Google Scholar] [CrossRef]
- Ghirri, A.; Bonizzoni, C.; Troiani, F.; Buccheri, N.; Beverina, L.; Cassinese, A.; Affronte, M. Coherently coupling distinct spin ensembles through a high-Tc superconducting resonator. Phys. Rev. A 2016, 93, 063855. [Google Scholar] [CrossRef]
- Bonizzoni, C.; Ghirri, A.; Bader, K.; van Slageren, J.; Perfetti, M.; Sorace, L.; Lan, Y.; Fuhr, O.; Ruben, M.; Affronte, M. Coupling molecular spin centers to microwave planar resonators: towards integration of molecular qubits in quantum circuits. Dalton Trans. 2016, 45, 16596–16603. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, M.D.; Zueco, D.; Roubeau, O.; Aromí, G.; Majer, J.; Luis, F. A scalable architecture for quantum computation with molecular nanomagnets. Dalton Trans. 2016, 45, 16682–16693. [Google Scholar] [CrossRef] [PubMed]
- Bienfait, A.; Pla, J.J.; Kubo, Y.; Stern, M.; Zhou, X.; Lo, C.C.; Weis, C.D.; Schenkel, T.; Thewalt, M.L.W.; Vion, D.; et al. Reaching the quantum limit of sensitivity in electron spin resonance. Nat. Nanotechnol. 2015, 11, 253–257. [Google Scholar] [CrossRef] [PubMed]
- Trif, M.; Troiani, F.; Stepanenko, D.; Loss, D. Spin-Electric Coupling in Molecular Magnets. Phys. Rev. Lett. 2008, 101, 217201. [Google Scholar] [CrossRef] [PubMed]
- George, R.E.; Edwards, J.P.; Ardavan, A. Coherent Spin Control by Electrical Manipulation of the Magnetic Anisotropy. Phys. Rev. Lett. 2013, 110, 027601. [Google Scholar] [CrossRef] [PubMed]
- Carretta, S.; Chiesa, A.; Troiani, F.; Gerace, D.; Amoretti, G.; Santini, P. Quantum Information Processing with Hybrid Spin-Photon Qubit Encoding. Phys. Rev. Lett. 2013, 111, 110501. [Google Scholar] [CrossRef] [PubMed]
- Grezes, C.; Julsgaard, B.; Kubo, Y.; Stern, M.; Umeda, T.; Isoya, J.; Sumiya, H.; Abe, H.; Onoda, S.; Ohshima, T.; et al. Multimode Storage and Retrieval of Microwave Fields in a Spin Ensemble. Phys. Rev. X 2014, 4, 021049. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghirri, A.; Candini, A.; Affronte, M. Molecular Spins in the Context of Quantum Technologies. Magnetochemistry 2017, 3, 12. https://doi.org/10.3390/magnetochemistry3010012
Ghirri A, Candini A, Affronte M. Molecular Spins in the Context of Quantum Technologies. Magnetochemistry. 2017; 3(1):12. https://doi.org/10.3390/magnetochemistry3010012
Chicago/Turabian StyleGhirri, Alberto, Andrea Candini, and Marco Affronte. 2017. "Molecular Spins in the Context of Quantum Technologies" Magnetochemistry 3, no. 1: 12. https://doi.org/10.3390/magnetochemistry3010012
APA StyleGhirri, A., Candini, A., & Affronte, M. (2017). Molecular Spins in the Context of Quantum Technologies. Magnetochemistry, 3(1), 12. https://doi.org/10.3390/magnetochemistry3010012





