Abstract
To our knowledge, no magnetic B2 phase in the Al–Mn system of near-equiatomic compositions has been reported so far. Here, we investigate the structural and magnetic characteristics of Al45Mn41.8X13.2 (X = Fe, Co or Ni) alloys. We demonstrate that adding 13.2 atomic percent magnetic 3d metal to AlMn stabilizes a ferromagnetic B2 structure, where Al and X occupy different sublattices. We employ density functional theory calculations and experimental characterizations to underscore the role of the late 3d metals for the phase stability of the quasi-ordered ternary systems. We show that these alloys possess large local magnetic moments primarily due to Mn atoms partitioned to the Al-free sublattice. The revealed magneto-chemical effect opens alternative routes for tailoring the magnetic properties of B2 intermetallic compounds for various magnetic applications.
1. Introduction
A promising strategy for the design of novel magnetic materials involves modulating the magnetic ordering through incorporating non-magnetic elements into itinerant magnetic metals. This approach allows for tailored magnetic properties, crucial for applications such as magnetic refrigeration and energy conversion. One representative example is the intermetallic compound FeRh, which crystallizes in the ordered B2 (CsCl-type) structure, characterized by an equiatomic distribution of Fe and Rh atoms occupying alternating sublattices [1]. FeRh exhibits a first-order metamagnetic phase transition from an antiferromagnetic (AFM) to a ferromagnetic (FM) state near 340 K. This transition is accompanied by a substantial entropy change, making the material particularly attractive for magnetocaloric applications [2,3].
Expanding this approach, recent studies have shown that the addition of non-magnetic elements, such as aluminum (Al), can stabilize the ordered B2-type structure in transition metal systems. For example, theoretical calculations by Li et al. [4] demonstrated that in AlCrCoNiFe high-entropy alloys (HEAs), the B2 structure becomes dominant when the Al concentration exceeds that of the other elements. An experimental study by Cieslak et al. [5] showed that above x = 0.75 in the AlxCoCrNiFe system, the ordered B2 and disordered BCC phases form simultaneously, exhibiting large differences in magnetization and magnetic transition temperature. Similarly, our previous work revealed that around 50 at.% Al promotes the formation of the B2 phase in the Al–V–Cr–Mn–Co HEA system [6], which is responsible for the observed ferromagnetic behavior.
Among the 3d transition metals, manganese (Mn) has attracted considerable attention due to its partially filled d-orbitals and its potential for magnetic applications. A notably promising and cost-effective alloy system is near-equiatomic Mn–Al (Al50Mn50), which combines good mechanical properties with magnetic functionality. The existence of a ferromagnetic phase in the Al–Mn system has been investigated in several works [7,8,9]. The good magnetic properties derive from the tetragonal τ phase, which forms from the non-magnetic hexagonal ε phase by annealing a quenched Mn50+xAl50−x alloy (x = 0–10) at 400–700 °C. Both phases are metastable at room temperature and therefore strongly related to the production route, making this system a candidate for permanent magnet applications.
However, binary Al–Mn alloys in the B2 structure are of particular interest due to theoretical predictions of strong ferromagnetism, with a magnetic moment around 1.87 μB per Mn atom [10], in contrast to the non-magnetic behavior for the B2 structures of AlFe, AlCo, and AlNi [11,12,13]. Despite that, the Al–Mn binary phase diagram indicates that the B2 phase is not stable under equilibrium conditions. This raises the question of whether stabilization of the B2 phase of Al–Mn with ferromagnetic behavior can be achieved through the addition of other transition metal elements. A recent study indicates that binary aluminides between Al and 3d magnetic transition elements (Cr, Mn, Fe, Co, and Ni) are more stable in the ordered B2 phase than in the disordered body centered cubic (BCC) phase, and Co is found to be the strongest B2-forming element with Al [10]. Moreover, Huang et al. reported that a dominant ferromagnetic B2 phase can be obtained in the Al50Mn38Ni12 alloy [14]. All these findings suggest that doping Al–Mn alloys with specific transition metals can offer a viable route for the formation of the magnetic B2 phase.
By using experimental methods and theoretical calculations, we show here that addition of a low concentration of Fe, Co, or Ni to Al–Mn induces a B2-type ferromagnetic structure. We recall that a higher concentration of Al results in a reduced fraction of the B2 phase and promotes the formation of intermetallic phases. Namely, in our recent study [15] on the Al–Mn–Co system, we investigated the effect of Al content in Alx (Mn0.76Co0.24)1−x (x = 0.45, 0.50, 0.55) alloys, maintaining a constant ratio of Mn/Co, and found that the x = 0.45 alloy exhibited the highest fraction of the B2 phase. Therefore, here, we keep the Al fraction at 45 at.%, the Mn fraction at 41.8 at.%, and change the third alloy component, keeping its atomic fraction at 13.2 at.%. We find that the measured magnetic response of the Al45Mn41.8X13.2 (X = Fe, Co, Ni) alloys indicates their potential as a promising ferromagnetic material for various magnetic applications. Since the magnetic transition temperature for the X = Fe alloy is relatively close to room temperature, we selected this system for measuring the magnetocaloric parameters. Although the magnetocaloric performance of our alloys is moderate compared to Gd, using Al, Mn, and a reduced amount of critical element (Co) makes them appealing candidates for continued investigation as rare-earth-free materials for magnetocaloric applications.
2. Materials and Methods
2.1. Theoretical Modeling
The ab initio calculations were conducted based on density functional theory (DFT), employing the exact muffin-tin orbitals (EMTO) method [16,17,18]. The exchange-correlation effects were described by adopting the local density approximation (LDA) in the self-consistent Kohn–Sham calculations and the Perdew–Burke–Ernzerhof (PBE) functional [19] for the total energy. The valence electron configurations for Al, Mn, Fe, Co and Ni were taken as 3s23p1, 3d54s2, 3d74s1, 3d74s2, and 3d84s2, respectively. We notice that although the core states are affected by the actual valence configuration, the results were not sensitive to this since we employed a soft-core scheme (i.e., the core states were recalculated for the actual Kohn–Sham potential after each DFT iteration).
The coherent potential approximation (CPA) [20,21] was used to describe the substitutional chemical disorder and the magnetic disorder in the paramagnetic (PM) state. The PM state was described using the disordered local magnetic moment approximation [22].
The Curie temperatures (TC) were estimated using a mean-field approach [22]:
where EPM and EFM denote the energies of the magnetically disordered (paramagnetic state) and the magnetically ordered ground state (ferromagnetic state), respectively, and c represents the atomic fraction of non-spin-polarized chemical species. A set of 13 × 13 × 13 k-point mesh was used based on the convergence tests. The calculations were conducted for the BCC and B2 structures in FM, PM, and NM states for reference, respectively.
The distribution of constituents (Al, Mn, and X) over the two sublattices had to be determined to model the B2-type atomic long-range ordered state in the Al45Mn41.8X13.2 (X = Fe, Co, Ni) at.% alloys. In theoretical calculations, it was observed that Al and X (Fe, Co, and Ni) showed a strong preference for occupying different sublattices, while Mn balanced between them [15]. Thus, B2 is occupied by 45 at.% Al and 5 at.% Mn in one sublattice, and 36.8 at.% Mn and 13.2 at.% X (X = Fe, Co, Ni) in the other sublattice.
2.2. Experimental Procedure
The ingots with a nominal composition of Al45Mn41.8X13.2 (X = Fe, Co, Ni) were prepared using induction melting of pure metals (99.99%, Sigma-Aldrich, St. Louis, MO, USA) of Al, Mn, Fe, Co, and Ni. Approximately 2–3 g of raw materials was induction melted in a water-cooled copper mold under ultrahigh-purity argon. Each ingot was remelted 4 times to improve chemical homogeneity.
Structural analysis was performed using X-ray diffraction (XRD, model SIEMENS D5000, Siemens AG, Karlsruhe, Germany) with Cu Kα radiation, in a 2θ range of 30–100° at a scanning rate of 0.02° per 2 s, employing a graphite monochromator. Phase composition was determined via scanning electron microscopy (SEM, Hitachi, Hitachi High-Technologies Corporation, Tokyo, Japan) equipped with an energy dispersive spectrometer (EDS), operating at 15 kV.
Magnetic hysteresis loops were recorded using a vibrating sample magnetometer (VSM, EG&G model 155, EG&G Princeton Applied Research, Princeton, NJ, USA) under an applied maximum magnetic field of 650 kA m−1 (0.82 T) at room temperature and at liquid nitrogen temperature. To determine the magnetic entropy change, isothermal magnetization curves were measured over an appropriate temperature range.
The temperature-dependent normalized magnetization was carried out by magneto-thermo-gravimetry (MTG, model TGS-2, Perkin-Elmer Corporation, Norwalk, CA, USA) using a low magnetic field of approximately 3 kA m−1 and a heating rate of 40 K min−1 under an argon atmosphere.
The magnetic entropy change, ΔSM, can be determined by using Equation (2) from Ref. [23]:
This equation involves measuring the magnetization of the material as a function of temperature and magnetic field and then determining the change in magnetization with respect to temperature (dM/dT). By integrating this change with respect to the field, we obtain the magnetic entropy change.
The direct adiabatic temperature change, ΔTa, was measured by gradually heating the sample at a constant rate in an evacuated tube from room temperature to maximum temperature. During this heating scan, the magnetic field alternates between zero field and a maximum of 650 kA m−1, with a period of about 20 s. The ΔT is the difference between two temperature traces, one with zero field and the other with maximum field. The thermometer consisted of a spot welded thermocouple of type E.
The relative cooling power (RCP) is given by the following equation [24]:
Here, is the peak value of the isothermal magnetic entropy change with associated peak temperature Tpeak, and δTFWHM is the full width at half maximum obtained from the temperature at half the maximum peak value of the ΔSM curve.
3. Results and Discussion
3.1. DFT Calculations of Al45Mn41.8X13.2 (X = Fe, Co, Ni) Alloys
To give an atomic-level understanding of structural stability, the total energy per atom as a function of Wigner–Seitz radius (w) is shown in Figure 1. Here, we present the results as a BCC structure, as it represents the chemically disordered B2 phase that is stable at high temperatures in the Al–Mn system. The equilibrium energy difference between the BCC and B2 structures indicates that the B2 phase is the most stable for Al45Mn41.8X13.2 (X = Fe, Co, Ni) alloys. Specifically, the FM state of the B2 structure exhibits the lowest energy, confirming its stability. This result demonstrates that the B2 structure in near-equiatomic Al–Mn alloys exhibits ferromagnetic behavior. Furthermore, the energy curves for all BCC FM and PM states indicate a bifurcation into low-spin and high-spin states. At reduced volumes, these structures favor low-spin configurations, whereas at increased volumes, they transition to high-spin configurations. Notably, the energy curve for the NM state corresponds with the low-spin curves. Hence, the low-spin state is in fact a NM configuration. Namely, at small volumes, all local magnetic moments vanish. With increasing volume, the density of state near the Fermi level increases and all three BCC systems start to fulfill the Stoner criterion for itinerant magnetism [25]. This leads to spontaneous spin polarization. These theoretical results are fully self-consistent and thus the actual valence and spin configurations are the solutions for the Kohn–Sham equations at particular volumes. We should mention that the present calculations assume collinear magnetism, i.e., non-collinear configurations are not considered.
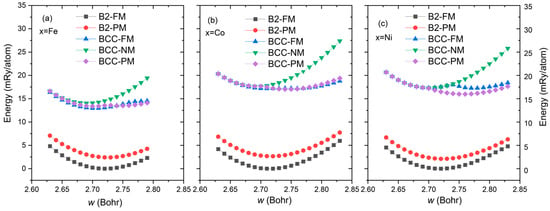
Figure 1.
Total energy as a function of Wigner–Seitz radius (w) for BCC and B2 structures in various magnetic states (FM, NM, and PM) for the Al45Mn41.8X13.2 alloys, (a) X = Fe, (b) X = Co and (c) X = Ni. The energy curve values are shown relative to the B2 phase energies in the FM state.
The total magnetic moment and Curie temperature (TC) for the B2 and BCC phases with the nominal composition calculated by ab initio are presented in Table 1. The values of the TC demonstrate that the B2 phase exhibits ferromagnetism at room temperature. The total magnetic moments are quantified as 0.53, 0.47, and 0.42 μB/atom for X = Fe, X = Co, and X = Ni, respectively. Conversely, the BCC structure is paramagnetic at room temperature. These theoretical data suggest that the ferromagnetic behavior is due to the B2 phase. As noted before, the calculations indicate a strong site preference for Al and X (Fe, Co, and Ni) to occupy different sublattices, whereas Mn tends to distribute between both sublattices. Analysis of the local magnetic moments of the constituents within the B2 phase in its ferromagnetic state reveals that the Al and X elements possess negligible magnetic moments. In contrast, Mn atoms exhibit significant local magnetic moments on both sublattices, with antiparallel spin orientations. This detailed magnetic characterization underscores the critical role of the B2 phase in the ferromagnetic properties of the samples.

Table 1.
The total magnetic moments, the Curie temperatures, and the local magnetic moments of alloy constituents (Al, Mn, and X) in the ferromagnetic state for the nominal composition in the BCC and B2 structures for the X = Fe, Co, and Ni alloys from DFT calculations.
3.2. Microstructural Characterization of Al45Mn41.8X13.2 (X = Fe, Co, Ni) Alloys
Figure 2 illustrates the XRD patterns for the as-cast Al45Mn41.8X13.2 (X = Fe, Co, Ni) alloys at room temperature. The diffraction data are indexed as a B2-type structure with the space group of Pm3m. It should be noted that although there is no distinct (111) peak for the B2 phase in the X = Fe alloy, its ferromagnetic behavior confirms the presence of the B2 phase. The SEM images of these alloys, as presented in Figure 2, reveal a single phase for X = Fe and X = Co alloys. For the X = Ni alloy, there are some white zones observed in its SEM image. However, the XRD cannot detect the low fraction of this secondary phase. The composition of the B2 phase based on the EDS analysis is Al40.0Mn44.2Fe15.8, Al40.7Mn45.3Co14.0, and Al40.3Mn44.8Ni14.9 for X = Fe, Co, and Ni, respectively.
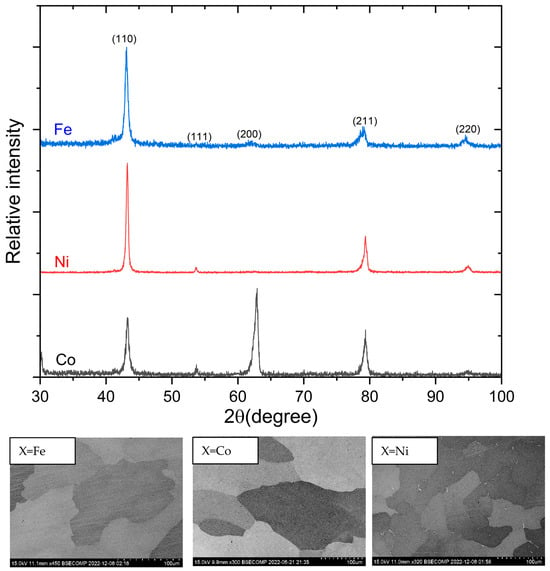
Figure 2.
(Top) XRD patterns and (bottom) the SEM images of the as-cast Al45Mn41.8X13.2 (X = Fe, Co, Ni) alloys at room temperature. The XRD patterns are indexed based on the peaks of the B2 phase.
3.3. Magnetic Measurements
The hysteresis loops for Al45Mn41.8X13.2 (X = Fe, Co, Ni) alloys at liquid nitrogen (77 K) and at room temperature (293 K) are shown in Figure 3. At 293 K, with all systems relatively close to the Curie temperature, the magnetization behavior is further away from the low-temperature behavior. Namely, the X = Fe sample has a Curie temperature of around 363 K (illustrated in Figure 4), leading to lower magnetization of 36 A m2 kg−1 at the maximum magnetic field. In contrast, the X = Co sample with a high TC is still strongly ferromagnetic at 293 K, resulting in the observed order of Co > Ni > Fe. At 77 K, all samples are well below their TC values, and the thermal effect is significantly reduced. Thus, magnetization is near saturation for all samples. This leads to the observed order of Fe > Ni > Co. It is important to mention that the calculated total magnetic moments and the experimental magnetizations differ from each other. We ascribe these differences to the fact that the calculations correspond to pure phases and are obtained at static conditions (absolute zero K), while the experimental magnetizations are per mass and measured at finite temperatures. Additionally, the theoretical magnetic moments are calculated for nominal compositions. While the Curie temperature for the actual compositions of the synthesized materials is very close to the TC for the nominal compositions (difference less than 8%), the total magnetic moment is more dependent on the composition, particularly the Mn content, despite the local magnetic moments of Mn differing by less than 6%. Nevertheless, even with considering the calculated moments for the real compositions, the conclusions remain valid.
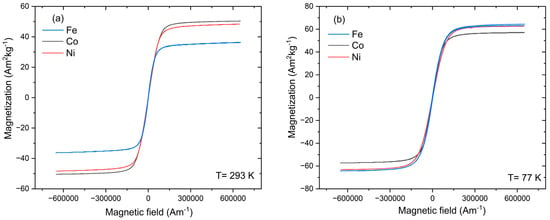
Figure 3.
The hysteresis loops for Al45Mn41.8X13.2 (X = Fe, Co, Ni) alloys at (a) 77 K and (b) 293 K.
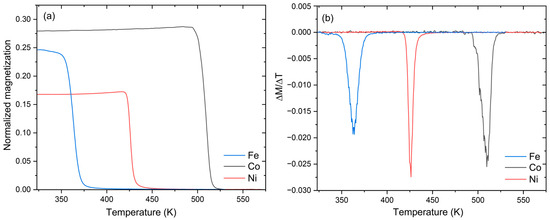
Figure 4.
(a) The normalized magnetization (M(T)) as a function of temperature for Al45Mn41.8X13.2 (X = Fe, Co, Ni) alloys at a magnetic field of about 3 kA m−1 and a heating rate of 40 K min−1 and (b) the temperature derivative of the magnetization vs. temperature. The Curie temperature is identified as the temperature corresponding to the inverted peak of the (∆M/∆T) curve.
The temperature dependences of magnetization, M(T), for Al45Mn41.8X13.2 (X = Fe, Co, Ni) alloys are presented in Figure 4a. The magnetization is in order of Co, Fe, and Ni, consistent with Figure 3a in a low magnetic field. The experimental Curie temperature TC measured by locating the peak in the change in magnetization with temperature (dM/dT) (Figure 4b) indicates that the TC values for X = Co, Ni, and Fe are 511, 426, and 363 K, respectively. We observe a slight discrepancy between the theoretical predictions and experimental values. This discrepancy can be attributed to the mean-field approximation, thermal effects, and differences in theoretical and experimental compositions. Nevertheless, the calculated TC values differ from the experimental values by 21% at most, which is acceptable.
Among these alloys, the X = Fe alloy was selected for the magnetocaloric study due to its magnetic transition temperature being close to room temperature. We analyzed the magnetocaloric effect of this alloy by evaluating the magnetic entropy change (ΔSM) and adiabatic temperature change (ΔTa). Figure 5 shows the ΔSM and ΔTa at a magnetic field of 650 kA m−1 (0.82 T) for the Al45Mn41.8Fe13.2 alloy. The observed peak in Figure 5a,b is near TC, attributed to the ferromagnetic to paramagnetic transition. The corresponding peaks for ΔSM and ΔTa were 0.54 J kg−1 K−1 and 0.27 K, respectively. The RCP value for the X = Fe alloy is 21 J kg−1. The comparison of magnetic entropy change and adiabatic temperature change in this alloy with Gd [26] (ΔSM = 2.8 J kg−1 K−1 and ΔTa = 3 K at 294 K ) shows that although these two values are modest as a promising magnetocaloric material, the RCP value (21 J kg−1) is sizable in comparison with Gd (63.4 J kg−1), which originates from the broad magnetic entropy changes. These results highlight the potential of this system and the need for further optimization and investigation.
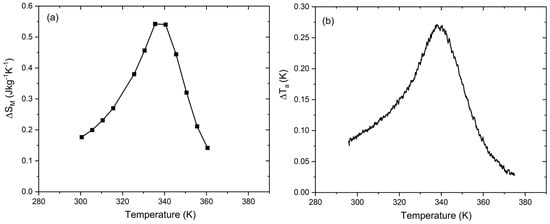
Figure 5.
(a) The magnetic entropy change (ΔSM) and (b) the adiabatic temperature change (ΔTad) of Al45Mn41.8Fe13.2 as a function of temperature under an applied magnetic field of 650 kA m−1 (0.82 T).
4. Conclusions
In this study, we investigated the structural and magnetic properties of ternary Al45Mn41.8X13.2 (X = Fe, Co, Ni) alloys by a combination of experimental analysis and theoretical calculations. Our findings reveal that the late 3d element X (X = Fe, Co, Ni) in the Al45Mn41.8X13.2 alloy leads to the stabilization of the B2-type structure as the main phase and induces ferromagnetic-like behavior. Notably, the Al45Mn41.8Fe13.2 alloy shows a magnetic entropy change (ΔSM) of 0.54 J kg−1 K−1, an adiabatic temperature change (ΔTa) of 0.27 K, and a relative cooling power (RCP) of 21 J kg−1 at 650 kA m−1 (0.82 T).
Author Contributions
Conceptualization, E.D. and L.V.; Methodology, V.S. and L.K.V.; Investigation, E.D.; Writing—original draft, E.D.; Formal analysis, H.A. and S.H.; Writing—review and editing, H.A., S.H., V.S., L.K.V., and L.V.; Supervision, L.V.; Funding acquisition, L.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Swedish Foundation for Strategic Research (SM23-0041), the Wallenberg Initiative Materials Science for Sustainability (WISE) funded by the Knut and Alice Wallenberg Foundation (KAW), the Formas-a Swedish Research Council for Sustainable Development (2023-00543), and the Carl Tryggers Foundation (CTS 22:1970). The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) at the National Supercomputing Centre (NSC, Tetralith cluster), partially funded by the Swedish Research Council through Grant Agreement No. 2022-06725.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to (specify the reason for the restriction).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AFM | Antiferromagnetic |
| FM | Ferromagnetic |
| NM | Non-magnetic |
| PM | Paramagnetic |
| BCC | Body-Centered Cubic |
| DFT | Density Functional Theory |
| HEA | High-Entropy Alloy |
| XRD | X-ray Diffraction |
| SEM | Scanning Electron Microscopy |
| EDS | Energy Dispersive Spectroscopy |
| LN2 | Liquid Nitrogen |
| ΔSM | Magnetic Entropy Change |
| ΔTa | Adiabatic temperature change |
| RCP | Relative Cooling Power |
| TC | Curie Temperature |
References
- Vieira, R.M.; Eriksson, O.; Bergman, A.; Herper, H.C. High-Throughput Compatible Approach for Entropy Estimation in Magnetocaloric Materials: FeRh as a Test Case. J. Alloys Compd. 2021, 857, 157811. [Google Scholar] [CrossRef]
- Scheibel, F.; Gottschall, T.; Taubel, A.; Fries, M.; Wende, H.; Farle, M.; Acet, M.; Gutfleisch, O. Hysteresis Design of Magnetocaloric Materials—From Basic Mechanisms to Applications. Energy Technol. 2018, 6, 1397–1428. [Google Scholar] [CrossRef]
- Annaorazov, M.P.; Asatryan, K.A.; Myalikgulyev, G.; Nikitin, S.A.; Tishin, A.M.; Tyurin, A.L. Alloys of the Fe–Rh System as a New Class of Working Material for Magnetic Refrigerators. Cryogenics 1992, 32, 867–872. [Google Scholar] [CrossRef]
- Li, C.; Zhao, M.; Li, J.C.; Jiang, Q. B2 Structure of High-Entropy Alloys with Addition of Al. J. Appl. Phys. 2008, 104, 113504. [Google Scholar] [CrossRef]
- Cieslak, J.; Tobola, J.; Berent, K.; Marciszko, M. Phase composition of AlxFeNiCrCo high entropy alloys prepared by sintering and arc-melting methods. J. Alloys Compd. 2018, 740, 264–272. [Google Scholar] [CrossRef]
- Dastanpour, E.; Huang, S.; Schönecker, S.; Mao, H.; Ström, V.; Eriksson, O.; Varga, L.K.; Vitos, L. On the Structural and Magnetic Properties of Al-Rich High Entropy Alloys: A Joint Experimental-Theoretical. J. Phys. D Appl. Phys. 2023, 56, 1–8. [Google Scholar] [CrossRef]
- Liu, Z.W.; Chen, C.; Zheng, Z.G.; Tan, B.H.; Ramanujan, R.V. Phase transitions and hard magnetic properties for rapidly solidified MnAl alloys doped with C, B, and rare earth elements. J. Mater. Sci. 2012, 47, 2333–2338. [Google Scholar] [CrossRef]
- Janotová, I.; Švec, P., Sr.; Švec, P.; Mat’ko, I.; Janičkovič, D.; Zigo, J.; Mihalkovič, M.; Marcin, J.; Škorvánek, I. Phase analysis and structure of rapidly quenched Al–Mn systems. J. Alloys Compd. 2017, 707, 137–141. [Google Scholar] [CrossRef]
- Kono, H. On the Ferromagnetic Phase in Manganese-Aluminum System. J. Phys. Soc. Jpn. 1958, 13, 1444–1451. [Google Scholar] [CrossRef]
- Aihemaiti, H.; Dastanpour, E.; Bergman, A.; Vitos, L. First-principles study of phase stability and magnetic properties of B2 AlCr, AlMn, AlFe, AlCo and AlNi aluminides. Phys. Rev. Mater. 2025. submitted. [Google Scholar]
- Chen, L.; Huang, R.; Ke, X.; Yu, J.; Zhang, T.; Maurice, J.L.; Li, J.; Li, K.; Ni, L.; Huang, S.; et al. Parallel aluminum-cobalt oxide nanosheet arrays with high-temperature ferromagnetism. Small 2023, 19, 2301513. [Google Scholar] [CrossRef]
- Menushenkov, V.P.; Gorshenkov, M.V.; Savchenko, E.S.; Zhukov, D.G. The Effect of the rate of cooling from high-temperature single-phase region on the microstructure and magnetic properties of AlNi alloys. Metall. Mater. Trans. A 2015, 46, 656–664. [Google Scholar] [CrossRef]
- Hernando, A.; Amils, X.; Nogués, J.; Suriñach, S.; Baró, M. Influence of magnetization on the reordering of nanostructured ball-milled Fe-40 at.% Al powders. Phys. Rev. B 1998, 58, R11864. [Google Scholar] [CrossRef]
- Huang, S.; Dastanpour, E.; Ström, V.; Varga, L.K.; Eriksson, O.; Jin, H.; Vitos, L. Lattice and spin entropy changes in B2-type magnetocaloric Al–Mn–Ni alloy. J. Phys. D Appl. Phys. 2025, 58, 075001. [Google Scholar] [CrossRef]
- Dastanpour, E.; Huang, S.; Schönecker, S.; Ström, V.; Varga, L.K.; Eriksson, O.; Vitos, L. Magnetocaloric properties of ternary Al–Mn–Co Alloys. J. Alloys Compd. 2025, 1035, 182006. [Google Scholar] [CrossRef]
- Vitos, L. Computational Quantum Mechanics for Materials Engineering; Springer: London, UK, 2007. [Google Scholar]
- Vitos, L. Total-Energy method based on the Exact Muffin-Tin Orbitals theory. Phys. Rev B 2001, 64, 014107. [Google Scholar] [CrossRef]
- Vitos, L.; Skriver, H.L.; Johansson, B.; Kollár, J. Application of the Exact Muffin-Tin Orbitals theory: The spherical cell approximation. Comput. Mater. Sci. 2000, 18, 24–38. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to Density-Functional Approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Soven, P. Coherent-Potential Model of Substitutional Disordered Alloys. Phys. Rev. 1967, 156, 809–813. [Google Scholar] [CrossRef]
- Gyorffy, B.L. Coherent-Potential Approximation for a Nonoverlapping-Muffin-Tin-Potential Model of Random Substitutional Alloys. Phys. Rev. B 1972, 5, 2382. [Google Scholar] [CrossRef]
- Gyorffy, B.L.; Pindor, A.J.; Staunton, J.; Stocks, G.M.; Winter, H. A first-principles theory of ferromagnetic phase transitions in metals. J. Phys. F Met. Phys. 1985, 15, 1337–1386. [Google Scholar] [CrossRef]
- Amaral, J.S.; Amaral, V.S. On Estimating the Magnetocaloric Effect from Magnetization Measurements. J. Magn. Magn. Mater. 2010, 322, 1552–1557. [Google Scholar] [CrossRef]
- Phan, M.H.; Yu, S.C. Review of the Magnetocaloric Effect in Manganite Materials. J. Magn. Magn. Mater. 2007, 302, 325–340. [Google Scholar] [CrossRef]
- Mohn, P. Magnetism in the Solid State; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Wang, D.; Han, Z.; Cao, Q.; Huang, S.; Zhang, J.; Du, Y. The Reduced Curie Temperature and Magnetic Entropy Changes in Gd1−xInx Alloys. J. Alloys Compd. 2005, 396, 22–24. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).