Lanthanoid Coordination Polymers Based on Homoditopic Picolinate Ligands: Synthesis, Structure and Magnetic Properties †
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
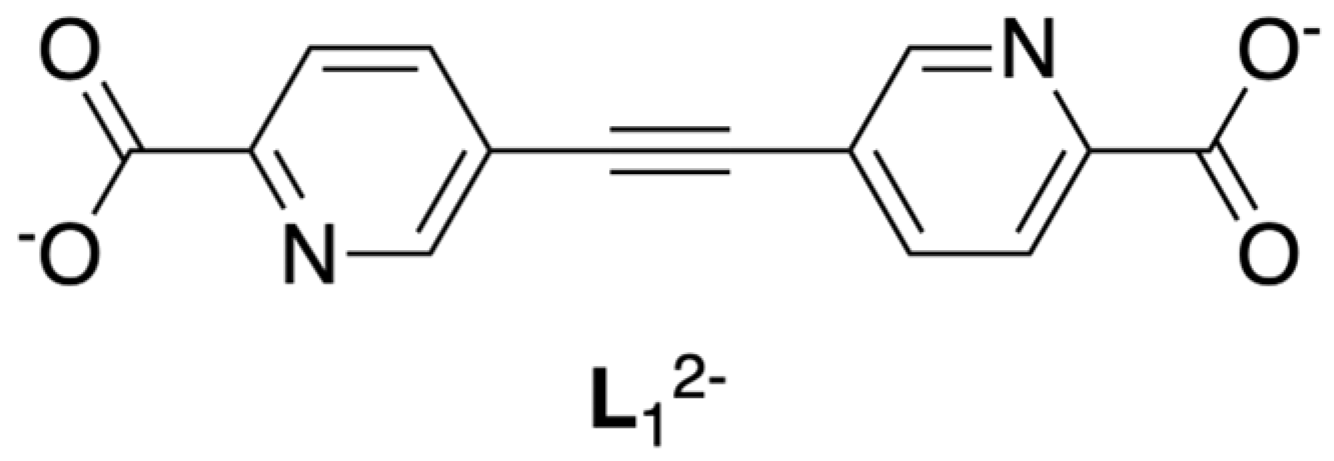
3.1. Synthesis and Characterization
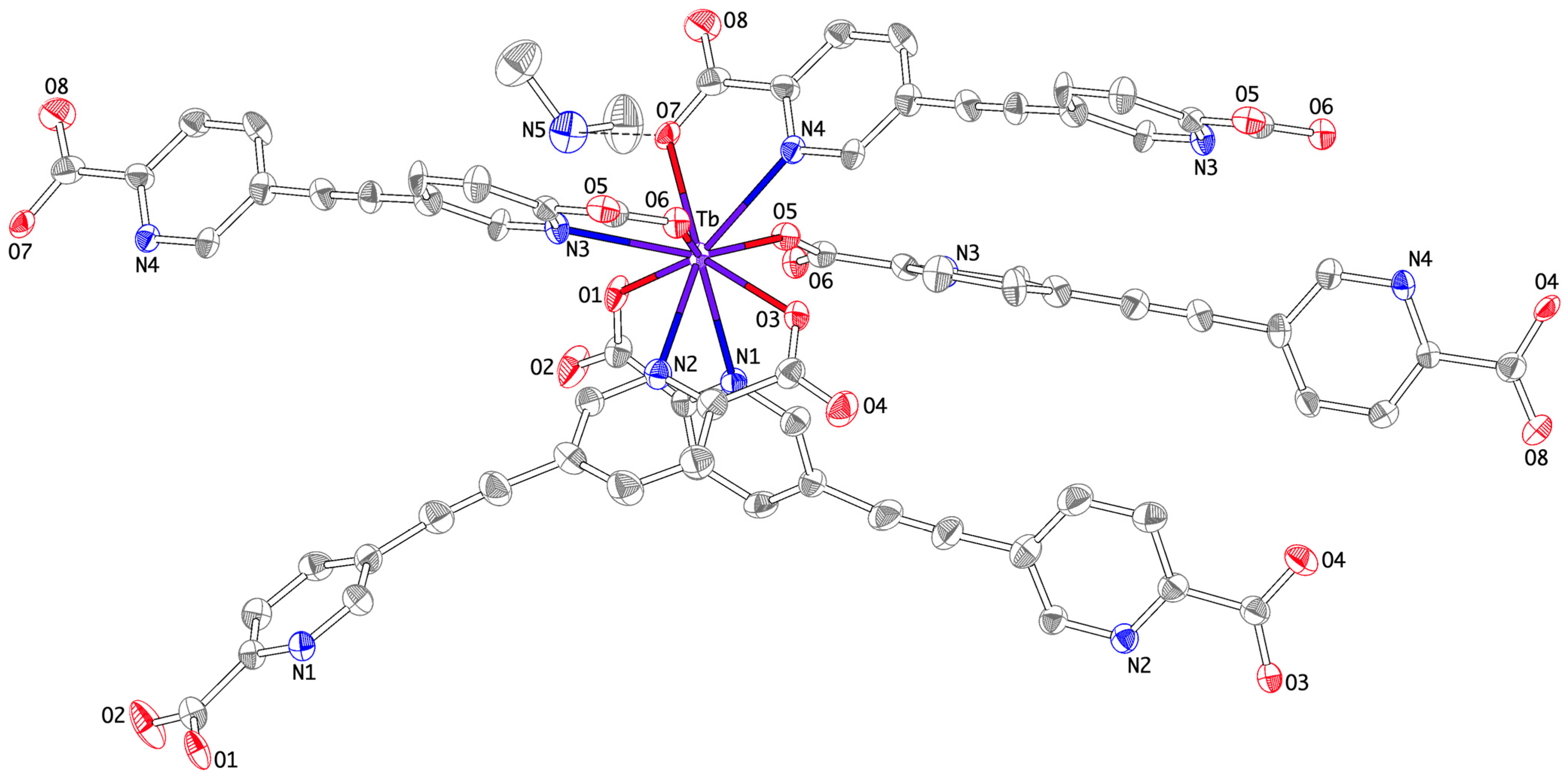
3.2. Structural Properties
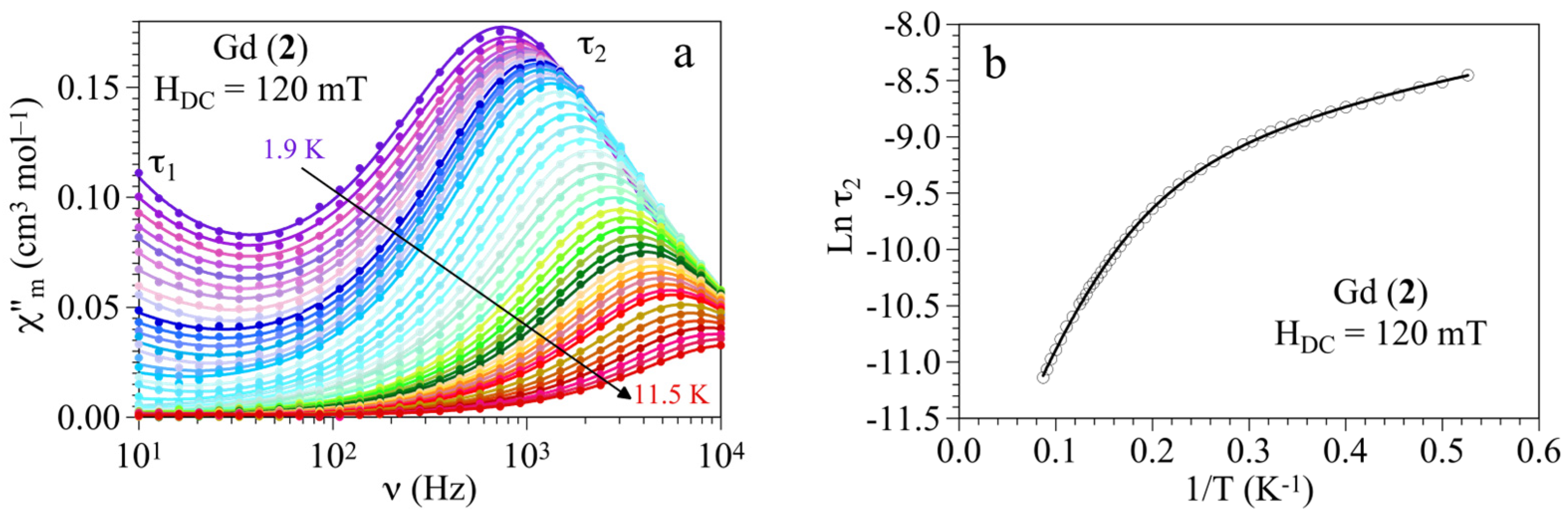
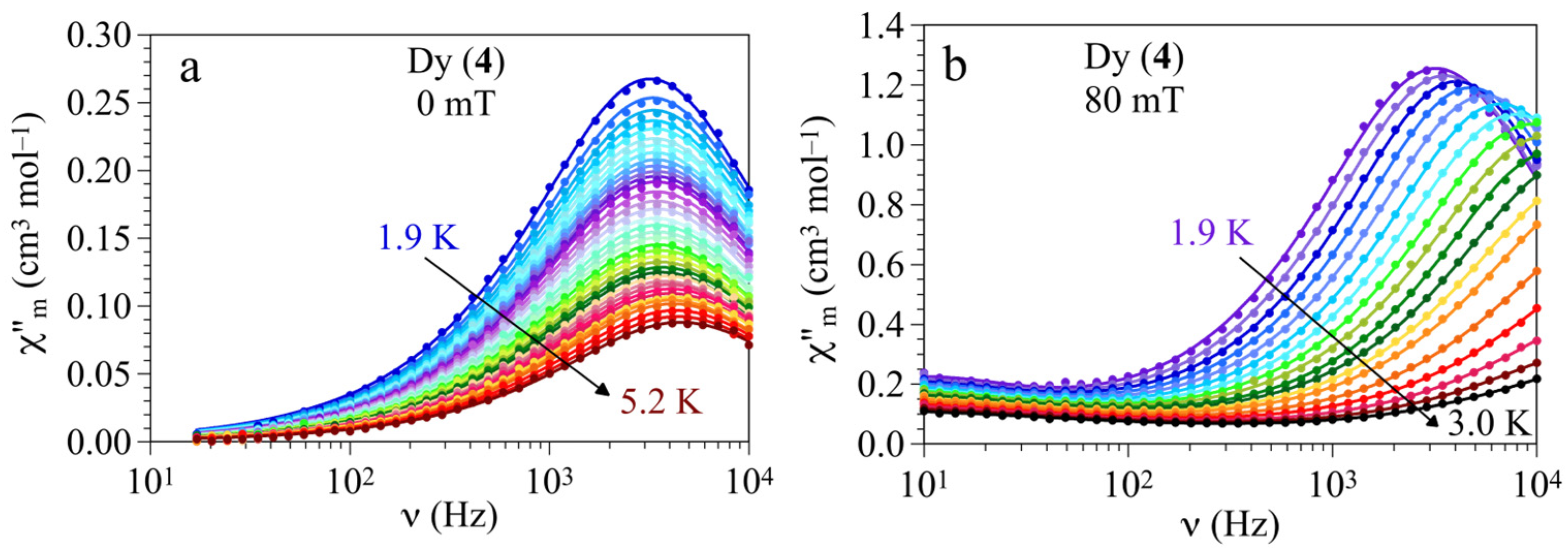
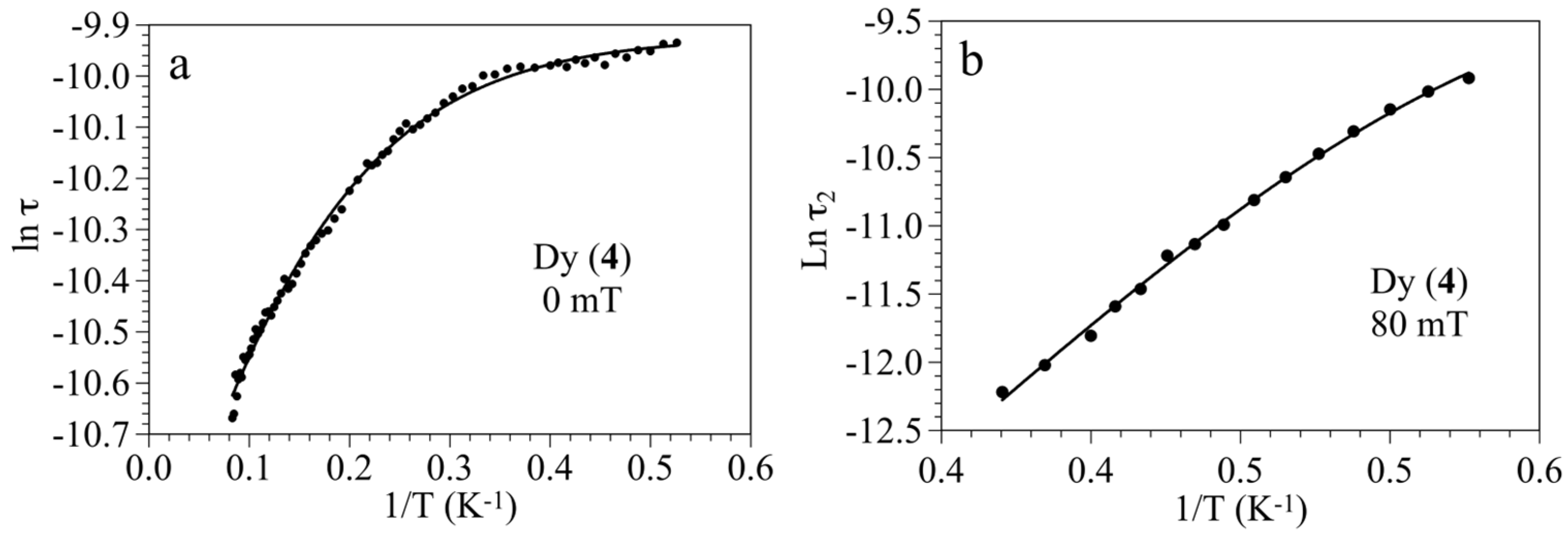
3.3. Magnetic Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, B. Lanthanide-functionalized metal–organic framework hybrid systems to create multiple luminescent centers for chemical sensing. Acc. Chem. Res. 2017, 50, 2789–2798. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Song, M.-M.; Tao, D.-L.; Bo, Q.-B. Diverse lanthanide coordination polymers with 3,3′-dimethylcyclopropane-1,2-dicarboxylate ligand: Synthesis, crystal structure, and properties. ACS Omega 2018, 3, 12122–12131. [Google Scholar] [CrossRef]
- Feng, X.; Shang, Y.; Zhang, H.; Li, R.; Wang, W.; Zhang, D.; Wang, L.; Li, Z. Enhanced luminescence and tunable magnetic properties of lanthanide coordination polymers based on fluorine substitution and phenanthroline ligand. RSC Adv. 2019, 9, 16328–16338. [Google Scholar] [CrossRef]
- Ruiz-Muelle, A.B.; García- García, A.; García-Valdivia, A.A.; Oyarzabal, I.; Cepeda, J.; Seco, J.M.; Colacio, E.; Rodríguez-Diéguez, A.; Fernández, I. Design and synthesis of a family of 1D-lanthanide-coordination polymers showing luminescence and slow relaxation of the magnetization. Dalton Trans. 2018, 47, 12783–12794. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-H.; Zhang, R.-T.; Zhang, J.; Zhao, D.; Li, X.-X.; Sun, Y.-Q.; Zheng, S.-T. A series of 3D porous lanthanide-substituted polyoxometalate frameworks based on rare hexadecahedral {Ln6W8O28} heterometallic cage-shaped clusters. Inorg. Chem. 2019, 58, 14734–14740. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, W.; Li, L.; Duan, E.; Cheng, P. Lanthanide coordination polymers with “fsy-type” topology based on 4, 4′-azobenzoic acid: Syntheses, crystal structures, and magnetic properties. Inorg. Chem. 2014, 53, 10340–10346. [Google Scholar] [CrossRef]
- Ma, F.; Sun, R.; Sun, A.-H.; Xiong, J.; Sun, H.-L.; Gao, S. Regulating the structural dimensionality and dynamic properties of a porous dysprosium coordination polymer through solvent molecules. Inorg. Chem. Front. 2020, 7, 930–938. [Google Scholar] [CrossRef]
- Blais, C.; Calvez, G.; Suffren, Y.; Daiguebonne, C.; Paranthoen, C.; Bazin, E.; Freslon, S.; Bernot, K.; Guillou, O. Luminance and brightness: Application to lanthanide-based coordination polymers. Inorg. Chem. 2022, 48, 19588–19596. [Google Scholar] [CrossRef]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef]
- Urdampilleta, M.; Nguyen, N.V.; Cleuziou, J.P.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W. Molecular quantum spintronics: Supramolecular spin valves based on single-molecule magnets and carbon nanotubes. Int. J. Mol. Sci. 2011, 12, 6656–6667. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.; Kaizu, Y. Lanthanide double-decker complexes functioning as magnets at the single-molecular level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.; Kaizu, Y. Mononuclear lanthanide complexes with a long magnetization relaxation time at high temperatures: A new category of magnets at the single-molecular level. J. Phys. Chem. B 2004, 108, 11265–11271. [Google Scholar] [CrossRef]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide single-molecule magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef]
- Ungur, L.; Chibotaru, L.F. Strategies toward high-temperature lanthanide-based single-molecule magnets. Inorg. Chem. 2016, 55, 10043–10056. [Google Scholar] [CrossRef] [PubMed]
- Bernot, K. Get under the umbrella: A comprehensive gateway for researchers on lanthanide-based single-molecule magnets. Eur. J. Inorg. Chem. 2023, 26, e202300336. [Google Scholar] [CrossRef]
- Zhang, P.; Guo, Y.-N.; Tang, J. Recent advances in dysprosium-based single molecule magnets: Structural overview and synthetic strategies. Coord. Chem. Rev. 2013, 257, 1728–1763. [Google Scholar] [CrossRef]
- AlDamen, M.A.; Clemente-Juan, J.M.; Coronado, E.; Martí-Gastaldo, C.; Gaita-Ariño, A. Mononuclear lanthanide single-molecule magnets based on polyoxometalates. J. Am. Chem. Soc. 2008, 130, 8874–8875. [Google Scholar] [CrossRef] [PubMed]
- Meihaus, K.R.; Long, J.R. Magnetic blocking at 10 K and a dipolar-mediated avalanche in salts of the bis(η8-cyclooctatetraenide) complex [Er(COT)2]−. J. Am. Chem. Soc. 2013, 135, 17952–17957. [Google Scholar] [CrossRef]
- Le Roy, J.J.; Jeletic, M.; Gorelsky, S.I.; Korobkov, I.; Ungur, L.; Chibotaru, L.F.; Murugesu, M. An organometallic building block approach to produce a multidecker 4f single-molecule magnet. J. Am. Chem. Soc. 2013, 135, 3502–3510. [Google Scholar] [CrossRef]
- Tang, J.; Hewitt, I.; Madhu, N.T.; Chastanet, G.; Wernsdorfer, W.; Anson, C.E.; Benelli, C.; Sessoli, R.; Powell, A.K. Dysprosium triangles showing single-molecule magnet behavior of thermally excited spin states. Angew. Chem. Int. Ed. 2006, 45, 1729–1733. [Google Scholar] [CrossRef]
- Wang, J.; Sun, C.-Y.; Zheng, Q.; Wang, D.-Q.; Chen, Y.-T.; Ju, J.-F.; Sun, T.-M.; Cui, Y.; Ding, Y.; Tang, Y.-F. Lanthanide single-molecule magnets: Synthetic strategy, structures, properties and recent advances. Chem. Asian J. 2023, 18, e202201297. [Google Scholar] [PubMed]
- Dolinar, B.S.; Alexandropoulos, D.I.; Vignesh, K.R.; James, T.; Dunbar, K.R. Lanthanide triangles supported by radical bridging ligands. J. Am. Chem. Soc. 2018, 140, 908–911. [Google Scholar] [PubMed]
- Boulon, M.-E.; Cucinotta, G.; Luzon, J.; Degl’Innocenti, C.; Perfetti, M.; Bernot, K.; Calvez, G.; Caneschi, A.; Sessoli, R. Magnetic anisotropy and spin-parity effect along the series of lanthanide complexes with DOTA. Angew. Chem. Int. Ed. 2013, 52, 350–354. [Google Scholar] [CrossRef]
- Wan, Q.; Wakizaka, M.; Yamashita, M. Single-ion magnetism behaviors in lanthanide (III) based coordination frameworks. Inorg. Chem. Front. 2023, 10, 5212–5224. [Google Scholar]
- Huang, G.; Fernandez-Garcia, G.; Badiane, I.; Camarra, M.; Freslon, S.; Guillou, O.; Daiguebonne, C.; Totti, F.; Cador, O.; Guizouarn, T.; et al. Magnetic slow relaxation in a metal–organic framework made of chains of ferromagnetically coupled single-molecule magnets. Chem. Eur. J. 2018, 24, 6983–6991. [Google Scholar] [CrossRef] [PubMed]
- Bernot, K.; Bogani, L.; Caneschi, A.; Gatteschi, D.; Sessoli, R. A family of rare-earth-based single chain magnets: Playing with anisotropy. J. Am. Chem. Soc. 2006, 128, 7947–7956. [Google Scholar]
- Gheorghe, R.; Madalan, A.M.; Costes, J.-P.; Wernsdorfer, W.; Andruh, M. A heterotrimetallic 3d–3d′–4f single chain magnet constructed from anisotropic high-spin 3d–4f nodes and paramagnetic spacers. Dalton Trans. 2010, 39, 4734–4736. [Google Scholar]
- Paulovič, J.; Cimpoesu, F.; Ferbinteanu, M.; Hirao, K. Mechanism of ferromagnetic coupling in copper (II)-gadolinium (III) complexes. J. Am. Chem. Soc. 2004, 126, 3321–3331. [Google Scholar]
- Singh, S.K.; Beg, M.F.; Rajaraman, G. Role of magnetic exchange interactions in the magnetization relaxation of {3d–4f} single-molecule magnets: A theoretical perspective. Chem. Eur. J. 2016, 22, 672–680. [Google Scholar]
- Dey, A.; Acharya, J.; Chandrasekhar, V. Heterometallic 3d–4f complexes as single-molecule magnets. Chem. Asian J. 2019, 14, 4433–4453. [Google Scholar]
- Girginova, P.I.; Pereira, L.C.J.; Coutinho, J.T.; Santos, I.C.; Almeida, M. Slow magnetic relaxation in lanthanide ladder type coordination polymers. Dalton Trans. 2014, 43, 1897–1905. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef]
- Tarannum, I.; Moorthy, S.; Singh, S.K. Understanding electrostatics and covalency effects in highly anisotropic organometallic sandwich dysprosium complexes [Dy(CmRm)2] (where R = H, SiH3, CH3 and m = 4 to 9): A computational perspective. Dalton Trans. 2023, 52, 15576–15589. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhang, X.; Meng, X.; Shi, W.; Cheng, P.; Powell, A.K. Constraining the coordination geometries of lanthanide centers and magnetic building blocks in frameworks: A new strategy for molecular nanomagnets. Chem. Soc. Rev. 2016, 45, 2423–2439. [Google Scholar] [CrossRef]
- Zhang, X.; Vieru, V.; Feng, X.; Liu, J.-L.; Zhang, Z.; Na, B.; Shi, W.; Wang, B.-W.; Powell, A.K.; Chibotaru, L.F.; et al. Influence of guest exchange on the magnetization dynamics of dilanthanide single-molecule-magnet nodes within a metal–organic framework. Angew. Chem. Int. Ed. 2015, 54, 9861–9865. [Google Scholar] [CrossRef]
- Caskey, S.R.; Wong-Foy, A.G.; Matzger, A.J. Dramatic tuning of carbon dioxide uptake via metal substitution in a coordination polymer with cylindrical pores. J. Am. Chem. Soc. 2008, 130, 10870–10871. [Google Scholar] [CrossRef] [PubMed]
- Bloch, E.D.; Murray, L.J.; Queen, W.L.; Chavan, S.; Maximoff, S.N.; Bigi, J.P.; Krishna, R.; Peterson, V.K.; Grandjean, F.; Long, G.J.; et al. Selective binding of O2 over N2 in a redox–active metal–organic framework with open iron(II) coordination sites. J. Am. Chem. Soc. 2011, 133, 14814–14822. [Google Scholar] [CrossRef]
- Kapelewski, M.T.; Geier, S.J.; Hudson, M.R.; Stück, D.; Mason, J.A.; Nelson, J.N.; Xiao, D.J.; Hulvey, Z.; Gilmour, E.; FitzGerald, S.A.; et al. M2(m-dobdc) (M = Mg, Mn, Fe, Co, Ni) metal–organic frameworks exhibiting increased charge density and enhanced H2 binding at the open metal sites. J. Am. Chem. Soc. 2014, 136, 12119–12129. [Google Scholar] [CrossRef]
- Hmadeh, M.; Lu, Z.; Liu, Z.; Gándara, F.; Furukawa, H.; Wan, S.; Augustyn, V.; Chang, R.; Liao, L.; Zhou, F.; et al. New porous crystals of extended metal-catecholates. Chem. Mater. 2012, 24, 3511–3513. [Google Scholar] [CrossRef]
- Park, B.G.; Pink, M.; Lee, D. Fluorogenic N,O-chelates built on a C2-symmetric aryleneethynylene platform: Spectroscopic and structural consequences of conformational preorganization and ligand denticity. J. Organomet. Chem. 2011, 696, 4039–4045. [Google Scholar] [CrossRef]
- Kodanko, J.J.; Lippard, S.J. Synthesis and characterization of a ditriflate-bridged, diiron(II) complex with syn-N-donor ligands: [Fe2(μ-OTf)2(PIC2DET)2](BARF)2. Inorg. Chim. Acta 2008, 361, 894–900. [Google Scholar]
- Kodanko, J.J.; Xu, D.; Song, D.; Lippard, S.J. Iron substitution for sodium in a carboxylate-bridged, heterodinuclear sodium–iron Complex. J. Am. Chem. Soc. 2005, 127, 16004–16005. [Google Scholar] [CrossRef]
- Severance, R.C.; Rountree, E.S.; Smith, M.D.; zur Loye, H.-C. Ligand-based luminescence in lead-containing complexes: The effect of conjugated organic ligands on fluorescence. Solid State Sci. 2012, 14, 1512–1519. [Google Scholar]
- Jornet-Mollá, V.; Romero, F.M. Synthesis of rigid ethynyl-bridged polytopic picolinate ligands for MOF applications. Tetrahedron Lett. 2015, 56, 6120–6122. [Google Scholar] [CrossRef]
- Jornet-Mollá, V.; Martín-Mezquita, C.; Giménez-Saiz, C.; Romero, F.M. Zinc (II) picolinate-based coordination polymers as luminescent sensors of Fe3+ ions and nitroaromatic compounds. Inorg. Chim. Acta 2022, 538, 120993. [Google Scholar] [CrossRef]
- Bünzli, J.-C.G.; Piguet, C. Taking advantage of luminescent lanthanide ions. Chem. Soc. Rev. 2005, 34, 1048–1077. [Google Scholar]
- Lamture, J.B.; Zhou, Z.H.; Kumar, A.S.; Wensel, T.G. Luminescence properties of terbium (III) complexes with 4-substituted dipicolinic acid analogs. Inorg. Chem. 1995, 34, 864–869. [Google Scholar] [CrossRef]
- Jornet-Mollá, V.; Dreessen, C.; Romero, F.M. Robust lanthanoid picolinate-based coordination polymers for luminescence and sensing applications. Inorg. Chem. 2021, 60, 10572–10584. [Google Scholar] [CrossRef]
- CrysAlisPro v38.46; Oxford Diffraction Ltd.: Abingdon, UK, 2017.
- Farrugia, L.J. WinGX suite for small-molecule single-crystal crystallography. J. Appl. Crystallogr. 1999, 32, 837–838. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. 2015, C71, 3–8. [Google Scholar]
- Bain, G.A.; Berry, J.F. Diamagnetic corrections and Pascal’s constants. J. Chem. Educ. 2008, 85, 532–536. [Google Scholar] [CrossRef]
- Flack, H.D. On enantiomorph-polarity estimation. Acta Cryst. 1983, A39, 876–881. [Google Scholar] [CrossRef]
- Wu, Y.-P.; Xu, G.-W.; Dong, W.-W.; Zhao, J.; Li, D.-S.; Zhang, J.; Bu, X. Anionic lanthanide MOFs as a platform for iron-selective sensing, systematic color tuning, and efficient nanoparticle catalysis. Inorg. Chem. 2017, 56, 1402–1411. [Google Scholar] [CrossRef]
- Casanova, D.; Alemany, P.; Bofill, J.M.; Alvarez, S. Shape and symmetry of heptacoordinate transition-metal complexes: Structural trends. Chem. Eur. J. 2003, 9, 1281–1295. [Google Scholar] [CrossRef]
- Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
- Llunell, M.; Casanova, D.; Cirera, J.; Bofill, J.M.; Alemany, P.; Alvarez, S. SHAPE, version 2.1; Universitat de Barcelona: Barcelona, Spain, 2013. [Google Scholar]
- Alvarez, S.; Avnir, D.; Llunell, M.; Pinsky, M. Continuous symmetry maps and shape classification. The case of six-coordinated metal compounds. New J. Chem. 2002, 26, 996–1009. [Google Scholar] [CrossRef]
- Sorace, L.; Gatteschi, D. Electronic Structure and Magnetic Properties of Lanthanide Molecular Complexes. In Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH: Hoboken, NJ, USA, 2015; pp. 1–26. [Google Scholar]
- de Oliveira Maciel, J.W.; Lemes, M.A.; Valdo, A.K.; Rabelo, R.; Martins, F.T.; Queiroz Maia, L.J.; de Santana, R.C.; Lloret, F.; Julve, M.; Cangussu, D. Europium(III), terbium(III), and gadolinium(III) oxamato-based coordination polymers: Visible luminescence and slow magnetic relaxation. Inorg. Chem. 2021, 60, 6176–6190. [Google Scholar] [CrossRef]
- Vostrikova, K.E.; Sukhikh, T.S.; Lavrov, A.N. The synthesis, crystal structure, and magnetic properties of mono-scorpionate Eu(III) complexes. Inorganics 2023, 11, 418. [Google Scholar] [CrossRef]
- Benmansour, S.; Cerezo-Navarrete, C.; Gómez-García, C.J. Slow relaxation of the magnetisation in a two-dimensional metal–organic framework with a layered square lattice. Magnetochemistry 2025, 11, 1. [Google Scholar] [CrossRef]
- AlDamen, M.A.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Martí-Gastaldo, C.; Luis, F.; Montero, O. Mononuclear lanthanide single molecule magnets based on the polyoxometalates [Ln(W5O18)2]9− and [Ln(β2-SiW11O39)2]13− (LnIII = Tb, Dy, Ho, Er, Tm, and Yb). Inorg. Chem. 2009, 48, 3467–3479. [Google Scholar] [CrossRef]
- Kalita, P.; Malakar, A.; Goura, J.; Nayak, S.; Herrera, J.M.; Colacio, E.; Chandrasekhar, V. Mononuclear lanthanide complexes assembled from a tridentate NNO donor ligand: Design of a DyIII single-ion magnet. Dalton Trans. 2019, 48, 4857–4866. [Google Scholar]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar]
- Dolai, M.; Ali, M.; Titiš, J.; Boča, R. Cu(II)–Dy(III) and Co(III)–Dy(III) based single molecule magnets with multiple slow magnetic relaxation processes in the Cu(II)–Dy(III) complex. Dalton Trans. 2015, 44, 13242–13249. [Google Scholar] [PubMed]
- Blagg, R.J.; Ungur, L.; Tuna, F.; Speak, J.; Comar, P.; Collison, D.; Wernsdorfer, W.; McInnes, E.J.L.; Chibotaru, L.; Winpenny, R.E.P. Magnetic relaxation pathways in lanthanide single-molecule magnets. Nature Chem. 2013, 5, 673–678. [Google Scholar]
- Wang, M.-H.; Tsai, M.-Y.; Su, Y.-C.; Chiu, S.-T.; Lin, P.-H.; Long, J. Zero-field single-molecule magnet behavior in a series of dinuclear dysprosium(III) complexes based on benzothiazolyl-based ligands and β-diketonates. Cryst. Growth Des. 2024, 24, 422–431. [Google Scholar]
- Demir, S.; Zadrozny, J.M.; Long, J.R. Large spin-relaxation barriers for the low-symmetry organolanthanide complexes [Cp*2Ln(BPh4)] (Cp*=pentamethylcyclopentadienyl; Ln=Tb, Dy). Chem. Eur. J. 2014, 20, 9524–9529. [Google Scholar]
- Zhu, Z.; Guo, M.; Li, X.; Tang, J. Molecular magnetism of lanthanide: Advances and perspectives. Coord. Chem. Rev. 2019, 378, 350–364. [Google Scholar]
- Parmar, V.S.; Mills, D.P.; Winpenny, R.E.P. Mononuclear dysprosium alkoxide and aryloxide single-molecule magnets. Chem. Eur. J. 2021, 27, 7625–7645. [Google Scholar] [CrossRef]
- Zabala-Lekuona, A.; Manuel Seco, J.; Colacio, E. Single-molecule magnets: From Mn12-ac to dysprosium metallocenes, a travel in time. Coord. Chem. Rev. 2021, 441, 213984. [Google Scholar]
- Ashebr, T.G.; Li, H.; Ying, X.; Li, X.-L.; Zhao, C.; Liu, S.; Tang, J. Emerging trends on designing high-performance dysprosium(III) single-molecule magnets. ACS Mater. Lett. 2022, 4, 307–319. [Google Scholar] [CrossRef]
- Orendáč, M.; Sedláková, L.; Čizmár, E.; Orendáčova, A.; Feher, A.; Zvyagin, S.A.; Wosnitza, J.; Zhu, W.H.; Wang, Z.M.; Gao, S. Spin relaxation and resonant phonon trapping in [Gd2(fum)3(H2O)4]⋅3H2O. Phys. Rev. B 2010, 81, 214410. [Google Scholar] [CrossRef]
- Rossin, A.; Giambastiani, G.; Peruzzini, M.; Sessoli, R. Amine-templated polymeric lanthanide formates: Synthesis, characterization, and applications in luminescence and magnetism. Inorg. Chem. 2012, 51, 6962–6968. [Google Scholar] [CrossRef] [PubMed]
- Orts-Arroyo, M.; Rabelo, R.; Carrasco-Berlanga, A.; Moliner, N.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Ruiz-García, R.; Mayans, J.; et al. Field-induced slow magnetic relaxation and magnetocaloric effects in an oxalato-bridged gadolinium(III)-based 2D MOF. Dalton Trans. 2021, 50, 3801–3805. [Google Scholar] [CrossRef] [PubMed]
- Orts-Arroyo, M.; Sanchis-Perucho, A.; Moliner, N.; Castro, I.; Lloret, F.; Martínez-Lillo, J. One-dimensional gadolinium(III) complexes based on alpha-and beta-amino acids exhibiting field-induced slow relaxation of magnetization. Inorganics 2022, 10, 32. [Google Scholar] [CrossRef]
- Chen, Y.C.; Peng, Y.-Y.; Liu, J.-L.; Tong, M.-L. Field-induced slow magnetic relaxation in a mononuclear Gd (III) complex. Inorg. Chem. Commun. 2019, 107, 107449. [Google Scholar] [CrossRef]
- Mayans, J.; Escuer, A. Correlating the axial zero field splitting with the slow magnetic relaxation in GdIII SIMs. Chem. Commun. 2021, 57, 721–724. [Google Scholar] [CrossRef]
- Liu, B.; Wang, B.; Wang, Z. Static field induced magnetic relaxations in dinuclear lanthanide compounds of [phen2Ln2(HCOO)4(HCOO)2−2x (NO3)2x ] (1, Ln = Gd and x = 0.52; 2, Ln = Er and x = 0.90; phen = 1,10-phenanthroline). Sci. China Chem. 2012, 55, 926–933. [Google Scholar] [CrossRef]
- Martínez-Pérez, M.J.; Cardona-Serra, S.; Schlegel, C.; Moro, F.; Alonso, P.J.; Prima-García, H.; Clemente-Juan, J.M.; Evangelisti, M.; Gaita-Ariño, A.; Sesé, J.; et al. Gd-based single-ion magnets with tunable magnetic anisotropy: Molecular design of spin qubits. Phys. Rev. Lett. 2012, 108, 247213. [Google Scholar] [CrossRef]
- Arauzo, A.; Lazarescu, A.; Shova, S.; Bartolomé, E.; Cases, R.; Luzón, J.; Bartolomé, J.; Turta, C. Structural and magnetic properties of some lanthanide (Ln = Eu(III), Gd(III) and Nd(III)) cyanoacetate polymers: Field-induced slow magnetic relaxation in the Gd and Nd substitutions. Dalton Trans. 2014, 43, 12342–12356. [Google Scholar] [CrossRef]
- Holmberg, R.J.; Anh Ho, L.T.; Ungur, L.; Korobkov, I.; Chibotaru, L.F.; Murugesu, M. Observation of unusual slow-relaxation of the magnetisation in a Gd-EDTA chelate. Dalton Trans. 2015, 44, 20321–20325. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, T.; Cosquer, G.; Izuogu, D.C.; Ohtsu, H.; Kawano, M.; Lan, Y.; Wernsdorfer, W.; Nojiri, H.; Breedlove, B.K.; Yamashita, M. Field-induced slow magnetic relaxation of GdIII complex with a Pt−Gd heterometallic bond. Chem. Eur. J. 2017, 23, 4551–4556. [Google Scholar] [CrossRef] [PubMed]
- Izuogu, D.C.; Yoshida, T.; Zhang, H.; Cosquer, G.; Katoh, K.; Ogata, S.; Hasegawa, M.; Nojiri, H.; Damjanović, M.; Wernsdorfer, W.; et al. Slow magnetic relaxation in a palladium–gadolinium complex induced by electron density donation from the palladium ion. Chem. Eur. J. 2018, 24, 9285–9294. [Google Scholar] [CrossRef] [PubMed]
- da Cunha, T.T.; Barbosa, V.M.M.; Oliveira, W.X.C.; Pinheiro, C.B.; Pedroso, E.F.; Nunes, W.C.; Pereira, C.L.M. Slow magnetic relaxation in mononuclear gadolinium(III) and dysprosium(III) oxamato complexes. Polyhedron 2019, 169, 102–113. [Google Scholar] [CrossRef]
- Vaz, R.C.A.; Esteves, I.O.; Oliveira, W.X.C.; Honorato, J.; Martins, F.T.; Marques, L.F.; dos Santos, G.L.; Freire, R.O.; Jesus, L.T.; Pedroso, E.F.; et al. Mononuclear lanthanide(III)-oxamate complexes as new photoluminescent field-induced single-molecule magnets: Solid-state photophysical and magnetic properties. Dalton Trans. 2020, 49, 16106–16124. [Google Scholar] [CrossRef]
- Handzlik, G.; Magott, M.; Arczyński, M.; Sheveleva, A.M.; Tuna, F.; Sarewicz, M.; Osyczka, A.; Rams, M.; Vieru, V.; Chibotaru, L.F.; et al. Magnetization dynamics and coherent spin manipulation of a propeller Gd(III) complex with the smallest helicene ligand. J. Phys. Chem. Lett. 2020, 11, 1508–1515. [Google Scholar] [CrossRef]
- Brzozowska, M.; Handzlik, G.; Zychowicz, M.; Pinkowicz, D. Low-coordinate dinuclear dysprosium(III) single molecule magnets utilizing LiCl as bridging moieties and tris(amido)amine as blocking ligands. Magnetochemistry 2021, 7, 125. [Google Scholar] [CrossRef]
- Tkáč, V.; Tarasenko, R.; Doroshenko, A.; Kavečansky, V.; Čizmár, E.; Orendáčová, A.; Smolko, R.; Černák, J.; Orendáč, M. Reciprocating thermal behavior in a magnetic field induced slow spin relaxation of [Gd2(H2O)6(C2O4)3]∙2.5H2O. Solid State Sci. 2023, 136, 107105. [Google Scholar] [CrossRef]
- Masuda, Y.; Sakata, S.; Kayahara, S.; Irie, N.; Kofu, M.; Kono, Y.; Sakakibara, T.; Horii, Y.; Kajiwara, T. Slow magnetic relaxation of linear trinuclear M(II)–Gd(III)–M(II) complexes with D3 point group symmetry (M(II) = Zn(II) and Mg(II)). J. Phys. Chem. C 2023, 127, 3295–3306. [Google Scholar] [CrossRef]
- Kumar, S.; Gabarró Riera, G.; Arauzo, A.; Hruby, J.; Hill, S.; Bogani, L.; Rubio-Zuazo, J.; Jover, J.; Bartolomé, E.; Sañudo, E.C. On-surface magnetocaloric effect for a van der Waals Gd(III) 2D MOF grown on Si. J. Mater. Chem. A 2024, 12, 6269–6279. [Google Scholar] [CrossRef]
- da Silveira, C.O.C.; Oliveira, W.X.C.; da Silva Júnior, E.N.; Alvarenga, M.E.; Martins, F.T.; Gatto, C.C.; Pinheiro, C.B.; Pedroso, E.F.; Silva, J.P.O.; Marques, L.F.; et al. Photoluminescence and magnetic properties of isostructural europium(III), gadolinium(III) and terbium(III) oxamate-based coordination polymers. Dalton Trans. 2024, 53, 14995–15009. [Google Scholar] [CrossRef] [PubMed]
- Orts-Arroyo, M.; Ten-Esteve, A.; Ginés-Cárdenas, S.; Cerdá-Alberich, L.; Martí-Bonmatí, L.; Martínez-Lillo, J. A gadolinium(III) complex based on pyridoxine molecule with single-ion magnet and magnetic resonance imaging properties. Int. J. Mol. Sci. 2024, 25, 2112. [Google Scholar] [CrossRef] [PubMed]



| 1 | 3 | |
|---|---|---|
| chemical formula | C32H26EuN5O11 | C32H26N5O11Tb |
| a (Å) | 19.6440(2) | 19.70340(10) |
| b (Å) | 12.35500(10) | 12.32080(10) |
| c (Å) | 13.21490(10) | 13.14510(10) |
| α (deg) | 90.00 | 90.00 |
| β (deg) | 90.00 | 90.00 |
| γ (deg) | 90.00 | 90.00 |
| V (Å3) | 3207.28(5) | 3191.13(4) |
| T (K) | 119.7(8) | 120.00(10) |
| Z | 4 | 4 |
| Mr (g/mol) | 808.54 | 815.50 |
| crystal system | orthorhombic | orthorhombic |
| space group | Pna21 (No. 33) | Pna21 (No. 33) |
| crystal dimensions (mm) | 0.124 0.105 0.073 | 0.180 0.136 0.122 |
| µ (Mo Kα) (mm−1) | 2.025 | 2.286 |
| λ (Å) | 0.71073 | 0.71073 |
| density (Mg/m3) | 1.674 | 1.697 |
| index ranges for h, k, l | −25/24, −16/16, −16/17 | −25/25, −16/15, −17/17 |
| θ range (deg) | 3.298 to 28.107 | 3.307 to 27.710 |
| goodness-of-fit on F2 | 1.082 | 1.115 |
| reflns collected | 118251 | 116487 |
| independent reflns (Rint) | 7383 (0.0975) | 7172 (0.0435) |
| data/restraints/parameters | 7383/33/453 | 7172/6/422 |
| R1, wR2 [I > 2σ(I)] 1 | 0.0389, 0.0765 | 0.0308, 0.0714 |
| R1, wR2 (all data) 1 | 0.0627, 0.0883 | 0.0356, 0.0747 |
| absolute structure parameter | −0.039(6) | −0.026(4) |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| Experimental χmT | 1.55 | 7.86 | 12.05 | 13.65 | 14.04 |
| Expected χmT | 0 (1.50) | 7.87 | 11.82 | 14.05 | 14.04 |
| λ (cm−1) | 389(2) | ||||
| Experimental g | 2.023(4) | 1.528(2) | 1.301(2) | 1.195(2) | |
| Expected g | 2.0 | 1.5 | 1.33 | 1.20 | |
| |D| (cm−1) | 0.27(3) | 0.15(1) | 1.35(6) | 1.14(2) | |
| zj (cm−1) | −0.018(2) | −0.091(2) | −0.032(1) | −0.079(1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jornet-Mollá, V.; Gómez-García, C.J.; Dolz-Lozano, M.J.; Romero, F.M. Lanthanoid Coordination Polymers Based on Homoditopic Picolinate Ligands: Synthesis, Structure and Magnetic Properties. Magnetochemistry 2025, 11, 31. https://doi.org/10.3390/magnetochemistry11040031
Jornet-Mollá V, Gómez-García CJ, Dolz-Lozano MJ, Romero FM. Lanthanoid Coordination Polymers Based on Homoditopic Picolinate Ligands: Synthesis, Structure and Magnetic Properties. Magnetochemistry. 2025; 11(4):31. https://doi.org/10.3390/magnetochemistry11040031
Chicago/Turabian StyleJornet-Mollá, Verónica, Carlos J. Gómez-García, Miquel J. Dolz-Lozano, and Francisco M. Romero. 2025. "Lanthanoid Coordination Polymers Based on Homoditopic Picolinate Ligands: Synthesis, Structure and Magnetic Properties" Magnetochemistry 11, no. 4: 31. https://doi.org/10.3390/magnetochemistry11040031
APA StyleJornet-Mollá, V., Gómez-García, C. J., Dolz-Lozano, M. J., & Romero, F. M. (2025). Lanthanoid Coordination Polymers Based on Homoditopic Picolinate Ligands: Synthesis, Structure and Magnetic Properties. Magnetochemistry, 11(4), 31. https://doi.org/10.3390/magnetochemistry11040031