Uniform Illumination Using Single-Surface Lens through Wavefront Engineering
Abstract
1. Introduction
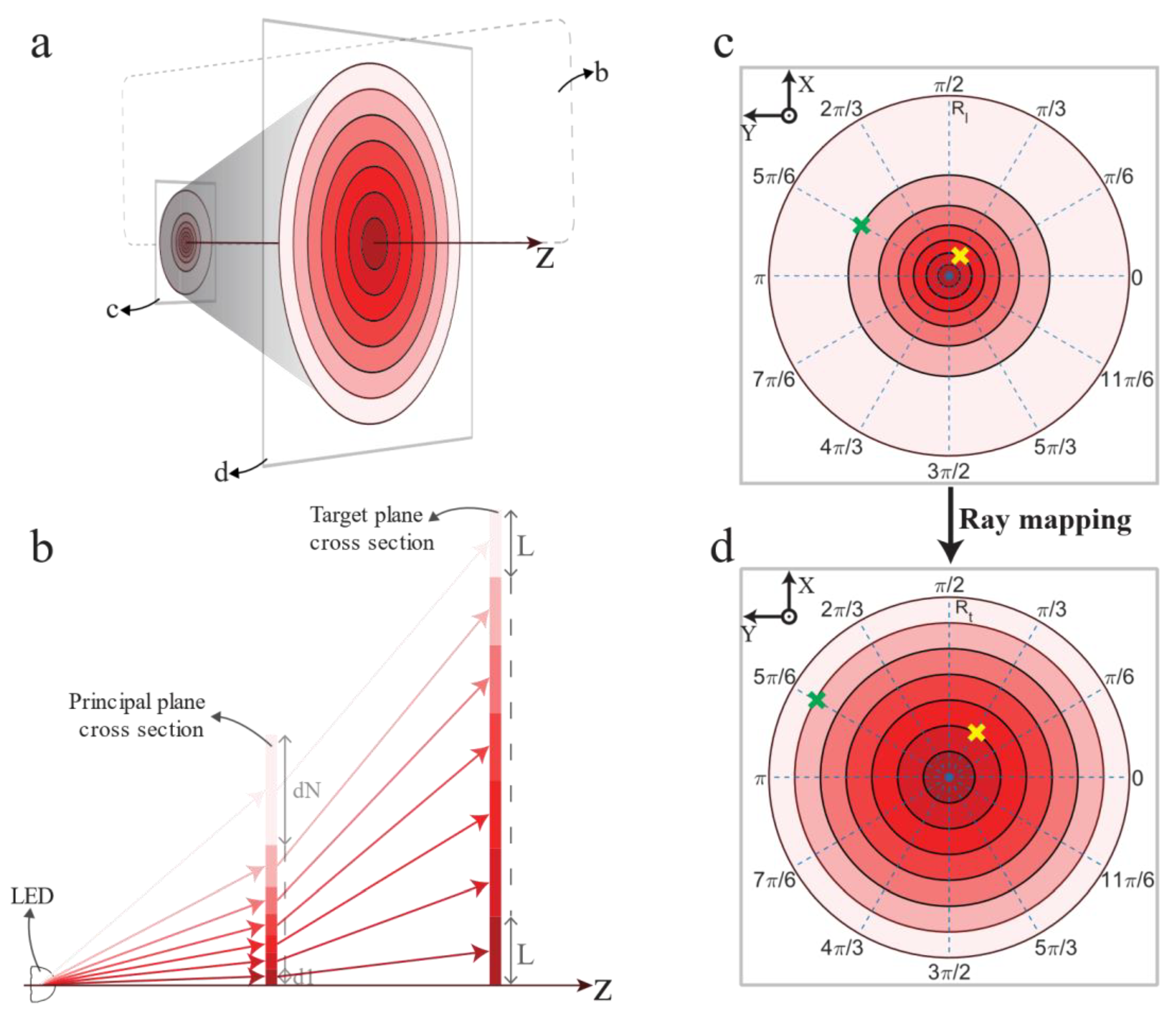
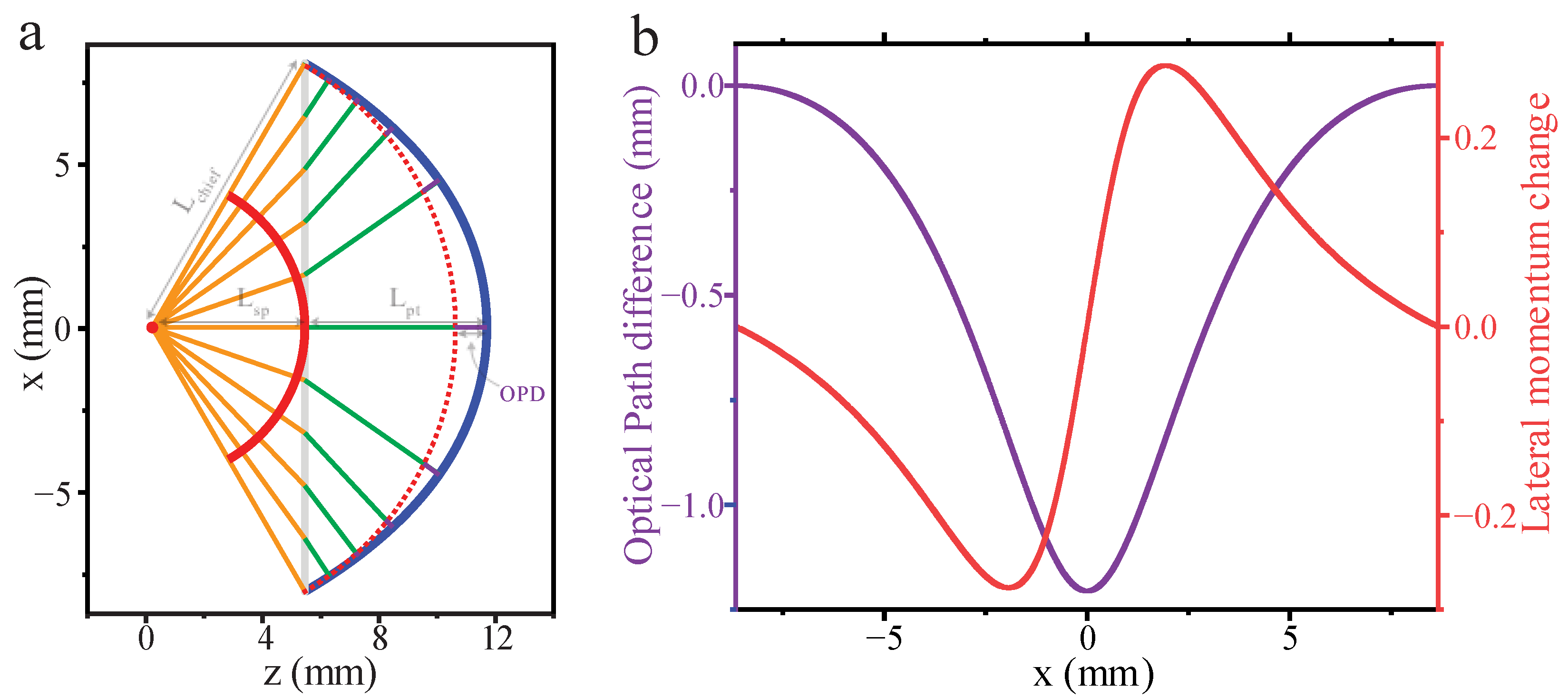
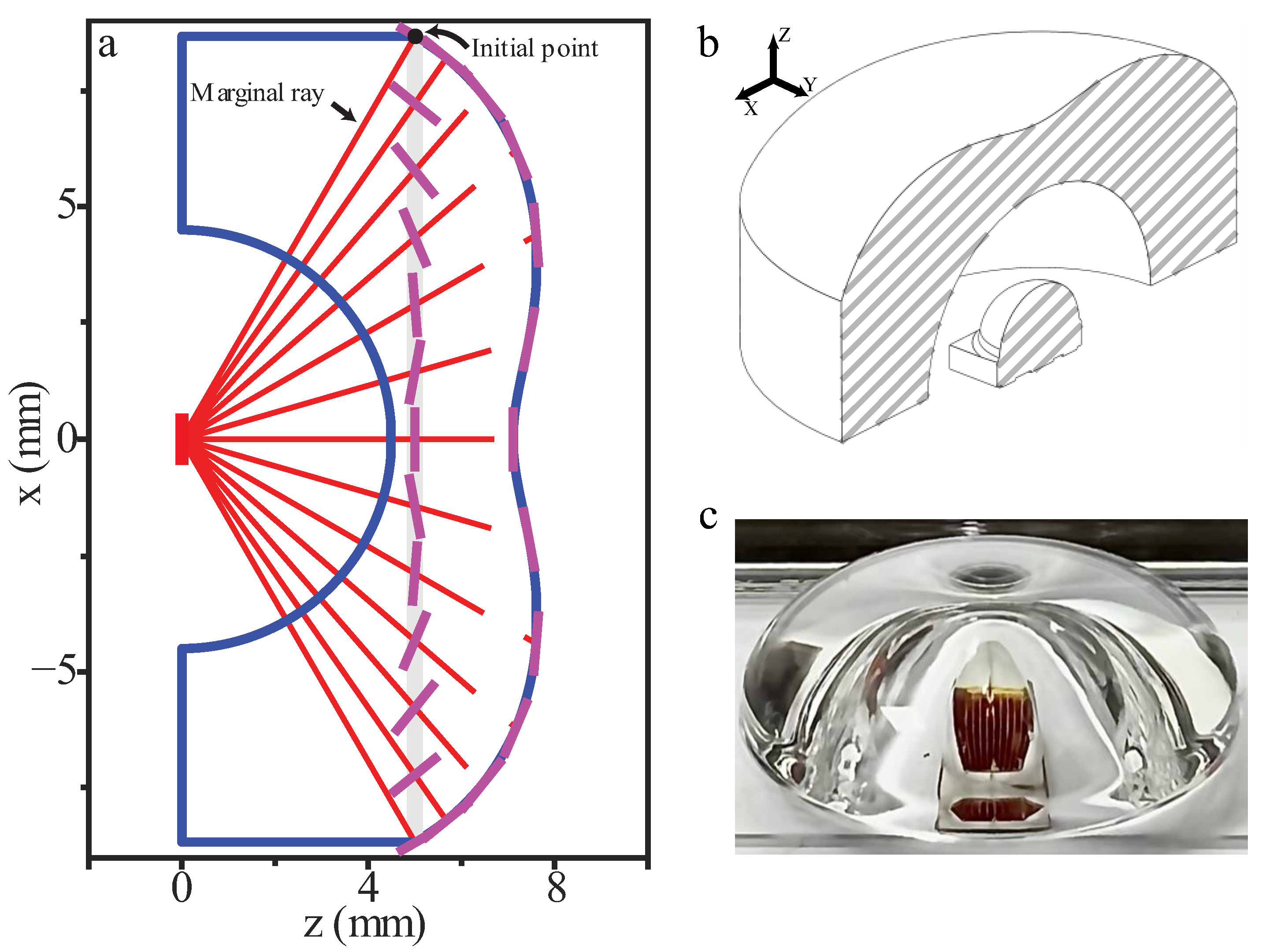
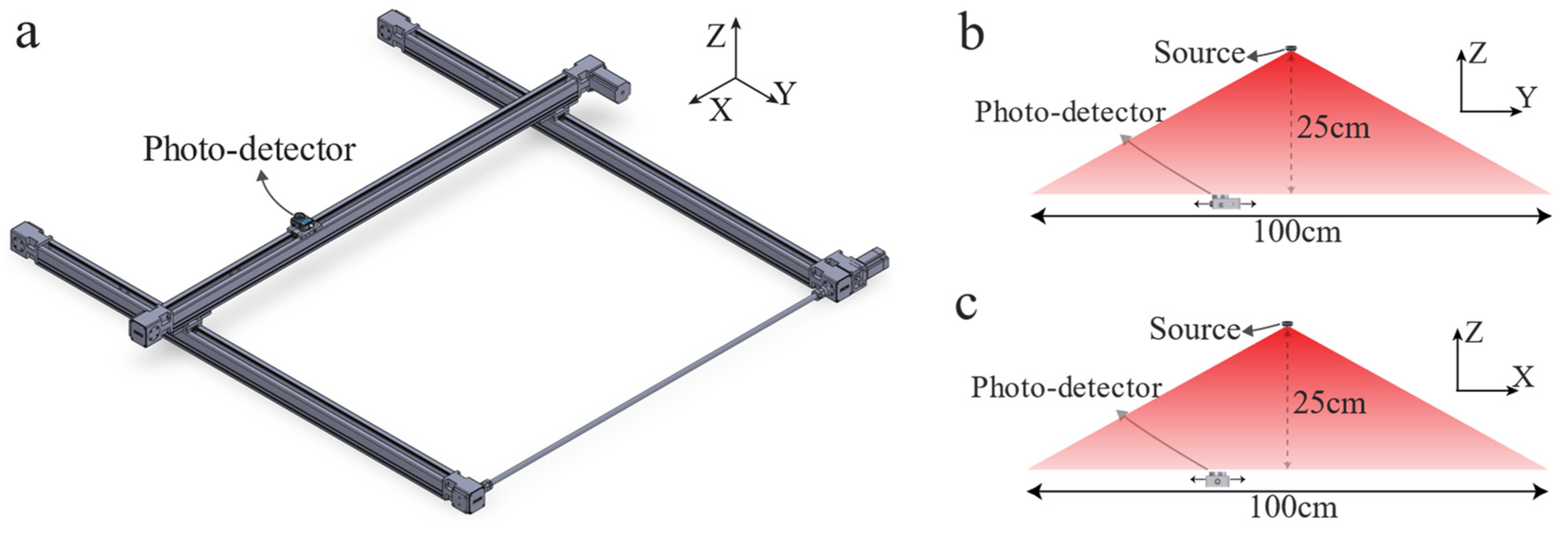
2. Materials and Methods
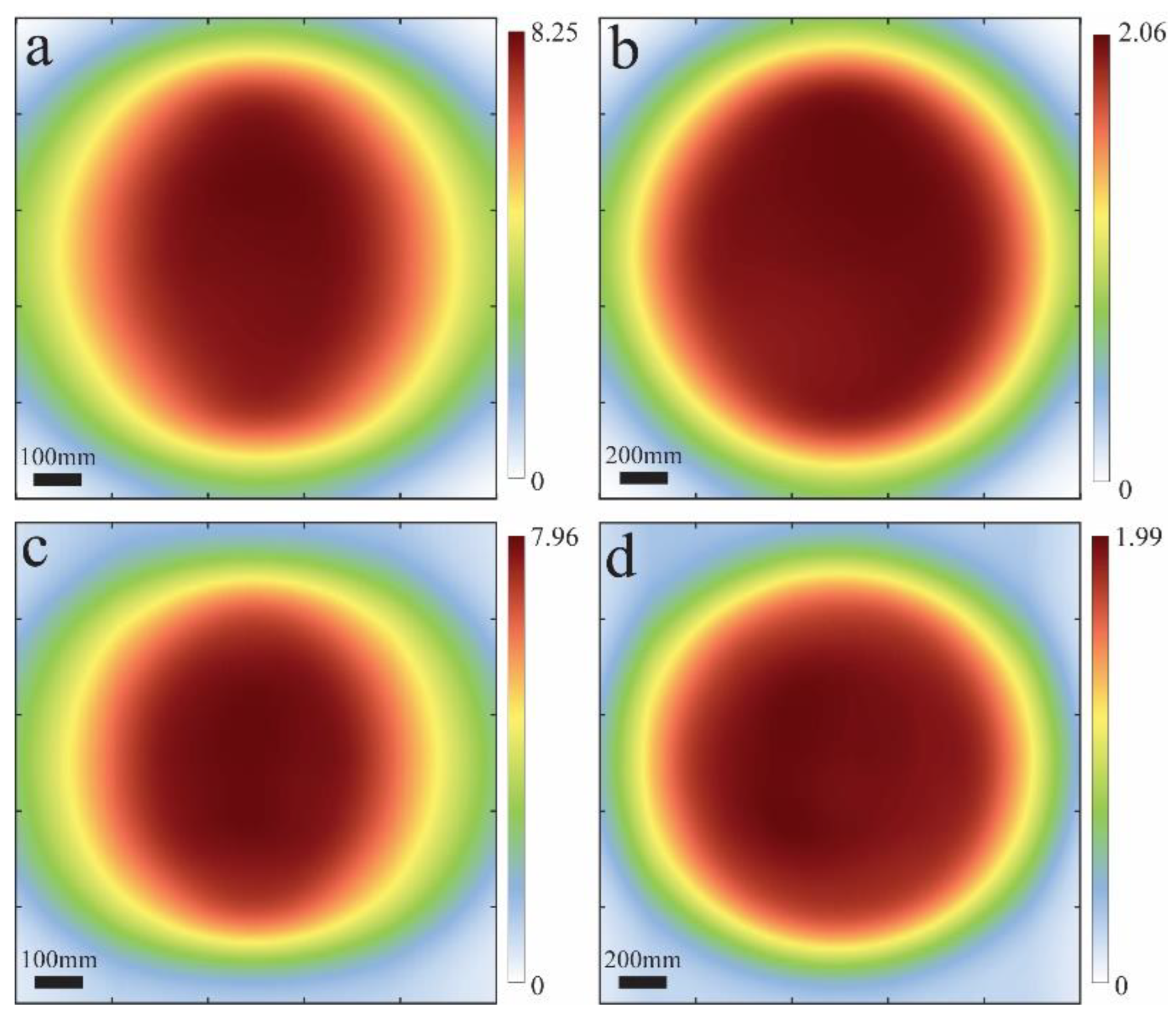
3. Results and Discussion
4. Conclusions
5. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haitz, R.; Tsao, J.Y. Solid-state lighting:‘The case’10 years after and future prospects. Phys. Status Solidi 2011, 208, 17–29. [Google Scholar] [CrossRef]
- Gupta, S.D.; Agarwal, A. LED Supplementary Lighting. In Light Emitting Diodes for Agriculture, 1st ed.; Springer: Singapore, 2017; pp. 27–36. [Google Scholar]
- Bula, R.J.; Morrow, R.C.; Tibbitts, T.; Barta, D.; Ignatius, R.; Martin, T. Light-emitting diodes as a radiation source for plants. HortScience 1991, 26, 203–205. [Google Scholar] [CrossRef] [PubMed]
- Nelson, J.A.; Bugbee, B. Economic analysis of greenhouse lighting: Light emitting diodes vs. high intensity discharge fixtures. PLoS ONE 2014, 9, e99010. [Google Scholar] [CrossRef]
- Kusuma, P.; Pattison, P.M.; Bugbee, B. From physics to fixtures to food: Current and potential LED efficacy. Hortic. Res. 2020, 7, 56. [Google Scholar] [CrossRef]
- Wu, B.-S.; Hitti, Y.; MacPherson, S.; Orsat, V.; Lefsrud, M.G. Comparison and perspective of conventional and LED lighting for photobiology and industry applications. Environ. Exp. Bot. 2020, 171, 103953. [Google Scholar] [CrossRef]
- Paucek, I.; Appolloni, E.; Pennisi, G.; Quaini, S.; Gianquinto, G.; Orsini, F. LED lighting systems for horticulture: Business growth and global distribution. Sustainability 2020, 12, 7516. [Google Scholar] [CrossRef]
- Katzin, D.; Marcelis, L.F.; van Mourik, S. Energy savings in greenhouses by transition from high-pressure sodium to LED lighting. Appl. Energy 2021, 281, 116019. [Google Scholar] [CrossRef]
- Shelford, T.J.; Both, A.-J. On the technical performance characteristics of horticultural lamps. AgriEngineering 2021, 3, 716–727. [Google Scholar] [CrossRef]
- Runkle, E. The Importance of Light Uniformity; Michigan State University: East Lansin, MI, USA, 2017. [Google Scholar]
- Poorter, H.; Niinemets, Ü.; Ntagkas, N.; Siebenkäs, A.; Mäenpää, M.; Matsubara, S.; Pons, T. A meta-analysis of plant responses to light intensity for 70 traits ranging from molecules to whole plant performance. New Phytol. 2019, 223, 1073–1105. [Google Scholar] [CrossRef] [PubMed]
- Balázs, L.; Dombi, Z.; Csambalik, L.; Sipos, L. Characterizing the Spatial Uniformity of Light Intensity and Spectrum for Indoor Crop Production. Horticulturae 2022, 8, 644. [Google Scholar] [CrossRef]
- Both, A.; Ciolkosz, D.E.; Albright, L. Evaluation of light uniformity underneath supplemental lighting systems. In Proceedings of the IV International ISHS Symposium on Artificial Lighting 580, Québec City, QC, Canada, 7 November 2000; pp. 183–190. [Google Scholar]
- Ciolkosz, D.E.; Both, A.J.; Albright, L.D. Selection and placement of greenhouse luminaires for uniformity. Appl. Eng. Agric. 2001, 17, 875. [Google Scholar] [CrossRef]
- Pan, J.; Li, Q.; Li, X.; Wen, Y. Spatial light distribution characterization and measurement of LED horticultural lights. In Proceedings of the 29th CIE Session, Washington, DC, USA, 14–16 June 2019; pp. 14–22. [Google Scholar]
- Ding, Y.; Liu, X.; Zheng, Z.-r.; Gu, P.-f. Freeform LED lens for uniform illumination. Opt. Express 2008, 16, 12958–12966. [Google Scholar] [CrossRef]
- Fang, F.; Zhang, X.; Weckenmann, A.; Zhang, G.; Evans, C. Manufacturing and measurement of freeform optics. CIRP Ann. 2013, 62, 823–846. [Google Scholar] [CrossRef]
- Desnijder, K.; Hanselaer, P.; Meuret, Y. Ray mapping method for off-axis and non-paraxial freeform illumination lens design. Opt. Lett. 2019, 44, 771–774. [Google Scholar] [CrossRef]
- Bösel, C.; Gross, H. Ray mapping approach for the efficient design of continuous freeform surfaces. Opt. Express 2016, 24, 14271–14282. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Cheng, D.; Wang, Y. Iterative wavefront tailoring to simplify freeform optical design for prescribed irradiance. Opt. Lett. 2019, 44, 2274–2277. [Google Scholar] [CrossRef]
- Bösel, C.; Gross, H. Double freeform illumination design for prescribed wavefronts and irradiances. JOSA A 2018, 35, 236–243. [Google Scholar] [CrossRef] [PubMed]
- Gannon, C.; Liang, R. Ray mapping with surface information for freeform illumination design. Opt. Express 2017, 25, 9426–9434. [Google Scholar] [CrossRef]
- Bruneton, A.; Bäuerle, A.; Wester, R.; Stollenwerk, J.; Loosen, P. High resolution irradiance tailoring using multiple freeform surfaces. Opt. Express 2013, 21, 10563–10571. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Huang, L.; Gong, M.; Jin, G. Beam shaping system design using double freeform optical surfaces. Opt. Express 2013, 21, 14728–14735. [Google Scholar] [CrossRef]
- Feng, Z.; Cheng, D.; Wang, Y. Iterative freeform lens design for prescribed irradiance on curved target. Opto-Electron. Adv. 2020, 3, 200010-200011–200010-200019. [Google Scholar] [CrossRef]
- Romijn, L.B.; ten Thije Boonkkamp, J.H.; IJzerman, W.L. Freeform lens design for a point source and far-field target. JOSA A 2019, 36, 1926–1939. [Google Scholar] [CrossRef]
- Byzov, E.V.; Kravchenko, S.V.; Moiseev, M.A.; Bezus, E.A.; Doskolovich, L.L. Optimization method for designing double-surface refractive optical elements for an extended light source. Opt. Express 2020, 28, 24431–24443. [Google Scholar] [CrossRef]
- Ma, D.; Feng, Z.; Liang, R. Freeform illumination lens design using composite ray mapping. Appl. Opt. 2015, 54, 498–503. [Google Scholar] [CrossRef]
- Bruneton, A.; Bäuerle, A.; Wester, R.; Stollenwerk, J.; Loosen, P. Limitations of the ray mapping approach in freeform optics design. Opt. Lett. 2013, 38, 1945–1947. [Google Scholar] [CrossRef]
- Wei, S.; Zhu, Z.; Fan, Z.; Ma, D. Least-squares ray mapping method for freeform illumination optics design. Opt. Express 2020, 28, 3811–3822. [Google Scholar] [CrossRef] [PubMed]
- Oliker, V.I.; Rubinstein, J.; Wolansky, G. Ray mapping and illumination control. J. Photonics Energy 2013, 3, 035599. [Google Scholar] [CrossRef]
- Ma, D.; Feng, Z.; Liang, R. Tailoring freeform illumination optics in a double-pole coordinate system. Appl. Opt. 2015, 54, 2395–2399. [Google Scholar] [CrossRef]
- Wu, R.; Feng, Z.; Zheng, Z.; Liang, R.; Benítez, P.; Miñano, J.C.; Duerr, F. Design of freeform illumination optics. Laser Photonics Rev. 2018, 12, 1700310. [Google Scholar] [CrossRef]
- Wang, K.; Liu, S.; Chen, F.; Qin, Z.; Liu, Z.; Luo, X. Freeform LED lens for rectangularly prescribed illumination. J. Opt. A Pure Appl. Opt. 2009, 11, 105501. [Google Scholar] [CrossRef]
- Zhenrong, Z.; Xiang, H.; Xu, L. Freeform surface lens for LED uniform illumination. Appl. Opt. 2009, 48, 6627–6634. [Google Scholar] [CrossRef] [PubMed]
- Sorgato, S.; Chaves, J.; Thienpont, H.; Duerr, F. Design of illumination optics with extended sources based on wavefront tailoring. Optica 2019, 6, 966–971. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moaven, A.; Pahlevaninezhad, H.; Pahlevaninezhad, M.; Pahlevani, M. Uniform Illumination Using Single-Surface Lens through Wavefront Engineering. Horticulturae 2022, 8, 1019. https://doi.org/10.3390/horticulturae8111019
Moaven A, Pahlevaninezhad H, Pahlevaninezhad M, Pahlevani M. Uniform Illumination Using Single-Surface Lens through Wavefront Engineering. Horticulturae. 2022; 8(11):1019. https://doi.org/10.3390/horticulturae8111019
Chicago/Turabian StyleMoaven, Aria, Hamid Pahlevaninezhad, Masoud Pahlevaninezhad, and Majid Pahlevani. 2022. "Uniform Illumination Using Single-Surface Lens through Wavefront Engineering" Horticulturae 8, no. 11: 1019. https://doi.org/10.3390/horticulturae8111019
APA StyleMoaven, A., Pahlevaninezhad, H., Pahlevaninezhad, M., & Pahlevani, M. (2022). Uniform Illumination Using Single-Surface Lens through Wavefront Engineering. Horticulturae, 8(11), 1019. https://doi.org/10.3390/horticulturae8111019






