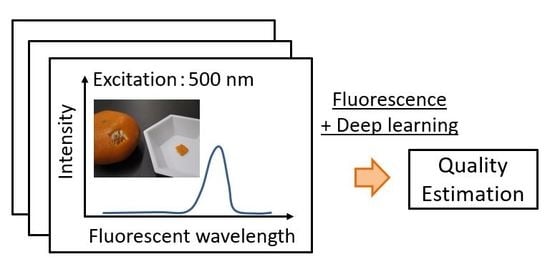
Estimation of Citrus Maturity with Fluorescence Spectroscopy Using Deep Learning
Abstract
1. Introduction
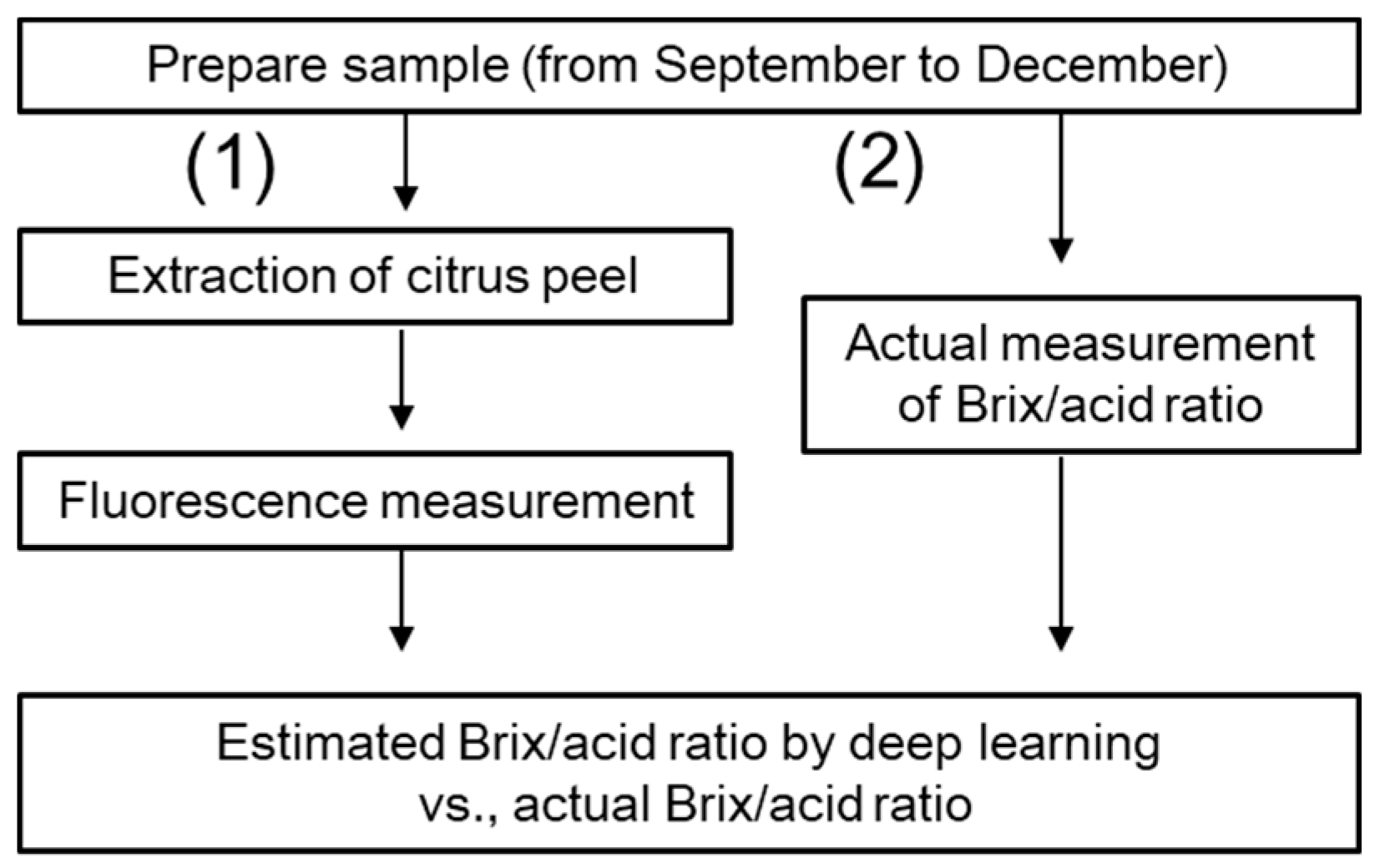
2. Materials and Methods
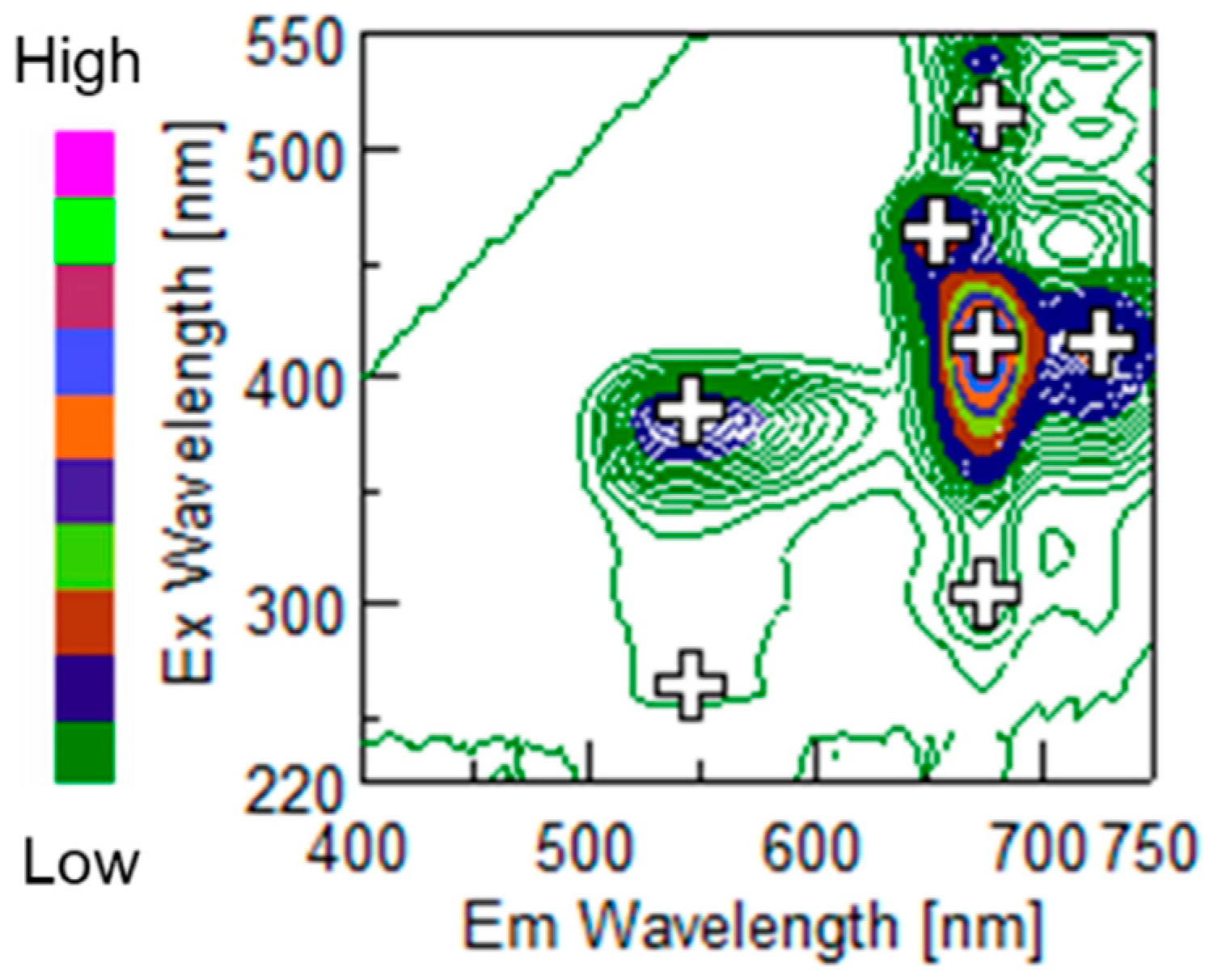
2.1. Materials and Spectra Measurement
2.2. Estimation of the Brix/Acid Ratio with CNN Regression
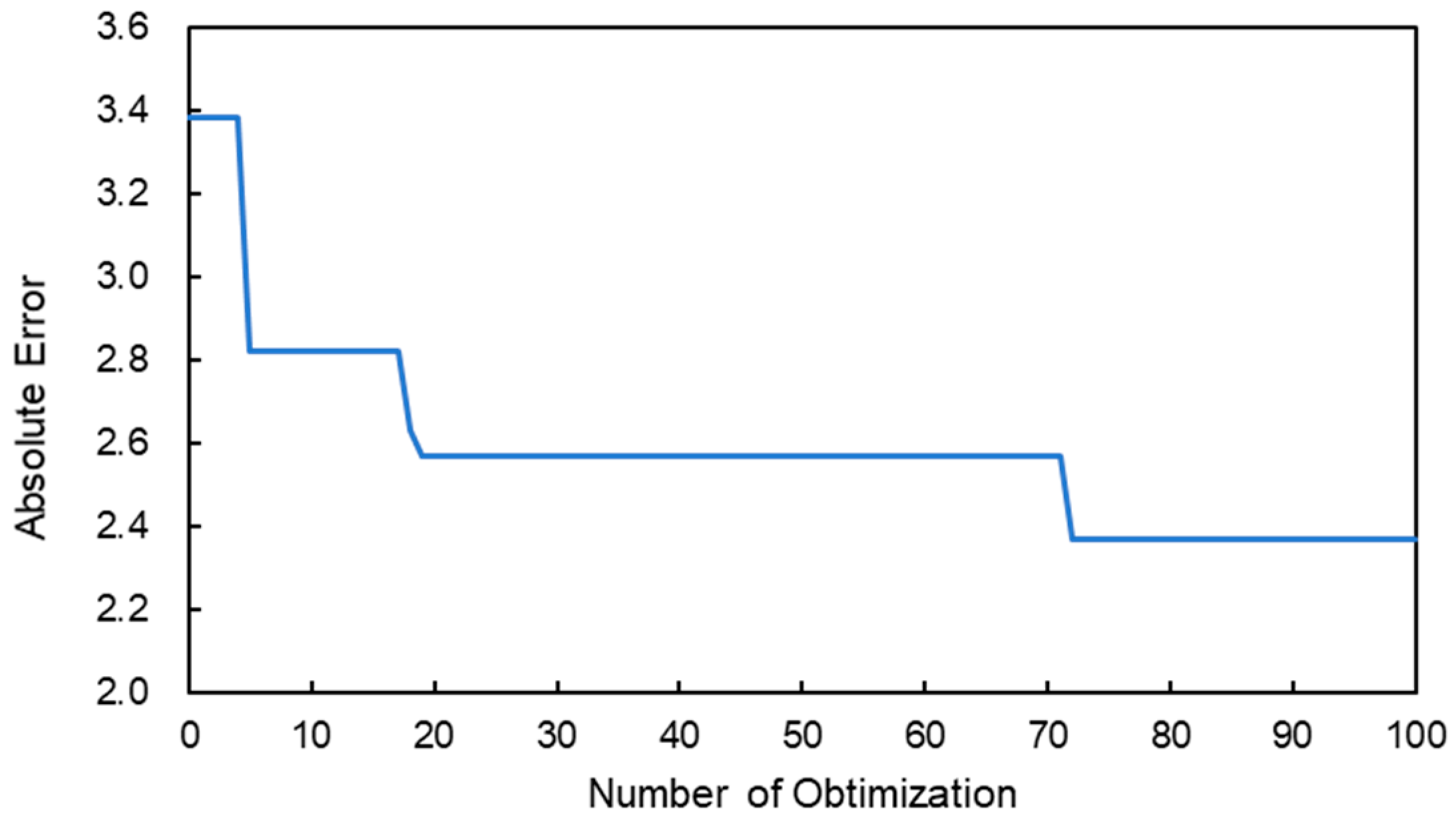
2.3. Bayesian Optimization
2.4. Evaluation of the Brix/Acid Ratio Estimation with Deep Learning
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgement
Conflicts of Interest
References
- Ministry of Agriculture, Forestry and Fisheries. The Situation Surrounding Fruits. Available online: http://www.maff.go.jp/j/seisan/ryutu/fruits/attach/pdf/index-57.pdf (accessed on 20 November 2018).
- Morimoto, T.; Chikaizumi, S.; Hashimoto, Y. Intelligent quality control of fruit storage factory. J. Shita 1994, 6, 191–196. [Google Scholar]
- Momin, A.M.; Kondo, N.; Ogawa, Y.; Shiigi, T.; Kurita, M.; Ninomiya, K. Machine vision system for detecting fluorescent area of citrus using fluorescence image. Proc. IFAC 2010, 43, 241–244. [Google Scholar] [CrossRef]
- Reid, M.S. Maturation and maturity indices. In Postharvest Technology of Horticultural Crops; University of California Division of Agriculture and Natural Resources Publication: Oakland, CA, USA, 2002; pp. 21–28. [Google Scholar]
- Cary, P.R. Citrus Fruit Maturity; MPKV: Rahuri, India, 1974; p. 26. [Google Scholar]
- Iglesias, D.J.; Cercós, M.; Colmenero-Flores, J.M.; Naranjo, M.A.; Ríos, G.; Carrera, E.; Ruiz-Rivero, O.; Lliso, I.; Morillon, R.; Tadeo, F.R.; et al. Physiology of citrus fruiting. Braz. J. Plant Physiol. 2007, 19, 333–362. [Google Scholar] [CrossRef]
- Kimball, D. Citrus Processing: Quality Control and Technology; Springer Science & Business Media: New York, NY, USA, 1991; p. 55. [Google Scholar]
- Kondo, N.; Ahmad, U.; Monta, M.; Murase, H. Machine vision based quality evaluation of Iyokan orange fruit using neural networks. Comput. Electron. Agric. 2000, 29, 135–147. [Google Scholar] [CrossRef]
- Antonucci, F.; Pallottino, F.; Paglia, G.; Palma, A.; D’Aquino, S.; Menesatti, P. Non-destructive estimation of mandarin maturity status through portable VIS-NIR spectrophotometer. Food Bioprocess. Technol. 2011, 4, 809–813. [Google Scholar] [CrossRef]
- Christensen, J.; Povlsen, V.T.; Sørensen, J. Application of fluorescence spectroscopy and chemometrics in the evaluation of processed cheese during storage. J. Dairy Sci. 2003, 86, 1101–1107. [Google Scholar] [CrossRef]
- Muharfiza; Riza, A.F.D.; Saito, Y.; Itakura, K.; Kohno, Y.; Suzuki, T.; Kuramoto, M.; Kondo, N. Monitoring of Fluorescence Characteristics of Satsuma Mandarin (Citrus unshiu Marc.) during the Maturation Period. Horticulturae 2017, 3, 51. [Google Scholar] [CrossRef]
- Wang, X.; Cao, L.; Yang, S.T.; Lu, F.; Meziani, M.J.; Tian, L.; Sun, K.W.; Bloodgood, M.A.; Sun, Y.P. Bandgap-Like strong fluorescence in functionalized carbon nanoparticles. Angew. Chem. Int. Ed. 2010, 49, 5310–5314. [Google Scholar] [CrossRef]
- Sugiyama, J.; Tsuta, M. Discrimination and quantification thechnology for food using fluorescence fingerprint. Nippon Shokuhin Kagaku Kogaku Kaishi 2013, 60, 457–465. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional neural networks for large-scale remote-sensing image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 645–657. [Google Scholar] [CrossRef]
- Barbedo, J.G.A. Impact of dataset size and variety on the effectiveness of deep learning and transfer learning for plant disease classification. Comput. Electron. Agric. 2018, 153, 46–53. [Google Scholar] [CrossRef]
- Barbedo, J.G.A. Factors influencing the use of deep learning for plant disease recognition. Biosyst. Eng. 2018, 172, 84–91. [Google Scholar] [CrossRef]
- Itakura, K.; Hosoi, F. Estimation of tree structural parameters from video frames with removal of blurred images using machine learning. J. Agric. Meteorol. 2018, 74, 154–161. [Google Scholar] [CrossRef]
- Suh, H.K.; Ijsselmuiden, J.; Hofstee, J.W.; van Henten, E.J. Transfer learning for the classification of sugar beet and volunteer potato under field conditions. Biosyst. Eng. 2018, 174, 50–65. [Google Scholar] [CrossRef]
- Miao, S.; Wang, Z.J.; Liao, R. A CNN regression approach for real-time 2D/3D registration. IEEE Trans. Med. Imaging 2016, 35, 1352–1363. [Google Scholar] [CrossRef]
- Deng, L.; Hinton, G.; Kingsbury, B. New types of deep neural network learning for speech recognition and related applications: An overview. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 8599–8603. [Google Scholar]
- Aloysius, N.; Geetha, M. A review on deep convolutional neural networks. In Proceedings of the 2017 International Conference on Communication and Signal Processing (ICCSP 2017), Chennai, India, 6–8 April 2017; pp. 0588–0592. [Google Scholar]
- Močkus, J. On Bayesian methods for seeking the extremum. In Proceedings of the Optimization Techniques IFIP Technical Conference, Novosibirsk, Russia, 1–7 July 1975; Springer: Berlin, Heidelberg, 1975; pp. 400–404. [Google Scholar]
- Zhang, Y.; Sohn, K.; Villegas, R.; Pan, G.; Lee, H. Improving object detection with deep convolutional networks via bayesian optimization and structured prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 249–258. [Google Scholar]
- Rawat, W.; Wang, Z. Deep convolutional neural networks for image classification: A comprehensive review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef]
- Gong, Y.; Jia, Y.; Leung, T.; Toshev, A.; Ioffe, S. Deep convolutional ranking for multilabel image annotation. arXiv, 2013; arXiv:1312.4894. [Google Scholar]
- Locatelli, M. Bayesian algorithms for one-dimensional global optimization. J. Glob. Optim. 1997, 10, 57–76. [Google Scholar] [CrossRef]
- Brochu, E.; Cora, M.; de Freitas, N.A. Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning; Technical Report TR-2009-23; Department of Computer Science, University of British Columbia: Vancouver, BC, Canada, 2009. [Google Scholar]
- Kano, M.; Yoshizaki, R. Operating condition optimization for efficient scale-up of manufacturing process by using Bayesian optimization and transfer learning. J. SICI 2017, 56, 695–698. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. 2012, 2, pp. 2951–2959. Available online: http://papers.nips.cc/paper/4522-practical-bayesian-optimization (accessed on 20 November 2018).
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, UK, 2016. [Google Scholar]
- Syukri, D.; Thammawong, M.; Naznin, H.A.; Kuroki, S.; Tsuta, M.; Yoshida, M.; Nakano, K. Identification of a freshness marker metabolite in stored soybean sprouts by comprehensive mass-spectrometric analysis of carbonyl compounds. Food Chem. 2018, 269, 588–594. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. NIPS 2012, 60, 84–90. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 28th IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.W.M.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Slaughter, D.C.; Obenland, D.M.; Thompson, J.F.; Arpaia, M.L.; Margosan, D.A. Non-destructive freeze damage detection in oranges using machine vision and ultraviolet fluorescence. Postharvest Biol. Technol. 2008, 48, 341–346. [Google Scholar] [CrossRef]
- Ogawa, Y.; Momin, A.M.; Kuramoto, M.; Kohno, Y.; Shiigi, T.; Yamamoto, K.; Kondo, N. Detection of rotten citrus fruit using fluorescent images. Rev. Laser Eng. 2011, 39, 255–261. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, H.; Sun, Y.; Zhang, Y.; Liu, H.; Cheng, J.; Bi, S.; Zhang, H. Study of interaction between protein and main active components in Citrus aurantium L. by optical spectroscopy. J. Lumin. 2010, 130, 270–279. [Google Scholar] [CrossRef]
- Daito, H.; Tominaga, S. Studies on fruit quality of navel oranges and several Japanese late and midseason citrus cultivars in Seto inland sea area IV seasonal changes in amino acid constituents of juice. Bull. Shikoku Agric. Exp. Stn. 1981, 37, 75–85. [Google Scholar]
| Name | Explanation |
|---|---|
| Image Input Layer | Image size: 32 × 32 |
| Convolution Layer 1 | Number of filter: 37, Filter size: 3 × 3, Stride: [1 1] |
| Batch Normalization 1 | Batch normalization with 37 channels |
| Relu Layer 1 | − |
| Maxpooling Layer 1 | 2 × 2 max pooling with stride [2 2], Padding: [0 0] |
| Convolution Layer 2 | Number of filter: 74, Filter size: 3 × 3 Stride: [1 1] |
| Batch Normalization 2 | Batch normalization with 74 channels |
| Relu Layer 2 | − |
| Maxpooling Layer 2 | 2 × 2 max pooling with stride [2 2], Padding: [0 0] |
| Convolution Layer 3 | Number of filter: 148, Filter size: 3 × 3, Stride: [1 1] |
| Batch Normalization 3 | Batch normalization with 148 channels |
| Relu Layer 3 | - |
| Average Pooling 1 | 8 × 8 Average pooling with stride [2 2], Padding: [0 0] |
| Dropout | 20% Dropout |
| Fully Connected Layer | One fully connected layer |
| Regression Layer | Regression (to minimize mean-squared error) |
| Estimation Method | Absolute Estimation Error of Brix/Acid Ratio | |
|---|---|---|
| 1 | Two peaks of polymethoxy flavone | 6.21 |
| 2 | Two peaks of Tryptophan and Chlorophyll | 4.49 |
| 3 | PCR (Principal Component Regression) | 4.04 |
| 4 | Present method (CNN regression) | 2.48 |
| Range of Excitation Wavelength Used for the Estimation | Absolute Estimation Error of Brix/Acid Ratio |
|---|---|
| (A) 300–400 nm | 3.66 |
| (B) 400–500 nm | 5.85 |
| (C) 500–600 nm | 4.23 |
| (D) 600–700 nm | 3.1 |
| 300–700 nm (full range) | 2.48 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Itakura, K.; Saito, Y.; Suzuki, T.; Kondo, N.; Hosoi, F. Estimation of Citrus Maturity with Fluorescence Spectroscopy Using Deep Learning. Horticulturae 2019, 5, 2. https://doi.org/10.3390/horticulturae5010002
Itakura K, Saito Y, Suzuki T, Kondo N, Hosoi F. Estimation of Citrus Maturity with Fluorescence Spectroscopy Using Deep Learning. Horticulturae. 2019; 5(1):2. https://doi.org/10.3390/horticulturae5010002
Chicago/Turabian StyleItakura, Kenta, Yoshito Saito, Tetsuhito Suzuki, Naoshi Kondo, and Fumiki Hosoi. 2019. "Estimation of Citrus Maturity with Fluorescence Spectroscopy Using Deep Learning" Horticulturae 5, no. 1: 2. https://doi.org/10.3390/horticulturae5010002
APA StyleItakura, K., Saito, Y., Suzuki, T., Kondo, N., & Hosoi, F. (2019). Estimation of Citrus Maturity with Fluorescence Spectroscopy Using Deep Learning. Horticulturae, 5(1), 2. https://doi.org/10.3390/horticulturae5010002