Optimising Crop Selection for Small Urban Food Gardens in Dry Climates
Abstract
:1. Introduction
2. Experimental Section
2.1. Method
- A relevant objective: the total value of food produced in a garden of a specified area, minus the total cost of inputs
- A set of decision variables: the area to allocate to each crop type in the garden
- A set of constraints: minimum and maximum representation of dietary food groups (as well as energy and protein); land area available; total cost
2.2. Modelled Scenario
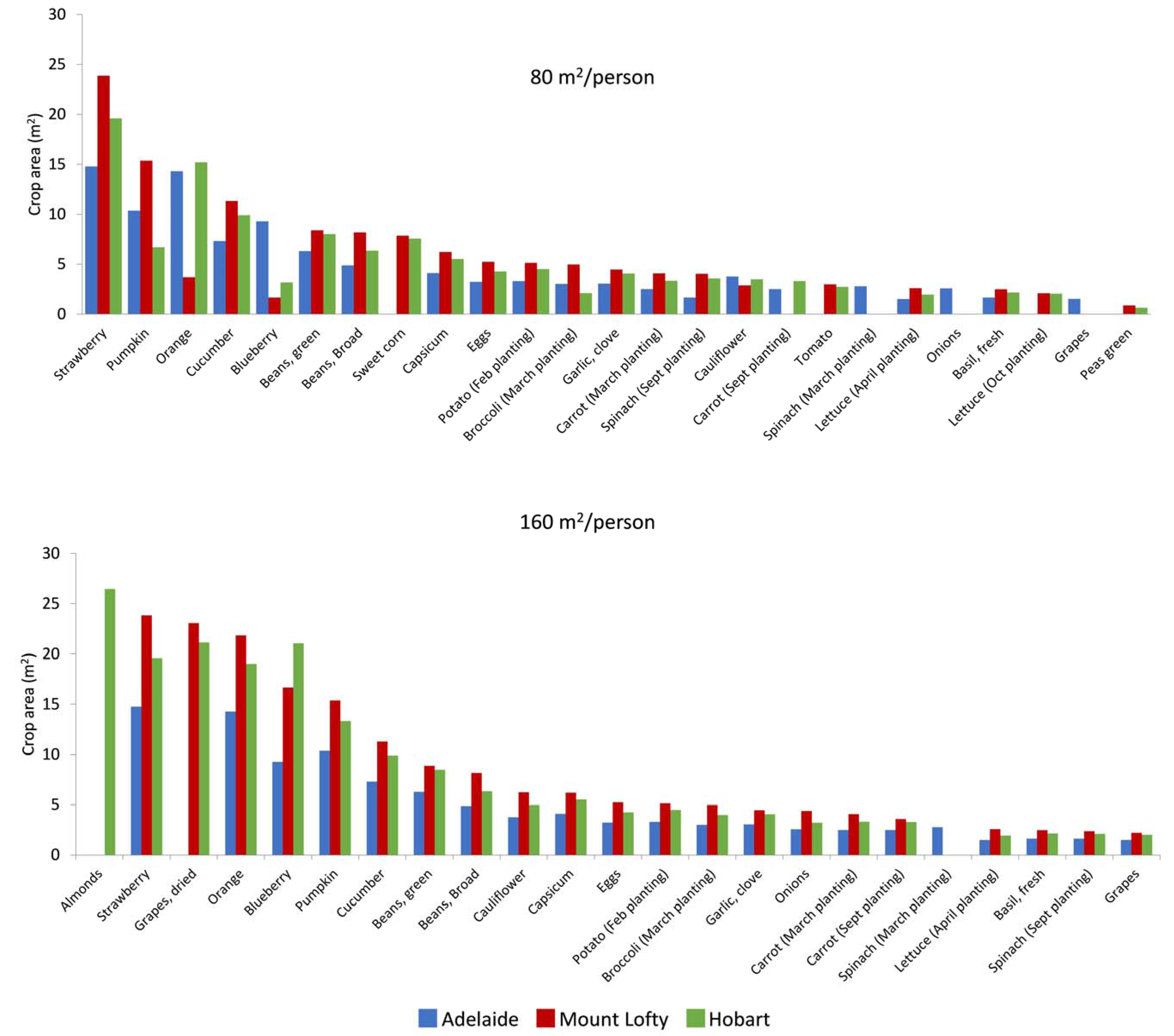
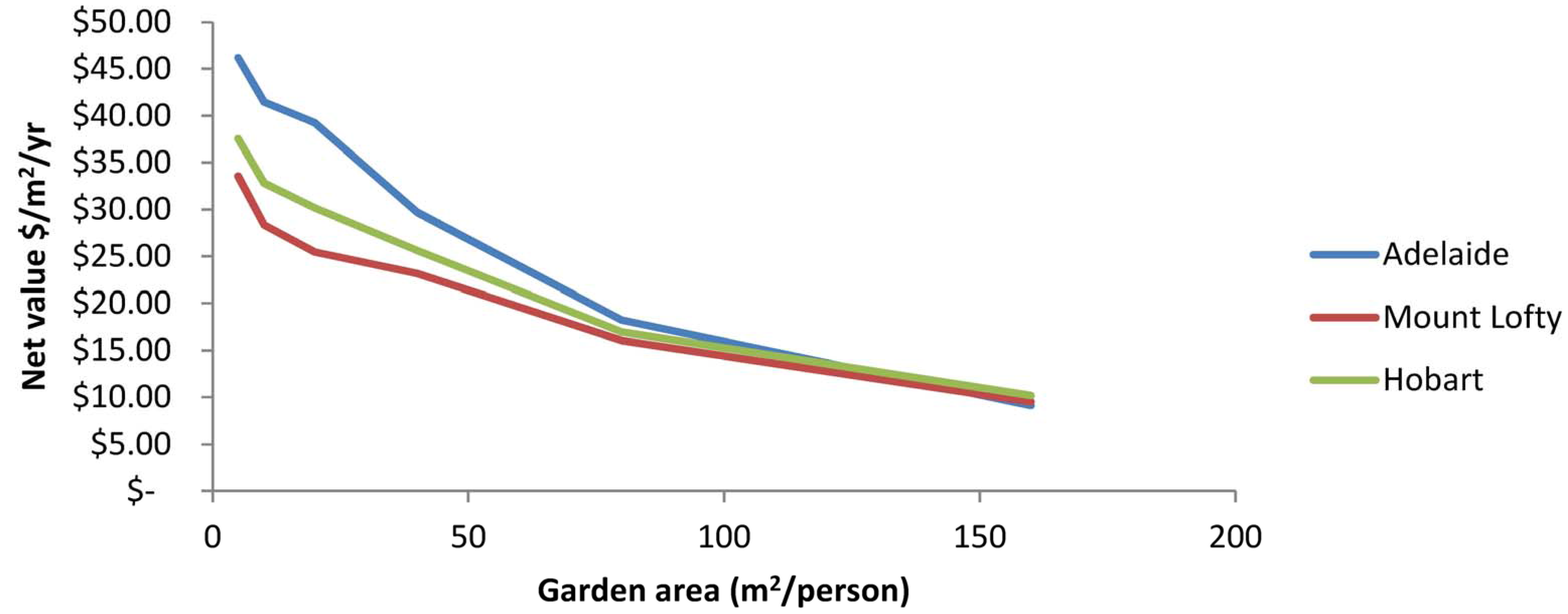
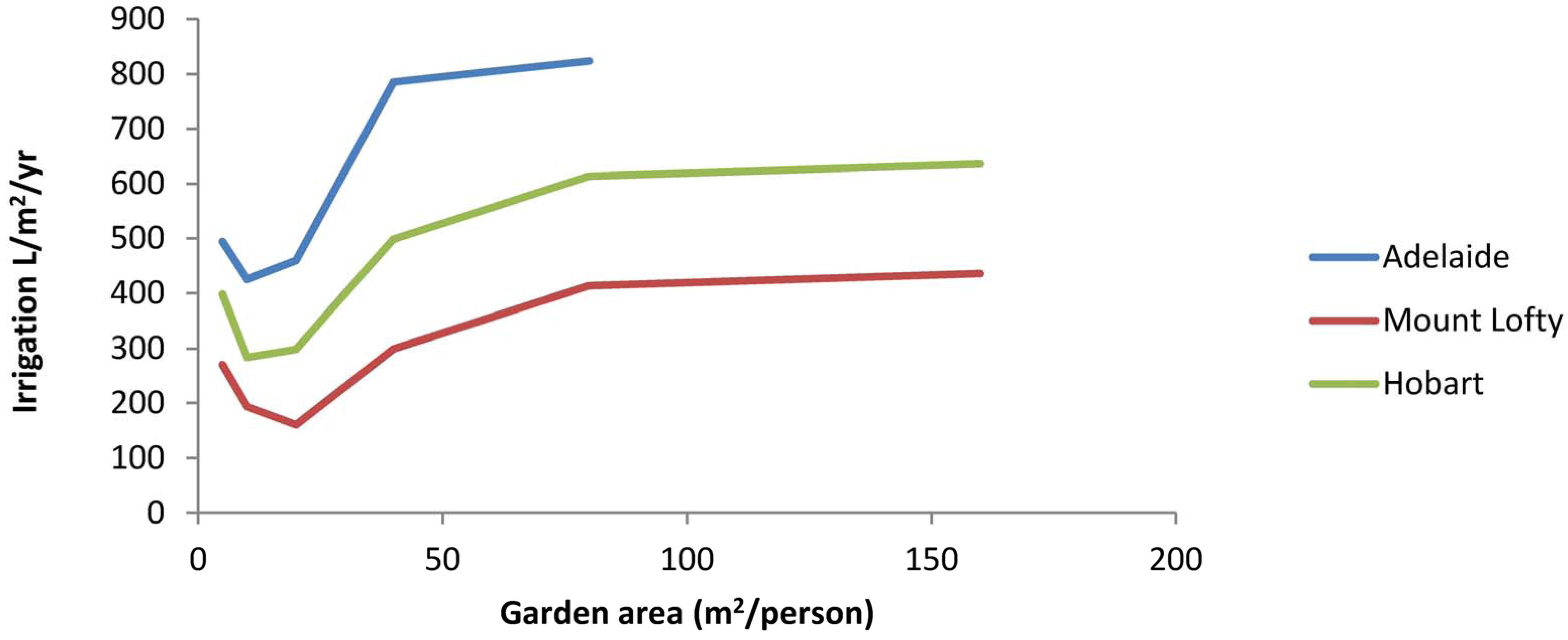
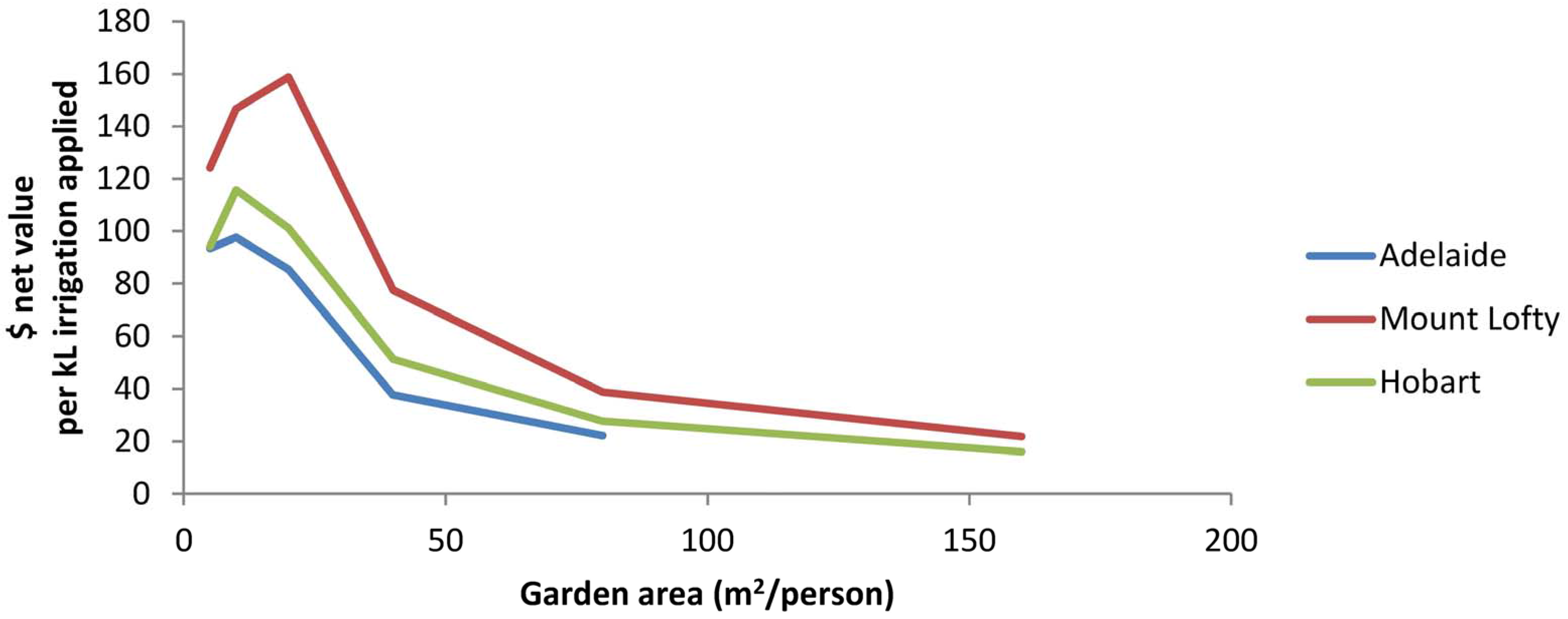
3. Results
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Blaylock, J.R.; Gallo, A.E. Modeling the decision to produce vegetables at home. Am. J. Agric. Econ. 1983, 65, 722–729. [Google Scholar] [CrossRef]
- Patel, I. Gardening’s Socioeconomic Impacts. J. Ext. 1991, 29, 7–8. [Google Scholar]
- Ghosh, S.; Vale, R.; Vale, B. Local food production in home gardens: measuring on-site sustainability potential of residential development. Int. J. Environ. Sustain. Dev. 2008, 7, 430–451. [Google Scholar] [CrossRef]
- Gray, L.; Guzman, P.; Glowa, K.M.; Drevno, A.G. Can home gardens scale up into movements for social change? The role of home gardens in providing food security and community change in San Jose, California. Local Environ. 2014, 19, 187–203. [Google Scholar] [CrossRef]
- Ward, J.; Ward, P.; Saint, C.; Mantzioris, E. The urban agriculture revolution. Water J. Aust. Water Assoc. 2014, 41, 69–74. [Google Scholar]
- Sanyé-Mengual, E.; Oliver-Solà, J.; Montero, J.I.; Rieradevall, J. An environmental and economic life cycle assessment of rooftop greenhouse (RTG) implementation in Barcelona, Spain. Assessing new forms of urban agriculture from the greenhouse structure to the final product level. Int. J. Life Cycle Assess. 2015, 20, 350–366. [Google Scholar]
- van Veenhuizen, R.; Danso, G. Profitability and sustainability of urban and periurban agriculture. In Agricultural Management, Marketing and Finance Occasional Paper No. 19; Food & Agriculture Organisation of the United Nations (FAO): Roma, Italy, 2007. [Google Scholar]
- Satzewich, W.; Christensen, R. SPIN-Farming Basics: How to Grow Commercially on Under an Acre; SPIN Farming LLC: USA, 2011; p. 114. [Google Scholar]
- Cleveland, D.A.; Orum, T.V.; Ferguson, N. Economic value of home vegetable gardens in an urban desert environment. HortScience 1985, 20, 694–696. [Google Scholar]
- City of Tucson Current Water Rate Schedules. Available online: http://www.tucsonaz.gov/water/rates (accessed on 7 April 2014).
- Wallin, C. Profitable Plants Digest. Available online: http://www.profitableplantsdigest.com/about/ (accessed on 7 April 2014).
- Gladek, E. Polydome: High Performance Polyculture Systems; InnovatieNetwerk: Utrecht, The Netherlands, 2011. [Google Scholar]
- Ward, J.; Ward, P.; Mantzioris, E.; Saint, C. Optimising diet decisions and urban agriculture using linear programming. Food Secur. 2014, 6, 701–718. [Google Scholar] [CrossRef]
- Clarke, F.G. The History of Australia; Greenwood Publishing Group: Westport, CT, USA, 2002. [Google Scholar]
- Davison, A. Stuck in a Cul-de-Sac? Suburban History and Urban Sustainability in Australia. Urban Policy Res. 2006, 24, 201–216. [Google Scholar] [CrossRef]
- Gaynor, A. Harvest of the Suburbs: An Environmental History of Growing Food in Australian Cities; University of Western Australia Press: Crawley, WA, Australia, 2006. [Google Scholar]
- AUSVEG. Australian Vegetable Industry Strategic Investment Plan 2012–2017; Horticulture Australia: Sydney, Australia, 2012. [Google Scholar]
- Grewal, S.S.; Grewal, P.S. Can cities become self-reliant in food? Cities 2012, 29, 1–11. [Google Scholar] [CrossRef]
- Jeavons, J. How to Grow More Vegetables: And Fruits, Nuts, Berries, Grains, and Other Crops Than You Ever Thought Possible on Less Land Than You Can Imagine; Ten Speed Press: Berkeley, CA, USA, 2012. [Google Scholar]
- Gommes, R. An Introduction into the Art of Agrometeorological Crop Yield Forecasting Using Multiple Regression; Food and Agriculture Organization of the United Nations, Crop Monitoring and Forecast Group: Rome, Italy, 2001. [Google Scholar]
- Steduto, P.; Hslao, T.; Fereres, E.; Raes, D. Crop Yield Response to Water; FAO Irrigation and Drainage Paper 66; Food and Agriculture Organization of the United Nations: Rome, Italy, 2012. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and drainage paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- NHMRC. Australian Dietary Guidelines; National Health and Medical Research Council: Canberra, Australia, 2013.
- Holmgren, D. Garden Agriculture: A revolution in efficient water use. Water J. Aust. Water Assoc. 2005, 32, 8–9. [Google Scholar]
- Mason, A.J. OpenSolver—An Open Source Add-in to Solve Linear and Integer Progammes in Excel. In Operations Research Proceedings 2011; Springer: Berlin, Germany, 2012; pp. 401–406. [Google Scholar]


| Dietary Food Group | Items Included for Garden Production | Items Included in Overall Diet |
|---|---|---|
| Dairy | none | Cheese (cheddar); Milk; Soy milk (calcium enriched); Yoghurt |
| Discretionary choices | none | Butter; Beer; Wine; Coriander (dried); Cardamom dried; Pepper (Piper spp.); Snack biscuits (savoury); Cane sugar; Coffee (from beans); Tea (from leaf) |
| Eggs | Eggs | Eggs |
| Fish/seafood | none | Wild fish |
| Fruit | Apple; Apricot; Blueberry; Grapes; Grapes (dried); Kiwifruit; Orange; Peach; Pear; Plum; Rockmelon; Strawberry | Apple; Apricot; Banana; Blueberry; Grapes; Grapes (dried); Kiwifruit; Orange; Peach; Pear; Plum; Rockmelon; Strawberry |
| Green and brassica vegetables | Beans (green); Broccoli (March & Dec plantings); Cauliflower; Lettuce (April & Oct plantings); Peas (green); Spinach (March & Sept plantings); Basil (fresh) | Beans (green); Broccoli; Cauliflower; Lettuce; Peas (green); Spinach; Basil (fresh) |
| Legumes | none | Beans (dry); Chick peas; Tofu; Lentils |
| Nuts and seeds | Almonds | Almonds; Sunflower seeds |
| Orange vegetables | Carrot (March planting); Carrot (Sept planting); Pumpkin | Carrot (March planting); Carrot (Sept planting); Pumpkin; Sweet potato |
| Other vegetables | Broad Beans; Avocado; Tomato; Onions; Zucchini; Garlic; Cucumber; Capsicum | Beans, Broad; Avocado; Tomato; Mushrooms; Onions; Zucchini; Chillies (dried); Garlic; Cucumber; Capsicum |
| Poultry | none | Chicken meat |
| Red meats | none | Beef, diced; Lamb; Pork |
| Refined/low fibre cereals/grains | none | Couscous; Pasta (Australian); Pasta (non-Australian); Polenta |
| Starchy vegetables | Potato (Feb planting); Potato (Sept planting); Sweet corn | Potato (Feb planting); Potato (Sept planting); Sweet corn |
| Unsaturated oils/spreads | none | Olive oil |
| Wholegrain/high fibre cereals/grains | none | Bread; Breakfast cereal (wheat flakes); Oats, porridge; Rice (Australian); Rice (non-Australian) |
| Garden Size (m2/person) | Min.% Dietary Protein Produced in Garden |
|---|---|
| 5 | 2.5% |
| 10 | 5% |
| 20 | 7.5% |
| 40 | 10% |
| 80 | 12.5% |
| 160 | 15% |
| Food Group | kJ/Serve | Min. Serves/Day | Max. Serves/Day |
|---|---|---|---|
| All Cereal | 4 | 6 | |
| Dairy | 600 | 1.5 | 4 |
| Discretionary Choices | 600 | 0 | 3 |
| Eggs | 600 | 0 | 0.5 |
| Fish/seafood | 600 | 0.1 | 0.4 |
| Fruit | 350 | 2 | 4 |
| Green and brassica vegetables | 100 | 1 | 2 |
| Legumes | 350 | 0 | 6 |
| Nuts and seeds | 750 | 0 | 2 |
| Orange vegetables | 150 | 1 | 2 |
| Other vegetables | 100 | 1 | 2 |
| Poultry | 600 | 0 | 1 |
| Red meats | 550 | 0 | 1 |
| Refined/low fibre cereals/grains | 550 | 0 | 2 |
| Starchy vegetables | 250 | 1 | 4 |
| Unsaturated oils/spreads | 250 | 0 | 5 |
| Wholegrain/high fibre cereals/grains | 450 | 2 | 6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ward, J.; Symons, J. Optimising Crop Selection for Small Urban Food Gardens in Dry Climates. Horticulturae 2017, 3, 33. https://doi.org/10.3390/horticulturae3020033
Ward J, Symons J. Optimising Crop Selection for Small Urban Food Gardens in Dry Climates. Horticulturae. 2017; 3(2):33. https://doi.org/10.3390/horticulturae3020033
Chicago/Turabian StyleWard, James, and John Symons. 2017. "Optimising Crop Selection for Small Urban Food Gardens in Dry Climates" Horticulturae 3, no. 2: 33. https://doi.org/10.3390/horticulturae3020033
APA StyleWard, J., & Symons, J. (2017). Optimising Crop Selection for Small Urban Food Gardens in Dry Climates. Horticulturae, 3(2), 33. https://doi.org/10.3390/horticulturae3020033






