Can Multi-Temporal Vegetation Indices and Machine Learning Algorithms Be Used for Estimation of Groundnut Canopy State Variables?
Abstract
1. Introduction
2. Materials and Methodology
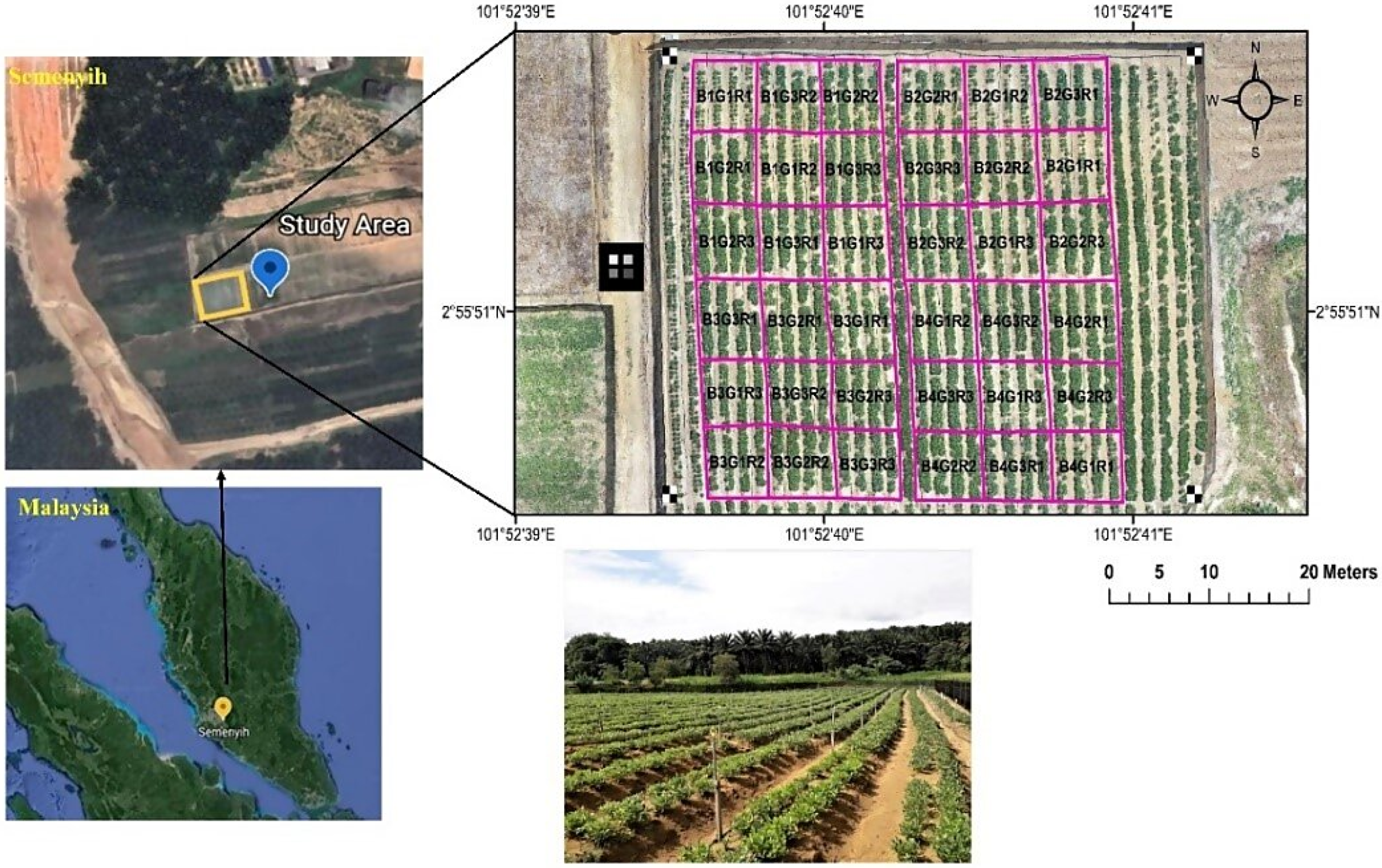
2.1. Study Site
2.2. Experimental Design
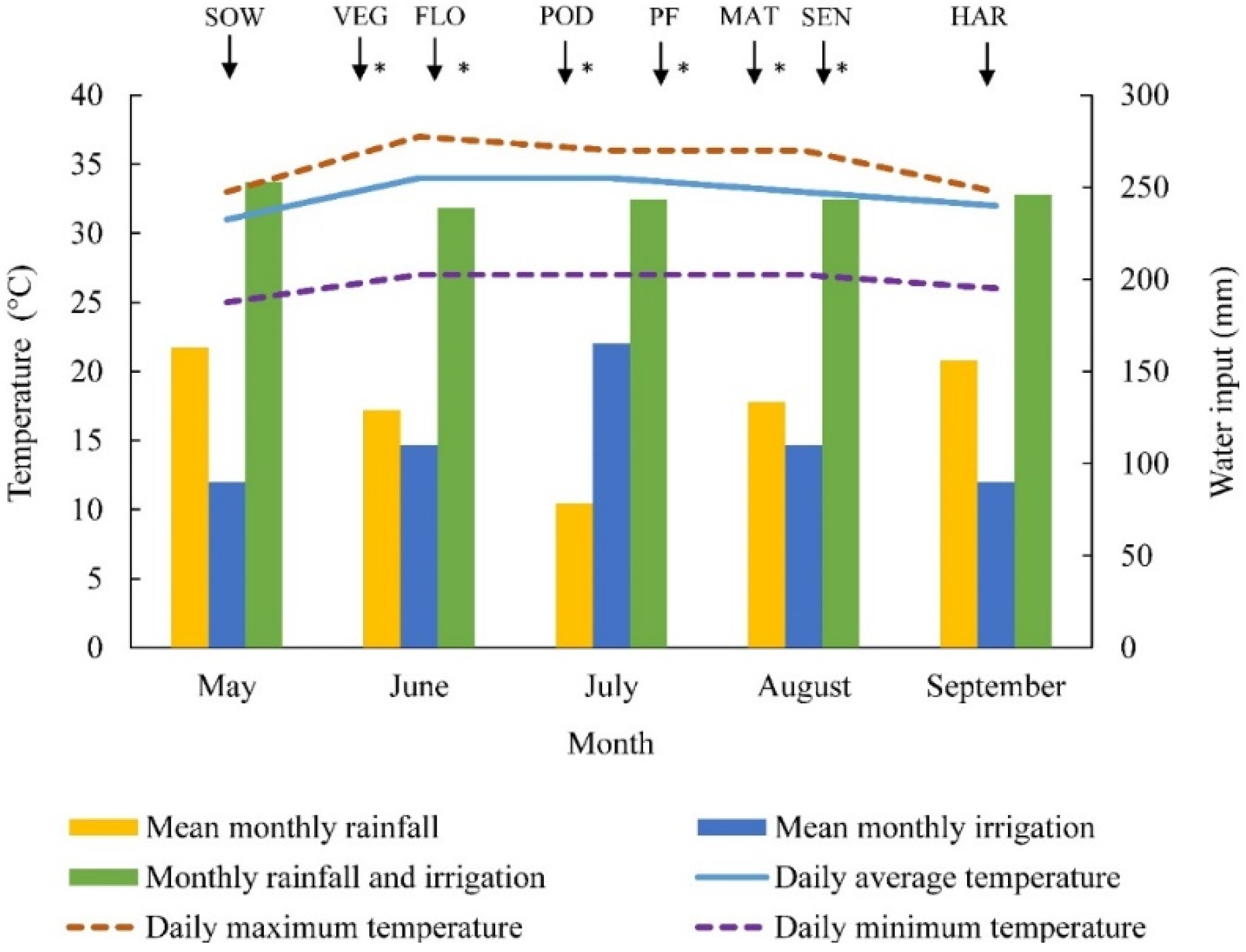
2.3. Agronomic Measurements
2.4. UAV, Sensor and Remote Sensing Data Acquisition Missions
2.5. Image Processing
2.6. Vegetation Indices and Cumulative Vegetation Indices Calculation
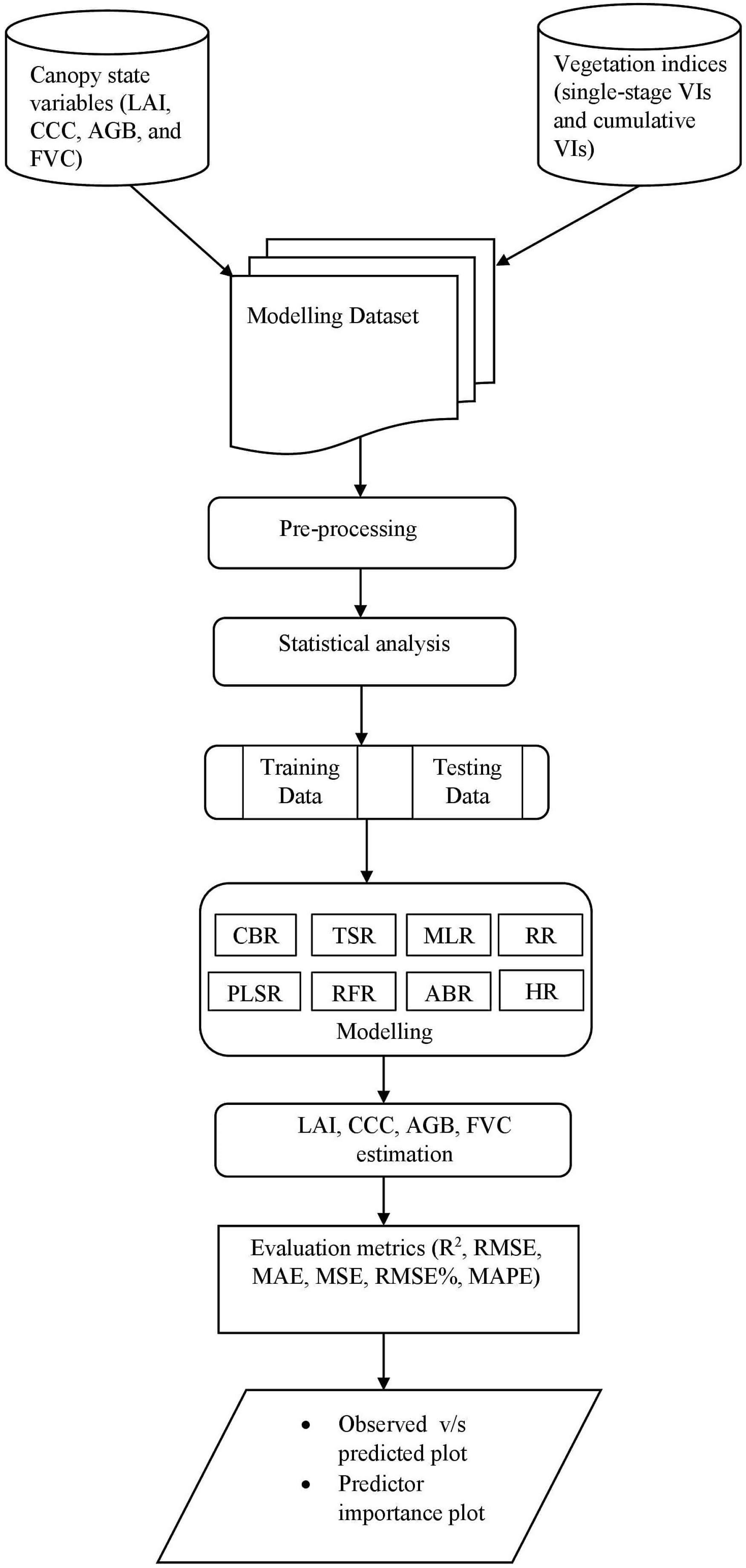
2.7. Model Selection and Modelling Strategy
3. Results and Discussion
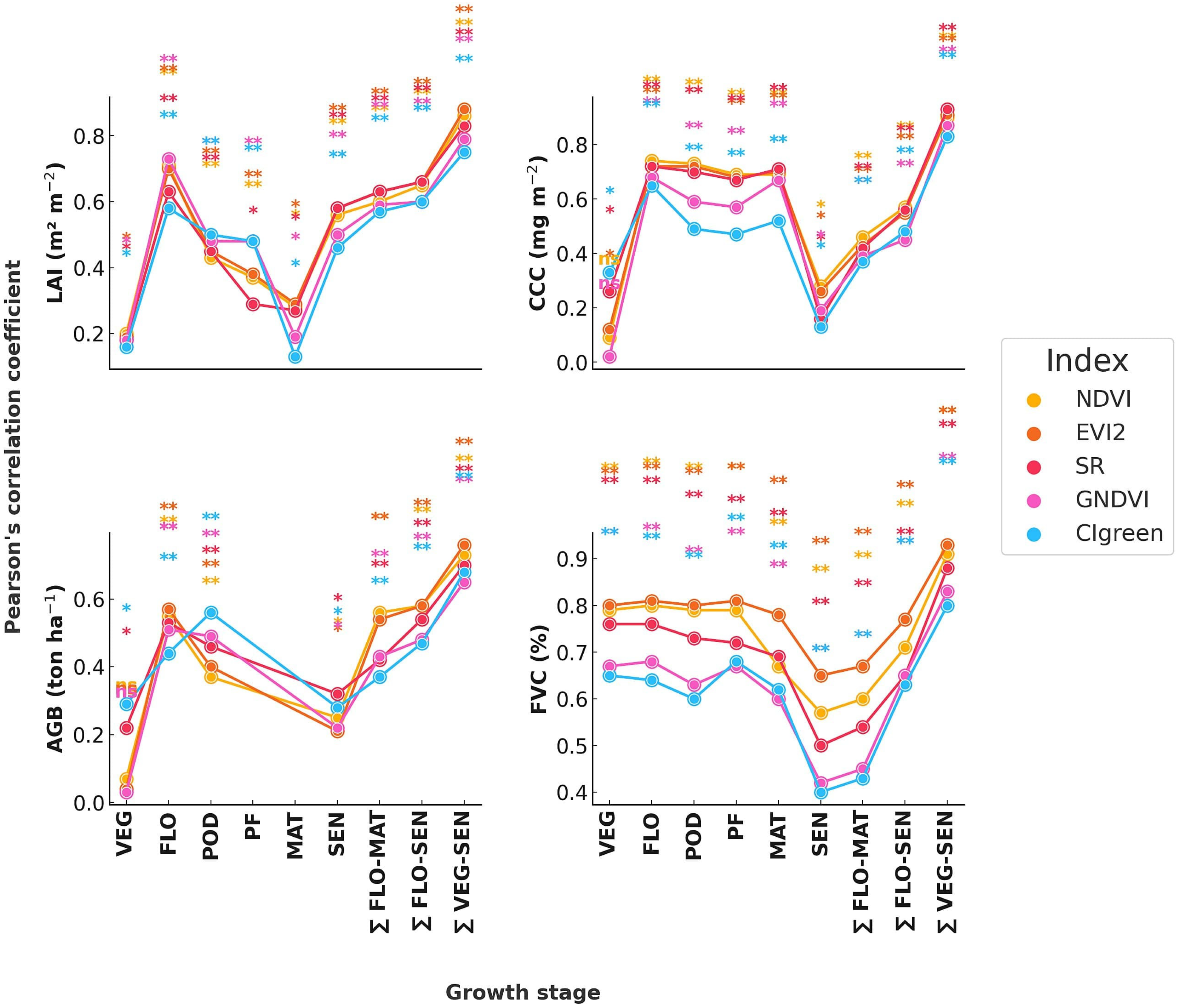
3.1. Correlation of Canopy State Variables with Vegetation Indices and Cumulative Vegetation Indices
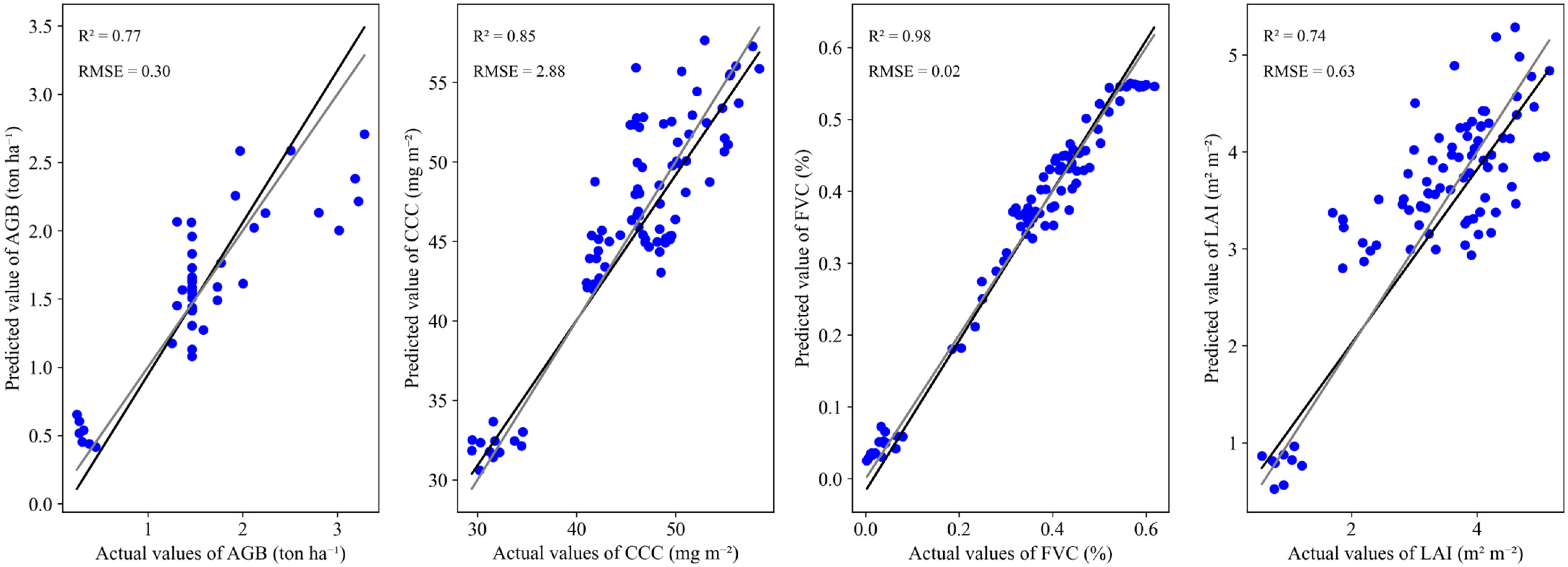
3.2. Modeling the Relationship between Canopy State Variables and Cumulative Vegetation Indices Using Machine-Learning Algorithms
3.3. Predictor Importance for Estimating Bambara Groundnut Canopy State Variables
4. Limitations and Future Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Yadav, R.; Siddique, K.H.M. Neglected and Underutilized Crop Species: The Key to Improving Dietary Diversity and Fighting Hunger and Malnutrition in Asia and the Pacific. Front. Nutr. 2020, 7, 593711. [Google Scholar] [CrossRef] [PubMed]
- Padulosi, S.; Heywood, V.; Hunter, D.; Jarvis, A. Underutilized Species and Climate Change: Current Status and Outlook. In Crop Adaptation to Climate Change; Wiley-Blackwell: Oxford, UK, 2011; pp. 507–521. [Google Scholar]
- Tan, X.L.; Azam-Ali, S.; Von Goh, E.; Mustafa, M.; Chai, H.H.; Ho, W.K.; Mayes, S.; Mabhaudhi, T.; Azam-Ali, S.; Massawe, F. Bambara Groundnut: An Underutilized Leguminous Crop for Global Food Security and Nutrition. Front. Nutr. 2020, 7, 601496. [Google Scholar] [CrossRef] [PubMed]
- Soumare, A.; Diedhiou, A.G.; Kane, A. Bambara groundnut: A neglected and underutilized climate-resilient crop with great potential to alleviate food insecurity in sub-Saharan Africa. J. Crop Improv. 2022, 36, 747–767. [Google Scholar] [CrossRef]
- Chibarabada, T.P.; Modi, A.T.; Mabhaudhi, T. Options for improving water productivity: A case study of bambara groundnut and groundnut. Phys. Chem. Earth Parts A/B/C 2020, 115, 102806. [Google Scholar] [CrossRef]
- Mayes, S.; Ho, W.K.; Chai, H.H.; Gao, X.; Kundy, A.C.; Mateva, K.I.; Zahrulakmal, M.; Hahiree, M.K.I.M.; Kendabie, P.; Licea, L.C.S.; et al. Bambara groundnut: An exemplar underutilised legume for resilience under climate change. Planta 2019, 250, 803–820. [Google Scholar] [CrossRef]
- Linneman, A. Phenological Development in Bambara Groundnut (Vigna subterranea) at Constant Exposure to Photoperiods of 10 to 16 h. Ann. Bot. 1993, 71, 445–452. [Google Scholar] [CrossRef]
- Jewan, S.Y.Y.; Pagay, V.; Billa, L.; Tyerman, S.D.; Gautam, D.; Sparkes, D.; Chai, H.H.; Singh, A. The feasibility of using a low-cost near-infrared, sensitive, consumer-grade digital camera mounted on a commercial UAV to assess Bambara groundnut yield. Int. J. Remote. Sens. 2021, 43, 393–423. [Google Scholar] [CrossRef]
- Qi, H.; Zhu, B.; Wu, Z.; Liang, Y.; Li, J.; Wang, L.; Chen, T.; Lan, Y.; Zhang, L. Estimation of Peanut Leaf Area Index from Unmanned Aerial Vehicle Multispectral Images. Sensors 2020, 20, 6732. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Sun, H.; Gao, D.; Qiao, L.; Liu, N.; Li, M.; Zhang, Y. Detection of Canopy Chlorophyll Content of Corn Based on Continuous Wavelet Transform Analysis. Remote Sens. 2020, 12, 2741. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, G.; Song, X.; Li, Z.; Xu, X.; Feng, H.; Zhao, C. Improved Estimation of Winter Wheat Aboveground Biomass Using Multiscale Textures Extracted from UAV-Based Digital Images and Hyperspectral Feature Analysis. Remote Sens. 2021, 13, 581. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, H.; Fu, Y.; Niu, H.; Yang, Y.; Zhang, B. Fractional Vegetation Cover Estimation of Different Vegetation Types in the Qaidam Basin. Sustainability 2019, 11, 864. [Google Scholar] [CrossRef]
- Feng, L.; Chen, S.; Zhang, C.; Zhang, Y.; He, Y. A comprehensive review on recent applications of unmanned aerial vehicle remote sensing with various sensors for high-throughput plant phenotyping. Comput. Electron. Agric. 2021, 182, 106033. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned aerial vehicle remote sensing for field-based crop phenotyping: Current status and perspectives. Front. Plant Sci. 2017, 8, 272832. [Google Scholar] [CrossRef] [PubMed]
- Tattaris, M.; Reynolds, M.P.; Chapman, S.C. A direct comparison of remote sensing approaches for high-throughput phenotyping in plant breeding. Front. Plant Sci. 2016, 7, 206105. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Rayhana, R.; Feng, K.; Liu, Z.; Xiao, G.; Ruan, Y.; Sangha, J.S. A Review on Sensing Technologies for High-Throughput Plant Phenotyping. IEEE Open J. Instrum. Meas. 2022, 1, 9500121. [Google Scholar] [CrossRef]
- Sharma, L.K.; Gupta, R.; Pandey, P.C. Future Aspects and Potential of the Remote Sensing Technology to Meet the Natural Resource Needs. In Advances in Remote Sensing for Natural Resource Monitoring; Springer: Cham, Switzerland, 2021; pp. 445–464. [Google Scholar]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Naveed Tahir, M.; Lan, Y.; Zhang, Y.; Wang, Y.; Nawaz, F.; Arslan Ahmed Shah, M.; Gulzar, A.; Shahid Qureshi, W.; Manshoor Naqvi, S.; Zaigham Abbas Naqvi, S. Real time estimation of leaf area index and groundnut yield using multispectral UAV. Int. J. Precis. Agric. Aviat. 2018, 1, 1–6. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.; Zhang, L.; Han, J.; Bian, C.; Li, G.; Liu, J.; Jin, L. Above-ground biomass estimation and yield prediction in potato by using UAV-based RGB and hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2020, 162, 161–172. [Google Scholar] [CrossRef]
- Chen, J.; Yi, S.; Qin, Y.; Wang, X. Improving estimates of fractional vegetation cover based on UAV in alpine grassland on the Qinghai–Tibetan Plateau. Int. J. Remote Sens. 2016, 37, 1922–1936. [Google Scholar] [CrossRef]
- Rouse, J.W.J.; Haas, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA/GSFC Type III Final Report; NASA: Greenbelt, MD, USA, 1974. [Google Scholar]
- Shamsuzzoha, M.; Noguchi, R.; Ahamed, T. Rice Yield Loss Area Assessment from Satellite-derived NDVI after Extreme Climatic Events Using a Fuzzy Approach. Agric. Inf. Res. 2022, 31, 32–46. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote sensing of chlorophyll concentration in higher plant leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Peng, Y.; Nguy-Robertson, A.; Arkebauer, T.; Gitelson, A.A. Assessment of Canopy Chlorophyll Content Retrieval in Maize and Soybean: Implications of Hysteresis on the Development of Generic Algorithms. Remote Sens. 2017, 9, 226. [Google Scholar] [CrossRef]
- Hu, J.; Yue, J.; Xu, X.; Han, S.; Sun, T.; Liu, Y.; Feng, H.; Qiao, H. UAV-Based Remote Sensing for Soybean FVC, LCC, and Maturity Monitoring. Agriculture 2023, 13, 692. [Google Scholar] [CrossRef]
- dos Santos, R.A.; Mantovani, E.C.; Filgueiras, R.; Fernandes-Filho, E.I.; da Silva, A.C.B.; Venancio, L.P. Actual Evapotranspiration and Biomass of Maize from a Red–Green-Near-Infrared (RGNIR) Sensor on Board an Unmanned Aerial Vehicle (UAV). Water 2020, 12, 2359. [Google Scholar] [CrossRef]
- Ma, Y.; Jiang, Q.; Wu, X.; Zhu, R.; Gong, Y.; Peng, Y.; Duan, B.; Fang, S. Feasibility of Combining Deep Learning and RGB Images Obtained by Unmanned Aerial Vehicle for Leaf Area Index Estimation in Rice. Remote Sens. 2020, 13, 84. [Google Scholar] [CrossRef]
- Shamsuzzoha, M.; Shaw, R.; Ahamed, T. Machine learning system to assess rice crop change detection from satellite-derived RGVI due to tropical cyclones using remote sensing dataset. Remote Sens. Appl. Soc. Environ. 2024, 35, 101201. [Google Scholar] [CrossRef]
- Li, Z.; Fan, C.; Zhao, Y.; Jin, X.; Casa, R.; Huang, W.; Song, X.; Blasch, G.; Yang, G.; Taylor, J.; et al. Remote sensing of quality traits in cereal and arable production systems: A review. Crop J. 2024, 12, 45–57. [Google Scholar] [CrossRef]
- Cozzolino, D.; Porker, K.; Laws, M. An Overview on the Use of Infrared Sensors for in Field, Proximal and at Harvest Monitoring of Cereal Crops. Agriculture 2015, 5, 713–722. [Google Scholar] [CrossRef]
- Khanal, S.; Kushal, K.C.; Fulton, J.P.; Shearer, S.; Ozkan, E. Remote Sensing in Agriculture—Accomplishments, Limitations, and Opportunities. Remote Sens. 2020, 12, 3783. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Sagan, V.; Sidike, P.; Kwasniewski, M.T. Dual Activation Function-Based Extreme Learning Machine (ELM) for Estimating Grapevine Berry Yield and Quality. Remote Sens. 2019, 11, 740. [Google Scholar] [CrossRef]
- Serrano, L.; Filella, I.; Peñuelas, J. Remote Sensing of Biomass and Yield of Winter Wheat under Different Nitrogen Supplies. Crop Sci. 2000, 40, 723–731. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Estimation of a Location Parameter. In Breakthroughs in Statistics; Kotz, S., Johnson, N.L., Eds.; Springer: New York, NY, USA, 1992; pp. 492–518. [Google Scholar]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis. In Henri Theil’s Contributions to Economics and Econometrics; Raj, B., Koerts, J., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 345–381. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018; pp. 6638–6648. [Google Scholar]
- Modak, A.; Chatterjee, T.N.; Nag, S.; Roy, R.B.; Tudu, B.; Bandyopadhyay, R. Linear regression modelling on epigallocatechin-3-gallate sensor data for green tea. In Proceedings of the 2018 Fourth International Conference on Research in Computational Intelligence and Communication Networks (ICRCICN), Kolkata, India, 22–23 November 2018; pp. 112–117. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Carrascal, L.M.; Galván, I.; Gordo, O. Partial least squares regression as an alternative to current regression methods used in ecology. Oikos 2009, 118, 681–690. [Google Scholar] [CrossRef]
- Schreiber-Gregory, D.N. Ridge Regression and multicollinearity: An in-depth review. Model Assist. Stat. Appl. 2018, 13, 359–365. [Google Scholar] [CrossRef]
- Dong, T.; Meng, J.; Shang, J.; Liu, J.; Wu, B.; Huffman, T. Modified vegetation indices for estimating crop fraction of absorbed photosynthetically active radiation. Int. J. Remote. Sens. 2015, 36, 3097–3113. [Google Scholar] [CrossRef]
- Tan, C.; Huang, W.; Liu, L.; Wang, J.; Zhao, C. Relationship between leaf area index and proper vegetation indices across a wide range of cultivars. Int. Geosci. Remote Sens. Symp. 2004, 6, 4070–4072. [Google Scholar]
- Ma, Y.; Zhang, Q.; Yi, X.; Ma, L.; Zhang, L.; Huang, C.; Zhang, Z.; Lv, X. Estimation of Cotton Leaf Area Index (LAI) Based on Spectral Transformation and Vegetation Index. Remote Sens. 2021, 14, 136. [Google Scholar] [CrossRef]
- Yang, H.; Ming, B.; Nie, C.; Xue, B.; Xin, J.; Lu, X.; Xue, J.; Hou, P.; Xie, R.; Wang, K.; et al. Maize Canopy and Leaf Chlorophyll Content Assessment from Leaf Spectral Reflectance: Estimation and Uncertainty Analysis across Growth Stages and Vertical Distribution. Remote Sens. 2022, 14, 2115. [Google Scholar] [CrossRef]
- Vásquez, R.A.R.; Heenkenda, M.K.; Nelson, R.; Segura Serrano, L. Developing a New Vegetation Index Using Cyan, Orange, and Near Infrared Bands to Analyze Soybean Growth Dynamics. Remote Sens. 2023, 15, 2888. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, Y.; Chen, P.; Yang, Y.; Fu, H.; Yang, F.; Raza, M.A.; Guo, C.; Shu, C.; Sun, Y.; et al. Estimation of Rice Aboveground Biomass by Combining Canopy Spectral Reflectance and Unmanned Aerial Vehicle-Based Red Green Blue Imagery Data. Front. Plant Sci. 2022, 13, 903643. [Google Scholar] [CrossRef] [PubMed]
- Hassan, M.A.; Yang, M.; Rasheed, A.; Jin, X.; Xia, X.; Xiao, Y.; He, Z. Time-Series Multispectral Indices from Unmanned Aerial Vehicle Imagery Reveal Senescence Rate in Bread Wheat. Remote Sens. 2018, 10, 809. [Google Scholar] [CrossRef]
- Zaman-Allah, M.; Vergara, O.; Araus, J.L.; Tarekegne, A.; Magorokosho, C.; Zarco-Tejada, P.J.; Hornero, A.; Albà, A.H.; Das, B.; Craufurd, P.; et al. Unmanned aerial platform-based multi-spectral imaging for field phenotyping of maize. Plant Methods 2015, 11, 35. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, S.; Adak, A.; Wilde, S.; Nakasagga, S.; Murray, S.C. Cumulative temporal vegetation indices from unoccupied aerial systems allow maize (Zea mays L.) hybrid yield to be estimated across environments with fewer flights. PLoS ONE 2023, 18, e0277804. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Wang, J.; Ding, L.; Lu, J.; Zhang, J.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.; Tian, Y. Grain yield prediction using multi-temporal UAV-based multispectral vegetation indices and endmember abundance in rice. Field Crop. Res. 2023, 299, 108992. [Google Scholar] [CrossRef]
- Marshall, M.; Thenkabail, P. Biomass Modeling of Four Leading World Crops Using Hyperspectral Narrowbands in Support of HyspIRI Mission. Photogramm. Eng. Remote Sens. 2014, 80, 757–772. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Qian, B.; Jing, Q.; Croft, H.; Chen, J.; Wang, J.; Huffman, T.; Shang, J.; Chen, P. Deriving Maximum Light Use Efficiency from Crop Growth Model and Satellite Data to Improve Crop Biomass Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 104–117. [Google Scholar] [CrossRef]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote estimation of crop chlorophyll content using spectral indices derived from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 423–436. [Google Scholar] [CrossRef]
- Han, Y.; Tang, R.; Liao, Z.; Zhai, B.; Fan, J. A Novel Hybrid GOA-XGB Model for Estimating Wheat Aboveground Biomass Using UAV-Based Multispectral Vegetation Indices. Remote Sens. 2022, 14, 3506. [Google Scholar] [CrossRef]
- Wai, P.; Su, H.; Li, M.; Chen, G.; Wai, P.; Su, H.; Li, M. Estimating Aboveground Biomass of Two Different Forest Types in Myanmar from Sentinel-2 Data with Machine Learning and Geostatistical Algorithms. Remote Sens. 2022, 14, 2146. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Elhadi, A.; Ismail, R. Intra-and-Inter Species Biomass Prediction in a Plantation Forest: Testing the Utility of High Spatial Resolution Spaceborne Multispectral RapidEye Sensor and Advanced Machine Learning Algorithms. Sensors 2014, 14, 15348–15370. [Google Scholar] [CrossRef] [PubMed]
- Ohsowski, B.M.; Dunfield, K.E.; Klironomos, J.N.; Hart, M.M. Improving plant biomass estimation in the field using partial least squares regression and ridge regression. Botany 2016, 94, 501–508. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, P.; Meng, F.; Yang, X.; Xu, J.; Cui, Y. Estimation algorithm for chlorophyll-a concentrations in water from hyperspectral images based on feature derivation and ensemble learning. Ecol. Inform. 2022, 71, 101783. [Google Scholar] [CrossRef]
- Lu, B.; He, Y. Evaluating Empirical Regression, Machine Learning, and Radiative Transfer Modelling for Estimating Vegetation Chlorophyll Content Using Bi-Seasonal Hyperspectral Images. Remote Sens. 2019, 11, 1979. [Google Scholar] [CrossRef]
- Niu, Y.; Han, W.; Zhang, H.; Zhang, L.; Chen, H. Estimating fractional vegetation cover of maize under water stress from UAV multispectral imagery using machine learning algorithms. Comput. Electron. Agric. 2021, 189, 106414. [Google Scholar] [CrossRef]
- Martinez, K.P.; Burgos, D.F.M.; Blanco, A.C.; Salmo, S.G. Multi-sensor approach to leaf area index estimation using statistical machine learning models: A case on mangrove forests. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, V-3-2021, 109–115. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Y.; Zhang, Q.; Duan, R.; Liu, J.; Qin, Y.; Wang, X. Toward Multi-Stage Phenotyping of Soybean with Multimodal UAV Sensor Data: A Comparison of Machine Learning Approaches for Leaf Area Index Estimation. Remote Sens. 2022, 15, 7. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Signature Analysis of Leaf Reflectance Spectra: Algorithm Development for Remote Sensing of Chlorophyll. J. Plant Physiol. 1996, 148, 494–500. [Google Scholar] [CrossRef]
- Sankaran, S.; Zhou, J.; Khot, L.R.; Trapp, J.J.; Mndolwa, E.; Miklas, P.N. High-throughput field phenotyping in dry bean using small unmanned aerial vehicle based multispectral imagery. Comput. Electron. Agric. 2018, 151, 84–92. [Google Scholar] [CrossRef]
- Macedo, F.L.; Nóbrega, H.; de Freitas, J.G.R.; Ragonezi, C.; Pinto, L.; Rosa, J.; Pinheiro de Carvalho, M.A.A. Estimation of Productivity and Above-Ground Biomass for Corn (Zea mays) via Vegetation Indices in Madeira Island. Agriculture 2023, 13, 1115. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, H.; Yue, J.; Jin, X.; Li, Z.; Yang, G. Estimation of potato above-ground biomass based on unmanned aerial vehicle red-green-blue images with different texture features and crop height. Front. Plant Sci. 2022, 13, 938216. [Google Scholar] [CrossRef] [PubMed]
- Tao, H.; Feng, H.; Xu, L.; Miao, M.; Long, H.; Yue, J.; Li, Z.; Yang, G.; Yang, X.; Fan, L. Estimation of Crop Growth Parameters Using UAV-Based Hyperspectral Remote Sensing Data. Sensors 2020, 20, 1296. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, C.; Yang, H.; Yang, G.; Han, L.; Li, Z.; Feng, H.; Xu, B.; Wu, J.; Lei, L. Estimation of maize above-ground biomass based on stem-leaf separation strategy integrated with LiDAR and optical remote sensing data. PeerJ 2019, 2019, e7593. [Google Scholar] [CrossRef] [PubMed]
- Tong, A.; He, Y. Remote sensing of grassland chlorophyll content: Assessing the spatial-temporal performance of spectral indices. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 2846–2849. [Google Scholar]
- Zillmann, E.; Schönert, M.; Lilienthal, H.; Siegmann, B.; Jarmer, T.; Rosso, P.; Weichelt, H. Crop Ground Cover Fraction and Canopy Chlorophyll Content Mapping using RapidEye imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-7/W3, 149–155. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, W.; Kong, W.; Ye, H.; Luo, J.; Chen, P. Remote estimation of canopy nitrogen content in winter wheat using airborne hyperspectral reflectance measurements. Adv. Space Res. 2016, 58, 1627–1637. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, G. Deriving a light use efficiency estimation algorithm using in situ hyperspectral and eddy covariance measurements for a maize canopy in Northeast China. Ecol. Evol. 2017, 7, 4735–4744. [Google Scholar] [CrossRef]
- Coops, N.C.; Stone, C.; Culvenor, D.S.; Chisholm, L.A.; Merton, R.N. Chlorophyll content in eucalypt vegetation at the leaf and canopy scales as derived from high resolution spectral data. Tree Physiol. 2003, 23, 23–31. [Google Scholar] [CrossRef]
- Thanyapraneedkul, J.; Muramatsu, K.; Daigo, M.; Furumi, S.; Soyama, N.; Nasahara, K.N.; Muraoka, H.; Noda, H.M.; Nagai, S.; Maeda, T.; et al. A Vegetation Index to Estimate Terrestrial Gross Primary Production Capacity for the Global Change Observation Mission-Climate (GCOM-C)/Second-Generation Global Imager (SGLI) Satellite Sensor. Remote Sens. 2012, 4, 3689–3720. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Rundquist, D.C.; Keydan, G.P.; Leavitt, B.; Schepers, J. Monitoring Maize (Zea mays L.) Phenology with Remote Sensing. Agron. J. 2004, 96, 1139–1147. [Google Scholar] [CrossRef]
- Luscier, J.D.; Thompson, W.L.; Wilson, J.M.; Gorham, B.E.; Dragut, L.D. Using digital photographs and object-based image analysis to estimate percent ground cover in vegetation plots. Front. Ecol. Environ. 2006, 4, 408–413. [Google Scholar] [CrossRef]
- Dai, S.; Luo, H.; Hu, Y.; Zheng, Q.; Li, H.; Li, M.; Yu, X.; Chen, B. Retrieving leaf area index of rubber plantation in Hainan Island using empirical and neural network models with Landsat images. J. Appl. Remote. Sens. 2023, 17, 014503. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Kang, Y.; Özdoğan, M.; Zipper, S.C.; Román, M.O.; Walker, J.; Hong, S.Y.; Marshall, M.; Magliulo, V.; Moreno, J.; Alonso, L.; et al. How Universal Is the Relationship between Remotely Sensed Vegetation Indices and Crop Leaf Area Index? A Global Assessment. Remote Sens. 2016, 8, 597. [Google Scholar] [CrossRef] [PubMed]
- Stenberg, P.; Rautiainen, M.; Manninen, T.; Voipio, P.; Smolander, H. Reduced simple ratio better than NDVI for estimating LAI in Finnish pine and spruce stands. Silva Fenn. 2004, 38, 3–14. [Google Scholar] [CrossRef]
- Ghasemzadeh, H.; Hillman, R.E.; Mehta, D.D. Toward Generalizable Machine Learning Models in Speech, Language, and Hearing Sciences: Sample Size Estimation and Reducing Overfitting Running Title: Power Analysis and Reducing Overfitting in Machine Learning. J. Speech Lang. Hear. Res. 2024, 11, 753–781. [Google Scholar] [CrossRef] [PubMed]
- Szabó, Z.C.; Mikita, T.; Négyesi, G.; Varga, O.G.; Burai, P.; Takács-Szilágyi, L.; Szabó, S. Uncertainty and Overfitting in Fluvial Landform Classification Using Laser Scanned Data and Machine Learning: A Comparison of Pixel and Object-Based Approaches. Remote Sens. 2020, 12, 3652. [Google Scholar] [CrossRef]
- Kolluri, J.; Kotte, V.K.; Phridviraj, M.S.B.; Razia, S. Reducing Overfitting Problem in Machine Learning Using Novel L1/4 Regularization Method. In Proceedings of the 2020 4th International Conference on Trends in Electronics and Informatics (ICOEI) (48184), Tirunelveli, India, 15–17 June 2020; pp. 934–938. [Google Scholar]
- Wang, W.; Pai, T.-W. Enhancing Small Tabular Clinical Trial Dataset through Hybrid Data Augmentation: Combining SMOTE and WCGAN-GP. Data 2023, 8, 135. [Google Scholar] [CrossRef]

| Canopy State Variables | Min | Mean | Max | SD | CV (%) |
|---|---|---|---|---|---|
| LAI (m2 m−2) | 1.39 | 2.79 | 4.19 | 1.40 | 50 |
| AGB (ton ha−1) | 0.59 | 1.46 | 2.33 | 0.87 | 60 |
| CCC (mg m−2) | 35.95 | 43.42 | 50.89 | 7.47 | 17 |
| FVC (%) | 14 | 32 | 50 | 18 | 57 |
| Index | Name | Formula | References |
|---|---|---|---|
| NDVI | Normalized difference vegetation index | (NIR − R)/(NIR + R) | [22] |
| GNDVI | Green normalized difference vegetation index | (NIR − G)/(NIR + G) | [25] |
| SR | Simple ratio | NIR/R | [24] |
| EVI2 | Enhanced vegetation index 2 | 2.5 × (NIR − R)/(1 + NIR + 2.4 × R) | [26] |
| CIgreen | Green chlorophyll index | (NIR/G) − 1 | [27] |
| Model | Hyperparameter | Description | Values Evaluated | Selected Hyperparameter |
|---|---|---|---|---|
| HR | epsilon | Tolerance to outliers | 0.01, 0.1, 0.5, 1.0, 2.0 | 0.1 |
| max_iter | Maximum iterations for optimisation | 100, 200, 500, 1000 | 500 | |
| alpha | Regularisation strength | 0.0001, 0.001, 0.01, 0.1, 1.0 | 0.01 | |
| warm_start | Reuse previous solution | True, False | False | |
| TSR | n_subsamples | Number of subsets for robust estimation | 100, 200, 500, 1000 | 500 |
| max_iter | Maximum iterations for optimisation | 100, 200, 500, 1000 | 1000 | |
| ABR | n_estimators | Number of weak learners (trees) | 50, 100, 200, 500 | 200 |
| learning_rate | Scaling factor for weak learners | 0.01, 0.1, 0.5, 1.0 | 0.1 | |
| CBR | iterations | Number of boosting iterations (trees) | 100, 200, 500, 1000 | 500 |
| learning_rate | Step size for adaptation during training | 0.01, 0.05, 0.1, 0.2 | 0.1 | |
| depth | Maximum depth of trees in the ensemble | 4, 6, 8, 10 | 6 | |
| l2_leaf_reg | L2 regularisation for leaf values | 1.0, 5.0, 10.0 | 5.0 | |
| MLR | n/a | n/a | n/a | n/a |
| RFR | n_estimators | Number of trees in the forest | 10, 50, 100, 200 | 100 |
| max_depth | Maximum depth of each tree | None, 10, 20, 30 | 20 | |
| min_samples_split | Minimum number of samples to split a node | 2, 5, 10 | 2 | |
| min_samples_leaf | Minimum number of samples in a leaf node | 1, 2, 4 | 1 | |
| PLSR | n_components | Number of components to keep | 1, 2, 3, 4 | 3 |
| scale | Whether to scale the data | True, False | True | |
| RR | alpha | Regularisation strength | 0.1, 1.0, 10.0 | 1.0 |
| solver | Algorithm to use in the optimisation | ‘auto’, ‘svd’, ‘cholesky’, ‘lsqr’, ‘saga’ | auto |
| Model | CBR | TSR | MLR | RR | PLSR | RFR | ABR | HR | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | |
| AGB | R2 | 0.99 | 0.55 | 0.47 | 0.66 | 0.65 | 0.77 | 0.27 | 0.49 | 0.04 | 0.21 | 0.91 | 0.57 | 0.90 | 0.47 | 0.50 | 0.66 |
| RMSE | 0.04 | 0.39 | 0.39 | 0.31 | 0.37 | 0.30 | 0.46 | 0.38 | 0.51 | 0.46 | 0.19 | 0.40 | 0.21 | 0.42 | 0.39 | 0.33 | |
| RMSE% | 3 | 27 | 26 | 21 | 25 | 20 | 31 | 26 | 34 | 31 | 13 | 27 | 14 | 28 | 26 | 22 | |
| MAE | 0.03 | 0.25 | 0.23 | 0.22 | 0.24 | 0.23 | 0.29 | 0.27 | 0.33 | 0.31 | 0.10 | 0.27 | 0.16 | 0.28 | 0.22 | 0.22 | |
| MSE | 0.00 | 0.16 | 0.15 | 0.10 | 0.14 | 0.09 | 0.21 | 0.15 | 0.26 | 0.21 | 0.04 | 0.16 | 0.04 | 0.18 | 0.15 | 0.11 | |
| MAPE | 2 | 17 | 16 | 15 | 16 | 18 | 22 | 21 | 23 | 22 | 5 | 16 | 11 | 19 | 15 | 17 | |
| CCC | R2 | 0.99 | 0.83 | 0.84 | 0.83 | 0.84 | 0.83 | 0.83 | 0.81 | 0.81 | 0.78 | 0.98 | 0.85 | 0.93 | 0.82 | 0.84 | 0.82 |
| RMSE | 0.25 | 2.91 | 3.06 | 3.10 | 2.87 | 2.97 | 2.94 | 3.11 | 3.09 | 3.30 | 1.01 | 2.88 | 1.98 | 2.91 | 2.88 | 3.06 | |
| RMSE% | 1 | 6 | 7 | 7 | 6 | 6 | 6 | 7 | 7 | 7 | 2 | 6 | 4 | 6 | 6 | 7 | |
| MAE | 0.21 | 2.29 | 2.42 | 2.43 | 2.27 | 2.35 | 2.33 | 2.52 | 2.45 | 2.69 | 0.74 | 2.29 | 1.70 | 2.28 | 2.26 | 2.40 | |
| MSE | 0.07 | 8.46 | 9.34 | 9.58 | 8.23 | 8.84 | 8.65 | 9.66 | 9.53 | 10.89 | 1.03 | 8.31 | 3.93 | 8.48 | 8.31 | 9.34 | |
| MAPE | 1 | 5 | 5 | 5 | 5 | 5 | 5 | 6 | 5 | 6 | 2 | 5 | 4 | 5 | 5 | 5 | |
| FVC | R2 | 0.99 | 0.97 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 0.98 | 0.97 | 0.99 | 0.98 | 0.99 | 0.97 | 0.98 | 0.98 |
| RMSE | 0.00 | 0.03 | 0.02 | 0.03 | 0.02 | 0.03 | 0.02 | 0.03 | 0.03 | 0.03 | 0.01 | 0.02 | 0.02 | 0.03 | 0.02 | 0.03 | |
| RMSE% | 1 | 7 | 6 | 8 | 6 | 7 | 6 | 8 | 7 | 8 | 3 | 6 | 5 | 7 | 6 | 7 | |
| MAE | 0.00 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | |
| MSE | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| MAPE | 1 | 11 | 31 | 24 | 16 | 25 | 18 | 17 | 42 | 13 | 3 | 10 | 9 | 11 | 24 | 24 | |
| LAI | R2 | 0.99 | 0.70 | 0.79 | 0.73 | 0.80 | 0.74 | 0.79 | 0.74 | 0.72 | 0.71 | 0.97 | 0.55 | 0.91 | 0.69 | 0.79 | 0.74 |
| RMSE | 0.08 | 0.64 | 0.58 | 0.65 | 0.56 | 0.63 | 0.57 | 0.62 | 0.64 | 0.66 | 0.21 | 0.74 | 0.39 | 0.65 | 0.56 | 0.63 | |
| RMSE% | 2 | 19 | 18 | 20 | 17 | 19 | 17 | 19 | 19 | 20 | 6 | 22 | 12 | 20 | 17 | 19 | |
| MAE | 0.06 | 0.52 | 0.45 | 0.50 | 0.43 | 0.48 | 0.44 | 0.48 | 0.51 | 0.53 | 0.16 | 0.60 | 0.33 | 0.52 | 0.43 | 0.49 | |
| MSE | 0.01 | 0.42 | 0.34 | 0.42 | 0.31 | 0.40 | 0.32 | 0.39 | 0.41 | 0.43 | 0.04 | 0.54 | 0.15 | 0.42 | 0.32 | 0.40 | |
| MAPE | 3 | 18 | 16 | 17 | 15 | 16 | 16 | 16 | 18 | 21 | 6 | 21 | 11 | 18 | 15 | 17 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jewan, S.Y.Y.; Singh, A.; Billa, L.; Sparkes, D.; Murchie, E.; Gautam, D.; Cogato, A.; Pagay, V. Can Multi-Temporal Vegetation Indices and Machine Learning Algorithms Be Used for Estimation of Groundnut Canopy State Variables? Horticulturae 2024, 10, 748. https://doi.org/10.3390/horticulturae10070748
Jewan SYY, Singh A, Billa L, Sparkes D, Murchie E, Gautam D, Cogato A, Pagay V. Can Multi-Temporal Vegetation Indices and Machine Learning Algorithms Be Used for Estimation of Groundnut Canopy State Variables? Horticulturae. 2024; 10(7):748. https://doi.org/10.3390/horticulturae10070748
Chicago/Turabian StyleJewan, Shaikh Yassir Yousouf, Ajit Singh, Lawal Billa, Debbie Sparkes, Erik Murchie, Deepak Gautam, Alessia Cogato, and Vinay Pagay. 2024. "Can Multi-Temporal Vegetation Indices and Machine Learning Algorithms Be Used for Estimation of Groundnut Canopy State Variables?" Horticulturae 10, no. 7: 748. https://doi.org/10.3390/horticulturae10070748
APA StyleJewan, S. Y. Y., Singh, A., Billa, L., Sparkes, D., Murchie, E., Gautam, D., Cogato, A., & Pagay, V. (2024). Can Multi-Temporal Vegetation Indices and Machine Learning Algorithms Be Used for Estimation of Groundnut Canopy State Variables? Horticulturae, 10(7), 748. https://doi.org/10.3390/horticulturae10070748











