Abstract
Industrial-sized fermenters differ from the laboratory environment in which bioprocess development initially took place. One of the issues that can lead to reduced productivity on a large scale or even early termination of the process is the presence of bioreactor heterogeneities. This work proposes and adopts a design–build–test–learn-type workflow that estimates the substrate, oxygen, and resulting growth heterogeneities through a compartmental modelling approach and maps Yarrowia lipolytica-specific behavior in this relevant range of conditions. The results indicate that at a growth rate of 0.1 h−1, the largest simulated volume (90 m3) reached partial oxygen limitation. Throughout the fed-batch, the cells experienced dissolved oxygen values from 0 to 75% and grew at rates of 0 to 0.2 h−1. These simulated large-scale conditions were tested in small-scale cultivations, which elucidated a transcriptome with a strong downregulation of various transporter and central carbon metabolism genes during oxygen limitation. The relation between oxygen availability and differential gene expression was dynamic and did not show a simple on–off behavior. This indicates that Y. lipolytica can differentiate between different available oxygen concentrations and adjust its transcription accordingly. The workflow presented can be used for Y. lipolytica-based strain engineering, thereby accelerating bioprocess development.
1. Introduction
The production volumes of biotechnological processes are much larger (10–100 s m3) than the typical volume in which strain screening and development take place (mL–Ls). It has been well described that this difference in scales leads to unforeseen adverse effects, such as a reduced titer, rate, yield, or health of the production strain [1,2]. One of the major contributors to these unwanted effects is the exposure to extrinsic sources of heterogeneity in large volumes. Combined with different hydrostatic pressures, this results in a setting where the production strain experiences varying environments throughout the vessel (e.g., changes in pH, substrate availabilities, and temperatures). Consequently, the optimal production conditions are not present in all bioreactor zones, resulting in altered metabolic activity and potentially in population heterogeneity [3,4]. Partly due to these issues, it is therefore recommended to work with the end in mind; by designing a theoretical process, including potential stressors, a conceptual process understanding can be obtained [5,6].
Computational fluid dynamics (CFD) efforts can provide a detailed prediction of the mixing and resulting mass flows in a large-scale bioreactor. An additional approach, which is often derived from CFD, is the compartmentalization of bioreactors based on factors such as liquid mixing, impellor orientation, and bioreactor size [7,8]. The introduction of metabolic models into the compartmental bioreactor design can directly link the simulated bioreactor conditions to metabolic performance [9]. The required tools or skillsets, however, might not always be present for these more complex exercises. Therefore, a useful first step is combining simple microbial black-box kinetics with the various predicted substrate availabilities. Translating the environmental conditions to different metabolic states or regimes would be a powerful predictive tool [10,11,12].
With bioreactor heterogeneities in mind, it is important to develop strains that are suitable for industrial conditions, a concept that has been pitched as the idea of fermenterphiles [13]. Ultimately, the goal is to design strains that show robustness against the adverse conditions that large-scale bioproduction can bring. One of the organisms that is gaining industrial interest is Yarrowia lipolytica. Its versatility in its substrate and product spectrum, alongside an increasing genomic understanding, makes Y. lipolytica a promising host for novel biochemical production [14,15]. To aid in the development of these projects, it is important to assess the robustness (i.e., unaltered microbial performance when exposed to perturbations [16]) of Y. lipolytica when exposed to different bioreactor heterogeneities. Aeration in industrial fermenters can be a challenging factor, and due to the relatively low solubility of oxygen, transport over the gas–liquid interface could become limiting [17]. Being a strict aerobe, Y. lipolytica might be challenged in an industrial bioreactor, and thus, the system boundaries must be defined.
Process development benefits from laboratory setups that have a good predictive power of large-scale conditions. Unfortunately, when assessing strain physiology, wet-lab scientists often do not have a tool to determine what the most relevant conditions are to test. Computational scientists, on the other hand, often rely on the literature to obtain the kinetic parameters for their strain of interest. This study aims to bridge both fields and illustrate Y. lipolytica’s physiological and transcriptional responses under relevant dissolved oxygen (DO) values.
Bridging these scales has proven to be of great importance, with similar efforts focusing on different processes [18]. This study aims to aid in the development of Y. lipolytica-based bioprocesses; as such, a targeted workflow is presented and followed. The framework starts with a process design, identifying the kinetic equations and parameters needed to describe microbial growth, which were estimated from continuous cultivations. The microbial growth kinetics were then combined to initialize and solve a compartmental model, describing mass exchanges and flows on an industrial scale. The model simulation resulted in substrate and oxygen heterogeneities and metabolic regimes that cells can experience throughout an industrial fed-batch fermentation. This range of conditions was experimentally simulated in small-scale bioreactors to assess the fundamental physiological and transcriptional landscape of Y. lipolytica. The results provide insights for either strain or process optimization. The workflow is summarized in Figure 1.
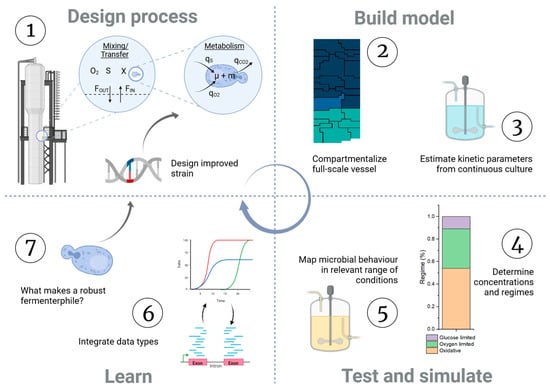
Figure 1.
Graphical summary of the design–build–test–learn type of workflow used in this manuscript.
2. Materials and Methods
2.1. Cultivation
The wild-type Yarrowia lipolytica W29 was used in this study. For the pre-culture, 25 mL of Delft media (20 g/L of glucose, 14.4 g/L of KH2PO4, 0.5 g/L of MgSO4, 7.5 g/L of (NH4)2SO4, 0.1 mg/L of biotin, 0.4 mg/L of 4-aminobenzoic acid, 2 mg/L of nicotinic acid, 2 mg/L of calcium pantothenate, 2 mg/L of pyridoxine, 2 mg/L of thiamine HCl, 50 mg/L of myo-inositol, 4.5 mg/L of CaCl2·2H2O, 4.5 mg/L of ZnSO4·7H2O, 3 mg/L of FeSO4·7H2O, 1 mg/L of boric acid, 1 mg/L of MnCl2·4H2O, 0.4 mg/L of Na2MoO4·2H2O, 0.3 mg/L of CoCl2·6H2O, 0.1 mg/L of CuSO4·5H2O, 0.1 mg/L of KI, and 15 mg/L of ethylenediaminetetraacetic acid (EDTA)) was inoculated with 250 µL of glycerol stock (25% v/v at −80 °C) and grown overnight at 30 °C and 225 rpm.
Continuous cultivations were started with a batch phase (OD600 0.1) on Delft media, where all media components were scaled to a glucose concentration of 10 g/L, with the addition of 1 mL/L of antifoam 204 (Merck, Darmstadt, Germany). Upon the end of the batch, external feed and harvest pumps were activated to maintain a constant volume. The weights of the feed and harvest bottles were monitored to determine the precise dilution rate. The feed media were similar to the batch media at 10 g/L of glucose. Five residence times were taken to reach the initial steady state, after which two residence times were deemed sufficient for the remaining dilution rates. The cultivation was performed in a 1 L Biostat Q plus vessel (Sartorius, Göttingen, Germany) with a working volume of 0.5 L. The bioreactor was operated at a constant stirring rate to limit the changes in liquid volume throughout the process. Thus, a DO control was performed through a cascade by adjusting the airflow and composition. To reach lower DO setpoints, pure nitrogen was mixed into the sparging air. The pH was maintained at 6 by the automatic addition of 5 M NaOH.
To obtain kinetic information for Y. lipolytica, continuous cultivations were operated at six different dilution rates that covered the range in which Y. lipolytica is able to grow (0.05, 0.1, 0.15, 0.2, 0.25, and 0.3 h−1) and the culture was sampled at the end of each steady state. To assess the effect of oxygen concentrations at different growth rates, three cultivations at constant dilution rates (0.05, 0.1, and 0.2 h−1) were brought to steady state at six different DO levels (50, 25, 10, 5, 2.5, and 0.5%) and sampled at the end of each steady state.
The UltiMate 3000 HPLC (Thermo Scientific, Waltham, MA, USA) with 9 mM sulfuric acid as the mobile phase was used to quantify and detect the levels of organic acids and the carbon source. The quantification of compounds was performed based on the refractive index (RI) chromatograms measured on the Refractomax 521 detector (Thermo Scientific, Waltham, MA, USA). Residual glucose concentrations were measured with a colorimetric detection kit (Invitrogen, Waltham, MA, USA). Off-gas concentrations of CO2 and O2 were determined using a PrimaBT Mass Spectrometer (Thermo Scientific, Waltham, MA, USA). The cell dry weight (CDW) was determined by drying known sample volumes after washing the cell pellet twice with a 0.9% NaCl solution. The samples were placed in pre-dried and weighed Eppendorf tubes and dried in an oven at 80 °C until a constant weight was reached. For RNA sequencing, 1 mL of broth was sampled in pre-cooled Eppendorf tubes and centrifuged directly for one minute at 4000× g and 2 °C. The supernatant was discarded and the remaining cell pellet was snap-frozen in liquid nitrogen.
2.2. RNA Sequencing
RNA extraction, quality control, library preparation, and paired-end sequencing were performed by an external service partner (BGI Europe, Copenhagen, Denmark). The resulting datasets were analyzed with FASTQc for quality control [19]. The Spliced Transcripts Alignment to a Reference (STAR) package was used to align the reads to the YALI1 reference genome of Y. lipolytica [20]. Feature counts were then used to convert the alignments into read counts for each gene by supplementing the expected exons per gene from the previously mentioned reference genome [21]. An expression analysis was performed with DESeq2 and the results were used for a principal component analysis [22,23]. Relevant ontology data were gathered from the Supplementary Materials in Lubuta et al. with a conversion from the YALI0 to YALI1 annotation using the information published by Magnan et al. [24,25]. A differential gene expression analysis was performed based on the TPM log2 difference against a reference condition. Log2 differences lower than −1 indicated a downregulation, whereas values higher than 1 were considered to be upregulated.
2.3. Parameter Estimation
Measurements from the continuous culture were used to estimate various fermentation parameters. With the growth rates and substrate concentrations available, the maximum growth rate and substrate affinity constant could be estimated through Monod:
where is the growth rate, S is the substrate concentration, and kS is the substrate affinity constant. The specific uptake and production rates (q) can be described by the Herbert–Pirt relation:
where i corresponds to either the substrate (S), oxygen (O2), or carbon dioxide (CO2); the growth-related term is a; the product-related term is b; and the maintenance coefficient is m.
The model equations were formulated and solved in MATLAB© R2019a. For parameter estimation, Bayesian inference with the Markov Chain Monte Carlo (MCMC) metropolis algorithm was used. For the prior distribution, a multivariate normal distribution of the Herbert–Pirt model parameters was used, with the parameters being estimated using the maximum likelihood (MLE) method. From the MLE method, the parameter estimators’ covariance matrix and mean values were obtained and subsequently used as previously for sampling the initial starting points for the MCMC chains. The inverse gamma distribution was used as previously for sampling the variance of the measurement errors. The sample variance was estimated from the residuals. For the jumping distribution, a multivariate normal with an efficient covariance scaling factor of ~2.4/sqrt(d) was applied, where d is the total number of parameters. Multi-chain simulations with a chain number of 10 and a sampling number of 10,000 were run. A burn ratio of 0.2 was applied and the remaining samples in the chains were analyzed for inferring the posterior distribution of the model parameters. All parameter estimation was performed using the guidelines as set by Sin et al. [26].
Secondly, the rates of oxygen consumption and carbon dioxide production were estimated based on their stoichiometric balance with substrate uptake and biomass growth. Two matrices describing C-moles and the degree of reduction of measured and unmeasured compounds, as well as two vectors describing the specific rates, were used [27]:
Rewriting allows for the determination of the undetermined specific rates:
In this equation, E is the conservation matrix whereas the columns refer to a conserved element and property. Meanwhile, q is a column vector that includes the measured rates for each compound. The subscript m indicates the measured values whereas u represents those that are unmeasured.
was used as the biomass composition of Y. lipolytica [28]. Solving the stoichiometric balance for each continuous steady state resulted in a set of estimated rates. These vectors could be further used to perform additional parameter estimation as described previously.
2.4. Sensitivity Analysis
Substrate uptake, oxygen consumption, and carbon dioxide production are all products of various estimated parameters. Therefore, it was relevant to include a sensitivity analysis, and the following function describing the various uptake or production rates was defined:
where i corresponds to either S, O2, or CO2.
The estimated values and standard deviations were used in a global sensitivity analysis to find the parameters that affect the final output the most. The easyGSA toolbox was used for this purpose, which works by identifying a model handle and a definition of the input space [29]. The model was defined as Equation (5) with one model output () and four model inputs (). The standard setup used a Sobol analysis with a sampling size of 2 × 103 and the Jansen estimator.
2.5. Compartmental Modelling
The work by Nadal-Rey et al. provides a compartmentalized understanding of an industrially sized bioreactor [30]. Through CFD-aided simulations, the authors were able to divide a vessel with varying filling volumes into a library of compartment maps. As a result, the heterogeneous bioreactor can now be described as a combination of multiple perfectly mixed compartments. This understanding of compartment volumes, exchange flows, kLa values, and oxygen solubility offers a tool to model the kinetic changes that a production strain undergoes as it circulates through the vessel. By coupling the required kinetic equations to each compartment, the dynamic compartmental model allows for both a spatial and temporal understanding of an industrial bioprocess. Here, this work is combined with the parameters estimated specifically for Y. lipolytica. A simplified version was used to simulate a snapshot of 6 min at three different fixed liquid volumes (40, 60, and 90 m3). The end of the batch phase corresponds to 40 m3 of liquid volume and an exponential feeding phase continues until 90 m3 is reached.
Based on the substrate and oxygen availability in each compartment, cells will have a different metabolic activity. Here, this was addressed as the strain being in a specific metabolic regime, with altered kinetics as a result. The maintenance coefficients were set as thresholds, below which the respective compartment was considered starved (glucose) or limited (oxygen). As Y. lipolytica is a strictly aerobic organism, no growth was assumed under oxygen limitation. The product terms and overflow metabolism were omitted from the list of equations and over the short simulation period, the biomass concentrations were maintained as constant. This resulted in a simplified setup that only assumed growth if both the oxygen and glucose concentrations were above their respective maintenance requirements. If the substrate supply was less than the maintenance requirements, the metabolic state became glucose starvation and the same goes for oxygen limitation. Thus, metabolism can be described by Monod and Herbert–Pirt through the following kinetics (Table 1) [30].

Table 1.
Definition of different metabolic states that can be encountered in the compartmental model alongside the description of microbial kinetics for each metabolic state.
Aeration was set at 1 vvm of the initial filling volume and was not adjusted throughout the fermentation. The system was fed from the top and designed to sustain a growth rate of 0.1 h−1. Given this growth rate, the biomass increased for each bioreactor volume, assuming a complete consumption of all substrate supplied. These settings allowed the model to be initialized for each filling volume as described in Table 2.

Table 2.
Initialization parameters for the compartmental model.
The compartmental model was implemented in MATLAB© R2019a as a set of ordinary differential equations. An ode15 solver was then used to solve the mass balances (Equations (6)–(8)) for the substrate and oxygen in each compartment over a period of 6 min. Both equations, i.e., Equations (6) and (7), address substrate levels, with Equation (7) applying to the compartment in which feeding takes place and Equation (6) covering the other compartments.
The liquid mass flows in and out of the compartment are indicated by F and were obtained from the CFD. First, the CFD results were compartmentalized based on the axial and radial velocities. Then, through an automated methodology, the compartment volumes, flows, and connections of the compartments were defined [7]. M refers to the total mass of each respective compound and S and O2 refer to the concentrations of the substrate and oxygen in the flows in and out of the compartments.
Oxygen was added to each individual compartment and not only to the one containing the sparging system. To achieve this, the model includes a kLa (oxygen transfer coefficient), O* (oxygen saturation concentration), and O (actual oxygen concentration) term for each compartment. The kLa and O* values were approximated based on the CFD and are used to calculate oxygen transfer from the gas to liquid phase based on mixing and pressure [30].
3. Results
3.1. Growth Physiology and Estimated Kinetics of Y. lipolytica at Different Growth Rates
A continuous cultivation of Y. lipolytica with six steady states at different growth rates was performed to obtain key performance parameters (Figure 2). It was hypothesized that the (by-)product formation is a function of environmental pressure rather than of dilution rate. pH has been known to affect the production of organic acids, whereas nutrient limitation is associated with the accumulation of lipids [31,32]. In this work, it was believed that under the selected conditions, no significant (by-)product formation was expected. This was also confirmed by the HPLC analysis. Hence, no product formation and a consistent biomass composition (CH1.675O0.523N0.153) were assumed for all growth rates [33]. The substrate consumption and product formation rates (R) were calculated and used to determine the biomass-specific (q) rates (Figure 2A). Carbon balancing consistently accounted for over 92% of the amount supplied (Figure 2B). Variations were observed across the growth rates, but in general, approximately 30% and 60% of the carbon was directed towards CO2 and biomass, respectively. An initial interpretation of the data indicated a linear relationship for all q-rates, as was expected since they were growth-coupled and no significant products were made. The specific uptake and production rates can be described by the Herbert–Pirt equation, in which the product term can now be omitted, thus confirming the linear relation. The resulting yield and maintenance coefficients were estimated from this relation.
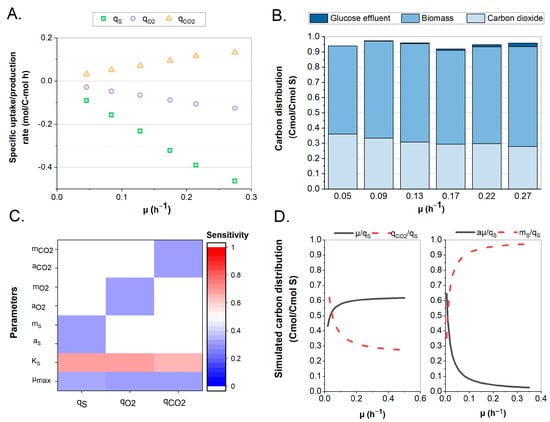
Figure 2.
Observed and simulated growth kinetics of Y. lipolytica W29. (A) Specific consumption rates of substrate (qS) and oxygen (qO2) and production rates of carbon dioxide (qCO2) were plotted from the values obtained from a continuous cultivation at six dilution rates. (B) Observed carbon balance and substrate distribution at various dilution rates of the continuous cultivation. (C) Sensitivity analysis of model kinetic parameters using the total Sobol indices. (D) (LEFT) Simulated values of substrate distribution to biomass production (YX/S) and to CO2 production (YCO2/S). (RIGHT) Simulated values of growth-dependent (aSµ/qS) and maintenance-dependent (mS/qS) glucose uptake.
The key parameters of the maximum growth rate (µmax) and substrate affinity constant (KS) were both estimated through a Monod-type equation. The growth rates and residual glucose concentrations enabled a Bayesian parameter estimation (Table 3). The Monte Carlo (MC) error was consistently low for all estimated parameters, indicating a good convergence of the applied sampling algorithm [26]. The MCMC chains and posterior simulations can be found in Supplementary File S1.

Table 3.
Parameter estimation of measured values of wild-type Y. lipolytica W29. The average, standard deviation, and Monte Carlo (MC) error of the estimated parameters are reported in the table below.
Through reaction stoichiometry, the following matrix describing the carbon balance and degree of reduction of the conversion of the substrate and O2 to biomass and CO2 was generated:
In this instance, the substrate uptake rate and growth rate were derived from measurements, which allowed for the determination of qO2 and qCO2. These values were then used in a parameter estimation of the yield factors and maintenance coefficients. A comparison of the stoichiometric values to the measurement-based values (Table 3) gave similar results, but with a large standard deviation. As a generalized biomass formula for Y. lipolytica has been used, this could introduce a larger uncertainty in the calculation. Moreover, the stoichiometric method would benefit from including nitrogen-containing components. Consequently, the measurement-based estimates were used in the compartmental model.
A sensitivity analysis showed a large contribution of the substrate affinity coefficient to the model outputs considered (Figure 2C). Analyses of the substrate uptake, O2 consumption, and CO2 production showed a similar pattern, where the substrate affinity coefficient seemed to be the source of the highest sensitivity. This high sensitivity underlines the need for rapid sampling and accurate parameter determination when describing enzyme kinetics [34]. From a kinetic perspective, the affinity constant is crucial, as it directly influences the growth rate obtained on a certain residual glucose level, and through the growth rate, it determines all other specific rates. This observation is supported by the correlation matrix of the parameter estimation, in which the maximum growth rate and substrate affinity constant had a strong positive correlation value of 0.9694 (Supplementary File S1).
Further, to understand the optimal carbon conversion efficiency, the estimates from the Herbert–Pirt relation were used to simulate yields and carbon distributions across varying growth rates, as shown in Figure 2D. At a growth rate of 0.1 h−1, these would be distributed as ∼55% towards biomass and ∼40% to CO2, while at the maximum growth rate, this distribution was closer to 60–30 on a C-mol basis. These simulated values can be compared against those obtained from the continuous culture, and indeed, a similar behavior was observed. The amount of carbon directed towards CO2 formation decreased (from ∼60% to ∼30%) as the growth increased, with a higher fraction of biomass. The maintenance term had a variable impact: i.e., at a growth rate of 0.1, approx. 10% of the carbon uptake was related to the maintenance of the biomass, while this fraction fell below 5% at higher growth rates.
3.2. Industrial-Scale Bioreactor Heterogeneities and Metabolic Regimes
Using the parameter values estimated from the chemostat experiments in Section 3.1, simulations were performed with the compartmental model describing the mixing, kinetics, and subsequent substrate and oxygen heterogeneities in a large-scale bioreactor. A high-density fed-batch cultivation was used as a case study bringing 5 gCDWL−1 culture (at the end of the batch phase) in 40 m3 up to 56 gCDWL−1 in 90 m3 at an exponential feeding rate of 0.1 h−1. The starting, intermediate, and final volumes were simulated by solving the mass balances across the compartments for a period of 6 min, resulting in a snapshot under those conditions. The compartmentalized model of the dissolved O2 concentrations throughout the bioreactor (Figure 3A) indicated the presence of gradients. The start of the fed-batch at 40 m3 and 5 gCDWL−1 did not result in significant heterogeneities. The oxygen concentrations were estimated at around 8 mg/L, which is close to the maximum solubility under ambient conditions. The growth rates throughout the bioreactor were relatively uniform at a value of about 0.1 h−1 (Figure 3B), corresponding to the applied exponential feeding rate. The residual substrate concentrations were also found to be relatively uniform throughout the bioreactor (Figure 3C). With increasing volume and cell concentrations, the 60 m3 liquid volume condition (31 gCDWL−1) showed a larger distribution of DO values. Since this was a top-fed system, there was a higher oxygen demand in the top compartments, resulting in lower DO values ranging from ∼0 to ∼6 mg/L or 0 to 75% solubility under ambient conditions. This distribution was also reflected in the estimated growth rates, showing a faster growth in the top compartments. Although some compartments were found to have a low oxygen concentration, the bioreactor at the 60 m3 liquid volume condition was still not oxygen-limited. Lower oxygen concentrations increased the driving force over the gas–liquid interface, which became a relevant factor. However, at the 60 m3 liquid volume condition, the substrate availability was found to vary with lower substrate concentrations in the bottom part of the vessel, thereby limiting the rate at which the microbes could grow. The 90 m3 liquid volume condition pushed the boundaries of this system with local oxygen limitations (Figure 3D). The growth rates became more uniform again, indicating that more substrate reached the lower compartments. Indeed, this can be seen in the substrate availability plot where the concentrations rose, and a further analysis showed that at this point, substrate accumulation occurred.
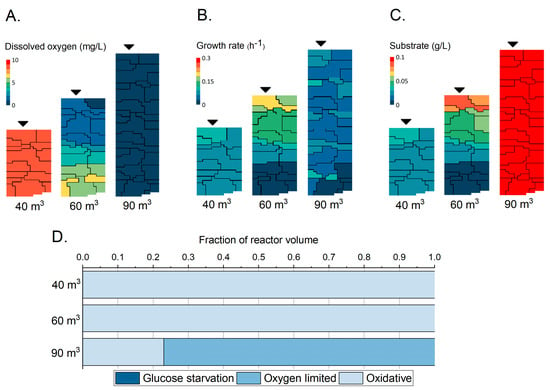
Figure 3.
Overview of industrial-scale bioreactor conditions and metabolic regimes. (A) Simulated compartmental overview of the dissolved oxygen (mg/L) concentrations in three large-scale liquid volume conditions. (B) Simulated compartmental overview of the growth rate (h−1). (C) Simulated compartmental overview of the substrate concentrations (g/L). (D) Expected metabolic regimes as a fraction of the total bioreactor volume.
Further, to validate that the estimated parameters hold true across the different scales, especially when the strains are exposed to suboptimal oxygen concentrations, the workflow was repeated. Data were included from the continuous cultures performed in the next section, covering DO values from 0.5 up to 50%. Although the increase in the data availability shifted the values of the parameter estimation, the compartmental modelling yielded similar results. The dissolved oxygen, growth rate, and substrate heterogeneities were simulated alike and the fraction of the 90 m3 bioreactor that was in an oxygen-limited metabolic state was comparable at 77%. The results are reported in Supplementary File S2.
3.3. Yarrowia lipolytica’s Transcriptional Response to Growth Rate and Dissolved Oxygen Variations
Compartmental modelling provides a range of realistic values that could be encountered in an industrial vessel. This approach of estimation can aid as a useful design tool for further scale-down or strain characterization. Mapping microbial behavior under industrially relevant conditions is important, as an improved understanding of cellular control mechanisms would allow for the design of a new genotype for a desired fermenterphile phenotype. Based on the compartmental model understanding, three distinct growth rates vs. six DO values were investigated in continuous cultivations. A standard analysis of the substrate, biomass, and off-gas was supplemented with a transcriptomic analysis to obtain a comprehensive understanding of the regulatory response.
The substrate and biomass profiles for the different conditions showed a relatively constant behavior. The main effects, however, were observed at the lowest DO values, where biomass production and substrate uptake decreased (Figure 4A,B). Consequently, an increase in glucose concentrations was observed with a decrease in biomass. Both are strong indicators that at this point, the continuous cultivation became oxygen-limited instead of substrate-limited, with the biomass being washed out. The onset of this phenomenon was observed at a DO percentage of 0.5% for the growth rates of 0.1 and 0.2 h−1, while it was observed at a DO of 5% for a lower growth rate of 0.05 h−1.
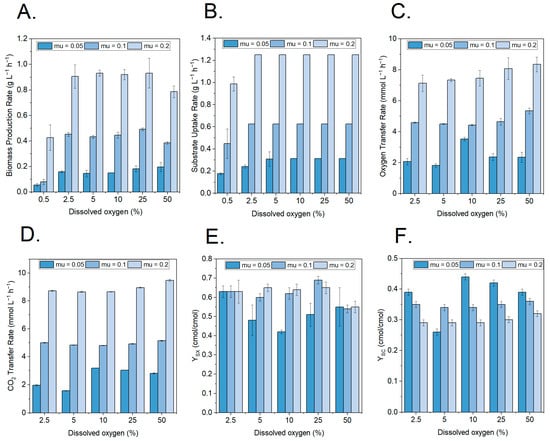
Figure 4.
Growth physiology at different growth rate and dissolved oxygen (DO) combinations. (A) Biomass production rate (gCDW L−1 h−1) at three different growth rates and six different dissolved oxygen concentrations. (B) Substrate uptake rate (gGLU L−1 h−1) at three different growth rates and six different dissolved oxygen concentrations. (C) Oxygen transfer rate (mmol L−1 h−1) at three different growth rates and five different dissolved oxygen concentrations. (D) CO2 transfer rate (mmol L−1 h−1) at three different growth rates and five different dissolved oxygen concentrations. (E) Yield of biomass on substrate (cmol cmol−1) at three different growth rates and five different dissolved oxygen concentrations. (F) Yield of CO2 on substrate (cmol cmol−1) at three different growth rates and five different dissolved oxygen concentrations.
For the non-limiting oxygen concentrations, the oxygen transfer rate, carbon dioxide transfer rate, yield of the biomass on the substrate, and yield of CO2 on the substrate (Figure 4C–F) confirm the carbon distribution presented in Section 3.1. Indeed, there was a growth rate dependency on the carbon distribution, as higher growth directed more towards biomass and less towards CO2.
A principal component analysis (PCA) of the transcriptome data identified 18 principal components (PC), with PC1 and PC2 explaining most of the variance at 42 and 26%, respectively (Figure 5A). A comparison of PC1 and PC2 revealed four distinct clusters, of which one cluster was representative of the oxygen-limited conditions (Figure 5B, cluster 1). The other three clusters appeared to spread out along PC2 based on their corresponding growth rates. Within each cluster, the data points moved along PC1 as the DO level was changed.
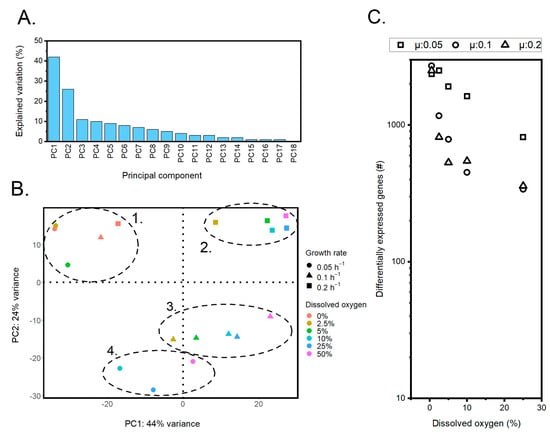
Figure 5.
An overview of transcriptome analysis with principal components and differentially expressed genes. (A) Explained variance by all principal components that were identified. (B) Explained variance by PC1 and PC2 plotted against one another. Four distinct clusters could be identified. The samples from the oxygen-limited conditions were grouped together in cluster one. Cluster two covered the setups with a growth rate of 0.2 h−1, while clusters three and four covered the growth rates of 0.1 h−1 and 0.05 h1, respectively. (C) Number of differentially expressed genes (log scale) when comparing the reference condition of 50% dissolved oxygen to 0.5, 2.5, 5, 10, and 25% dissolved oxygen for each individual growth rate.
Although many genes contributed to PC1, the 10 genes with the highest and lowest loading were further investigated (Supplementary File S3). Nine out of these twenty were associated with transporter functionality, indicating that transport is affected by oxygen availability. Many of the genes, however, were found to be uncharacterized, thereby limiting the interpretation possibilities.
While the PCA analysis was useful for analyzing general patterns in the transcriptome data, differential gene expression was performed to further understand the transcriptome response of Yarrowia’s core metabolism. The highest experimentally tested DO level of 50% was selected as the reference to which all other concentrations were compared. The transcripts per million (TPM) values were calculated and the log2 difference was determined against the reference condition. A log2-fold difference smaller than −1 was considered downregulated, whereas values higher than 1 were upregulated.
This analysis yielded different profiles when comparing the various growth rates (Figure 5C). While the number of differentially expressed genes at a DO% of 0 was approximately the same (2363, 2710, and 2510 for the growth rates of 0.05, 0.1, and 0.2, respectively), the number dropped more rapidly for the two higher growth rates as the DO went up. At a DO% of 25, all states still showed a differential expression with a count of 817, 339, and 359 for the three respective growth rates.
A detailed analysis of the differential gene expression of the central carbon metabolism genes showed a downregulation of various genes involved (Figure 6). In multiple instances, this involved the first steps of a pathway, thereby affecting downstream activity. Often, this response was limited to the states with the lowest growth rate (0.05 h−1). An especially strong response was observed at the start of glycolysis, where glucose is phosphorylated to glucose-6P by the enzyme hexokinase. Two genes (YALI1_E24028g and YALI1_E18539g) that have been proposed to encode for proteins with hexokinase activity were significantly downregulated during oxygen limitation. For YALI1_E18539g, this downregulation was not only observed for the lowest growth rate, but also held true for the other growth rates. As this step is crucial to all subsequent central carbon metabolisms, this can be seen as a strong regulatory response.
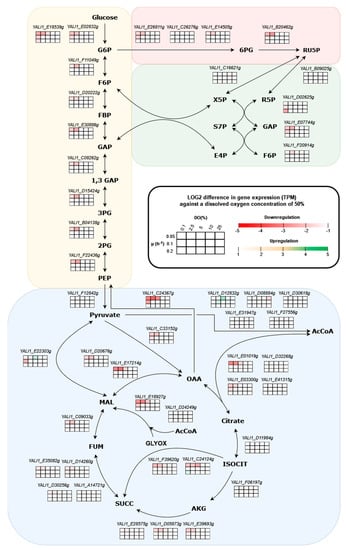
Figure 6.
Differential expression of genes involved in the central carbon metabolism of Y. lipolytica. The 5 × 3 table indicates 15 experimental conditions. Horizontally, 5 different dissolved oxygen (DO) percentages and vertically, 3 growth rates are shown. The coloring of the table is based on the log2 difference in gene expression as TPM values compared to a DO value of 50% at each respective growth rate. The red color scheme indicates gene downregulation and the green values indicate upregulation. White cells indicate a log2 difference between −1 and 1 and are considered not significant.
Meanwhile, a similar response was seen in the pentose phosphate pathway, most notably through the downregulation of 6-phosphogluconate dehydrogenase (YALI1_B20462g) in the oxidative part and two transketolases (YALI1_D02625g and YALI1_E07744g) in the non-oxidative part. Moreover, the entry points into the citric acid cycle (TCA) showed downregulation during oxygen limitation. The TCA cycle serves several purposes, with a major one being the supplying of NADH during oxidative phosphorylation. Citrate synthase converts acetyl-CoA and oxaloacetate into citrate, and as such, it serves to enter carbon into the TCA cycle. Both genes encoding this protein (YALI1_E01019 and YALI1_E03300g) showed significant downregulation. Interestingly, the genes responsible for the conversion of pyruvate into acetyl-CoA appeared to be unaffected and even slightly upregulated at a growth rate of 0.05 and a DO of 5%, and at a growth rate of 0.1 with a DO of 2.5%. The gene coding for the enzyme phosphoenolpyruvate carboxykinase (YALI1_C24367g), which facilitates the conversion of oxaloacetate into phosphoenolpyruvate and malate dehydrogenase (YALI1_D20679g and YALI1_E17214g), showed a strong downregulation. Additionally, the glyoxylate cycle genes were found to be downregulated, whereas iso-citrate lyase (YALI1_F39620g and YALI1_C24124g) and malate synthase (YALI1_E18927g and YALI1_D24249g) both showed downregulation.
4. Discussion
In this study, a better understanding of industrial-scale bioreactor O2 and growth rate heterogeneities was approximated to design experiments and test strain characteristics under relevant conditions. Ultimately, with this DBTL approach, the dynamic relation between gene expression and O2 availability in Y. lipolytica was better understood.
By the application of a compartmental modeling approach, industrial-scale bioreactor fed-batch conditions were simulated at snapshots of 40, 60, and 90 m3 liquid volumes. To solve the model, the appropriate kinetic parameters were estimated from continuous cultivations at varying growth rates. In these efforts, the microbial kinetic equations were simplified under the assumption that only cell growth would occur under the selected conditions. However, Y. lipolytica is known to be able to produce various (intracellular) products and alter its lipid contents based on triggers such as N limitation [35,36]. Nonetheless, consistent carbon balancing gave confidence that no major metabolites were missed in these estimations. While the biomass yields and maintenance coefficients were in agreement with previous studies [28,37], the estimated maximum growth rate of 0.399 h−1 is high compared to the previously reported values of approx. 0.25 h−1 [32,37]. In this work, the chemostat was operated to a high dilution rate of 0.3 h−1, at which the washout of the culture was observed (data not shown). Thus, it is likely that indeed the given maximum growth rate is an overestimation of reality. The parameter estimation indicated that the maximum growth rate and affinity constant had a strong positive correlation, meaning that an inaccurate residual glucose measurement can carry over into the maximum growth rate determination. The affinity constant on glucose was estimated to be 0.1 g/L, which is in line with the assay manufacturer’s reported sensitivity of 4 mg/L. Comparable residual glucose concentrations have been reported in an accelerostat study [38] and estimated values for glycerol have indicated an affinity constant of 0.196 g/L [39].
With the estimated parameters, the compartmental model could be initialized and solved for the various bioreactor volumes. For the selected process, cells experienced heterogeneities with respect to oxygen and the substrate. Consequently, different metabolic states were observed through varying growth rates. At the volumes of 40 and 60 m3, none of these heterogeneities led to a local limitation for either oxygen or the substrate. All the cells still experienced an environment in which complete oxidation was possible. For the 90 m3 setup, the vessel became severely oxygen-limited; thus, growth was hindered and the substrate accumulated. Through these simulations, two types of heterogeneities could be identified, both of which are important to consider in process development. First, there is the spatial aspect, meaning that at any given time, there will be varying substrate and oxygen availabilities throughout the vessel. Secondly, there is the temporal effect, i.e., as the fed-batch progresses, the volume and cell density increase, and these heterogeneities develop over time as a result. This is an important factor, as cells bring with them a certain “history” that is not determined only by the heterogeneities at that given time. The approach presented in this work did not fully cover this history, as the kinetic equations and parameters were static over time and did not change as a result of potential intracellular changes. In order to adequately cover these phenomena, the concept of microbial lifelines could be very valuable [12,40].
These simulations did not fully represent true industrial vessels, and therefore do not necessarily hold true for all scales. However, they do act as useful design tools for subsequent experimental designs. The validation of the estimated parameters showed that the compartmental outcome was robust to changes in the parameter estimation. Argumentation for these similar outcomes can most likely be found in the fact that the description of metabolism was kept relatively simple. All product formation was omitted from the kinetic equations, and only growth and maintenance were assumed. With only two distinct metabolic states, there was a limited sensitivity to the estimated parameters used across the different scales.
Thus, the first logical and insightful step would be to define more metabolic states and include terms that describe (by-) product formation. Ultimately, however, this will be achieved in small incremental steps, adding kinetic and metabolic data as they become available. Large-scale conditions will impose many additional stressors on the strain, which can in turn affect all parameters involved. These stressors are not just limited to oxygen and substrate availability; (hydrostatic) pressure, temperature, pH, and other transport and mixing phenomena will most certainly have their effect.
The main drawbacks of the presented compartmental method are the fixed bioreactor geometry and the mode of operation. The chosen bioreactor geometry, however, can be considered relatively standard, especially for larger volume processes. Much more flexibility lies in the selection of biological parameters, as the biomass concentration and kinetics can be altered. Little has been reported about industrial DO values and growth rates, as they are both process-dependent and often part of an industry secret. Therefore, the theoretical approach from this study can provide useful insights. Concrete values allow for a more rational design of laboratory experiments and, from a process development point of view, it is relevant to gain an understanding of when limitations occur.
The simulated values from compartmental modelling were used to frame a design space for strain characterization. In several continuous fermentations, it was observed that the transcriptomic and physiological response of Y. lipolytica to lower DO values was, to some extent, dependent on the growth rate of the cells. In this study, a strong contribution from principal component 2 was found to separate the transcriptomic results based on the set growth rate. Similarly, in S. cerevisiae, it has previously been reported that the growth rate has a large impact on the transcriptome, and that half of the transcriptome is affected by the specific growth rate [41]. Potentially, the increased maintenance at these lower growth rates could be an important contributor to these observed differences. Another relevant finding was that genes that were associated with a stress response were upregulated at lower growth rates [41]. A similar pattern of stress gene upregulation was seen in Escherichia coli at lower growth rates [42]. Hence, a similar hypothesis for Y. lipolytica could be that lower growth rates are more likely to induce a stress response. This finding could also explain why different studies with respect to the DO response of Y. lipolytica have reached different conclusions regarding morphological changes. In the slow-growing cells of Y. lipolytica, in a chemostat with a dilution rate of 0.032 h−1, low DO values of 1–2% led to filamentous growth, while higher DO levels of around 20% reversed the transition back to cells in their non-filamentous, yeast-like form [43]. In a chemostat with a dilution rate of 0.1 h−1, no morphological changes were observed when a low DO value (2%) was selected [28]. A differential gene expression analysis also revealed this dependency of the transcriptomic landscape on the selected growth rate. Altogether, these results underline the importance of understanding substrate and oxygen heterogeneities in industrial environments, as they can lead to a distribution of growth rates. Suboptimal growth rates can lead to unwanted stress responses and changes in metabolism that reduce the productivity of the bioreactor.
In this study, the main effect of low DO values was centered around the downregulation of the central carbon metabolism and transporter functionality. The central carbon metabolism was affected in multiple crucial locations, underlining the large impact of oxygen limitation. Though carbon was not depleted in the extracellular space, Y. lipolytica cells appeared to actively minimize fluxes through the central carbon metabolism. This raises the underlying question as to what regulatory events cause this downregulation. Research on S. cerevisiae suggests that heme plays a role in oxygen-sensing pathways by controlling the transcription of varying genes [44]. Further research also suggests that eukaryotes deploy so-called hypoxic signaling through increased reactive oxygen species (ROS) production [45]. The exact mechanisms in Y. lipolytica remain unknown, but more insights would allow for a better understanding of cellular regulation in industrial settings.
The relation between oxygen availability and differential gene expression is a dynamic interplay and does not show a simple on–off behavior. Therefore, it is hypothesized that there is not one distinct oxygen-limited and one oxidative metabolic state. A difference in gene expression was observed under conditions where oxygen was considered a non-limiting factor (at DO values of 5, 10, 25, and 50%). This is a crucial insight, as it suggests that cells can differentiate between the available oxygen concentrations and steer their transcription accordingly. Compared to many prokaryotic strains, little is known about the transcription regulatory network (TRN) in Y. lipolytica. As such, new insights into the potential sensing pathways interacting with the TRN are of great value to further develop Y. lipolytica as a production strain.
The experiments were performed in continuous cultivations with constant values. As a result, one should be careful when translating these results to what might happen in response to the constant fluctuating DO environments that are observed in a large-scale bioreactor. The response of the cells to transient fluctuations is likely more relevant, and experiments assessing those conditions could prove very useful. Further research efforts could therefore focus on obtaining a higher resolution understanding of the cellular response over both a single and repeated oscillation, thereby also focusing on unraveling the regulatory mechanisms deployed under those conditions. Relevant experimental designs could be built on previous studies, i.e., by using appropriate scale-down simulators such as the STR–STR(–STR) or STR–PFR systems [18,46,47,48]. Additionally, the development of single multicompartmental bioreactors would allow for the recreation of heterogeneities in a single vessel, thereby decreasing the experimental complexity of these studies [49,50].
5. Conclusions
In this study, a framework was demonstrated that bridges process modelling, fermentation engineering, and bioinformatics, thereby streamlining bioprocess development. This showcases how an interdisciplinary approach can help in predicting what conditions a production strain can be exposed to and how these conditions could reduce the process performance. By combining strain-specific kinetic information with a compartmentalized industrial bioreactor understanding, bioreactor heterogeneities and metabolic regimes can be predicted. This information is not only useful for searching for the boundaries of a given system, but it also acts as a design aid for strain characterization. Concrete simulated industrial values served as a clear guideline in experimental design. Continuous cultures in the range of relevant conditions provided a baseline understanding of Y. lipolytica’s behavior. The predicted metabolic regimes could enable many more detailed experiments under oscillating conditions. Specific physiological and transcriptional responses to relevant oxygen concentrations can be obtained, thereby further supporting the development of Y. lipolytica as a fermenterphile for an industrial-scale bioprocess.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/fermentation9010074/s1, File S1: MCMC chains, simulations and correlation matrices; File S2: Parameter estimation, including multiple DO values; File S3: Highly weighted genes in PCA.
Author Contributions
Conceptualization, S.S., G.S. and A.A.J.K.; methodology, S.S., G.S., S.Ø. and A.A.J.K.; software, S.Ø. and A.A.J.K.; validation, S.Ø. and A.A.J.K.; formal analysis, S.Ø. and A.A.J.K.; investigation, S.S., G.S., S.Ø. and A.A.J.K.; resources, S.S. and G.S.; data curation, A.A.J.K.; writing—original draft preparation, A.A.J.K.; writing—review and editing, S.S., G.S., S.Ø. and A.A.J.K.; visualization, A.A.J.K.; supervision, S.S. and G.S.; project administration, S.S.; funding acquisition, S.S. and A.A.J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Novo Nordisk Foundation within the framework of the Fermentation-based Biomanufacturing Initiative (FBM), grant number NNF17SA0031362 and through NNF20CC0035580.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All RNA-seq. data has been uploaded to the Sequence Read Archive (SRA) and is further described under BioProject number PRJNA906726.
Acknowledgments
The authors want to thank Gisela Nadal-Rey for sharing the Matlab scripts on the dynamic compartmental modelling as well as the compartmentalization of the different filling volumes based on CFD. We thank the Yeast Metabolic Engineering group at the Novo Nordisk Foundation Center for Biosustainability for providing the W29 strain used in this research. Figure 1 was made through BioRender.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lara, A.R.; Galindo, E.; Ramírez, O.T.; Palomares, L.A. Living with heterogeneities in bioreactors. Mol. Biotechnol. 2006, 34, 355–381. [Google Scholar] [CrossRef]
- Nadal-Rey, G.; McClure, D.D.; Kavanagh, J.M.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Understanding gradients in industrial bioreactors. Biotechnol. Adv. 2021, 46, 107660. [Google Scholar] [CrossRef]
- Neubauer, P.; Junne, S. Scale-down simulators for metabolic analysis of large-scale bioprocesses. Curr. Opin. Biotechnol. 2010, 21, 114–121. [Google Scholar] [CrossRef]
- Heins, A.L.; Weuster-Botz, D. Population heterogeneity in microbial bioprocesses: Origin, analysis, mechanisms, and future perspectives. Bioprocess Biosyst. Eng. 2018, 41, 889–916. [Google Scholar] [CrossRef]
- Wehrs, M.; Tanjore, D.; Eng, T.; Lievense, J.; Pray, T.R.; Mukhopadhyay, A. Engineering Robust Production Microbes for Large-Scale Cultivation. Trends Microbiol. 2019, 27, 524–537. [Google Scholar] [CrossRef]
- Noorman, H.J.; Heijnen, J.J. Biochemical engineering’s grand adventure. Chem. Eng. Sci. 2017, 170, 677–693. [Google Scholar] [CrossRef]
- Tajsoleiman, T.; Spann, R.; Bach, C.; Gernaey, K.V.; Huusom, J.K.; Krühne, U. A CFD based automatic method for compartment model development. Comput. Chem. Eng. 2019, 123, 236–245. [Google Scholar] [CrossRef]
- Bisgaard, J.; Zahn, J.A.; Tajsoleiman, T.; Rasmussen, T.; Huusom, J.K.; Gernaey, K. V Data-based dynamic compartment model: Modeling of E. coli fed-batch fermentation in a 600 m3 bubble column. J. Ind. Microbiol. Biotechnol. 2022, 49, 21. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.; Wang, G.; Deshmukh, A.T.; van Winden, W.A.; Chu, J.; van Gulik, W.M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Computational fluid dynamics simulation of an industrial P. chrysogenum fermentation with a coupled 9-pool metabolic model: Towards rational scale-down and design optimization. Chem. Eng. Sci. 2018, 175, 12–24. [Google Scholar] [CrossRef]
- Wang, G.; Tang, W.; Xia, J.; Chu, J.; Noorman, H.; van Gulik, W.M. Integration of microbial kinetics and fluid dynamics toward model-driven scale-up of industrial bioprocesses. Eng. Life Sci. 2015, 15, 20–29. [Google Scholar] [CrossRef]
- Schmidt, F.R. Optimization and scale up of industrial fermentation processes. Appl. Microbiol. Biotechnol. 2005, 68, 425–435. [Google Scholar] [CrossRef]
- Blöbaum, L.; Haringa, C.; Grünberger, A. Microbial lifelines in bioprocesses: From concept to application. Biotechnol. Adv. 2023, 62, 108071. [Google Scholar] [CrossRef]
- Straathof, A.J.J.; Wahl, S.A.; Benjamin, K.R.; Takors, R.; Wierckx, N.; Noorman, H.J. Grand Research Challenges for Sustainable Industrial Biotechnology. Trends Biotechnol. 2019, 37, 1042–1050. [Google Scholar] [CrossRef]
- Coelho, M.A.Z.; Amaral, P.F.F.; Belo, I. Yarrowia lipolytica: An Industrial Workhorse; Formatex Research Center: Badajoz, Spain, 2010. [Google Scholar]
- Nicaud, J.M. Yarrowia lipolytica. Yeast 2012, 29, 409–418. [Google Scholar] [CrossRef]
- Kitano, H. Biological robustness. Nat. Rev. Genet. 2004, 5, 826–837. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E.; Santos, V.E.; Merchuk, J.C. Oxygen uptake rate in microbial processes: An overview. Biochem. Eng. J. 2010, 49, 289–307. [Google Scholar] [CrossRef]
- Janoska, A.; Buijs, J.; van Gulik, W.M. Predicting the influence of combined oxygen and glucose gradients based on scale-down and modelling approaches for the scale-up of penicillin fermentations. Process Biochem. 2023, 124, 100–112. [Google Scholar] [CrossRef]
- Andrews, S. FastQC: A Quality Control Tool for High Throughput Sequence Data; Babraham Bioinformatics, Babraham Institute: Cambridge, UK, 2010. [Google Scholar]
- Dobin, A.; Davis, C.A.; Schlesinger, F.; Drenkow, J.; Zaleski, C.; Jha, S.; Batut, P.; Chaisson, M.; Gingeras, T.R. STAR: Ultrafast universal RNA-seq aligner. Bioinformatics 2013, 29, 15–21. [Google Scholar] [CrossRef]
- Liao, Y.; Smyth, G.K.; Shi, W. featureCounts: An efficient general purpose program for assigning sequence reads to genomic features. Bioinformatics 2014, 30, 923–930. [Google Scholar] [CrossRef]
- Love, M.I.; Huber, W.; Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014, 15, 550. [Google Scholar] [CrossRef]
- Young, M.D.; Wakefield, M.J.; Smyth, G.K.; Oshlack, A. Gene ontology analysis for RNA-seq: Accounting for selection bias. Genome Biol. 2010, 11, R14. [Google Scholar] [CrossRef]
- Lubuta, P.; Workman, M.; Kerkhoven, E.J.; Workman, C.T. Investigating the Influence of Glycerol on the Utilization of Glucose in Yarrowia lipolytica Using RNA-Seq-Based Transcriptomics. G3 Genes Genomes Genet. 2019, 9, 4059–4071. [Google Scholar] [CrossRef]
- Magnan, C.; Yu, J.; Chang, I.; Jahn, E.; Kanomata, Y.; Wu, J.; Zeller, M.; Oakes, M.; Baldi, P.; Sandmeyer, S. Sequence Assembly of Yarrowia lipolytica Strain W29/CLIB89 Shows Transposable Element Diversity. PLoS ONE 2016, 11, e0162363. [Google Scholar] [CrossRef]
- Sin, G.; Gernaey, K.V.; Lantz, A.E. Good modeling practice for PAT applications: Propagation of input uncertainty and sensitivity analysis. Biotechnol. Prog. 2009, 25, 1043–1053. [Google Scholar] [CrossRef]
- Sin, G.; Gernaey, K.V. Data Handling and Parameter Estimation. Exp. Methods Wastewater Treat. 2016, 9781780404, 201–234. [Google Scholar]
- Timoumi, A.; Bideaux, C.; Guillouet, S.E.; Allouche, Y.; Molina-Jouve, C.; Fillaudeau, L.; Gorret, N. Influence of oxygen availability on the metabolism and morphology of Yarrowia lipolytica: Insights into the impact of glucose levels on dimorphism. Appl. Microbiol. Biotechnol. 2017, 101, 7317–7333. [Google Scholar] [CrossRef]
- Al, R.; Behera, C.R.; Zubov, A.; Gernaey, K.V.; Sin, G. Meta-modeling based efficient global sensitivity analysis for wastewater treatment plants—An application to the BSM2 model. Comput. Chem. Eng. 2019, 127, 233–246. [Google Scholar] [CrossRef]
- Nadal-Rey, G.; McClure, D.D.; Kavanagh, J.M.; Cassells, B.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Development of dynamic compartment models for industrial aerobic fed-batch fermentation processes. Chem. Eng. J. 2021, 420, 130402. [Google Scholar] [CrossRef]
- Moeller, L.; Strehlitz, B.; Aurich, A.; Zehnsdort, A.; Bley, T. Optimization of Citric Acid Production from Glucose by Yarrowia lipolytica. Eng. Life Sci. 2007, 7, 504–511. [Google Scholar] [CrossRef]
- Beopoulos, A.; Cescut, J.; Haddouche, R.; Uribelarrea, J.L.; Molina-Jouve, C.; Nicaud, J.M. Yarrowia lipolytica as a model for bio-oil production. Prog. Lipid Res. 2009, 48, 375–387. [Google Scholar] [CrossRef]
- Timoumi, A.; Cléret, M.; Bideaux, C.; Guillouet, S.E.; Allouche, Y.; Molina-Jouve, C.; Fillaudeau, L.; Gorret, N. Dynamic behavior of Yarrowia lipolytica in response to pH perturbations: Dependence of the stress response on the culture mode. Appl. Microbiol. Biotechnol. 2017, 101, 351–366. [Google Scholar] [CrossRef] [PubMed]
- Theobald, U.; Mailinger, W.; Baltes, M.; Rizzi, M.; Reuss, M. In Vivo Analysis of Metabolic Dynamics in Saccharomyces cerevisiae: I. Experimental Observations. Biotechnol. Bioeng. 1997, 55, 305–316. [Google Scholar] [CrossRef]
- Bellou, S.; Triantaphyllidou, I.E.; Mizerakis, P.; Aggelis, G. High lipid accumulation in Yarrowia lipolytica cultivated under double limitation of nitrogen and magnesium. J. Biotechnol. 2016, 234, 116–126. [Google Scholar] [CrossRef] [PubMed]
- Beopoulos, A.; Nicaud, J.-M.; Gaillardin, C. An overview of lipid metabolism in yeasts and its impact on biotechnological processes. Appl. Microbiol. Biotechnol. 2011, 90, 1193–1206. [Google Scholar] [CrossRef]
- Workman, M.; Holt, P.; Thykaer, J. Comparing cellular performance of Yarrowia lipolytica during growth on glucose and glycerol in submerged cultivations. AMB Express 2013, 3, 58. [Google Scholar] [CrossRef]
- Lesage, J.; Timoumi, A.; Cenard, S.; Lombard, E.; Lee, H.L.T.; Guillouet, S.E.; Gorret, N. Accelerostat study in conventional and microfluidic bioreactors to assess the key role of residual glucose in the dimorphic transition of Yarrowia lipolytica in response to environmental stimuli. New Biotechnol. 2021, 64, 37–45. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Aggelis, G. Modelling aspects of the biotechnological valorization of raw glycerol: Production of citric acid by Yarrowia lipolytica and 1,3-propanediol by Clostridium butyricum. J. Chem. Technol. Biotechnol. 2003, 78, 542–547. [Google Scholar] [CrossRef]
- Lapin, A.; Müller, D.; Reuss, M. Dynamic behavior of microbial populations in stirred bioreactors simulated with Euler-Lagrange methods: Traveling along the lifelines of single cells. Ind. Eng. Chem. Res. 2004, 43, 4647–4656. [Google Scholar] [CrossRef]
- Regenberg, B.; Grotkjær, T.; Winther, O.; Fausbøll, A.; Åkesson, M.; Bro, C.; Hansen, L.K.; Brunak, S.; Nielsen, J. Growth-rate regulated genes have profound impact on interpretation of transcriptome profiling in Saccharomyces cerevisiae. Genome Biol. 2006, 7, R107. [Google Scholar] [CrossRef]
- Ihssen, J.; Egli, T. Specific growth rate and not cell density controls the general stress response in Escherichia coli. Microbiology 2004, 150, 1637–1648. [Google Scholar] [CrossRef]
- Bellou, S.; Makri, A.; Triantaphyllidou, I.-E.; Papanikolaou, S.; Aggelis, G. Morphological and metabolic shifts of Yarrowia lipolytica induced by alteration of the dissolved oxygen concentration in the growth environment. Microbiology 2014, 160, 807–817. [Google Scholar] [CrossRef] [PubMed]
- Kwast, K.E.; Burke, P.V.; Poyton, R.O. Oxygen sensing and the transcriptional regulation of oxygen-responsive genes in yeast. J. Exp. Biol. 1998, 201, 1177–1195. [Google Scholar] [CrossRef] [PubMed]
- Castello, P.R.; David, P.S.; McClure, T.; Crook, Z.; Poyton, R.O. Mitochondrial cytochrome oxidase produces nitric oxide under hypoxic conditions: Implications for oxygen sensing and hypoxic signaling in eukaryotes. Cell Metab. 2006, 3, 277–287. [Google Scholar] [CrossRef]
- Buchholz, J.; Graf, M.; Freund, A.; Busche, T.; Kalinowski, J.; Blombach, B.; Takors, R. CO2/HCO3—Perturbations of simulated large scale gradients in a scale-down device cause fast transcriptional responses in Corynebacterium glutamicum. Appl. Microbiol. Biotechnol. 2014, 98, 8563–8572. [Google Scholar] [PubMed]
- Ankenbauer, A.; Schäfer, R.A.; Viegas, S.C.; Pobre, V.; Voß, B.; Arraiano, C.M.; Takors, R. Pseudomonas putida KT2440 is naturally endowed to withstand industrial-scale stress conditions. Microb. Biotechnol. 2020, 13, 1145–1161. [Google Scholar]
- Risager Wright, N.; Rønnest, N.P.; Thykaer, J. Scale-down of continuous protein producing Saccharomyces cerevisiae cultivations using a two-compartment system. Biotechnol. Prog. 2016, 32, 152–159. [Google Scholar] [CrossRef]
- Gaugler, L.; Mast, Y.; Fitschen, J.; Hofmann, S.; Schlüter, M.; Takors, R. Scaling-down biopharmaceutical production processes via a single multi-compartment bioreactor (SMCB). Eng. Life Sci. 2022, 23, e2100161. [Google Scholar] [CrossRef]
- Schilling, B.M.; Pfefferle, W.; Bachmann, B.; Leuchtenberger, W.; Deckwer, W.-D. A Special Reactor Design for Investigations of Mixing Time Effects in a Scaled-Down Industrial L-Lysine Fed-Batch Fermentation Process. Biotechnol. Bioeng. 1999, 64, 599–606. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).