Abstract
A novel 2D carbon allotrope, pentagraphyne (PG-yne), was introduced in a recent theoretical study. This unique structure is derived from pentagraphene by incorporating acetylenic linkages between sp and sp hybridized carbon atoms. Given its intriguing electronic and structural properties, it is imperative to investigate the mechanical characteristics and thermal responses of PG-yne in both monolayer and nanotube configurations, which encompass different chiralities and diameters. We conducted fully atomistic reactive molecular dynamics (MD) simulations employing the ReaxFF potential to address these aspects. Our findings reveal that Young’s modulus of PG-yne monolayers stands at approximately 51 GPa at room temperature. In contrast, for the studied nanotubes, regardless of their chirality, it hovers around 45 GPa. Furthermore, our observations indicate that PG-yne-based systems feature an extensive and relatively flat plastic region before reaching the point of total fracture, irrespective of their topology. Regarding their thermal properties, we identified a melting point at approximately 3600 K, accompanied by a phase transition around 1100 K.
1. Introduction
Two-dimensional (2D) carbon-based materials have garnered significant attention owing to their exceptional physical and chemical properties, which have found utility in the realm of flat electronics []. Among these materials, graphene emerges as one of the most prominent choices []. Graphene exhibits remarkable characteristics, comprising a single layer of carbon atoms arranged in a hexagonal lattice, including outstanding electrical conductivity, robust mechanical strength, and excellent thermal properties [,]. The combination of these properties positions graphene as an up-and-coming candidate for a diverse array of applications, encompassing electronics [], energy storage [], and sensor technology [,].
Several other 2D carbon allotropes, such as -graphyne [], monolayers of biphenylene [], amorphous carbon [], and fullerene networks [], have been successfully synthesized. Despite these achievements, ongoing efforts are focused on creating new materials that can overcome certain limitations associated with graphene. Notably, graphene’s absence of an electronic bandgap hinders its application in digital devices, and researchers are actively seeking alternatives to address this issue.
One study introduced the concept of pentagraphene (PG), a material entirely composed of pentagonal carbon rings arranged in a pattern reminiscent of Cairo pentagonal tiling []. This unique material offers a compelling combination of high stability, a negative Poisson’s ratio, and anisotropic conductivity. It possesses a semiconducting and indirect band gap measuring 3.25 eV, along with Young’s modulus and Poisson’s ratio values of approximately 263.8 GPa·nm and −0.068, respectively. Although the synthesis of PG has not yet been realized, its innovative properties have sparked further research to develop new materials with similar topological features. These efforts involve fused pentagonal rings, which aim to retain the attractive properties of PG.
A recent theoretical study introduced a novel 2D carbon allotrope named pentagraphyne (PG-yne) []. In comparison to other graphyne variants, including experimentally synthesized graphyne monolayers [] and graphdiyne [], PG-yne exhibits greater thermodynamic stability and energy favorability. It derives from PG by introducing acetylenic linkages between sp and sp hybridized carbon atoms, much like graphynes originate from graphene [].
Computational calculations have confirmed PG-yne’s dynamic, thermal, and mechanical stability, enabling it to withstand temperatures of up to 1000 K []. Furthermore, PG-yne exhibits inherent semiconducting properties, characterized by an electronic bandgap of approximately 1.0 eV, which can be fine-tuned by applying strain. These exceptional attributes drive our comprehensive exploration of PG-yne’s mechanical properties and fracture patterns to broaden the understanding of its potential applications and inspire further investigations into its synthesis.
In this study, we have conducted fully atomistic reactive molecular dynamics (MD) simulations employing the ReaxFF force field. Our primary objective was to investigate the mechanical properties, fracture patterns, and thermal behavior of PG-yne monolayers and nanotubes. Our simulations encompassed a monolayer and spanned a range of tube diameters and chiralities within the PG-yne system. At room temperature, we determined Young’s modulus of the monolayers to be approximately 50 GPa. The nanotubes considered in this study exhibited values hovering around 45 GPa. The well-known impact of rising temperature on the elastic constants, as reported in existing literature [], was also evident in our findings. A noteworthy observation emerged after subjecting both PG-yne and PG-yneNTs and PG-yneNTs to specific strain levels. In each case, a distinct flat plastic region was between the elastic and fully fractured areas, brought about by a phase transition within PG-yne. This phase transition led to a transformation of the material into an amorphous graphyne-like structure. A comparable transformation was observed when increasing the temperature. Under a constant temperature ramp, the system converted at around 1100 K, completely melting the structure at approximately 3600 K.
2. Methodology
To explore the mechanical properties and fracture patterns of PG-yne monolayers and PG-yneNTs, we conducted fully atomistic reactive molecular dynamics (MD) simulations. These simulations were carried out using the LAMMPS code [] in conjunction with the ReaxFF potential []. The ReaxFF potential is widely employed to study nanostructures’ mechanical properties due to its capability to model atomic-level bond formation and breakage []. In our simulation setup, we utilized a PG-yne supercell model (refer to Figure 1). For the nanotubes, we explored two distinct chirality types, namely and , as depicted in Figure 1.
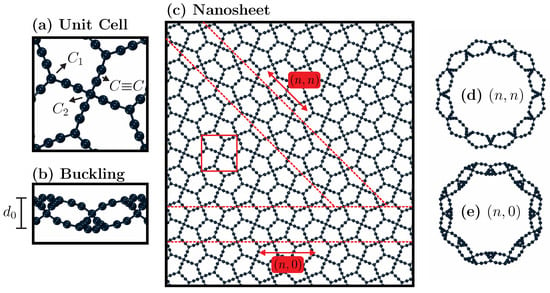
Figure 1.
The schematic representations of the systems under investigation are presented here. In Panel (a), the unit cell comprises 26 atoms. Within this unit cell, one can observe particles exhibiting different hybridizations, including sp (involved in bonds), sp (type- atoms), and sp (type- atoms). This unit cell is square, with sides measuring 9.85 Å. In Panel (b), the buckling of the system is highlighted, denoted as , and it has a value of 3.45 Å. Moving to Panel (c), we present the frontal view of the PG-yne nanosheet. The red square outlined by solid lines represents the unit cell, whereas the dashed lines indicate the two chiral directions we considered to form nanotubes: and . Frontal views are depicted in Panels (d,e) for the corresponding nanotubes for the respective chirality types.
We performed extensive tests of various force fields, including Tersoff [], AIREBO [], and two ReaxFF potentials [,]. Throughout these simulations, we encountered several challenges when attempting to model the system accurately. For instance, when using AIREBO, we observed a system collapse in the direction perpendicular to the applied uniaxial stress. On the other hand, applying the Tersoff force field led to deviations within the system during the equilibration simulation. After a thorough assessment, the force field presented in [] emerged as the most suitable choice among our explored options. This force field accurately represented triple bonds and the unique penta-graphene allotrope structure, allowing us to achieve the desired results.
In our computational modeling of PG-yneNTs, we establish the chiral vector, denoted as , as , where and represent the lattice vectors, and n and m are integers that dictate the chirality of the nanotube. The nanotube’s diameter, , is determined as . Furthermore, we establish the translational vector, , which is perpendicular to , and this is defined as , with and being integers derived from the inner product relationship . The length of the nanotube is represented as , and the chiral and translational vectors jointly define the nanotube’s unit cell. It is worth noting that because the PG-yne unit cell is square (), configurations labeled as and for PG-yneNTs are fundamentally equivalent, with the only distinction being a rotational difference.
Figure 1 provides an illustrative overview of the systems under investigation, emphasizing key elements relevant to their thermal and mechanical characteristics. In Figure 1a, we present the unit cell of the system, consisting of 26 atoms and featuring a symmetrical structure with a side length of 9.85 Å. Within PG-yne, acetylene linkages are introduced between sp hybridized () and sp hybridized () atoms. These acetylenes give rise to triple bonds of the sp type. When viewed from the side, PG-yne, much like pentagraphene, deviates from being perfectly flat. We denote the difference between the maximum and minimum values in the direction perpendicular to the 2D plane as . In calculations of the stress–strain curve, this value is added to the graphene thickness ( Å), making it an essential parameter. Figure 1c showcases the monolayer of PG-yne employed in this study. The red square denotes the unit cell. At the same time, the chiral directions for the nanotubes, namely and , are indicated by dashed red lines. Frontal views of these nanotube configurations are presented in items Figure 1d,e.
In the case of the 2D system, a supercell of dimensions was employed, with an area of 117.4 nm measuring 108.35 Å on each side, comprising a total of 3146 atoms. Periodic boundary conditions were applied for the x and y directions, and mirror boundary conditions for z. For the nanotubes, the systems , , and with diameters of 12.5, 25.0, and 37.6 Å, respectively, were considered. Furthermore, the , , and nanotubes, with diameters of 13.3, 26.6, and 35.5 Å, respectively, were also studied. These values were chosen to compare nanotubes with different chiralities and similar diameters. In the cases, where the unit cell coincides in terms of length with the 2D unit cell (9.85 Å), a supercell was considered, totaling 1144, 2288, and 3432 atoms for the , , and systems, respectively. The , , and systems have 1248, 2496, and 3328 atoms, respectively, with a total length of 111.44 Å in all cases. In all nanotubes, periodic boundary conditions were applied in the z-direction, with mirror boundary conditions in the x and y directions.
In our computational approach, we first minimized the energy of the PG-yne and PG-yneNTs systems. Subsequently, we coupled them to a thermostat chain for thermodynamic equilibrium. We performed constant NPT ensemble integration at null pressure and 300 K to ensure no remaining stress. We used a Nose/Hoover [] pressure barostat for 50 ps. Following this, we coupled all the systems in the canonical NVT ensemble for an additional 50 ps. This approach enabled the generation of sampled positions and velocities at room temperature. In all simulations, the time step was set to 0.05 fs.
For the study of thermal stability, after equilibration and thermalization at room temperature and zero pressure, the system is subjected to a temperature ramp using a canonical ensemble, ranging from 300 K to 7000 K over a 2 ns simulation, equivalent to a rate of 3.35 K/ps. To characterize the system’s response, considering the first law of thermodynamics, , it is possible to express the internal energy as a function of temperature and volume as:
In the case of the canonical ensemble, the volume is constant, i.e., the heat capacity can defined as , and so it helps identify phase transitions in the system when the energy response varies significantly with temperature.
To investigate the overall mechanical behavior of PG-yne and PG-yneNTs, we conducted tensile tests by stretching the systems until rupture. The tests were performed using a constant engineering tensile strain rate of /fs concerning the simulation box in the strain direction. An NPT ensemble was employed for the 2D case, maintaining zero pressure in the direction orthogonal to the strain direction, and an NVT ensemble was used for the 1D case, also varying the chirality ( and ). In this way, the strain rate was applied to PG-yne along the x-direction and to PG-yneNTs along the z-direction. We analyzed the stress–strain curves to extract the elastic properties of each structure at room temperature. Furthermore, we described bond breaks and defined fracture patterns of the PG-yne and PG-yneNTs structures by analyzing the snapshots from MD simulations.
In the generation of the stress–strain curves, we calculated the percentage of strain and the stress tensor divided by the volume, where a takes on values x or z, depending on whether it’s a 2D or 1D system []. In the two-dimensional case, the volume is given by , where , with representing the system’s buckling, as the thickness of graphene, and and denotes the lengths in x- and y-direction, respectively. In the 1D system, , with the radius R, and length in z-direction. The term is defined as:
where is the neighbor of atom i, and , are the positions of the two atoms in the pairwise interaction, and and are the forces resulting of this pairwise interaction. , , , and are the number of bonds, angles, dihedrals, and impropers of i-atom, respectively. To visualize the MD snapshots, we used the VMD software version 1.9.4 [].
3. Results
We start the discussion by analyzing the PG-yne structure after optimization at 0 K, equilibration at zero pressure and room temperature, and thermalization at constant volume at room temperature. In Figure 1a, the unit cell of PG-yne contains 26 atoms, and the bond lengths are distributed essentially in three values. In the case of the bonds between acetylene atoms, there is a bond length of approximately 1.22 Å, and these bonds are known for their sp hybridization. In PG-yne, the bonds involving atoms denoted as and have bond lengths of around 1.45 Å and 1.54 Å.
Graphyne-like systems have an interesting aspect: replacing a bond with an acetylene bond leads to a more energetically favorable atomic angle rearrangement []. Here, the angles centered on atoms of type- are close to 120, whereas the angles centered on type- atoms are approximately 108, typical values for sp and sp hybridization, respectively. These results are consistent with the original work [] and indicate the structural stability of PG-yne with the coexistence of bonds involving sp and sp hybridized carbon atoms. On the other hand, the two types of nanotubes, and , exhibit almost the same configuration, with the expected difference in the widening of the outer bonds, compensated by the narrowing of the inner bonds. The angles are only slightly altered.
A characteristic of PG, which extends to PG-yne, is the presence of a buckling structure (see Figure 1b). After the system equilibration, Å. Additionally, a 50 ps simulation was conducted with the finite PG-yne monolayer using a canonical ensemble at room temperature to verify the integrity of the buckling in the case of a non-periodic system. The value of remained unchanged.
As mentioned in the previous section, we conducted a temperature ramp simulation to explore the thermal properties of PG-yne. This simulation considers the thermally equilibrated system at room temperature and zero pressure as input. The total simulation time is 2 ns, with the temperature incrementing at a rate of 3.35 K/ps concerning the system’s thermal bath. We monitored the system’s temperature and total energy during this simulation, computing these values following the equipartition theorem.
Subsequently, we established a linear fit between temperature and time, which allowed us to confirm the correlation between temperature and energy. This relationship is illustrated by the green curve in Figure 2. Notably, there are two shifts in the energy variation rate with increasing temperature: the first corresponds to a phase change in the 2D system’s topology. In contrast, the second indicates the transition to a gaseous state.
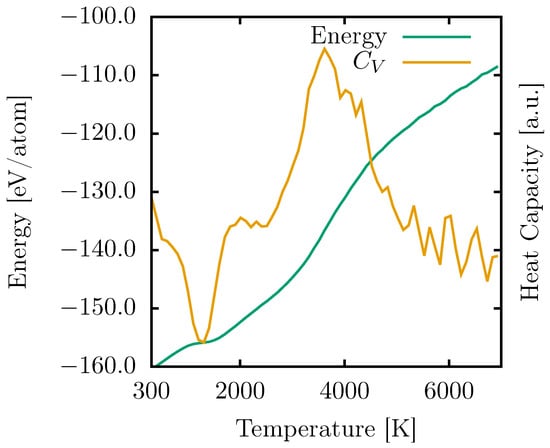
Figure 2.
Response of the total energy (green curve) and heat capacity (, yellow curve) of PG-yne as a function of increasing temperature from 300 to 7000 K.
We quantified these values by employing Equation (1), which calculates the heat capacity by assessing the rate of energy change concerning temperature within a system held at a constant volume. The results are depicted in Figure 2 (illustrated by the orange curve).
The observed PG-yne phase transition manifests as a transformation into an amorphous graphyne-like system, taking place around 1100 K. Consequently, the resulting topology proves to be more energetically stable than PG-yne when temperatures exceed 1000 K. The most substantial shift in energy occurs at 3616 K when the original PG-yne transitions to a gaseous state. This behavior aligns with that of PG, which exhibits two notable phase changes: the first at 1593 K, resulting in a more stable configuration within that temperature range, and the second at 4944 K, signifying the onset of the melting process [].
Figure 3 provides a visual representation of selected snapshots depicting the behavior of the PG-yne monolayer throughout the heating simulation, as quantified in Figure 2. The system’s initial state was already thermally equilibrated at 300 K and maintained zero pressure in the x and y directions. As previously noted, the system undergoes a significant phase transition around 1100 K. Figure 3a captures the system’s state at 2000 K, portraying a discernible transformation. Many acetylene structures and atoms of type with sp hybridization remain intact. In contrast, those of type exhibiting sp hybridization have experienced bond breakage. This observation suggests that the latter group of atoms is less susceptible to the temperature increase in this particular system.
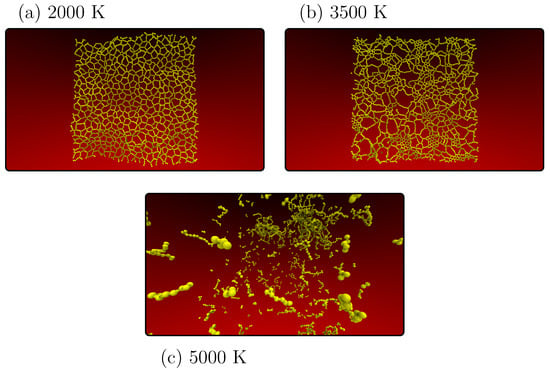
Figure 3.
Representative MD snapshots of the heating process of PG-yne monolayers at different temperatures: 2000 K (a), 3500 K (b), and 5000 K (c) to mark critical temperatures for phase transition in the lattice arrangement of the system.
In Figure 3b, as the system approaches the point of collapse (occurring at 3600 K), we observe a solid system characterized by a notable presence of linear atomic chains (LACs) and small graphene domains. This behavior can be attributed to the stability and proximity of sp hybridized atoms within the structure. Moving on to Figure 3c at 5000 K, we observe that the system has melted, resulting in multiple clusters comprising dispersed LACs scattered throughout the simulation box. At 7000 K, the system has transitioned into a gaseous state. See the supplementary material for more information on this process. Notably, beyond the initial phase transition up to 1000 K, the melting pattern resembles that of various other two-dimensional carbon allotropes [,]. Notably, the change in system topology does not significantly alter its response to increasing temperature.
Regarding the mechanical properties of PG-yne, Figure 4 presents the stress–strain curve for the 2D case. In these simulations, uniaxial stress is applied in the x direction, inducing deformation in the periodic box at a rate of fs. Given the system’s symmetry, a simulation with deformation in the y direction would yield analogous results. To prevent the accumulation of stress in the direction perpendicular to the strain, we used an NPT ensemble, ensuring zero pressure in the y direction is maintained.
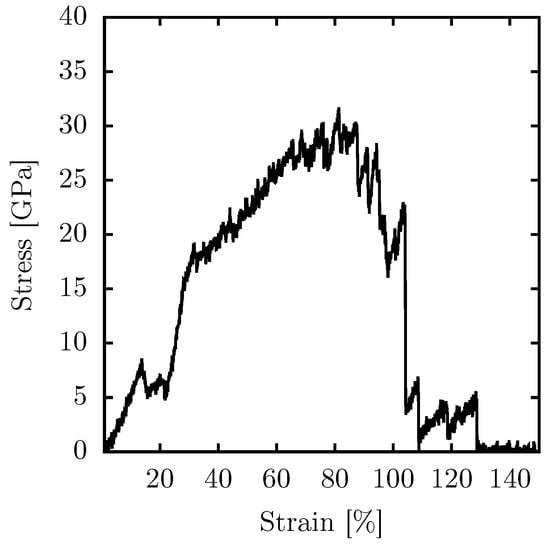
Figure 4.
Stress–strain curve for PG-yne monolayers at room temperature when subjected to uniaxial stress in the x direction, using an NPT ensemble.
In general, acetylene is typically associated with a rigid structure. However, it forms micropores within the lattice when it replaces bonds in 2D carbon allotropes characterized by sp and sp hybridization. This presence of micropores is known to reduce the overall rigidity of the materials. The specific case of PG-yne consists of rings containing 16 atoms. Given a buckling of 6.8 Å and a 1% strain, Young’s modulus of PG-yne is approximately 51 GPa. This value represents only one-tenth of the reported Young’s modulus for pure PG, which exhibits a much smaller buckling of 0.6 Å, measuring approximately 500 GPa. This value was calculated using both Density Functional Theory (DFT) [] and classical (reactive) MD [] approaches.
Similar to the scenario with temperature increase, a critical transformation in the system occurs with a relatively modest strain percentage of around 12%. At this stage, we observe the conversion to an amorphous graphyne-like system. Consequently, the elastic region of PG-yne is constrained to an approximate maximum of 12%. This limitation arises due to the implementation of the NPT approach, preventing stress accumulation in the y direction. This constraint prompts the system to reconfigure itself, averting persistent high-stress conditions. The system can endure significant strain before reaching complete fracture, accommodating up to 108% of strain. Beyond this point, up to 130% of strain, the system still encounters stress due to linear atomic chains (LACs) forming during rupture. The ultimate strength supported by the system approximates 32 GPa.
The adaptability of periodic 2D graphyne-type structures and their related mechanical properties have been examined regarding the stress–strain curve, as depicted in Figure 4. Complementing this, Figure 5 provides insights into the fracture patterns. In Figure 5a, we observe the system in an equilibrium state characterized by zero constant pressure. At this point, it has been thermally equilibrated to room temperature with no applied strain.
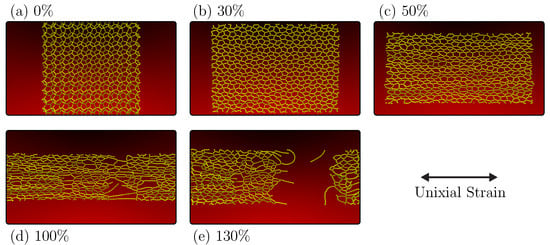
Figure 5.
Representative MD snapshots of the fracture pattern of the PG-yne monolayer with uniaxial tension applied in the x direction, while the y direction is stress-free, as obtained from the NPT ensemble. Panel (a) depicts the system thermalized and equilibrated at 300 K with no applied strain. Panels (b–e) show snapshots of the system with strains of 30%, 50%, 100%, and 130%, respectively.
In Figure 5b, a 30% strain is introduced to the system, leading to the conversion of the material into an amorphous graphyne-like structure. This transformation involves a distinct pattern of transitioning atoms of type with sp hybridization into atoms featuring sp hybridization. Additionally, the system loses its inherent buckling. This yielded product from PG-yne accumulates more significant stress than the original system, prompting the reorganization of bonds to prevent abrupt stress escalation.
Moving on to Figure 5c, one can note that the linear atomic chains (LACs) formed are increasingly aligned with the direction of strain, accompanied by the onset of a Poisson effect. This effect is marked by continuously reducing the simulation box’s dimensions in the y direction. At 100% strain (Figure 5d), the system takes on a highly porous quality characterized by extended LACs in the region that will eventually fracture entirely at 108%, as previously discussed. Finally, Figure 5e captures the system in a fully fractured state, marked by the rupture of the last remaining LAC connecting the system at 130%. Notably, when considering an NVT ensemble for the crack of this system (see Supplementary Material), the breakage occurs abruptly due to the accumulation of stress in the direction perpendicular to the applied strain. For more details about the PG-yne fracture process, see Supplementary Material.
The transition in the topology of PG-yne has a relatively modest impact on the system’s response to longitudinal strain. When simulating nanotubes, we maintained most parameters, except the ensemble, which was changed to NVT due to the one-dimensional nature of the system. Periodic boundary conditions were preserved in the z-direction. Figure 6 showcases two nanotubes with differing chiralities but similar diameters. In Figure 6a, we observe the PG-yneNT at 0% strain, with the system in equilibrium and thermally equilibrated. In Figure 6b, at 30% strain, we witness the same phase transition previously discussed for monolayers. This transition involves the disruption of the sp hybridization of type- atoms.

Figure 6.
Representative MD snapshots for the PG-yne nanotube deformation for chiralities (panels (a–d)) and (panels (e–h)). Both nanotubes have similar diameters and are shown at 0% strain (panels (a,e)), 30% strain (panels (b,f)), 50% strain (panels (c,g)), and at the specific fracture moments for each of them, which are 91.5% for PG-yneNT (d) and 73.5% for PG-yneNT (h).
Advancing to 50% strain Figure 6c, we note the alignment of linear atomic chains (LACs) with the direction of strain. Finally, in Figure 6d, at 91.5% strain, the system is on the verge of complete fracture, with only a few LACs remaining. The critical observation is the infinite nature of stress dissipation in the y-direction for monolayers. In contrast, despite their ability to adapt concerning diameter, nanotubes cannot as effectively accommodate changes in the direction perpendicular to the applied strain, particularly compared to the two-dimensional case. Consequently, despite a similar fracture pattern, nanotubes tend to fracture significantly earlier than the 2D case.
A similar pattern is evident when considering the PG-yneNT case. Figure 6e–g represent the system in equilibrium, the phase transition triggered by sp hybridization disruption, and the alignment of linear atomic chains (LACs) alongside the formation of increasing micropores. Figure 6h depicts the system with 73.5% strain, teetering on the brink of complete fracture following the emergence of LACs. In all these instances, the Poisson effect is observable, manifesting as a distinct reduction in tube diameter with increasing deformation.
In addition to the nanotube discussions presented earlier, Figure 7 provides stress–strain curves. The left panel illustrates the cases, whereas the right panel displays the cases. As mentioned, all systems employ 1% strain with a Å thickness. Young’s modulus for all systems is about 45 GPa in this case. The marginal variance compared to the monolayer can be attributed to the system’s topology, as it possesses limited capacity for adjustments in the direction perpendicular to the strain. Furthermore, within the study of PG-yneNTs’ mechanical properties, two distinct groups can be identified based on behavior.
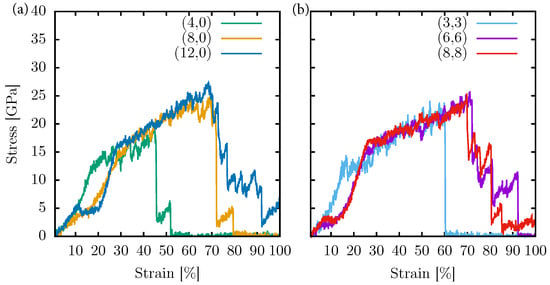
Figure 7.
Stress–strain curves for PG-yneNTs (a) and PG-yneNTs (b) with different diameters at room temperature. The NVT ensemble was considered with a longitudinal strain application.
An interesting observation for cases with smaller diameters is the topology change resulting from the disruption of sp hybridization. However, it is worth noting that the system’s stress does not immediately become flat after this transition, as observed in the monolayer case. In the case of PG-yneNT, the smaller diameter leads to a unique occurrence where the system collapses due to van der Waals interactions between the inner walls (see the Supplementary Material for a video of this dynamic process). This collapse is reversed when the stress surpasses the vdW forces involved, causing a surge in stress within the system, occurring around 10–20% of strain.
A similar situation occurs in the case of PG-yneNT, where the vdW interaction is even stronger, given the exceptionally narrow diameter of this nanotube. Due to their topology, specifically their narrow diameters, both nanotubes reach an ultimate strength of 18 GPa with a critical strain of 45% for PG-yneNT (green curve, left panel of Figure 7), and 22 GPa with a critical strain of 60% for PG-yneNT (cyan curve, right panel of Figure 7).
In the case of PG-yneNT systems (left panel of Figure 7), as the diameter increases, the fracture pattern becomes more akin to that of the monolayer. Specifically, the nanotube reaches an ultimate strength of 25 GPa. The nanotube achieves a similar 27 GPa, exhibiting a critical deformation of approximately 70%. In both cases, linear atomic chains (LACs) are formed until the system experiences complete rupture.
Notably, PG-yneNTs (right panel of Figure 7) similarly behave with larger diameters, showing nearly identical ultimate strength (26 GPa) and critical strain (72%). This observation underscores that the topology directly affects the elastic constants of the system due to the limited reorganization of atoms in the direction perpendicular to the strain. However, the fracture pattern remains almost identical across these systems. Detailed videos are available in the supplementary material for a comprehensive view of all these simulations.
4. Conclusions
In summary, our investigation relied on fully atomistic MD simulations using the ReaxFF potential to delve into the mechanical properties and fracture patterns of PG-yne and PG-yneNT systems. We explored a range of nanotube diameters and considered two distinct chiralities in our analyses. We examined the system’s response to temperature increases, uncovering two significant phase transitions. At approximately 1100 K, the sp hybridized bonds exhibited decreased stability, leading to the formation of atoms with sp bonds, which are more stable. This transformation significantly altered the system’s behavior as it approached higher temperatures. It resulted in an amorphous monolayer reminiscent of graphyne with sp and sp hybridization. Consequently, the system’s buckling was also affected. As the temperature climbed to 3600 K, the system transitioned from solid to gaseous.
Regarding mechanical properties, our observations consistently reveal that the structural topology of PG-yne, whether in the form of 2D nanotubes or 1D monolayers, influences their elastic constants. Despite this structural influence, both types of structures exhibit a parallel fracture pattern. Each system can withstand strains from 45% to 130% before reaching complete fracture. However, at around 10% strain, they undergo a phase transition akin to the transformation observed during the heating process. Consequently, the elastic region is comparatively limited.
The Young’s modulus for these systems falls within the range of 45–51 GPa, approximately one-tenth of the Young’s modulus for pure PG. This result is an anticipated result since PG-yne is inherently porous and comprises highly rigid acetylenic bonds. The ultimate strength for all cases does not exceed 30 GPa. The critical difference in the mechanical properties of these systems lies in their capacity to dissipate stress in the direction perpendicular to the applied strain. The monolayer is treated as an infinite system, allowing it to endure significantly higher critical deformation than tubular systems. Furthermore, it’s worth noting that the larger the tube, the more closely the system’s behavior resembles that of the monolayer.
Supplementary Materials
The following supporting information can be downloaded at: www.mdpi.com/article/10.3390/c9040110/s1, Video S1: Mechanical response of (3,3)PG-yneNT. Video S2: Mechanical response of (4,0)PG-yneNT. Video S3: Mechanical response of (6,6)PG-yneNT. Video S4: Mechanical response of (8,0)PG-yneNT. Video S5: Mechanical response of (8,8)PG-yneNT. Video S6: Mechanical response of (12,0)PG-yneNT. Video S7: Thermal Response of PG-yne.
Author Contributions
W.L.A.P.S., J.M.d.S. and W.H.d.S.B.: Data curation, Formal analysis, Methodology, Writing—original draft. L.A.R.J., D.S.G. and M.L.P.J.: Conceptualization, Supervision, Funding acquisition, Writing—review, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
Brazilian Research Councils CNPq, CAPES, FAPEPI, FAPDF, and FAPESP.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is available upon reasonable request to the authors.
Acknowledgments
This work received partial support from Brazilian agencies CAPES, CNPq, FAPDF, FAPESP, and FAPEPI. J.M.S and D.S.G thank the Center for Computational Engineering and Sciences at Unicamp for financial support through the FAPESP/CEPID Grant #2013/08293-7. L.A.R.J. acknowledges CAPES for partially financing this study—Finance Code 88887.691997/2022-00. CENAPAD-SP (Centro Nacional de Alto Desenpenho em São Paulo – Universidade Estadual de Campinas—UNICAMP) provided computational support for L.A.R.J, J.M.S and M.L.P.J (proj634, proj842, and proj960). W.H.S.B. and J.M.S were supported by Laboratório de Simulação Computacional Cajuína (LSCC) at Universidade Federal do Piauí. L.A.R.J thanks the financial support from Brazilian Research Council FAP-DF grant 00193.00001808/2022-71, FAPDF-PRONEM grant 00193.00001247/2021-20, and CNPq grants 350176/2022-1. M.L.P.J acknowledges the financial support from FAP-DF grant 00193-00001807/2023-16. L.A.R.J and M.L.P.J also thanks Núcleo de Computação de Alto Desempenho (NACAD) for computational facilities through the Lobo Carneiro supercomputer. This research also used computing resources and assistance from the John David Rogers Computing Center (CCJDR) in the Institute of Physics “Gleb Wataghin”, at the State University of Campinas.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Stoller, M.D.; Park, S.; Zhu, Y.; An, J.; Ruoff, R.S. Graphene-based ultracapacitors. Nano Lett. 2008, 8, 3498–3502. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, C.; Pan, Q.; Jin, Y.; Lyu, R.; Martinez, V.; Huang, S.; Wu, J.; Wayment, L.J.; Clark, N.A.; et al. Synthesis of γ-graphyne using dynamic covalent chemistry. Nat. Synth. 2022, 1, 449–454. [Google Scholar] [CrossRef]
- Fan, Q.; Yan, L.; Tripp, M.W.; Krejčí, O.; Dimosthenous, S.; Kachel, S.R.; Chen, M.; Foster, A.S.; Koert, U.; Liljeroth, P.; et al. Biphenylene network: A nonbenzenoid carbon allotrope. Science 2021, 372, 852–856. [Google Scholar] [CrossRef]
- Toh, C.T.; Zhang, H.; Lin, J.; Mayorov, A.S.; Wang, Y.P.; Orofeo, C.M.; Ferry, D.B.; Andersen, H.; Kakenov, N.; Guo, Z.; et al. Synthesis and properties of free-standing monolayer amorphous carbon. Nature 2020, 577, 199–203. [Google Scholar] [CrossRef]
- Hou, L.; Cui, X.; Guan, B.; Wang, S.; Li, R.; Liu, Y.; Zhu, D.; Zheng, J. Synthesis of a monolayer fullerene network. Nature 2022, 606, 507–510. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, J.; Wang, Q.; Chen, X.; Kawazoe, Y.; Jena, P. Penta-graphene: A new carbon allotrope. Proc. Natl. Acad. Sci. USA 2015, 112, 2372–2377. [Google Scholar] [CrossRef]
- Deb, J.; Paul, D.; Sarkar, U. Pentagraphyne: A new carbon allotrope with superior electronic and optical property. J. Mater. Chem. C 2020, 8, 16143–16150. [Google Scholar] [CrossRef]
- Gao, X.; Liu, H.; Wang, D.; Zhang, J. Graphdiyne: Synthesis, properties, and applications. Chem. Soc. Rev. 2019, 48, 908–936. [Google Scholar] [CrossRef] [PubMed]
- Desyatkin, V.G.; Martin, W.B.; Aliev, A.E.; Chapman, N.E.; Fonseca, A.F.; Galvão, D.S.; Miller, E.R.; Stone, K.H.; Wang, Z.; Zakhidov, D.; et al. Scalable synthesis and characterization of multilayer γ-graphyne, new carbon crystals with a small direct band gap. J. Am. Chem. Soc. 2022, 144, 17999–18008. [Google Scholar] [CrossRef]
- Andrievski, R.A.; Glezer, A.M. Strength of nanostructures. Phys.-Uspekhi 2009, 52, 315. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Van Duin, A.C.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Mueller, J.E.; van Duin, A.C.; Goddard, W.A., III. Development and validation of ReaxFF reactive force field for hydrocarbon chemistry catalyzed by nickel. J. Phys. Chem. C 2010, 114, 4939–4949. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Physics Condens. Matter 2002, 14, 783. [Google Scholar] [CrossRef]
- Chenoweth, K.; Van Duin, A.C.; Goddard, W.A. ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef]
- Ashraf, C.; Van Duin, A.C. Extension of the ReaxFF combustion force field toward syngas combustion and initial oxidation kinetics. J. Phys. Chem. A 2017, 121, 1051–1068. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.J.; Holian, B.L. The nose–hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Oliveira, T.A.; Silva, P.V.; Saraiva-Souza, A.; da Silva Filho, J.G.; Girão, E.C. Structural and electronic properties of nonconventional α-graphyne nanocarbons. Phys. Rev. Mater. 2022, 6, 016001. [Google Scholar] [CrossRef]
- Fu, R.; Xu, Y.; Liu, Y.; Lin, Y.; Xu, K.; Chang, Y.; Fu, Y.; Zhang, Z.; Wu, J. Thermally induced hex-graphene transitions in 2D carbon crystals. Nanotechnol. Rev. 2022, 11, 1101–1114. [Google Scholar] [CrossRef]
- Júnior, M.P.; da Cunha, W.; Giozza, W.; de Sousa Junior, R.; Junior, L.R. Irida-Graphene: A New 2D Carbon Allotrope. FlatChem 2023, 37, 100469. [Google Scholar] [CrossRef]
- Júnior, M.L.P.; Júnior, L.A.R. Thermomechanical insight into the stability of nanoporous graphene membranes. FlatChem 2020, 24, 100196. [Google Scholar]
- Li, X.; Zhang, S.; Wang, F.Q.; Guo, Y.; Liu, J.; Wang, Q. Tuning the electronic and mechanical properties of penta-graphene via hydrogenation and fluorination. Phys. Chem. Chem. Phys. 2016, 18, 14191–14197. [Google Scholar] [CrossRef]
- Le, M.Q. Mechanical properties of penta-graphene, hydrogenated penta-graphene, and penta-CN2 sheets. Comput. Mater. Sci. 2017, 136, 181–190. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).