Carbide-Derived Carbons: WAXS and Raman Spectra for Detailed Structural Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Carbide-Derived Carbons
2.2. Wide-Angle X-Ray Scattering Measurements
2.3. Raman Spectroscopy
3. Results
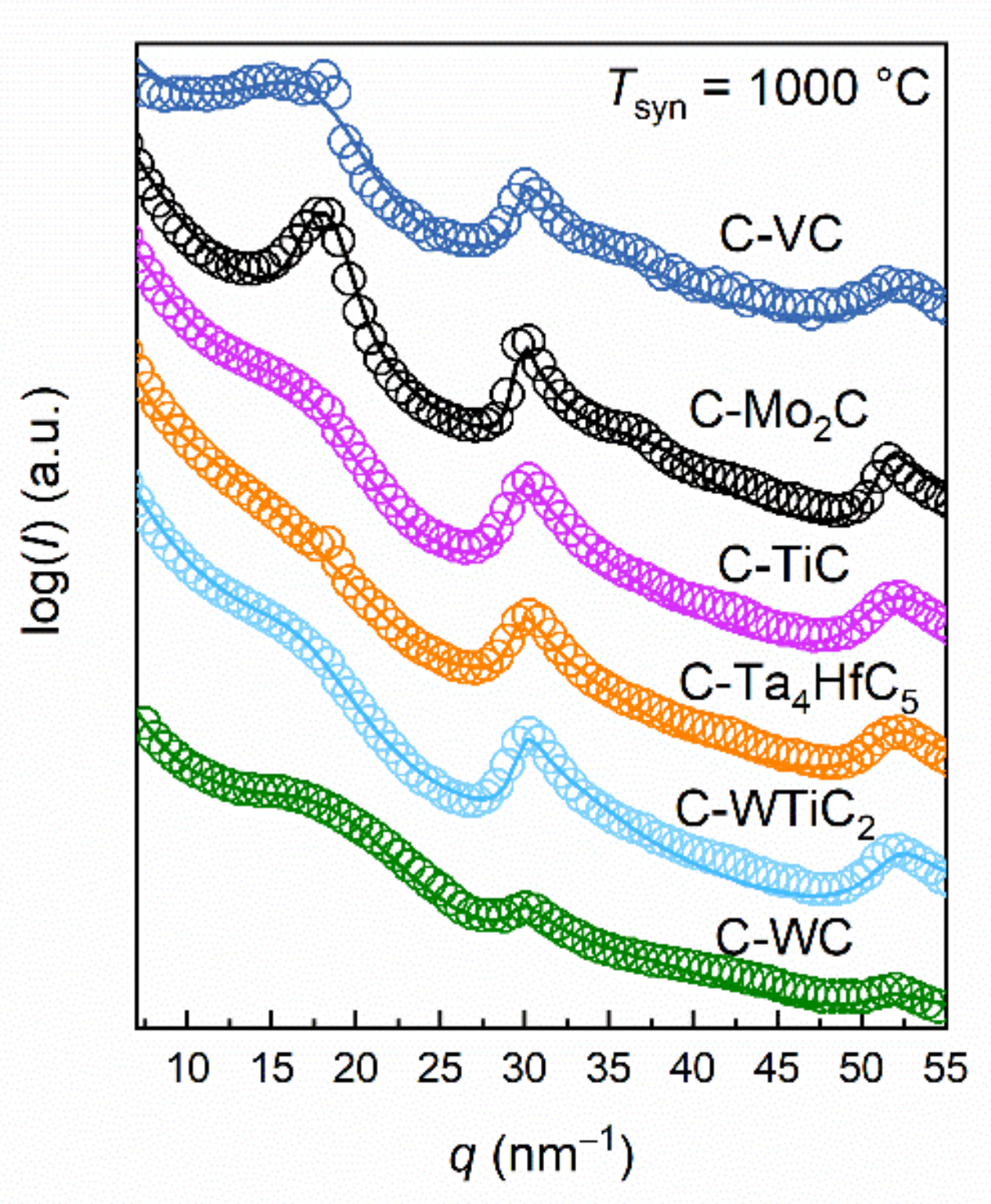
3.1. Wide-Angle X-Ray Scattering
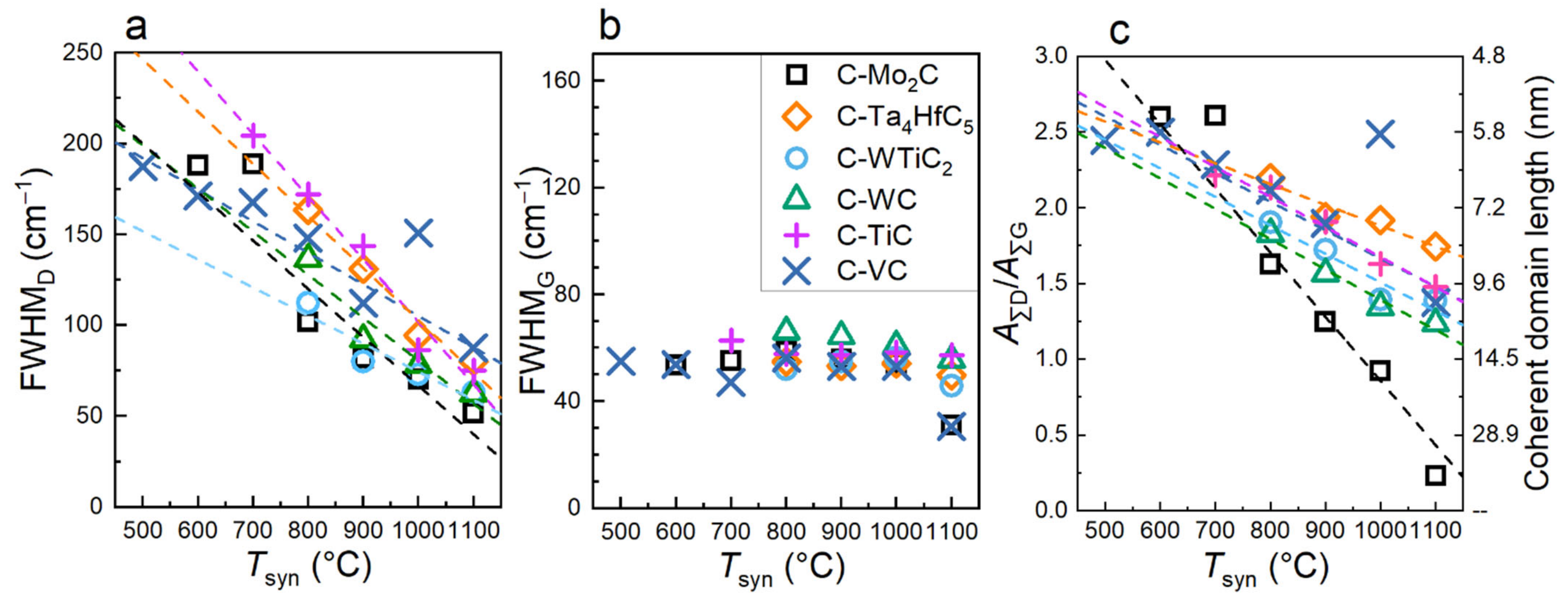
3.2. The Raman Spectra of CDCs: The Stages of Graphitization
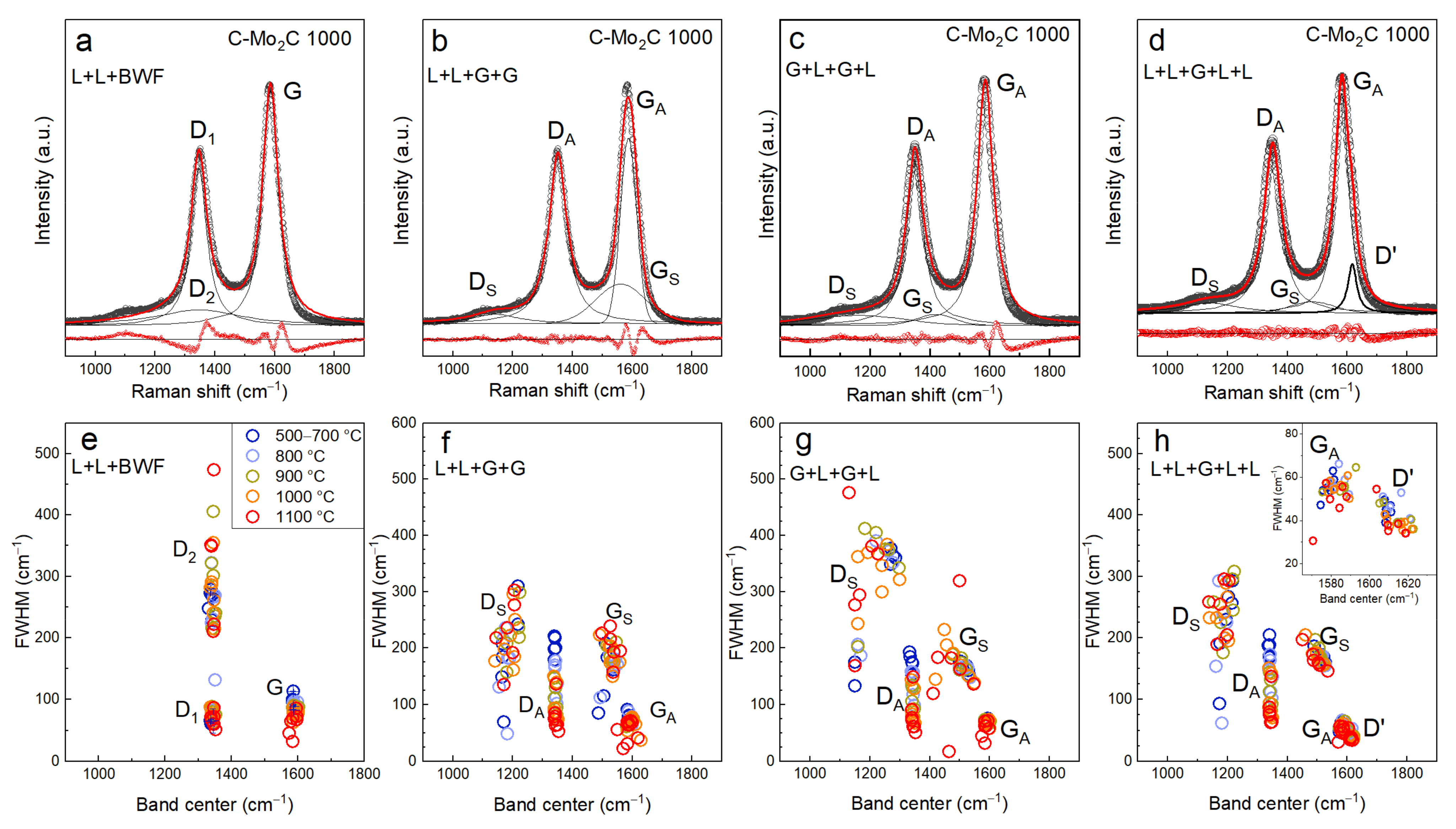
3.3. Impact of Band Deconvolution Method on Calculated Peak Properties
- Deconvolution by two Lorentzian functions centered at ~1350 cm−1 (denoted as D) and 1500 cm−1 (denoted as G), respectively, and two Gaussian functions (Equation (2)) centered at both sides of the D-band (denoted as DS and GS, respectively) as proposed by Ribeiro-Soares [27], henceforth denoted as G + L + G + L (Figure 3b).
- Deconvolution by two Lorentzian functions centered at ~1200 cm−1 and 1350 cm−1 (DS and D, respectively) and two Gaussian functions centered at wavenumbers ~1450 cm−1 and 1500 cm−1 (GS and G, respectively), henceforth denoted as L + L + G + G (Figure 3c).
3.4. First Order Raman Spectra Deconvolution Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schimmel, H.G.; Kearley, G.J.; Nijkamp, M.G.; Visser, C.T.; De Jong, K.P.; Mulder, F.M. Hydrogen Adsorption in Carbon Nanostructures: Comparison of Nanotubes, Fibers, and Coals. Chem. Eur. J. 2003, 9, 4764–4770. [Google Scholar] [CrossRef]
- Brown, R.C. Review: Activated Carbon Filters in Respiratory Protective Equipment. Int. J. Occup. Saf. Ergon. 1995, 1, 330–373. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Candelaria, S.L.; Shao, Y.; Zhou, W.; Li, X.; Xiao, J.; Zhang, J.-G.; Wang, Y.; Liu, J.; Li, J.; Cao, G. Nanostructured carbon for energy storage and conversion. Nano Energy 2012, 1, 195–220. [Google Scholar] [CrossRef]
- Härmas, R.; Palm, R.; Härmas, M.; Pohl, M.; Kurig, H.; Tallo, I.; Tee, E.; Vaas, I.; Väli, R.; Romann, T.; et al. Influence of porosity parameters and electrolyte chemical composition on the power densities of non-aqueous and ionic liquid based supercapacitors. Electrochim. Acta 2018, 283, 931–948. [Google Scholar] [CrossRef]
- Jänes, A.; Thomberg, T.; Kurig, H.; Lust, E. Nanoscale fine-tuning of porosity of carbide-derived carbon prepared from molybdenum carbide. Carbon 2009, 47, 23–29. [Google Scholar] [CrossRef]
- Tallo, I.; Thomberg, T.; Kurig, H.; Kontturi, K.; Jänes, A.; Lust, E. Novel micromesoporous carbon materials synthesized from tantalum hafnium carbide and tungsten titanium carbide. Carbon 2014, 67, 607–616. [Google Scholar] [CrossRef]
- Tallo, I.; Thomberg, T.; Kontturi, K.; Jänes, A.; Lust, E. Nanostructured carbide-derived carbon synthesized by chlorination of tungsten carbide. Carbon 2011, 49, 4427–4433. [Google Scholar] [CrossRef]
- Tallo, I.; Thomberg, T.; Jänes, A.; Lust, E. Replacing Chlorine with Hydrogen Chloride as a Possible Reactant for Synthesis of Titanium Carbide Derived Carbon Powders for High-Technology Devices. IOP Conf. Ser. Mater. Sci. Eng. 2013, 49, 012018. [Google Scholar] [CrossRef]
- Jänes, A.; Thomberg, T.; Lust, E. Synthesis and characterisation of nanoporous carbide-derived carbon by chlorination of vanadium carbide. Carbon 2007, 45, 2717–2722. [Google Scholar] [CrossRef]
- Tee, E.; Tallo, I.; Kurig, H.; Thomberg, T.; Jänes, A.; Lust, E. Huge enhancement of energy storage capacity and power density of supercapacitors based on the carbon dioxide activated microporous SiC-CDC. Electrochim. Acta 2015, 161, 364–370. [Google Scholar] [CrossRef]
- Jäger, R.; Härk, E.; Romann, T.; Joost, U.; Lust, E. C(Mo2C) and Pt–C(Mo2C) based mixed catalysts for oxygen reduction reaction. J. Electroanal. Chem. 2016, 761, 89–97. [Google Scholar] [CrossRef]
- Palm, R.; Tallo, I.; Romann, T.; Kurig, H. Methane adsorption on specially designed TiC and Mo 2 C derived carbons with different pore size and surface morphology. Microporous Mesoporous Mater. 2015, 218, 167–173. [Google Scholar] [CrossRef]
- Härmas, R.; Palm, R.; Russina, M.; Kurig, H.; Grzimek, V.; Härk, E.; Koppel, M.; Tallo, I.; Paalo, M.; Oll, O.; et al. Transport properties of H2 confined in carbide-derived carbons with different pore shapes and sizes. Carbon 2019, 155, 122–128. [Google Scholar] [CrossRef]
- Kim, H.S.; Singer, J.P.; Gogotsi, Y.; Fischer, J.E. Molybdenum carbide-derived carbon for hydrogen storage. Microporous Mesoporous Mater. 2009, 120, 267–271. [Google Scholar] [CrossRef]
- Härk, E.; Petzold, A.; Goerigk, G.; Risse, S.; Tallo, I.; Härmas, R.; Lust, E.; Ballauff, M. Carbide derived carbons investigated by small angle X-ray scattering: Inner surface and porosity vs. graphitization. Carbon 2019, 146, 284–292. [Google Scholar] [CrossRef]
- Kurig, H.; Russina, M.; Tallo, I.; Siebenbürger, M.; Romann, T.; Lust, E. The suitability of infinite slit-shaped pore model to describe the pores in highly porous carbon materials. Carbon 2016, 100, 617–624. [Google Scholar] [CrossRef]
- Tuinstra, F.; Koenig, J.L. Raman Spectrum of Graphite. J. Chem. Phys. 1970, 53, 1126–1130. [Google Scholar] [CrossRef]
- Cuesta, A.; Dhamelincourt, P.; Laureyns, J.; Martínez-Alonso, A.; Tascón, J. Raman microprobe studies on carbon materials. Carbon 1994, 32, 1523–1532. [Google Scholar] [CrossRef]
- Puech, P.; Kandara, M.; Paredes, G.; Moulin, L.; Weiss-Hortala, E.; Kundu, A.; Ratel-Ramond, N.; Plewa, J.-M.; Pellenq, R.; Monthioux, M. Analyzing the Raman Spectra of Graphenic Carbon Materials from Kerogens to Nanotubes: What Type of Information Can Be Extracted from Defect Bands? C 2019, 5, 69. [Google Scholar] [CrossRef]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar] [CrossRef]
- Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S.; Cançado, L.G.; Jorio, A.; Saito, R. Studying disorder in graphite-based systems by Raman spectroscopy. Phys. Chem. Chem. Phys. 2007, 9, 1276–1290. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Robertson, J. Interpretation of Raman spectra of disordered and amorphous carbon. Phys. Rev. B 2000, 61, 14095–14107. [Google Scholar] [CrossRef]
- Urbonaite, S.; Hälldahl, L.; Svensson, G. Raman spectroscopy studies of carbide derived carbons. Carbon 2008, 46, 1942–1947. [Google Scholar] [CrossRef]
- Zickler, G.A.; Smarsly, B.; Gierlinger, N.; Peterlik, H.; Paris, O. A reconsideration of the relationship between the crystallite size La of carbons determined by X-ray diffraction and Raman spectroscopy. Carbon 2006, 44, 3239–3246. [Google Scholar] [CrossRef]
- Hu, C.; Sedghi, S.; Silvestre-Albero, A.; Andersson, G.G.; Sharma, A.; Pendleton, P.; Rodríguez-Reinoso, F.; Kaneko, K.; Biggs, M.J. Raman spectroscopy study of the transformation of the carbonaceous skeleton of a polymer-based nanoporous carbon along the thermal annealing pathway. Carbon 2015, 85, 147–158. [Google Scholar] [CrossRef]
- Sadezky, A.; Muckenhuber, H.; Grothe, H.; Niessner, R.; Pöschl, U. Raman microspectroscopy of soot and related carbonaceous materials: Spectral analysis and structural information. Carbon 2005, 43, 1731–1742. [Google Scholar] [CrossRef]
- Ribeiro-Soares, J.; Oliveros, M.E.; Garin, C.; David, M.V.; Martins, L.G.P.; Almeida, C.A.; Martins-Ferreira, E.H.; Takai, K.; Enoki, T.; Magalhães-Paniago, R.; et al. Structural analysis of polycrystalline graphene systems by Raman spectroscopy. Carbon 2015, 95, 646–652. [Google Scholar] [CrossRef]
- Shimodaira, N.; Masui, A. Raman spectroscopic investigations of activated carbon materials. J. Appl. Phys. 2002, 92, 902–909. [Google Scholar] [CrossRef]
- Mallet-Ladeira, P.; Puech, P.; Toulouse, C.; Cazayous, M.; Ratel-Ramond, N.; Weisbecker, P.; Vignoles, G.L.; Monthioux, M. A Raman study to obtain crystallite size of carbon materials: A better alternative to the Tuinstra–Koenig law. Carbon 2014, 80, 629–639. [Google Scholar] [CrossRef]
- Schuepfer, D.B.; Badaczewski, F.; Guerra-Castro, J.M.; Hofmann, D.M.; Heiliger, C.; Smarsly, B.; Klar, P.J. Assessing the structural properties of graphitic and non-graphitic carbons by Raman spectroscopy. Carbon 2020, 161, 359–372. [Google Scholar] [CrossRef]
- Ruland, W.; Smarsly, B. X-ray scattering of non-graphitic carbon: An improved method of evaluation. J. Appl. Crystallogr. 2002, 35, 624–633. [Google Scholar] [CrossRef]
- Pfaff, T.; Simmermacher, M.; Smarsly, B.M. CarbX: A program for the evaluation of wide-angle X-ray scattering data of non-graphitic carbons. J. Appl. Crystallogr. 2018, 51, 219–229. [Google Scholar] [CrossRef]
- Faber, K.; Badaczewski, F.; Oschatz, M.; Mondin, G.; Nickel, W.; Kaskel, S.; Smarsly, B.M. In-Depth Investigation of the Carbon Microstructure of Silicon Carbide-Derived Carbons by Wide-Angle X-ray Scattering. J. Phys. Chem. C 2014, 118, 15705–15715. [Google Scholar] [CrossRef]
- Christians, H.; Brunnengräber, K.; Gläsel, J.; Etzold, B.J. Mesoporous and crystalline carbide-derived carbons: Towards a general correlation on synthesis temperature and precursor structure influence. Carbon 2021, 175, 215–222. [Google Scholar] [CrossRef]
- Nič, M.; Jirát, J.; Košata, B.; Jenkins, A.; McNaught, A. (Eds.) IUPAC Compendium of Chemical Terminology: Gold Book; 2.1.0.; IUPAC: Research Triagle Park, NC, USA, 2009; ISBN 978–0-9678550–9-7. [Google Scholar]
- Ferrari, A.C.; Basko, D.M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8, 235–246. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Alsmeyer, D.C.; McCreery, R.L. Raman spectroscopy of carbon materials: Structural basis of observed spectra. Chem. Mater. 1990, 2, 557–563. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Jorio, A.; Saito, R. Characterizing Graphene, Graphite, and Carbon Nanotubes by Raman Spectroscopy. Annu. Rev. Condens. Matter Phys. 2010, 1, 89–108. [Google Scholar] [CrossRef]
- Lee, Y.-J. The second order Raman spectroscopy in carbon crystallinity. J. Nucl. Mater. 2004, 325, 174–179. [Google Scholar] [CrossRef]
- Matthews, M.J.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S.; Endo, M. Origin of dispersive effects of the RamanDband in carbon materials. Phys. Rev. B 1999, 59, R6585–R6588. [Google Scholar] [CrossRef]
- Sato, K.; Saito, R.; Oyama, Y.; Jiang, J.; Cançado, L.; Pimenta, M.; Jorio, A.; Samsonidze, G.; Dresselhaus, G.; Dresselhaus, M. D-band Raman intensity of graphitic materials as a function of laser energy and crystallite size. Chem. Phys. Lett. 2006, 427, 117–121. [Google Scholar] [CrossRef]
- Deldicque, D.; Rouzaud, J.-N.; Velde, B. A Raman–HRTEM study of the carbonization of wood: A new Raman-based paleothermometer dedicated to archaeometry. Carbon 2016, 102, 319–329. [Google Scholar] [CrossRef]
- Vallerot, J.-M.; Bourrat, X.; Mouchon, A.; Chollon, G. Quantitative structural and textural assessment of laminar pyrocarbons through Raman spectroscopy, electron diffraction and few other techniques. Carbon 2006, 44, 1833–1844. [Google Scholar] [CrossRef]
- Merlen, A.; Buijnsters, J.G.; Pardanaud, C. A Guide to and Review of the Use of Multiwavelength Raman Spectroscopy for Characterizing Defective Aromatic Carbon Solids: From Graphene to Amorphous Carbons. Coatings 2017, 7, 153. [Google Scholar] [CrossRef]
- Mallet-Ladeira, P.; Puech, P.; Weisbecker, P.; Vignoles, G.L.; Monthioux, M. Behavior of Raman D band for pyrocarbons with crystallite size in the 2–5 nm range. Appl. Phys. A 2013, 114, 759–763. [Google Scholar] [CrossRef]
- Cançado, L.G.; Takai, K.; Enoki, T.; Endo, M.; Kim, Y.A.; Mizusaki, H.; Jorio, A.; Coelho, L.N.; Magalhães-Paniago, R.; Pimenta, M.A. General equation for the determination of the crystallite size La of nanographite by Raman spectroscopy. Appl. Phys. Lett. 2006, 88, 163106. [Google Scholar] [CrossRef]
- Vázquez-Santos, M.B.; Geissler, E.; László, K.; Rouzaud, J.-N.; Martínez-Alonso, A.; Tascón, J.M. Comparative XRD, Raman, and TEM Study on Graphitization of PBO-Derived Carbon Fibers. J. Phys. Chem. C 2012, 116, 257–268. [Google Scholar] [CrossRef]
- Cançado, L.G.; Da Silva, M.G.; Ferreira, E.H.M.; Hof, F.; Kampioti, K.; Huang, K.; Pénicaud, A.; Achete, C.A.; Capaz, R.B.; Jorio, A. Disentangling contributions of point and line defects in the Raman spectra of graphene-related materials. 2D Mater. 2017, 4, 025039. [Google Scholar] [CrossRef]
- Gupta, A.K.; Nisoli, C.; Lammert, P.E.; Crespi, V.H.; Eklund, P.C. Curvature-induced D-band Raman scattering in folded graphene. J. Phys. Condens. Matter 2010, 22, 334205. [Google Scholar] [CrossRef]
- Palm, R.; Härmas, R.; Härk, E.; Kent, B.; Kurig, H.; Koppel, M.; Russina, M.; Tallo, I.; Romann, T.; Mata, J.; et al. Study of the structural curvature in Mo2C derived carbons with contrast matched small-angle neutron scattering. Carbon 2021, 171, 695–703. [Google Scholar] [CrossRef]

| Precursor Carbide | Chlorination Temperature (°C) | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|
| Mo2C | 600 | 700 | 800 | 900 | 1000 | 1100 | [5] | |
| Ta4HfC5 | 800 | 900 | 1000 | 1100 | [6] | |||
| WTiC2 | 800 | 900 | 1000 | 1100 | [6] | |||
| WC | 800 | 900 | 1000 | 1100 | [7] | |||
| TiC | 800 | 900 | 1000 | 1100 | [8] | |||
| VC | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | [9] |
| C-Mo2C | C-Ta4HfC5 | C-WTiC2 | C-WC | C-TiC | C-VC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tsyn | 800 | 1000 | 800 | 1000 | 800 | 1000 | 800 | 1000 | 800 | 1000 | 600 | 1100 |
| La, nm | 3.8 ± 0.6 | 8.3 ± 2.9 | 2.5 ± 0.3 | 5.6 ± 1.3 | 2.6 ± 0.3 | 7.1 ± 2.1 | 2.8 ± 0.3 | 4.5 ± 0.8 | 2.6 ± 0.3 | 5.6 ± 1.3 | 2.5 ± 0.3 | 6.3 ± 1.6 |
| lcc, nm | 0.1412 | 0.1410 | 0.1381 | 0.1409 | 0.1405 | 0.1400 | 0.1411 | 0.1411 | 0.1410 | 0.1414 | 0.1416 | 0.1406 |
| σ1, nm | 0.016 | 0.012 | 0.013 | 0.016 | 0.022 | 0.016 | 0.016 | 0.015 | 0.021 | 0.018 | 0.020 | 0.011 |
| ⟨N⟩ | 1.05 | 6.74 | 0.19 | 1.21 | 0.66 | 1.02 | 1.40 | 1.90 | 1.08 | 0.97 | 1.51 | 0.09 |
| Lc, nm | 1.3 ± 0.2 | 2.7 ± 0.2 | 0.7 ± 0.1 | 0.52 ± 0.05 | 0.37 ± 0.05 | 0.56 ± 0.1 | 0.55 ± 0.03 | 0.8 ± 0.1 | 0.5 ± 0.1 | 0.6 ± 0.1 | 0.82 ± 0.05 | 3.1 ± 0.7 |
| a3, nm | 0.364 | 0.351 | 0.333 | 0.380 | 0.354 | 0.369 | 0.314 | 0.347 | 0.365 | 0.365 | 0.395 | 0.343 |
| σ3, nm | 0.061 | 0.048 | 0.110 | 0.001 | 0.024 | 0.00 | 0.057 | 0.021 | 0.038 | 0.039 | 0.051 | 0.011 |
| 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | |
| C-Mo2C | Stage I | Stage II | Stage III | ||||
| C-Ta4HfC5 | Stage I | Stage II | |||||
| C-WTiC2 | Stage II | ||||||
| C-WC | Stage II | ||||||
| C-TiC | Stage I | Stage II | |||||
| C-VC | Stage I | Stage II | Stage III | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Härmas, R.; Palm, R.; Kurig, H.; Puusepp, L.; Pfaff, T.; Romann, T.; Aruväli, J.; Tallo, I.; Thomberg, T.; Jänes, A.; et al. Carbide-Derived Carbons: WAXS and Raman Spectra for Detailed Structural Analysis. C 2021, 7, 29. https://doi.org/10.3390/c7010029
Härmas R, Palm R, Kurig H, Puusepp L, Pfaff T, Romann T, Aruväli J, Tallo I, Thomberg T, Jänes A, et al. Carbide-Derived Carbons: WAXS and Raman Spectra for Detailed Structural Analysis. C. 2021; 7(1):29. https://doi.org/10.3390/c7010029
Chicago/Turabian StyleHärmas, Riinu, Rasmus Palm, Heisi Kurig, Laura Puusepp, Torben Pfaff, Tavo Romann, Jaan Aruväli, Indrek Tallo, Thomas Thomberg, Alar Jänes, and et al. 2021. "Carbide-Derived Carbons: WAXS and Raman Spectra for Detailed Structural Analysis" C 7, no. 1: 29. https://doi.org/10.3390/c7010029
APA StyleHärmas, R., Palm, R., Kurig, H., Puusepp, L., Pfaff, T., Romann, T., Aruväli, J., Tallo, I., Thomberg, T., Jänes, A., & Lust, E. (2021). Carbide-Derived Carbons: WAXS and Raman Spectra for Detailed Structural Analysis. C, 7(1), 29. https://doi.org/10.3390/c7010029






