RKKY Interaction in Graphene at Finite Temperature
Abstract
:1. Introduction
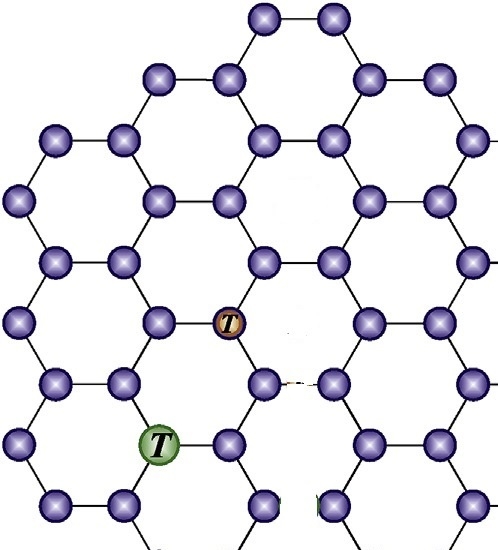
2. Theoretical Methods
3. Results
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Zyuzin, Y.A.; Spivak, B.Z. Friedel oscillations and Ruderman-Kittel interaction in disordered conductors. JETP Lett. 1986, 43, 234–237. [Google Scholar]
- Abrikosov, A.A. Fundamentals of the Theory of Metals; Elsevier Science Publishers: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Aristov, D.N.; Maleyev, S.V.; Yashenkin, A.G. RKKY interaction in layered superconductors with anisotropic pairing. Z. Phys. B Condens. 1997, 102, 467–471. [Google Scholar] [CrossRef]
- Galitski, V.M.; Larkin, A.I. Spin glass versus superconductivity. Phys. Rev. B 2002, 66, 064526. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, C.-X.; Xu, C.; Qi, X.-L.; Zhang, S.-C. Magnetic Impurities on the Surface of a Topological Insulator. Phys. Rev. Lett. 2009, 102, 156603. [Google Scholar] [CrossRef]
- Biswas, R.R.; Balatsky, A.V. Impurity-induced states on the surface of three-dimensional topological insulators. Phys. Rev. B 2010, 81, 233405. [Google Scholar] [CrossRef]
- Garate, I.; Franz, M. Magnetoelectric response of the time-reversal invariant helical metal. Phys. Rev. B 2010, 81, 172408. [Google Scholar] [CrossRef]
- Zhu, J.-J.; Yao, D.-X.; Zhang, S.-C.; Chang, K. Electrically Controllable Surface Magnetism on the Surface of Topological Insulators. Phys. Rev. Lett. 2011, 106, 097201. [Google Scholar] [CrossRef] [PubMed]
- Abanin, D.A.; Pesin, D.A. Ordering of Magnetic Impurities and Tunable Electronic Properties of Topological Insulators. Phys. Rev. Lett. 2011, 106, 136802. [Google Scholar] [CrossRef] [PubMed]
- Checkelsky, J.G.; Ye, J.; Onose, Y.; Iwasa, Y.; Tokura, Y. Dirac-fermion-mediated ferromagnetism in a topological insulator. Nat. Phys. 2012, 8, 729–733. [Google Scholar] [CrossRef]
- Zyuzin, A.A.; Loss, D. RKKY interaction on surfaces of topological insulators with superconducting proximity effect. Phys. Rev. B 2014, 90, 125443. [Google Scholar] [CrossRef]
- Klier, N.; Sharma, S.; Pankratov, O.; Shallcross, S. Tuning topological surface magnetism by bulk alloying. arXiv 2017, arXiv:1711.10760. [Google Scholar]
- Braunecker, B.; Simon, P.; Loss, D. Nuclear Magnetism and Electronic Order in 13C Nanotubes. Phys. Rev. Lett. 2009, 102, 116403. [Google Scholar] [CrossRef]
- Klinovaja, J.; Loss, D. RKKY interaction in carbon nanotubes and graphene nanoribbons. Phys. Rev. B 2013, 87, 045422. [Google Scholar] [CrossRef]
- Braunecker, B.; Simon, P.; Loss, D. Nuclear magnetism and electron order in interacting one-dimensional conductors. Phys. Rev. B 2009, 80, 165119. [Google Scholar] [CrossRef]
- Sun, J.-H.; Xu, D.-H.; Zhang, F.-C.; Zhou, Y. Magnetic impurity in a Weyl semimetal. Phys. Rev. B 2015, 92, 195124. [Google Scholar] [CrossRef]
- Chang, H.-R.; Zhou, J.; Wang, S.-X.; Shan, W.; Xiao, D. RKKY interaction of magnetic impurities in Dirac and Weyl semimetals. Phys. Rev. B 2015, 92, 241103. [Google Scholar] [CrossRef]
- Hosseini, M.V.; Askari, M. Ruderman-KittelKasuya-Yosida interaction in Weyl semimetals. Phys. Rev. B 2015, 92, 224435. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, A. RKKY interaction of magnetic impurities in multi-Weyl semimetals. J. Phys. Condens. Matter 2017, 2, 435306. [Google Scholar] [CrossRef] [PubMed]
- Yevtushenko, O.M.; Yudson, V.I. Kondo Impurities Coupled to a Helical Luttinger Liquid: RKKY-Kondo Physics Revisited. Phys. Rev. Lett. 2018, 120, 147201. [Google Scholar] [CrossRef]
- Kaladzhyan, V.; Zyuzin, A.A.; Simon, P. RKKY interaction on the surface of 3D Dirac semimetals. arXiv 2018, arXiv:1811.05750. [Google Scholar]
- Vozmediano, M.A.H.; Lopez-Sancho, M.P.; Stauber, T.; Guinea, F. Local defects and ferromagnetism in graphene layers. Phys. Rev. B 2005, 72, 155121. [Google Scholar] [CrossRef]
- Dugaev, V.K.; Litvinov, V.I.; Barnas, J. Exchange interaction of magnetic impurities in graphene. Phys. Rev. B 2006, 74, 224438. [Google Scholar] [CrossRef]
- Brey, L.; Fertig, H.A.; Sarma, S.D. Diluted Graphene Antiferromagnet. Phys. Rev. Lett. 2007, 99, 116802. [Google Scholar] [CrossRef]
- Saremi, S. RKKY in half-filled bipartite lattices: Graphene as an example. Phys. Rev. B 2007, 76, 184430. [Google Scholar] [CrossRef]
- Hwang, E.H.; Sarma, S.D. Screening, Kohn Anomaly, Friedel Oscillation, and RKKY Interaction in Bilayer Graphene. Phys. Rev. Lett. 2008, 101, 156802. [Google Scholar] [CrossRef] [PubMed]
- Black–Schaffer, A.M. RKKY coupling in graphene. Phys. Rev. B 2010, 81, 205416. [Google Scholar] [CrossRef]
- Sherafati, M.; Satpathy, S. RKKY interaction in graphene from the lattice Green’s function. Phys. Rev. B 2011, 83, 165425. [Google Scholar] [CrossRef]
- Uchoa, B.; Rappoport, T.G.; Castro Neto, A.H. Kondo Quantum Criticality of Magnetic Adatoms in Graphene. Phys. Rev. Lett. 2011, 106, 016801. [Google Scholar] [CrossRef] [PubMed]
- Power, S.R.; Guimaraes, F.M.S.; Costa, A.T.; Muniz, R.B.; Ferreira, M.S. Dynamic RKKY interaction in graphene. Phys. Rev. B 2012, 85, 195411. [Google Scholar] [CrossRef]
- Patrone, P.N.; Einstein, T.L. Anisotropic surface-state-mediated RKKY interaction between adatoms. Phys. Rev. B 2012, 85, 045429. [Google Scholar] [CrossRef]
- Kogan, E. RKKY Interaction in Gapped or Doped Graphene. Graphene 2013, 2, 8–12. [Google Scholar] [CrossRef]
- Gorman, P.D.; Duffy, J.M.; Ferreira, M.S.; Power, S.R. RKKY interaction between adsorbed magnetic impurities in graphene: Symmetry and strain effects. Phys. Rev. B 2013, 88, 085405. [Google Scholar] [CrossRef]
- Stano, P.; Klinovaja, J.; Yacoby, A.; Loss, D. Local spin susceptibilities of low-dimensional electron systems. Phys. Rev. B 2013, 88, 045441. [Google Scholar] [CrossRef]
- Szalowski, K. Indirect RKKY interaction between localized magnetic moments in armchair graphene nanoribbons. J. Phys. Condens. Matter 2013, 25, 166001. [Google Scholar] [CrossRef]
- Roslyak, O.; Gumbs, G.; Huang, D. Gap-modulated doping effects on indirect exchange interaction between magnetic impurities in graphene. J. Appl. Phys. 2013, 1, 123702. [Google Scholar] [CrossRef]
- Xiao, X.; Liu, Y.; Wen, W. Ruderman-Kittel-Kasuya-Yosida interaction in silicene. J. Phys. Condens. Matter 2014, 26, 266001. [Google Scholar] [CrossRef] [PubMed]
- Shirakawa, T.; Yunoki, S. Block Lanczos density-matrix renormalization group method for general Anderson impurity models: Application to magnetic impurity problems in graphene. Phys. Rev. B 2014, 90, 195109. [Google Scholar] [CrossRef]
- Zare, M.; Parhizgar, F.; Asgari, R. Topological phase and edge states dependence of the RKKY interaction in zigzag silicene nanoribbon. Phys. Rev. B 2016, 94, 045443. [Google Scholar] [CrossRef]
- Fransson, J.; Black-Schaffer, A.M.; Balatsky, A.V. Magnon Dirac materials. Phys. Rev. B 2016, 94, 075401. [Google Scholar] [CrossRef]
- Rezania, H.; Azizi, F. RKKY interaction in spin polarized armchair graphene nanoribbon. JMMM 2016, 417, 272–278. [Google Scholar] [CrossRef]
- Agarwal, M.; Mishchenko, E.G. Long-range exchange interaction between magnetic impurities in graphene. Phys. Rev. B 2017, 95, 075411. [Google Scholar] [CrossRef]
- Sousa, J.F.; Amorim, B.; Castro, E.V. Dilute magnetism in graphene. arXiv 2019, arXiv:1901.08614. [Google Scholar]
- Kogan, E. RKKY interaction in graphene. Phys. Rev. B 2011, 84, 115119. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Gorkov, L.P.; Dzyloshinski, I.E. Methods of Quantum Field Theory in Statistical Physics; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Wang, S.; Yang, B.; Chen, H.; Ruckenstein, E. Popgraphene: a new 2D planar carbon allotrope composed of 5–8–5 carbon rings for high-performance lithium-ion battery anodes from bottom-up programming. J. Mater. Chem. A 2018, 6, 6815–6821. [Google Scholar] [CrossRef]
- Wang, S.; Yang, B.; Chen, H.; Ruckenstein, E. Reconfiguring graphene for high-performance metal-ion battery anodes. Energy Storage Mater. 2019, 16, 619–624. [Google Scholar] [CrossRef]
- Wu, D.; Yang, B.; Ruckenstein, E.; Chen, H. Functionalization: An Effective Approach to Open and Close Channels for Electron Transfer in Nitrogenated Holey Graphene C2N Anodes in Sodium-Ion Batteries. J. Phys. Chem. Lett. 2019, 10, 721–726. [Google Scholar] [CrossRef]
- Kogan, E.; Noda, K.; Yunoki, S. Spin-anisotropic magnetic impurity in a Fermi gas: Integration of poor man’s scaling equations. Phys. Rev. B 2017, 95, 165412. [Google Scholar] [CrossRef]
- Kogan, E. Poor man’s scaling: anisotropic Kondo and Coqblin–Schrieffer models. J. Phys. Commun. 2018, 2, 085001. [Google Scholar] [CrossRef]
- Pruser, H.; Dargel, P.E.; Bouhassoune, M.; Ulbrich, R.G.; Pruschke, T.; Lounis, S.; Wenderoth, M. Interplay between the Kondo effect and the Ruderman–Kittel–Kasuya–Yosida interaction. Nat. Commun. 2014, 5, 5417. [Google Scholar] [CrossRef]
- Nejati, A.; Kroha, J. Oscillation and suppression of Kondo temperature by RKKY coupling in two-site Kondo systems. J. Phys. Conf. Ser. 2017, 807, 082004. [Google Scholar] [CrossRef]
- Kroha, J. Ser. Model. Simulat. 2017; 7, 12.1–12.27, (Verlag Forschungszentrum Julich, 2017).
- Cheianov, V.V.; Syljuasen, O.; Altshuler, B.L.; Fal’ko, V. Ordered states of adatoms on graphene. Phys. Rev. B 2009, 80, 233409. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series; Gordon and Breach Science Publishers: London, UK, 1986; Volume 2. [Google Scholar]
- Klier, N.; Shallcross, S.; Sharma, S.; Pankratov, O. Ruderman-Kittel-Kasuya-Yosida interaction at finite temperature: Graphene and bilayer graphene. Phys. Rev. B 2015, 92, 205414. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kogan, E. RKKY Interaction in Graphene at Finite Temperature. C 2019, 5, 14. https://doi.org/10.3390/c5020014
Kogan E. RKKY Interaction in Graphene at Finite Temperature. C. 2019; 5(2):14. https://doi.org/10.3390/c5020014
Chicago/Turabian StyleKogan, Eugene. 2019. "RKKY Interaction in Graphene at Finite Temperature" C 5, no. 2: 14. https://doi.org/10.3390/c5020014
APA StyleKogan, E. (2019). RKKY Interaction in Graphene at Finite Temperature. C, 5(2), 14. https://doi.org/10.3390/c5020014