Convenient Preparation of Graphene Oxide from Expandable Graphite and Its Characterization by Positron Annihilation Lifetime Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
Preparation of Graphene Oxide (GO)
3. Results and Discussion
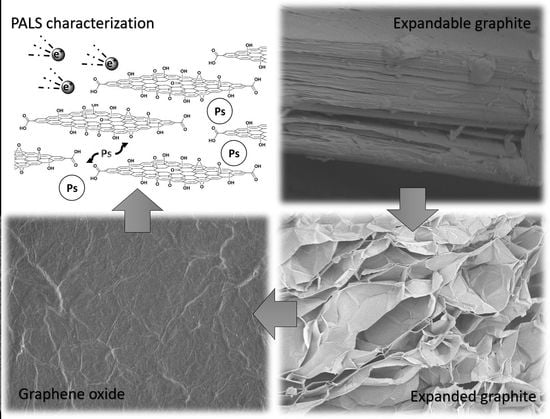
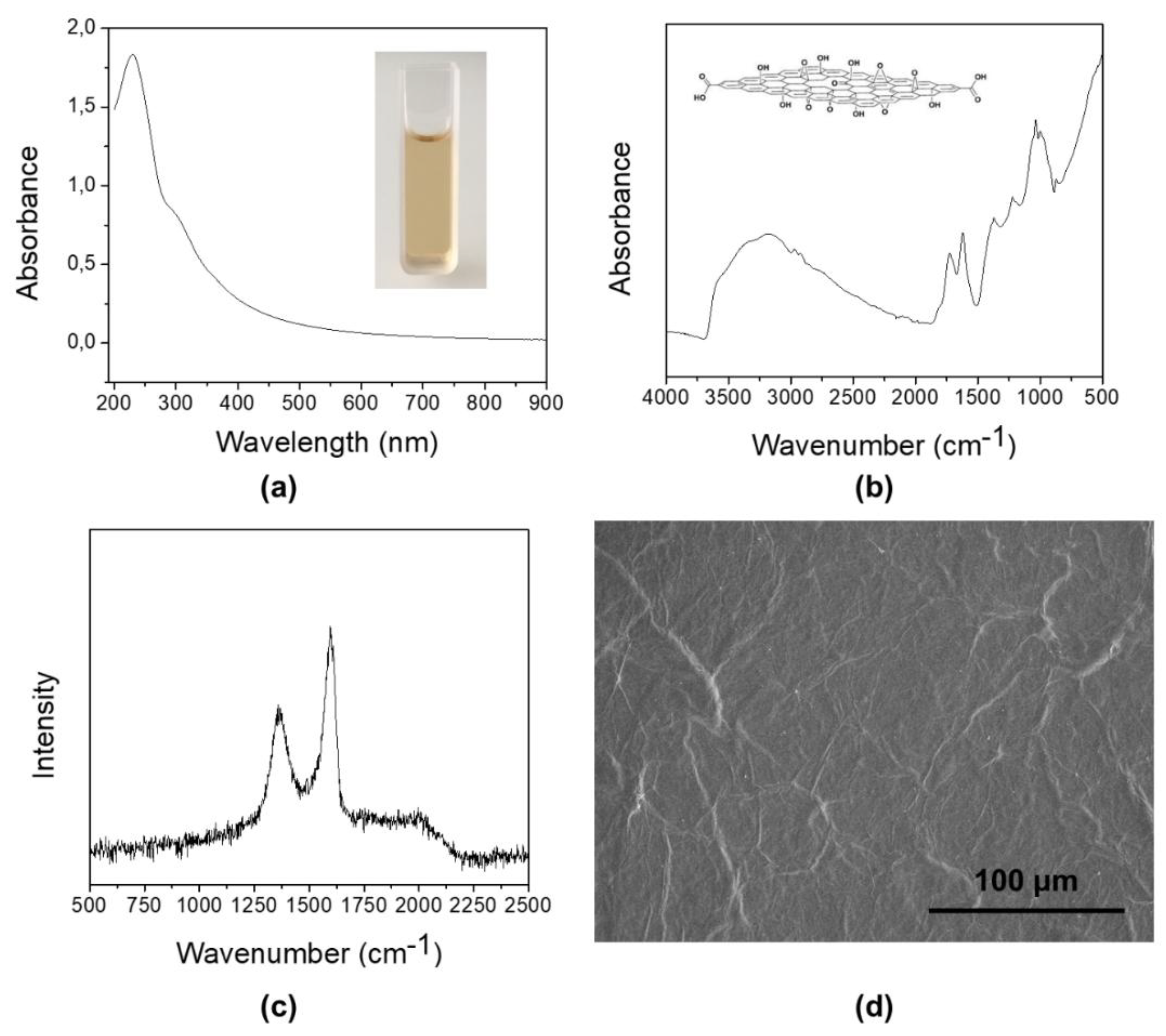
3.1. Graphene Oxide from Expanded Graphite by a Simplified Hummers’ Method
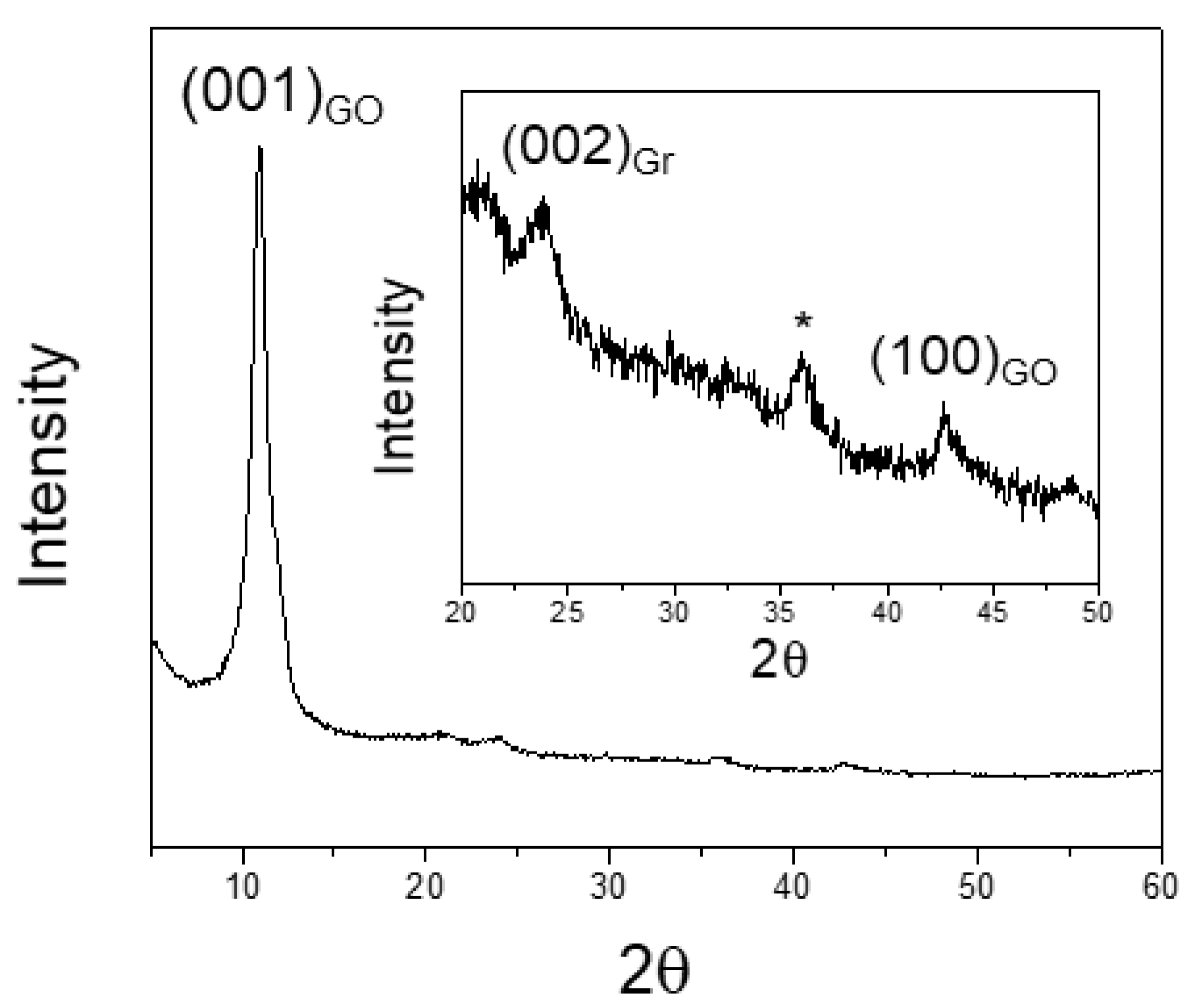
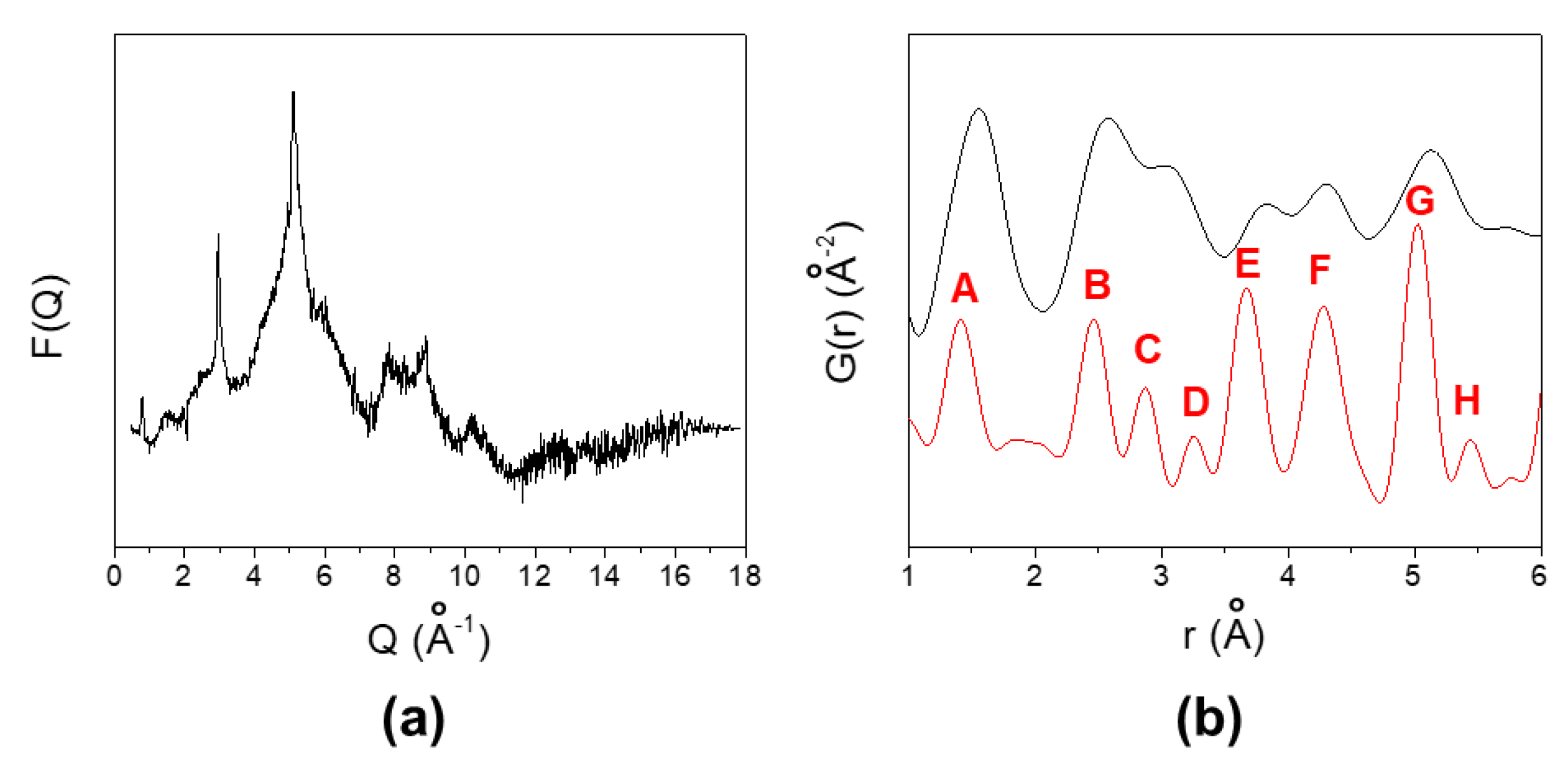
3.2. X-ray Powder Diffraction (XRPD) Results
3.3. Positron Annihilation Lifetime Spectroscopy (PALS) of GO
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.J.; Tung, V.C.; Kaner, R.B. Honeycomb carbon: A review of graphene. Chem. Rev. 2010, 110, 132–145. [Google Scholar] [CrossRef]
- Georgakilas, V.; Otyepka, M.; Bourlinos, A.B.; Chandra, V.; Kim, N.; Kemp, K.C.; Hobza, P.; Zboril, R.; Kim, K.S. Functionalization of graphene: Covalent and non-covalent approaches, derivatives and applications. Chem. Rev. 2012, 112, 6156–6214. [Google Scholar] [CrossRef] [PubMed]
- Hummers, W.S.; Offeman, R.E. Preparation of Graphitic Oxide. J. Am. Chem. Soc. 1958, 80, 1339. [Google Scholar] [CrossRef]
- Roisnel, T.; Rodríquez-Carvajal, J. WinPLOTR: A Windows Tool for Powder Diffraction Pattern Analysis. Mater. Sci. Forum 2001, 378–381, 118–123. [Google Scholar] [CrossRef]
- Ashiotis, G.; Deschildre, A.; Nawaz, Z.; Wright, J.P.; Karkoulis, D.; Picca, F.E.; Kieffer, J. The fast azimuthal integration Python library: PyFAI. J. Appl. Crystallogr. 2015, 48, 510–519. [Google Scholar] [CrossRef] [PubMed]
- Knudsen, E.B.; Sørensen, H.O.; Wright, J.P.; Goret, G.; Kieffer, J. FabIO: Easy access to two-dimensional X-ray detector images in Python. J. Appl. Crystallogr. 2013, 46, 537–539. [Google Scholar] [CrossRef]
- Egami, T.; Billinge, S.J.L. Underneath Bragg Peaks; Pergamon: New York, NY, USA, 2003. [Google Scholar]
- Qiu, X.; Thompson, J.W.; Billinge, S.J.L. PDFgetX2: A GUI-driven program to obtain the pair distribution function from X-ray powder diffraction data. J. Appl. Crystallogr. 2004, 37, 678. [Google Scholar] [CrossRef]
- Kansy, J. Microcomputer program for analysis of positron annihilation lifetime spectra. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1996, 374, 235–244. [Google Scholar] [CrossRef]
- Focke, W.W.; Badenhorst, H.; Mhike, W.; Kruger, H.J.; Lombaard, D. Characterization of commercial expandable graphite fire retardants. Thermochim. Acta 2014, 584, 8–16. [Google Scholar] [CrossRef]
- Modesti, M.; Lorenzetti, A.; Simioni, F.; Camino, G. Expandable graphite as an intumescent flame retardant in polyisocyanurate-polyurethane foams. Polym. Degrad. Stab. 2002, 77, 195–202. [Google Scholar] [CrossRef]
- Sun, L.; Fugetsu, B. Mass production of graphene oxide from expanded graphite. Mater. Lett. 2013, 109, 207–210. [Google Scholar] [CrossRef]
- Konkena, B.; Vasudevan, S. Understanding aqueous dispersibility of graphene oxide and reduced graphene oxide through pKa measurements. J. Phys. Chem. Lett. 2012, 3, 867–872. [Google Scholar] [CrossRef] [PubMed]
- Arrais, A.; Diana, E.; Boccaleri, E. A study on the carbon soot derived from the wood combustion and on the relative alkali-extractable fraction. J. Mater. Sci. 2006, 41, 6035–6045. [Google Scholar] [CrossRef]
- Arrais, A.; Diana, E.; Rossetti, R.; Boccaleri, E. Spectral and chemical evidence for the direct formation of carboxylic groups in aerobically oxidised water-soluble fullerenes. Carbon 2007, 13, 2502–2510. [Google Scholar] [CrossRef]
- Hontoria-Lucas, C.; López-Peinado, A.J.; de López-González, J.D.; Rojas-Cervantes, M.L.; Martín-Aranda, R.M. Study of oxygen-containing groups in a series of graphite oxides: Physical and chemical characterization. Carbon N. Y. 1995, 33, 1585–1592. [Google Scholar] [CrossRef]
- Wu, J.B.; Lin, M.L.; Cong, X.; Liu, H.N.; Tan, P.H. Raman spectroscopy of graphene-based materials and its applications in related devices. Chem. Soc. Rev. 2018, 47, 1822–1873. [Google Scholar] [CrossRef]
- Kudin, K.N.; Ozbas, B.; Schniepp, H.C.; Prud’homme, R.K.; Aksay, I.A.; Car, R. Raman spectra of graphite oxide and functionalized graphene sheets. Nano Lett. 2008, 8, 36–41. [Google Scholar] [CrossRef]
- Krishnamoorthy, K.; Veerapandian, M.; Yun, K.; Kim, S.J. The chemical and structural analysis of graphene oxide with different degrees of oxidation. Carbon N. Y. 2013, 53, 38–49. [Google Scholar] [CrossRef]
- Wyckoff, R.W.G. Crystal Structure; Interscience Publishers: New York, NY, USA, 1963. [Google Scholar]
- Longhi, M.; Marzorati, S.; Checchia, S.; Sacchi, B.; Santo, N.; Zaffino, C.; Scavini, M. Sugar-based catalysts for oxygen reduction reaction. Effects of the functionalization of the nitrogen precursors on the electrocatalytic activity. Electrochim. Acta 2016, 222, 781–792. [Google Scholar] [CrossRef]
- Sormann, H.; Kontrym-Sznajd, G. Many-body effects on the electron-positron momentum density in simple and transition metals: Comparison with positron annihilation spectroscopy data. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 075111. [Google Scholar] [CrossRef]
- Tuomisto, F.; Makkonen, I. Defect identification in semiconductors with positron annihilation: Experiment and theory. Rev. Mod. Phys. 2013, 85, 1583–1631. [Google Scholar] [CrossRef]
- Jean, Y.C.; Van Horn, J.D.; Hung, W.S.; Lee, K.R. Perspective of positron annihilation spectroscopy in polymers. Macromolecules 2013, 46, 7133–7145. [Google Scholar] [CrossRef]
- Panzarasa, G.; Aghion, S.; Soliveri, G.; Consolati, G.; Ferragut, R. Positron annihilation spectroscopy: A new frontier for understanding nanoparticle-loaded polymer brushes. Nanotechnology 2016, 27, 02LT03. [Google Scholar] [CrossRef] [PubMed]
- Panzarasa, G.; Aghion, S.; Marra, G.; Wagner, A.; Liedke, M.O.; Elsayed, M.; Krause-Rehberg, R.; Ferragut, R.; Consolati, G. Probing the Impact of the Initiator Layer on Grafted-from Polymer Brushes: A Positron Annihilation Spectroscopy Study. Macromolecules 2017, 50, 5574–5581. [Google Scholar] [CrossRef]
- Pandini, S.; Bignotti, F.; Baldi, F.; Sartore, L.; Consolati, G.; Panzarasa, G. Thermomechanical and large deformation behaviors of antiplasticized epoxy resins: Effect of material formulation and network architecture. Polym. Eng. Sci. 2017, 57, 553–565. [Google Scholar] [CrossRef]
- Dehghani, E.S.; Aghion, S.; Anwand, W.; Consolati, G.; Ferragut, R.; Panzarasa, G. Investigating the structure of crosslinked polymer brushes (brush-gels) by means of Positron Annihilation Spectroscopy. Eur. Polym. J. 2018, 99, 415–421. [Google Scholar] [CrossRef]
- Consolati, G.; Panzarasa, G.; Quasso, F. Morphology of free volume holes in an amorphous polyether-polyester polyurethane of biomedical interest. Polym. Test. 2018, 68, 208–212. [Google Scholar] [CrossRef]
- Tang, Y.P.; Paul, D.R.; Chung, T.S. Free-standing graphene oxide thin films assembled by a pressurized ultrafiltration method for dehydration of ethanol. J. Memb. Sci. 2014, 458, 199–208. [Google Scholar] [CrossRef]
- Gong, W.; He, D.; Tao, J.; Zhao, P.; Kong, L.; Luo, Y.; Peng, Z.; Wang, H. Formation of defects in the graphite oxidization process: A positron study. RSC Adv. 2015, 5, 88908–88914. [Google Scholar] [CrossRef]
- Tao, S.J. Positronium annihilation in molecular substances. J. Chem. Phys. 1972, 56, 5499. [Google Scholar] [CrossRef]
- Eldrup, M.; Lightbody, D.; Sherwood, J.N. The temperature dependence of positron lifetimes in solid pivalic acid. Chem. Phys. 1981, 63, 51–58. [Google Scholar] [CrossRef]
- Nakanishi, H.; Wang, S.J.; Jean, Y.C. Positron Annihilation Studies of Fluids; Sharma, S.C., Ed.; World Scientific: Singapore, 1988. [Google Scholar]
- Jasinska, B.; Koziol, A.E.; Goworek, T. Void shapes and o-Ps lifetimes in molecular crystals. Acta Phys. Pol. A 1999, 95, 557–561. [Google Scholar] [CrossRef]
- He, H.; Riedl, T.; Lerf, A.; Klinowski, J. Solid-state NMR studies of the structure of graphite oxide. J. Phys. Chem. 1996, 100, 19954–19958. [Google Scholar] [CrossRef]

| Lifetime Components τ (ns) | Intensity Components I (%) |
|---|---|
| τ1 = 0.20 ± 0.02 | I1 = 54.2 ± 7.0 |
| τ2 = 0.44 ± 0.03 | I2 = 42.0 ± 5.0 |
| τ3 = 2.42 ± 0.04 | I3 = 3.8 ± 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panzarasa, G.; Consolati, G.; Scavini, M.; Longhi, M.; Quasso, F. Convenient Preparation of Graphene Oxide from Expandable Graphite and Its Characterization by Positron Annihilation Lifetime Spectroscopy. C 2019, 5, 6. https://doi.org/10.3390/c5010006
Panzarasa G, Consolati G, Scavini M, Longhi M, Quasso F. Convenient Preparation of Graphene Oxide from Expandable Graphite and Its Characterization by Positron Annihilation Lifetime Spectroscopy. C. 2019; 5(1):6. https://doi.org/10.3390/c5010006
Chicago/Turabian StylePanzarasa, Guido, Giovanni Consolati, Marco Scavini, Mariangela Longhi, and Fiorenza Quasso. 2019. "Convenient Preparation of Graphene Oxide from Expandable Graphite and Its Characterization by Positron Annihilation Lifetime Spectroscopy" C 5, no. 1: 6. https://doi.org/10.3390/c5010006
APA StylePanzarasa, G., Consolati, G., Scavini, M., Longhi, M., & Quasso, F. (2019). Convenient Preparation of Graphene Oxide from Expandable Graphite and Its Characterization by Positron Annihilation Lifetime Spectroscopy. C, 5(1), 6. https://doi.org/10.3390/c5010006