Aligned Carbon Nanotube Arrays Bonded to Solid Graphite Substrates: Thermal Analysis for Future Device Cooling Applications
Abstract
1. Introduction
2. Experimental
2.1. CNT Growth
2.2. Microscopy
2.3. Thermal Analysis
3. Results and Discussion
3.1. Microscopy and Characterization
3.2. Thermal Analysis
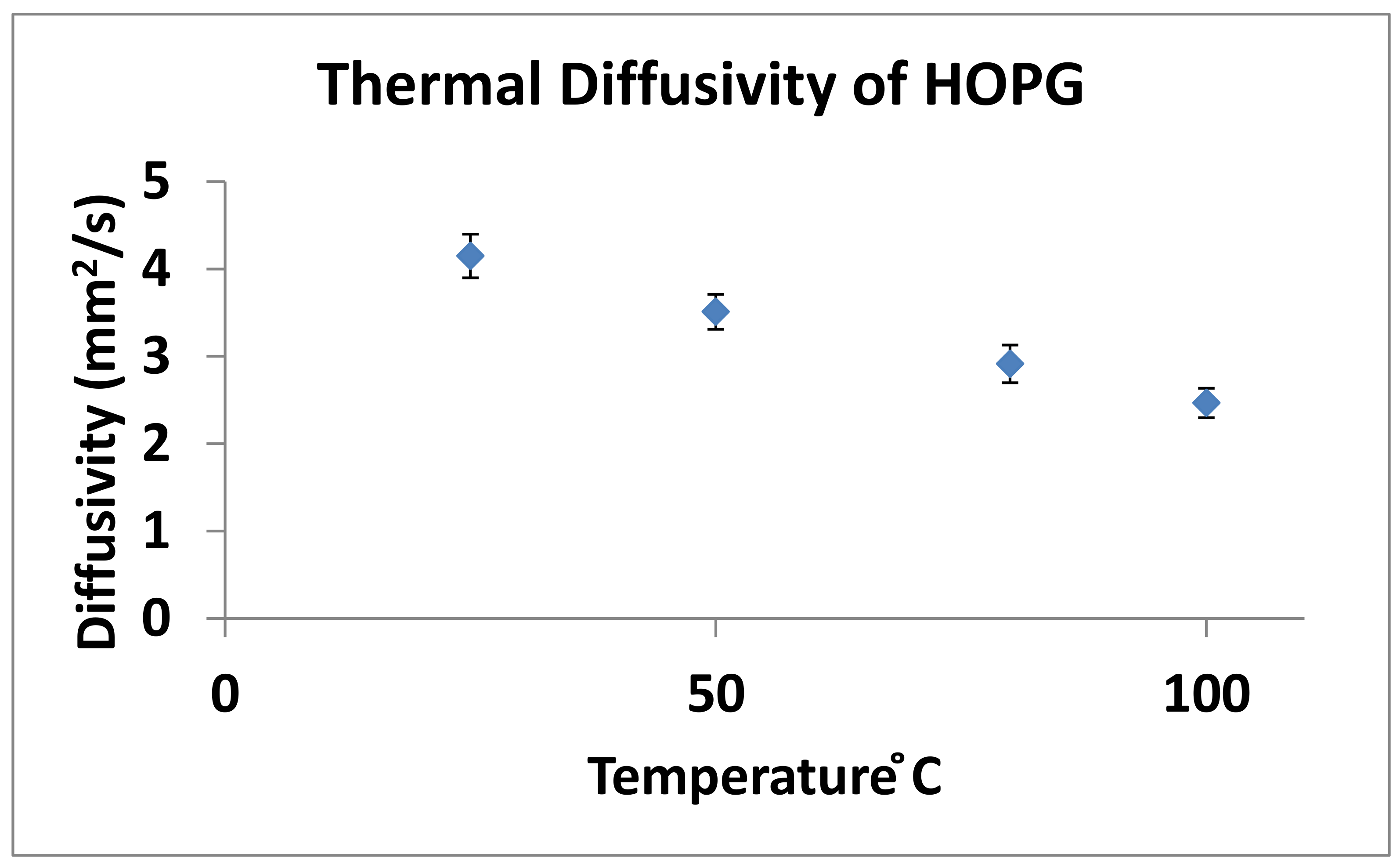
3.2.1. Thermal Analysis of the Substrate (HOPG)
3.2.2. Thermal Analysis of Substrates with a Buffer Layer
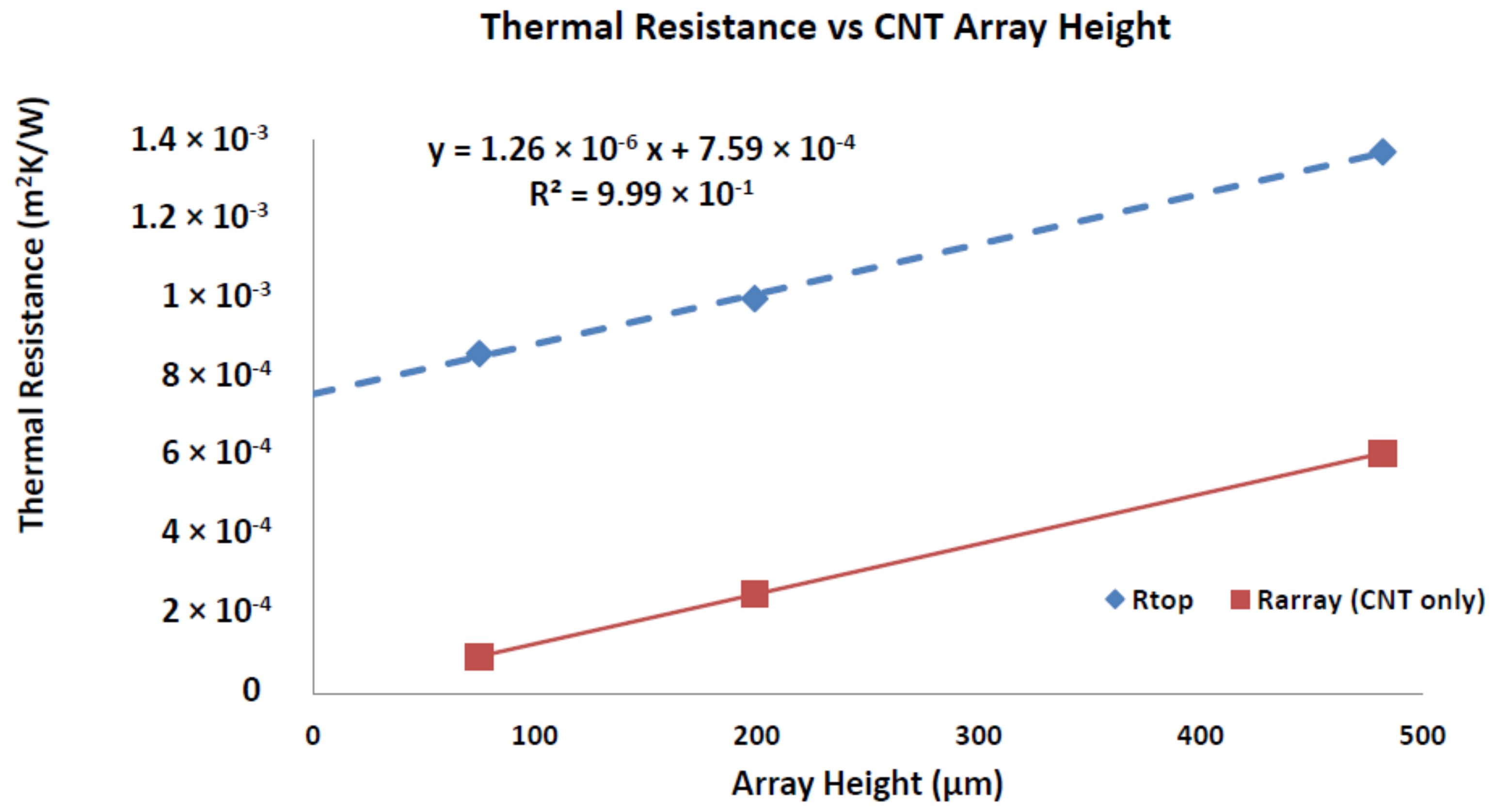
3.2.3. Thermal Analysis of Substrates with a Buffer Layer and CNT Array Film
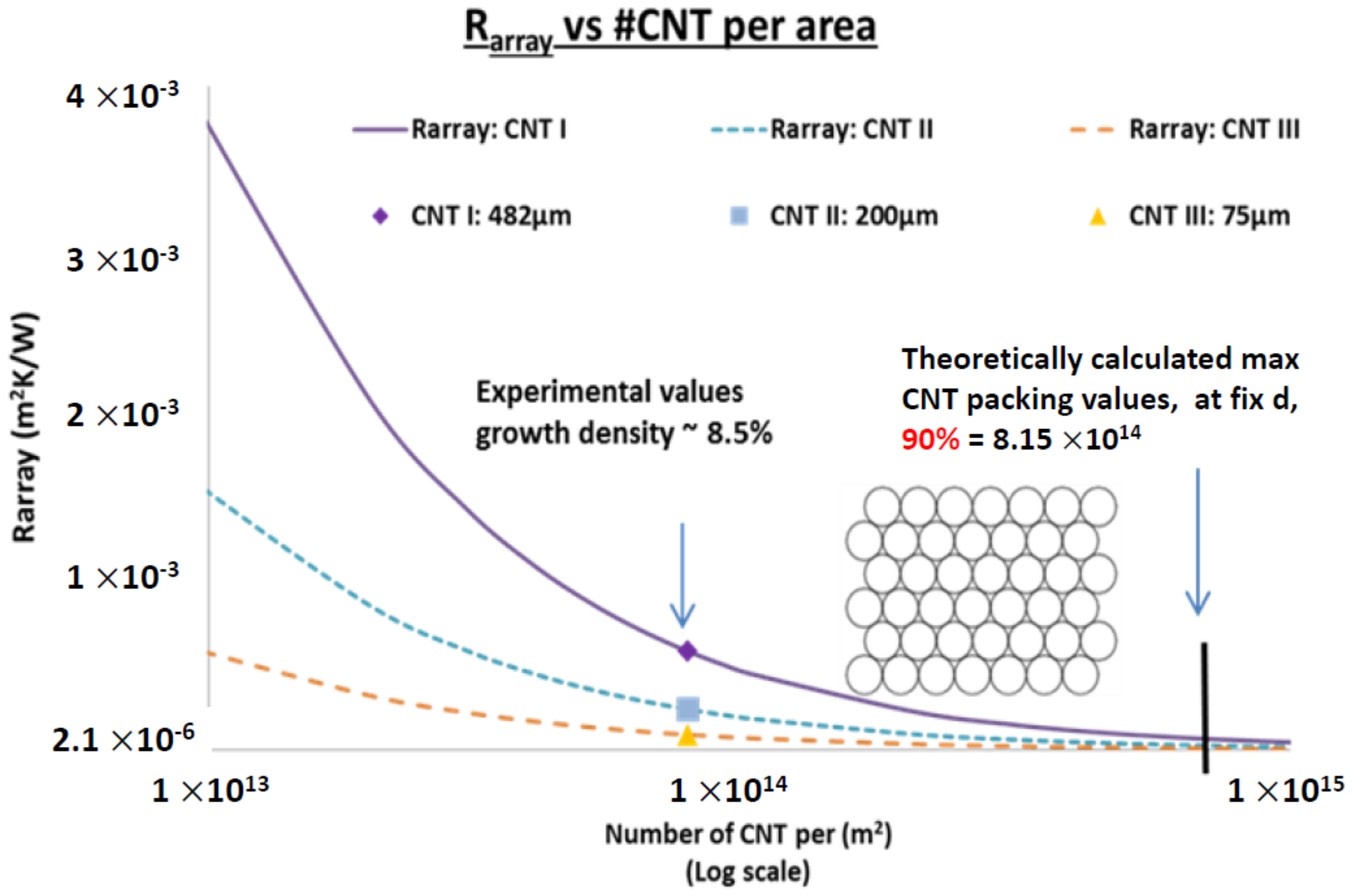
3.2.4. CNT Thermal Conductivity Analysis
3.2.5. Thermal Resistance Analytical Model
4. Concluding Remarks
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Incropera, F.P.; DeWitt, D.P. Fundamental of Heat and Mass Transfer, 5th ed.; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Ganguli, S.; Roy, A.K.; Wheeler, R.; Varshney, V.; Du, F.; Dai, L. Superior thermal interface via vertically aligned carbon nanotubes grown on graphite foils. J. Mater. Res. 2012, 28, 933–939. [Google Scholar] [CrossRef][Green Version]
- Sarvar, F.; Whalley, D.; Conway, P. Thermal Interface Materials—A Review of the State of the Art. In Proceedings of the 2006 1st Electronic Systemintegration Technology Conference, Dresden, Germany, 5–7 September 2006; Volume 2, pp. 1292–1302. [Google Scholar]
- Balandin, A. Thermal Properties of graphene and nanostructured carbon material. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef] [PubMed]
- Renteria, J.D.; Nika, D.L.; Balandin, A.A. Graphene thermal Properties: Applications in Thermal Management and Energy Storage. Appl. Sci. 2014, 4, 525–547. [Google Scholar] [CrossRef]
- Nika, D.L.; Balanddin, A. Phonons and thermal transport in graphene and graphene-based materials. Rep. Prog. Phys. 2017, 80, 036502. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Timmermans, M.Y.; Tian, Y.; Nasibulin, A.G.; Kauppinen, E.I.; Kishimoto, S.; Mizutani, T.; Ohno, Y. Flexible high-performance carbon nanotube integrated circuits. Nat. Nanotechnol. 2011, 6, 156–161. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Kim, H.; Pimparkar, N.; Kulkarni, J.P.; Wang, C.; Shim, M.; Roy, K.; Alam, M.A.; Rogers, J.A. Medium-scale carbon nanotube thin-film integrated circuits on flexible plastic substrates. Nature 2008, 454, 495–500. [Google Scholar] [CrossRef] [PubMed]
- Prestes, E.; Souza, T.; Pandolfelli, V.; Gomes, D. Thermal Expansion Mismatch Analysis of Nano-bonded Refractory Castables. Int. J. Appl. Ceram. Technol. 2014, 11, 984–992. [Google Scholar] [CrossRef]
- Prieto, R.; Molina, J.M.; Narciso, J.; Louis, E. Fabrication and properties of graphite flakes/metal composites for thermal management applications. Scr. Mater. 2008, 59, 11–14. [Google Scholar] [CrossRef]
- Molina, J.M.; Narciso, J.; Weber, L.; Mortensen, A.; Louis, E. Thermal conductivity of Al-SiC composites with monomodal and bimodal particle size distribution. Mater. Sci. Eng. A 2008, 480, 483–488. [Google Scholar] [CrossRef]
- Molina, J.M.; Rodríguez-Guerrero, A.; Louis, E.; Rodríguez-Reinoso, F.; Narciso, J. Porosity effect on thermal properties of Al-12 wt % Si/graphite composites. Materials (Basel) 2017, 10, 177. [Google Scholar] [CrossRef] [PubMed]
- Malekpour, H.; Chang, K.H.; Chen, J.C.; Lu, C.Y.; Nika, D.L.; Novoselov, K.S.; Balandin, A.A. Thermal conductivity of graphene laminate. Nano Lett. 2014, 14, 5155–5161. [Google Scholar] [CrossRef] [PubMed]
- Renteria, J.D.; Ramirez, S.; Malekpour, H.; Alonso, B.; Centeno, A.; Zurutuza, A.; Cocemasov, A.I.; Nika, D.L.; Balandin, A.A. Strongly Anisotropic Thermal Conductivity of Free-Standing Reduced Graphene Oxide Films Annealed at High Temperature. Adv. Funct. Mater. 2015, 25, 4664–4672. [Google Scholar] [CrossRef]
- Gulotty, R.; Castellino, M.; Jagdale, P.; Tagliaferro, A.; Balandin, A.A. Effects of functionalization on thermal properties of single-wall and multi-wall carbon nanotube-polymer nanocomposites. ACS Nano 2013, 7, 5114–5121. [Google Scholar] [CrossRef] [PubMed]
- Renteria, J.; Legedza, S.; Salgado, R.; Balandin, M.P.; Ramirez, S.; Saadah, M.; Kargar, F.; Balandin, A.A. Magnetically-functionalized self-aligning graphene fillers for high-efficiency thermal management applications. Mater. Des. 2015, 88, 214–221. [Google Scholar] [CrossRef]
- Berber, S.; Kwon, Y.; Tomanek, D. Unusually high thermal conductivity of carbon nanotubes. Phys. Rev. Lett. 2000, 84, 4613. [Google Scholar] [CrossRef] [PubMed]
- Akoshima, M.; Hata, K.; Futaba, D.N.; Mizuno, K.; Baba, T.; Yumura, M. Thermal diffusivity of single-walled carbon nanotube forest measured by laser flash method. Jpn. J. Appl. Phys. 2009, 48, 05EC07. [Google Scholar] [CrossRef]
- Hone, J.; Whitney, M.; Piskoti, C.; Zettl, A. Thermal conductivity of single-walled carbon nanotubes. Phys. Rev. B 1999, 59, R2514–R2516. [Google Scholar] [CrossRef]
- Hone, J. Carbon Nanotubes: Thermal Properties. In Dekker Encyclopedia of Nanoscience and Nanotechnology; CRC Press: Boca Raton, FL, USA, 2004; pp. 603–611. [Google Scholar]
- Sato, K.; Shiraiwa, T.; Maruyama, T.; Naritsuka, S. Effect of buffer thickness on single-walled Carbon Nanotube Growth Using Aluminum Oxide Buffer Layer with Alcohol Gas Source Method. J. Nanosci. Nanotechnol. 2010, 10, 3929–3933. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Miao, T.; Zhang, X.; Yang, L.; Cai, A.; Yong, Z.; Li, Q. Thermal performance of vertically-aligned multi-walled carbon nanotube array grown on platinum film. Carbon 2014, 77, 266–274. [Google Scholar] [CrossRef]
- Fujii, M.; Zhang, X.; Xie, H.; Ago, H.; Takahashi, K.; Ikuta, T.; Abe, H.; Shimizu, T. Measuring the Thermal Conductivity of a Single Carbon Nanotube. Phys. Rev. Lett. 2005, 95, 65502. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Shi, L.; Yao, Z.; Li, D.; Majumdar, A. Thermal conductance and thermopower of an individual single-wall carbon nanotube. Nano Lett. 2005, 5, 1842–1846. [Google Scholar] [CrossRef] [PubMed]
- Kim, P.; Shi, L.; Majumdar, A.; McEuen, P.L. Thermal Transport Measurements of Individual Multiwalled Nanotubes. Phys. Rev. Lett. 2001, 87, 215502. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Liu, C.; Wang, X.; Fan, S. Measuring the thermal conductivity of individual carbon nanotubes by the Raman shift method. Nanotechnology 2009, 20, 145702. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.J.; Zhang, Q.; Chen, G.; Yoon, S.F.; Ahn, J.; Wang, S.G.; Zhou, Q.; Wang, Q.; Li, J.Q. Thermal conductivity of multiwalled carbon nanotubes. Phys. Rev. B 2002, 66, 165440. [Google Scholar] [CrossRef]
- Ivanov, I.; Puretzky, A.; Eres, G.; Wang, H.; Pan, Z.; Cui, H.; Jin, R.; Howe, J.; Geohegan, D.B. Fast and highly anisotropic thermal transport through vertically aligned carbon nanotube arrays. Appl. Phys. Lett. 2006, 89, 174–177. [Google Scholar] [CrossRef]
- Hu, M.; Keblinski, P.; Wang, J.-S.; Raravikar, N. Interfacial thermal conductance between silicon and a vertical carbon nanotube. J. Appl. Phys. 2008, 104, 83503. [Google Scholar] [CrossRef]
- Lin, W.; Shang, J.; Gu, W.; Wong, C.P. Parametric study of intrinsic thermal transport in vertically aligned multi-walled carbon nanotubes using a laser flash technique. Carbon 2012, 50, 1591–1603. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, Z.; Xu, J. Noncontact thermal characterization of multiwall carbon nanotubes. J. Appl. Phys. 2005, 97, 064302. [Google Scholar] [CrossRef]
- Shaikh, S.; Li, L.; Lafdi, K.; Huie, J. Thermal conductivity of an aligned carbon nanotube array. Carbon 2007, 45, 2608–2613. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.M.; Karumuri, A.; Barney, I.T. Hierarchical nanostructures by nanotube grafting on porous cellular surfaces. J. Phys. D Appl. Phys. 2009, 42, 195503. [Google Scholar] [CrossRef]
- Barney, I.T.; Ganguli, S.; Roy, A.K.; Mukhopadhyay, S.M. Improved Thermal Response in Encapsullated Phase change materials by nanotube Attachment on Encapsulating Solid. J. Nanotechnol. Eng. Med. 2012, 3, 031005. [Google Scholar] [CrossRef]
- Quinton, B.T.; Leedy, K.D.; Lawson, J.W.; Tsao, B.; Scofield, J.D.; Merrett, J.N.; Zhang, Q.; Yost, K.; Mukhopadhyay, S.M. Influence of oxide buffer layers on the growth of carbon nanotube arrays on carbon substrates. Carbon 2015, 87, 175–185. [Google Scholar] [CrossRef]
- Pulikollu, R.V. Nano-Coatings on Carbon Structures for Interfacial Modification. Ph.D. Dissertation, Wright State University, Dayton, OH, USA, 2005. [Google Scholar]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbott, G.L. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. J. Appl. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
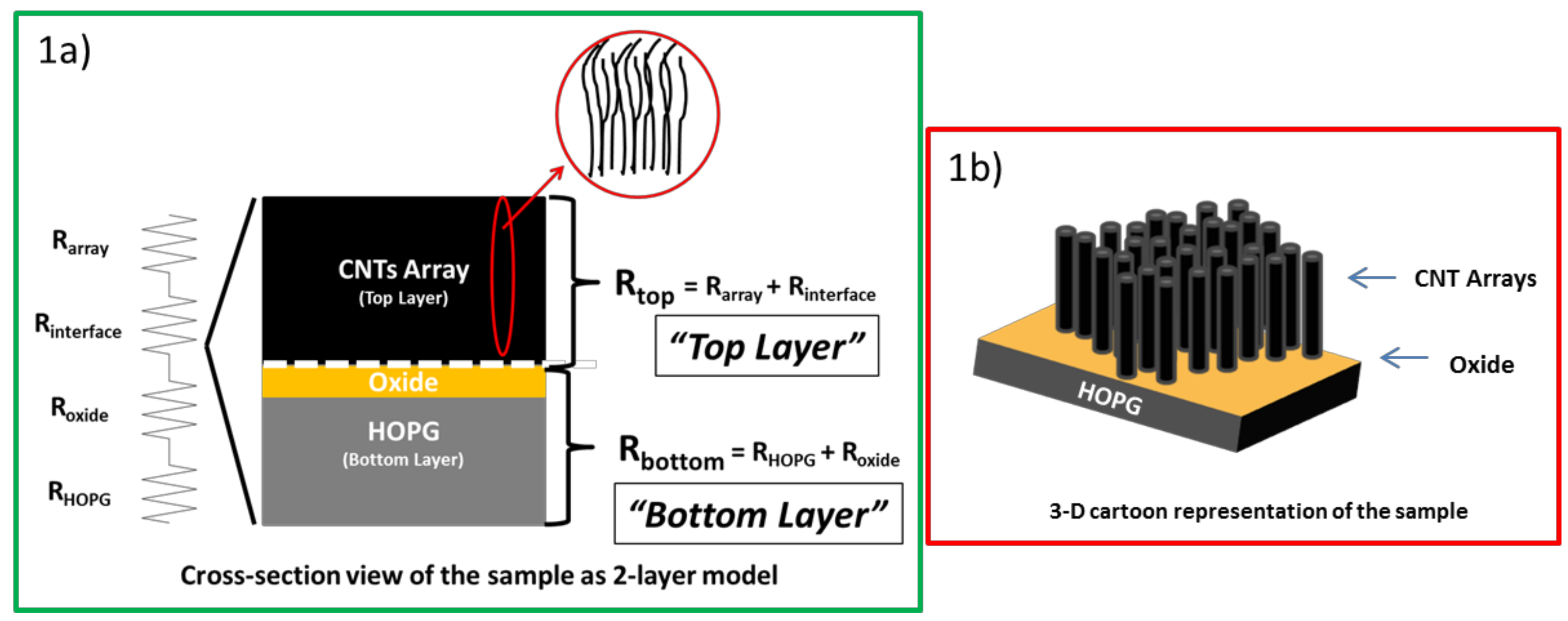


| Bottom Layer Samples | Cap | Top Layer Samples | |||||
|---|---|---|---|---|---|---|---|
| Units | HOPG 1 | HOPG 2 | HOPG 3 | HOPG Cap | CNT I (482 μm) | CNT II (199 μm) | CNT III (75 μm) |
| mm | 10 mm × 10 mm (nominal sample Size) | ||||||
| mm | 1.23 ± 0.01 | 1.37 ± 0.01 | 1.42 ± 0.01 | 1.15 ± 0.01 | 0.482 ± 8 × 10−4 | 0.199 ± 7 × 10−4 | 0.075 ± 6 × 10−4 |
| g | 0.2518 | 0.306 | 0.3148 | 0.2363 | 4.2 × 10−3 | 2.1 × 10−3 | 1.90 × 10−3 |
| g/cm3 | 2.16 ± 0.01 | 0.091 | 0.102 | 0.248 | |||
| Bottom Layer Samples | Top Layer Samples | ||||||
|---|---|---|---|---|---|---|---|
| Units | HOPG 1 | HOPG 2 | HOPG 3 | CNT I (482 μm) | CNT II (199 μm) | CNT III (75 μm) | |
| α | mm2/s | 3.864 ± 0.06 | 4.053 ± 0.08 | 4.177 ± 0.09 | 6.099 ± 0.04 | 3.088 ± 0.04 | 0.558 ± 0.03 |
| Cp | J/(g × K) | 0.63 ± 0.01 | |||||
| κ | W/mK | 5.23 | 5.52 | 5.71 | 0.351 | 0.199 | 0.087 |
| Rbottom = Rsub + Roxide | m2 K/W | 2.35 × 10−4 | 2.48 × 10−4 | 2.49 × 10−4 | - | ||
| Roxide | m2 K/W | 5.21 × 10−8 | |||||
| Rtop = Rarray + Rinterface | m2 K/W | - | 1.37 × 10−3 | 1 × 10−3 | 8.61 × 10−4 | ||
| Rinterface (Figure 5) | m2 K/W | 7.59 × 10−4 | |||||
| κarray (Figure 5) | m2 K/W | 7.91 × 10−1 | |||||
| Rarray | m2 K/W | 6.09 × 10−4 | 2.52 × 10−4 | 9.48 × 10−5 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quinton, B.T.; Elston, L.; Scofield, J.D.; Mukhopadhyay, S.M. Aligned Carbon Nanotube Arrays Bonded to Solid Graphite Substrates: Thermal Analysis for Future Device Cooling Applications. C 2018, 4, 28. https://doi.org/10.3390/c4020028
Quinton BT, Elston L, Scofield JD, Mukhopadhyay SM. Aligned Carbon Nanotube Arrays Bonded to Solid Graphite Substrates: Thermal Analysis for Future Device Cooling Applications. C. 2018; 4(2):28. https://doi.org/10.3390/c4020028
Chicago/Turabian StyleQuinton, Betty T., Levi Elston, James D. Scofield, and Sharmila M. Mukhopadhyay. 2018. "Aligned Carbon Nanotube Arrays Bonded to Solid Graphite Substrates: Thermal Analysis for Future Device Cooling Applications" C 4, no. 2: 28. https://doi.org/10.3390/c4020028
APA StyleQuinton, B. T., Elston, L., Scofield, J. D., & Mukhopadhyay, S. M. (2018). Aligned Carbon Nanotube Arrays Bonded to Solid Graphite Substrates: Thermal Analysis for Future Device Cooling Applications. C, 4(2), 28. https://doi.org/10.3390/c4020028





