Abstract
In this study, the vibrational properties of single- and double-layer graphene sheets (GSs) with attached nanoparticles are analyzed based on the nonlocal elasticity theory. The potential applications of atomic-scale mass sensing are presented using GSs with simply supported boundary condition. The frequency equation for GSs with an attached nanoparticle is derived to investigate the vibration frequency of the GSs under thermal environment. Using the proposed model, the relationship between the frequency shifts of graphene-based mass sensor and the attached nanoparticles is obtained. The nonlocal effect and the temperature dependence on the variation of frequency shifts with the attached nanomass and the positions on the GS are investigated and discussed in detail. The obtained results show that the nanomass can be easily detected by using GS resonator which provides a highly sensitive nanomechanical element in sensor systems. The vibrational frequency shift of GS increases with increasing the temperature dependence. The double-layer GSs (DLGSs) have higher sensitivity than the single-layer GSs (SLGSs) due to high frequency shifts.
1. Introduction
Graphene sheets (GSs) are an excellent two-dimensional (2D) material, and have drawn attention in recent years. Due to the unique properties of small size, super mechanical properties, and high vibration frequency, graphene sheets have been considered an ideal structure element for fabricating nanoelectromechanical systems (NEMS) [,,]. Novel graphene-based nanostructures are believed to have tremendous potential applications for developing sensors of various types such as magnetic and electric field sensors, strain and nanoscale mass sensors [,,,,]. The mechanism of using GSs as nanoscale mass sensing is based on the fact that the resonant frequency of GSs is shifted upward when a nanoparticle is loaded onto the GSs and the shift frequency is sensitive to the attached nanomass. One relevant application of the GSs is given by carbon nanotubes (CNTs) which can be obtained by rolling a graphene sheet into a cylinder. Due to their mechanical and physical properties, CNTs are applied as ultrahigh-frequency nano-mechanical resonators in a large number of NEMS such as sensors, oscillators and charge detectors [,,,,,,].
At present, the elastic continuum theory and model have been regarded as an effective way to investigate the vibration behavior of GSs [,]. The vibration analysis of multilayered graphene sheets (MLGSs) using a continuum model has been reported by Kitipornchai et al. []. They indicated that the vibration modes of the graphene sheets that were associated with the resonant frequencies were quite different due to the influence of the Van der Waals (vdW) interaction between any two nanosheets. The lowest natural frequency of a MLGS was independent of the vdW interaction, but all of the other higher natural frequencies depended largely on the vdW interaction. Natsuki’s group has investigated the vibrational characteristics of embedded double-layer graphene nanoribbons (DLGNRs) based on the nonlocal elasticity theory []. The results showed that the vibrational frequency of DLGNRs had a significant difference between the in-phase mode (IPM) and the anti-phase mode (APM). The nonlocal parameter affected the natural frequencies, especially for higher modes of vibration. Moreover, the natural frequencies of the APM were less sensitive to the vibration modes than those of the IPM. The operation of a NEMS mass sensor relied on monitoring how the resonance frequency of a nanomechanical resonator changed when an additional nanomass was adsorbed onto its surface [,,,]. Many studies have shown that GSs exhibit ultrahigh frequency ranges up to the terahertz order because of the inherent characteristics of the materials [,,,,]. These inherent characteristics led to a higher sensitivity to atomic-scale mass detection, whereby the attached nanomass can easily cause a shift in the resonant frequency of the GS resonator.
Ultrasonic vibration and attenuation are the important properties for design and performance of the sensor devices. Graphene sheets appear to be excellent element materials for structures of nanomechanical resonators because they can generate terahertz frequency vibration. Some studies have been carried out on utilizing the molecular dynamics (MD) method [,], molecular structural mechanics [] or continuum mechanics [,,,,] to investigate the applications of single-layer graphene sheets (SLGSs) for NEMS mass sensors. However, there is very little investigation of the resonant frequency of double-layer graphene sheets (DLGSs) used as mass sensors and how temperature affects the vibration frequency of GSs [].
In this paper, an analytical method based on the nonlocal elasticity theory [,,] is introduced to predict the vibrational property of GSs as nanoscale sensing. The potential applications using single- and double-layer GSs with a simply supported boundary condition are illustrated. To investigate the vibration frequency of GSs under a thermal environment, the frequency equation in GSs for attaching a nanoparticle is derived. Using the present theory, the relationship between the frequency shifts of the graphene-based mass sensor and the attached nanoparticles is investigated in detail.
2. Theoretical Approach
2.1. Governing Equation Based on Nonlocal Elasticity
We present a continuum elastic model to analyze the vibration frequency of the nanomechanical mass sensor when temperature effects are considered. As shown in Figure 1, a nanoparticle is attached to a simply supported graphene sheet (GS) in an arbitrary position , thereby inducing a vibrational frequency shift due to the attached mass. The origin is taken at a corner of the mid-plane of the nanoplate. The coordinates x and y are taken along the length and the width of the GSs, respectively. The coordinate z is taken along the thickness direction of the GSs.
Figure 1.
Schematic illustration showing graphene sheet with an attached mass.
In the analysis, the vibration frequency of GSs is analyzed based on nonlocal elasticity theory. For the nonlocal linear elastic solids, Hook’s law of nanoplates can be expressed as
where and are the normal stress and the shear stress. and are the axial strain and shear strain. , and are the tensile, shear elastic modulus and Poisson’s ratio, respectively. is the coefficient of thermal expansion, and is the temperature change. The parameter is the nonlocal parameter appropriate to GSs, where is a constant appropriate to the material and has to be determined for each material independently by experiment or atomistic simulation. is the internal characteristic length of a carbon-carbon bond (e.g., lattice parameter, granular size, distance between atoms’ bond) [,].
The expressions between the strain and the displacement are []
where is the transverse displacement.
The bending and shear moments can be defined by
Substituting Equation (1) into Equation (3) and using Equation (2), we obtain
and
According to the elastic theory of thin plates, the governing equation of the vibration for GSs with the external load is given in
where is an attached nanoparticle mass, is the thickness of GSs, is the time, δ is the Dirac delta function, and is the load caused by the temperature change given by
Substituting Equation (4) into Equation (6), we yield
The bi-harmonic operator is given by
2.2. Dynamic Analysis for Single-Layer Graphene Sheet (SLGSs)
We can introduce the following substitution to obtain the vibration frequency of the governing equations for SLGSs
where is the shape function of deflection, and ω is the resonant frequency of the GSs.
Substituting Equation (10) into Equation (8), the governing equation is written as
To obtain the solution of Equation (11), we consider GSs subjected to a simply supported condition. For the simply supported GSs, we have
To satisfy the above set of boundary conditions, therefore, the shape function of deflection in Equation (10) can be expressed as:
where is the vibration amplitude of oscillation. m and n indicate the mode numbers.
Substituting Equation (13) into Equation (11), we get
Multiplying Equation (14) by and integrating over the whole region with respect to x and y with the limits to and to , we obtain the following frequency equation after simplifications,
where , is the non-dimensional position of the attached nanoparticle. According to the Equation (15), the natural frequency of GSs can be given as .
2.3. Dynamic Analysis for Double-Layer Graphene Sheet (DLGSs)
In the analysis for DLGSs with attached nanoparticles, the governing equations are given by the two coupled equations
where are the flexural deflections of the upper sheet (j = 1) and lower sheet (j = 2). c is the vdW interaction coefficient between the upper and lower layers, which can be obtained from the Lennard-Jones pair potential [], given as:
where and are parameters chosen to fit the physical properties of GSs. , where is the coordinate of the jth layer in the direction of thickness with the origin at the midplane of the GSs, and is the C–C bond length.
To obtain the vibration frequency for the governing equations Equation (16), we can introduce the following substitution
where is the shape function of deflection in the upper and the lower sheets, whereas ω is the resonant frequency of the DLGS sensor.
Substituting Equation (18) into Equation (16), the coupled governing equations of the vibration in DLGSs are written in the following matrix form:
and
Algebraic manipulation of Equation (20) reduces it to a single equation, which is
where , or .
For simply supported boundary condition, we can obtain the following frequency equation based on the same method with single-layer GSs.
and
The solution of Equation (22) yields the sought natural frequency of DLGSs. The anti-phase mode of the sought natural frequency, in which the deflection of the upper and lower layers occurs in the opposite direction, is obtained from:
3. Results and Discussion
In this simulation, GSs used as the nanomechanical resonator are considered to be simply supported. The vibration mode takes the fundamental frequency , and the anti-phase vibration for the DLGSs, in which the deflection of the upper and lower layers occurs in the opposite direction. In order to investigate the vibrational behavior of a GS mass sensor, the geometrical dimensions and the material constants are given as follows: The effective thickness h of each layer of GS was 0.127 nm. The aspect ratio of GSs is 20, which is defined as the side length to the thickness. The Young’s modulus E and the density ρ of GSs were 2.81 TPa and 2300 kg/m3 []. The coefficient of thermal expansion of GSs was 2.2×10−6/K [].
The Young’s modulus and the thickness of GSs from the literature [] are given in Table 1, and the frequency shifts of GSs with attached nanomass of 100 zg (1 zg = 10−24 kg are obtained based on the proposed analytical mode.

Table 1.
Young’s modulus, thickness and the frequency shifts of GSs [].
Here, the frequency shift is defined as the difference between the natural frequency of a GS with and without attached nanoparticles, that is . It can be observed that the frequency shifts of GSs with attached nanoparticles are larger for the temperature dependence. The variation errors of frequency shifts are about 2% when the temperature change is only 5 K, especially if the error value increases up to 8.45 % at the Young’s modulus (6.88 TPa) and there is a small thickness of around 0.052 nm of the GS. This suggests that the temperature dependence of the frequency shift is affected largely by the Young’s modulus and the thickness of GSs.
Figure 2 shows the location dependence of attached nanoparticles on the frequency shift of the SLGSs as a function of the attached mass under the temperature difference of 100 K. The attached mass is located at the center of the GSs; near to the corner ; and near to the edge . The frequency shift value of GSs increases with increasing attached mass because the attached nanoparticles increase the overall mass of the GS resonator. It can be deduced from Figure 2 that the location influence of the nanoparticles on the frequency shift is significant within a mass range from 10 to 1000 zg. The value of frequency shifts of GSs at the center load is larger than those away from the center location. This suggests that the sensitivity of the GS mass sensor is high when nanoparticles are located at the center of GSs.
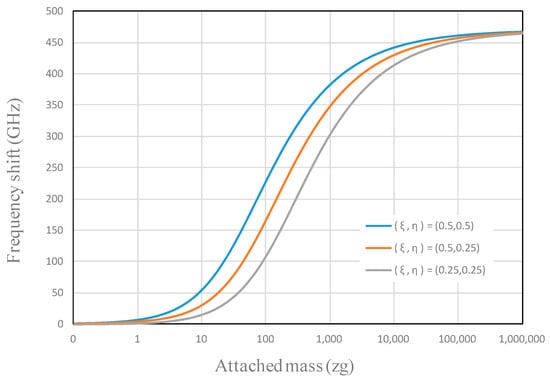
Figure 2.
Location influence of the attached nanoparticle on the frequency shift of single-layer graphene sheets (SLGSs) (e0a = 2.0 nm, ΔT = 100 K).
As shown in Figure 3, the effects of temperature difference and nonlocal parameter on the vibration frequency shift of GSs are investigated for an attached mass of 100 zg. In this simulation, we assume that the nonlocal parameter is 0, 2.0 and 4.0 nm []. It is found that the nonlocal parameter affects the vibrational frequency shift of GSs. The value of the frequency shift decreases with increasing nonlocal parameter, and increases with the temperature difference. Figure 4 shows the relationship between frequency shift and temperature difference. It is evident that the effect of temperature difference on the frequency shift is greater for a small mass than for a large mass.
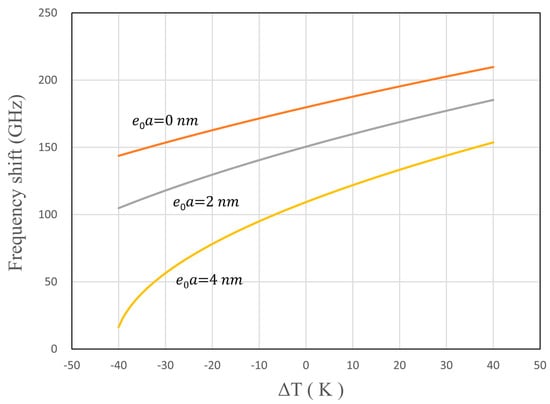
Figure 3.
Variation of the vibration frequency shift with the temperature difference for different nonlocal parameters (m = 100 zg, ξ = η = 0.5).
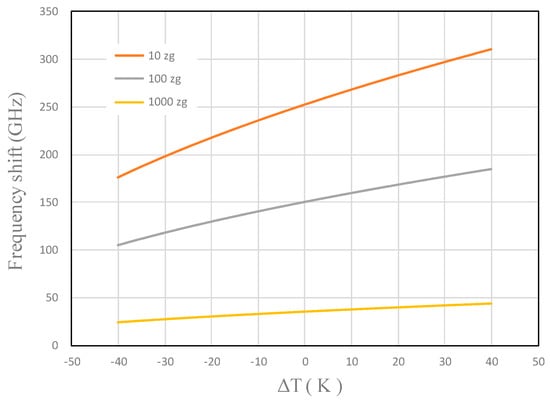
Figure 4.
Variation of the vibration frequency shift with the temperature difference for different nanomass sizes (e0a = 2.0 nm, ξ = η = 0.5).
Figure 5 shows a comparison of the frequency shift between SLGSs and DLGSs with the temperature difference of 100 K. The frequency shift of the GS resonator increases with increasing mass of nanoparticles. The DLGSs used as a nanomechanical resonator can provide higher sensitivity than the SLGSs due to large change in the vibrational frequency shift. It can be found that the frequency shift versus the attached mass show a nearly logarithmic linear relationship within a certain range. According to this simulation, the relationship between the frequency shift and the attached mass can be well represented by the exponential function , which has the double logarithmic linear relationship. The values of the parameters α and β can be determined easily by fitting the simulated curve and to obtain high accuracy calibration between frequency shift and attached mass. A logarithmically linear relationship is found between the frequency shift and the attached mass when the total mass attached to the GSs is less than 1.0 zg.
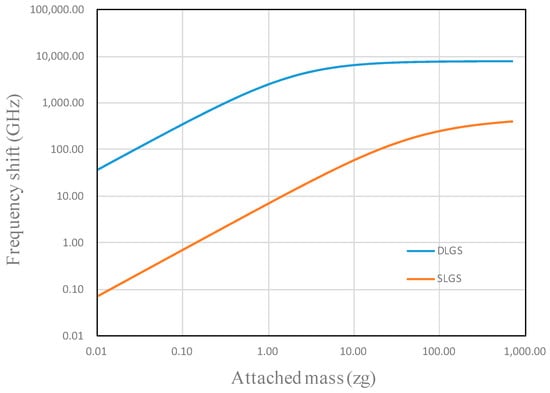
Figure 5.
Comparison of the frequency shift between DLGSs and SLGSs with attached nanoparticle for the temperature difference of ΔT = 100 K (e0a = 0 nm, ξ = η = 0.5).
4. Conclusions
In this study, we propose an analytical model to investigate the vibration frequency of simply supported graphene sheets (GSs) using the nonlocal elasticity theory. The relationship between the vibrational frequency of GSs and the attached mass is derived analytically, and the influences of the position of the nanoparticles and the mass on the frequency shifts of GSs are analyzed in detail. Because the mass of a GS is quite small, the frequency shifts can easily change when a relatively small mass of a nanoparticle is added to the GS. Based on the simulation, the results indicate the resolution of a mass sensor could achieve an order of 100 zg. The result demonstrates that the temperature and the nonlocal parameter affect the vibration frequency shift of the GSs. Moreover, the double-layer graphene sheets (DLGSs) used as a nanomechanical mass sensor provide higher sensitivity than the SLGSs. In this simulation, the results show that the Young’s modulus and the thickness of the GS affect temperature dependence of frequency shifts, especially the error value which increases for high Young’s modulus and small thickness. It is evident that the variation errors of frequency shifts are about 2% when the temperature change is only 5 K. The simulation technology and the parameters of investigation, such as temperature, nonlocal coefficient, geometric and material parameters, are thus very useful in designing GSs used as nano-scale sensing.
Acknowledgments
This work was supported by JSPS KAKENHI Grant Number 26420698.
Author Contributions
Toshiaki Natsuki contributed to the planning, the analytical model and its solutions. Atsushi Yiwada performed the program of the analytical solution and obtained the analytical results. Jun Natsuki wrote and edited the manuscript. All authors approved the final version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, H.J.; Zhu, K.D. Graphene-based nanoresonator with applications in optical transistor and mass sensing. Sensors 2014, 14, 16740–16753. [Google Scholar] [CrossRef] [PubMed]
- Fazelzadeh, S.A.; Ghavanloo, E. Nanoscale mass sensing based on vibration of single-layered graphene sheet in thermal environments. Acta Mech. Sin. 2014, 30, 84–91. [Google Scholar] [CrossRef]
- Ekinci, K.L.; Huang, X.M.H.; Roukes, M.L. Ultrasensitive nanoelectromechanical mass detection. Appl. Phys. Lett. 2004, 84, 4469–4471. [Google Scholar] [CrossRef]
- Hill, E.W.; Vijayaragahvan, A.; Novoselov, K. Graphene sensors. IEEE Sens. J. 2011, 11, 3161–3170. [Google Scholar] [CrossRef]
- Varghese, S.S.; Varghese, S.H.; Swaminathan, S.; Singh, K.K.; Mittal, V. Two-dimensional materials for sensing: Graphene and beyond. Electronics 2015, 4, 651–687. [Google Scholar] [CrossRef]
- Babaei, H.; Shahidi, A.R. Vibration of quadrilateral embedded multilayered graphene sheets based on nonlocal continuum models using the Galerkin method. Acta Mech. Sin. 2011, 27, 967–976. [Google Scholar] [CrossRef]
- Xiong, W.; Liu, J.Z.; Zhang, Z.L.; Zheng, Q.S. Control of surface wettability via strain engineering. Acta Mech. Sin. 2013, 29, 543–549. [Google Scholar] [CrossRef]
- Endo, M.; Hayashi, T.; Kim, Y.A.; Terrones, M.; Dresselhaus, M.S. Applications of carbon nanotubes in the twenty-first century. Philos. Trans. R. Soc. Lond. A 2004, 362, 2223–2238. [Google Scholar] [CrossRef] [PubMed]
- Baughman, R.H.; Zakhidov, A.A.; de Heer, W.A. Carbon nanotubes. The route toward applications. Science 2002, 297, 787–792. [Google Scholar] [CrossRef] [PubMed]
- De Volder, M.F.L.; Tawfick, S.H.; Baughman, R.H.; Hart, A.J. Carbon Nanotubes: Present and future commercial applications. Science 2013, 339, 535–539. [Google Scholar] [CrossRef] [PubMed]
- Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Milani, M.; Pellicano, F. Nonlinear vibrations and energy exchange of single-walled carbon nanotubes. Circumferential flexural modes. J. Sound Vib. 2016, 381, 156–178. [Google Scholar] [CrossRef]
- Mahar, B.; Laslau, C.; Yip, R.; Sun, Y. Development of carbon nanotube-based sensors: A Review. IEEE Sens. J. 2007, 7, 266–284. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. Nonlinear dynamics of electrically actuated carbon nanotube resonators. J. Comput. Nonlinear Dyn. 2010, 5, 011009. [Google Scholar] [CrossRef]
- Li, C.; Thostenson, E.T.; Chou, T.W. Sensors and actuators based on carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2008, 68, 1227–1249. [Google Scholar] [CrossRef]
- Kitipornchai, S.; He, X.Q.; Liew, K.M. Continuum model for the vibration of multilayered graphene sheets. Phys Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Shi, J.X.; Ni, Q.Q.; Lei, X.W.; Natsuki, T. Nonlocal vibration of embedded double-layer graphene nanoribbons in in-phase and anti-phase modes. Physica E 2012, 44, 1136–1141. [Google Scholar] [CrossRef]
- Chaste, J.; Eichler, A.; Moser, J.; Ceballos, G.; Rurali, R.; Bachtold, A. A Nanomechanical Mass Sensor with Yoctogram Resolution. Nat. Nanotechnol. 2012, 7, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Eichler, A.; Moser, J.; Chaste, J.; Zdrojek, M.; Wilson-Rae, I.; Bachtold, A. Nonlinear damping in mechanical resonators made from carbon nanotubes and graphene. Nat. Nanotechnol. 2011, 6, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Pang, W.; Yan, L.; Zhang, H.; Yu, H.Y.; Kim, E.S.; Tang, W.C. Femtogram mass sensing platform based on lateral extensional mode piezoelectric resonator. Appl. Phys. Lett. 2006, 88. [Google Scholar] [CrossRef]
- Natsuki, T. Theoretical analysis of vibration frequency of graphene sheet used as nanomechanical mass sensor. Electronics 2015, 4, 723–738. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Kumar, A. Vibration analysis of orthotropic graphene sheets embedded in Pasternak elastic medium using nonlocal elasticity theory and differential quadrature method. Comput. Mater. Sci. 2010, 50, 239–245. [Google Scholar] [CrossRef]
- Chowdhury, R.; Adhikari, S.; Scarpa, F.; Friswell, M.I. Transverse vibration of single-layer graphene sheets. J. Phys. D Appl. Phys. 2011, 44, 205401. [Google Scholar] [CrossRef]
- Gupta, S.S.; Batra, R.C. Elastic Properties and Frequencies of Free Vibrations of Single-Layer Graphene Sheets. J. Comput. Theor. Nanosci. 2010, 7, 1–14. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q.; Duan, W.H. Detection of gas atoms via vibration of graphenes. Phys. Lett. A 2011, 375, 2411–2415. [Google Scholar] [CrossRef]
- Jiang, J.W.; Park, H.S.; Rabczuk, T. Enhancing the mass sensitivity of graphene nanoresonators via nonlinear oscillations: The effective strain mechanism. Nanotechnology 2012, 23. [Google Scholar] [CrossRef] [PubMed]
- Sakhaee-Pour, A.; Ahmadiana, M.T.; Vafaib, A. Applications of single-layered graphene sheets as mass sensors and atomistic dust detectors. Solid State Commun. 2008, 145, 168–172. [Google Scholar] [CrossRef]
- Lei, X.W.; Natsuki, T.; Shi, J.X.; Ni, Q.Q. Vibration analysis of circular double-layered graphene sheets. J. Appl. Phys. 2013, 113. [Google Scholar] [CrossRef]
- Dai, M.D.; Kim, C.W.; Eom, K. Nonlinear vibration behavior of graphene resonators and their applications in sensitive mass detection. Nanoscale Res. Lett. 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.B.; Tang, H.L.; Li, D.K.; Tang, G.J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal kirchhoff plate theory. Comput. Mater. Sci. 2012, 61, 200–205. [Google Scholar] [CrossRef]
- Lee, H.L.; Yang, Y.C.; Chang, W.J. Mass Detection Using a Graphene-Based Nanomechanical Resonator. Jpn. J. Appl. Phys. 2013, 52, 025101. [Google Scholar] [CrossRef]
- Benvenuti, E.; Simone, A. One-dimensional nonlocal and gradient elasticity: Closed-form solution and size effect. Mech. Res. Commun. 2013, 48, 46–51. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; de Marotti Sciarra, F. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2016. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Comment on the paper “Exact solution of Eringen’s nonlocal integral model for bending of Euler-Bernoulli and Timoshenko beams” by Meral Tuna & Mesut Kirca. Int. J. Eng. Sci. 2016, 109, 240–242. [Google Scholar]
- Decolon, C. Analysis of Composite Structure; HPS: London, UK, 2002; pp. 159–194. [Google Scholar]
- Shi, J.-X.; Natsuki, T.; Lei, X.-W.; Ni, Q.-Q. Equivalent Young’s modulus and thickness of graphene sheets for the continuum mechanical models. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).