A Multi-Input Neural Network Model for Accurate MicroRNA Target Site Detection
Abstract
1. Introduction
2. Data Collection Procedure
2.1. Computing Probabilities of All Possible Base Pairs Between Two Bases
2.2. Preparing MicroRNA Target-Site Dataset
2.2.1. MirTarBase
2.2.2. Helwak et al. Dataset
2.2.3. Diana-TarBase
2.2.4. Creating Training and Test Sets
3. Results
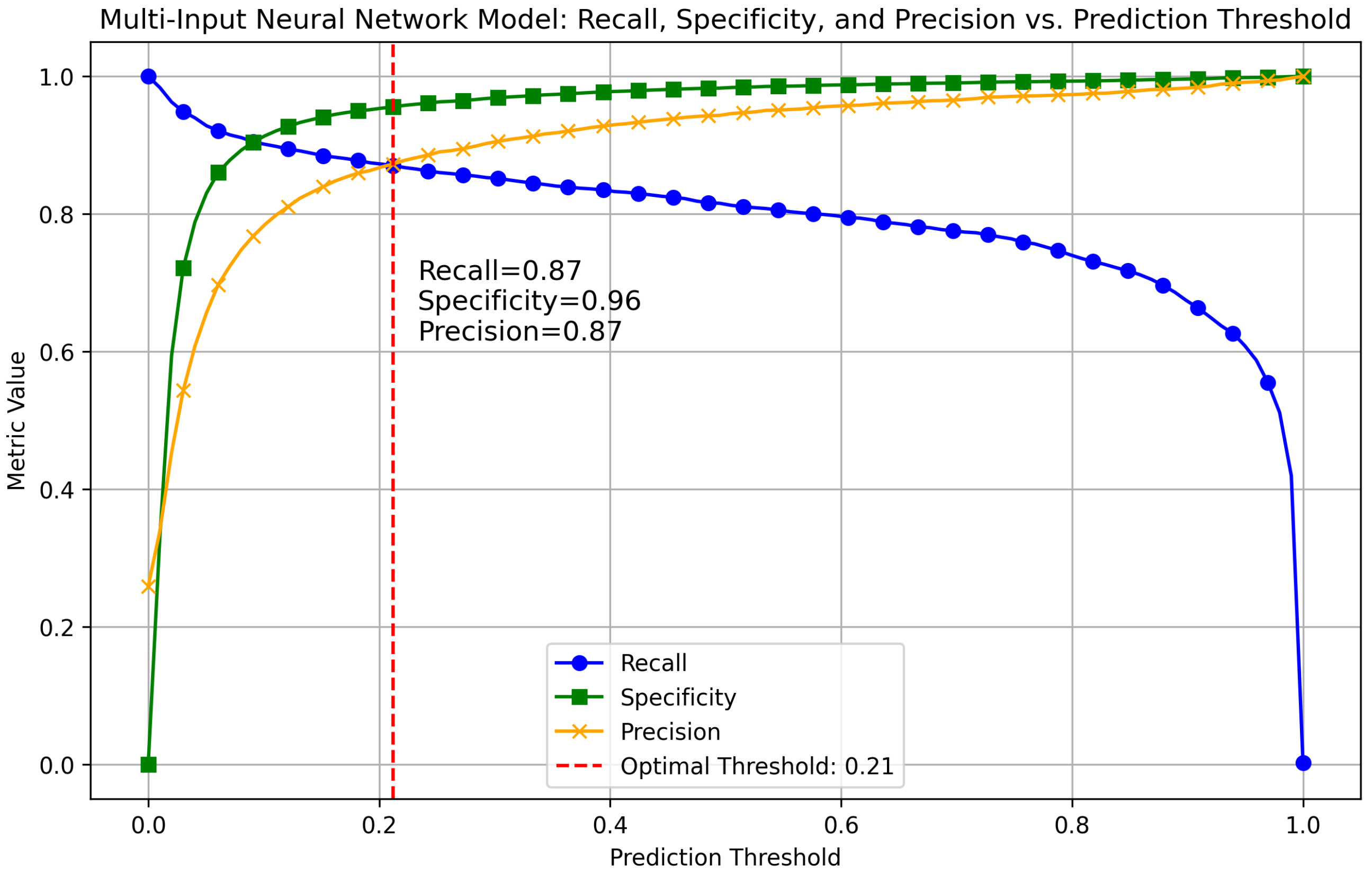
3.1. Hyperparameter Optimization and Model Selection
3.2. Performance Analysis of Computational Methods
3.3. Evaluating Generalization Capacity of MINN on an Independent Dataset
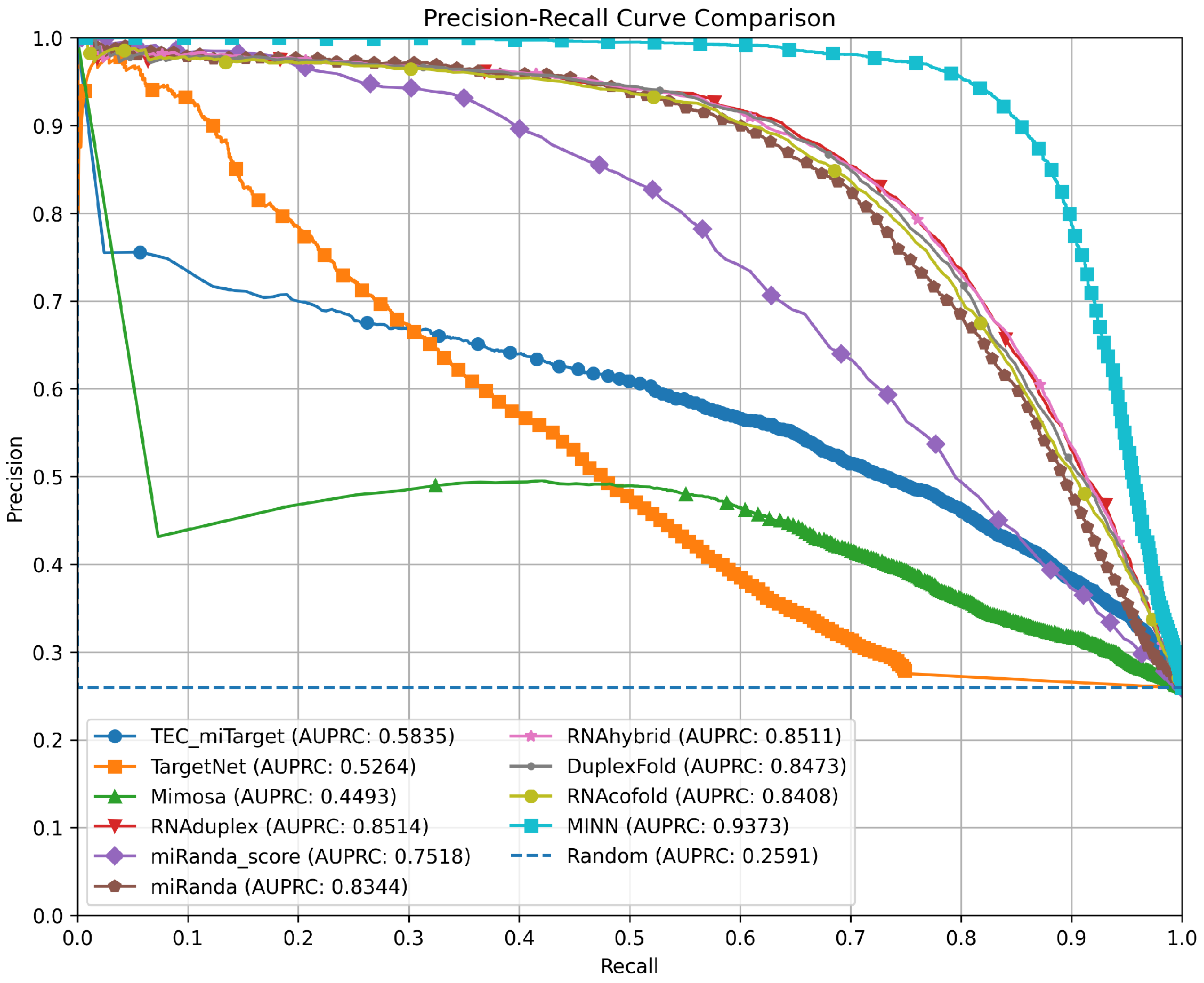
3.4. Precision–Recall Curves for Method Comparison
3.5. Bootstrap-Based Statistical Comparison of Model Performance
3.6. Logical Basis and Biological Interpretability of Feature Representations in the MINN Model
3.6.1. Importance of the Duplex Structure Matrix for Capturing Base-Pairing Preferences
3.6.2. Enhancing Structural Accuracy with the DP Scoring Table
3.6.3. Thermodynamic Insights from the DP MFE Table
3.6.4. Base Pairing Probabilities Matrix: Integrating Canonical and Non-Canonical Interactions
3.6.5. Integration of Features for Enhanced Predictive Power
3.7. Advantages and Limitations of the MINN Model
3.8. How the MINN Model Can Be Used and Its Potential Applications in MicroRNA Research
4. Materials and Methods
4.1. MicroRNA-Specific Secondary Structure Prediction
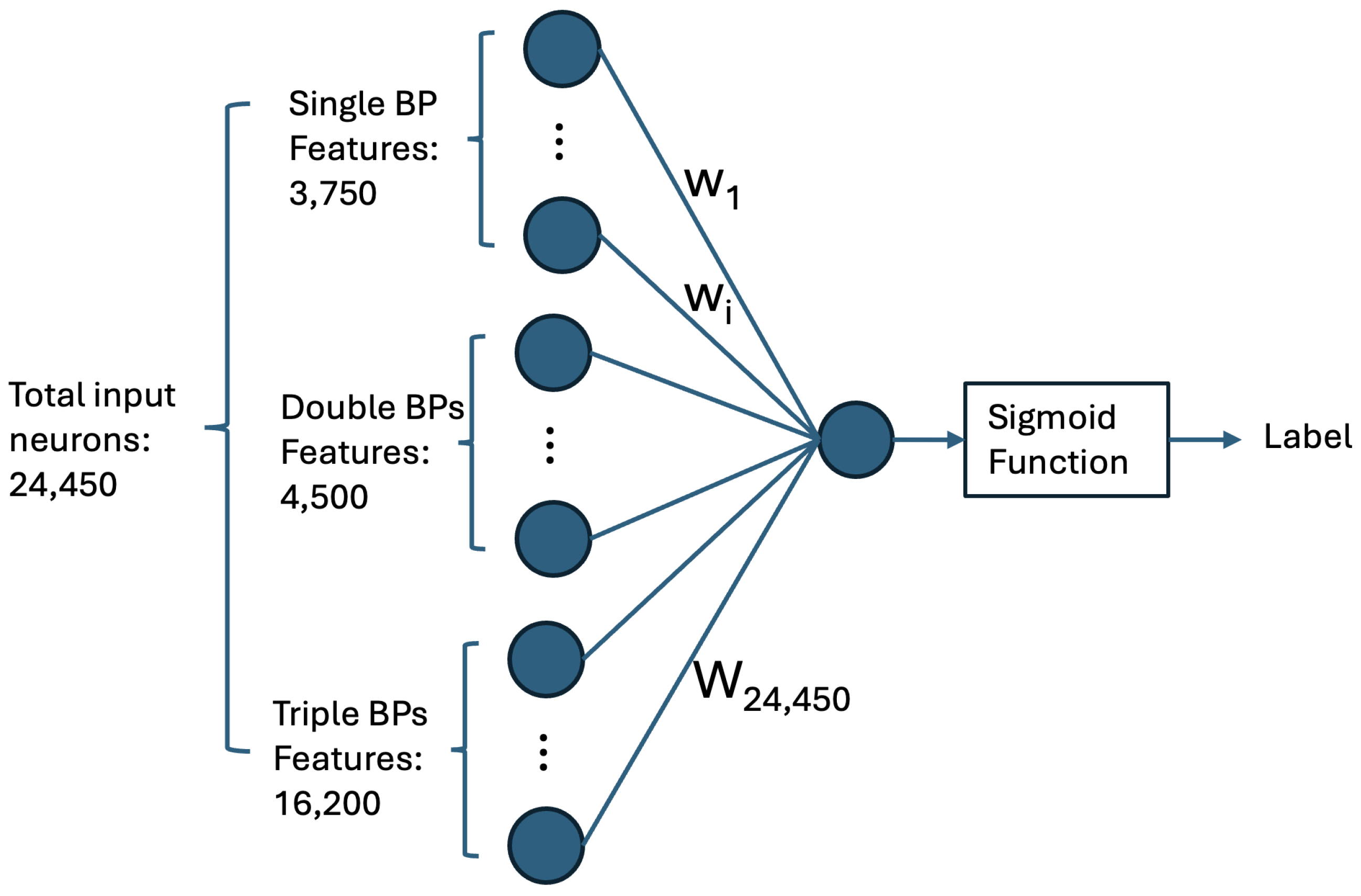
4.1.1. Computing Base-Pairing Preferences via a Single-Neuron Neural Network
4.1.2. Distribution of Base-Pair Types in MicroRNA Seed Region
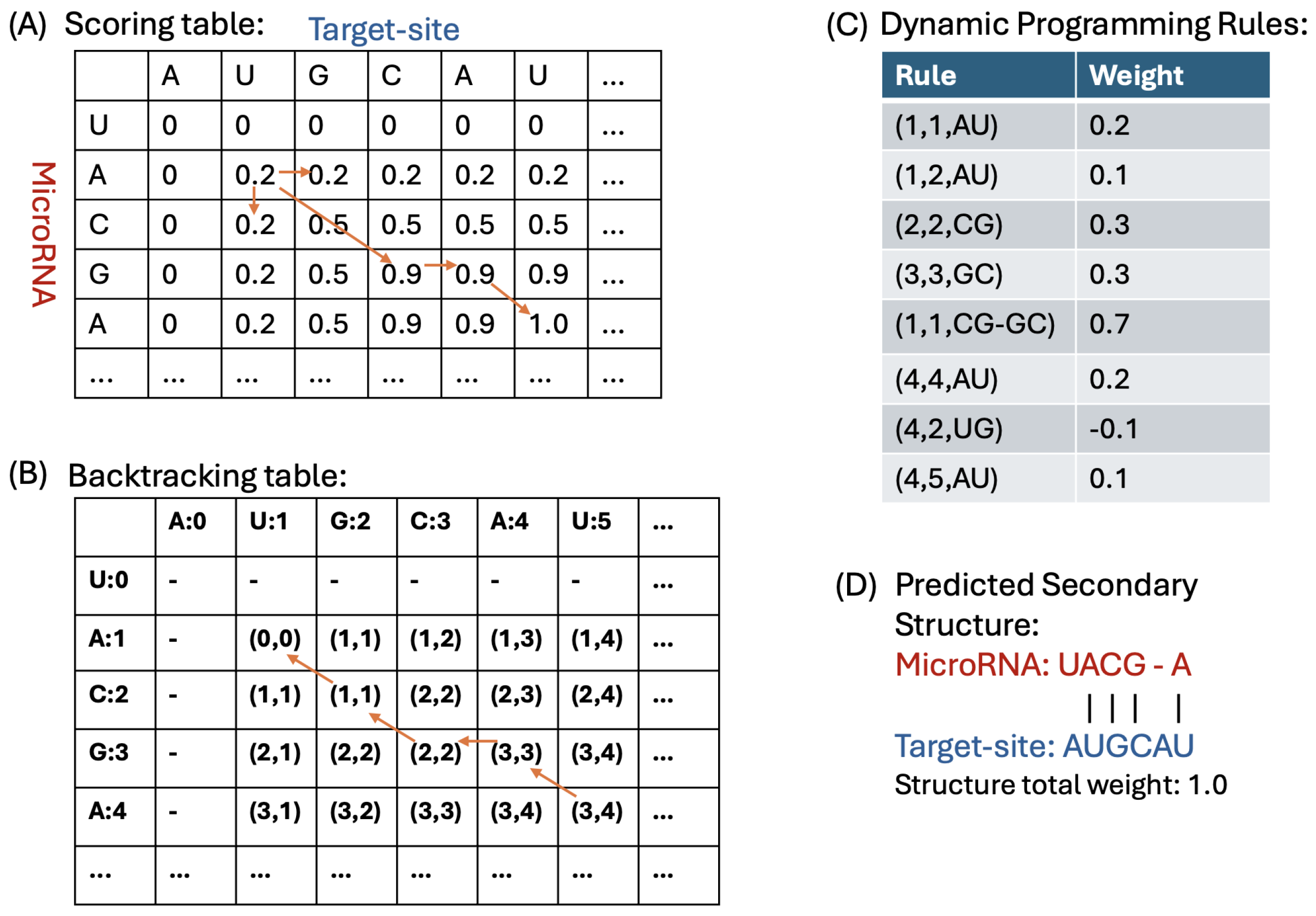
4.1.3. Dynamic Programming Algorithm for Duplex Prediction
- (a)
- Ignoring the i-th base of microRNA;
- (b)
- Ignoring the j-th base of the target-site;
- (c)
- Matching k consecutive base pair(s) where .
4.1.4. Backtracking and Constructing the Duplex Structure
- No Pairing Case: If the pointer’s value indicates a transition to either or , we move the pointer to one of these cells. In this scenario, it implies that there is no base pairing between the corresponding nucleotides, the and the target-site.
- Base-Pairing Case: If the pointer’s value is for k values in {1, 2, 3}, it indicates that there are k base pairs formed between the nucleotides and . We record these base pairings and then move the pointer to to continue the backtracking process.
4.1.5. Computing Minimum Free Energy of the Duplex Structure
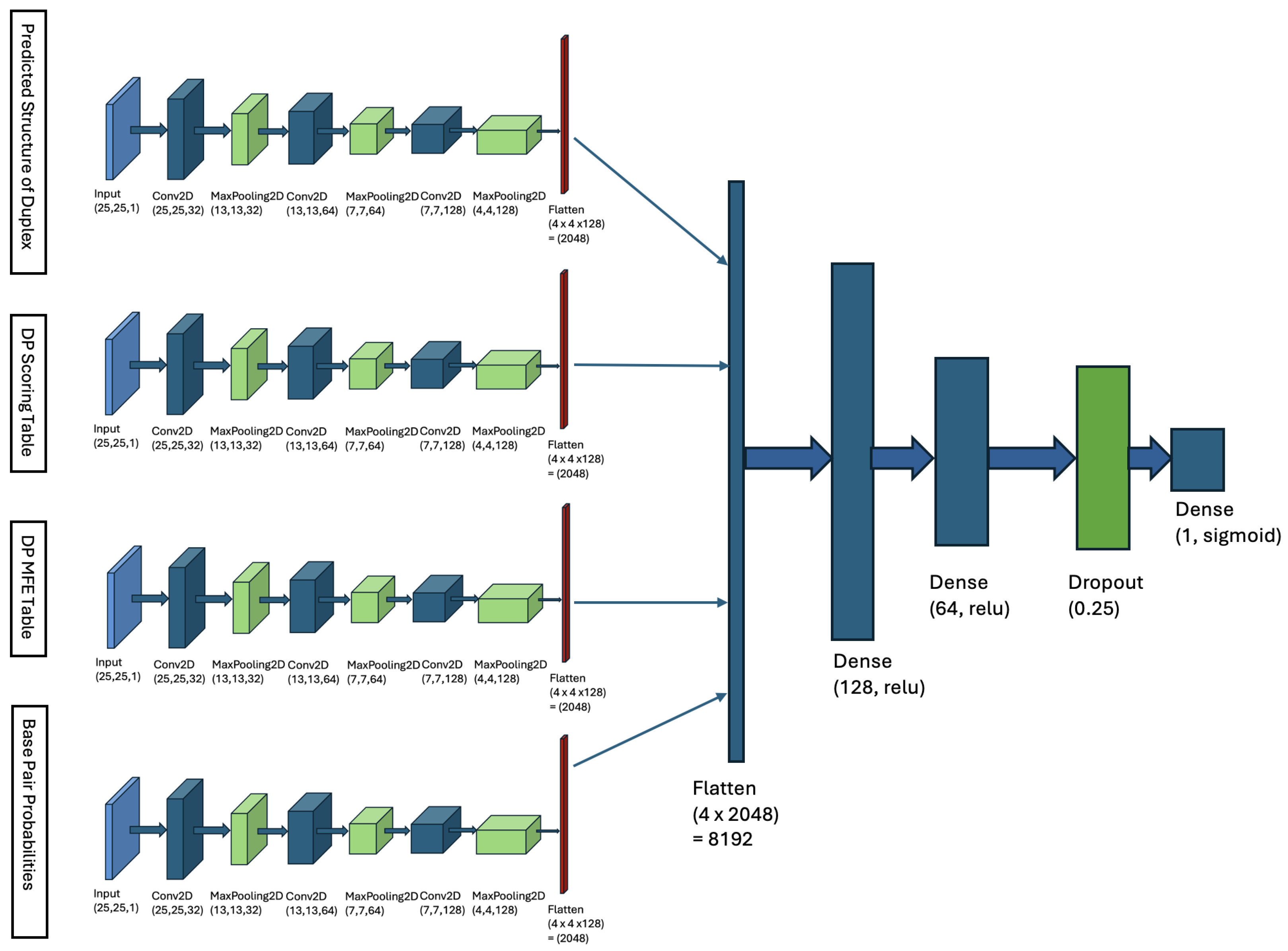
4.2. Multi-Input Neural Network Architecture
- Matrix of Duplex Structure:For the input sequences microRNA () and CTS (), we compute a matrix. For each index r in and each index c in , we examine whether our DP algorithm’s predicted structure includes a base pair between and . If a base pair is present, we store the base pair probability in the matrix entry . This probability is derived from Table 1. The matrix entry is filled with zero, if no such base pair is predicted. When is computed, it serves as an image, representing the duplex base pairs and the probability of each pairing, and it is fed to the first channel of our model.
- DP Scoring Table: For the sequences () and (), our DP algorithm (described in Section 4.1.3) computes a scoring table DPs. Each cell contains the total weight of the optimal duplex between the subsequences and . This table stores the weights of all substructures formed by every possible pair of subsequences.
- DP MFE Table: Our DP algorithm also computes a MFE table, denoted as DPm. For indices r in and c in , cell contains the minimum free energy (MFE) of the optimal duplex formed between the subsequences and . This table captures the thermodynamic stability of all possible substructures by storing their MFE values, where r and c represent indices in and , respectively.
- Base-Pair Probabilities Matrix: For the inputs () and (), this matrix captures the likelihood of nucleotide base pairing between the two sequences. Each cell contains the probability of a base pair forming between the nucleotides and . These probabilities are derived from Table 1. The BP matrix provides a comprehensive view of the pairing potential across all nucleotide positions in the duplex structure.
4.3. Evaluation Metrics and Model Comparison
- TN (True Negatives): Negative samples predicted correctly.
- TP (True Positives): Positive samples predicted correctly.
- FP (False Positives): Negative samples incorrectly predicted as positive.
- FN (False Negatives): Positive samples incorrectly predicted as negative [63].
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AgoTRIBE | Argonaut TRIBE |
| AGO | Argonaut |
| CLASH | Crosslinking, Ligation, and Sequencing of Hybrids |
| CLIP | Crosslinking and Immunoprecipitation |
| CLIP-seq | Crosslinking Immunoprecipitation Sequencing |
| CTS | Candidate Target-Site |
| DNN | Deep Neural Network |
| DP | Dynamic Programming |
| DSSR | Dihedral Angle Stepwise Sequence Realignment |
| miRISC | MicroRNA-Induced Silencing Complex |
| miRNA | MicroRNA |
| miTarBase | MicroRNA Target DataBase |
| mRNA | Messenger RNA |
| MFE | Minimum Free Energy |
| MTI | MicroRNA-Target Interaction |
| PDB | Protein Data Bank |
| qPCR | Quantitative Polymerase Chain Reaction |
| RISC | RNA-Induced Silencing Complex |
| RNAhybrid | RNA-RNA Hybridization Tool |
| rRNA | Ribosomal RNA |
| SdAE | Stacked Denoising Autoencoder |
| UNAfold | Unified Nucleic Acid Folding Algorithm |
| UTR | Untranslated Region |
Appendix A
Appendix A.1. Finding Optimal Threshold for RNAhybrid

Appendix A.2. Method Comparison
| Method | Threshold | Confusion Matrix (TP, FN, FP, TN) |
|---|---|---|
| RNAduplex | 0.3232 | 12,288, 1120, 1023, 3665 |
| miRanda score | 0.4848 | 11,661, 1747, 1493, 3195 |
| miRanda MFE | 0.2929 | 12,262, 1146, 1179, 3509 |
| RNAhybrid | 0.3535 | 12,291, 1117, 1040, 3648 |
| DuplexFold | 0.3030 | 12,358, 1050, 1105, 3583 |
| RNAcofold | 0.3131 | 12,256, 1152, 1086, 3602 |
| MINN | 0.2121 | 12,812, 596, 608, 4080 |
| TEC-miTarget | 0.9899 | 11,263, 2145, 1878, 2810 |
| TargetNet | 0.4545 | 11,069, 2339, 2429, 2259 |
| Mimosa | 0.5000 | 6709, 6699, 928, 3760 |
| TargetScan | N/A | 12,755, 653, 4311, 377 |
| RNA22 | N/A | 13,169, 239, 3821, 867 |

References
- Bartel, D.P. MicroRNAs: Target Recognition and Regulatory Functions. Cell 2009, 136, 215–233. [Google Scholar] [CrossRef] [PubMed]
- Thomas, M.; Lieberman, J.; Lal, A. Desperately seeking microRNA targets. Nat. Struct. Mol. Biol. 2010, 17, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
- Diener, C.; Keller, A.; Meese, E. Emerging concepts of microRNA therapeutics: From cells to clinic. Trends Genet. 2022, 38, 613–626. [Google Scholar] [CrossRef]
- Fehlmann, T.; Lehallier, B.; Schaum, N.; Hahn, O.; Kahraman, M.; Li, Y.; Backes, C. Common diseases alter the physiological age-related blood microRNA profile. Nat. Commun. 2020, 11, 5958. [Google Scholar] [CrossRef]
- Baek, D.; Villén, J.; Shin, C.; Camargo, F.D.; Gygi, S.P.; Bartel, D.P. The Impact of microRNAs on Protein Output. Nature 2008, 455, 64–71. [Google Scholar] [CrossRef]
- Selbach, M.; Schwanhäusser, B.; Thierfelder, N.; Fang, Z.; Khanin, R.; Rajewsky, N. Widespread changes in protein synthesis induced by microRNAs. Nature 2008, 455, 58–63. [Google Scholar] [CrossRef]
- Eulalio, A.; Huntzinger, E.; Izaurralde, E. GW182 interaction with Argonaute is essential for microRNA-mediated translational repression and mRNA decay. Nat. Struct. Mol. Biol. 2008, 15, 346–353. [Google Scholar] [CrossRef]
- Lim, L.P.; Lau, N.C.; Garrett-Engele, P.; Grimson, A.; Schelter, J.M.; Castle, J.; Bartel, D.P.; Linsley, P.S.; Johnson, J.M. Microarray analysis shows that some microRNAs downregulate large numbers of target mRNAs. Nature 2005, 433, 769–773. [Google Scholar] [CrossRef]
- Thomson, D.W.; Bracken, C.P.; Goodall, G.J. Experimental strategies for microRNA target identification. Nucleic Acids Res. 2011, 39, 6845–6853. [Google Scholar] [CrossRef]
- Chi, S.W.; Zang, J.B.; Mele, A.; Darnell, R.B. Argonaute HITS-CLIP decodes microRNA-mRNA interaction maps. Nature 2009, 460, 479–486. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, T.; Liu, C.; Xu, J.; Li, Y. AgoTRIBE: A Single-cell Resolution Method to Identify Direct MicroRNA Targets. Mol. Cell 2023, 83, 1511–1524.e7. [Google Scholar]
- German, M.A.; Pillay, M.; Jeong, D.H.; Hetawal, A.; Luo, S.; Janardhanan, P.; Kannan, V.; Rymarquis, L.A.; Nobuta, K.; German, R.; et al. Global identification of microRNA-target RNA pairs by parallel analysis of RNA ends. Nat. Biotechnol. 2008, 26, 1384–1389. [Google Scholar] [CrossRef] [PubMed]
- Helwak, A.; Kudla, G.; Dudnakova, T.; Tollervey, D. Mapping the human microRNA interactome by CLASH reveals frequent noncanonical binding. Cell 2013, 153, 654–665. [Google Scholar] [CrossRef] [PubMed]
- Bartel, D.P. Computational methods for microRNA target prediction. Nat. Rev. Genet. 2014, 15, 703–715. [Google Scholar] [CrossRef]
- Mohebbi, M.; Ding, L.; Malmberg, R.L.; Cai, L. Human MicroRNA target prediction via multi-hypotheses learning. J. Comput. Biol. 2021, 28, 117–132. [Google Scholar] [CrossRef]
- Enright, A.J.; John, B.; Gaul, U.; Tuschl, T.; Sander, C.; Marks, D.S. MicroRNA targets in Drosophila. Genome Biol. 2004, 5, R1. [Google Scholar] [CrossRef]
- Agarwal, V.; Bell, G.W.; Nam, J.W.; Bartel, D.P. Predicting effective microRNA target sites in mammalian mRNAs. eLife 2015, 4, e05005. [Google Scholar] [CrossRef]
- McGeary, S.E.; Lin, K.S.; Shi, C.Y.; Pham, T.M.; Bisaria, N.; Kelley, G.M.; Bartel, D.P. The biochemical basis of microRNA targeting efficacy. Science 2019, 366, eaav1741. [Google Scholar] [CrossRef]
- Miranda, K.C.; Huynh, T.; Tay, Y.; Ang, Y.S.; Tam, W.L.; Thomson, A.M.; Lim, B.; Rigoutsos, I. A pattern-based method for the identification of MicroRNA binding sites and their corresponding heteroduplexes. Cell 2006, 126, 1203–1217. [Google Scholar] [CrossRef]
- Kertesz, M.; Iovino, N.; Unnerstall, U.; Gaul, U.; Segal, E. The role of site accessibility in microRNA target recognition. Nat. Genet. 2007, 39, 1278–1284. [Google Scholar] [CrossRef]
- Rehmsmeier, M.; Steffen, P.; Höchsmann, M.; Giegerich, R. Fast and effective prediction of microRNA/target duplexes. RNA 2004, 10, 1507–1517. [Google Scholar] [CrossRef] [PubMed]
- Mohebbi, M.; Sesser, S.; Williams, P.; Wodtke, M.; Highton, S.; Shaik, S. Beyond Sequence: A Novel Image-Based Model for MicroRNA Target Prediction. In Proceedings of the SoutheastCon 2024, Virtual, 22–24 March 2024; pp. 922–927. [Google Scholar] [CrossRef]
- Mohebbi, M.; Ding, L.; Malmberg, R.L.; Momany, C.; Rasheed, K.; Cai, L. Accurate prediction of human miRNA targets via graph modeling of the miRNA-target duplex. J. Bioinform. Comput. Biol. 2018, 16, 1850013. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.; Zadeh, M.; Mazzocchi, F. Machine learning in the era of big data: An overview. Front. Bioeng. Biotechnol. 2019, 7, 33. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Wen, M.; Cong, P.; Zhang, Z.; Lu, H.; Li, T. DeepMirTar: A deep-learning approach for predicting human miRNA targets. Bioinformatics 2018, 34, 3781–3787. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, Y.; Jiang, D.; Zhang, X.; Dai, W.; Xiong, H.; Tian, Q. Sdae: Self-distillated masked autoencoder. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 108–124. [Google Scholar]
- Pla, A.; Zhong, X.; Rayner, S. miRAW: A deep learning-based approach to predict microRNA targets by analyzing whole microRNA transcripts. PLoS Comput. Biol. 2018, 14, e1006185. [Google Scholar] [CrossRef]
- Min, S.; Lee, B.; Yoon, S. TargetNet: Functional microRNA target prediction with deep neural networks. Bioinformatics 2022, 38, 671–677. [Google Scholar] [CrossRef]
- Koonce, B.; Koonce, B. ResNet 50. In Convolutional Neural Networks with Swift for Tensorflow: Image Recognition and Dataset Categorization; Apress: Berkeley, CA, USA, 2021; pp. 63–72. [Google Scholar]
- Yang, T.; Wang, Y.; He, Y. TEC-miTarget: Enhancing microRNA target prediction based on deep learning of ribonucleic acid sequences. BMC Bioinform. 2024, 25, 159. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Bi, Y.; Li, F.; Wang, C.; Pan, T.; Davidovich, C.; Webb, G.I.; Song, J. Advancing microRNA target site prediction with transformer and base-pairing patterns. Nucleic Acids Res. 2024, 52, 11455–11465. [Google Scholar] [CrossRef]
- Colasanti, A.V.; Lu, X.J.; Olson, W.K. Analyzing and building nucleic acid structures with 3DNA. JoVE (J. Vis. Exp.) 2013, 74, e4401. [Google Scholar]
- Burley, S.K.; Bhikadiya, C.; Bi, C.; Bittrich, S.; Chao, H.; Chen, L.; Craig, P.A.; Crichlow, G.V.; Dalenberg, K.; Duarte, J.M.; et al. RCSB Protein Data Bank (RCSB. org): Delivery of experimentally-determined PDB structures alongside one million computed structure models of proteins from artificial intelligence machine learning. Nucleic Acids Res. 2023, 51, D488–D508. [Google Scholar] [CrossRef] [PubMed]
- Kushner, A.; Petrov, A.S.; Dao Duc, K. RiboXYZ: A comprehensive database for visualizing and analyzing ribosome structures. Nucleic Acids Res. 2023, 51, D509–D516. [Google Scholar] [CrossRef]
- Zheng, G.; Lu, X.J.; Olson, W.K. Web 3DNA–a web server for the analysis, reconstruction, and visualization of three-dimensional nucleic-acid structures. Nucleic Acids Res. 2009, 37, W240–W246. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.Y.; Huang, H.Y.; Huang, H.Y. miRTarBase update 2023: An informative resource for experimentally validated miRNA-target interactions. Nucleic Acids Res. 2023, 51, D215–D221. [Google Scholar]
- Vlachos, I.S.; Paraskevopoulou, M.D.; Karagkouni, D.; Georgakilas, G.; Vergoulis, T.; Kanellos, I.; Anastasopoulos, I.L.; Maniou, S.; Karathanou, K.; Kalfakakou, D.; et al. DIANA-TarBase v7. 0: Indexing more than half a million experimentally supported miRNA: mRNA interactions. Nucleic Acids Res. 2015, 43, D153–D159. [Google Scholar] [CrossRef]
- Reuter, J.S.; Mathews, D.H. RNAstructure: Software for RNA secondary structure prediction and analysis. BMC Bioinform. 2010, 11, 129. [Google Scholar] [CrossRef]
- Markham, N.R.; Zuker, M. UNAFold: Software for nucleic acid folding and hybridization. In Bioinformatics: Structure, Function and Applications; Humana: New York, NY, USA, 2008; pp. 3–31. [Google Scholar]
- Cochran, W.G. Sampling Techniques; Johan Wiley & Sons Inc.: Hoboken, NJ, USA, 1977. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Tibshirani, R.J.; Efron, B. An introduction to the bootstrap. Monogr. Stat. Appl. Probab. 1993, 57, 1–436. [Google Scholar]
- Freedman, D.A.; Pisani, R.; Purves, O. Statistics, 4th ed.; W.W. Norton & Company: New York, NY, USA, 2007. [Google Scholar]
- Efron, B.; Tibshirani, R.J. Better bootstrap confidence intervals. J. Am. Stat. Assoc. 1987, 82, 171–185. [Google Scholar] [CrossRef]
- Fabian, M.R. Of seeds and supplements: Structural insights into extended microRNA–target pairing. EMBO J. 2019, 38, e102477. [Google Scholar] [CrossRef] [PubMed]
- Mathews, D.H.; Disney, M.D.; Childs, J.L.; Schroeder, S.J.; Zuker, M.; Turner, D.H. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl. Acad. Sci. USA 2004, 101, 7287–7292. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, R.; Bernhart, S.H.; Höner Zu Siederdissen, C.; Tafer, H.; Flamm, C.; Stadler, P.F.; Hofacker, I.L. ViennaRNA Package 2.0. Algorithms Mol. Biol. 2011, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- Bartel, D.P. MicroRNAs: Genomics, Biogenesis, Mechanism, and Function. Cell 2004, 116, 281–297. [Google Scholar] [CrossRef]
- Schirle, N.T.; Sheu Gruttadauria, J.; MacRae, I.J. Structural basis for microRNA targeting. Science 2014, 346, 608–613. [Google Scholar] [CrossRef]
- Sheu-Gruttadauria, J.; MacRae, I.J. Structural foundations of RNA silencing by Argonaute. J. Mol. Biol. 2017, 429, 2619–2639. [Google Scholar] [CrossRef]
- Mathews, D.H.; Sabina, J.; Zuker, M.; Turner, D.H. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999, 288, 911–940. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Bartel, D.P. Metazoan MicroRNAs. Cell 2018, 173, 20–51. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Xia, T.; SantaLucia, J.; Burkard, M.E.; Kierzek, R.; Schroeder, S.J.; Jiao, X.; Cox, C.; Turner, D.H. Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson–Crick base pairs. Biochemistry 1998, 37, 14719–14735. [Google Scholar] [CrossRef]
- Turner, D.H.; Mathews, D.H. NNDB: The nearest neighbor parameter database for predicting stability of nucleic acid secondary structure. Nucleic Acids Res. 2010, 38, D280–D282. [Google Scholar] [CrossRef] [PubMed]
- Mittal, A.; Turner, D.H.; Mathews, D.H. NNDB: An Expanded Database of Nearest Neighbor Parameters for Predicting Stability of Nucleic Acid Secondary Structures. J. Mol. Biol. 2024, 436, 168549. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Rehmsmeier, M. Precision-Recall Plot Is More Informative Than Receiver Operating Characteristic Plot. Bioinformatics 2015, 31, 3509–3511. [Google Scholar]
- Davis, J.; Goadrich, M. The relationship between precision-recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning (ICML), Honolulu, HI, USA, 25–29 June 2006; ACM: New York, NY, USA, 2006; pp. 233–240. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
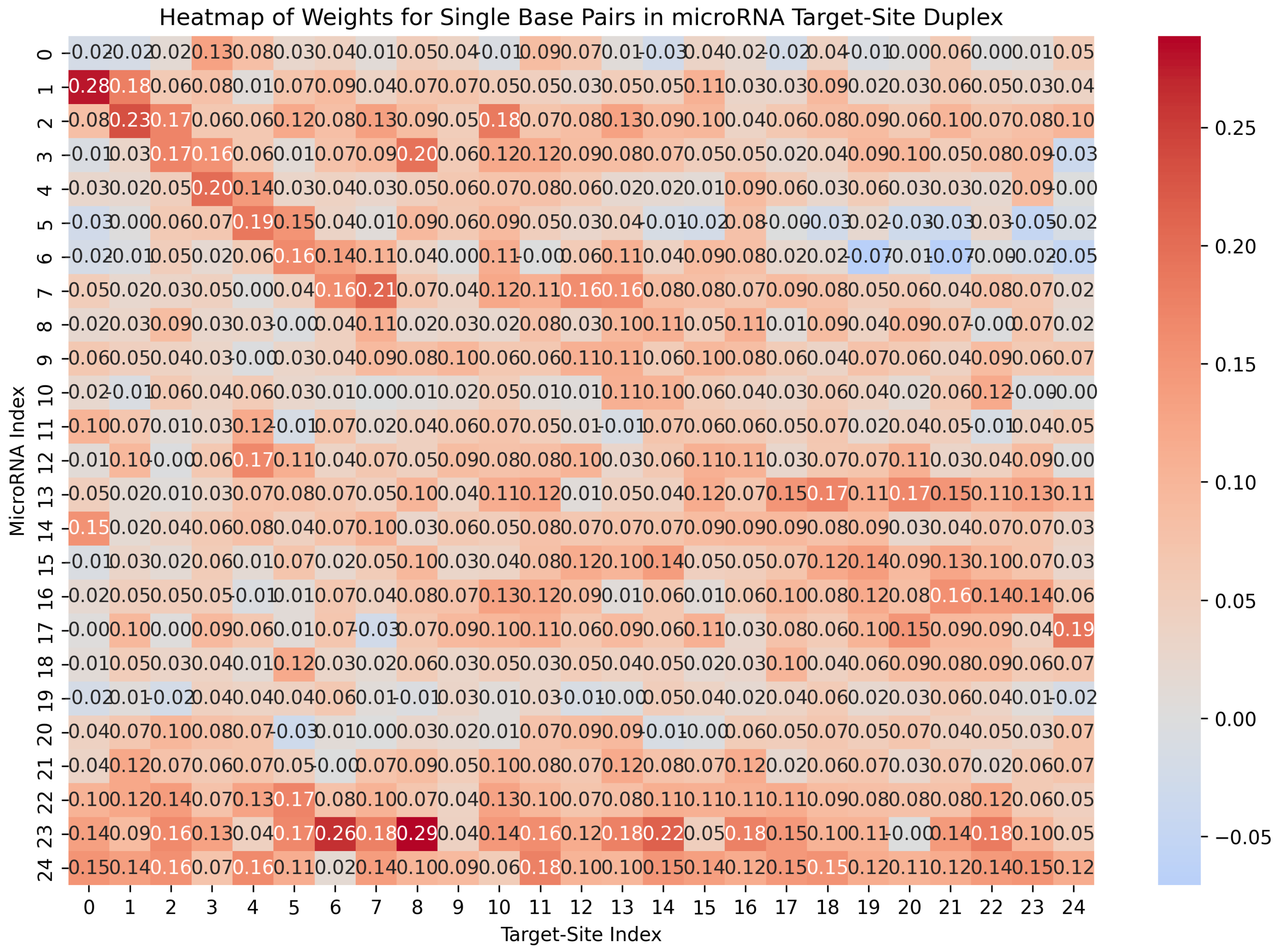
| Base Pair Type | Probability |
|---|---|
| AA | 0.0519 |
| AC/CA | 0.0870 |
| AG/GA | 0.1566 |
| AU/UA | 0.4965 |
| CC | 0.0189 |
| CG/GC | 0.6979 |
| CU/UC | 0.0473 |
| GG | 0.0303 |
| GU/UG | 0.1210 |
| UU | 0.0455 |
| Method | AUPRC | Thrs. | PPV | Rec. | F1 | Acc. | Spec. | NPV |
|---|---|---|---|---|---|---|---|---|
| RNAduplex | 0.8514 | 0.3232 | 0.7659 | 0.7818 | 0.7738 | 0.8816 | 0.9165 | 0.9231 |
| miRanda score | 0.7518 | 0.4848 | 0.6465 | 0.6815 | 0.6636 | 0.821 | 0.8697 | 0.8865 |
| miRanda MFE | 0.8344 | 0.2929 | 0.7538 | 0.7485 | 0.7512 | 0.8715 | 0.9145 | 0.9123 |
| RNAhybrid | 0.8511 | 0.3535 | 0.7656 | 0.7782 | 0.7718 | 0.8808 | 0.9167 | 0.9220 |
| DuplexFold | 0.8473 | 0.303 | 0.7734 | 0.7643 | 0.7688 | 0.8809 | 0.9217 | 0.9179 |
| RNAcofold | 0.8408 | 0.3131 | 0.7577 | 0.7683 | 0.763 | 0.8763 | 0.9141 | 0.9186 |
| MINN | 0.9373 | 0.2121 | 0.8725 | 0.8703 | 0.8714 | 0.9335 | 0.9555 | 0.9547 |
| TEC-miTarget | 0.5835 | 0.9899 | 0.5671 | 0.5994 | 0.5828 | 0.7777 | 0.8400 | 0.8571 |
| TargetNet | 0.5264 | 0.4545 | 0.4913 | 0.4819 | 0.4865 | 0.7365 | 0.8256 | 0.8200 |
| Mimosa | 0.4493 | 0.5000 | 0.3595 | 0.8020 | 0.4965 | 0.5785 | 0.5004 | 0.8785 |
| TargetScan | N/A | N/A | 0.3660 | 0.0804 | 0.1319 | 0.7257 | 0.9513 | 0.3660 |
| RNA22 | N/A | N/A | 0.7839 | 0.1849 | 0.2993 | 0.7756 | 0.9822 | 0.7839 |
| Method | AUPRC | 95% CI | Mean Diff. | p-Value | % Diff. AUPRC |
|---|---|---|---|---|---|
| MINN * | 0.9373 | [0.9323, 0.9422] | 0 | 0 | 0.00% |
| RNAduplex | 0.8503 | [0.8409, 0.8597] | 0.0871 | 0 | 10.24% |
| miRanda score | 0.7473 | [0.7357, 0.7586] | 0.19 | 0 | 25.43% |
| miRanda MFE | 0.8343 | [0.8246, 0.8436] | 0.103 | 0 | 12.35% |
| RNAhybrid | 0.8499 | [0.8408, 0.8591] | 0.0875 | 0 | 10.29% |
| DuplexFold | 0.8461 | [0.8369, 0.8557] | 0.0912 | 0 | 10.78% |
| RNAcofold | 0.8395 | [0.8298, 0.8498] | 0.0979 | 0 | 11.65% |
| TEC-miTarget | 0.5801 | [0.5657, 0.5965] | 0.3571 | 0 | 61.58% |
| TargetNet | 0.5245 | [0.5106, 0.5386] | 0.4128 | 0 | 78.72% |
| Mimosa | 0.4311 | [0.4187, 0.4456] | 0.5058 | 0 | 117.42% |
| Canonical Base-Pair Type | Percentage |
|---|---|
| AU | 22.0% |
| CG | 16.0% |
| GC | 44.0% |
| UA | 18.0% |
| UG | 0.0% |
| GU | 0.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohebbi, M.; Manzourolajdad, A.; Bennett, E.; Williams, P. A Multi-Input Neural Network Model for Accurate MicroRNA Target Site Detection. Non-Coding RNA 2025, 11, 23. https://doi.org/10.3390/ncrna11020023
Mohebbi M, Manzourolajdad A, Bennett E, Williams P. A Multi-Input Neural Network Model for Accurate MicroRNA Target Site Detection. Non-Coding RNA. 2025; 11(2):23. https://doi.org/10.3390/ncrna11020023
Chicago/Turabian StyleMohebbi, Mohammad, Amirhossein Manzourolajdad, Ethan Bennett, and Phillip Williams. 2025. "A Multi-Input Neural Network Model for Accurate MicroRNA Target Site Detection" Non-Coding RNA 11, no. 2: 23. https://doi.org/10.3390/ncrna11020023
APA StyleMohebbi, M., Manzourolajdad, A., Bennett, E., & Williams, P. (2025). A Multi-Input Neural Network Model for Accurate MicroRNA Target Site Detection. Non-Coding RNA, 11(2), 23. https://doi.org/10.3390/ncrna11020023








