Dynamics of a Gel-Based Artificial Tear Film with an Emphasis on Dry Disease Treatment Applications
Abstract
:1. Introduction
2. Results and Discussion
2.1. Influence of the Tear Gel Rheological Parameters
2.1.1. Effect of Flow Behavior Index, n
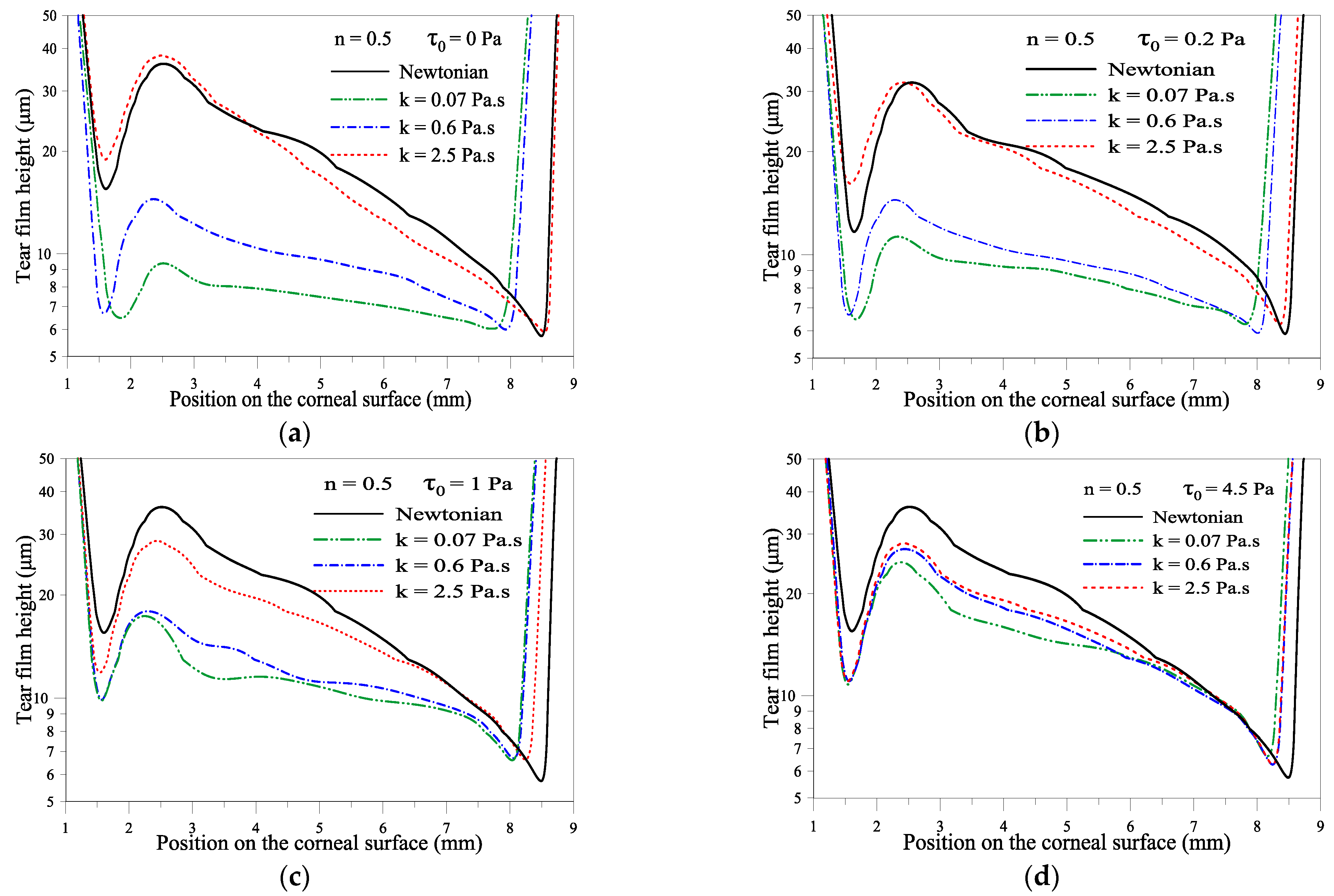
2.1.2. Effect of Consistency Index, k
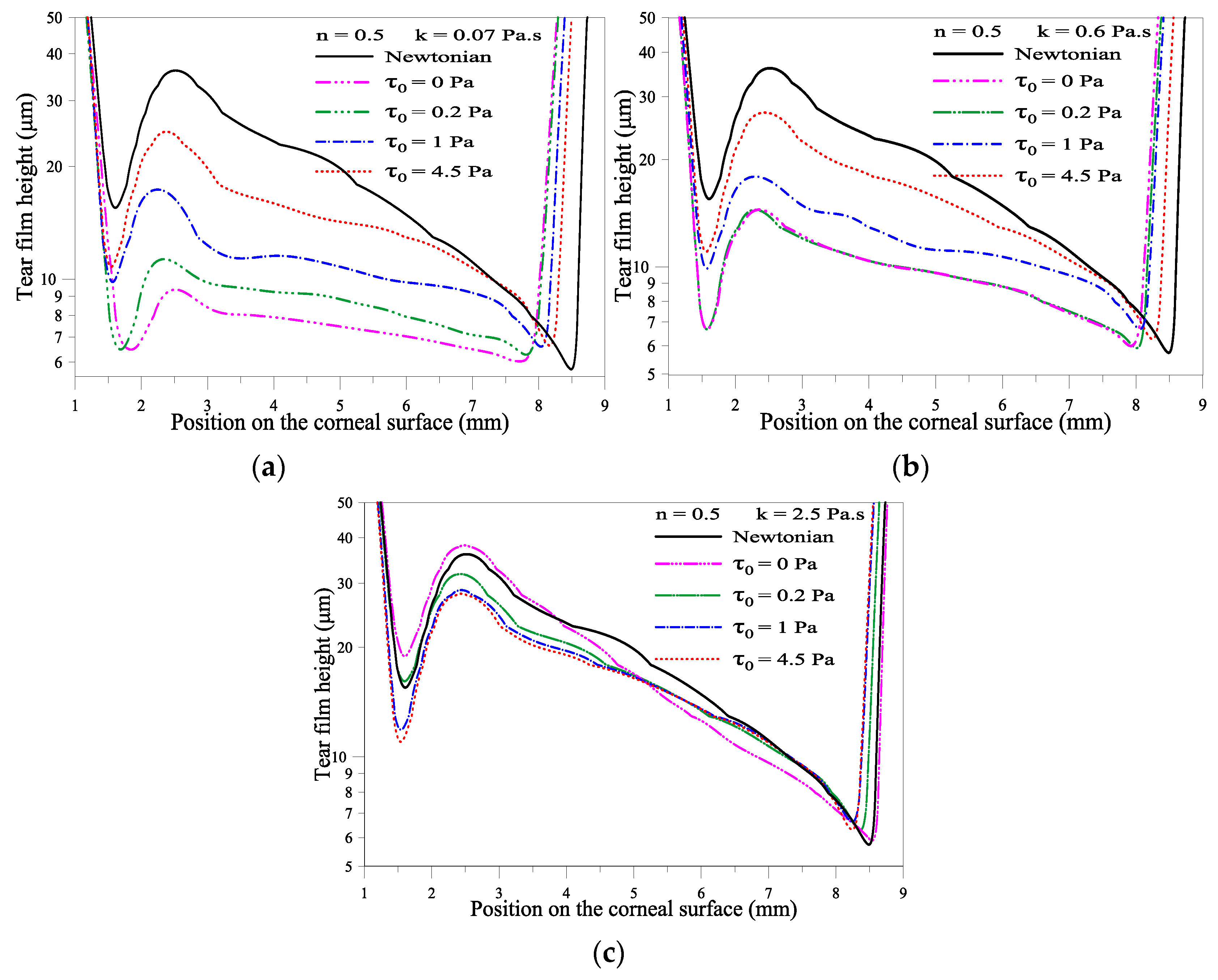
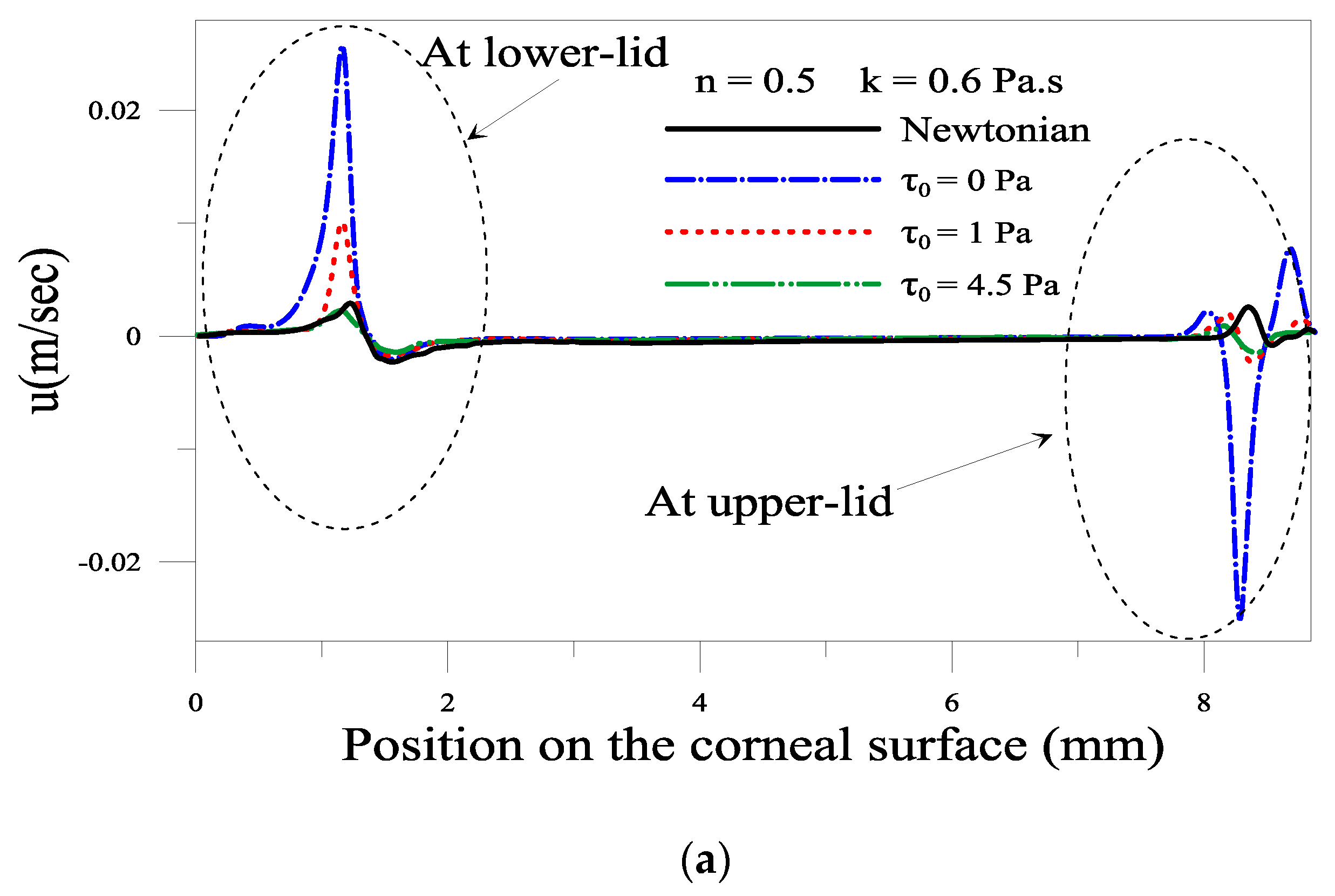
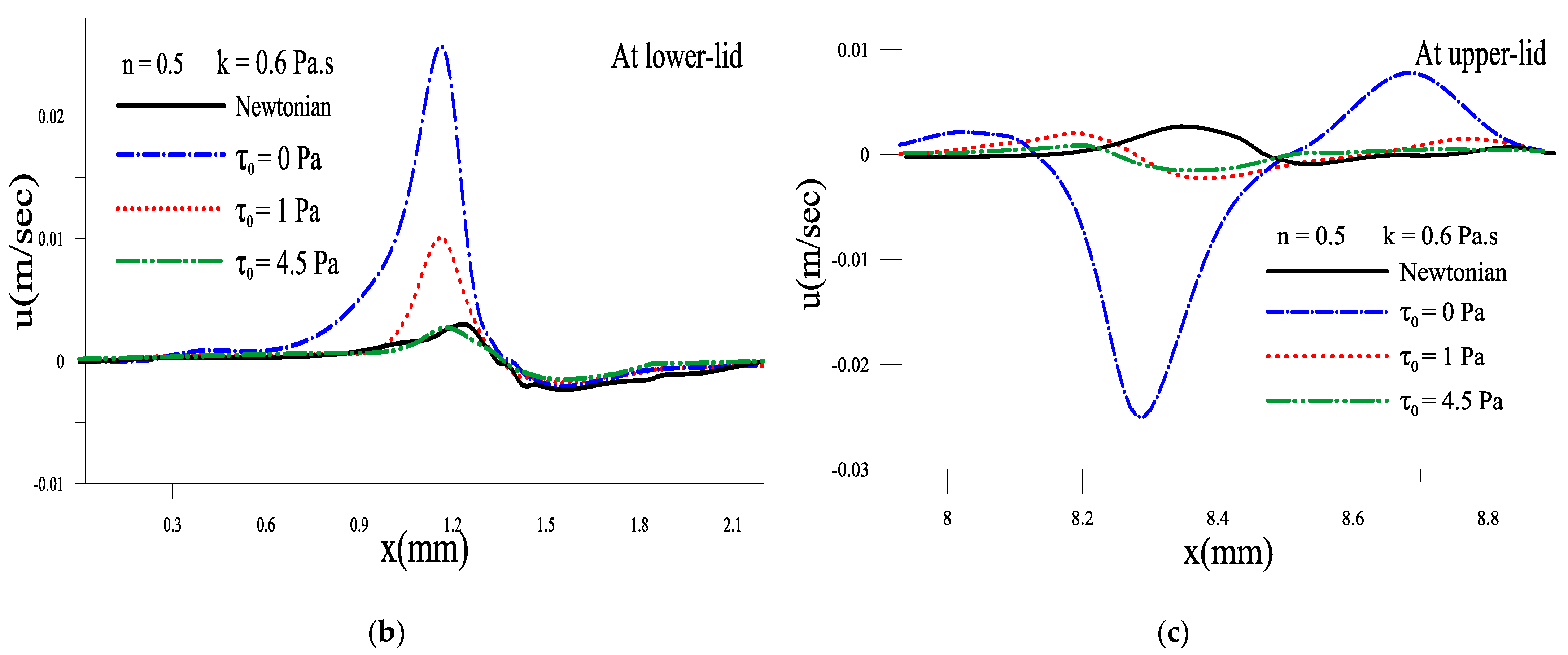
2.1.3. Effect of the Yield Stress τ0
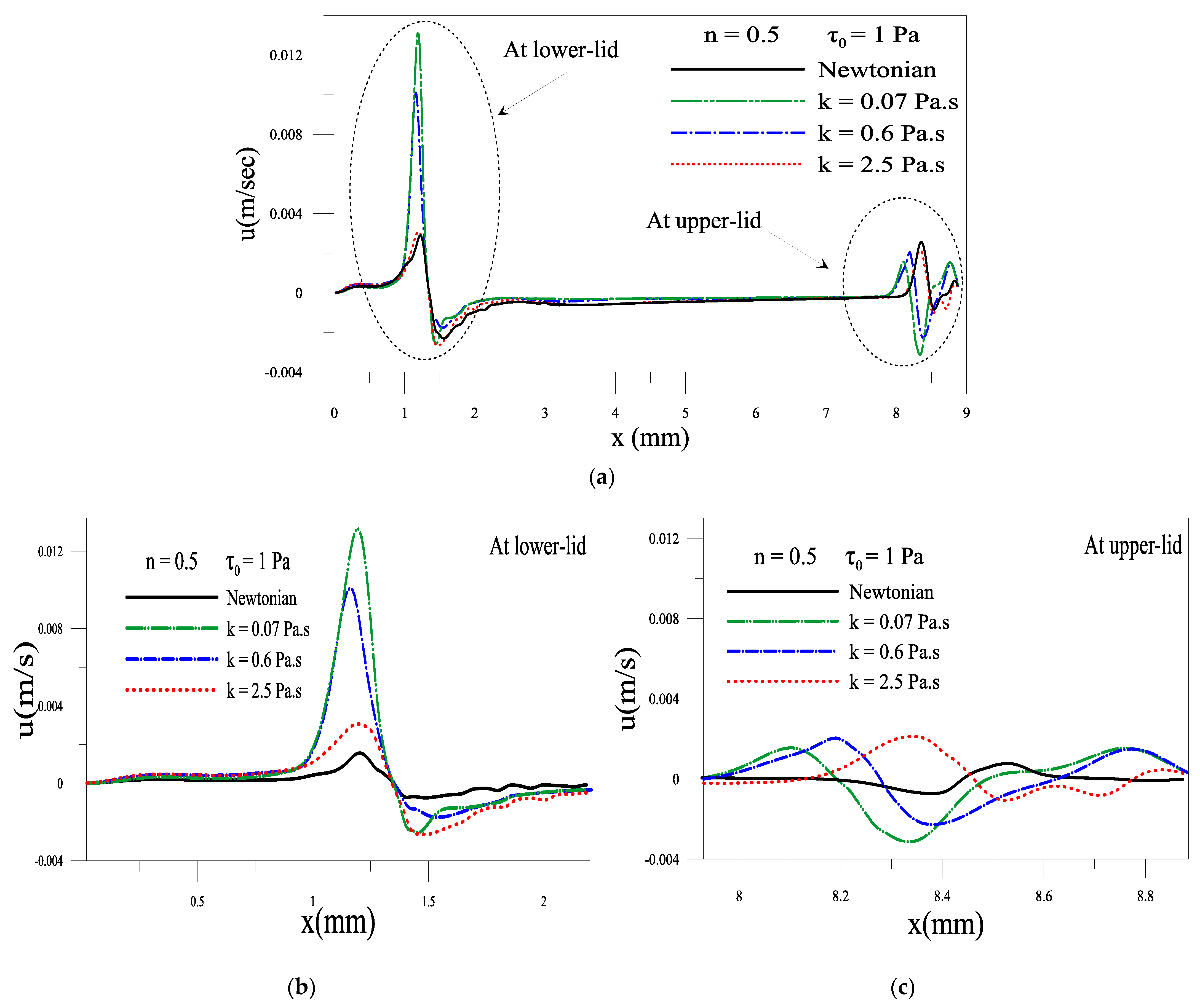
2.1.4. Evolution of Local Velocity at the Eyelids
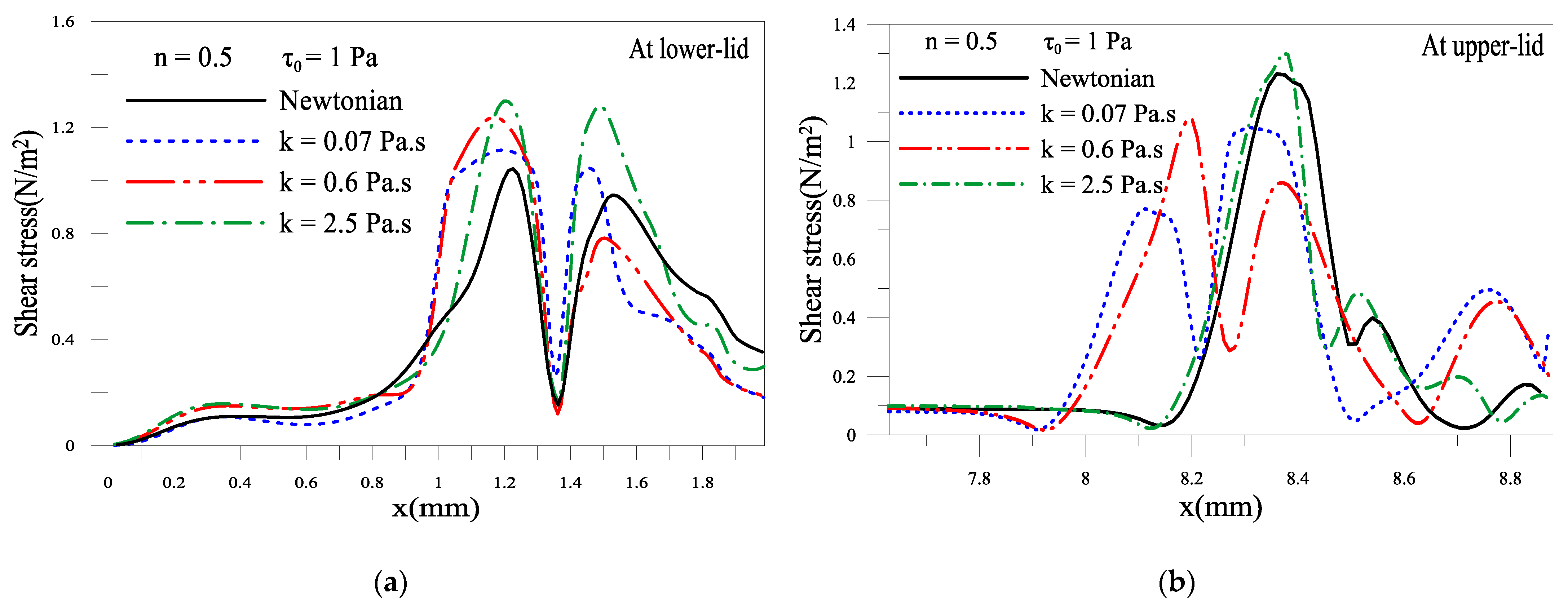
2.1.5. Shear Stress of the Tear Film near Eyelids
3. Conclusions
4. Materials and Methods
4.1. Rheology and Spreading of Tear Substitutes
4.2. Numerical Simulations
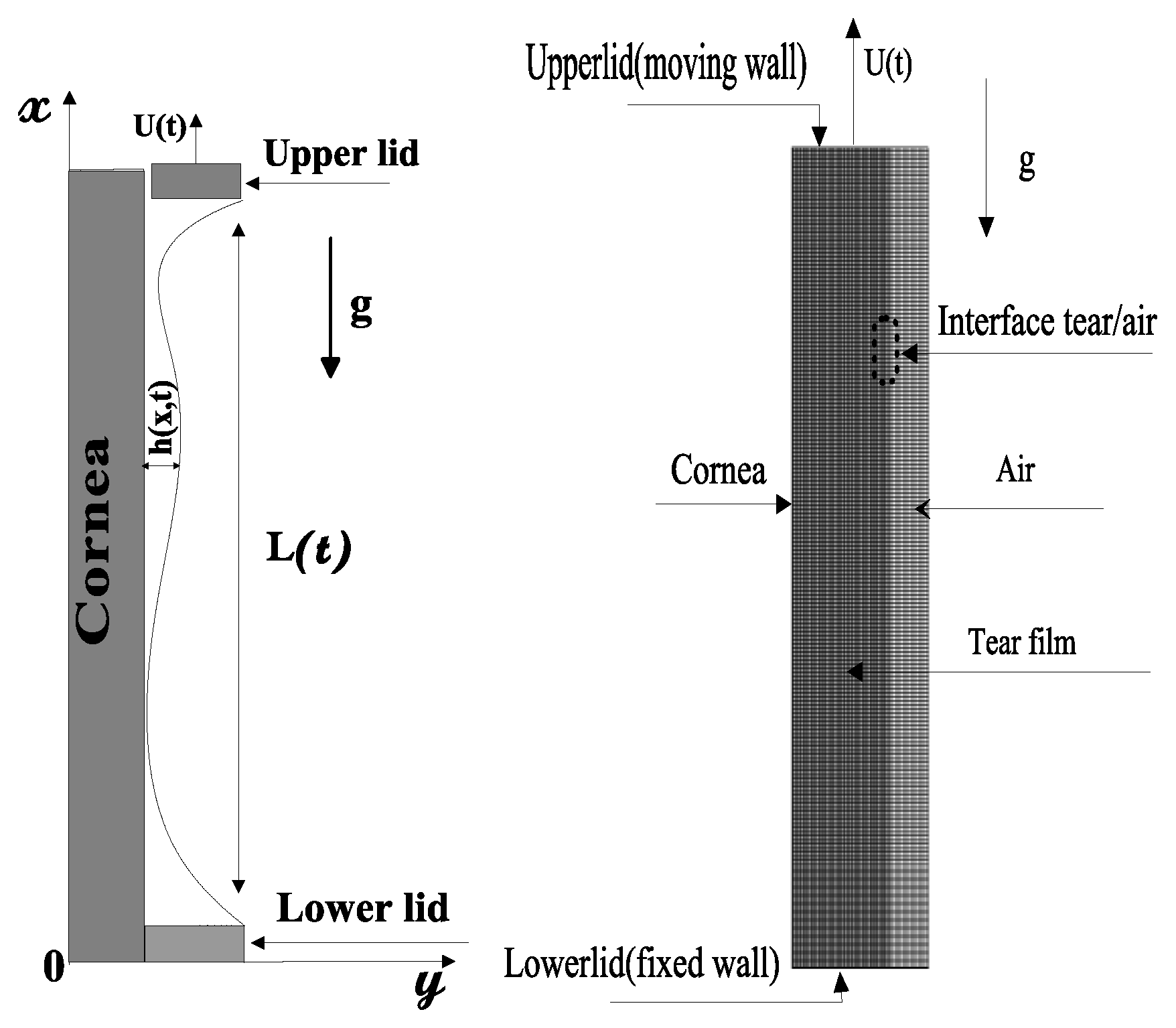
4.2.1. Formulation of the Problem
Governing Equations
- = 0: the cell is empty.
- = 1: the cell is full.
- 0 << 1: the cell contains the interface between the two fluids.
Boundary Conditions
- : at the corneal surface.
- : at the lower eyelid.
- at the upper eyelid.
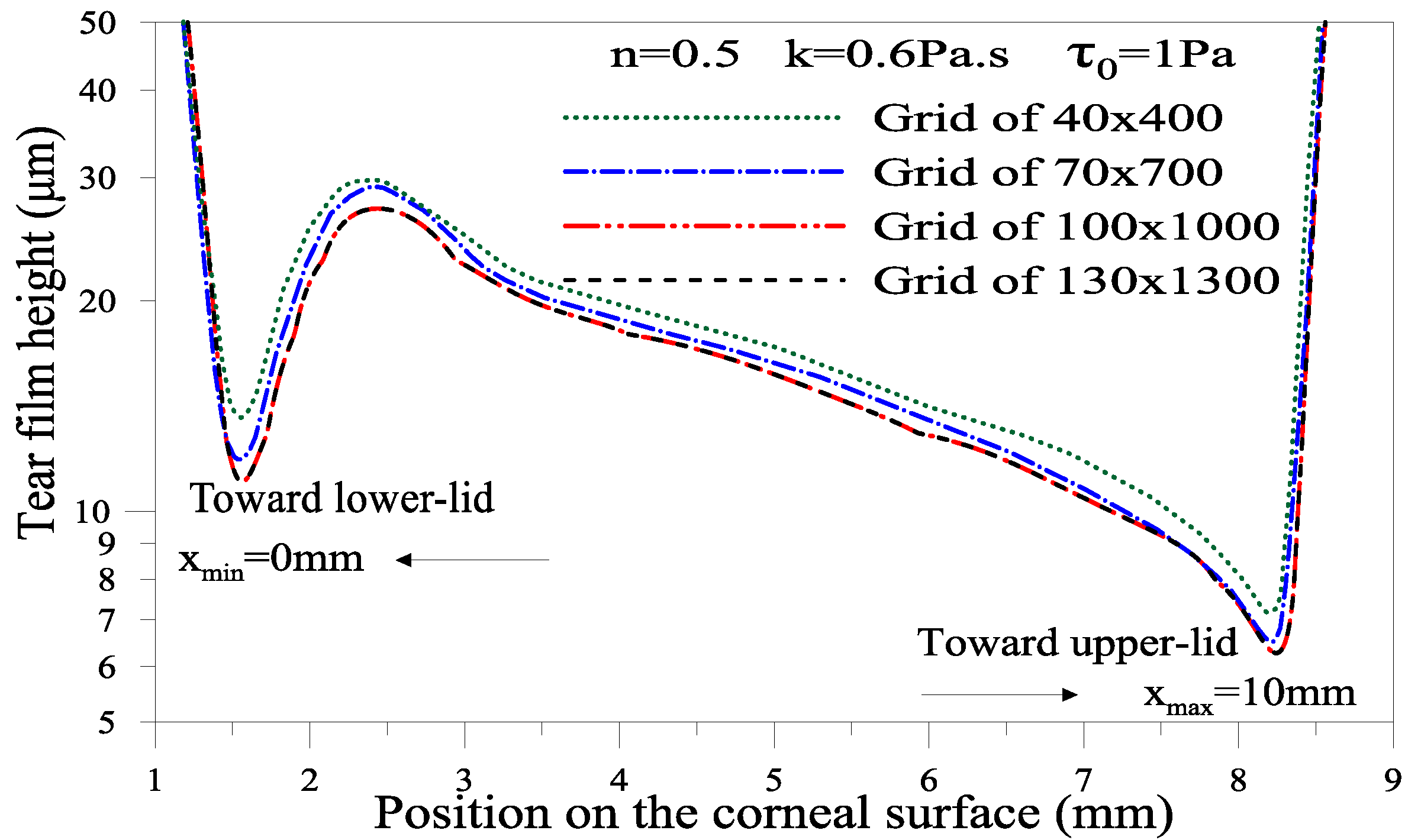
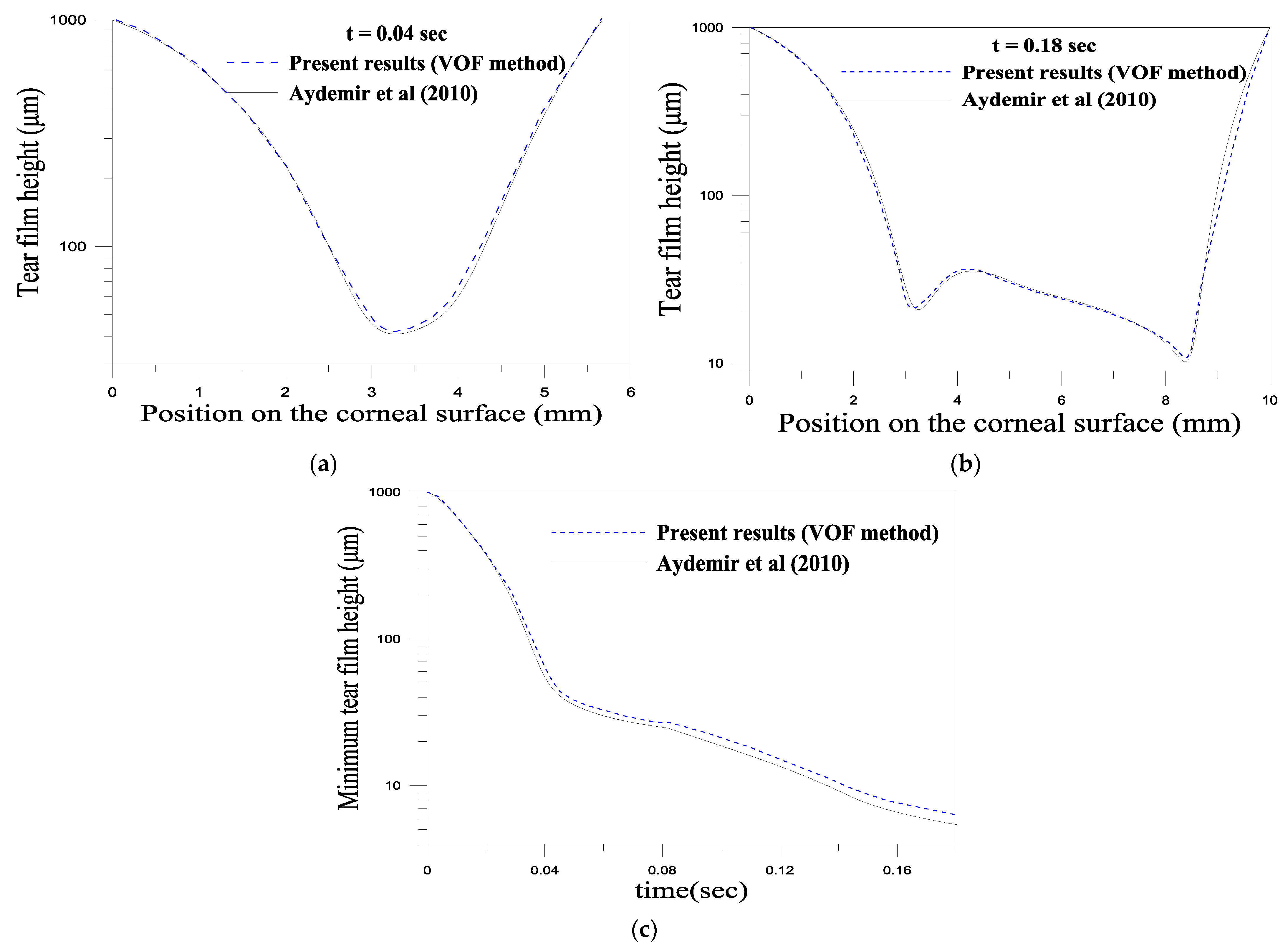
4.2.2. Numerical Method and Validation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Jones, M.B.; McElwain, D.L.S.; Fulford, G.R.; Collins, M.J.; Roberts, A.P. The effect of the lipid layer on tear film behavior. Bull. Math. Biol. 2006, 68, 1355–1381. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.A.; Albeitz, J.; Begley, C.; Barbara, C.; Nichols, K.; Schaumberg, D.; Schein, O. The Epidemiology of Dry Eye Disease: Report of the Epidemiology Subcommittee of the International Dry Eye WorkShop (2007). Ocul. Surf. 2007, 5, 93–107. [Google Scholar]
- Stapleton, F.; Alves, M.; Bunya, V.Y.; Jalbert, I.; Lekhanont, K.; Malet, F.; Na, K.S.; Schaumberg, D.; Uchino, M.; Vehof, J.; et al. TFOS DEWS II epidemiology report. Ocul. Surf. 2017, 15, 334–365. [Google Scholar] [CrossRef] [PubMed]
- Luke, R.A.; Braun, R.J.; Begley, C.G. Mechanistic determination of tear film thinning via fitting simplified models to tear breakup. arXiv 2021, arXiv:2101.08351. [Google Scholar]
- Wei, Y.; Asbell, P.A. The Core Mechanism of Dry Eye Disease Is Inflammation. Eye Contact Lens Sci. Clin. Pr. 2014, 40, 248–256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.; Begley, C.; Chen, M.; Bradley, A.; Bonanno, J.; McNamara, N.A.; Nelson, J.D.; Simpson, T. A Link between Tear Instability and Hyperosmolarity in Dry Eye. Investig. Opthalmology Vis. Sci. 2009, 50, 3671–3679. [Google Scholar] [CrossRef]
- Chao, W.; Belmonte, C.; del Castillo, J.M.B.; Bron, A.J.; Dua, H.S.; Nichols, K.K.; Novack, G.; Schrader, S.; Willcox, M.; Wolffsohn, J.S.; et al. Report of the Inaugural Meeting of the TFOS i2 = initiating innovation Series: Targeting the Unmet Need for Dry Eye Treatment. Ocul. Surf. 2016, 14, 264–316. [Google Scholar] [CrossRef] [Green Version]
- Mehra, D.; Galor, A. Digital Screen Use and Dry Eye: A Review, Asia-Pacific. J. Ophthalmol. 2020, 9, 491–497. [Google Scholar]
- Bahkir, F.A.; Grandee, S.S. Impact of the COVID-19 lockdown on digital device-related ocular health. Indian J. Ophthalmol. 2020, 68, 2378–2383. [Google Scholar] [CrossRef]
- Lemp, M.A.; Baudouin, C.; Baum, J.; Dogru, M.; Foulks, G.N.; Kinoshita, S.; Laibson, P.; McCulley, J.; Murube, J.; Pflugfelder, S.C.; et al. The Definition and Classification of Dry Eye Disease: Report of the Definition and Classification Subcommittee of the International Dry Eye Workshop (2007). Ocul. Surf. 2007, 5, 75–92. [Google Scholar]
- Daull, P.; Raymond, E.; Feraille, L.; Garrigue, J.-S. Safety and Tolerability of Overdosed Artificial Tears by Abraded Rabbit Corneas. J. Ocul. Pharmacol. Ther. 2018, 34, 670–676. [Google Scholar] [CrossRef] [Green Version]
- Tiffany, J.M.; Macey-Dare, B.V. Artificial Tear Formulation. U.S. Patent US6565861B1, 20 May 2003. [Google Scholar]
- Paugh, J.R.; Nguyen, A.L.; Ketelson, H.A.; Christensen, M.T.; Meadows, D.L. Precorneal Residence Time of Artificial Tears Measured in Dry Eye Subjects. Optom. Vis. Sci. 2008, 85, 725–731. [Google Scholar] [CrossRef] [PubMed]
- Arshinoff, S.; Hofmann, I.; Hemi, N. Role of rheology in tears and artificial tears. J. Cataract. Refract. Surg. 2021, 47, 655–661. [Google Scholar] [CrossRef]
- Arshinoff, S.; Hofmann, I.; Nae, H. Rheological behavior of commercial artificial tear solutions. J. Cataract. Refract. Surg. 2021, 47, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Wee, W.R.; Wang, X.W.; McDonnell, P.J. Effect of Artificial Tears on Cultured Keratocytes in Vitro. Cornea 1995, 14, 273–279. [Google Scholar] [CrossRef]
- Braun, R.J. Dynamics of the Tear Film. Annu. Rev. Fluid Mech. 2012, 44, 267–297. [Google Scholar] [CrossRef]
- Braun, R.J.; Fitt, A.D. Modelling drainage of the precorneal tear film after a blink. Math. Med. Biol. 2003, 20, 1–28. [Google Scholar] [CrossRef]
- Wong, H.; Fatt, I.; Radke, C. Deposition and Thinning of the Human Tear Film. J. Colloid Interface Sci. 1996, 184, 44–51. [Google Scholar] [CrossRef]
- Heryudono, A.; Braun, R.J.; Driscoll, T.A.; Maki, K.L.; Cook, L.P.; King-Smith, P.E. Single-equation models for the tear film in a blink cycle: Realistic lid motion. Math. Med. Biol. 2007, 24, 347–377. [Google Scholar] [CrossRef]
- Braun, R.J.; King-Smith, P.E. Model problems for the tear film in a blink cycle: Single-equation models. J. Fluid Mech. 2007, 586, 465–490. [Google Scholar] [CrossRef] [Green Version]
- Deng, Q.; Braun, R.J.; Driscoll, T.A.; King-Smith, P.E. A Model for the Tear Film and Ocular Surface Temperature for Partial Blinks. Interfacial Phenom. Heat Transf. 2013, 1, 357–381. [Google Scholar] [CrossRef] [PubMed]
- Zubkov, V.S.; Breward, C.J.W.; Gaffney, E.A. Meniscal Tear Film Fluid Dynamics near Marx’s Line. Bull. Math. Biol. 2013, 75, 1524–1543. [Google Scholar] [CrossRef] [PubMed]
- Aydemir, E.; Breward, C.J.W.; Witelski, T.P. The Effect of Polar Lipids on Tear Film Dynamics. Bull. Math. Biol. 2010, 73, 1171–1201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bruna, M.; Breward, C.J.W. The influence of non-polar lipids on tear film dynamics. J. Fluid Mech. 2014, 746, 565–605. [Google Scholar] [CrossRef] [Green Version]
- Jossic, L.; Lefevre, P.; de Loubens, C.; Magnin, A.; Corre, C. The fluid mechanics of shear-thinning tear substitutes. J. Non-Newtonian Fluid Mech. 2009, 161, 1–9. [Google Scholar] [CrossRef]
- Mehdaoui, H.; Abderrahmane, H.A.; Bouda, F.N.; Koulali, A.; Hamani, S. 2D numerical simulation of tear film dynamics: Effects of shear-thinning properties. Eur. J. Mech.-B/Fluids 2021, 90, 128–136. [Google Scholar] [CrossRef]
- Daull, P.; Amrane, M.; Ismail, D.; Georgiev, G.; Cwiklik, L.; Baudouin, C.; Leonardi, A.; Garhofer, G.; Garrigue, J.S. Cationic Emulsion-Based Artificial Tears as a Mimic of Functional Healthy Tear Film for Restoration of Ocular Surface Homeostasis in Dry Eye Disease. J. Ocul. Pharmacol. Ther. 2020, 36, 355–365. [Google Scholar] [CrossRef]
- King-Smith, P.E.; Fink, B.A.; Nichols, J.J.; Nichols, K.K.; Braun, R.J.; McFadden, G.B. The Contribution of Lipid Layer Movement to Tear Film Thinning and Breakup. Investig. Opthalmology Vis. Sci. 2009, 50, 2747–2756. [Google Scholar] [CrossRef]
- Cwiklik, L. Tear film lipid layer: A molecular level view. Biochim. Et Biophys. Acta (BBA)-Biomembr. 2016, 1858, 2421–2430. [Google Scholar] [CrossRef]
- Coffey, M.J.; DeCory, H.H.; Lane, S.S. Development of a non-settling gel formulation of 0.5% loteprednol etabonate for anti-inflammatory use as an ophthalmic drop. Clin. Ophthalmol. 2013, 7, 299–312. [Google Scholar]
- Yu, Y.; Chow, D.W.Y.; Lau, C.M.L.; Zhou, G.; Back, W.; Xu, J.; Carim, S.; Chau, Y. A bioinspired synthetic soft hydrogel for the treatment of dry eye. Bioeng. Transl. Med. 2021, 6, e10227. [Google Scholar] [CrossRef] [PubMed]
- Acar, D. Bio-Adhesive Polymers Containing Liposomes for DED Treatment. Ph.D. Thesis, Aston University, Birmingham, UK, 2019. [Google Scholar]
- Willcox, M.D.; Argüeso, P.; Georgiev, G.; Holopainen, J.M.; Laurie, G.; Millar, T.J.; Papas, E.B.; Rolland, J.P.; Schmidt, T.A.; Stahl, U.; et al. TFOS DEWS II Tear Film Report. Ocul. Surf. 2017, 15, 366–403. [Google Scholar] [CrossRef] [Green Version]
- Piau, J.M. Carbopol gels: Elastoviscoplastic and slippery glasses made of individual swollen sponges: Meso- and macroscopic properties, constitutive equations and scaling laws. J. Non-Newtonian Fluid Mech. 2007, 144, 1–29. [Google Scholar] [CrossRef]
- Herschel, W.H.; Bulkley, R. Consistency measurements of rubber benzene solutions. Kolloid-Z 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Jones, M.B.; Please, C.; McElwain, S.; Fulford, G.; Roberts, A.P.; Collins, M. Dynamics of tear film deposition and draining. Math. Med. Biol. 2005, 22, 265–288. [Google Scholar] [CrossRef] [PubMed]
- Tutt, R.; Bradley, A.; Begley, C.; Thibos, L.N. Optical and Visual Impact of Tear Break-up in Human Eyes. Investig. Ophthalmol. Vis. Sci. 2000, 41, 4117–4123. [Google Scholar]
- Magnin, A.; Piau, J. Cone-and-plate rheometry of yield stress fluids. Study of an aqueous gel. J. Non-Newtonian Fluid Mech. 1990, 36, 85–108. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Le, H.D.; De Schutter, G.; Kadri, E.H.; Aggoun, S.; Vierendeels, J.; Tichko, S.; Troch, P. Computational fluid dynamics calibration of tattersall MK-II TYPE rheometer for concrete. Appl. Rheol. 2013, 23, 34741-12. [Google Scholar]
- ANSYS FLUENT 17.0: User’s Guide. Available online: https://manualzz.com/doc/47147783/fluent-in-workbench-user-s-guide (accessed on 9 July 2021).
- Allouche, M.; Abderrahmane, H.A.; Djouadi, S.M.; Mansouri, K. Influence of curvature on tear film dynamics. Eur. J. Mech.-B/Fluids 2017, 66, 81–91. [Google Scholar] [CrossRef]
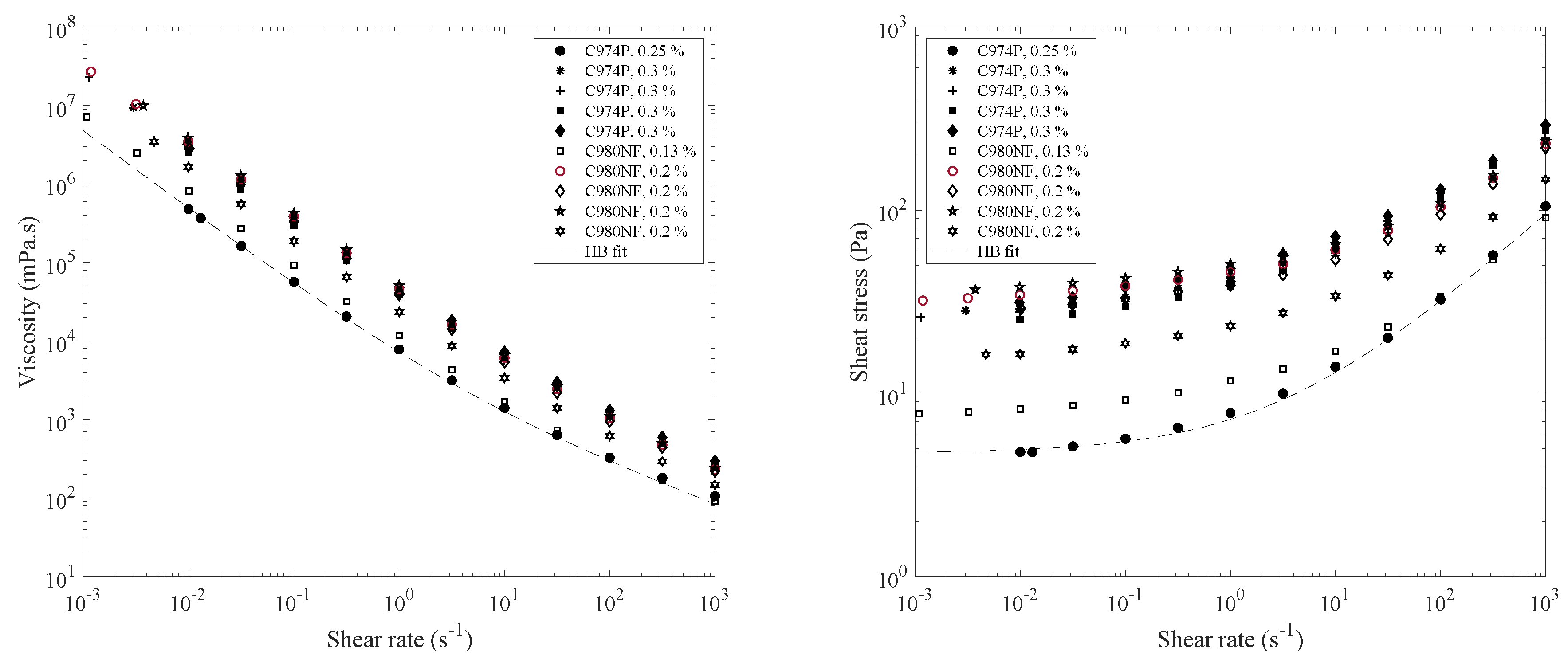



| Composition | Concentration (%) | Yield Stress (Pa) | k (Pa.sn) | n |
|---|---|---|---|---|
| Carbopol® 974 P | 0.25 | 4.7 | 2.5 | 0.5 |
| 0.3 | 23.8 | 18.1 | 0.4 | |
| 0.3 | 26 | 14.4 | 0.4 | |
| 0.3 | 27.7 | 20.5 | 0.4 | |
| 0.3 | 28.1 | 16.9 | 0.4 | |
| Carbopol® 980 NF | 0.13 | 7.3 | 3.4 | 0.5 |
| 0.2 | 15.9 | 7.9 | 0.4 | |
| 0.2 | 31.3 | 12.4 | 0.4 | |
| 0.2 | 32.1 | 15 | 0.4 | |
| 0.2 | 33.8 | 15.5 | 0.4 |
| hmin at Upper-Lid (10−7 m) | |||||
|---|---|---|---|---|---|
| τ0 = 0 Pa | τ0 = 0.2 Pa | τ0 = 1 Pa | τ0 = 4.5 Pa | ||
| n = 0.5 | Newtonian | 0.574 | |||
| k = 0.07 Pa·s | 0.603 | 0.628 | 0.660 | 0.664 | |
| k = 0.6 Pa·s | 0.599 | 0.591 | 0.671 | 0.625 | |
| k = 2.5 Pa·s | 0.589 | 0.627 | 0.641 | 0.631 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehdaoui, H.; Ait Abderrahmane, H.; de Loubens, C.; Nait Bouda, F.; Hamani, S. Dynamics of a Gel-Based Artificial Tear Film with an Emphasis on Dry Disease Treatment Applications. Gels 2021, 7, 215. https://doi.org/10.3390/gels7040215
Mehdaoui H, Ait Abderrahmane H, de Loubens C, Nait Bouda F, Hamani S. Dynamics of a Gel-Based Artificial Tear Film with an Emphasis on Dry Disease Treatment Applications. Gels. 2021; 7(4):215. https://doi.org/10.3390/gels7040215
Chicago/Turabian StyleMehdaoui, Hamza, Hamid Ait Abderrahmane, Clement de Loubens, Faïçal Nait Bouda, and Sofiane Hamani. 2021. "Dynamics of a Gel-Based Artificial Tear Film with an Emphasis on Dry Disease Treatment Applications" Gels 7, no. 4: 215. https://doi.org/10.3390/gels7040215
APA StyleMehdaoui, H., Ait Abderrahmane, H., de Loubens, C., Nait Bouda, F., & Hamani, S. (2021). Dynamics of a Gel-Based Artificial Tear Film with an Emphasis on Dry Disease Treatment Applications. Gels, 7(4), 215. https://doi.org/10.3390/gels7040215






