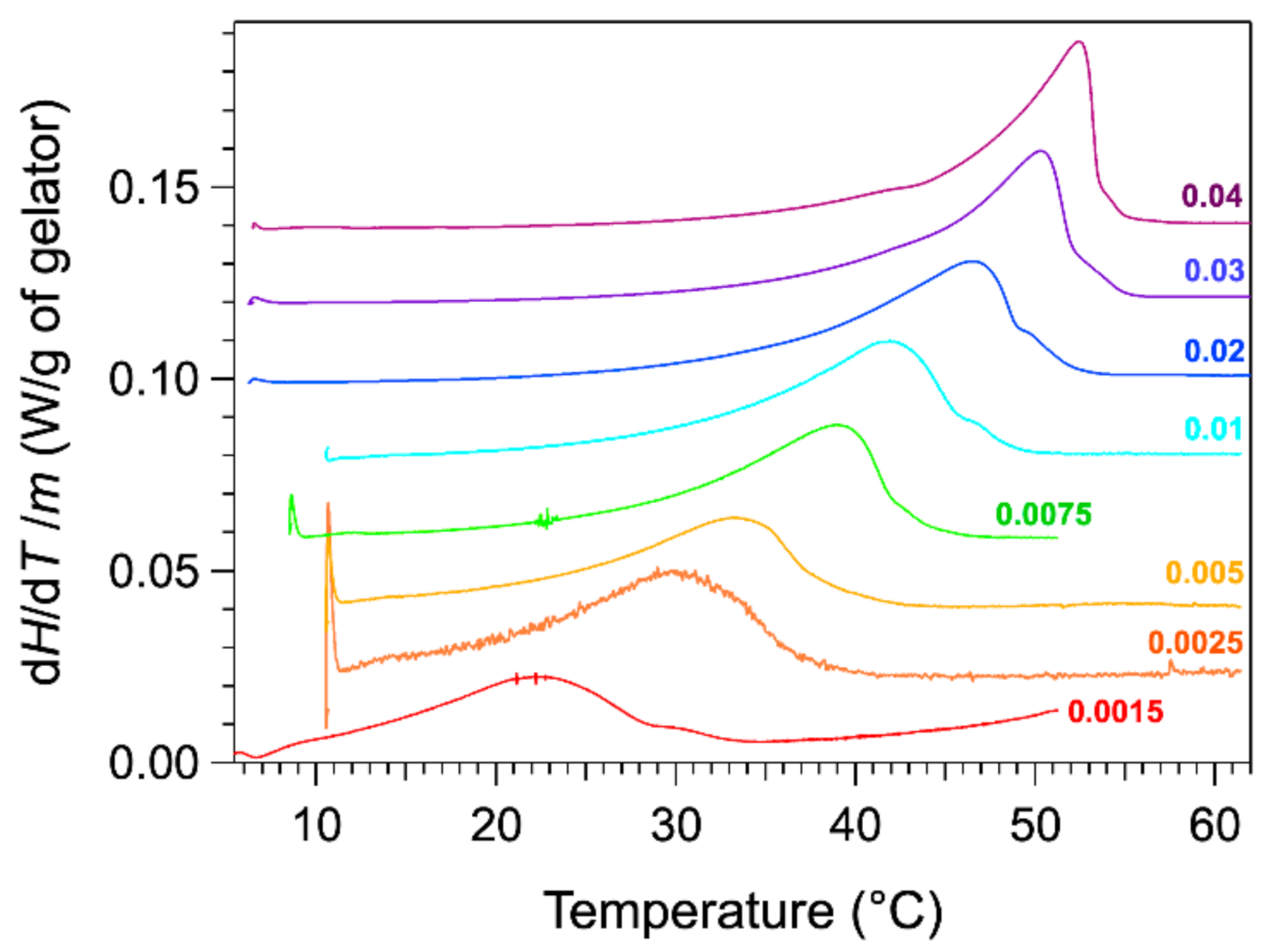
2.1. Aspect of the Thermograms
The thermograms were measured with a microcalorimeter. The apparatus measures the heat flow difference between the gel and the solvent as the reference. The advantage of the microcalorimeter is its sensitivity at low heating rates. The rate used in our studies is 0.1 °C/min. The low rates provide a lower signal, but they reduce the effects due to the heat transfer and kinetics. For instance, the observed peaks are not shifted to higher temperature values than actual temperatures. The thermograms of HSA/nitrobenzene gels were recorded for total weight fractions
W comprised between 0.0015 and 0.04. The thermograms normalized to the mass of HSA are presented in
Figure 1.
The thermograms for weight fractions W exhibit an endothermic peak, stretched out from low temperature, increasing slowly up to a maximum, and followed by steep decrease. The heat flow diminishes to the baseline only a few degrees after its maximal value. For samples at lower concentrations, the decrease after the peak is less abrupt and much slower. For the last curve, the heat flow reaches the baseline 10 °C above the temperature of the maximal flow. At the maximum of the peak , the thermal events are far to be finished, and the choice of the temperature of this maximum as is not obvious. This will be discussed later.
2.2. Measurements of the Molar Enthalpies
From these thermograms, the enthalpies can be measured by integration, and one may wonder whether the change of shape of the curves with concentration affects the enthalpies. We have integrated the heat flows either with the software of the apparatus or home-made software. In both cases, the signal is integrated between two temperatures after a baseline is subtracted. This baseline is simply the straight line joining both points. As a consequence, at the temperatures chosen as the integration limits, the heat flow is set to zero. In this first part, we have followed this procedure, and we will discuss its accuracy later. For each thermogram, the curves were integrated from the same starting temperature 14 °C up to temperatures after the peaks, when the heat flows are equal to the baseline. The calculated enthalpy ∆
H was normalized to the number of moles of gelator
n in the sample to yield the molar melting enthalpies
L (
Figure 2). For weight fractions above 0.01, the values are the same with an average value of 62.1 ± 0.3 kJ/mol. However, the values diminish for lower concentrations. The thermograms at a rate of 0.25 °C/min afford the same values of ∆
H within an error of 3%, thus showing no effect of the rate. The low concentrations are subjects to the errors in weighing low masses, and in the sensibility of the calorimeter, but these errors do not exceed 10% of total area and cannot explain a drop of 50% for
W = 0.0015.
The apparent lower values at low concentrations are easily explained by the solubility of the gelator. If the measured enthalpy is assumed to come only from the melting of the gel, the heat flow is given by Equation (1).
where
L is the molar enthalpy of melting of the gel and d
ns is the number of moles of gelators transitioning from the solid state to the liquid phase, opposite to
, the increment in the number of moles appearing in the liquid phase. If the heat flow is integrated between a temperature
(chosen as low as possible) and a temperature
T, the corresponding enthalpy is:
where
and
are the number of moles of gelator in the solid phase at
T and
;
and
are the same in the liquid phase. The integral
increases with
T and reaches a plateau when
T is above the melting temperature of the gel
. This plateau, noted simply
, is the value used above to derive molar enthalpy (
). When
, all the gelator is solubilized, there is no longer solid:
= 0; the corresponding integral
, with
n representing the total number of moles of the gelator. There is always a proportion of the gelator soluble in the liquid phase even if it is small. It is related to the concentration
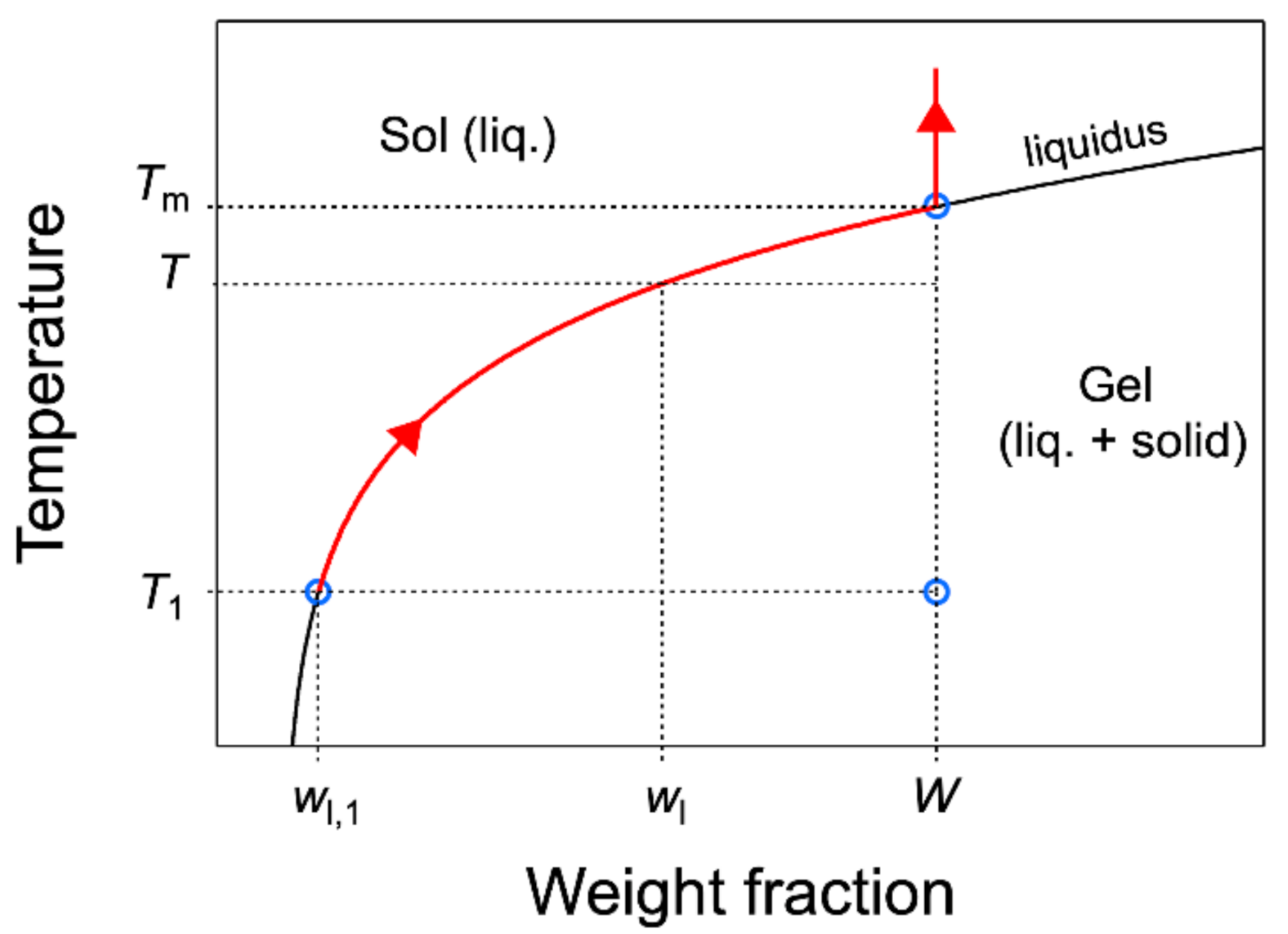
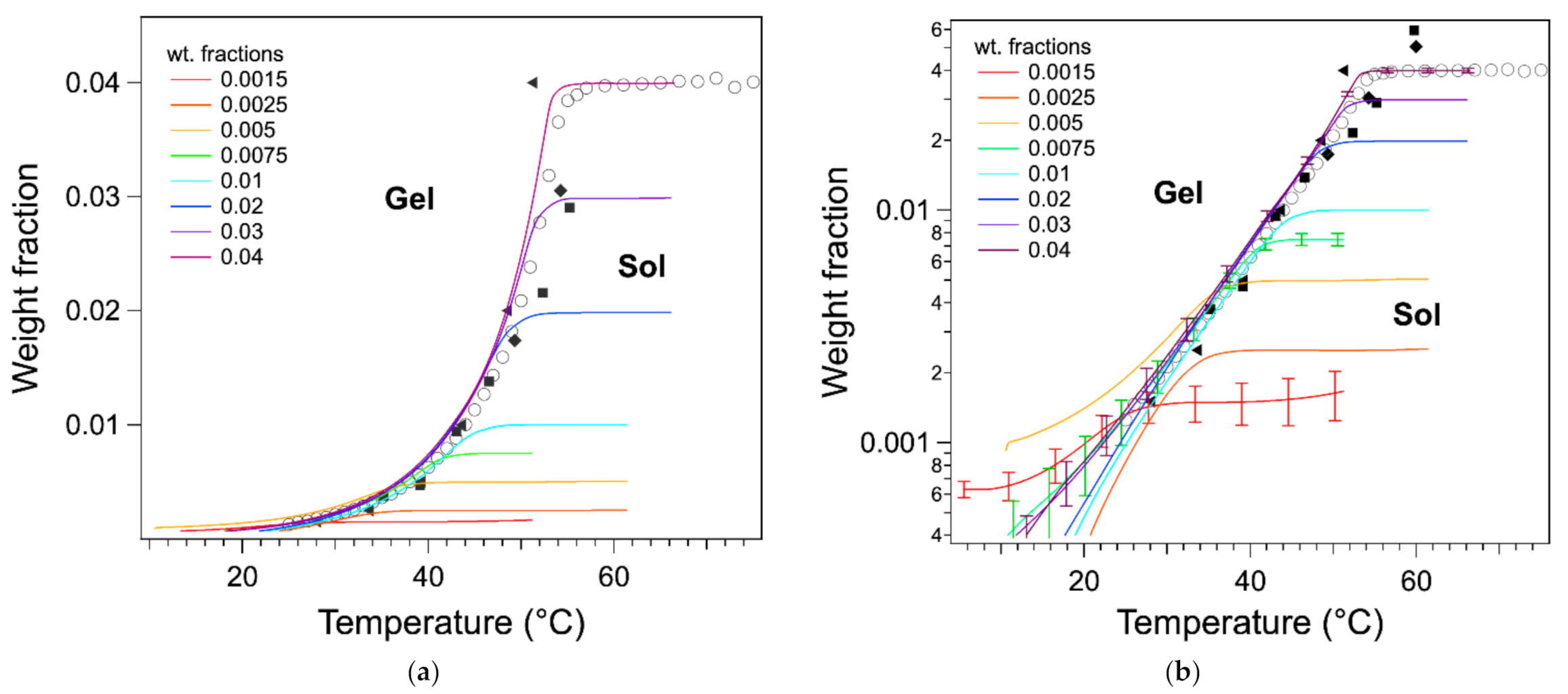
of the gelator in the liquid, or solubility; it depends on the temperature only, and it is given by the gel-to-sol line in the phase diagram (the abscissa at a given
T; see
Figure 3).
When the total fraction
W in the gelator is high, the fraction of the soluble fraction of the gelator is negligible before the solid fraction:
n ∼
and
∆H =
Ln. For high
W values, it is a good approximation to consider that all the gelator in the mixture transitions from the solid to the liquid phase. However, this approximation is no longer valid when
W is in the same order of magnitude as the solubility of the gelator. The lever rule allows quantifying the weight fraction of the solid phase:
where
is the mass of the solid gelator at
and
is the total mass of the gel;
is the solubility at
(
). From this equation, the number of moles of gelator
ns in the solid phase can be calculated and hence the quantity ∆
H/
n (Equation (4)).
In this equation, is the integral of the heat flow between a low temperature and a temperature above the transition, and is the fraction of gelator in the liquid at .
∆
H/
n =
L only when W >>
.
Figure 2 shows the fit of the values from Equation (4). This fit accounts for the variations of
∆H/
n, with a parameter
in the expected order of magnitude (about half of 0.0015). The most important point is that the value of
L can be given by DSC only if the concentration
W is significantly higher than the solubility
at low temperature. In conclusion, the phase diagram can explain the dependance of the integrals with concentrations.
2.3. Measurement of Transition Temperatures
As an introduction, it is necessary to define the melting temperature
of organogels. For a binary system such as organogels, according to Gibb’s phase rule, at fixed pressure, the sol–gel equilibrium is monovariant, which means that the gel melts in a range of temperatures, not at a single temperature. Even at low temperatures, a fraction of the solid melts upon heating, and the fraction of melted solid increases with
T. This fraction is given by the lever rule, as explained above. When the temperature reaches
the liquidus composition is the total concentration
W, and all the gelator is solubilized (
Figure 3). In summary, the solid fraction dissolves gradually from low temperature up to
where the dissolution is complete.
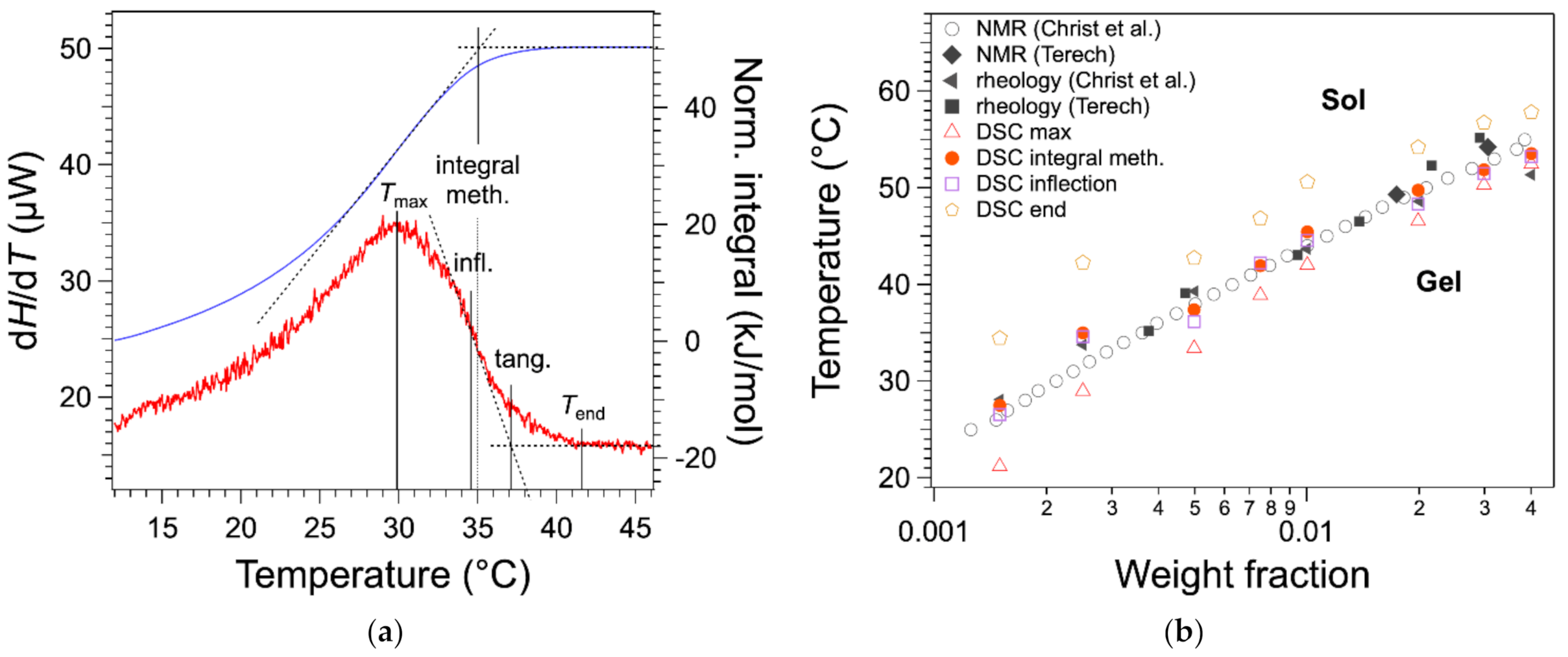
In previous work [
20], we have considered
as the temperature of the maximum
(
Figure 4a), as practiced in earlier work or recommended in textbooks [
11,
13]. We have compared the
values with those obtained by other techniques. The binary
c-
T phase diagram of HSA/nitrobenzene provides a good comparison because it has been studied by two groups, each with different techniques and five sets of data with a good agreement [
12,
19]. There a bias between the measured
values temperature and the other measurements as shown in
Figure 4b. All
values (red triangles) measured from DSC are lower than the values from other measurements.
For the highest two concentrations, there is a good agreement between
and the temperatures measured with the other techniques; for lower
W values, a gap appears and increases when
W decreases. In the literature, it has been suggested that the melting temperature is given by the temperature
of the end of the exotherm, when the heat flow joins the baseline (
Figure 4a) [
17]. This definition is legitimate, since the liquidus is defined by the line above which the mixture is completely liquid, that is when the last solid fraction has melted. For instance, it is applied to map phase diagrams of metal alloys [
14]. However, in the case of organogels, the heat flow broadens after the peak, especially for low concentration
W. As a result,
values are well above the transition temperature values, as measured by other techniques (
Figure 4b).
The tangent method is another classical method to measure the full solubilization temperature of organic compounds by DSC [
21]. It consists of drawing the tangent at the inflection point and determining its intersection with the baseline (
Figure 4a). This method is very precise for concentrated solution (a few tens of wt %) because the baseline is well defined. However, for lower concentrations, the baseline is not linear and noisy, which leads to large uncertainties. However, the inflection point can be located with accuracy and very reproducibly even for a heat flow with a low signal/noise ratio, as shown in
Figure 4a. The temperature of full solubilization can be visualized by the integral of the heat flow. This integral varies linearly with the amount of gelator in the liquid phase (Equation (2)). At the plateau, the gelator is fully soluble and in the ascending branch increasing with
T, the gelator is transforming from solid to liquid. The temperature of full solubilization can be taken as the intersection of the plateau and the tangent of the integral at its inflection. It is closer to the liquidus and to the
measured by rheology than
; it presents errors but less bias. The determination of the melting temperature by the integral is rather lengthy. However, as shown in
Figure 4a,b, the values are close to the inflection points within 1 °C, and the inflection point is simpler to determine, either graphically or by software. Therefore,
can be measured conveniently with a good precision by the inflection point temperature.
2.4. Calculation of the Soluble Fraction of Gelator from the Thermograms
When the thermograms are normalized to the total mass of the gel, their ascending branches superimpose approximately (
Figure 5a). In this section, we try to study whether this superimposition and the shape of the thermograms reflect the thermodynamics of the organogels. We have hypothesized that the heat flows are related only to the transformations of the gel at quasi-equilibrium. The baseline of the thermograms was corrected from the difference in capacity between cells, as described in Materials and Methods, which made the superimposition more accurate, as shown in
Figure 5b.
After this correction of the baselines, the heat flows correspond to Equation (5).
where
is the weight fraction of solubilized gelator in the whole mixture,
M is the molar weight of the gelator,
L is the molar melting enthalpy, and
is the difference between the heat capacity of the solid and liquid gelator.
is close to the weight fraction
of the gelator in the liquid (Equation (6)).
When the gel is heated but not melted, the solubility
is equal the liquidus (
Figure 3). Hence, when the heat flows are normalized to the total mass
, they depend only on intensive quantities. It explains why the curves superimpose before the melting of the gels. After the transition,
=
W and
= 0, and the heat flows reach a plateau of different values.
In a first approximation, the capacity effects are neglected, and the heat flows are:
The integration of the curves should yield the solubility and retrace the liquidus in the phase diagram. The weight fraction
of the gelator in the mixture is expressed simply with
, the integral between a reference temperature
and
T, and
is the maximal value of this integral (as defined in
Section 2.3):
When the heat flow is integrated after the subtraction of a straight baseline joining the integration limits, the
values yielded by Equations (4) and (6) superimpose with the liquidus only at high T and depart significantly from it at low T or concentrations. This error is due to the straight baseline that neglects the partial melting at low
T, as explained in
Section 2.2. In order to better estimate the baseline,
was multiplied by a factor to adjust the value of its plateau (
W) to the baseline of the normalized heat flow after
. It amounts to multiplying by
, and we verified that the factor is close to the
value calculated from the fit in material and method. Since Equation (5) deals with d
H/d
T,the conversion to the heat flow d
H/d
t is done by multiplying the resukt by another factor
r, the heating rate.
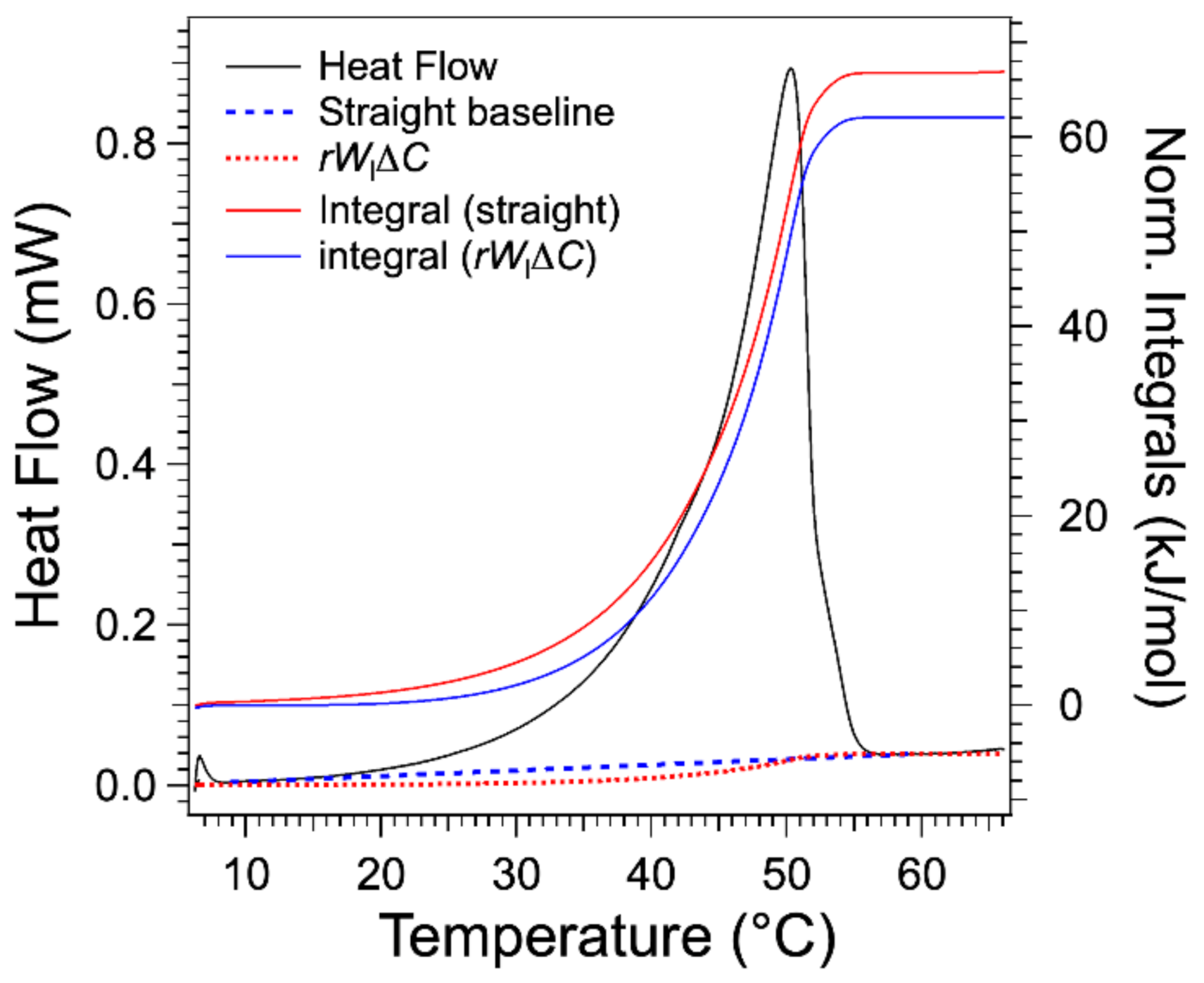
Figure 6 compares the term
and the straight baseline for the gel at 3 wt %. It lies below the straight baseline joining both integral limits. Therefore, the integral after subtraction of this term yields a higher molar enthalpy of about 7% in the selected example, and this error increases when the concentration
W decreases to reach more than 50% for the lowest concentrations. Indeed, the order of magnitude of the error is
. The integrals calculated after subtraction of the
yield a value of molar melting enthalpy
L of 67.1 ± 0.7 kJ/mol.
The ascending parts of the
curves superimpose well with the liquidus as measured by other techniques (
Figure 7). For the sample of concentration
W > 0.075, the curves superimpose from high to low temperatures within 2 °C in their upper parts. For the samples of concentration below 0.005, the curves superimpose only roughly to the phase diagram. Part of this error can be attributed to the low signal/noise ratio at lower
W and the difficulty of calculating the baseline. The uncertainties of
were calculated by taking into account the noise, the errors on
W, and the measured
L values. For the curves corresponding to high concentrations, the uncertainties are below 10% for temperatures above 35 °C and increase when T increases. For lower concentrations, the uncertainties are greater than 10% even if it decreases with decreasing
T. In addition to the errors due to the signal, and more fundamentally, at low temperature, the heat flows cannot be modeled only by thermodynamics at equilibrium, but the heat transfer and kinetics should be taken into account. However, this superimposition shows that the shape of the endotherms above ≈34 °C are directly related to the phase diagram. It also confirms that the determination of the melting temperature by the integrals is more accurate: the temperature of the maximum of the endotherm is too low because it corresponds to the inflection point of the integral, not to the start of the plateau.
2.5. Comparison of the Endotherms with the Exotherms
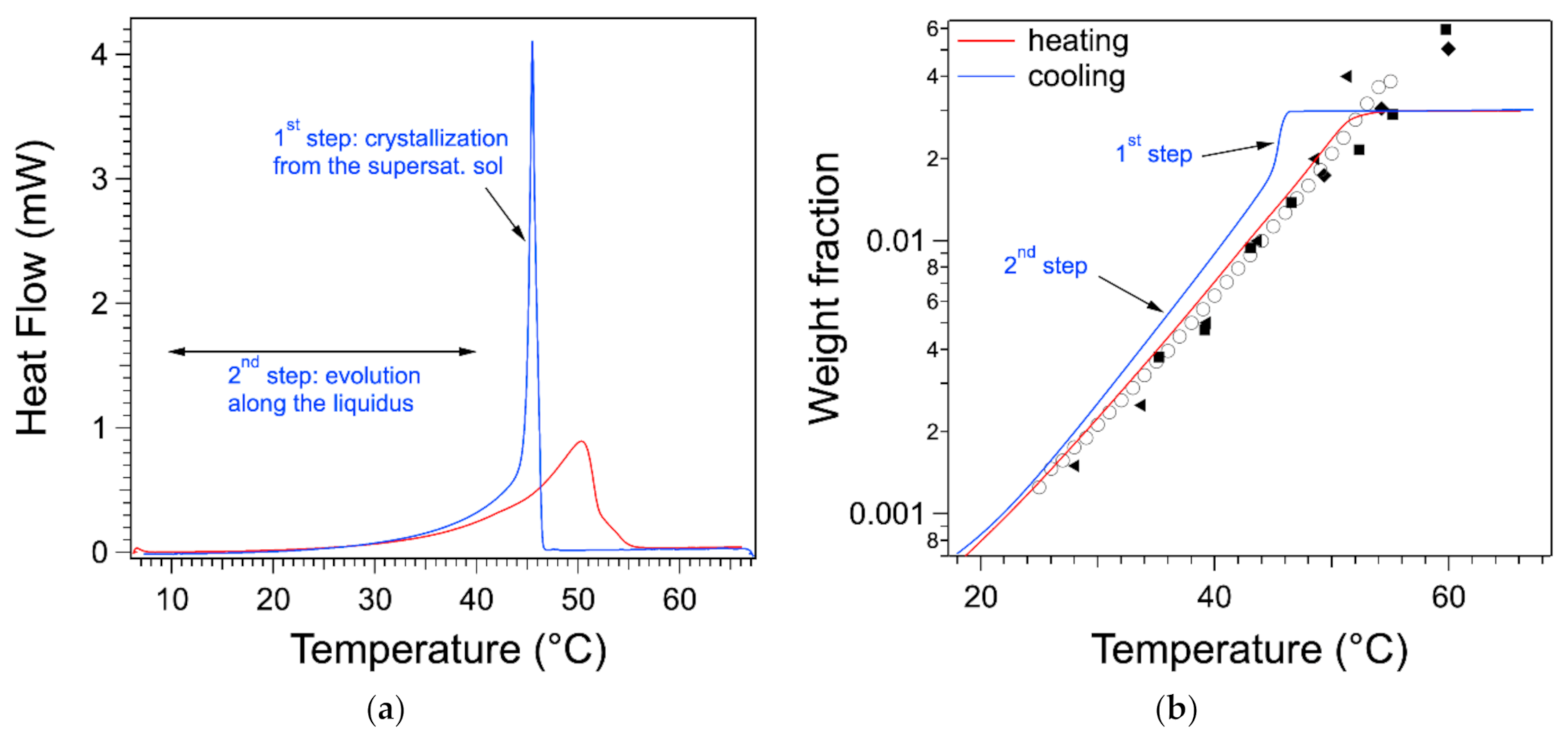
As discussed in the introduction, the thermogram measured upon cooling exhibits a sharp peak. In
Figure 8a, the endotherm and the exotherm of the gel at 0.03 are represented. The exotherm has been multiplied by −1 to compare directly both flows. On the cooling curve, after the heat flow reaches its peaks, when
T decreases, the flow decreases first abruptly and then slowly. In the second step, at low temperatures, it superimposes with the heating curve. This can be explained by correlating the signal with the phase diagram.
The heat flow measured during cooling can be treated and integrated in the same way as the one during heating. It yields the variation of the weight fraction
during the cooling phase.
starts from the plateau where all of the gelator is soluble. When
T decreases,
remains on the plateau, which shows that all of the gelator is in the liquid phase and passes the liquidus: the gelator remains dissolved but in a supersaturated state. At the transition temperature (almost equal to the peak temperature), the concentration drops suddenly. In a second stage, it decreases slowly with
T, and it is close to the liquidus. The drop in
corresponds to the solidification of part of the gelator. This stops when the solution returns to its saturation state, i.e., on the liquidus. This return is slow and incomplete. It can be due to the kinetics of formation of the aggregates. Nevertheless, the heat flow shows both steps, as indicated on
Figure 8a. The whole signal includes both stages, and the integral of the peak itself is only half of the whole integral. Therefore, integration limits close to the edges of the peak will yield erroneously a lower enthalpy than for the endotherm.