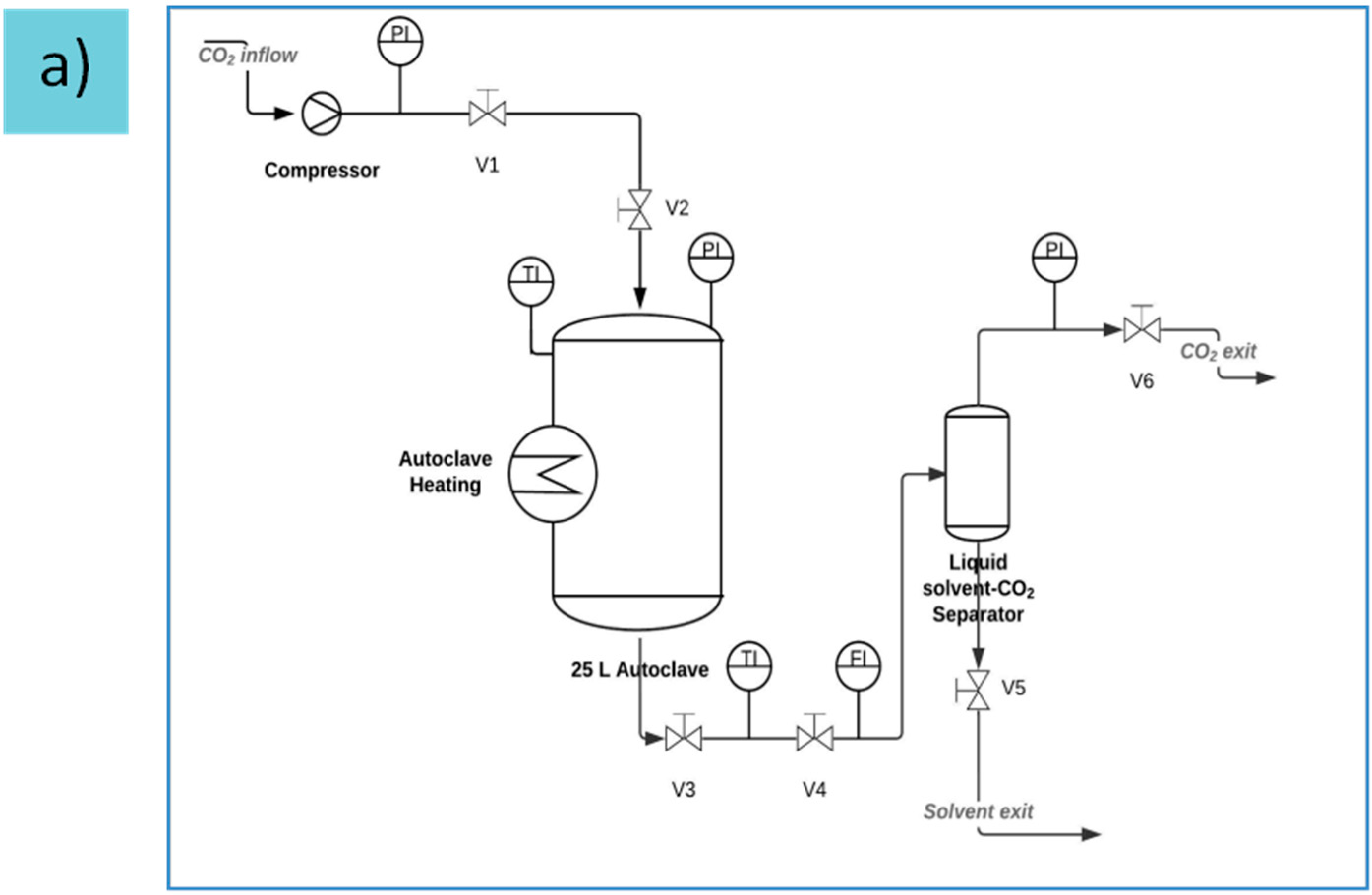
2.1. Role of Solvent-matrix Interactions during the Solvent Exchange Process
To reveal the influence of solvent nature on the shrinkage of alginate hydrogel (0.5 wt %, Q1; see
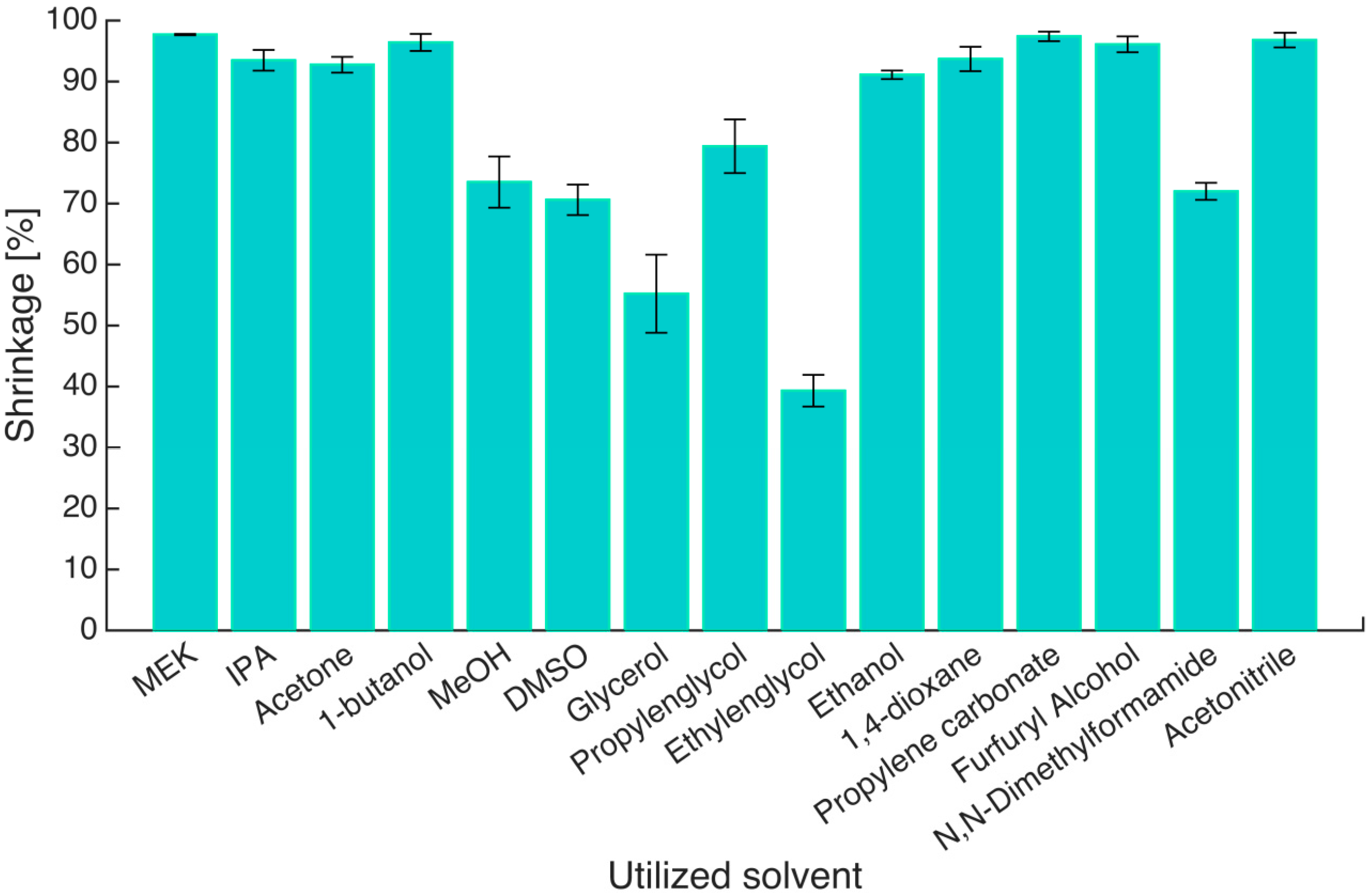
Section 4 for details), one step solvent exchange was performed with 15 different solvents. One step procedure is known to cause considerable shrinkage [
6] and was used in this study intentionally to simulate the worst-case scenario and to potentially discriminate between the solvents. The final solvent concentration for this procedure was >95 wt %. Appearance of the original hydrogel and the gel subjected to solvent exchange is shown in
Figure 1.
To quantify the effect of the solvent, volumetric shrinkage was calculated (
Figure 2, see
Section 4.8, Equation (12)). Only six of the 15 solvents were able to retain gels with volume shrinkage less than 90%. They are methanol, DMSO, glycerol, propylene glycol, ethylene glycol and DMF. It is interesting to note that ethanol does not make this list even though it is the solvent of choice for solvent exchange and supercritical drying [
6,
23]. The reason lies in the fact that only stepwise solvent exchange with ethanol leads to volume shrinkage at a more acceptable level [
3,
6]. Much lower volumetric shrinkages for all other solvents can be expected when a stepwise solvent exchange procedure is used. In addition to volume shrinkage, the solvents also cause the change of other properties of the gels during shrinking, such as the shape, texture style, strength, transparency and even the color. The gels which showed extreme shrinkage,
i.e., in MEK, IPA, 1-butanol, 1,4-dioxane, propylene carbonate, furfuryl alcohol and acetonitrile, changed into hard rubber-like texture. The gels immersed in ethylene glycol became extremely brittle and broke despite the low volume shrinkage, and the ones immersed in glycerol had significant deformation. The appearance and texture of gels immersed in pure methanol, DMSO, propylene glycol and DMF could be inferred as the best out of all the cases.
Figure 1.
Pictures of shrunk gels compared to an original hydrogel. The hydrogels are placed on the left in each picture, and on the right are the gels once soaked in (a) methyl ethyl ketone (MEK); (b) isopropanol (IPA); (c) acetone; (d) 1-butanol; (e) methanol (MeOH); (f) dimethyl sulfoxide (DMSO); (g) glycerol; (h) propylene glycol; (i) ethylene glycol; (j) ethanol; (k) 1,4-dioxane; (l) propylene carbonate; (m) furfuryl alcohol; (n) N,N-dimethylformamide (DMF) and (o) acetonitrile.
Figure 1.
Pictures of shrunk gels compared to an original hydrogel. The hydrogels are placed on the left in each picture, and on the right are the gels once soaked in (a) methyl ethyl ketone (MEK); (b) isopropanol (IPA); (c) acetone; (d) 1-butanol; (e) methanol (MeOH); (f) dimethyl sulfoxide (DMSO); (g) glycerol; (h) propylene glycol; (i) ethylene glycol; (j) ethanol; (k) 1,4-dioxane; (l) propylene carbonate; (m) furfuryl alcohol; (n) N,N-dimethylformamide (DMF) and (o) acetonitrile.
Figure 2.
Volumetric shrinkage (S1) of gels in different solvents after one step solvent exchange. The horizontal labels are the names of solvents, in which hydrogels were immersed. Error bars represent standard deviation of three parallel measurements.
Figure 2.
Volumetric shrinkage (S1) of gels in different solvents after one step solvent exchange. The horizontal labels are the names of solvents, in which hydrogels were immersed. Error bars represent standard deviation of three parallel measurements.
Solvent/biopolymer interactions and the matrix shrinkage during solvent exchange can be further understood and related to each other through solubility parameters [
27]. Solubility parameters are widely used not only to predict solubility, but also to predict the compatibility of polymers and affinities to surfaces to improve dispersion and adhesion [
28]. Even for insoluble polymers the solubility parameters can be correlated with swelling. Hansen solubility parameters are one such parameter usually used to predict the polymer solubility. It takes into consideration three major types of interaction between molecules: dispersion (d), dipole-dipole (p) and the hydrogen bonding (h) interactions. The basic Equation (1) which governs the assignment of Hansen parameter is that the total cohesion energy
E equals the sum of the individual energies
Dividing this by the molar volume of the solvent gives the square of the total solubility parameter which is the sum of the squares of the Hansen d, p and h components, Equation (2). The total solubility parameter δt is also the so-called Hildebrand solubility parameter.
The d, p and h components of the Hildebrand parameter for each individual solvent were taken from [
28] and listed
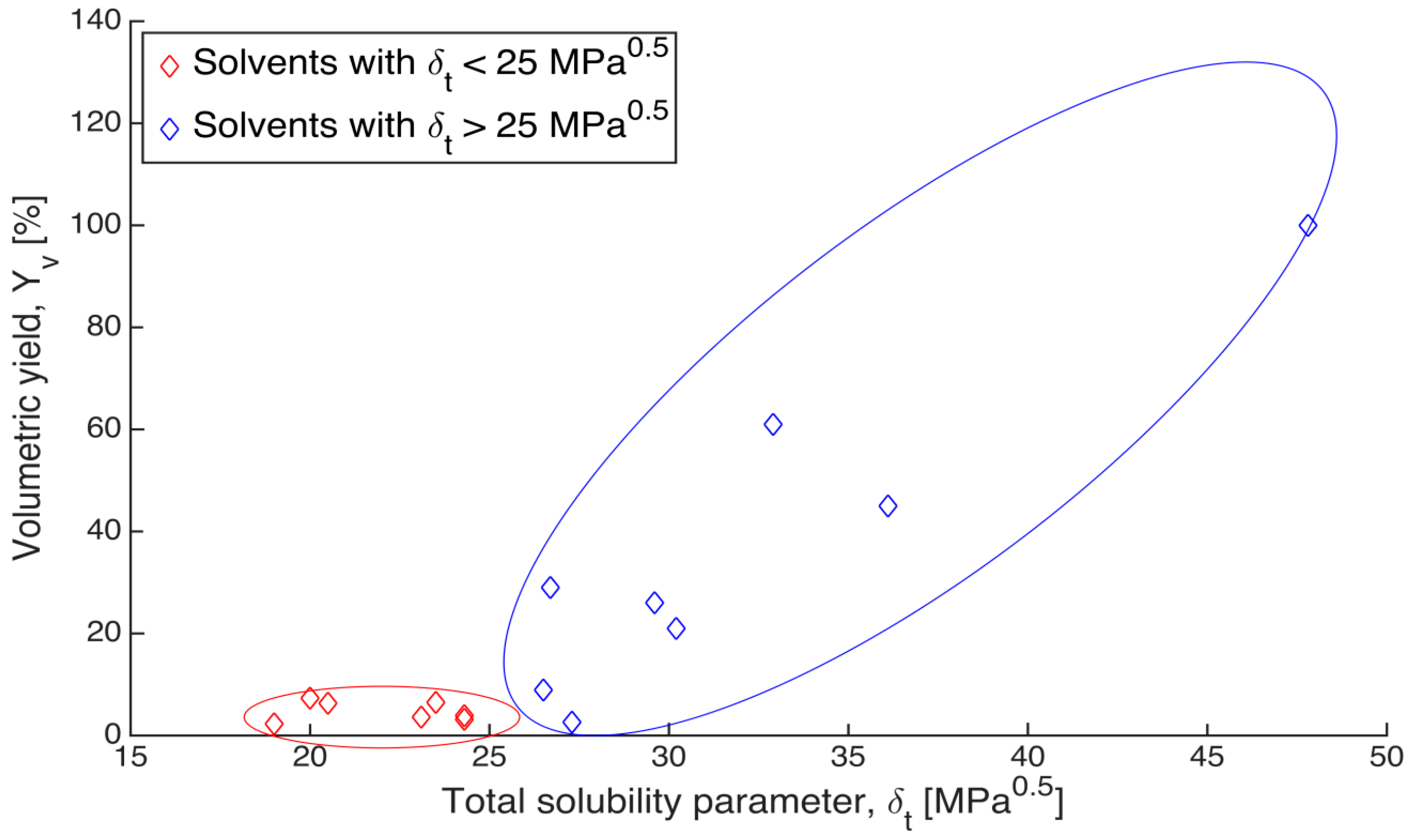
Table 1. The volumetric yield
of all gels after the one step solvent exchange was plotted against the total solubility parameter δ
t of the respective solvents (
Figure 3). The volumetric yield is a measure of remaining volume relative to initial volume (see Equation (13)).
Table 1.
The Hansen solubility parameters of solvents and experimentally measured volumetric yields after one step solvent exchange.
Table 1.
The Hansen solubility parameters of solvents and experimentally measured volumetric yields after one step solvent exchange.
| Solvents | δd MPa0.5 | δp MPa0.5 | δh MPa0.5 | δt MPa0.5 | Volumetric Yield |
|---|
| Water | 15.6 | 16.0 | 42.3 | 47.8 | 100 |
| MEK | 16.0 | 9.0 | 5.1 | 19.0 | 2.30 ± 0.11 |
| IPA | 15.8 | 6.1 | 16.4 | 23.5 | 6.5 ± 1.7 |
| Acetone | 15.5 | 10.4 | 7.0 | 20.0 | 7.3 ± 1.3 |
| 1-butanol | 16.0 | 5.7 | 15.8 | 23.1 | 3.6 ± 1.4 |
| Methanol | 15.1 | 12.3 | 22.3 | 29.6 | 26.4 ± 4.2 |
| DMSO | 18.4 | 16.4 | 10.2 | 26.7 | 29.4 ± 2.5 |
| Glycerol | 17.4 | 12.1 | 29.3 | 36.1 | 44.8 ± 6.4 |
| Propylene glycol | 16.8 | 9.4 | 23.3 | 30.2 | 20.6 ± 4.4 |
| Ethylene glycol | 17.0 | 11.0 | 26.0 | 32.9 | 60.7 ± 2.6 |
| Ethanol | 15.8 | 8.8 | 19.4 | 26.5 | 8.94 ± 0.71 |
| 1,4-dioxane | 19.0 | 1.8 | 7.4 | 20.5 | 6.3 ± 2.0 |
| Propylene carbonate | 20.0 | 18.0 | 4.1 | 27.3 | 2.60 ± 0.78 |
| Furfuryl alcohol | 17.4 | 7.6 | 15.1 | 24.3 | 3.9 ± 1.3 |
| DMF | 17.4 | 13.7 | 11.3 | 24.8 | 28.0 ± 1.4 |
| Acetonitrile | 15.3 | 18.0 | 6.1 | 24.3 | 3.2 ± 1.2 |
As shown in
Figure 3, although the data points are rather scattered, a clear trend is observed that the alginate gels shrank less in the solvents with higher solubility parameters. The volumetric yield of gels immersed in the solvents, which have total solubility parameter below 25 MPa
0.5, stays at a low level and does not increase as solubility parameter increases (red points in
Figure 3). On the other hand, the volumetric yield of gels in solvent with solubility parameter higher than 25 MPa
0.5 has an increasing trend with increasing solubility parameter (blue points in
Figure 3). Since the total solubility parameter (δ
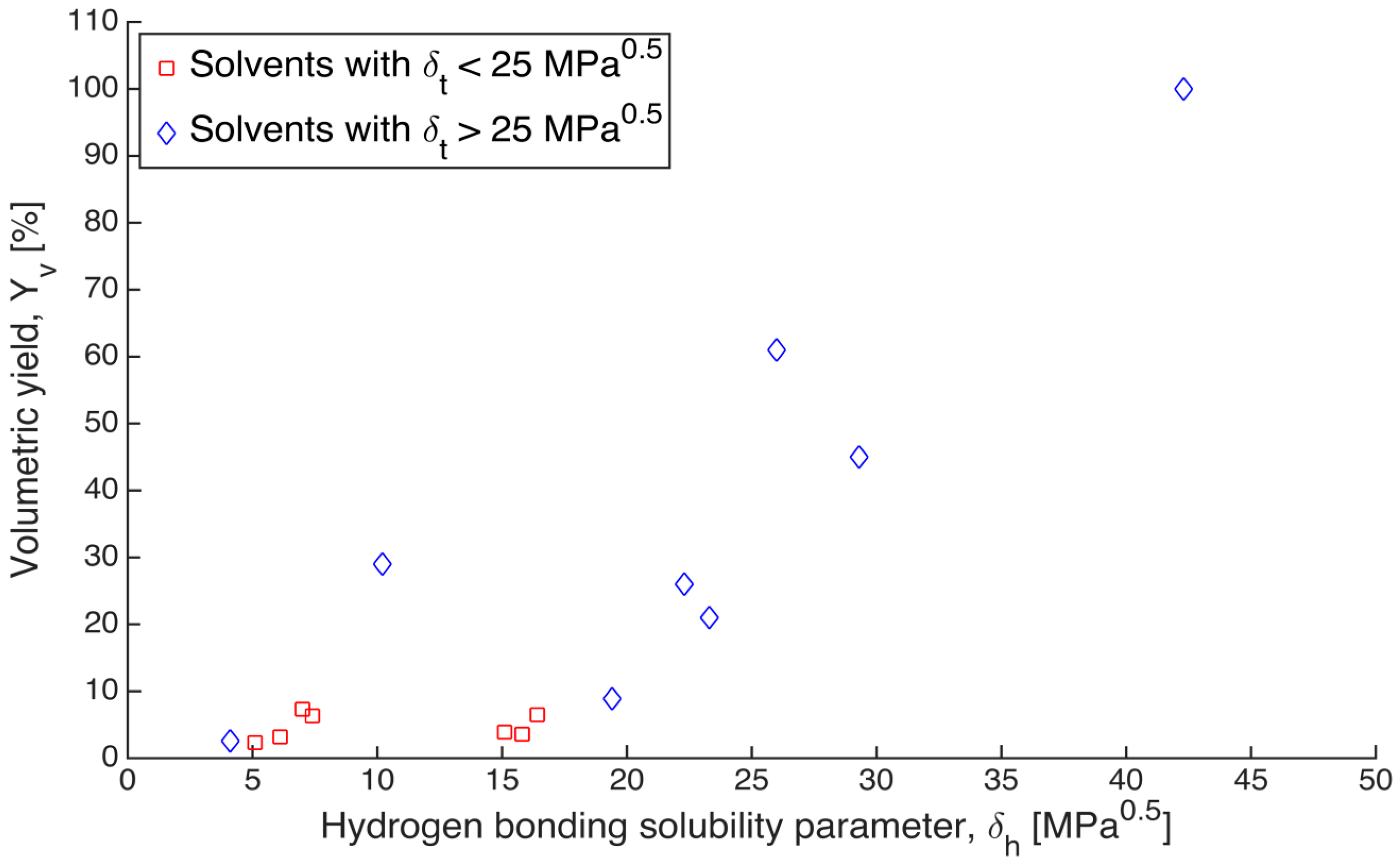
t) is composed of three individual components, the volumetric yield could be influenced by a single dominant parameter rather than all the three together. To determine this, the individual Hansen d, p and h components (δ
d, δ
p, δ
h) were also plotted against the volumetric yields (
). There was no clear trend observed according to d and p components (data not shown); however, a relation between relative volume and Hansen h component δ
h was observed similar to the trend between relative volume and total Hansen parameter δ
t (
Figure 4).
Figure 3.
Relation between the volumetric yields of gels after solvent exchange and the total solubility parameter (δt) of the respective solvents. Blue points refer to solvents with total solubility parameter above 25 MPa0.5, and red points refer to solvents with total solubility parameter below 25 MPa0.5.
Figure 3.
Relation between the volumetric yields of gels after solvent exchange and the total solubility parameter (δt) of the respective solvents. Blue points refer to solvents with total solubility parameter above 25 MPa0.5, and red points refer to solvents with total solubility parameter below 25 MPa0.5.
Figure 4.
Relation between the volumetric yields of gels after solvent exchange and Hansen h component (δh) of the respective solvents. Blue points refer to solvents with total solubility parameter above 25 MPa0.5, and red points refer to solvents with total solubility parameter below 25 MPa0.5.
Figure 4.
Relation between the volumetric yields of gels after solvent exchange and Hansen h component (δh) of the respective solvents. Blue points refer to solvents with total solubility parameter above 25 MPa0.5, and red points refer to solvents with total solubility parameter below 25 MPa0.5.
Although the data points in
Figure 4 are also rather scattered, a clear trend can be seen that the volumetric yields of alginate gels were higher in solvents with higher δ
h components. It is highly likely that conformations of alginate chains are strongly affected by the solvent. Solvents with less capability of forming hydrogen bonds may cause partial folding of the polymer coil. The effect of hydrogen bonding has been clearly exemplified by Antoniou
et al., (2010) [
29]: the coil radius of dextran molecules when dissolved in four solvents increases with increase of the h component, δ
h, whereas δ
d and δ
p show no correlation. This indicates that hydrogen bonding is the most important contributor to the solubility of dextran in the examined solvents. As alginate chains possess ionizable COOH groups, the effect of hydrogen bonding is expected be more pronounced.
Two remarks should be made. First, the above-described analysis is a first attempt to quantify the role the solvent can play in alginate hydrogel shrinkage during solvent exchange. They can be further developed to serve as a general framework. The first apparent extension is to evaluate solvent affinity to biopolymer. This is achieved by calculating the ”solubility distance”
Ra between a solvent and a biopolymer based on the partial solubility parameter components using the following equation [
28,
30]:
Here δ
X,S are Hansen component parameters for the solvent, and δ
X,P are Hansen component parameters for the biopolymer. To the best of our knowledge, there has been only one rough estimation of the total solubility parameter (δ
t) for sodium alginate (37 MPa
0.5) [
31] and no estimations for the individual Hansen parameters δ
d, δ
p, δ
h. In addition, ionic strength, cation concentration and the pH play a prominent role in the swelling and shrinkage behavior of biopolymer [
32]. Even though the system considered here is calcium alginate, some of the better solvents (methanol, glycerol, ethylene and propylene glycol)—which show higher volumetric yields (26%–61%) during the one step solvent exchange—possess total solubility parameters (29.6–36.1 MPa
0.5) close to the values reported for sodium alginate. However, solubility parameters only provide a direction for solvent selection [
33] and the possibility of no alginate shrinkage or even some swelling for solvents δ
t > 37 MPa
0.5 remains an open question. Nevertheless, one could also estimate the Hansen parameters of biopolymers using numerical methods and experimentally validate them [
34]. Once obtained, parameters δ
d,P, δ
p,P, δ
h,P can then be used to calculate the distance according to Equation (3). This distance is expected to serve as a reliable measure of the similarity between a biopolymer and a solvent [
28]. In addition, the solubility distance
Ra could help in comparing across biopolymers and possibly their hybrids.
Second, the calcium alginate hydrogel under consideration for solvent exchange is already in a solvent, namely water. Therefore the solvent exchange process cannot be purely ascertained by considering individual solvent/polymer interactions. A framework addressing the matrix changes and resistance during the solvent transfer needs to be developed. Recently, methodologies for correlating gel forming capabilities using solvents and solvent blends on a three dimensional Hansen space have been reported [
35]. This method would directly be applicable to evaluate the recently reported formation of polysaccharide gels in solvents [
36]. Further, this methodology can also be extended to solvent exchange process; replacing gel forming capability with volume shrinkage and studying the effects of solvent, solvent mixtures and polymer blends on a three dimensional Hansen space. Such an endeavor is part of our future work.
2.2. Concentration Gradient as a Control Parameter to Reduce Shrinkage during the Solvent Exchange
In the previous section, it was demonstrated that immersing an alginate hydrogel in pure ethanol can result in more than 90% shrinkage. Despite this, ethanol remains one of the best solvents to yield aerogels due to different reasons, a case which will also be supported during the course of this discussion. The large shrinkage during solvent exchange can be overcome by performing a stepwise solvent exchange instead of a one-step immersion [
6]. In brief, when an alginate hydrogel is immersed in pure ethanol, the gel is subjected to an initial concentration gradient of 100% resulting in a huge driving force. At macroscopic level a severe shrinkage of the gel network is observed. However, when the gradient is reduced by using ethanol/water mixtures with increasing concentration instead of pure ethanol, the driving force is reduced along with the shrinkage. The provision of lower concentration gradients increases however the overall duration of the solvent exchange process. As processing time reduction is the prime focus for aerogel production, an optimization problem is presented balancing aerogel properties such as density and surface area with production times.
To understand the role of gel composition (alginate concentration and the crosslinking degree) in the solvent exchange process, hydrogels of three different concentrations and two crosslinking degrees were prepared by CO
2 induced gelation. Then they were subjected to the solvent exchange wherein two solvents, ethanol and DMSO, were used at two initial concentration gradients, 30 and 50 wt %.
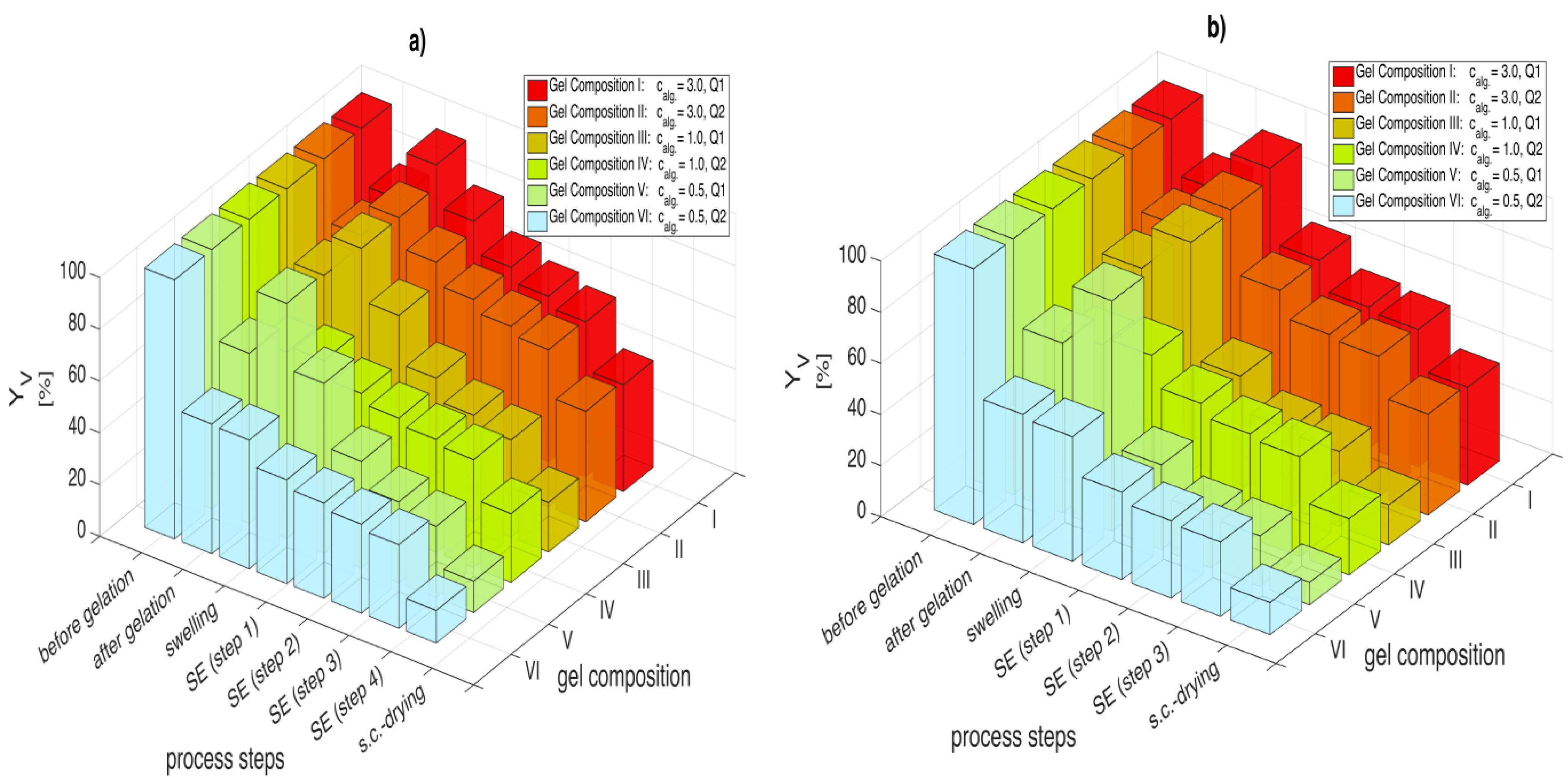
Figure 5a,b illustrate the calculated volumetric yields for all six gel compositions, treated with an initial concentration gradient of 30 wt % and 50 wt % ethanol respectively.
Figure 5.
Volumetric yields after gelation, swelling, each process step for solvent exchange with ethanol and supercritical CO2 drying; for (a) Δc = 30 wt % and (b) Δc = 50 wt %. Numerical data for each solvent composition are given in supplementary materials associated with this paper (Tables S1 and S2).
Figure 5.
Volumetric yields after gelation, swelling, each process step for solvent exchange with ethanol and supercritical CO2 drying; for (a) Δc = 30 wt % and (b) Δc = 50 wt %. Numerical data for each solvent composition are given in supplementary materials associated with this paper (Tables S1 and S2).
Generally, four phenomena are observed during biopolymer aerogel transformation: (1) volume loss during CO
2 induced gelation (syneresis); (2) swelling of the freshly prepared hydrogels in water; (3) shrinkage in solvent/water mixtures and (4) shrinkage during supercritical CO
2 drying. The first observation is that the gel’s loss of volume after CO
2 induced gelation is strongly dependent on the crosslinking degree at given alginate concentration. For soft gels derived from 0.5 wt % and 1 wt % alginate solution, syneresis is more pronounced for Q2 than for Q1. Previous studies investigating the syneresis [
2,
3] interpreted it as a release of water by the gel, resulting in a condensing and strengthening of the gel matrix facilitated by the presence of more crosslinking ions (higher crosslinking degree, Q2). Reasons for this syneresis could be explained by the lateral chain associations of alginate at higher calcium ion concentrations [
37]. Also, pressurized CO
2 could favor inter-chain interactions [
8]. Swelling is also strongly dependent on the cross linking degree where weakly crosslinked gels swell between 16% and 24% However, syneresis and swelling tendencies diminish with higher alginate concentrations (3 wt %) and cross linking degree in these cases is observed to have a low influence.
Analyzing gel volumes during solvent exchange with a solvent concentration gradient of 30 wt % (
Figure 5a) shows that high alginate concentration gels exhibit higher volumetric yields (gel composition II:
Yv,4 = 60.6%, gel composition V:
Yv,4 = 27.6%) after solvent exchange (steps 1 to 4). Lower crosslinking degree results in very high shrinkage during solvent exchange (gel composition V: Δ
Yv (swelling → step 4) = 63.1%, gel composition VI: Δ
Yv (swelling → step 4) = 17.5%). It is also observed that the shrinkage is most severe during the early steps of the solvent exchange (70%–80% of the total shrinkage occurs in the first two solvent exchange steps).
The influence of the initial concentration gradient on shrinkage can be obtained by comparing
Figure 5a,b. As samples were prepared using the same procedure for both measurement sets, shrinkage after CO
2 induced gelation and swelling in water are identical but start to deviate when considering the solvent exchange. When comparing gel volumes, it can be said that the volumetric yields of the solvent exchange with Δ
c = 30 wt % are higher after each respective step compared to the Δ
c = 50 wt % case. For example, the softest gel (gel composition
V) after solvent exchange showed a 30% volumetric yield deterioration, when the concentration gradient was increased to Δ
c = 50 wt % (
Yv,3 = 19.6%) from Δ
c = 30 wt % (
Yv,4 = 27.6%). These observations are in line with previous studies analyzing this topic [
6]. While lower concentration gradients lead to a slower and gentler exchange between water and solvent molecules within the gel, an increase in the initial concentration accelerates the solvent exchange increasing the stresses on the gel backbone. Consequently, higher volumetric yields can be achieved when small concentration gradients are applied. Higher crosslinking degree can also mitigate the shrinkage to some extent.
DMSO is a much better solvent for solvent exchange of alginate than ethanol. When comparing solvent exchange performance of ethanol and DMSO (
Yv,4) for a constant concentration gradient Δ
c = 30 wt % (
Figure 5a and
Figure 6a), a 20%–60% improvement in the volumetric yield across all gel compositions is observed for DMSO. This increase in the volumetric yield is even higher for Δ
c = 50 wt % (
Figure 5b and
Figure 6b) especially for soft gels (gels III and V), where 60%–100% improvement in the volumetric yield is observed. The superiority of DMSO over ethanol regarding shrinkage during solvent exchange can most likely be attributed to a higher affinity of alginate molecules towards DMSO and thus a replacement of structural water by solvent molecules instead of an extraction of water from the gel matrix. Most likely, methanol, propylene glycol and DMF (as discussed in the previous section) would also show similar low shrinkage behavior during solvent exchange like DMSO. However, the use of solvents is application specific: methanol and DMF are toxic solvents and may not be suitable for certain food and pharmaceutical applications.
Figure 6.
Volumetric yields after gelation, swelling, each process step for solvent exchange with DMSO and supercritical CO2 drying; for (a) Δc = 30 wt % and (b) Δc = 50 wt %. Numerical data for each solvent composition are given in supplementary materials associated with this paper (Tables S3 and S4).
Figure 6.
Volumetric yields after gelation, swelling, each process step for solvent exchange with DMSO and supercritical CO2 drying; for (a) Δc = 30 wt % and (b) Δc = 50 wt %. Numerical data for each solvent composition are given in supplementary materials associated with this paper (Tables S3 and S4).
2.3. Shrinkage during Sc-Drying and Minimum Concentration Requirements for Drying
In the previous section, it was shown that DMSO is much better solvent for solvent exchange in terms of the overall shrinkage as compared to ethanol. However, it is observed that the final volumetric yields of the aerogels obtained after supercritical drying are similar regardless of the solvent used.
Table 2 summarizes the shrinkages after complete solvent exchange (suspension → organogel), during supercritical drying (organogel → aerogel) and the overall volumetric shrinkage (suspension → aerogel). Data shows that the shrinkage during drying is much higher for DMSO compared to ethanol even though both solvents are miscible in supercritical CO
2 at operating conditions (
p = 120 bar, 40 °C) [
25]. One plausible reason could be that the affinity of DMSO to the alginate matrix causes scaffold collapse during extraction with CO
2 and thereby a higher shrinkage. Here one caveat can be established. Miscible solvents that are gentle for solvent exchange may be harsh on the matrix during supercritical CO
2 drying as observed in the case of DMSO. This scenario can be tackled by using solvent combinations instead of a single solvent alone. For example in case of alginate, combination of DMSO (mild for solvent exchange) and ethanol (mild during supercritical drying) can be used. The use of two complete solvent exchange procedures (DMSO exchange first and then to ethanol before supercritical CO
2 drying), or DMSO/ethanol solvent mixture compositions for solvent exchange and supercritical drying are in the scope of our ongoing work.
Table 2.
Shrinkage during complete transformation from suspension to aerogel; solvent concentration gradient ΔC = 50%.
Table 2.
Shrinkage during complete transformation from suspension to aerogel; solvent concentration gradient ΔC = 50%.
| Composition | Shrinkage, ΔYv, % |
|---|
| Suspension → Organogel * | Organogel * → Aerogel | Suspension → Aerogel |
|---|
| Ethanol | DMSO | Ethanol | DMSO | Ethanol | DMSO |
|---|
| I (3.0% Q1) | 46 | 32 | 16 | 31 | 62 | 63 |
| II (3.0% Q2) | 45 | 32 | 16 | 32 | 61 | 64 |
| III (1.0% Q1) | 71 | 53 | 14 | 31 | 85 | 84 |
| IV (1.0% Q2) | 61 | 52 | 17 | 22 | 78 | 74 |
| V (0.5% Q1) | 80 | 60 | 11 | 35 | 91 | 95 |
| VI (0.5% Q2) | 71 | 63 | 17 | 23 | 88 | 86 |
As for other solvents, propylene glycol with limited solubility in supercritical CO
2 is not a suitable solvent for aerogel production as it would then require longer processing times and harsher processing conditions (higher operating pressures). Methanol is an excellent solvent for both solvent exchange as determined in this study and supercritical drying as demonstrated in literature with TMOS based silica aerogels. It is also considered a green solvent similar to ethanol [
26]. However, in view of methanol anticipated toxicity related issues for food and pharmaceutical applications, ethanol was considered to be the best green solvent for biopolymer aerogels and thereby chosen for further kinetic evaluation of alginate aerogels. DMF solvent exchange and supercritical drying performance is expected to be comparable to DMSO, however it is also toxic and thereby excluded from further analysis. It should nevertheless be noted that drying with supercritical CO
2 allows to extract even residuals of low-molecular weight compounds such as highly cytotoxic glutaraldehyde from chitosan aerogels [
38]. Thus, more work should be done to draw firm conclusions on applicability of a particular solvent.
An important question that arises during solvent exchange is the extent of solvent exchange required prior to supercritical CO
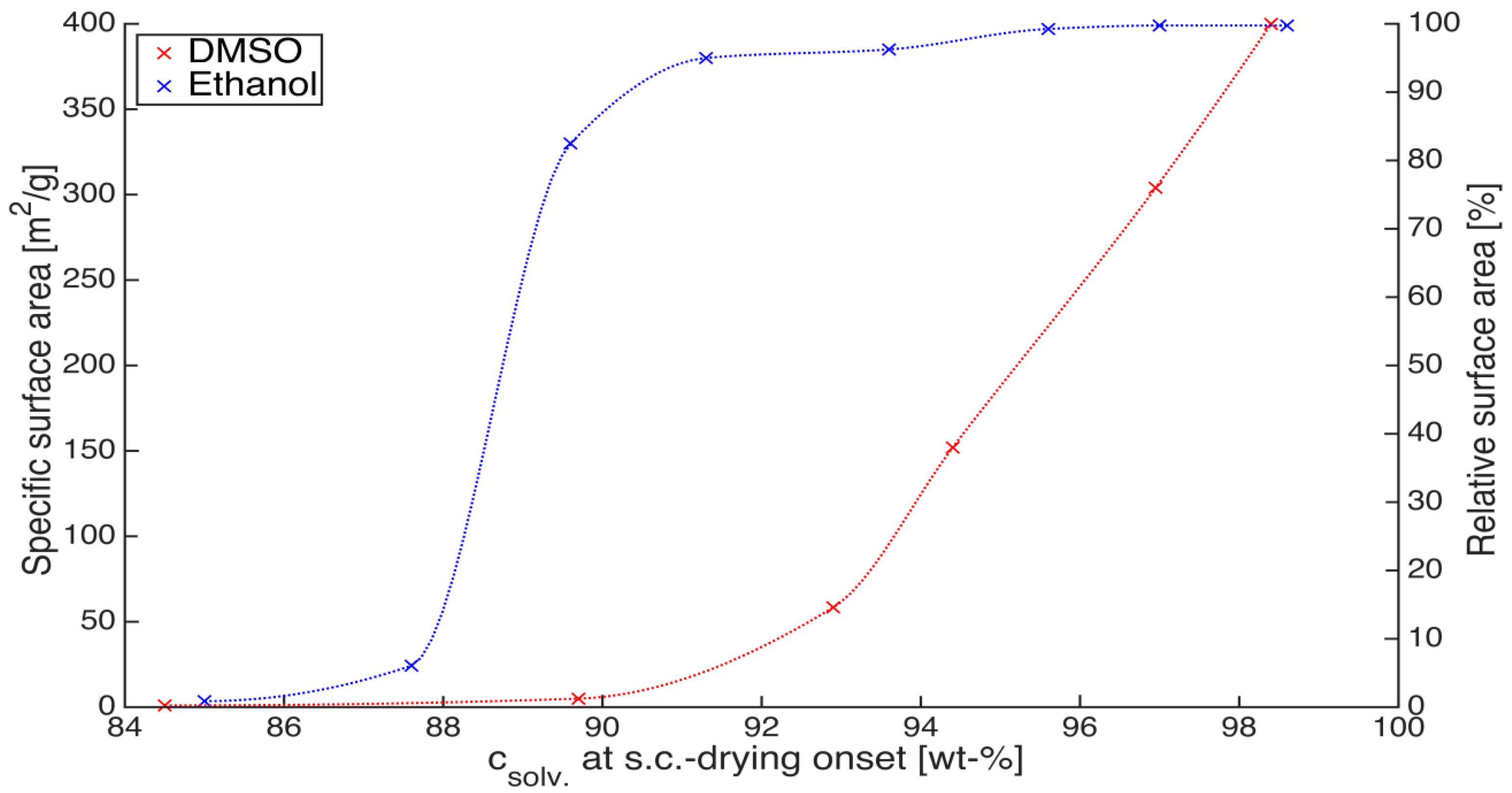
2 drying. This is an important aspect when considering solvent recycling in a production setup. For example, ethanol forms an azeotrope with water at 96 wt %. In case higher solvent concentrations inside the gel are required, alternative solvent recovery solutions such as azeotropic or pressure swing distillation, membrane separation or molecular sieving techniques should be considered instead of simple distillation. Surface area measurement can provide a sensitive assessment of aerogel quality to varying operating conditions. Insufficient solvent concentration inside the gel results in shrinkage and deformation but this information can be more precisely captured by measuring the drop in surface area due to pore collapse than the quantification of gel shrinkage. A plot of surface area against solvent concentration at which supercritical drying commenced is indicated in
Figure 7 for two solvents, ethanol and DMSO. The experiments were performed on 1 wt % calcium alginate with higher crosslinking degree (Q2).
Figure 7.
Surface area as a function of solvent concentration achieved before supercritical CO2 drying onset; gel composition: 1 wt % calcium alginate, Q2.
Figure 7.
Surface area as a function of solvent concentration achieved before supercritical CO2 drying onset; gel composition: 1 wt % calcium alginate, Q2.
The plot shows that supercritical CO
2 drying of alginate can proceed at ethanol concentrations as low as 93 wt % without any drop in surface area. Concentrations lower than 93 wt % result in first, a slow drop in the surface area till 90 wt % where ca. 90% of the total surface area is still retained. A further 3% lower concentration (87%) results in a steep drop where only 5% of the maximum achievable surface area is obtained. The behavior is completely different for DMSO gels where solvent concentrations higher than 98 wt % are required prior to the commencement of supercritical drying to achieve the maximum surface area. It is interesting at this juncture to point out that even in the pioneering works of Kistler [
18], minimum ethanol concentrations required prior to supercritical drying was presented (95%) although, the process under consideration was the direct supercritical drying of silica aerogels. The reason for this lower solvent concentration sufficiency could be attributed to strong water-matrix interactions (hydrogen bonding or covalent bonding) which do not allow formation of the liquid phase after complete extraction of ethanol. This water may be adsorbed on the aerogel backbone and can only be removed at higher temperatures. However this hypothesis requires further verification and is a part of our ongoing work.
2.4. Pseudo Second Order Kinetics to Evaluate Solvent Exchange Process
The question of how fast hydrogel-solvent system attains concentration equilibrium is important to ascertain process times required during production cycles. The solvent/matrix interactions play a crucial role in the solvent exchange process. However, the quantification of the solvent exchange kinetics still remains a challenge. In literature, there are two typical methods to evaluate the kinetics of a sorption process [
39]. The first method is the mass transfer method which involves the evaluation of film diffusion, surface diffusion, pore diffusion or their combination by setting up a set of partial differential equations and numerically solving them to yield solutions matching the experimental data [
40,
41]. The diffusion and mass transfer coefficients thus obtained are very useful and directly applicable in the process design and scale up. However, setting up equations catering to a real system taking the actual components such as shapes, size, and morphology into account (without simplification) and obtaining a robust solution might be a challenge, especially due to volume shrinkage associated with the solvent exchange. The other method is the reaction method [
39], which uses simple kinetic models such as pseudo-first order, Langmuir or pseudo second order kinetic models [
42]. The kinetic parameters are obtained by fitting the experimental data to the kinetic models but these parameters are not directly applicable in process design. However, when used under controlled experimental conditions, they can provide a quantitative assessment for example, when comparing solvents regarding their exchange kinetics. Moreover, simplified methods using kinetic parameters from batch adsorption data to calculate the film mass transfer and surface diffusion coefficients have recently been developed [
39].
The kinetics calculation procedure employed in this study is as follows. First the variation in ethanol concentration
vs. time for various alginate concentrations and crosslinking degree were measured at given initial concentration gradients.
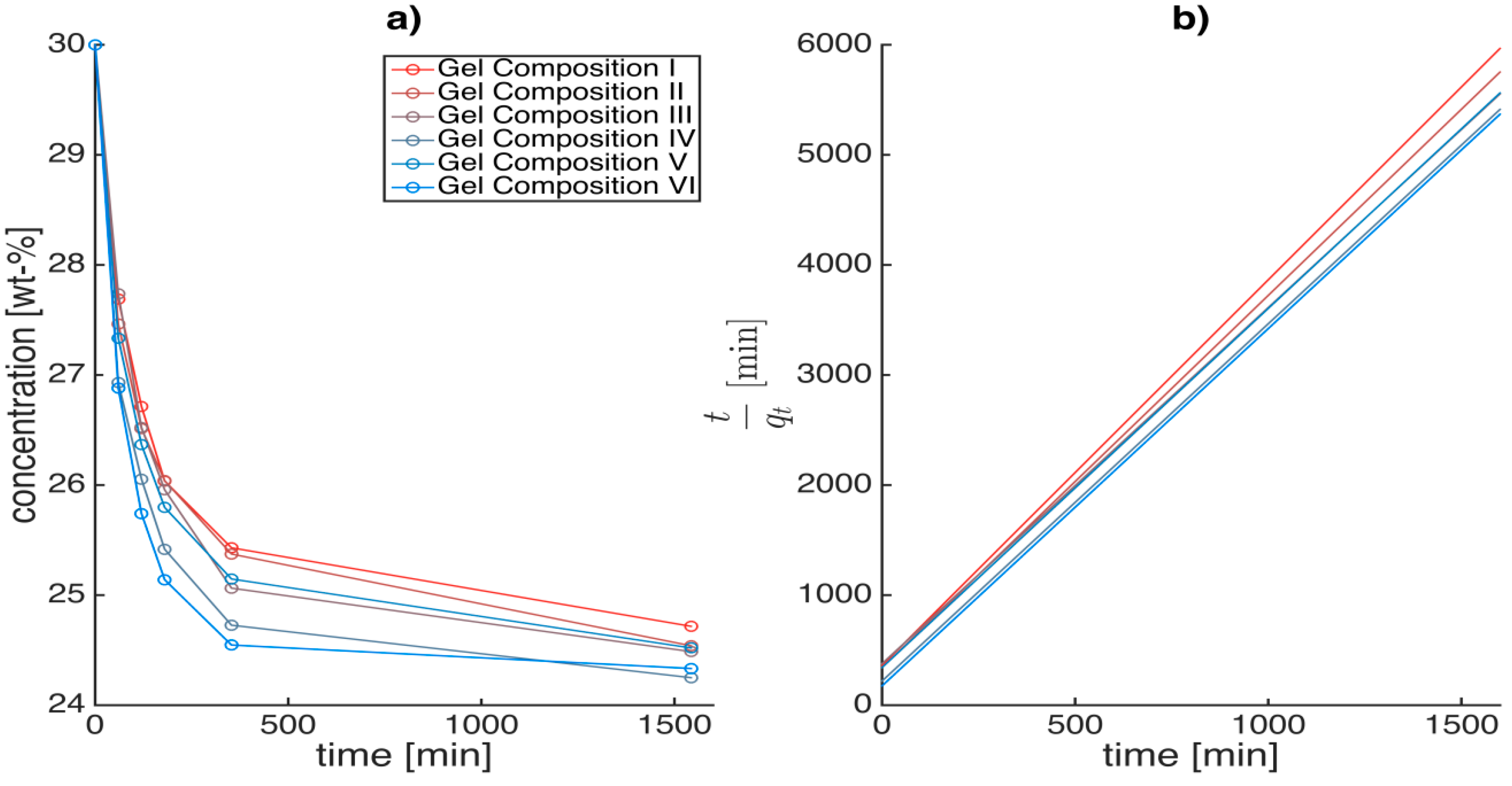
Figure 8a shows the concentration drop during the first step of the solvent exchange process with an initial concentration gradient of 30 wt % (Step 1), when a hydrogel (0 wt % ethanol) is placed in a 30 wt % ethanol water mixture (gel-to-solvent mass ratio 1:5).
Figure 8.
Concentration drop vs. time (a) and t/qt vs. time (b) when a hydrogel (0 wt % ethanol) of a given alginate concentration and crosslinking degree is placed in a 30 wt % ethanol/water mixture (step 1); 1:5 gel-to solvent ratio, w/w. Similar plots were determined for subsequent higher concentration steps (with constant concentration gradient).
Figure 8.
Concentration drop vs. time (a) and t/qt vs. time (b) when a hydrogel (0 wt % ethanol) of a given alginate concentration and crosslinking degree is placed in a 30 wt % ethanol/water mixture (step 1); 1:5 gel-to solvent ratio, w/w. Similar plots were determined for subsequent higher concentration steps (with constant concentration gradient).
A typical pseudo second-order equation based on adsorption equilibrium capacity can be expressed in the form [
42]:
Which upon integration can be linearized into the following equation
The ethanol uptake (
) is defined as the mass of ethanol (
absorbed/adsorbed till time t per unit mass of gel
). Here it is necessary to indicate that the mass of the gel varies due to the gel shrinkage during solvent exchange; therefore, an approximate mass of the gel (
) was estimated for time
t with the assumption that the mass loss of the gel varies linearly with the concentration drop. However, the total mass of the system is fixed during a solvent exchange step.
where
,
,
are the concentration of the solution and mass of the gel before and after the solvent exchange step.
The solvent uptake is calculated as
In this study, pseudo second order model (
Figure 8b) was best to fit the experimental data (R
2 > 0.99). It is interesting to note that the swelling behavior of alginate also follows the second order kinetics [
43]. The solvent replacement inside the hydrogels could be imagined as a simultaneous adsorption and permeation process, where the solvent not only (1) adsorbs onto the hydrogel matrix, similar to the adsorption of phenol from aqueous solution on activated carbon [
41] but also (2) the solvent can permeate into and through the hydrogel matrix scaffold depending on the solvent affinity to the matrix and the crosslinking degree similar to water uptake during the alginate swelling process [
43].
There are three parameters that can be derived from the pseudo second order equation: first, the equilibrium uptake
qe (
gsolv/
ggel), which is dependent on both the concentration gradient and the solvent amount and provides information regarding the maximum solvent the hydrogel can take in after infinite exposure time. In our case, we assume that the equilibrium is attained after 24 h. Second, the kinetic coefficient
k2 (
ggel/
gsolv·min
−1) which is indicative of how fast the equilibrium uptake
qe is reached. The sorption capacity and thereby the kinetic parameters are dependent on the initial adsorbate concentration, temperature, pH, adsorbent size and nature of the solute [
42]. Thereby, to compare across solvents, the concentration gradient (Δ
C) and the solvent amount (
) (initial adsorbate amount) were fixed prior to experiment and analysis. The last parameter, the initial sorption rate
h (
gsolv/
ggel·min
−1) is derived from the y-intercept reciprocal (
) and is a better parameter for comparison as
k2 is strong function of
qe. When the concentration gradient and solvent amount is fixed, the initial sorption rate (
h) should indicate the solvent affinity to the gel matrix.
2.5. Physical Interpretation of Solvent Exchange Process Derived from the Fitting Parameters of the Pseudo Second Order Model and Volumetric Shrinkage
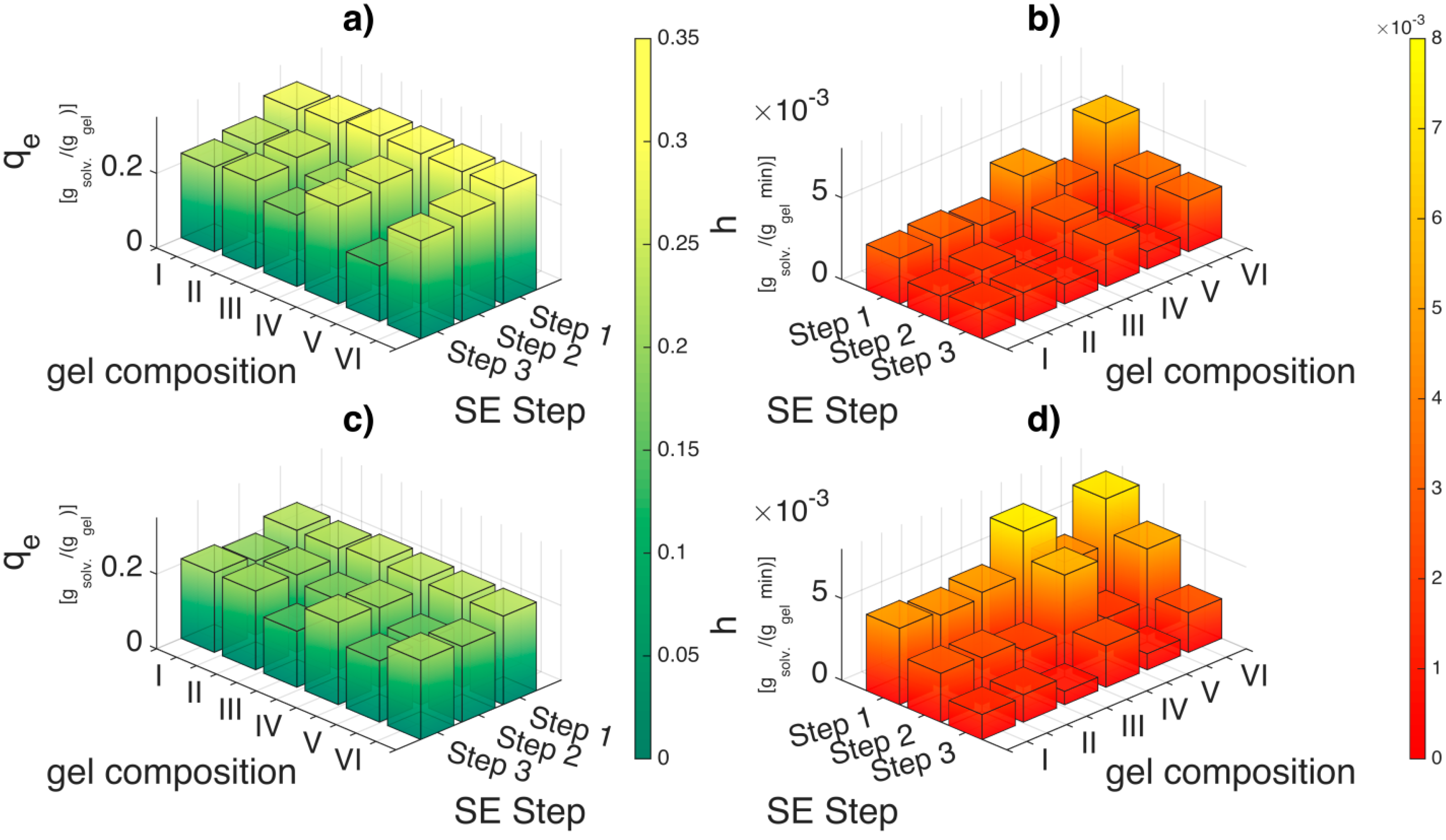
The first conclusion that could be drawn is that the solvent exchange process is also dependent on the alginate composition and crosslinking degree. The equilibrium uptake
qe (
Figure 9a) for step 1 of the solvent exchange is constant across alginate composition. However, based on the initial sorption rates (
h) for step 1 (
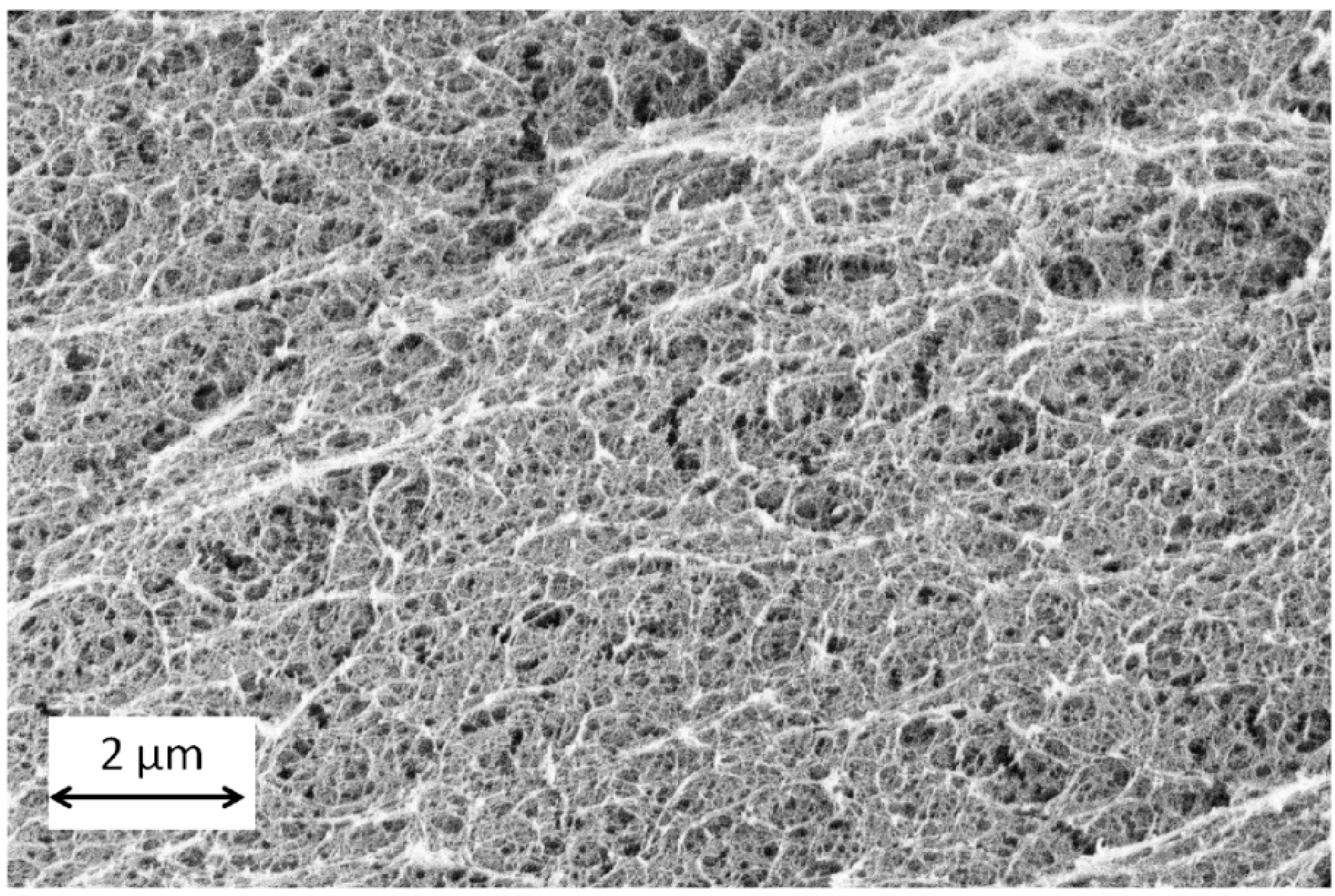
Figure 9b), the solvent exchange is fastest for highly crosslinked soft gels (gel VI). When comparing across the highly crosslinked gels (II, IV and VI), it is observed that the initial sorption rates decreases with increasing alginate concentration. Calcium alginate hydrogel consists of a fibrillar matrix (
Figure 10) with water trapped in its pores. With increasing biopolymer concentration, the tortuosity increases and also there might be additional resistances in the form of surface adsorption, hydrogen bonding or water dissolution in the matrix resulting in decrease in the sorption rates.
Figure 9.
Comparison of equilibrium uptake (qe) and initial sorption rates (h) for ethanol ((a) and (b)) and DMSO ((c) and (d)) for various alginate concentration and crosslinking degree. The applied concentration gradient is 30 wt %. Please refer the supplementary tables (Tables S5 to S10) for qe, k2 and h values.
Figure 9.
Comparison of equilibrium uptake (qe) and initial sorption rates (h) for ethanol ((a) and (b)) and DMSO ((c) and (d)) for various alginate concentration and crosslinking degree. The applied concentration gradient is 30 wt %. Please refer the supplementary tables (Tables S5 to S10) for qe, k2 and h values.
Figure 10.
Alginate aerogel microstructure (gel VI: concentration 0.5 wt %, Q2).
Figure 10.
Alginate aerogel microstructure (gel VI: concentration 0.5 wt %, Q2).
The initial sorption rates (
h) are lower for low crosslinked alginate hydrogels when compared to high crosslinked hydrogels (
Figure 9b). It is also very interesting to observe that during subsequent solvent exchange steps (step 2 and step 3) in
Figure 9a, the equilibrium uptake (
qe) drops substantially for the low crosslinked soft gels (III, V) but slightly for high crosslinked soft gels (IV, VI) with increasing ethanol concentration. This implies presence of solvent–water–matrix interactions as the concentration gradient and the solvent to gel ratio is maintained constant. The drop in the equilibrium uptake for the high crosslinked alginate gels with increasing ethanol concentration can be explained by strong bonding of water molecules to the hydrophilic gel matrix. This implies that the driving force due to ethanol concentration gradient progressively decreases in its capacity to remove the water from the matrix with increasing solvent concentration. This is probably also the reason why supercritical CO
2 drying can proceed at a lower ethanol concentration instead of pure solvent since water is an integral part of the gel matrix and can neither be extracted by the solvent during solvent exchange nor the CO
2 during supercritical drying. However, this reasoning is not sufficient to explain the steep drop in equilibrium uptake for low crosslinked alginate gels.
A closer inspection of the volumetric shrinkage for low crosslinked gels (gels I, III, V) shows that, with lowering of alginate concentration from 3 to 0.5 wt %, the water holding capacity increases from 33 to 180 grams water per gram alginate. The ionic crosslinking of alginate can be explained through the “egg box model” [
44] in which, lower calcium ion concentration leads to open positions where the water can enter resulting in swelling. The water amount held within the fibrillar matrix can be as much as 85% of the total water the pores themselves can hold (as calculated for 0.5 wt % alginate gels by the mass ratio between the low and high crosslinked hydrogels after the swelling step). This number decreases with increasing alginate concentration (57% for 1 wt % alginate and 10% for 3 wt % alginate). When fresh solvent is added, the ethanol not only enters the pore of the hydrogel matrix but also permeates into the fibrillar matrix through these positions. This permeation process is probably slow and thereby decreases the initial sorption rates (
h) when compared to the highly crosslinked gels. The ionic interactions of calcium ions with water changes due to the presence of an organic moeity resulting in shrinking of the fibrillar matrix and ejection of the water. This is probably the reason why large shrinkage is observed in the initial steps of the solvent exchange (
Figure 5). But during this process, ethanol is probably also embedded in the matrix on the inside in addition to adsorbing onto it from the pores on the outside which hinders or reduces matrix affinity to further solvent exchange. Thereby, both the solvent uptake and initial sorption rates decrease with increasing ethanol concentration for low concentration soft gels.
The decrease in the uptake behavior (
qe) and initial sorption rates (
h) with increasing solvent concentration is also observed during solvent exchange with DMSO (
Figure 9c,d) for low crosslinked alginate gels. However, the initial sorption rates (h) of DMSO when compared to ethanol during the first solvent exchange step are 30%–60% higher for high crosslinked gels and 50%–80% higher for the low crosslinked gels (also refer Tables S5–S10 in supplementary materials). This highlights not only the affinity of DMSO to enter the pores of the biopolymer matrix but also an affinity to enter the fibrillar matrix of the biopolymer. In addition, the 50%–100% improvement in the volumetric yields for low crosslinked soft gels (gels III and V) after solvent exchange process for DMSO compared to ethanol indicates that DMSO stiffens the hydrophilic fibrillar matrix of the alginate during the solvent exchange process; thus making it more resistant to collapse due to the driving forces during solvent exchange.
During supercritical drying, the CO2 extracts DMSO not only from the pores but also from alginate’s fibrillar matrix scaffold. This process is probably strenuous on the fibrillar structure leading to collapse of the alginate organogel resulting in shrinkage and final aerogel volumetric yields comparable to ethanol. As DMSO actively interacts with the matrix, supercritical drying onset cannot proceed at lower DMSO concentrations as compared to ethanol. Thereby, solvents considered to be good for solvent exchange might have adverse effects on the matrix during supercritical drying though miscible in supercritical CO2.