A Quantitative Model to Estimate Drug Resistance in Pathogens
Abstract
:1. Introduction
2. Materials and Methods
2.1. Formulation of the Quantitative Model
2.2. Experimental Data
3. Results
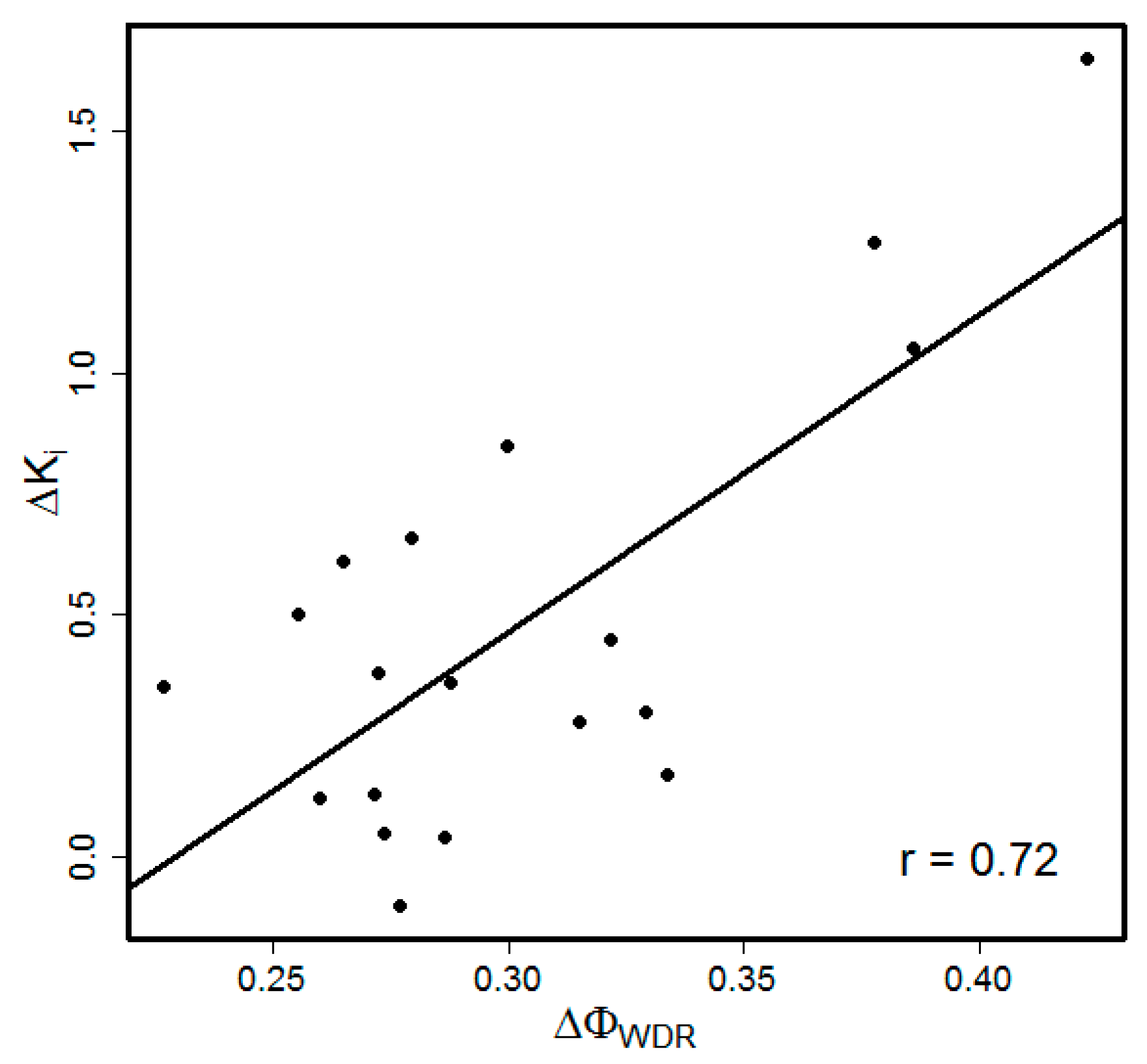
3.1. Choice of the Model
3.2. Evaluation of the Model
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Para, M.F.; Finkelstein, D.; Becker, S.; Dohn, M.; Walawander, A.; Black, J.R. Reduced toxicity with gradual initiation of trimethoprim-sulfamethoxazole as primary prophylaxis for Pneumocystis carinii pneumonia: Aids clinical trials group 268. J. Acquir Immune Defic. Syndr. 2000, 24, 337–343. [Google Scholar] [CrossRef] [PubMed]
- Koopmans, P.P.; Burger, D.M. Managing drug reactions to sulfonamides and other drugs in HIV infection: Desensitization rather than rechallenge? Pharm. World Sci. 1998, 20, 253–257. [Google Scholar] [CrossRef] [PubMed]
- Walker, D.J.; Meshnick, S.R. Drug resistance in Pneumocystis carinii: An emerging problem. Drug Resist. Updat. 1998, 1, 201–204. [Google Scholar] [CrossRef]
- Nahimana, A.; Rabodonirina, M.; Bille, J.; Francioli, P.; Hauser, P.M. Mutations of Pneumocystis jirovecii dihydrofolate reductase associated with failure of prophylaxis. Antimicrob. Agents Chemother. 2004, 48, 4301–4305. [Google Scholar] [CrossRef] [PubMed]
- Lane, B.R.; Ast, J.C.; Hossler, P.A.; Mindell, D.P.; Bartlett, M.S.; Smith, J.W.; Meshnick, S.R. Dihydropteroate synthase polymorphisms in Pneumocystis carinii. J. Infect. Dis. 1997, 175, 482–485. [Google Scholar] [CrossRef] [PubMed]
- Mei, Q.; Gurunathan, S.; Masur, H.; Kovacs, J.A. Failure of co-trimoxazole in Pneumocystis carinii infection and mutations in dihydropteroate synthase gene. Lancet 1998, 351, 1631–1632. [Google Scholar] [CrossRef]
- Helweg-Larsen, J.; Benfield, T.L.; Eugen-Olsen, J.; Lundgren, J.D.; Lundgren, B. Effects of mutations in Pneumocystis carinii dihydropteroate synthase gene on outcome of AIDS-associated P. carinii pneumonia. Lancet 1999, 354, 1347–1351. [Google Scholar] [CrossRef]
- Kazanjian, P.; Armstrong, W.; Hossler, P.A.; Burman, W.; Richardson, J.; Lee, C.H.; Crane, L.; Katz, J.; Meshnick, S.R. Pneumocystis carinii mutations are associated with duration of sulfa or sulfone prophylaxis exposure in AIDS patients. J. Infect. Dis. 2000, 182, 551–557. [Google Scholar] [CrossRef] [PubMed]
- Navin, T.R.; Beard, C.B.; Huang, L.; del Rio, C.; Lee, S.; Pieniazek, N.J.; Carter, J.L.; Le, T.; Hightower, A.; Rimland, D. Effect of mutations in Pneumocystis carinii dihydropteroate synthase gene on outcome of P. carinii pneumonia in patients with HIV-1: A prospective study. Lancet 2001, 358, 545–549. [Google Scholar] [CrossRef]
- Visconti, E.; Ortona, E.; Mencarini, P.; Margutti, P.; Marinaci, S.; Zolfo, M.; Siracusano, A.; Tamburrini, E. Mutations in dihydropteroate synthase gene of Pneumocystis carinii in HIV patients with Pneumocystis carinii pneumonia. Int. J. Antimicrob. Agents 2001, 18, 547–551. [Google Scholar] [CrossRef]
- Costa, M.C.; Helweg-Larsen, J.; Lundgren, B.; Antunes, F.; Matos, O. Mutations in the dihydropteroate synthase gene of Pneumocystis jirovecii isolates from portuguese patients with pneumocystis pneumonia. Int. J. Antimicrob. Agents 2003, 22, 516–520. [Google Scholar] [CrossRef]
- Iliades, P.; Meshnick, S.R.; Macreadie, I.G. Dihydropteroate synthase mutations in Pneumocystis jirovecii can affect sulfamethoxazole resistance in a Saccharomyces cerevisiae model. Antimicrob. Agents Chemother. 2004, 48, 2617–2623. [Google Scholar] [CrossRef] [PubMed]
- Iliades, P.; Meshnick, S.R.; Macreadie, I.G. Mutations in the Pneumocystis jirovecii DHPS gene confer cross-resistance to sulfa drugs. Antimicrob. Agents Chemother. 2005, 49, 741–748. [Google Scholar] [CrossRef] [PubMed]
- Moukhlis, R.; Boyer, J.; Lacube, P.; Bolognini, J.; Roux, P.; Hennequin, C. Linking Pneumocystis jirovecii sulfamethoxazole resistance to the alleles of the DHPS gene using functional complementation in Saccharomyces cerevisiae. Clin. Microbiol. Infect. 2010, 16, 501–507. [Google Scholar] [CrossRef] [PubMed]
- Cody, V.; Pace, J.; Makin, J.; Piraino, J.; Queener, S.F.; Rosowsky, A. Correlations of inhibitor kinetics for Pneumocystis jirovecii and human dihydrofolate reductase with structural data for human active site mutant enzyme complexes. Biochemistry 2009, 48, 1702–1711. [Google Scholar] [CrossRef] [PubMed]
- Cody, V.; Pace, J.; Queener, S.F.; Adair, O.O.; Gangjee, A. Kinetic and structural analysis for potent antifolate inhibition of Pneumocystis jirovecii, Pneumocystis carinii, and human dihydrofolate reductases and their active-site variants. Antimicrob. Agents. Chemother. 2013, 57, 2669–2677. [Google Scholar] [CrossRef] [PubMed]
- Queener, S.F.; Cody, V.; Pace, J.; Torkelson, P.; Gangjee, A. Trimethoprim resistance of dihydrofolate reductase variants from clinical isolates of Pneumocystis jirovecii. Antimicrob. Agents Chemother. 2013, 57, 4990–4998. [Google Scholar] [CrossRef] [PubMed]
- Figliuzzi, M.; Jacquier, H.; Schug, A.; Tenaillon, O.; Weigt, M. Coevolutionary landscape inference and the context-dependence of mutations in β-lactamase tem-1. Mol. Biol. Evol. 2016, 33, 268–280. [Google Scholar] [CrossRef] [PubMed]
- Jacquier, H.; Birgy, A.; Le Nagard, H.; Mechulam, Y.; Schmitt, E.; Glodt, J.; Bercot, B.; Petit, E.; Poulain, J.; Barnaud, G.; et al. Capturing the mutational landscape of the β-lactamase tem-1. Proc. Natl. Acad. Sci. USA 2013, 110, 13067–13072. [Google Scholar] [CrossRef] [PubMed]
- Ng, P.C.; Henikoff, S. Sift: Predicting amino acid changes that affect protein function. Nucleic Acids Res. 2003, 31, 3812–3814. [Google Scholar] [CrossRef] [PubMed]
- Adzhubei, I.A.; Schmidt, S.; Peshkin, L.; Ramensky, V.E.; Gerasimova, A.; Bork, P.; Kondrashov, A.S.; Sunyaev, S.R. A method and server for predicting damaging missense mutations. Nat. Methods 2010, 7, 248–249. [Google Scholar] [CrossRef] [PubMed]
- Capriotti, E.; Fariselli, P.; Casadio, R. I-mutant2.0: Predicting stability changes upon mutation from the protein sequence or structure. Nucleic Acids Res. 2005, 33, W306–W310. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Randall, A.; Baldi, P. Prediction of protein stability changes for single-site mutations using support vector machines. Proteins 2006, 62, 1125–1132. [Google Scholar] [CrossRef] [PubMed]
- Dehouck, Y.; Kwasigroch, J.M.; Gilis, D.; Rooman, M. Popmusic 2.1: A web server for the estimation of protein stability changes upon mutation and sequence optimality. BMC Bioinformatics 2011, 12, 151. [Google Scholar] [CrossRef] [PubMed]
- Morcos, F.; Pagnani, A.; Lunt, B.; Bertolino, A.; Marks, D.S.; Sander, C.; Zecchina, R.; Onuchic, J.N.; Hwa, T.; Weigt, M. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. USA 2011, 108, E1293–E1301. [Google Scholar] [CrossRef] [PubMed]
- Weigt, M.; White, R.A.; Szurmant, H.; Hoch, J.A.; Hwa, T. Identification of direct residue contacts in protein-protein interaction by message passing. Proc. Natl. Acad. Sci. USA 2009, 106, 67–72. [Google Scholar] [CrossRef] [PubMed]
- Baker, F.N.; Porollo, A. Coeviz: A web-based tool for coevolution analysis of protein residues. BMC Bioinformatics 2016, 17, 119. [Google Scholar] [CrossRef] [PubMed]
- Dunn, S.D.; Wahl, L.M.; Gloor, G.B. Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics 2008, 24, 333–340. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F.; Madden, T.L.; Schaffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped blast and PSI-blast: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [PubMed]
- Dale, G.E.; Broger, C.; D’Arcy, A.; Hartman, P.G.; DeHoogt, R.; Jolidon, S.; Kompis, I.; Labhardt, A.M.; Langen, H.; Locher, H.; et al. A single amino acid substitution in Staphylococcus aureus dihydrofolate reductase determines trimethoprim resistance. J. Mol. Biol. 1997, 266, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Fermer, C.; Swedberg, G. Adaptation to sulfonamide resistance in Neisseria meningitidis may have required compensatory changes to retain enzyme function: Kinetic analysis of dihydropteroate synthases from N. meningitidis expressed in a knockout mutant of Escherichia coli. J. Bacteriol. 1997, 179, 831–837. [Google Scholar] [CrossRef] [PubMed]
- Iliades, P.; Berglez, J.; Meshnick, S.; Macreadie, I. Promoter strength of folic acid synthesis genes affects sulfa drug resistance in Saccharomyces cerevisiae. Microb. Drug Resist. 2003, 9, 249–255. [Google Scholar] [CrossRef] [PubMed]
- Brochet, M.; Couve, E.; Zouine, M.; Poyart, C.; Glaser, P. A naturally occurring gene amplification leading to sulfonamide and trimethoprim resistance in Streptococcus agalactiae. J. Bacteriol. 2008, 190, 672–680. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, W.; Meshnick, S.; Kazanjian, P. Pneumocystis carinii mutations associated with sulfa and sulfone prophylaxis failures in immunocompromised patients. Microbes Infect. 2000, 2, 61–67. [Google Scholar] [CrossRef]
- Wolfger, H.; Mamnun, Y.M.; Kuchler, K. Fungal ABC proteins: Pleiotropic drug resistance, stress response and cellular detoxification. Res. Microbiol. 2001, 152, 375–389. [Google Scholar] [CrossRef]
- Chang, G.; Roth, C.B. Structure of msba from E. coli: A homolog of the multidrug resistance ATP binding cassette (ABC) transporters. Science 2001, 293, 1793–1800. [Google Scholar] [CrossRef] [PubMed]
- Pfaller, M.A. Antifungal drug resistance: Mechanisms, epidemiology, and consequences for treatment. Am. J. Med. 2012, 125, S3–S13. [Google Scholar] [CrossRef] [PubMed]
| Organism Protein (UniProt ID) | Mutants | Kinetic Parameter | Refs. | Purpose (Drug/Inhibitor) |
|---|---|---|---|---|
| P. jirovecii DHFR (Q9UUP5) | T14A, P26Q | Ki | [17] | Train the model on one target (TMP) |
| N23S | ||||
| S31F | ||||
| F36C | ||||
| L65P | ||||
| F36C, L65P | ||||
| S37T | ||||
| A67V | ||||
| A67V, C166Y | ||||
| R59G, A67V | ||||
| V79I | ||||
| S106P | ||||
| S106P, E127G | ||||
| T144A | ||||
| T144A, K171E | ||||
| D153V | ||||
| I158V | ||||
| C166Y | ||||
| R170G | ||||
| P. jirovecii DHFR (Q9UUP5) | T14A, P26Q | Ki | [17] | Evaluate on the same target, different inhibitor (OAAG324) |
| N23S | ||||
| S31F | ||||
| F36C | ||||
| L65P | ||||
| F36C, L65P | ||||
| S37T | ||||
| A67V | ||||
| A67V, C166Y | ||||
| R59G, A67V | ||||
| V79I | ||||
| S106P | ||||
| S106P, E127G | ||||
| T144A | ||||
| T144A, K171E | ||||
| D153V | ||||
| I158V | ||||
| R170G | ||||
| P. jirovecii DHFR (Q9UUP5) | S69F | Ki | [16] | Evaluate on the same target, artificially mutated (TMP, OAAG324) |
| S37K, S69F | ||||
| S37Q | ||||
| S69N | ||||
| S37Q, S69N | ||||
| S37K, S69N | ||||
| S37Q, S69F | ||||
| S. aureus DHFR (P0A017) | F99Y | IC50 | [30] | Evaluate on the same target, different organism (TMP) |
| H31N, F99Y | ||||
| F99Y, H150R | ||||
| L21V, N60I, F99Y | ||||
| P. jirovecii DHPS (L0P7Z1) | T519A | IC50 | [13] | Evaluate on a different drug target, different drug (SMX) |
| P521S | ||||
| T519A, P521S | ||||
| T519V, P521S |
| Co-Variance Metric | |||||||
|---|---|---|---|---|---|---|---|
| χ2 | −0.67 ± 0.05 | −0.53 ± 0.05 | −0.62 ± 0.05 | −0.29 ± 0.05 | 0.68 ± 0.04 | 0.29 ± 0.05 | 0.64 ± 0.04 |
| MI | −0.67 ± 0.05 | −0.53 ± 0.05 | −0.62 ± 0.05 | −0.05 ± 0.05 | 0.68 ± 0.04 | 0.05 ± 0.05 | 0.70 ± 0.04 |
| APC (MI) | −0.67 ± 0.05 | −0.53 ± 0.05 | −0.62 ± 0.05 | −0.28 ± 0.06 | 0.68 ± 0.04 | 0.28 ± 0.06 | 0.72 ± 0.05 |
| r | −0.67 ± 0.05 | −0.53 ± 0.05 | −0.62 ± 0.05 | −0.20 ± 0.07 | 0.68 ± 0.04 | 0.20 ± 0.07 | 0.65 ± 0.05 |
| Target | Inhibitor | The Number of Mutations: Single/Double/Triple | SIFT | |
|---|---|---|---|---|
| PjDHFR | OAAG324 | 12/6/0 | 0.60 ± 0.03 | −0.22 |
| 1 PjDHFR->PcDHFR/HsDHFR | TMP | 3/4/0 | 0.41 ± 0.10 | −0.48 |
| 1 PjDHFR->PcDHFR/HsDHFR | OAAG324 | 3/4/0 | −0.39 ± 0.16 | −0.07 |
| SaDHFR | TMP | 1/2/1 | 0.91 ± 0.12 | −0.59 |
| PjDHPS | SMX | 2/2/0 | 0.79 ± 0.18 | ND 2 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baker, F.N.; Cushion, M.T.; Porollo, A. A Quantitative Model to Estimate Drug Resistance in Pathogens. J. Fungi 2016, 2, 30. https://doi.org/10.3390/jof2040030
Baker FN, Cushion MT, Porollo A. A Quantitative Model to Estimate Drug Resistance in Pathogens. Journal of Fungi. 2016; 2(4):30. https://doi.org/10.3390/jof2040030
Chicago/Turabian StyleBaker, Frazier N., Melanie T. Cushion, and Aleksey Porollo. 2016. "A Quantitative Model to Estimate Drug Resistance in Pathogens" Journal of Fungi 2, no. 4: 30. https://doi.org/10.3390/jof2040030
APA StyleBaker, F. N., Cushion, M. T., & Porollo, A. (2016). A Quantitative Model to Estimate Drug Resistance in Pathogens. Journal of Fungi, 2(4), 30. https://doi.org/10.3390/jof2040030







