The Application of an Augmented Gravity Model to Measure the Effects of a Regionalization of Potential Risk Distribution of the US Cull Sow Market
Abstract
:1. Introduction
- (1)
- Detect, control, and contain the disease in animals as quickly as possible;
- (2)
- Eradicate the disease using strategies that seek to stabilize animal agriculture, the food supply, and the economy and to protect public health and the environment;
- (3)
- Provide science- and risk-based approaches and systems to facilitate continuity of business for non-infected animals.
2. Materials and Methods
2.1. Data Collection
2.2. Mathematical Description of the Cull Marketing Network
2.3. Model Validation
2.4. Stop Movement Scenarios
3. Results
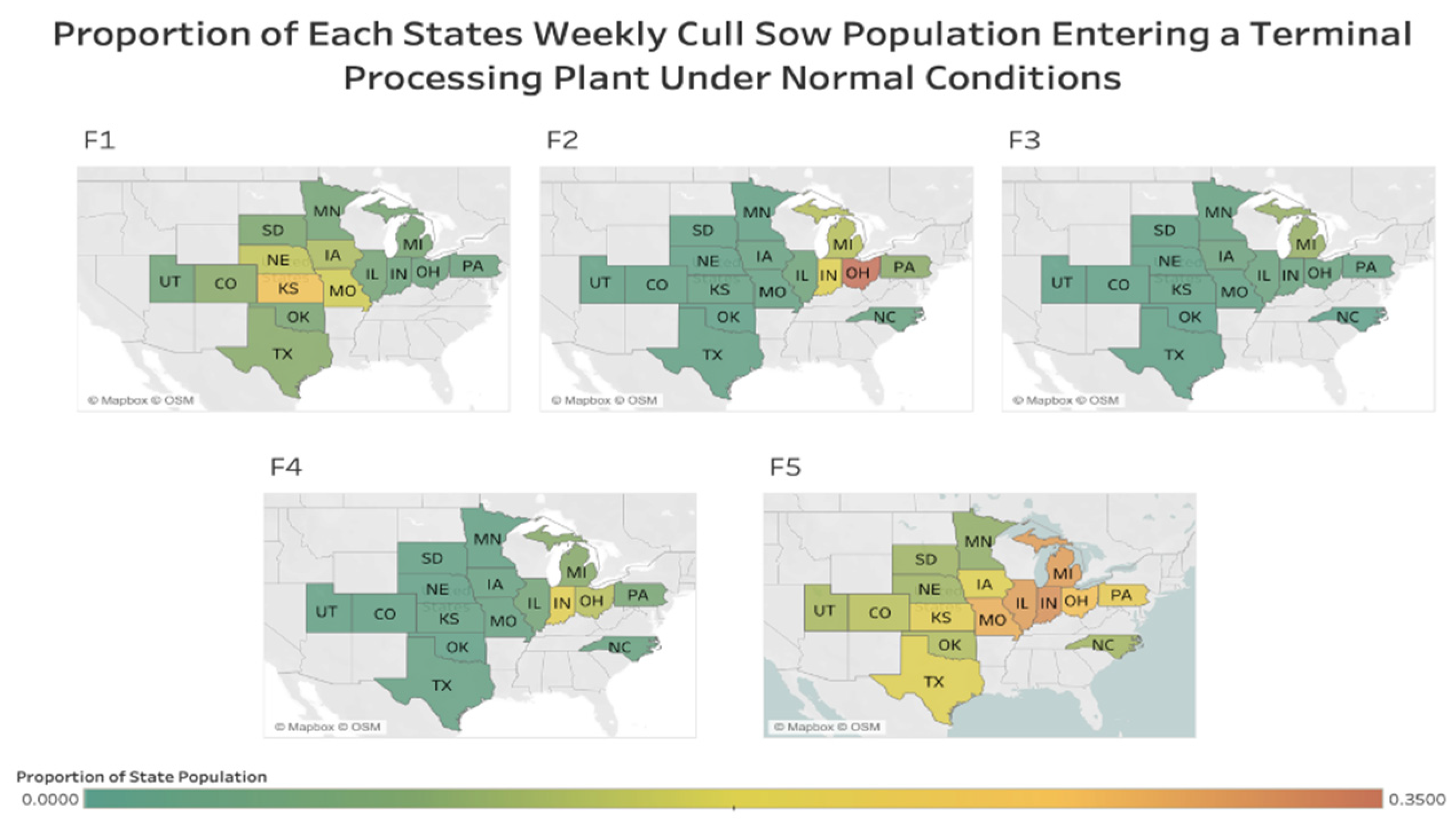
3.1. Mathematical Description of the Cull Sow Marketing Network
3.2. Model Validation Results
3.3. Processing Facility Closure Scenario
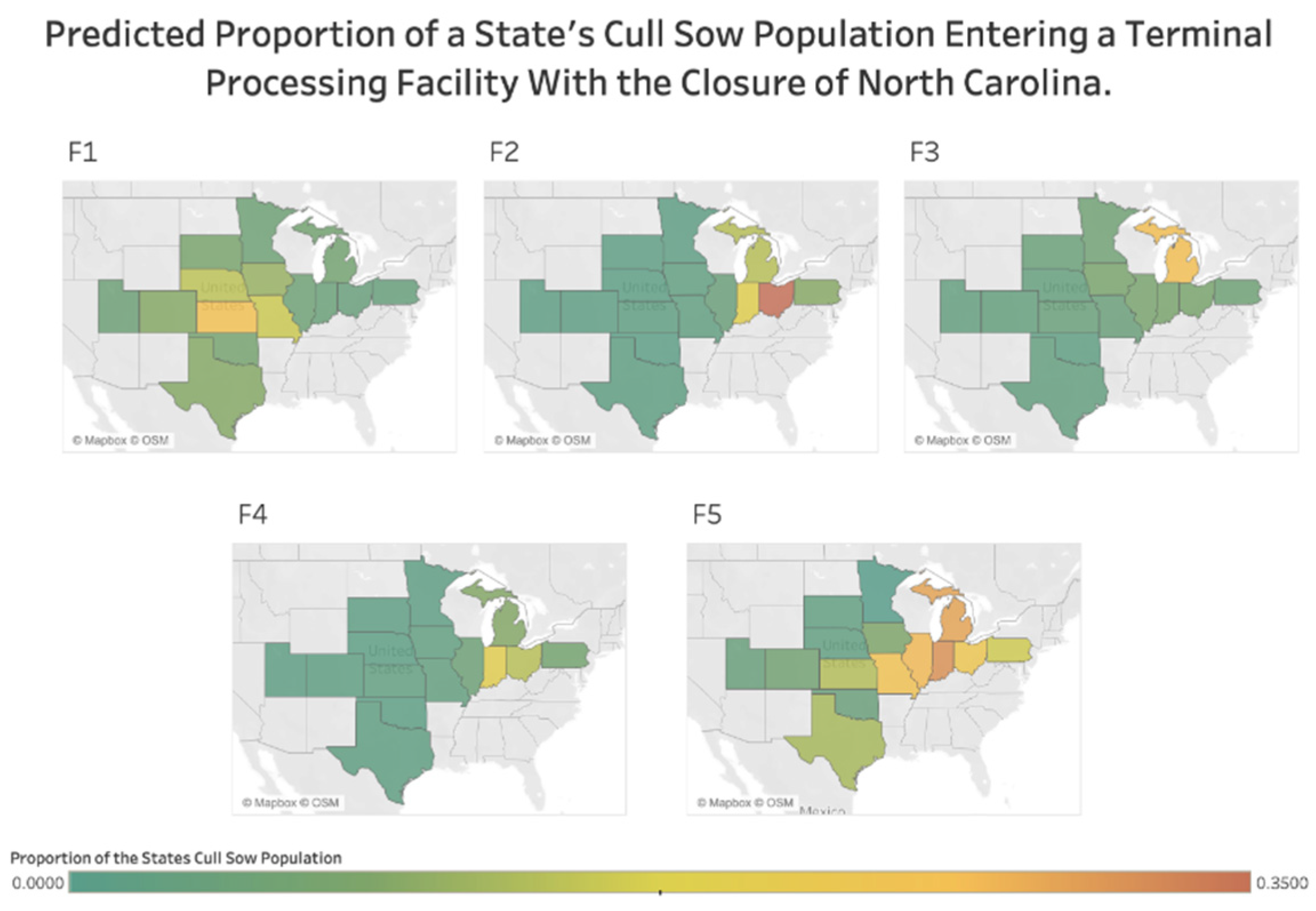
3.4. North Carolina Scenario
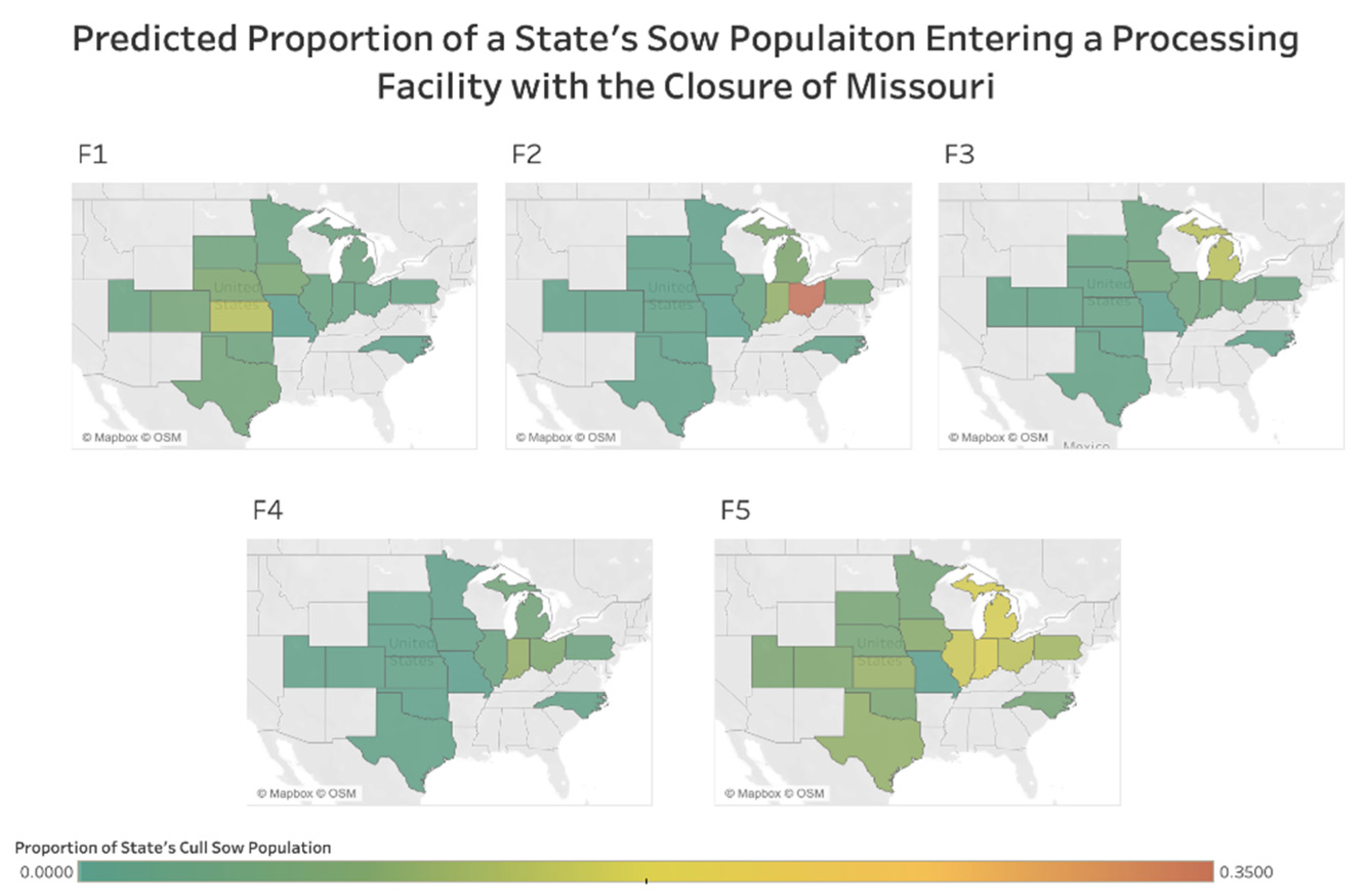
3.5. Missouri Scenario
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hamer, H. Quarterly Hogs and Pigs Inventory—United States: Chairperson. Statistics 2016, 1–16. [Google Scholar]
- Blair, B.; Lowe, J. Describing the cull sow market network in the US: A pilot project. Prev. Vet. Med. 2019, 162, 107–109. [Google Scholar] [CrossRef] [PubMed]
- Blair, B.; Lowe, J.F. A Novel Data Collection and Exploration of The Risk of Movements Within the United States’ Cull Sow Marketing Network. J. Swine Health Prod. 2022, 30, 72–78. [Google Scholar] [CrossRef]
- Sutherland, D. The Marketing Journey of Cull Sows and Secondary Market Pigs. Swine Health Inf. Cent. 2018, 2018. Available online: https://www.swinehealth.org/the-marketing-journey/ (accessed on 6 January 2021).
- Abell, C.E. Evaluation of litters per sow per year as a means to reduce non-productive sow days in commercial swine breeding herds and its association with other economically important traits. Anim. Sci. Commons 2011, 17, 1–87. [Google Scholar]
- Fitzgerald, R.F.; Stalder, K.J.; Johnson, C.D.; Layman, L.L.; Karriker, L.A. An Economic Analysis of Feeding Cull Sows11. Prof. Anim. Sci. 2008, 24, 355–362. [Google Scholar] [CrossRef]
- Huang, Y.W.; Dickerman, A.W.; Piñeyro, P.; Li, L.; Fang, L.; Kiehne, R.; Opriessnig, T.; Meng, X.J. Origin, evolution, and genotyping of emergent porcine epidemic diarrhea virus strains in the united states. MBio 2013, 4, e00737-13. [Google Scholar] [CrossRef] [Green Version]
- Hause, B.; Myers, O.; Duff, J.; Hesse, R. Senecavirus A in pigs, United States, 2015. Emerg. Infect. Dis. 2016, 22, 1323–1325. [Google Scholar] [CrossRef]
- Baker, K.L.; Mowrer, C.; Canon, A.; Linhares, D.C.L.; Rademacher, C.; Karriker, L.A.; Holtkamp, D.J. Systematic Epidemiological Investigations of Cases of Senecavirus A in US Swine Breeding Herds. Transbound. Emerg. Dis. 2017, 64, 11–18. [Google Scholar] [CrossRef]
- Dixon, L.K.; Sun, H.; Roberts, H. African swine fever. Antivir. Res. 2019, 165, 34–41. [Google Scholar] [CrossRef]
- Moennig, V. Introduction to classical swine fever: Virus, disease and control policy. Vet. Microbiol. 2000, 73, 93–102. [Google Scholar] [CrossRef]
- Orsel, K.; Bouma, A.; Dekker, A.; Stegeman, J.A.; de Jong, M.C.M. Foot and mouth disease virus transmission during the incubation period of the disease in piglets, lambs, calves, and dairy cows. Prev. Vet. Med. 2009, 88, 158–163. [Google Scholar] [CrossRef] [PubMed]
- Porphyre, T.; Bronsvoort, B.M.d.C.; Gunn, G.J.; Correia-Gomes, C. Multilayer network analysis unravels haulage vehicles as a hidden threat to the British swine industry. Transbound. Emerg. Dis. 2020, 67, 1231–1246. [Google Scholar] [CrossRef]
- Machado, G.; Vilalta, C.; Recamonde-Mendoza, M.; Corzo, C.; Torremorell, M.; Perez, A.; VanderWaal, K. Identifying outbreaks of Porcine Epidemic Diarrhea virus through animal movements and spatial neighborhoods. Sci. Rep. 2019, 9, 457. [Google Scholar] [CrossRef] [Green Version]
- Mathew, L.; Menon, D.G. Economic impact of FMD in Chazhoor Panchayath. Vet. World 2008, 1, 5–6. [Google Scholar]
- McLaws, M.; Ribble, C. Description of recent foot and mouth disease outbreaks in nonendemic areas: Exploring the relationship between detection and epidemic size. Can. Vet. J. 2007, 48, 1051–1062. [Google Scholar]
- Rushton, J.T.K.-J. The Impact of Foot and Mouth Disease. In Proceedings of the FAO/OIE Global Conference on Foot and Mouth Disease Control Ensuring Excellence and Ethics of the Veterinary Profession, Bangkok, Thailand, 27–29 June 2012; pp. 27–29. [Google Scholar]
- Ge, S.; Li, J.; Fan, X.; Liu, F.; Li, L.; Wang, Q.; Ren, W.; Bao, J.; Liu, C.; Wang, H.; et al. Molecular characterization of African swine fever virus, China, 2018. Emerg. Infect. Dis. 2018, 24, 2131–2133. [Google Scholar] [CrossRef] [Green Version]
- Moon, S.A.; Ferdousi, T.; Self, A.; Scoglio, C.M. Estimation of swine movement network at farm level in the US from the Census of Agriculture data. Sci. Rep. 2019, 9, 6237. [Google Scholar] [CrossRef] [Green Version]
- Bajardi, P.; Barrat, A.; Natale, F.; Savini, L.; Colizza, V. Dynamical patterns of cattle trade movements. PLoS ONE 2011, 6, e19869. [Google Scholar] [CrossRef]
- de Benedictis, L.; Vicarelli, C. Trade Potentials in Gravity Panel Data Models. Top. Econ. Anal. Policy 2005, 5, 1–52. [Google Scholar] [CrossRef]
- Egger, P. An econmetric view on the estimation of gravity models and the calculation of trade potentials. World Econ. 2002, 25, 297–312. [Google Scholar] [CrossRef] [Green Version]
- Natale, F.; Giovannini, A.; Savini, L.; Palma, D.; Possenti, L.; Fiore, G.; Calistri, P. Network analysis of Italian cattle trade patterns and evaluation of risks for potential disease spread. Prev. Vet. Med. 2009, 92, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Isard, W. Location Theory and Trade Theory: Short-Run Analysis. Q. J. Econ. 1954, 68, 305–320. [Google Scholar] [CrossRef]
- Battersby, B.; Ewing, R. International Trade Performance: The Gravity of Australia’s Remoteness. Gene 2005, 3, 1–37. [Google Scholar]
- Carrère, C. Revisiting the effects of regional trade agreements on trade flows with proper specification of the gravity model. Eur. Econ. Rev. 2006, 50, 223–247. [Google Scholar] [CrossRef] [Green Version]
- Kucheryavyy, K.; Rodríguez-Clare, A. Grounded by gravity: A well-behaved trade model with industry-level economies of scale. Natl. Bur. Econ. Res. 2013, 53, 1689–1699. [Google Scholar] [CrossRef]
- Özer, O.O. Determinants of Turkey’s textiles exportation: The gravitation model approach. Tekst. Konfeksiyon 2014, 24, 252–258. [Google Scholar]
- Rahman, M.; Shadat, W.B.; Narayan, C.D. Trade potential in SAFTA—An application of augmented gravity model. CPD Occas. Pap. Ser. 2006, 61, 1–28. [Google Scholar]
- Batra, A. India’s global trade potential: The gravity model approach. Glob. Econ. Rev. 2006, 35, 327–361. [Google Scholar] [CrossRef] [Green Version]
- Thompson, J.M.; Pendell, D.L.; Hagerman, A.D.; Johnson, K.K. International Trade Implications of Highly Pathogenic Poultry Disease Events. Agric. Resour. Econ. Rev. 2020, 49, 517–537. [Google Scholar] [CrossRef] [Green Version]
- Celko, J. National Animal Identification System (NAIS). In Joe Celko’s Data, Measurements and Standards in SQL; Morgan Kaufmann: San Francisco, CA, USA, 2010; pp. 217–222. [Google Scholar] [CrossRef]
- Google Maps. (n.d.). [Google Maps of the United States]. Available online: https://www.google.com/maps (accessed on 1 August 2020).
- U.S. Packing Sector—Pork Checkoff. Available online: https://www.pork.org/facts/stats/u-s-packing-sector/ (accessed on 15 March 2018).
- Agriculture Marketing Service. (LM_HG234) Daily Direct Prior Day Sow and Boar. Retrieved 2020. Available online: https://www.ams.usda.gov (accessed on 15 March 2018).
- Wölwer, A.L.; Breßlein, M.; Burgard, J.P. Gravity models in R. Austrian J. Stat. 2018, 47, 16–35. [Google Scholar] [CrossRef] [Green Version]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
| Variable | Normal Function | North Carolina Closure | Missouri Closure |
|---|---|---|---|
| Distance | −1.158 (0.091) *** | −1.302 (0.088) *** | −0.783 (0.120) *** |
| Facility’s Weekly Slaughter Capacity | 1.053 (0.080) *** | 1.124 (0.084) *** | 0.4299 (0.125) *** |
| State’s Weekly Slaughter Capacity | 0.803 (0.081) *** | 0.550 (0.081) *** | - |
| Regional Basis | - | - | - |
| Variable | F1 Closure Scenario | F1 Closure Actual |
|---|---|---|
| Distance | −0.744 (0.108) *** | −0.899 (0.214) *** |
| Facility’s Weekly Slaughter Capacity | 0.950 (0.092) *** | 1.00 (0.186) *** |
| State’s Weekly Slaughter Capacity | 0.334 (0.089) *** | - |
| Regional Basis | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blair, B.; Lowe, J. The Application of an Augmented Gravity Model to Measure the Effects of a Regionalization of Potential Risk Distribution of the US Cull Sow Market. Vet. Sci. 2022, 9, 215. https://doi.org/10.3390/vetsci9050215
Blair B, Lowe J. The Application of an Augmented Gravity Model to Measure the Effects of a Regionalization of Potential Risk Distribution of the US Cull Sow Market. Veterinary Sciences. 2022; 9(5):215. https://doi.org/10.3390/vetsci9050215
Chicago/Turabian StyleBlair, Benjamin, and James Lowe. 2022. "The Application of an Augmented Gravity Model to Measure the Effects of a Regionalization of Potential Risk Distribution of the US Cull Sow Market" Veterinary Sciences 9, no. 5: 215. https://doi.org/10.3390/vetsci9050215
APA StyleBlair, B., & Lowe, J. (2022). The Application of an Augmented Gravity Model to Measure the Effects of a Regionalization of Potential Risk Distribution of the US Cull Sow Market. Veterinary Sciences, 9(5), 215. https://doi.org/10.3390/vetsci9050215






