Next Article in Journal
Fertility Rate and Assessment of the Cytoprotective Capacity of Various Types of Holothuroidea Extracts on Spermatozoa
Previous Article in Journal
Molecular Detection of Equine Adenovirus 1 in Nasal Swabs from Horses in the Republic of Korea
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Veterinary Sciences
Volume 9
Issue 4
10.3390/vetsci9040188
vetsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of Non-Genetic Factors Affecting Wood’s Model of Daily Milk Fat Percentage of Holstein Cattle

by
Fuzhen Zhou
1,
Yan Liang
1,
Abdelaziz Adam Idriss Arbab
1,2,
Mingxun Li
1,
Zhangping Yang
1,
Niel A. Karrow
3 and
Yongjiang Mao
1,*
1
College of Animal Science and Technology, Yangzhou University, Yangzhou 225009, China
2
Biomedical Research Institute, Darfur College, Nyala 63313, Sudan
3
Center for Genetic Improvement of Livestock, Department of Animal Biosciences, University of Guelph, Guelph, ON N1G 2W1, Canada
*
Author to whom correspondence should be addressed.
Vet. Sci. 2022, 9(4), 188; https://doi.org/10.3390/vetsci9040188
Submission received: 15 March 2022 / Revised: 8 April 2022 / Accepted: 12 April 2022 / Published: 14 April 2022
Browse Figures
Versions Notes

Abstract

:
This research paper aimed to explore the characteristics of Holstein cattle’s milk fat percentage lactation curve and its influencing factors. The Wood model was used for fitting the lactation curve of 398,449 DHI test-day milk fat percentage records of Holstein cows from 2018 to 2020 in 12 dairy farms in Jiangsu province, and the influencing factors—including farm size, parity, calving season, calving interval, and 305-days milk production—on the parameters of the lactation curve were analyzed. The results showed that the non-genetic factors such as dairy farm size, calving season, parity, calving interval, and 305-days milk yield have a significant impact on milk fat percentage (p < 0.01); the average R2 of the daily milk fat percentage curve was 0.9699; the lowest milk fat percentage was 3.54%; the time to reach the lowest milk fat percentage was 126 days; and the persistence of milk fat percentage was 3.59%. All of these factors explored in this study fit at different levels above 0.96. The Wood model performed well in the fitting and analysis of the milk fat percentage curve of Holstein cattle in Jiangsu Province. This study provides a reference for improving the milk fat percentage of Holstein cattle.

1. Introduction

Milk fat is a kind of high-quality natural fat, which is synthesized and secreted by dairy cow mammary epithelial cells. It is an important nutritional component of milk and dairy products. The content of fat in milk will significantly affect the price of milk, and milk with high milk fat content is preferred. Lactation curve is a mathematical model describing the variation of milk yield during lactation, which is applied to predict lactation traits, potential genetic estimation, breeding stock selection, etc. Related studies have shown that milk fat percentage decreases gradually in the early stage of lactation, reaches the lowest point after a certain period of time, and gradually increases over time, showing rhythmic changes in different stages of lactation [1,2,3]. Many scholars have analyzed, described and quantified this law of change by establishing or drawing lessons from various mathematical models. Previous studies have shown that the Wood incomplete gamma function model (Wood model), the Nelder model, the Wilmink model, the Ali–Schaeffer model, and the Dijkstra model have good fitting effects on the lactation curve [4,5,6,7,8,9,10,11]. Compared with the Wood model, most of the models are more complex, the number of estimated parameters is increased, and the amount of data required is larger, therefore they may be difficult to calculate [12]. Sun et al. [13] found that the Wood model was suitable for fitting the milk fat percentage curve of Holstein cattle in the Yangtze River Delta. Mao et al. [14] found that the fitting degree of the Wood model to the lactation curve of southern Chinese Holstein cattle was more than 0.99.
Related studies have shown that the parameters of the dairy cow lactation curve model are affected by many non-genetic factors, such as dairy farm size, parity, calving season, etc, [15]. The changes in these factors must have a certain influence on the lactation curve of dairy cows’ daily milk fat percentage. Previous studies have only focused on the calculation of variance components and genetic parameters of dairy farm size, parity and calving season on milk, and there have been few reports on the effect of the dairy cows’ lactation [16,17,18]. Therefore, this study set out to use the Wood model to fit the curve of the daily milk fat percentage of Holstein cattle in 12 farms in Jiangsu Province from 2018 to 2020. The changing trend of all data was described quantitatively, and the effects of non-genetic factors such as dairy farm size, parity, calving season, calving interval, and 305-days milk yield on the parameters of the daily milk fat percentage Wood lactation curve of Holstein cattle were analyzed. The aim of this study was to provide referential and technical support for the breeding process and scientific feeding and management of Holstein cattle in Jiangsu Province.

2. Materials and Methods

2.1. Farm and Animal Information

The 12 dairy herds in the study were located in Jiangsu Province. The farms belonged to the monsoon climate area, with a mild climate and four distinct seasons. The annual average temperature was between 13.6 °C and 16.1 °C, and the annual precipitation was 704–1250 mm. The calving season was classified by average climate variables, as spring (March to May), summer (June to August), autumn (September to November) and winter (December to February next year).
All the dairy farm cattle were raised in the free stall, with three feeding and milking times per day, and all were fed with Total Mixed Ration (TMR). Dairy cows were divided into different groups in dairy farms. The formula for one of the farms is shown in Table 1.

2.2. Data Source

A total of 580,025 Dairy Herd Improvement (DHI) records of Holstein cattle, including cow number, determination date, calving season, parity, calving interval, lactation days, milk fat percentage, and 305-days milk yield were collected from 12 dairy farms in Jiangsu Province from 2018 to 2020. Extremely abnormal data was screened and eliminated to ensure the accuracy of the final results. The screening criteria were as follows: the number of births was 1–5 parities, the number of days of lactation was less than 305 days, and the milk fat percentage was 1–7%. After screening, the total number of qualified records was 398,449.

2.3. Statistical Analysis

The change in daily milk fat percentage was measured by the Wood incomplete gamma function model. The basic model is as follows:
Y t = a t − b e c t
where t represents the month of lactation, Yt represents the milk fat percentage of time t, and a, b and c are the model parameters. Parameter a represents the lactation potential, c represents the speed at which the milk fat percentage reaches the lowest point, and b represents the percentage at which the milk fat percentage rises from the lowest point [19]. The expressions of a, b and c are all “mean ± standard error”. In curve fitting, the initial values of each parameter are determined by the results calculated by Olori et al. [20]. The parameters calculated in the first step (a, b, and c), along with the following three formulas, are used to calculate the secondary parameters:
Tmin = b/c
Ymin = a(b/c)−b eb
Per = −(b + 1) lnc
In the above formula, Tmin is the number of days to reach the lowest milk fat percentage; Ymin is the lowest value of milk fat percentage; and Per is the lactation persistence of milk fat. Firstly, all the milk fat percentage data were sorted out in Microsoft Excel (2021), and then fitted with the SPSS (Ver 26.0) nonlinear regression subroutine. The fitting effect was evaluated by the degree of fit (R2) and the mean square of error. The least-square model was used to analyze the effects of non-genetic factors such as dairy farm size, parity, calving season, calving interval, and 305-days milk yield on the milk fat percentage of dairy cows. The model can be represented as follows:
Yijklmn = μ + Fi + Pj + Sk + Dl + Nm + eijklmn
where Yijklmn is the observed value of milk fat percentage; Fi is the fixed effect of dairy farm size; Pj is the fixed effect of parity; Sk is the fixed effect of calving season; Dl is the fixed effect of calving interval; Nm is the fixed effect of 305-days milk yield; and eijklmn is a residual random effect. The multiple comparisons between different levels of factors were made by Duncan’s method. The lactation month was divided into 1 lactation month every 30 days, and more than 300 days was the last lactation month, a total of 11 lactation months. The significance level was defined as follows: p ≤ 0.01, that the difference was extremely significant; p ≤ 0.05, that the difference reached a significant level; p > 0.05, that the difference was not significant. According to the above factors and levels affecting the daily milk fat percentage, the corresponding data were selected, the Wood lactation curve was fitted by the method mentioned above, and the corresponding parameters were calculated.

3. Results

3.1. Effects of Different Factors on Milk Fat Percentage of Holstein Cattle

Table 2 shows the basic situation of each parity of dairy cows’ milk fat percentage. The dairy farm size, parity, calving season, calving interval, and 305-days milk yield significantly impacted the milk fat percentage of Holstein cattle (Table 3, p < 0.01). The Holstein cow in the dairy farm with 2001 to 5000 cows had the highest milk fat percentage (3.93%), and the Holstein cow in the dairy farm with 1000 to 2000 cows had the lowest milk fat percentage (3.59%). The milk fat percentage of Holstein cows with fifth parity was 4.01%, which was significantly higher than those of the other parities (p < 0.01). The milk fat percentage of Holstein cows with first parity was 3.76%, which was significantly lower than those of the other parities (p < 0.01). The milk fat percentage of Holstein calving in autumn was 3.88%, which was significantly higher than in other calving seasons (p < 0.01). In spring, the milk fat percentage was 3.77%, which was significantly lower than in the other calving seasons (p < 0.01). The milk fat percentage of Holstein cattle with a calving interval of more than 441 days was 3.90%, which was significantly higher than those of other calving intervals (p < 0.01). When the calving interval was 300 to 365 days, the milk fat percentage was 3.88%, which was significantly lower than the percentage during other calving seasons (p < 0.01). The milk fat percentage was significantly higher for Holstein cows with a 305-days milk yield of 3000–5000 kg than in other 305-days milk yield cows (p < 0.01).

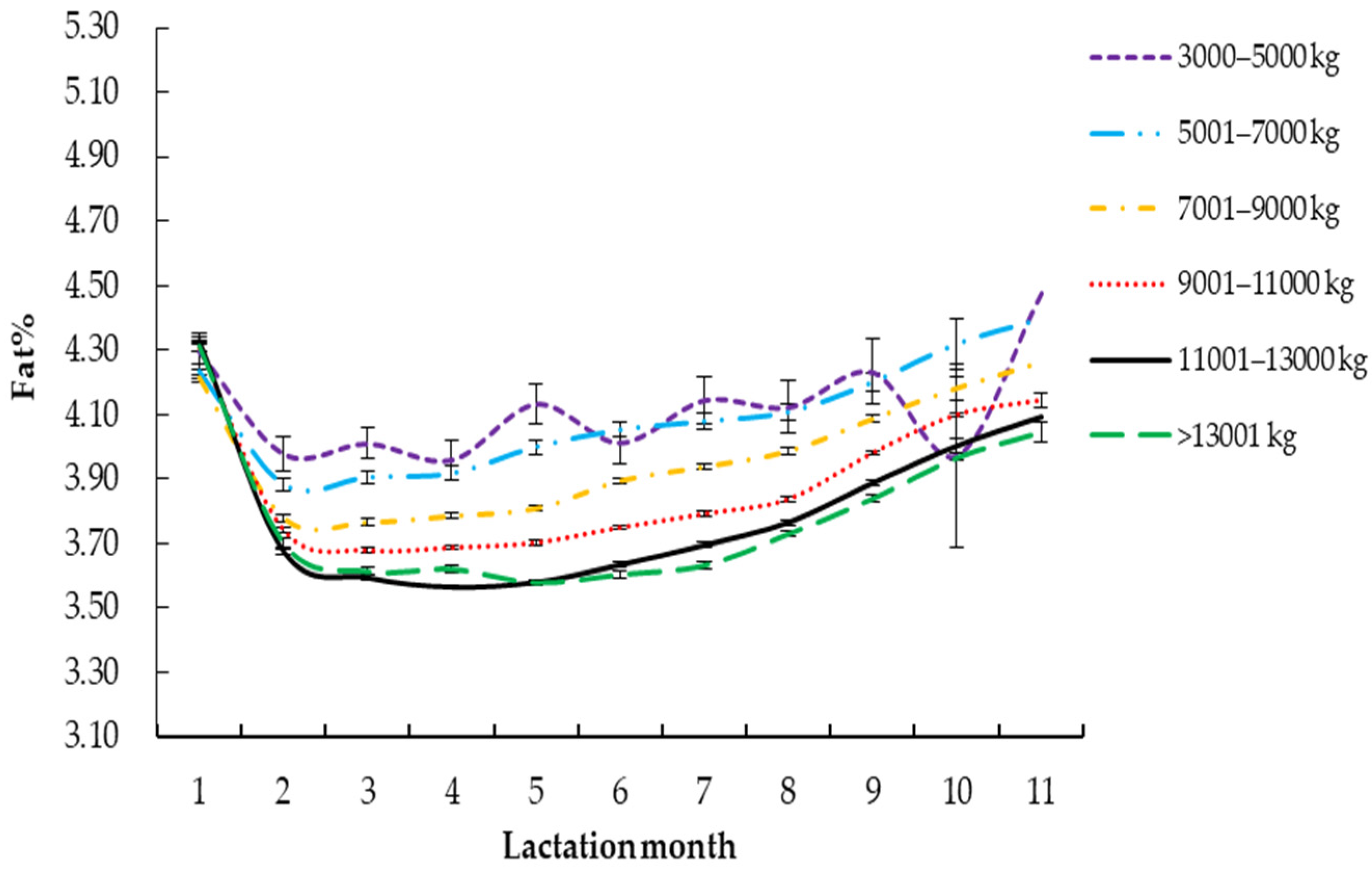
3.2. Effects of Different Factors on Lactation Curve and Fitting Parameters of Daily Milk Fat Percentage

The fitting parameters of the daily milk fat percentage Wood lactation curve with different factors are shown in Table 4. The daily milk fat percentage Wood lactation curve changes were drawn according to the different parameters.

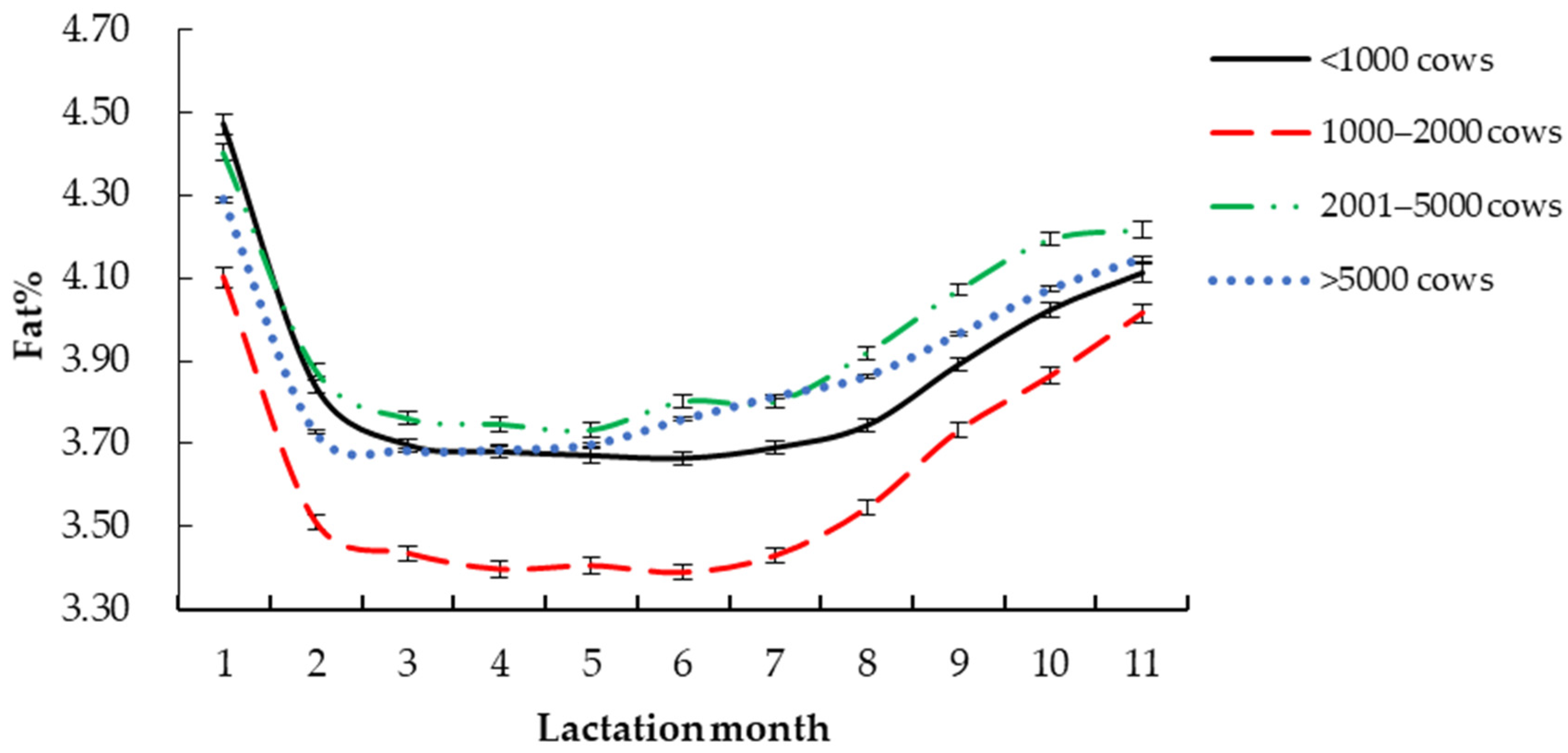
3.2.1. Dairy Farm Size

The R2 of the milk fat percentage curve was the highest (0.9798), and the mean square error was the lowest (0.036), on farms with fewer than 1000 cows (Figure 1, Table 4). When the number of dairy cows in the dairy farm was 1000 to 2000, the R2 of the milk fat percentage curve was the lowest (0.9483). The Ymin of dairy cows was the highest when the number of dairy cows was more than 5000 (3.58%). The Tmin of dairy cows with less than 1000 cows in the dairy farm was the highest (142 days). The Per of dairy cows with a size less than 1000 was the highest (3.65), while the Per of dairy cows with a scale of 1000 to 2000 was the lowest (3.44). The a of dairy cows with a size less than 1000 was the highest (4.10). When the number of dairy cows was 1000 to 2000, the c and b of the lactation curve were the highest, which were 0.07 and 0.3, respectively.

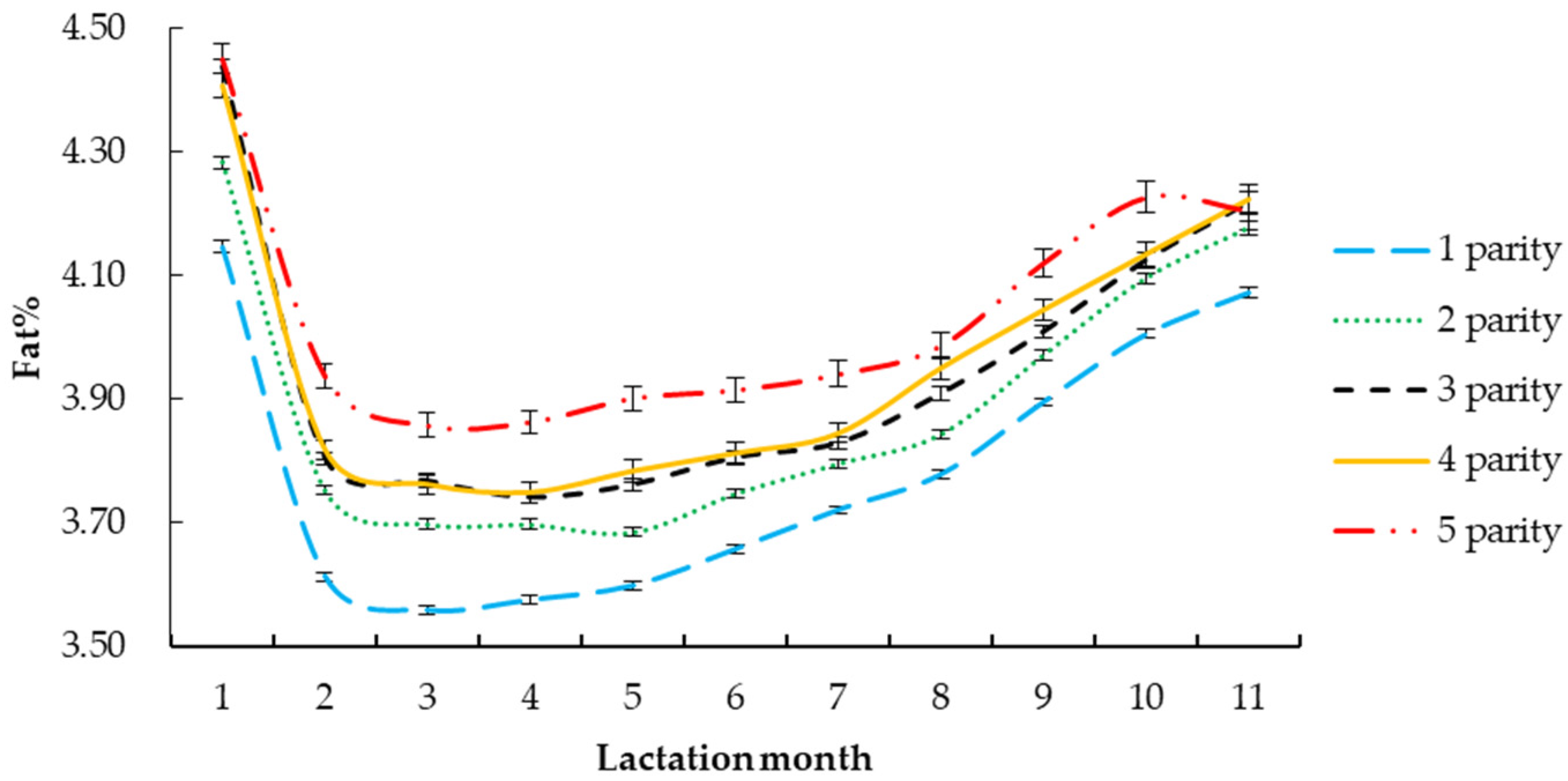
3.2.2. Parity

The R2 of the milk fat percentage curve of the first birth of Holstein cattle was the highest (0.9710), the mean square error was the lowest (0.050), and the R2 of the fifth birth was the lowest (0.9685), as shown in Figure 2 and Table 4. The Ymin of the fifth parity of Holstein cattle was the highest (3.74%). The Tmin of Holstein cattle was the highest in the third parity (129 days). The fifth fetus had the highest Per of milk fat percentage (3.68). The a of the fifth parity of Holstein cattle was the highest (4.07). Among different parities, the c of lactation curve of the third and fourth parity was the largest (0.06), and the b of the third parity was the largest (0.24).

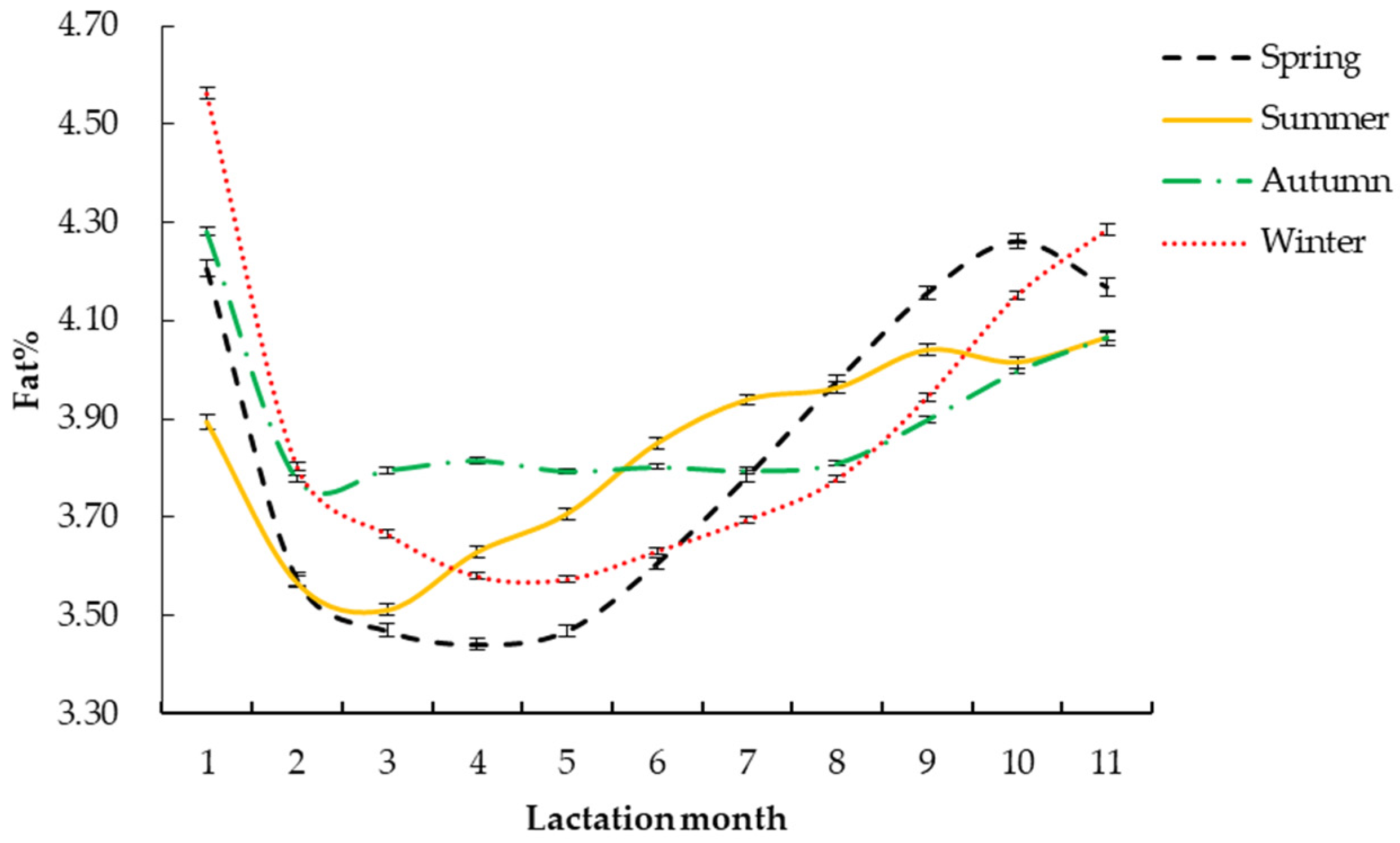
3.2.3. Calving Season

The lactation curves and fitting parameters of different calving seasons are shown in Figure 3 and Table 4. Among them, the R2 of the milk fat percentage curve of calving in autumn was the highest (0.9720). The Ymin of calving in autumn was the highest (3.65%), and that of calving in spring was the lowest (3.36%). The Tmin for Holstein calving in autumn was the highest (137 days). The Per of calving in spring was the lowest (3.24). The a and b of the lactation curve of Holstein calving cows in winter were the largest, 4.07 and 0.35, respectively, and the c was lowest in autumn (0.03).

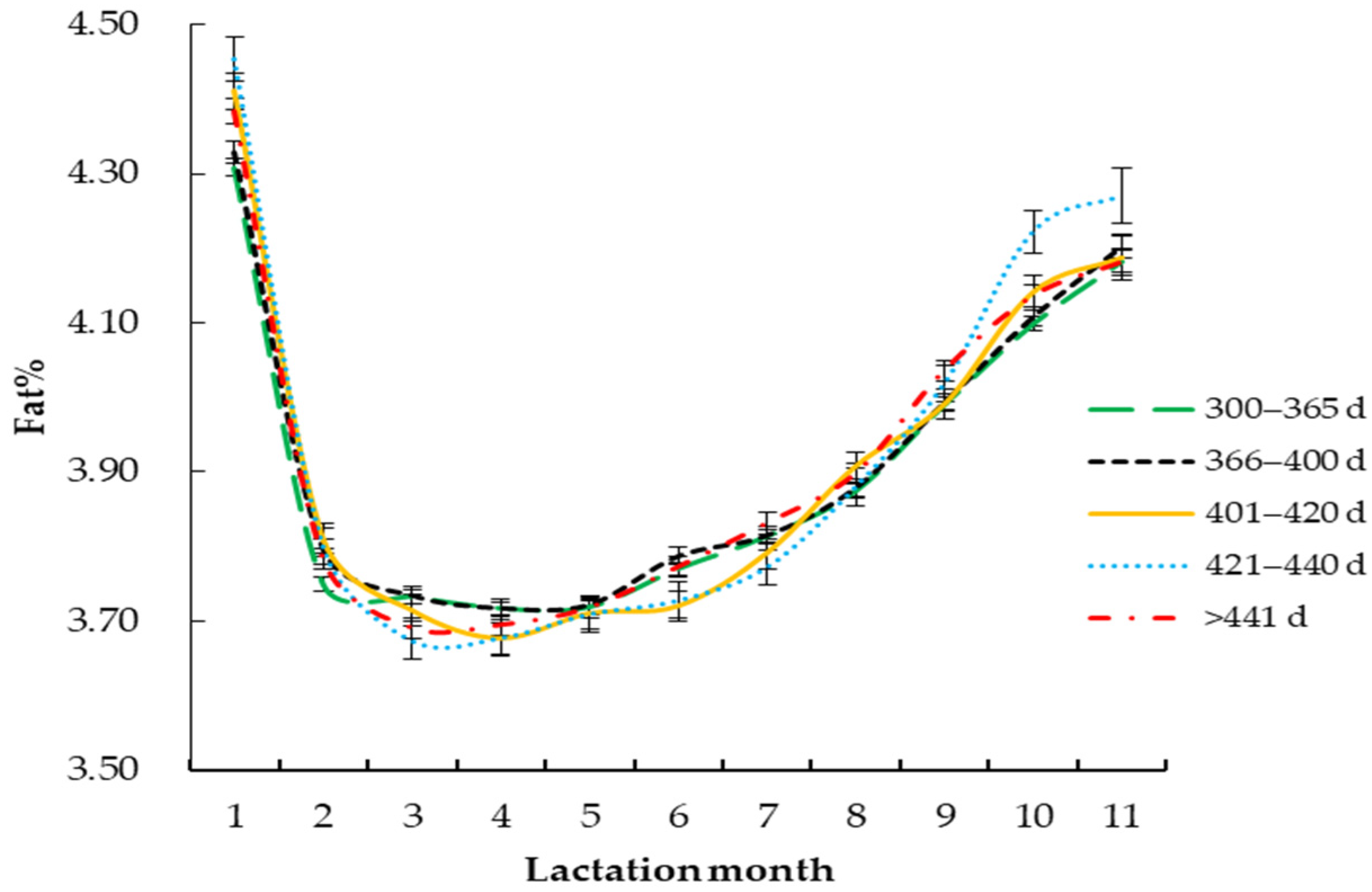
3.2.4. Calving Interval

The R2 of the milk fat percentage curve was the highest (0.9704), and the mean square error was the lowest (0.054), when the calving interval of Holstein cattle was 366–400 days (Figure 4 and Table 4). The Ymin was the highest (3.59%) when the calving interval was 366–400 days. The Tmin was the highest when the calving interval was 401–420 days (128 days). When the calving interval was 300–365 days, the Per was the highest (3.60), and when the calving interval was 421–440 days, the Per was the lowest (3.45). The a was the highest (4.00) when the calving interval was 421–440 days, and the a was the lowest (3.91) when the calving interval was 300–365 days. The maximum speed of c and b were 0.07 and 0.28, respectively, when the calving interval was 421–440 days.

3.2.5. 305-Day Milk Yield

As shown in Figure 5 and Table 4, the R2 of the milk fat percentage curve of Holstein cows with a 305-days milk yield of 5001–7000 kg was the highest (0.9734). The Ymin of Holstein cows with milk yield of 5001–7000 kg was the highest (3.67%). The Tmin was the highest when milk yield was 9001–11,000 kg (128 days). Holstein cows with milk yield of 3000–5000 kg had the highest Per (4.22), and Holstein cows with milk yield of 11,001–13,000 kg had the lowest Per (3.54). The a, c and b of Holstein cattle with milk yield greater than 13,001 kg in 305-days milk yield were the highest, with their corresponding values 4.14, 0.07 and 0.34, respectively.

4. Discussion

Wang et al. [15] and Zhang et al. [21] have shown that the size of farm has a significant effect on the parameters of the Holstein lactation curve model. Kuevi et al. [22] found that the size of the dairy farm had a significant effect on the milk fat percentage of dairy cows. This study found that the farm size had a certain effect on the Holstein milk fat percentage Wood lactation curve model parameters. Large-scale dairy farms adopt modern equipment and more meticulous feeding management to shorten the period of milk fat percentage declining before the peak period of cow intake. Therefore, dairy farms with more than 5000 cows have the shortest Tmin and the highest milk fat percentage. Related studies have shown that large-scale farm equipment has a high degree of mechanization, and that the establishment of a digital standardized management system can enable various departments to cooperate with each other, to have strong technical strength of operation, and to diversify the types of formulations, which is helpful for improving the lactation performance and efficiency of dairy cows [23,24]. Cows in large-scale dairy farms have been improved by standard and scientific breeding, and their genetic basis and production performance have improved. Holstein cows’ milk fat percentage curve, with a size of less than 1000, has the highest R2, the greatest Per, and the greatest potential of milk fat percentage. Small-scale pastures generally have a low degree of mechanization; although the number of cattle is small, the management of individuals is more thorough. On the other hand, medium-sized farms may be using low mechanization and poor cattle management, because of cost considerations; besides, the DHI records of medium-sized farms are not comprehensive. This may be the reason why 1000–2000 pastures have the lowest R2, the least Per, and the least potential of milk fat percentage. Therefore, the management of medium-sized pastures should be strengthened to ensure lactation performance.
This study found that the R2 of the fifth parity dairy cow was the smallest, the Ymin was the highest, the Per was the highest, and the lactation potential was the greatest. The R2 of the first parity dairy cow was the highest, the Ymin was the lowest, the Per was the lowest, and the potential of the milk fat percentage was the least. Roberto et al. [25] found that the parameters of the population lactation curve fitted by the Wood model were significantly affected by parity, and that the lactation potential of first-born cattle was low. The change of milk fat percentage of the first parity cows was relatively small, and the data were limited, which may be due to the fact that the majority of the first parity cattle had just reached body maturity. The dairy cows’ body development was not perfect, and the nutrient intake required to maintain the dairy cows’ energy consumption and tissue development wass not good, resulting in poor milk fat percentage. For first-born cattle, the potential of milk fat percentage was low, the milk fat percentage increased slowly in the later stage of lactation, and the Per was strong, which was consistent with the findings of Rao and Sundaresan [26]. High-parity cows had a small R2 because some individuals showed superior production performance, and there were significant differences between individuals. Capuco et al. [27] and Val-Arreola et al. [28] found that milk fat percentage increased significantly with the increase of parity, which was consistent with the findings of this study, and that lactation performance reached its peak at the fifth fetal stage. Amongst all the parities, Holstein cattle of the third parity first reached the lowest point of milk fat percentage and then increased the fastest, and this showed that the body recovery ability of dairy cows with third parity was the fastest, such that they could quickly eliminate negative effects after calving, and enter a state of efficient production. Knaus et al. [29] and Oltenacu et al. [30] showed that the average calving number of dairy cows in Austria and the United States was 3.3 when they were eliminated. Yan et al. [31] found that the average calving number of Chinese Holstein cattle was 2.86 when they were eliminated. Therefore, the productive lifetime of the dairy cow should be improved to improve the actual production income.
Qi et al. [32] found that the calving season has a certain influence on the Wood lactation curve model parameters. In this study, different calving seasons had corresponding effects on milk fat percentage and the Wood lactation curve model parameters of Holstein cattle. Among them, the R2 of calving in autumn, the Ymin, the shortest Tmin, and the Per were the highest, and the milk fat percentage was the highest; similar results have also been found by Tekerli et al. [33], Keown et al. [34], and Schneeberger [35]. This may be due to the suitable temperature in autumn, when the calving environment is less stressful on dairy cows; coupled with the supplementary feeding of fresh green feed in autumn, the lactation of dairy cattle can be brought into full play. When calving in spring, the R2, the shortest Tmin and the Per are the lowest. This could be because the calving cows in spring have just experienced a cold winter and are recovering, when calving increases the burden on the body; on the other hand, there is no high-quality green feed in spring, and the demand for nutrition of dairy cows cannot be met, resulting in low lactation performance. García et al. [36] found that the milk fat content of cows during calving in spring was significantly lower than that in other seasons, which was consistent with the results of this study. The potential of milk fat percentage and the shortest Tmin in summer calving cows are the smallest, which may be due to the influence of heat stress during summer calving, which reduces the dry matter intake and adipose tissue mobilization ability of dairy cows [37,38,39,40]; the dairy cow’s need for energy to maintain itself increases, and the energy used to produce milk decreases. However, as dairy cows drink a lot of water due to hot weather, the milk fat percentage decreases rapidly, and the shortest Tmin is also the smallest. Therefore, the dairy farm should reasonably arrange the breeding time of the herd to avoid calving in spring as far as possible, to improve the production income.
In this study, it was found that calving intervals had a significant effect on milk fat percentage and the parameters of the Wood lactation curve model: when the calving interval was 366 to 400 days, the R2 was the highest, and the Ymin was greatest. Related studies [41,42,43] have shown that production performance and production benefit are best when the calving interval of dairy cows is 12–13 months; using the production data at this time to fit, the R2 is the highest. The lactation potential is minimum when the calving interval is 300–365 days; a short calving interval means that there are more aborted cattle in the herd, and the production performance of the herd decreases [44]. The R2 of Holstein cattle with a calving interval of more than 441 days was the lowest, and this may have been due to the negative balance of IGF-I [45], the signal factor secreted by the body. The secretion capacity of reproductive hormones decreased while reproductive diseases increased, resulting in longer calving intervals and longer lactation days, so the R2 of dairy cows was the lowest. Therefore, matching the appropriate calving interval in production will help to improve the economic benefit of breeding.
Baiyila [46] showed that the difference in milk yield over 305 days had a certain effect on the Wood lactation curve model. This study found that the R2 of Holstein cattle was the highest when the 305-days milk yield was 5001–7000 kg. Among them, the milk fat percentage of Holstein cattle with a 305-days milk yield of 3000–5000 kg was the highest, and it was found that the milk fat percentage decreased significantly with the increase of milk yield. Umphrey et al. [47] and Liang et al. [48] showed a significant negative correlation between milk yield and milk fat percentage. The Holstein cows with 305-days milk yield above 13,001 kg were high-yield dairy cows; the results showed that the lactation potential of this kind of dairy cow was the best, the speed of reaching and rising from the lowest point of milk fat percentage was the highest, and Ymin was the highest. However, related studies [49,50] have shown that high-yield dairy cows may increase their own diseases at the same time as high milk yield, implying that some high-yield dairy cows may get sick, which may affect the milk fat content during lactation, resulting in great individual differences amongst individuals as a whole; this may be the reason for the least R2. The Holstein cattle with milk yield of 3000–5000 kg reached the lowest point of milk fat percentage at the slowest speed, and the speed of rising from the lowest point was the least, this may be due to the decline of lactation performance in some Holstein cattle due to heredity and disease, and the specific reasons need to be further studied.

5. Conclusions

The findings of this study show that the Wood model is suitable for fitting the curve of milk fat percentage of Holstein cattle in Jiangsu Province. Non-genetic factors such as dairy farm scale, calving season, parity, calving interval, and 305-days milk yield have significant effects on milk fat percentage and milk fat percentage curve fitting parameters. This study of non-genetic factors provides a referential basis for regulating and controlling the milk fat percentage of Holstein cattle in Chinese dairy farms.

Author Contributions

Conceptualization, F.Z. and Y.M.; methodology, F.Z. and Y.M.; software, F.Z. and Y.L.; validation, F.Z. and Y.L.; formal analysis, F.Z.; investigation, M.L. and Z.Y.; resources, Y.M.; data curation, Y.L.; writing—original draft preparation, F.Z.; writing—review and editing, F.Z.; N.A.K., A.A.I.A. and M.L.; funding acquisition, Y.M. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the National Natural Science Foundation of China (31972555), the Postgraduate Research and Practice Innovation Program of Yangzhou University (KYCX21_3264), Natural Science Research Project of Colleges and Universities in Jiangsu Province(18KJA230003), Jiangsu Province “Six talent peaks” Project Funding (ny-093), and Mod-ern Agricultural Development Project of Jiangsu Province (2019-SJ-039-08-04).

Institutional Review Board Statement

The animal study protocol was approved by the Institutional Re-view Board of The Ministry of Science and Technology of the People’s Republic of China (protocol code 2006–398). for studies involving animals.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Salfer, I.; Dechow, C.D.; Harvatine, K.J. Annual rhythms of milk and milk fat and protein production in dairy cattle in the United States. J. Dairy Sci. 2019, 102, 742–753. [Google Scholar] [CrossRef] [Green Version]
  2. García, S.; Holmes, C. Lactation curves of autumn- and spring-calved cows in pasture-based dairy systems. Livest. Prod. Sci. 2001, 68, 189–203. [Google Scholar] [CrossRef]
  3. Macciotta, N.; Vicario, D.; Cappio-Borlino, A. Detection of Different Shapes of Lactation Curve for Milk Yield in Dairy Cattle by Empirical Mathematical Models. J. Dairy Sci. 2005, 88, 1178–1191. [Google Scholar] [CrossRef] [Green Version]
  4. Rekik, B.; Ben Gara, A.; Ben Hamouda, M.; Hammami, H. Fitting lactation curves of dairy cattle in different types of herds in Tunisia. Livest. Prod. Sci. 2003, 83, 309–315. [Google Scholar] [CrossRef]
  5. Gantner, V.; Potočnik, K.; Kuterovac, K.; Gantner, R.; Antunović, B. Methods for early prediction of lactation flow in Holstein heifers. Mljekarstvo 2010, 60, 260–265. [Google Scholar]
  6. Gradiz, L.; Alvarado, L.; Kahi, A.; Hirooka, H. Fit of Wood’s function to daily milk records and estimation of environmental and additive and non-additive genetic effects on lactation curve and lactation parameters of crossbred dual purpose cattle. Livest. Sci. 2009, 124, 321–329. [Google Scholar] [CrossRef]
  7. Stachurska, A.; Bartyzel, K. Judging dressage competitions in the view of improving horse performance assessment. Acta Agric. Scand. Sect. A Anim. Sci. 2011, 61, 92–102. [Google Scholar] [CrossRef]
  8. Marek, J.; Rajmon, R.; Haloun, T. Critical Evaluation of Seven Lactation Curve Estimation Models; Springer Science and Business Media LLC: New York, NY, USA, 2015; pp. 73–84. [Google Scholar]
  9. Mao, Y.J.; Zhang, M.R.; Xu, Z.J.; Liu, S.; Zhang, Y.Q.; Chen, D.; Wang, X.L.; Yang, Z.P. Lactation curve fittings of Wood‘s non-linear model for milk yield, milk fat, milk protein and somatic cell score for Chinese Holstein in southern China. Chin. J. Anim. Vet. Sci. 2012, 43, 1904–1909. [Google Scholar]
  10. Cunha, D.D.N.F.V.D.; Pereira, J.C.; E Silva, F.F.; De Campos, O.F.; Braga, J.L.; Martuscello, J.A. Selection of models of lactation curves to use in milk production simulation systems. Rev. Bras. Zootec. 2010, 39, 891–902. [Google Scholar] [CrossRef] [Green Version]
  11. Silvestre, A.; Petim-Batista, F.; Colaço, J. The Accuracy of Seven Mathematical Functions in Modeling Dairy Cattle Lactation Curves Based on Test-Day Records from Varying Sample Schemes. J. Dairy Sci. 2006, 89, 1813–1821. [Google Scholar] [CrossRef] [Green Version]
  12. Wood, P.D.P. Algebraic Model of the Lactation Curve in Cattle. Nature 1967, 216, 164–165. [Google Scholar] [CrossRef]
  13. Sun, X.Z.; An, P.P.; Guo, M.; Sun, Y.; Jin, T.; Liu, G. Fitting of changing curves of milk yield and milk composition of Chi-nese Holstein dairy cows in Yangtze river delta using Wood’s model. Chin. J. Anim. Nutr. 2018, 30, 2136–2142. [Google Scholar]
  14. Mao, Y.J.; Zhang, Y.Q.; Xu, Z.J.; Liu, S.; Zhang, M.R.; Chang, L.L.; Yang, Z.P. Fitting of lactation curves for Chinese Holstein. Chin. J. Anim. Vet. Sci. 2011, 42, 1239–1248. [Google Scholar]
  15. Wang, R.J.; Zhang, Z.G.; Wu, H.J.; Wang, D.S.; Wu, E.Q.; Su, R.; Zhang, Y.J.; Wang, Y.C.; Li, J.Q. Study of non-genetic factors affecting on lactation curve traits of inner Mongolia Sanhe cattle. China Anim. Husb. Vet. Med. 2010, 37, 99–102. [Google Scholar]
  16. Togashi, K.; Lin, C. Genetic Improvement of Total Milk Yield and Total Lactation Persistency of the First Three Lactations in Dairy Cattle. J. Dairy Sci. 2008, 91, 2836–2843. [Google Scholar] [CrossRef]
  17. Pozveh, S.T.; Shadparvar, A.A.; Shahrbabak, M.M.; Taromsari, M.D. Genetic analysis of reproduction traits and their relationship with conformation traits in Holstein cows. Livest. Sci. 2009, 125, 84–87. [Google Scholar] [CrossRef]
  18. Xu, S.Z.; Chen, Y.C.; Zhang, Z.S. Studies on estimating milk yield of dairy cows by using gamma procedureIIpath analysis of the gamma lactation curve estimates of 305 days milk yield and other lactation characteristics. Chin. J. Anim. Vet. Sci. 1988, 19, 85–90. [Google Scholar]
  19. Silvestre, A.; Martins, A.; Santos, V.; Ginja, M.; Colaço, J. Lactation curves for milk, fat and protein in dairy cows: A full approach. Livest. Sci. 2009, 122, 308–313. [Google Scholar] [CrossRef]
  20. Olori, V.; Brotherstone, S.; Hill, W.; McGuirk, B. Fit of standard models of the lactation curve to weekly records of milk production of cows in a single herd. Livest. Prod. Sci. 1999, 58, 55–63. [Google Scholar] [CrossRef]
  21. Zhang, J.L.; Ru, C.X.; Zhao, W.H. The lactation curves fitting and parameters analysis in different dairy cattle farms. Hubei Agric. Sci. 2012, 12, 140–142. [Google Scholar] [CrossRef]
  22. Kucevic, D.; Trivunovic, S.; Radinovic, M.; Plavsic, M.; Skalicki, Z.; Perisic, P. The effect of the farm size on milk traits of cows. Biotehnol. Anim. Husb. 2011, 27, 951–958. [Google Scholar] [CrossRef] [Green Version]
  23. Ma, X.Y.; Gao, Z.L.; Gao, Y.X.; Gu, Q.S.; Li, J.G.; Ma, W.Q. Milk production, nitrogen balance and utilization efficiency of lactating cows in dairy operations with different sizes. J. Hebei Agric. Univ. 2014, 37, 88–93. [Google Scholar] [CrossRef]
  24. Wu, H.C.; Fan, X.Z.; Xu, K.Y.; Dong, J.H.; Sun, Z.G.; Wang, J.M.; Tan, J.H. Study on Devopment and Applion of Computer Assisted Breeding System in Modern Cattle Farm. J. Domest. Anim. Ecol. 2006, 6, 19–22. [Google Scholar] [CrossRef]
  25. Roberto, S.; Aldo, C.B.; Macciotta, N.P.P. Modelling extended lactation curves for milk production traits in Italian Holsteins. Ital. J. Anim. Sci. 2009, 8, 165–167. [Google Scholar] [CrossRef]
  26. Rao, M.K.; Sundaresan, D. Influence of environment and heredity on the shape of lactation curves in Sahiwal cows. J. Agric. Sci. 1979, 92, 393–401. [Google Scholar] [CrossRef]
  27. Capuco, A.V.; Wood, D.L.; Baldwin, R.; Mcleod, K.; Paape, M.J. Mammary cell number, proliferation, and apoptosis during a bovine lactation: Relation to milk production and effect of bST. J. Dairy Sci. 2001, 84, 2177–2187. [Google Scholar] [CrossRef]
  28. Val-Arreola, D.; Kebreab, E.; Dijkstra, J.; France, J. Study of the Lactation Curve in Dairy Cattle on Farms in Central Mexico. J. Dairy Sci. 2004, 87, 3789–3799. [Google Scholar] [CrossRef]
  29. Knaus, W. Dairy cows trapped between performance demands and adaptability. J. Sci. Food Agric. 2009, 89, 1107–1114. [Google Scholar] [CrossRef]
  30. Werner, C.; Wecke, C.; Liebert, F.; Wicke, M. Increasing the incubation temperature between embryonic day 7 and 10 has no influence on the growth and slaughter characteristics as well as meat quality of broilers. Animal 2010, 4, 810–816. [Google Scholar] [CrossRef] [Green Version]
  31. Yan, X.Y.; Liu, A.X.; Dong, G.H.; Guo, G.; Wang, X.Y.; Liu, L.; Zhang, S.L.; Wang, Y.C. Analysis of longevity and its influenc-ing factors in Chinese Holstein population in Beijing. Chin. J. Anim. Sci. 2016, 52, 1–5. [Google Scholar]
  32. Qi, J.G.; Yang, Z.C.; Li, X.; Yan, X.Y.; Dong, G.H.; Li, X.Z.; Huang, X.X.; Wang, Y.C. Effects of calving season on the parame-ters of Wood lactation curve of Holstein dairy cow in Beijing area. China Anim. Husb. Vet. Med. 2018, 45, 197–205. [Google Scholar] [CrossRef]
  33. Tekerli, M.; Akinci, Z.; Dogan, I.; Akcan, A. Factors Affecting the Shape of Lactation Curves of Holstein Cows from the Balikesir Province of Turkey. J. Dairy Sci. 2000, 83, 1381–1386. [Google Scholar] [CrossRef]
  34. Keown, J.; Everett, R.; Empet, N.; Wadell, L. Lactation Curves. J. Dairy Sci. 1986, 69, 769–781. [Google Scholar] [CrossRef]
  35. Schneeberger, M. Inheritance of Lactation Curve in Swiss Brown Cattle. J. Dairy Sci. 1981, 64, 475–483. [Google Scholar] [CrossRef]
  36. García, S.C.; Cayzer, F.J.; Holmes, C.W.; MacDonald, A. The effect of calving season on milk production A system study. Proc. N. Z. Soc. Anim. Prod. 1998, 58, 61–63. [Google Scholar]
  37. Gorniak, T.; Meyer, U.; Südekum, K.-H.; Dänicke, S. Impact of mild heat stress on dry matter intake, milk yield and milk composition in mid-lactation Holstein dairy cows in a temperate climate. Arch. Anim. Nutr. 2014, 68, 358–369. [Google Scholar] [CrossRef]
  38. Baumgard, L.H.; Rhoads, R.P. Ruminant nutrition symposium: Ruminant Production and Metabolic Responses to Heat Stress. J. Anim. Sci. 2012, 90, 1855–1865. [Google Scholar] [CrossRef] [Green Version]
  39. Wheelock, J.B.; Rhoads, R.P.; VanBaale, M.J.; Sanders, S.R.; Baumgard, L.H. Effects of heat stress on energetic metabolism in lactating Holstein cows. J. Dairy Sci. 2010, 93, 644–655. [Google Scholar] [CrossRef]
  40. Xie, G.H. Metabolic and Endocrine Adaptations to Heat Stress in Lactating Dairy Cows; The Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2015. [Google Scholar]
  41. Holmann, F.J.; Shumway, C.R.; Blake, R.W.; Schwart, R.B.; Sudweeks, E.M. Economic Value of Days Open for Holstein Cows of Alternative Milk Yields with Varying Calving Intervals. J. Dairy Sci. 1984, 67, 636–643. [Google Scholar] [CrossRef]
  42. Schmidt, G. Effect of Length of Calving Intervals on Income over Feed and Variable Costs. J. Dairy Sci. 1989, 72, 1605–1611. [Google Scholar] [CrossRef]
  43. Lehmann, J.; Fadel, J.; Mogensen, L.; Kristensen, T.; Gaillard, C.; Kebreab, E. Effect of calving interval and parity on milk yield per feeding day in Danish commercial dairy herds. J. Dairy Sci. 2016, 99, 621–633. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Lv, W.L. Correct interpretation of DHI report. Today Anim. Husb. Vet. Med. 2014, 8, 53–55. [Google Scholar]
  45. Meikle, A.; Kulcsar, M.; Chilliard, Y.; Febel, H.; Delavaud, C.; Cavestany, D.; Chilibroste, P. Effects of parity and body condition at parturition on endocrine and reproductive parameters of the cow. Reproduction 2004, 127, 727–737. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  46. Baiyila, T. Analysis of 305d Milk Yield and Lactation Curve of Dairy Cows Born in Different Seasons; Inner Mongolia Agricultural University: Hohhot, China, 2018. [Google Scholar]
  47. Umphrey, J.; Moss, B.; Wilcox, C.; Van Horn, H. Interrelationships in Lactating Holsteins of Rectal and Skin Temperatures, Milk Yield and Composition, Dry Matter Intake, Body Weight, and Feed Efficiency in Summer in Alabama. J. Dairy Sci. 2001, 84, 2680–2685. [Google Scholar] [CrossRef]
  48. Liang, Y.; Zhang, Q.; Tang, C.; Guo, J.G.; Wang, M.Q.; Zhang, H.M.; Li, M.X.; Yang, Z.P.; Mao, Y.J. Analysis of factors af-fecting 305-days milking traits of Holstein cows. Chin. J. Anim. Sci. 2020, 56, 56–59. [Google Scholar] [CrossRef]
  49. Fang, Y.; Li, S.J.; Yu, W.L.; Zhong, R.Z. Management measures and nutrition regulation of high-yield dairy cows. Heilongjiang Anim. Sci. Vet. Med. 2006, 2, 9–11. [Google Scholar] [CrossRef]
  50. Wu, F.X.; Tong, J.J.; Zhang, H.; Fang, L.Y.; Xiong, B.H.; Jiang, L.S. Behavioral differences of different milk yield dairy cows and its correlation with lactation performance. Chin. J. Anim. Nutr. 2019, 31, 3156–3163. [Google Scholar] [CrossRef]
Vetsci 09 00188 g001 550
Figure 1. Lactation curves of Wood model for different dairy farm sizes.
Figure 1. Lactation curves of Wood model for different dairy farm sizes.
Vetsci 09 00188 g001
Vetsci 09 00188 g002 550
Figure 2. Lactation curves of Wood model for different parities.
Figure 2. Lactation curves of Wood model for different parities.
Vetsci 09 00188 g002
Vetsci 09 00188 g003 550
Figure 3. Lactation curves of Wood model for different calving seasons.
Figure 3. Lactation curves of Wood model for different calving seasons.
Vetsci 09 00188 g003
Vetsci 09 00188 g004 550
Figure 4. Lactation curves of Wood model for different calving intervals.
Figure 4. Lactation curves of Wood model for different calving intervals.
Vetsci 09 00188 g004
Vetsci 09 00188 g005 550
Figure 5. Lactation curves of Wood model for different 305-days milk yield.
Figure 5. Lactation curves of Wood model for different 305-days milk yield.
Vetsci 09 00188 g005
Table
Table 1. Ingredients and nutrient composition of the diet (dry matter basis).
Table 1. Ingredients and nutrient composition of the diet (dry matter basis).
ItemPercentage
Ingredient, % of DM
Alfalfa hay25.41
Corn silage28.40
Oat hay6.16
Ground corn17.48
Soybean meal5.26
Cottonseed meal4.06
Distillers dried grains with solubles5.31
Barely5.17
Limestone0.32
NaHCO30.36
NaCl0.31
CaHPO40.56
Premix1.20
Composition, % of DM
Crude protein15.02
Ether extract3.96
Neutral detergent fiber41.11
Acid detergent fiber22.04
Calcium0.82
Phosphorus0.42
NEL, 1 Mcal/kg6.29
The premix provided the following per kg of the concentrate: VA 300000 IU, VD 385000 IU, VE 1455 IU, nicotinic acid 550 mg, Cu 770 mg, Mn 930 mg, Fe 1200 mg, Zn 3600 mg, Se 21 mg, I 50 mg, Co 12 mg. 1 NEL was a calculated value according to NRC(2001), while the others were measured values.
Table
Table 2. Basic information of milk fat percentage data for dairy cows at each parity.
Table 2. Basic information of milk fat percentage data for dairy cows at each parity.
ParityNumberMeanStandard DeviationMinimumMaximum
1157,4833.760.371.026.93
2123,3403.850.391.116.99
369,0223.920.401.046.94
428,3153.940.391.136.83
520,2894.010.391.036.72
Total398,4493.900.391.016.98
Table
Table 3. Effects of different factors on milk fat percentage (LSM ± SE).
Table 3. Effects of different factors on milk fat percentage (LSM ± SE).
FactorNumberMilk Fat Percentage
Dairy farm size<100019,1893.84 ± 0.01 B
1000~200030,0203.59 ± 0.01 C
2001~500045,8533.93 ± 0.01 A
>5000303,3873.85 ± 0.00 B
F value 436.331 **
Parity1157,4833.76 ± 0.00 D
2123,3403.85 ± 0.00 C
369,0223.92 ± 0.00 B
428,3153.94 ± 0.01 B
520,2894.01 ± 0.01 A
F value 195.399 **
Calving seasonSpring46,2973.77 ± 0.00 D
Summer53,3023.81 ± 0.00 C
Autumn178,6393.88 ± 0.00 A
Winter120,2113.83 ± 0.00 B
F value 59.986 **
Calving interval (Days)300~36589,2593.88 ± 0.00 B
366~40057,7893.89 ± 0.00 AB
401~42018,5253.89 ± 0.01 AB
421~44012,5613.89 ± 0.01 AB
>44140,1543.90 ± 0.01 A
F value 129.525 **
305-days milk yield (kg)3000~500021804.07 ± 0.02 A
5001~700013,2764.04 ± 0.01 B
7001~900059,5893.93 ± 0.00 C
9001~11,000125,9813.84 ± 0.00 D
11,001~13,000102,6053.75 ± 0.00 E
13,001~15,00054,9603.74 ± 0.00 E
F value 382.315 **
In the same factor and column, the superscript does not contain the same capital letters to indicate that the difference is extremely significant (p < 0.01); the same letter means no significant difference (p > 0.05). ** indicated that the difference reached a highly significant level (p < 0.01).
Table
Table 4. Wood model fitting parameters of daily milk fat percentage by different factors.
Table 4. Wood model fitting parameters of daily milk fat percentage by different factors.
FactorabcTmin (month)Tmin (day)Ymin (%)Per.R2Residual Mean Squares
Dairy farm size<10004.10 ± 0.020.26 ± 0.010.06 ± 0.004.711423.563.650.97980.036
1000–20003.65 ± 0.020.30 ± 0.010.07 ± 0.004.211273.213.440.94830.084
2001–50003.96 ± 0.010.26 ± 0.010.06 ± 0.004.181263.553.510.95600.082
>50003.89 ± 0.010.21 ± 0.000.05 ± 0.004.081233.583.590.97370.047
Parity13.74 ± 0.010.21 ± 0.000.05 ± 0.003.891173.473.540.97100.050
23.89 ± 0.010.22 ± 0.000.05 ± 0.004.131243.553.580.96960.055
34.02 ± 0.010.24 ± 0.000.06 ± 0.004.291293.613.580.97010.055
43.99 ± 0.010.23 ± 0.010.06 ± 0.004.161253.623.560.96850.059
54.07 ± 0.020.19 ± 0.010.05 ± 0.004.221273.743.680.96950.058
Calving seasonSpring3.68 ± 0.010.31 ± 0.010.08 ± 0.003.651103.363.240.96740.057
Summer3.54 ± 0.010.11 ± 0.000.04 ± 0.002.86863.523.650.97160.050
Autumn3.95 ± 0.010.16 ± 0.000.03 ± 0.014.561373.653.910.97200.051
Winter4.07 ± 0.010.35 ± 0.000.08 ± 0.004.371323.463.410.96850.056
Calving interval (Days)300–3653.91 ± 0.010.22 ± 0.000.05 ± 0.004.151253.573.600.96910.056
366–4003.94 ± 0.010.22 ± 0.000.05 ± 0.004.131243.593.580.97040.054
401–4203.99 ± 0.020.26 ± 0.010.06 ± 0.004.261283.553.520.96880.057
421–4404.00 ± 0.020.28 ± 0.010.07 ± 0.004.161253.543.450.96910.057
>4413.95 ± 0.010.24 ± 0.010.06 ± 0.004.161253.563.530.96850.058
305-day milk yield (kg)3000–50003.62 ± 0.170.00 ± 0.070.02 ± 0.010.2793.654.220.97140.055
5001–70003.60 ± 0.060.05 ± 0.020.03 ± 0.001.81553.673.820.97340.050
7001–90003.57 ± 0.030.09 ± 0.010.03 ± 0.002.62793.583.680.97280.050
9001–11,0003.74 ± 0.030.17 ± 0.100.05 ± 0.003.78 1143.533.630.97130.051
11,001–13,0003.62 ± 0.040.18 ± 0.010.05 ± 0.003.661103.433.540.97070.051
>13,0004.14 ± 0.070.34 ± 0.020.07 ± 0.004.791443.433.550.96990.051
Total 3.89 ± 0.000.22 ± 0.000.05 ± 0.004.171263.543.590.96990.054
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhou, F.; Liang, Y.; Arbab, A.A.I.; Li, M.; Yang, Z.; Karrow, N.A.; Mao, Y. Analysis of Non-Genetic Factors Affecting Wood’s Model of Daily Milk Fat Percentage of Holstein Cattle. Vet. Sci. 2022, 9, 188. https://doi.org/10.3390/vetsci9040188

AMA Style

Zhou F, Liang Y, Arbab AAI, Li M, Yang Z, Karrow NA, Mao Y. Analysis of Non-Genetic Factors Affecting Wood’s Model of Daily Milk Fat Percentage of Holstein Cattle. Veterinary Sciences. 2022; 9(4):188. https://doi.org/10.3390/vetsci9040188

Chicago/Turabian Style

Zhou, Fuzhen, Yan Liang, Abdelaziz Adam Idriss Arbab, Mingxun Li, Zhangping Yang, Niel A. Karrow, and Yongjiang Mao. 2022. "Analysis of Non-Genetic Factors Affecting Wood’s Model of Daily Milk Fat Percentage of Holstein Cattle" Veterinary Sciences 9, no. 4: 188. https://doi.org/10.3390/vetsci9040188

APA Style

Zhou, F., Liang, Y., Arbab, A. A. I., Li, M., Yang, Z., Karrow, N. A., & Mao, Y. (2022). Analysis of Non-Genetic Factors Affecting Wood’s Model of Daily Milk Fat Percentage of Holstein Cattle. Veterinary Sciences, 9(4), 188. https://doi.org/10.3390/vetsci9040188

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop