MEF: Multidimensional Examination Framework for Prioritization of COVID-19 Severe Patients and Promote Precision Medicine Based on Hybrid Multi-Criteria Decision-Making Approaches
Abstract
:1. Introduction
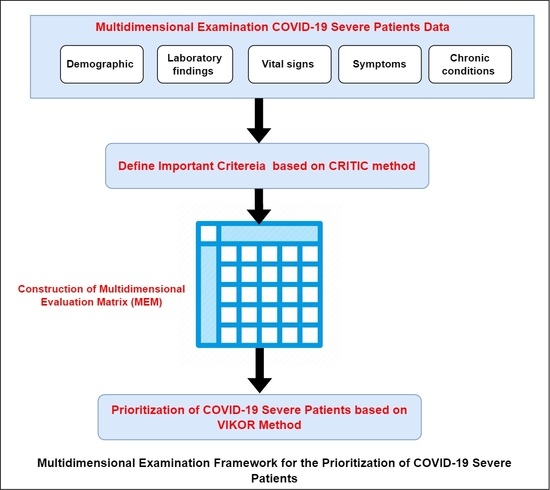
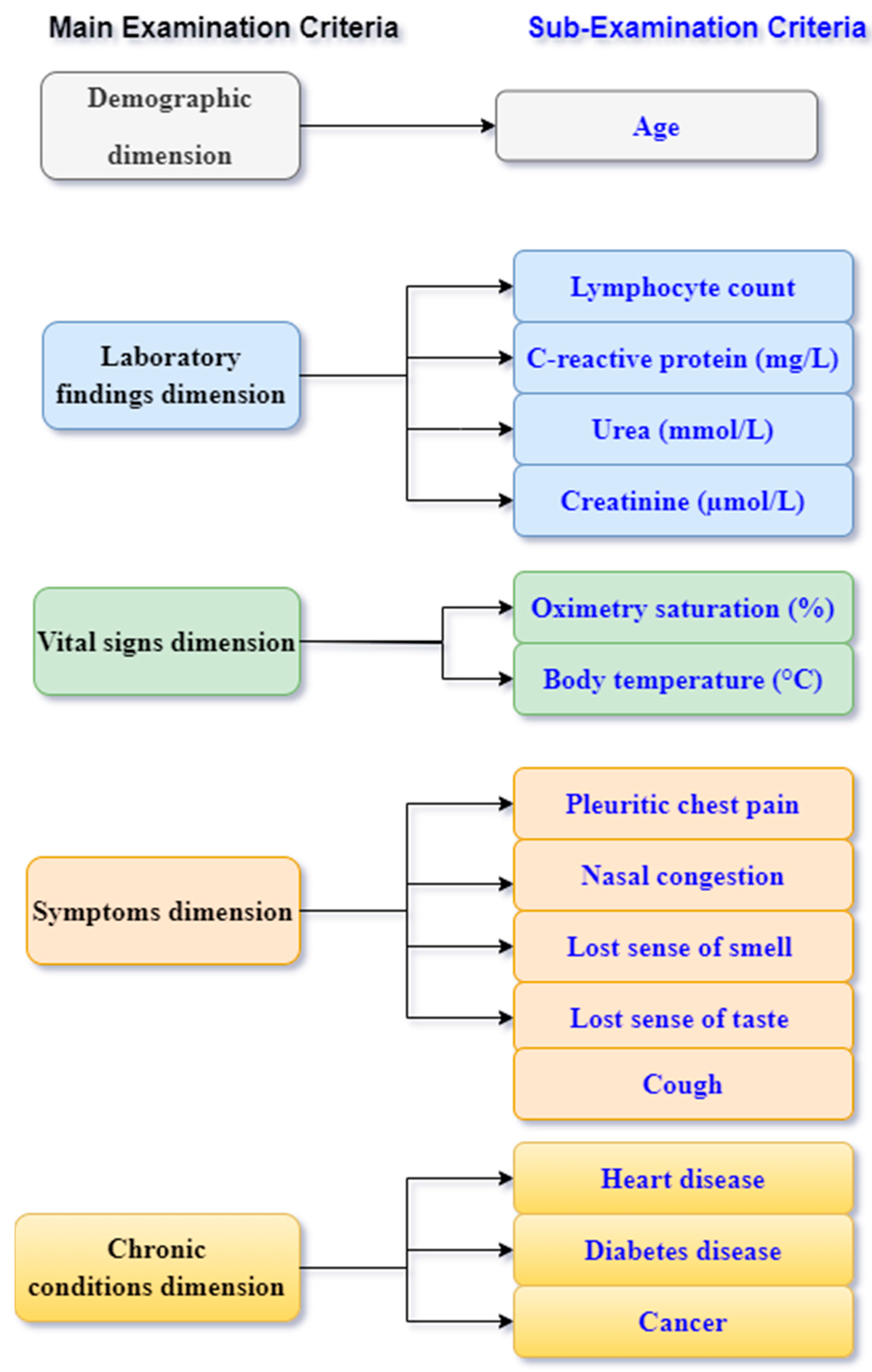
- Creation of a Multidimensional Evaluation Matrix (MEM) based on real data for different COVID-19 patients’ examination characteristics, such as demographic, laboratory findings, vital signs, symptoms, and chronic conditions.
- Based on multidimensional examination criteria and CRITIC (CRiteria Importance Through Intercriteria Correlation) approach, we provide an evaluation for the most examination criteria for sever COVID-19 patients.
- Develop a framework for prioritization of COVID-19 severe patients on the basis of the real data of constructed MEM and hybrid decision-making approaches (CRITIC and VIekriterijumsko KOmpromisno Rangiranje (VIKOR)). Therefore, we can help health authorities prioritize sever patients by considering the results of different examination criteria for patients infected with COVID-19 to provide the desired intensive care facilities and manage the health conditions of patients.
2. Related Works
- (a)
- Real data: With the spread of SARS-CoV-2 worldwide, understanding the basic epidemiological parameter values of COVID-19 from real-world data in mega-cities is essential for disease prevention and control [36]. Comparing them with other models depends on simulated data, which need more validation before being adopted [37].
- (b)
- (c)
- Multi-perspective (multidimensional): The identification of hospitalized COVID-19 patients at risk for severe deterioration can be performed by using risk scores that combine several factors, including age; sex; and comorbidities, i.e., diseases such as hypertension, diabetes, and cancer or tumor [40,41,42]. Some risk scores also include additional markers of severity, such as low level of oxygen in the blood, clinical symptoms, and biological factors reflecting multi-organ failures [42,43,44,45,46]. However, there are many unresolved interferences between these factors, including both clinical and biological markers [47]; therefore, there is a need for a comprehensive decision matrix that is inclusive of all of the markers mentioned earlier.
3. The Proposed Multidimensional Framework for COVID-19 Patients’ Prioritization
3.1. Construction of Multidimensional Evaluation Matrix (MEM)
3.2. Hybridization of CRITIC and VIKOR
3.2.1. Weighting of COVID-19 Examination Criteria Based on CRITIC Method
3.2.2. Ranking of COVID-19 Severe Patients Based on VIKOR Method
- C1. Acceptable advantage:
- 2.
- C2. Acceptable stability in decision-making:
4. Results and Discussions
4.1. MEM Results
4.2. CRITIC Weighting Results
4.3. Ranking Results based on VIKOR Method
5. Evaluation and Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Demographic | Laboratory Findings | Vital Signs | Symptoms | Chronic Conditions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patients | Age | Lymphocyte Count | C-reactive Protein | Urea | Creatinine | Oximetry Saturation | Body Temperature | Pleuritic Chest Pain | Nasal Congestion | Cough | Lost Sense of Smell | Lost Sense of Taste | Heart Disease | Diabetes Disease | Cancer |
| 1 | 0.703 | 0.287 | 0.5 | 0.162 | 0.069 | 0.432 | 0.512 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 2 | 1.000 | 0.550 | 1 | 0.277 | 0.106 | 0.750 | 0.756 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 3 | 0.797 | 0.248 | 1 | 0.050 | 0.023 | 0.636 | 0.878 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 4 | 0.676 | 0.364 | 1 | 0.032 | 0.032 | 0.318 | 1.000 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 5 | 0.568 | 0.132 | 1 | 0.068 | 0.028 | 0.250 | 0.756 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 6 | 0.743 | 0.264 | 1 | 1.000 | 1.000 | 0.659 | 0.756 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 7 | 0.838 | 0.147 | 1 | 0.201 | 0.042 | 0.864 | 1.000 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 8 | 0.892 | 0.287 | 1 | 0.284 | 0.134 | 1.000 | 1.000 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 0.635 | 0.628 | 1 | 0.101 | 0.069 | 0.273 | 0.512 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 10 | 0.595 | 0.837 | 1 | 0.061 | 0.005 | 0.705 | 0.756 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 11 | 0.635 | 0.612 | 1 | 0.097 | 0.012 | 0.636 | 0.659 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 12 | 0.878 | 0.000 | 1 | 0.237 | 0.014 | 0.386 | 0.268 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 13 | 0.635 | 0.116 | 1 | 0.036 | 0.014 | 0.341 | 0.756 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 14 | 0.338 | 0.031 | 0.5 | 0.014 | 0.005 | 0.295 | 0.268 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 15 | 0.284 | 0.008 | 0.5 | 0.036 | 0.009 | 0.205 | 0.268 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 16 | 0.338 | 0.372 | 1 | 0.050 | 0.014 | 0.432 | 0.756 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 17 | 0.432 | 0.039 | 0.5 | 0.058 | 0.014 | 0.341 | 0.268 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 18 | 0.973 | 0.008 | 1 | 0.230 | 0.074 | 0.273 | 0.756 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 19 | 0.635 | 0.132 | 1 | 0.104 | 0.032 | 0.455 | 0.512 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 20 | 0.905 | 0.008 | 1 | 0.237 | 0.083 | 0.545 | 0.756 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 21 | 0.568 | 1.000 | 0.5 | 0.068 | 0.028 | 0.182 | 0.268 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 22 | 0.905 | 0.798 | 1 | 0.086 | 0.032 | 0.432 | 0.512 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 23 | 0.568 | 0.186 | 0.5 | 0.014 | 0.000 | 0.136 | 0.268 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 24 | 0.635 | 0.078 | 0.5 | 0.086 | 0.032 | 0.341 | 0.756 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 25 | 0.595 | 0.233 | 0.5 | 0.025 | 0.009 | 0.273 | 0.268 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 26 | 0.500 | 0.295 | 0.5 | 0.036 | 0.019 | 0.205 | 0.268 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 27 | 0.770 | 0.256 | 0 | 0.004 | 0.009 | 0.386 | 0.268 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 28 | 0.568 | 0.109 | 0.5 | 0.068 | 0.028 | 0.159 | 0.512 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 29 | 0.635 | 0.124 | 0.5 | 0.007 | 0.007 | 0.250 | 0.512 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 30 | 0.446 | 0.078 | 0.5 | 0.032 | 0.006 | 0.318 | 0.634 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 31 | 0.297 | 0.101 | 0.5 | 0.043 | 0.009 | 0.205 | 0.268 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 32 | 0.324 | 0.054 | 0.5 | 0.058 | 0.010 | 0.750 | 0.512 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 33 | 0.703 | 0.062 | 0.5 | 0.011 | 0.000 | 0.432 | 0.268 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 34 | 0.297 | 0.054 | 0.5 | 0.004 | 0.005 | 0.364 | 0.756 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 35 | 0.392 | 0.047 | 0 | 0.058 | 0.009 | 0.250 | 0.268 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 36 | 0.838 | 0.070 | 0 | 0.104 | 0.028 | 0.409 | 0.512 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 37 | 0.432 | 0.031 | 0.5 | 0.054 | 0.019 | 0.295 | 0.878 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 38 | 0.230 | 0.132 | 0.5 | 0.061 | 0.023 | 0.205 | 0.268 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 39 | 0.297 | 0.070 | 0.5 | 0.083 | 0.019 | 0.250 | 0.268 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 40 | 0.703 | 0.062 | 0 | 0.054 | 0.009 | 0.432 | 0.512 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 41 | 0.581 | 0.062 | 0.5 | 0.104 | 0.023 | 0.227 | 0.268 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 42 | 0.608 | 0.031 | 0 | 0.155 | 0.009 | 0.409 | 0.756 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 43 | 0.595 | 0.101 | 0.5 | 0.061 | 0.014 | 0.250 | 0.512 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 44 | 0.230 | 0.062 | 0.5 | 0.032 | 0.014 | 0.273 | 0.634 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 45 | 0.446 | 0.047 | 0.5 | 0.065 | 0.019 | 0.205 | 0.634 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 46 | 0.365 | 0.039 | 0.5 | 0.025 | 0.005 | 0.227 | 0.268 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 47 | 0.297 | 0.093 | 0.5 | 0.061 | 0.012 | 0.295 | 0.268 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 48 | 0.635 | 0.101 | 0.5 | 0.043 | 0.000 | 0.318 | 0.756 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 49 | 0.703 | 0.140 | 0.5 | 0.129 | 0.026 | 0.182 | 0.268 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 50 | 0.635 | 0.039 | 0 | 0.032 | 0.019 | 0.205 | 0.512 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 51 | 0.419 | 0.109 | 0.5 | 0.043 | 0.028 | 0.205 | 0.390 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 52 | 0.703 | 0.186 | 0 | 0.086 | 0.023 | 0.159 | 0.512 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 53 | 0.541 | 0.233 | 0.5 | 0.097 | 0.046 | 0.227 | 0.512 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 54 | 0.581 | 0.287 | 0 | 0.029 | 0.032 | 0.250 | 0.268 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 55 | 0.486 | 0.256 | 0 | 0.058 | 0.019 | 0.205 | 0.463 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 56 | 0.608 | 0.194 | 0 | 0.101 | 0.028 | 0.136 | 0.439 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 57 | 0.649 | 0.225 | 0.5 | 0.086 | 0.042 | 0.182 | 0.561 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 58 | 0.730 | 0.062 | 0 | 0.115 | 0.074 | 0.250 | 0.512 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 59 | 0.784 | 0.031 | 0.5 | 0.248 | 0.120 | 0.364 | 0.512 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 60 | 0.365 | 0.248 | 0 | 0.022 | 0.014 | 0.091 | 0.268 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 61 | 0.824 | 0.043 | 0 | 0.133 | 0.028 | 0.205 | 0.512 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 62 | 0.716 | 0.074 | 0 | 0.108 | 0.028 | 0.318 | 0.512 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 63 | 0.703 | 0.054 | 0 | 0.079 | 0.019 | 0.205 | 0.512 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 64 | 0.189 | 0.031 | 0 | 0.029 | 0.005 | 0.023 | 0.268 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 65 | 0.432 | 0.140 | 0 | 0.014 | 0.009 | 0.114 | 0.268 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 66 | 0.162 | 0.039 | 0 | 0.018 | 0.000 | 0.114 | 0.268 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 67 | 0.500 | 0.070 | 0 | 0.054 | 0.005 | 0.000 | 0.634 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 68 | 0.905 | 0.047 | 0 | 0.022 | 0.023 | 0.250 | 0.512 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 69 | 0.568 | 0.039 | 0 | 0.094 | 0.023 | 0.182 | 0.024 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 70 | 0.095 | 0.039 | 0 | 0.011 | 0.019 | 0.068 | 0.439 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 71 | 0.041 | 0.674 | 0 | 0.000 | 0.030 | 0.068 | 0.000 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 72 | 0.270 | 0.240 | 0 | 0.043 | 0.037 | 0.023 | 0.024 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 73 | 0.297 | 0.287 | 0 | 0.050 | 0.042 | 0.000 | 0.024 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 74 | 0.176 | 0.178 | 0 | 0.018 | 0.023 | 0.091 | 0.512 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 75 | 0.378 | 0.217 | 0 | 0.000 | 0.023 | 0.091 | 0.463 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 76 | 0.446 | 0.295 | 0 | 0.086 | 0.042 | 0.114 | 0.512 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 77 | 0.000 | 0.225 | 0 | 0.043 | 0.028 | 0.000 | 0.512 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 78 | 0.122 | 0.085 | 0 | 0.029 | 0.029 | 0.045 | 0.512 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| Sigma (standard deviation) | 0.232 | 0.201 | 0.382 | 0.123 | 0.113 | 0.199 | 0.231 | 0.502 | 0.497 | 0.495 | 0.288 | 0.268 | 0.502 | 0.439 | 0.247 |
Appendix B
| Age | Lymphocyte Count | C-reactive Protein | Urea | Creatinine | Oximetry Saturation | Body Temperature | Pleuritic Chest Pain | Nasal Congestion | Cough | Lost Sense of Smell | Lost Sense of Taste | Heart Disease | Diabetes Disease | Cancer | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age | 1.000 | 0.091 | 0.397 | 0.419 | 0.199 | −0.558 | 0.425 | 0.471 | 0.318 | 0.101 | 0.055 | −0.133 | 0.512 | 0.378 | 0.310 |
| Lymphocyte count | 0.091 | 1.000 | 0.371 | 0.044 | 0.084 | −0.189 | 0.028 | 0.066 | −0.038 | 0.125 | 0.003 | 0.150 | 0.008 | 0.378 | 0.218 |
| C-reactive protein | 0.397 | 0.285 | 1.000 | 0.362 | 0.232 | −0.652 | 0.508 | 0.339 | 0.325 | 0.195 | 0.227 | 0.127 | 0.204 | 0.245 | 0.334 |
| Urea | 0.419 | 0.044 | 0.362 | 1.000 | 0.919 | −0.457 | 0.306 | 0.257 | 0.271 | 0.171 | 0.088 | 0.060 | 0.091 | 0.363 | 0.630 |
| Creatinine | 0.199 | 0.084 | 0.232 | 0.919 | 1.000 | 0.284 | 0.199 | 0.166 | 0.197 | 0.131 | 0.050 | 0.050 | −0.064 | 0.284 | 0.548 |
| Oximetry saturation | 0.558 | 0.189 | 0.652 | 0.457 | 0.284 | 1.000 | 0.584 | 0.374 | 0.359 | 0.169 | 0.187 | 0.097 | 0.210 | 0.194 | 0.518 |
| Body temperature | 0.425 | 0.028 | 0.508 | 0.306 | 0.199 | 0.584 | 1.000 | 0.401 | 0.277 | 0.069 | 0.158 | 0.093 | 0.196 | 0.239 | 0.288 |
| Pleuritic chest pain | 0.471 | 0.066 | 0.339 | 0.257 | 0.166 | 0.374 | 0.401 | 1.000 | 0.116 | 0.221 | 0.159 | 0.119 | 0.290 | 0.249 | 0.242 |
| Nasal congestion | 0.318 | −0.038 | 0.325 | 0.271 | 0.197 | 0.359 | 0.277 | 0.116 | 1.000 | −0.024 | −0.003 | −0.045 | 0.248 | 0.270 | 0.200 |
| Cough | 0.101 | 0.125 | 0.195 | 0.171 | 0.131 | 0.169 | 0.069 | 0.221 | −0.024 | 1.000 | −0.003 | −0.045 | 0.248 | 0.270 | 0.200 |
| Lost sense of smell | 0.055 | 0.003 | 0.227 | 0.088 | 0.050 | 0.187 | 0.158 | 0.159 | −0.003 | 0.285 | 1.000 | 0.150 | 0.040 | 0.132 | 0.218 |
| Lost sense of taste | −0.133 | 0.150 | 0.127 | 0.060 | 0.050 | 0.097 | 0.093 | 0.119 | −0.045 | 0.150 | 0.751 | 1.000 | −0.159 | −0.021 | 0.082 |
| Heart Disease | 0.512 | 0.008 | 0.204 | 0.091 | −0.064 | 0.210 | 0.196 | 0.290 | 0.248 | 0.040 | −0.159 | −0.215 | 1.000 | −0.051 | 0.076 |
| Diabetes Disease | 0.378 | 0.378 | 0.245 | 0.363 | 0.284 | 0.194 | 0.239 | 0.249 | 0.270 | 0.132 | −0.021 | −0.051 | 0.399 | 1.000 | 0.073 |
| Cancer | 0.310 | 0.218 | 0.334 | 0.630 | 0.548 | 0.518 | 0.288 | 0.242 | 0.200 | 0.218 | 0.082 | 0.076 | 0.073 | 0.206 | 1.000 |
Appendix C
| Medical Source | Sigma | Sum | Cj |
|---|---|---|---|
| Age | 0.232 | 11.015 | 2.550 |
| Lymphocyte count | 0.201 | 13.032 | 2.621 |
| C-reactive protein | 0.382 | 10.873 | 4.148 |
| Urea | 0.123 | 10.475 | 1.293 |
| Creatinine | 0.113 | 10.721 | 1.213 |
| Oximetry saturation | 0.199 | 9.167 | 1.827 |
| Body temperature | 0.231 | 10.229 | 2.359 |
| Pleuritic chest pain | 0.502 | 10.530 | 5.284 |
| Nasal congestion | 0.497 | 11.529 | 5.733 |
| Cough | 0.495 | 12.173 | 6.027 |
| Lost sense of smell | 0.288 | 12.251 | 3.524 |
| Lost sense of taste | 0.268 | 12.678 | 3.400 |
| Heart Disease | 0.502 | 12.615 | 6.329 |
| Diabetes Disease | 0.439 | 10.867 | 4.776 |
| Cancer | 0.247 | 10.059 | 2.480 |
| Sum | 53.564 |
References
- Mohammed, M.A.; Al-Khateeb, B.; Yousif, M.; Mostafa, S.A.; Kadry, S.; Abdulkareem, K.H.; Garcia-Zapirain, B. Novel Crow Swarm Optimization Algorithm and Selection Approach for Optimal Deep Learning COVID-19 Diagnostic Model. Comput. Intell. Neurosci. 2022, 2022, 1307944. [Google Scholar] [CrossRef]
- Saeed, M.; Ahsan, M.; Saeed, M.H.; Rahman, A.U.; Mehmood, A.; Mohammed, M.A.; Jaber, M.M.; Damaševičius, R. An Optimized Decision Support Model for COVID-19 Diagnostics Based on Complex Fuzzy Hypersoft Mapping. Mathematics 2022, 10, 2472. [Google Scholar] [CrossRef]
- Allioui, H.; Mohammed, M.A.; Benameur, N.; Al-Khateeb, B.; Abdulkareem, K.H.; Garcia-Zapirain, B.; Damaševičius, R.; Maskeliūnas, R. A Multi-Agent Deep Reinforcement Learning Approach for Enhancement of COVID-19 CT Image Segmentation. J. Pers. Med. 2022, 12, 309. [Google Scholar] [CrossRef] [PubMed]
- Albahli, S.; Algsham, A.; Aeraj, S.; Alsaeed, M.; Alrashed, M.; Rauf, H.T.; Arif, M.; Mohammed, M.A. COVID-19 Public Sentiment Insights: A Text Mining Approach to the Gulf Countries. Comput. Mater. Contin. 2021, 67, 1613–1627. [Google Scholar] [CrossRef]
- Harun, M.A.A.; Hossain, M.M.; Bari, M.A.; Rubel, N.A.S.; Karim, M.E.; Siddiquee, N.; Hossain, M.D.; Sultana, F.; Taous, A.; Islam, A.K.M.M.; et al. Pulse Oximetry Is Essential in Home Management of Elderly COVID-19 Patients. Bangladesh J. Otorhinolaryngol. 2020, 26, 55–67. [Google Scholar] [CrossRef]
- Chavez, S.; Long, B.; Koyfman, A.; Liang, S.Y. Coronavirus Disease (COVID-19): A Primer for Emergency Physicians. Am. J. Emerg. Med. 2021, 44, 220–229. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, Y.; Liu, X.; Tan, J. The Impact of the COVID-19 Epidemic on the Utilization of Emergency Dental Services. J. Dent. Sci. 2020, 15, 564–567. [Google Scholar] [CrossRef]
- Dinar, A.M.; Raheem, E.A.; Abdulkareem, K.H.; Mohammed, M.A.; Oleiwie, M.G.; Zayr, F.H.; Al-Boridi, O.; Al-Mhiqani, M.N.; Al-Andoli, M.N. Towards Automated Multiclass Severity Prediction Approach for COVID-19 Infections Based on Combinations of Clinical Data. Mob. Inf. Syst. 2022, 2022, 7675925. [Google Scholar] [CrossRef]
- Chen, N.; Zhou, M.; Dong, X.; Qu, J.; Gong, F.; Han, Y.; Qiu, Y.; Wang, J.; Liu, Y.; Wei, Y.; et al. Epidemiological and Clinical Characteristics of 99 Cases of 2019 Novel Coronavirus Pneumonia in Wuhan, China: A Descriptive Study. Lancet 2020, 395, 507–513. [Google Scholar] [CrossRef]
- Dong, E.; Du, H.; Gardner, L. An Interactive Web-Based Dashboard to Track COVID-19 in Real Time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Bai, Y.; Yao, L.; Wei, T.; Tian, F.; Jin, D.-Y.; Chen, L.; Wang, M. Presumed Asymptomatic Carrier Transmission of COVID-19. JAMA 2020, 323, 1406–1407. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical Features of Patients Infected with 2019 Novel Coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Montgomery, A.A.; Fahey, T. How Do Patients’ Treatment Preferences Compare with Those of Clinicians? Qual. Heal. Care 2001, 10, i39–i43. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.N.; Hultman, C.S.; Sepucha, K. Do Patients and Providers Agree About the Most Important Facts and Goals for Breast Reconstruction Decisions? Ann. Plast. Surg. 2010, 64, 563–566. [Google Scholar] [CrossRef] [PubMed]
- Petrilli, C.M.; Jones, S.A.; Yang, J.; Rajagopalan, H.; O’Donnell, L.; Chernyak, Y.; Tobin, K.A.; Cerfolio, R.J.; Francois, F.; Horwitz, L.I. Factors Associated with Hospital Admission and Critical Illness among 5279 People with Coronavirus Disease 2019 in New York City: Prospective Cohort Study. BMJ 2020, 369, m1966. [Google Scholar] [CrossRef]
- Jin, X.; Pang, B.; Zhang, J.; Liu, Q.; Yang, Z.; Feng, J.; Liu, X.; Zhang, L.; Wang, B.; Huang, Y.; et al. Core Outcome Set for Clinical Trials on Coronavirus Disease 2019 (COS-COVID). Engineering 2020, 6, 1147–1152. [Google Scholar] [CrossRef]
- Quiroz, J.C.; Feng, Y.-Z.; Cheng, Z.-Y.; Rezazadegan, D.; Chen, P.-K.; Lin, Q.-T.; Qian, L.; Liu, X.-F.; Berkovsky, S.; Coiera, E.; et al. Development and Validation of a Machine Learning Approach for Automated Severity Assessment of COVID-19 Based on Clinical and Imaging Data: Retrospective Study. JMIR Med. Inf. 2021, 9, e24572. [Google Scholar] [CrossRef]
- Albahri, A.S.; Al-Obaidi, J.R.; Zaidan, A.A.; Albahri, O.S.; Hamid, R.A.; Zaidan, B.B.; Alamoodi, A.H.; Hashim, M. Multi-Biological Laboratory Examination Framework for the Prioritization of Patients with COVID-19 Based on Integrated AHP and Group VIKOR Methods. Int. J. Inf. Technol. Decis. Mak. 2020, 19, 1247–1269. [Google Scholar] [CrossRef]
- Mohammed, R.T.; Zaidan, A.A.; Yaakob, R.; Sharef, N.M.; Abdullah, R.H.; Zaidan, B.B.; Albahri, O.S.; Abdulkareem, K.H. Determining Importance of Many-Objective Optimisation Competitive Algorithms Evaluation Criteria Based on a Novel Fuzzy-Weighted Zero-Inconsistency Method. Int. J. Inf. Technol. Decis. Mak. 2021, 21, 195–241. [Google Scholar] [CrossRef]
- Albahri, A.S.; Hamid, R.A.; Albahri, O.S.; Zaidan, A.A. Detection-Based Prioritisation: Framework of Multi-Laboratory Characteristics for Asymptomatic COVID-19 Carriers Based on Integrated Entropy–TOPSIS Methods. Artif. Intell. Med. 2021, 111, 101983. [Google Scholar] [CrossRef]
- Al-Mhiqani, M.N.; Ahmad, R.; Abidin, Z.Z.; Abdulkareem, K.H.; Mohammed, M.A.; Gupta, D.; Shankar, K. A New Intelligent Multilayer Framework for Insider Threat Detection. Comput. Electr. Eng. 2022, 97, 1075977. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.-H. Compromise Solution by MCDM Methods: A Comparative Analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.-H. Extended VIKOR Method in Comparison with Outranking Methods. Eur. J. Oper. Res. 2007, 178, 514–529. [Google Scholar] [CrossRef]
- Mohammed, M.A.; Abdulkareem, K.H.; Al-Waisy, A.S.; Mostafa, S.A.; Al-Fahdawi, S.; Dinar, A.M.; Alhakami, W.; BAZ, A.; Al-Mhiqani, M.N.; Alhakami, H.; et al. Benchmarking Methodology for Selection of Optimal COVID-19 Diagnostic Model Based on Entropy and TOPSIS Methods. IEEE Access 2020, 8, 99115–99131. [Google Scholar] [CrossRef]
- Žižović, M.; Pamucar, D.; Miljković, B.; Karan, A. Multiple-Criteria Evaluation Model for Medical Professionals Assigned to Temporary SARS-CoV-2 Hospitals. Decis. Mak. Appl. Manag. Eng. 2021, 4, 153–173. [Google Scholar] [CrossRef]
- May, R.M. Uses and Abuses of Mathematics in Biology. Science 2004, 303, 790–793. [Google Scholar] [CrossRef]
- Ghosh, I.; Datta Chaudhuri, T. FEB-Stacking and FEB-DNN Models for Stock Trend Prediction: A Performance Analysis for Pre and Post Covid-19 Periods. Decis. Mak. Appl. Manag. Eng. 2021, 4, 51–84. [Google Scholar] [CrossRef]
- Kayapinar Kaya, S. Evaluation of the Effect of COVID-19 on Countries’ Sustainable Development Level: A Comparative MCDM Framework. Oper. Res. Eng. Sci. Theory Appl. 2020, 3, 101–122. [Google Scholar] [CrossRef]
- Emanuel, E.J.; Persad, G.; Upshur, R.; Thome, B.; Parker, M.; Glickman, A.; Zhang, C.; Boyle, C.; Smith, M.; Phillips, J.P. Fair Allocation of Scarce Medical Resources in the Time of COVID-19. N. Engl. J. Med. 2020, 382, 2049–2055. [Google Scholar] [CrossRef]
- Özkan, B.; Özceylan, E.; Kabak, M.; Dikmen, A.U. Evaluation of Criteria and COVID-19 Patients for Intensive Care Unit Admission in the Era of Pandemic: A Multi-Criteria Decision Making Approach. Comput. Methods Programs Biomed. 2021, 209, 106348. [Google Scholar] [CrossRef]
- Parsons, L.M.; Ákos, S.; Cristina, G.; Evan, L.; Paramasivan, C.N.; Alash’le, A.; Steven, S.; Giorgio, R.; John, N. Laboratory Diagnosis of Tuberculosis in Resource-Poor Countries: Challenges and Opportunities. Clin. Microbiol. Rev. 2011, 24, 314–350. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Guo, J.; Wang, C.; Luo, F.; Yu, X.; Zhang, W.; Li, J.; Zhao, D.; Xu, D.; Gong, Q.; et al. Clinical Characteristics and Intrauterine Vertical Transmission Potential of COVID-19 Infection in Nine Pregnant Women: A Retrospective Review of Medical Records. Lancet 2020, 395, 809–815. [Google Scholar] [CrossRef]
- Abdel-Basst, M.; Mohamed, R.; Elhoseny, M. A Model for the Effective COVID-19 Identification in Uncertainty Environment Using Primary Symptoms and CT Scans. Health Inform. J. 2020, 26, 3088–3105. [Google Scholar] [CrossRef]
- Majumder, P.; Biswas, P.; Majumder, S. Application of New Topsis Approach to Identify the Most Significant Risk Factor and Continuous Monitoring of Death of COVID-19. Electron. J. Gen. Med. 2020, 17, em234. [Google Scholar] [CrossRef]
- Singh, R.; Avikal, S. COVID-19: A Decision-Making Approach for Prioritization of Preventive Activities. Int. J. Healthc. Manag. 2020, 13, 257–262. [Google Scholar] [CrossRef]
- Wang, X.; Pan, Y.; Zhang, D.; Chen, L.; Jia, L.; Li, X.; Yang, P.; Wang, Q.; Macintyre, C.R. Basic Epidemiological Parameter Values from Data of Real-World in Mega-Cities: The Characteristics of COVID-19 in Beijing, China. BMC Infect. Dis. 2020, 20, 526. [Google Scholar] [CrossRef] [PubMed]
- Artigaud, S.; Gauthier, O.; Pichereau, V. Identifying Differentially Expressed Proteins in Two-Dimensional Electrophoresis Experiments: Inputs from Transcriptomics Statistical Tools. Bioinformatics 2013, 29, 2729–2734. [Google Scholar] [CrossRef]
- Hodges, G.; Pallisgaard, J.; Schjerning Olsen, A.-M.; McGettigan, P.; Andersen, M.; Krogager, M.; Kragholm, K.; Køber, L.; Gislason, G.H.; Torp-Pedersen, C.; et al. Association between Biomarkers and COVID-19 Severity and Mortality: A Nationwide Danish Cohort Study. BMJ Open 2020, 10, e041295. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Shah, N.; Mushtaq, H.; Jehanzeb, V. Profiling Laboratory Biomarkers Associated with COVID-19 Disease Progression: A Single-Center Experience. Int. J. Microbiol. 2021, 2021, 6643333. [Google Scholar] [CrossRef]
- Liang, W.; Liang, H.; Ou, L.; Chen, B.; Chen, A.; Li, C.; Li, Y.; Guan, W.; Sang, L.; Lu, J.; et al. Development and Validation of a Clinical Risk Score to Predict the Occurrence of Critical Illness in Hospitalized Patients With COVID-19. JAMA Intern. Med. 2020, 180, 1081–1089. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, H.-T.; Goncalves, J.; Xiao, Y.; Wang, M.; Guo, Y.; Sun, C.; Tang, X.; Jing, L.; Zhang, M.; et al. An Interpretable Mortality Prediction Model for COVID-19 Patients. Nat. Mach. Intell. 2020, 2, 283–288. [Google Scholar] [CrossRef]
- Levy, T.J.; Richardson, S.; Coppa, K.; Barnaby, D.P.; McGinn, T.; Becker, L.B.; Davidson, K.W.; Cohen, S.L.; Hirsch, J.S.; Zanos, T.P.; et al. Development and Validation of a Survival Calculator for Hospitalized Patients with COVID-19. medRxiv 2020. preprint. [Google Scholar] [CrossRef]
- Mejía-Vilet, J.M.; Córdova-Sánchez, B.M.; Fernández-Camargo, D.A.; Méndez-Pérez, R.A.; Morales-Buenrostro, L.E.; Hernández-Gilsoul, T. A Risk Score to Predict Admission to the Intensive Care Unit in Patients with COVID-19: The ABC-GOALS Score. Salud Publica Mex. 2020, 63, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Covassin, N.; Fan, Z.; Singh, P.; Gao, W.; Li, G.; Kara, T.; Somers, V.K. Association Between Hypoxemia and Mortality in Patients With COVID-19. Mayo Clin. Proc. 2020, 95, 1138–1147. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical Course and Risk Factors for Mortality of Adult Inpatients with COVID-19 in Wuhan, China: A Retrospective Cohort Study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Lippi, G.; Plebani, M. Laboratory Abnormalities in Patients with COVID-2019 Infection. Clin. Chem. Lab. Med. (CCLM) 2020, 58, 1131–1134. [Google Scholar] [CrossRef] [PubMed]
- Lassau, N.; Ammari, S.; Chouzenoux, E.; Gortais, H.; Herent, P.; Devilder, M.; Soliman, S.; Meyrignac, O.; Talabard, M.-P.; Lamarque, J.-P.; et al. Integrating Deep Learning CT-Scan Model, Biological and Clinical Variables to Predict Severity of COVID-19 Patients. Nat. Commun. 2021, 12, 634. [Google Scholar] [CrossRef]
- Hameed Abdulkareem, K.; Awad Mutlag, A.; Musa Dinar, A.; Frnda, J.; Abed Mohammed, M.; Hasan Zayr, F.; Lakhan, A.; Kadry, S.; Ali Khattak, H.; Nedoma, J. Smart Healthcare System for Severity Prediction and Critical Tasks Management of COVID-19 Patients in IoT-Fog Computing Environments. Comput. Intell. Neurosci. 2022, 2022, 5012962. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining Objective Weights in Multiple Criteria Problems: The Critic Method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Jahan, A.; Mustapha, F.; Sapuan, S.M.; Ismail, M.Y.; Bahraminasab, M. A Framework for Weighting of Criteria in Ranking Stage of Material Selection Process. Int. J. Adv. Manuf. Technol. 2012, 58, 411–420. [Google Scholar] [CrossRef]
- Saaty, T.L.; Ergu, D. When Is a Decision-Making Method Trustworthy? Criteria for Evaluating Multi-Criteria Decision-Making Methods. Int. J. Inf. Technol. Decis. Mak. 2015, 14, 1171–1187. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable Supplier Selection in Healthcare Industries Using a New MCDM Method: Measurement of Alternatives and Ranking According to COmpromise Solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Mukhametzyanov, I.; Pamucar, D. A Sensitivity Analysis in MCDM Problems: A Statistical Approach. Decis. Mak. Appl. Manag. Eng. 2018, 1, 51–80. [Google Scholar] [CrossRef]
- Stewart, T.J.; French, S.; Rios, J. Integrating Multicriteria Decision Analysis and Scenario Planning—Review and Extension. Omega 2013, 41, 679–688. [Google Scholar] [CrossRef]
- Pamucar, D.; Yazdani, M.; Montero-Simo, M.J.; Araque-Padilla, R.A.; Mohammed, A. Multi-Criteria Decision Analysis towards Robust Service Quality Measurement. Expert Syst. Appl. 2021, 170, 114508. [Google Scholar] [CrossRef]
- Zhao, H.; Li, N. Optimal Siting of Charging Stations for Electric Vehicles Based on Fuzzy Delphi and Hybrid Multi-Criteria Decision Making Approaches from an Extended Sustainability Perspective. Energies 2016, 9, 270. [Google Scholar] [CrossRef] [Green Version]




| Ref. | Aim of the Study | Case Study | Criteria Used | Multidimensional |
|---|---|---|---|---|
| [33] | Differentiate between COVID-19 and other four viral chest diseases under uncertain environment using the viruses primary symptoms and CT scans | Based on other cases studies | Primary symptoms and CT scans | No |
| [18] | COVID-19 patient prioritization dependent on their health conditions | Real data of 6 patients from the literature | Laboratory characteristics | No |
| [20] | Prioritization of asymptomatic carriers | Real data from the literature were extended to 56, using simulated data | Laboratory characteristics | No |
| [24] | Benchmarking Methodology for Selection of Optimal COVID-19 Diagnostic Model | Real data (publicly available) | CT scans data | No |
| [34] | Identify and select the significant risk factor and continuous monitoring of death due to COVID-19 | Real data (publicly available) | Confirmed and death cases number of COVID-19 | No |
| [35] | Identify some of the suggested activities not to be performed during the pandemic period | Real data (publicly available) | WHO Guidelines | No |
| Proposed | COVID-19 patient prioritization based on multidimensional criteria | Real data of 78 patients (self-collected or own dataset) | (General factors and comorbidities), (multi-clinical characteristics with SpO2 sensor) and (multi-biological characteristics) | Yes |
| Demographic | Laboratory Findings | Vital Signs | Symptoms | Chronic Conditions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patients | Age | Lymphocyte Count | C-reactive Protein (mg/L) | Urea (mmol/L) | Creatinine (µmol/L) | Oximetry Saturation (%) | Body Temperature (°C) | Pleuritic Chest Pain | Nasal Congestion | Cough | Lost Sense of Smell (1/0) | Lost Sense of Taste (1/0) | Heart Disease | Diabetes Disease | Cancer |
| P1 | AV (P1/Ts) | LCV (P1/Ts) | CrPV (P1/Ts) | UrV (P1/Ts) | CrV (P1/Ts) | OSV (P1/Ts) | BTV (P1/Ts) | PCPV (P1/Ts) | NCV (P1/Ts) | CoV (P1/Ts) | LSV (P1/Ts) | LTV (P1/Ts) | HDV (P1/Ts) | DDV (P1/Ts) | CaV (P1/Ts) |
| P2 | AV (P2/Ts) | LCV (P2/Ts) | CrPV (P2/Ts) | UrV (P2/Ts) | CrV (P2/Ts) | OSV (P2/Ts) | BTV (P2/Ts) | PCPV (P2/Ts) | NCV (P2/Ts) | CoV (P2/Ts) | LSV (P2/Ts) | LTV (P2/Ts) | HDV (P2/Ts) | DDV (P2/Ts) | CaV (P2/Ts) |
| P3 | AV (P3/Ts) | LCV (P3/Ts) | CrPV (P3/Ts) | UrV (P3/Ts) | CrV (P3/Ts) | OSV (P3/Ts) | BTV (P3/Ts) | PCPV (P3/Ts) | NCV (P3/Ts) | CoV (P3/Ts) | LSV (P3/Ts) | LTV (P3/Ts) | HDV (P3/Ts) | DDV (P3/Ts) | CaV (P3/Ts) |
| ..…. | …… | …… | …… | …… | …… | …… | …… | …… | …… | …… | …… | …… | …… | …… | …… |
| Pn | AV (Pn/Ts) | LCV (Pn/Ts) | CrPV (Pn/Ts) | UrV (Pn/Ts) | CrV (Pn/Ts) | OSV (Pn/Ts) | BTV (Pn/Ts) | PCPV (Pn/Ts) | NCV (Pn/Ts) | CoV (Pn/Ts) | LSV (Pn/Ts) | LTV (Pn/Ts) | HDV (Pn/Ts) | DDV (Pn/Ts) | CaV (Pn/Ts) |
| Demographic | Laboratory Findings | Vital Signs | Symptoms | Chronic Conditions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patients | Age | Lymphocyte Count | C-reactive Protein | Urea | Creatinine | Oximetry Saturation | Body Temperature | Pleuritic Chest Pain | Nasal Congestion | Cough | Lost Sense of Smell | Lost Sense of Taste | Heart Disease | Diabetes Disease | Cancer |
| 1 | 65 | 4.1 | 1 | 66 | 1.8 | 80 | 38 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 2 | 87 | 7.5 | 2 | 98 | 2.6 | 66 | 39 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 3 | 72 | 3.6 | 2 | 35 | 0.8 | 71 | 39.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 4 | 63 | 5.1 | 2 | 30 | 1 | 85 | 40 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 5 | 55 | 2.1 | 2 | 40 | 0.9 | 88 | 39 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 6 | 68 | 3.8 | 2 | 299 | 21.9 | 70 | 39 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 7 | 75 | 2.3 | 2 | 77 | 1.2 | 61 | 40 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 8 | 79 | 4.1 | 2 | 100 | 3.2 | 55 | 40 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 60 | 8.5 | 2 | 49 | 1.8 | 87 | 38 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 10 | 57 | 11.2 | 2 | 38 | 0.4 | 68 | 39 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 11 | 60 | 8.3 | 2 | 48 | 0.56 | 71 | 38.6 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 12 | 78 | 0.4 | 2 | 87 | 0.6 | 82 | 37 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 13 | 60 | 1.9 | 2 | 31 | 0.6 | 84 | 39 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 14 | 38 | 0.8 | 1 | 25 | 0.4 | 86 | 37 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 15 | 34 | 0.5 | 1 | 31 | 0.5 | 90 | 37 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 16 | 38 | 5.2 | 2 | 35 | 0.6 | 80 | 39 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 17 | 45 | 0.9 | 1 | 37 | 0.6 | 84 | 37 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 18 | 85 | 0.5 | 2 | 85 | 1.9 | 87 | 39 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 19 | 60 | 2.1 | 2 | 50 | 1 | 79 | 38 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 20 | 80 | 0.5 | 2 | 87 | 2.1 | 75 | 39 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 21 | 55 | 13.3 | 1 | 40 | 0.9 | 91 | 37 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 22 | 80 | 10.7 | 2 | 45 | 1 | 80 | 38 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 23 | 55 | 2.8 | 1 | 25 | 0.3 | 93 | 37 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 24 | 60 | 1.4 | 1 | 45 | 1 | 84 | 39 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 25 | 57 | 3.4 | 1 | 28 | 0.5 | 87 | 37 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 26 | 50 | 4.2 | 1 | 31 | 0.7 | 90 | 37 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 27 | 70 | 3.7 | 0 | 22 | 0.5 | 82 | 37 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 28 | 55 | 1.8 | 1 | 40 | 0.9 | 92 | 38 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 29 | 60 | 2 | 1 | 23 | 0.45 | 88 | 38 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 30 | 46 | 1.4 | 1 | 30 | 0.42 | 85 | 38.5 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 31 | 35 | 1.7 | 1 | 33 | 0.5 | 90 | 37 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 32 | 37 | 1.1 | 1 | 37 | 0.52 | 66 | 38 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 33 | 65 | 1.2 | 1 | 24 | 0.3 | 80 | 37 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 34 | 35 | 1.1 | 1 | 22 | 0.4 | 83 | 39 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 35 | 42 | 1 | 0 | 37 | 0.5 | 88 | 37 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 36 | 75 | 1.3 | 0 | 50 | 0.9 | 81 | 38 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 37 | 45 | 0.8 | 1 | 36 | 0.7 | 86 | 39.5 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 38 | 30 | 2.1 | 1 | 38 | 0.8 | 90 | 37 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 39 | 35 | 1.3 | 1 | 44 | 0.7 | 88 | 37 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 40 | 65 | 1.2 | 0 | 36 | 0.5 | 80 | 38 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 41 | 56 | 1.2 | 1 | 50 | 0.8 | 89 | 37 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 42 | 58 | 0.8 | 0 | 64 | 0.5 | 81 | 39 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 43 | 57 | 1.7 | 1 | 38 | 0.6 | 88 | 38 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 44 | 30 | 1.2 | 1 | 30 | 0.6 | 87 | 38.5 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 45 | 46 | 1 | 1 | 39 | 0.7 | 90 | 38.5 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 46 | 40 | 0.9 | 1 | 28 | 0.4 | 89 | 37 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 47 | 35 | 1.6 | 1 | 38 | 0.55 | 86 | 37 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 48 | 60 | 1.7 | 1 | 33 | 0.3 | 85 | 39 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 49 | 65 | 2.2 | 1 | 57 | 0.86 | 91 | 37 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 50 | 60 | 0.9 | 0 | 30 | 0.7 | 90 | 38 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 51 | 44 | 1.8 | 1 | 33 | 0.9 | 90 | 37.5 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 52 | 65 | 2.8 | 0 | 45 | 0.8 | 92 | 38 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 53 | 53 | 3.4 | 1 | 48 | 1.3 | 89 | 38 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 54 | 56 | 4.1 | 0 | 29 | 1 | 88 | 37 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 55 | 49 | 3.7 | 0 | 37 | 0.7 | 90 | 37.8 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 56 | 58 | 2.9 | 0 | 49 | 0.9 | 93 | 37.7 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 57 | 61 | 3.3 | 1 | 45 | 1.2 | 91 | 38.2 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 58 | 67 | 1.2 | 0 | 53 | 1.9 | 88 | 38 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 59 | 71 | 0.8 | 1 | 90 | 2.9 | 83 | 38 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 60 | 40 | 3.6 | 0 | 27 | 0.6 | 95 | 37 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 61 | 74 | 0.95 | 0 | 58 | 0.9 | 90 | 38 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 62 | 66 | 1.35 | 0 | 51 | 0.9 | 85 | 38 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 63 | 65 | 1.1 | 0 | 43 | 0.7 | 90 | 38 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 64 | 27 | 0.8 | 0 | 29 | 0.4 | 98 | 37 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 65 | 45 | 2.2 | 0 | 25 | 0.5 | 94 | 37 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 66 | 25 | 0.9 | 0 | 26 | 0.3 | 94 | 37 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 67 | 50 | 1.3 | 0 | 36 | 0.4 | 99 | 38.5 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 68 | 80 | 1 | 0 | 27 | 0.8 | 88 | 38 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 69 | 55 | 0.9 | 0 | 47 | 0.8 | 91 | 36 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 70 | 20 | 0.9 | 0 | 24 | 0.7 | 96 | 37.7 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 71 | 16 | 9.1 | 0 | 21 | 0.95 | 96 | 35.9 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 72 | 33 | 3.5 | 0 | 33 | 1.1 | 98 | 36 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 73 | 35 | 4.1 | 0 | 35 | 1.2 | 99 | 36 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 74 | 26 | 2.7 | 0 | 26 | 0.8 | 95 | 38 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 75 | 41 | 3.2 | 0 | 21 | 0.79 | 95 | 37.8 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 76 | 46 | 4.2 | 0 | 45 | 1.2 | 94 | 38 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 77 | 13 | 3.3 | 0 | 33 | 0.9 | 99 | 38 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 78 | 22 | 1.5 | 0 | 29 | 0.93 | 97 | 38 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| Calculate Weight, W | Wj |
|---|---|
| Age | 0.048 |
| Lymphocyte count | 0.049 |
| C-reactive protein | 0.077 |
| Urea | 0.024 |
| Creatinine | 0.023 |
| Oximetry saturation | 0.034 |
| Body temperature | 0.044 |
| Pleuritic chest pain | 0.099 |
| Nasal congestion | 0.107 |
| Cough | 0.113 |
| Lost sense of smell | 0.066 |
| Lost sense of taste | 0.063 |
| Heart Disease | 0.118 |
| Diabetes Disease | 0.089 |
| Cancer | 0.046 |
| Demographic | Laboratory Findings | Vital Signs | Symptoms | Chronic Conditions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patients | Age | Lymphocyte Count | C-reactive Protein | Urea | Creatinine | Oximetry Saturation | Body Temperature | Pleuritic Chest Pain | Nasal Congestion | Cough | Lost Sense of Smell | Lost Sense of Taste | Heart Disease | Diabetes Disease | Cancer |
| Weight | 0.047613 | 0.048938 | 0.077444 | 0.024142 | 0.022652 | 0.034111 | 0.044037 | 0.098639 | 0.107028 | 0.112511 | 0.065791 | 0.063479 | 0.118163 | 0.089159 | 0.046293 |
| 1 | 0.014 | 0.035 | 0.039 | 0.020 | 0.021 | 0.019 | 0.021 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 2 | 0.000 | 0.022 | 0.000 | 0.017 | 0.020 | 0.009 | 0.011 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.000 |
| 3 | 0.010 | 0.037 | 0.000 | 0.023 | 0.022 | 0.012 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 4 | 0.015 | 0.031 | 0.000 | 0.023 | 0.022 | 0.023 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 5 | 0.021 | 0.042 | 0.000 | 0.022 | 0.022 | 0.026 | 0.011 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 6 | 0.012 | 0.036 | 0.000 | 0.000 | 0.000 | 0.012 | 0.011 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.118 | 0.000 | 0.000 |
| 7 | 0.008 | 0.042 | 0.000 | 0.019 | 0.022 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 8 | 0.005 | 0.035 | 0.000 | 0.017 | 0.020 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 9 | 0.017 | 0.018 | 0.000 | 0.022 | 0.021 | 0.025 | 0.021 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 10 | 0.019 | 0.008 | 0.000 | 0.023 | 0.023 | 0.010 | 0.011 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 11 | 0.017 | 0.019 | 0.000 | 0.022 | 0.022 | 0.012 | 0.015 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.000 |
| 12 | 0.006 | 0.049 | 0.000 | 0.018 | 0.022 | 0.021 | 0.032 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 13 | 0.017 | 0.043 | 0.000 | 0.023 | 0.022 | 0.022 | 0.011 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 14 | 0.032 | 0.047 | 0.039 | 0.024 | 0.023 | 0.024 | 0.032 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.118 | 0.000 | 0.046 |
| 15 | 0.034 | 0.049 | 0.039 | 0.023 | 0.022 | 0.027 | 0.032 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 16 | 0.032 | 0.031 | 0.000 | 0.023 | 0.022 | 0.019 | 0.011 | 0.099 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 17 | 0.027 | 0.047 | 0.039 | 0.023 | 0.022 | 0.022 | 0.032 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 18 | 0.001 | 0.049 | 0.000 | 0.019 | 0.021 | 0.025 | 0.011 | 0.099 | 0.000 | 0.113 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 19 | 0.017 | 0.042 | 0.000 | 0.022 | 0.022 | 0.019 | 0.021 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 20 | 0.005 | 0.049 | 0.000 | 0.018 | 0.021 | 0.016 | 0.011 | 0.000 | 0.000 | 0.113 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 21 | 0.021 | 0.000 | 0.039 | 0.022 | 0.022 | 0.028 | 0.032 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 22 | 0.005 | 0.010 | 0.000 | 0.022 | 0.022 | 0.019 | 0.021 | 0.000 | 0.000 | 0.113 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 23 | 0.021 | 0.040 | 0.039 | 0.024 | 0.023 | 0.029 | 0.032 | 0.099 | 0.000 | 0.113 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 24 | 0.017 | 0.045 | 0.039 | 0.022 | 0.022 | 0.022 | 0.011 | 0.000 | 0.107 | 0.113 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 25 | 0.019 | 0.038 | 0.039 | 0.024 | 0.022 | 0.025 | 0.032 | 0.099 | 0.000 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 26 | 0.024 | 0.035 | 0.039 | 0.023 | 0.022 | 0.027 | 0.032 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 27 | 0.011 | 0.036 | 0.077 | 0.024 | 0.022 | 0.021 | 0.032 | 0.099 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 28 | 0.021 | 0.044 | 0.039 | 0.022 | 0.022 | 0.029 | 0.021 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 29 | 0.017 | 0.043 | 0.039 | 0.024 | 0.022 | 0.026 | 0.021 | 0.000 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 30 | 0.026 | 0.045 | 0.039 | 0.023 | 0.023 | 0.023 | 0.016 | 0.099 | 0.000 | 0.113 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 31 | 0.033 | 0.044 | 0.039 | 0.023 | 0.022 | 0.027 | 0.032 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 32 | 0.032 | 0.046 | 0.039 | 0.023 | 0.022 | 0.009 | 0.021 | 0.099 | 0.000 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 33 | 0.014 | 0.046 | 0.039 | 0.024 | 0.023 | 0.019 | 0.032 | 0.099 | 0.000 | 0.113 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 34 | 0.033 | 0.046 | 0.039 | 0.024 | 0.023 | 0.022 | 0.011 | 0.099 | 0.000 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 35 | 0.029 | 0.047 | 0.077 | 0.023 | 0.022 | 0.026 | 0.032 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 36 | 0.008 | 0.046 | 0.077 | 0.022 | 0.022 | 0.020 | 0.021 | 0.000 | 0.107 | 0.113 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 37 | 0.027 | 0.047 | 0.039 | 0.023 | 0.022 | 0.024 | 0.005 | 0.000 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 38 | 0.037 | 0.042 | 0.039 | 0.023 | 0.022 | 0.027 | 0.032 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 39 | 0.033 | 0.046 | 0.039 | 0.022 | 0.022 | 0.026 | 0.032 | 0.099 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 40 | 0.014 | 0.046 | 0.077 | 0.023 | 0.022 | 0.019 | 0.021 | 0.000 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 41 | 0.020 | 0.046 | 0.039 | 0.022 | 0.022 | 0.026 | 0.032 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 42 | 0.019 | 0.047 | 0.077 | 0.020 | 0.022 | 0.020 | 0.011 | 0.099 | 0.000 | 0.113 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 43 | 0.019 | 0.044 | 0.039 | 0.023 | 0.022 | 0.026 | 0.021 | 0.000 | 0.000 | 0.113 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 44 | 0.037 | 0.046 | 0.039 | 0.023 | 0.022 | 0.025 | 0.016 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 45 | 0.026 | 0.047 | 0.039 | 0.023 | 0.022 | 0.027 | 0.016 | 0.000 | 0.000 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 46 | 0.030 | 0.047 | 0.039 | 0.024 | 0.023 | 0.026 | 0.032 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 47 | 0.033 | 0.044 | 0.039 | 0.023 | 0.022 | 0.024 | 0.032 | 0.099 | 0.000 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 48 | 0.017 | 0.044 | 0.039 | 0.023 | 0.023 | 0.023 | 0.011 | 0.000 | 0.107 | 0.113 | 0.066 | 0.063 | 0.000 | 0.000 | 0.046 |
| 49 | 0.014 | 0.042 | 0.039 | 0.021 | 0.022 | 0.028 | 0.032 | 0.099 | 0.000 | 0.113 | 0.066 | 0.063 | 0.000 | 0.000 | 0.046 |
| 50 | 0.017 | 0.047 | 0.077 | 0.023 | 0.022 | 0.027 | 0.021 | 0.099 | 0.000 | 0.113 | 0.066 | 0.063 | 0.000 | 0.089 | 0.046 |
| 51 | 0.028 | 0.044 | 0.039 | 0.023 | 0.022 | 0.027 | 0.027 | 0.099 | 0.107 | 0.000 | 0.000 | 0.063 | 0.118 | 0.089 | 0.046 |
| 52 | 0.014 | 0.040 | 0.077 | 0.022 | 0.022 | 0.029 | 0.021 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 53 | 0.022 | 0.038 | 0.039 | 0.022 | 0.022 | 0.026 | 0.021 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 54 | 0.020 | 0.035 | 0.077 | 0.023 | 0.022 | 0.026 | 0.032 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 55 | 0.024 | 0.036 | 0.077 | 0.023 | 0.022 | 0.027 | 0.024 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 56 | 0.019 | 0.039 | 0.077 | 0.022 | 0.022 | 0.029 | 0.025 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.046 |
| 57 | 0.017 | 0.038 | 0.039 | 0.022 | 0.022 | 0.028 | 0.019 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.000 | 0.046 |
| 58 | 0.013 | 0.046 | 0.077 | 0.021 | 0.021 | 0.026 | 0.021 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.118 | 0.000 | 0.046 |
| 59 | 0.010 | 0.047 | 0.039 | 0.018 | 0.020 | 0.022 | 0.021 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 60 | 0.030 | 0.037 | 0.077 | 0.024 | 0.022 | 0.031 | 0.032 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 61 | 0.008 | 0.047 | 0.077 | 0.021 | 0.022 | 0.027 | 0.021 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 62 | 0.014 | 0.045 | 0.077 | 0.022 | 0.022 | 0.023 | 0.021 | 0.000 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 63 | 0.014 | 0.046 | 0.077 | 0.022 | 0.022 | 0.027 | 0.021 | 0.000 | 0.107 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 64 | 0.039 | 0.047 | 0.077 | 0.023 | 0.023 | 0.033 | 0.032 | 0.099 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 65 | 0.027 | 0.042 | 0.077 | 0.024 | 0.022 | 0.030 | 0.032 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 66 | 0.040 | 0.047 | 0.077 | 0.024 | 0.023 | 0.030 | 0.032 | 0.099 | 0.000 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 67 | 0.024 | 0.046 | 0.077 | 0.023 | 0.023 | 0.034 | 0.016 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 68 | 0.005 | 0.047 | 0.077 | 0.024 | 0.022 | 0.026 | 0.021 | 0.000 | 0.000 | 0.000 | 0.066 | 0.063 | 0.000 | 0.089 | 0.046 |
| 69 | 0.021 | 0.047 | 0.077 | 0.022 | 0.022 | 0.028 | 0.043 | 0.099 | 0.107 | 0.113 | 0.066 | 0.063 | 0.000 | 0.089 | 0.046 |
| 70 | 0.043 | 0.047 | 0.077 | 0.024 | 0.022 | 0.032 | 0.025 | 0.099 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 71 | 0.046 | 0.016 | 0.077 | 0.024 | 0.022 | 0.032 | 0.044 | 0.099 | 0.107 | 0.113 | 0.066 | 0.000 | 0.118 | 0.089 | 0.046 |
| 72 | 0.035 | 0.037 | 0.077 | 0.023 | 0.022 | 0.033 | 0.043 | 0.000 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 73 | 0.033 | 0.035 | 0.077 | 0.023 | 0.022 | 0.034 | 0.043 | 0.099 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 74 | 0.039 | 0.040 | 0.077 | 0.024 | 0.022 | 0.031 | 0.021 | 0.099 | 0.107 | 0.000 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 75 | 0.030 | 0.038 | 0.077 | 0.024 | 0.022 | 0.031 | 0.024 | 0.000 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| 76 | 0.026 | 0.035 | 0.077 | 0.022 | 0.022 | 0.030 | 0.021 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.089 | 0.046 |
| 77 | 0.048 | 0.038 | 0.077 | 0.023 | 0.022 | 0.034 | 0.021 | 0.099 | 0.107 | 0.113 | 0.066 | 0.000 | 0.118 | 0.089 | 0.046 |
| 78 | 0.042 | 0.045 | 0.077 | 0.023 | 0.022 | 0.033 | 0.021 | 0.099 | 0.107 | 0.113 | 0.000 | 0.000 | 0.118 | 0.089 | 0.046 |
| Patient No. | S | R | Q | Rank | Patient No. | S | R | Q | Rank |
|---|---|---|---|---|---|---|---|---|---|
| 8 | 0.077 | 0.035 | 0.000 | 1 | 48 | 0.575 | 0.113 | 0.768 | 40 |
| 3 | 0.156 | 0.046 | 0.116 | 2 | 49 | 0.585 | 0.113 | 0.774 | 41 |
| 9 | 0.171 | 0.046 | 0.125 | 3 | 32 | 0.545 | 0.118 | 0.784 | 42 |
| 59 | 0.178 | 0.047 | 0.136 | 4 | 57 | 0.555 | 0.118 | 0.790 | 43 |
| 1 | 0.216 | 0.046 | 0.153 | 5 | 26 | 0.563 | 0.118 | 0.795 | 44 |
| 5 | 0.279 | 0.089 | 0.449 | 6 | 45 | 0.566 | 0.118 | 0.797 | 45 |
| 76 | 0.369 | 0.089 | 0.503 | 7 | 44 | 0.569 | 0.118 | 0.798 | 46 |
| 55 | 0.370 | 0.089 | 0.503 | 8 | 17 | 0.573 | 0.118 | 0.801 | 47 |
| 39 | 0.365 | 0.099 | 0.557 | 9 | 21 | 0.623 | 0.118 | 0.831 | 48 |
| 13 | 0.293 | 0.107 | 0.564 | 10 | 66 | 0.625 | 0.118 | 0.833 | 49 |
| 6 | 0.189 | 0.118 | 0.568 | 11 | 53 | 0.649 | 0.118 | 0.847 | 50 |
| 11 | 0.304 | 0.107 | 0.571 | 12 | 50 | 0.712 | 0.113 | 0.851 | 51 |
| 68 | 0.486 | 0.089 | 0.574 | 13 | 37 | 0.661 | 0.118 | 0.854 | 52 |
| 20 | 0.277 | 0.113 | 0.588 | 14 | 34 | 0.662 | 0.118 | 0.855 | 53 |
| 10 | 0.336 | 0.107 | 0.590 | 15 | 25 | 0.663 | 0.118 | 0.856 | 54 |
| 28 | 0.351 | 0.107 | 0.599 | 16 | 29 | 0.666 | 0.118 | 0.857 | 55 |
| 19 | 0.386 | 0.107 | 0.621 | 17 | 31 | 0.680 | 0.118 | 0.866 | 56 |
| 56 | 0.387 | 0.107 | 0.621 | 18 | 38 | 0.681 | 0.118 | 0.867 | 57 |
| 12 | 0.391 | 0.107 | 0.624 | 19 | 47 | 0.683 | 0.118 | 0.867 | 58 |
| 2 | 0.286 | 0.118 | 0.627 | 20 | 15 | 0.686 | 0.118 | 0.869 | 59 |
| 22 | 0.347 | 0.113 | 0.630 | 21 | 40 | 0.697 | 0.118 | 0.876 | 60 |
| 43 | 0.353 | 0.113 | 0.633 | 22 | 62 | 0.698 | 0.118 | 0.877 | 61 |
| 18 | 0.382 | 0.113 | 0.651 | 23 | 67 | 0.702 | 0.118 | 0.879 | 62 |
| 7 | 0.349 | 0.118 | 0.665 | 24 | 16 | 0.709 | 0.118 | 0.884 | 63 |
| 46 | 0.463 | 0.107 | 0.667 | 25 | 60 | 0.713 | 0.118 | 0.886 | 64 |
| 61 | 0.467 | 0.107 | 0.670 | 26 | 74 | 0.715 | 0.118 | 0.887 | 65 |
| 63 | 0.473 | 0.107 | 0.674 | 27 | 65 | 0.715 | 0.118 | 0.887 | 66 |
| 52 | 0.478 | 0.107 | 0.676 | 28 | 35 | 0.715 | 0.118 | 0.887 | 67 |
| 4 | 0.369 | 0.118 | 0.677 | 29 | 75 | 0.719 | 0.118 | 0.890 | 68 |
| 14 | 0.385 | 0.118 | 0.687 | 30 | 51 | 0.732 | 0.118 | 0.897 | 69 |
| 58 | 0.390 | 0.118 | 0.690 | 31 | 72 | 0.744 | 0.118 | 0.904 | 70 |
| 36 | 0.482 | 0.113 | 0.712 | 32 | 69 | 0.843 | 0.113 | 0.931 | 71 |
| 41 | 0.461 | 0.118 | 0.733 | 33 | 27 | 0.796 | 0.118 | 0.936 | 72 |
| 54 | 0.577 | 0.107 | 0.736 | 34 | 78 | 0.835 | 0.118 | 0.960 | 73 |
| 24 | 0.533 | 0.113 | 0.743 | 35 | 73 | 0.839 | 0.118 | 0.962 | 74 |
| 30 | 0.542 | 0.113 | 0.748 | 36 | 70 | 0.842 | 0.118 | 0.964 | 75 |
| 33 | 0.544 | 0.113 | 0.749 | 37 | 64 | 0.847 | 0.118 | 0.967 | 76 |
| 23 | 0.554 | 0.113 | 0.755 | 38 | 71 | 0.899 | 0.118 | 0.998 | 77 |
| 42 | 0.564 | 0.113 | 0.761 | 39 | 77 | 0.901 | 0.118 | 1.000 | 78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulkareem, K.H.; Al-Mhiqani, M.N.; Dinar, A.M.; Mohammed, M.A.; Al-Imari, M.J.; Al-Waisy, A.S.; Alghawli, A.S.; Al-Qaness, M.A.A. MEF: Multidimensional Examination Framework for Prioritization of COVID-19 Severe Patients and Promote Precision Medicine Based on Hybrid Multi-Criteria Decision-Making Approaches. Bioengineering 2022, 9, 457. https://doi.org/10.3390/bioengineering9090457
Abdulkareem KH, Al-Mhiqani MN, Dinar AM, Mohammed MA, Al-Imari MJ, Al-Waisy AS, Alghawli AS, Al-Qaness MAA. MEF: Multidimensional Examination Framework for Prioritization of COVID-19 Severe Patients and Promote Precision Medicine Based on Hybrid Multi-Criteria Decision-Making Approaches. Bioengineering. 2022; 9(9):457. https://doi.org/10.3390/bioengineering9090457
Chicago/Turabian StyleAbdulkareem, Karrar Hameed, Mohammed Nasser Al-Mhiqani, Ahmed M. Dinar, Mazin Abed Mohammed, Mustafa Jawad Al-Imari, Alaa S. Al-Waisy, Abed Saif Alghawli, and Mohammed A. A. Al-Qaness. 2022. "MEF: Multidimensional Examination Framework for Prioritization of COVID-19 Severe Patients and Promote Precision Medicine Based on Hybrid Multi-Criteria Decision-Making Approaches" Bioengineering 9, no. 9: 457. https://doi.org/10.3390/bioengineering9090457
APA StyleAbdulkareem, K. H., Al-Mhiqani, M. N., Dinar, A. M., Mohammed, M. A., Al-Imari, M. J., Al-Waisy, A. S., Alghawli, A. S., & Al-Qaness, M. A. A. (2022). MEF: Multidimensional Examination Framework for Prioritization of COVID-19 Severe Patients and Promote Precision Medicine Based on Hybrid Multi-Criteria Decision-Making Approaches. Bioengineering, 9(9), 457. https://doi.org/10.3390/bioengineering9090457