A Benchmark Dataset for Evaluating Practical Performance of Model Quality Assessment of Homology Models
Abstract
:1. Introduction
2. Methods
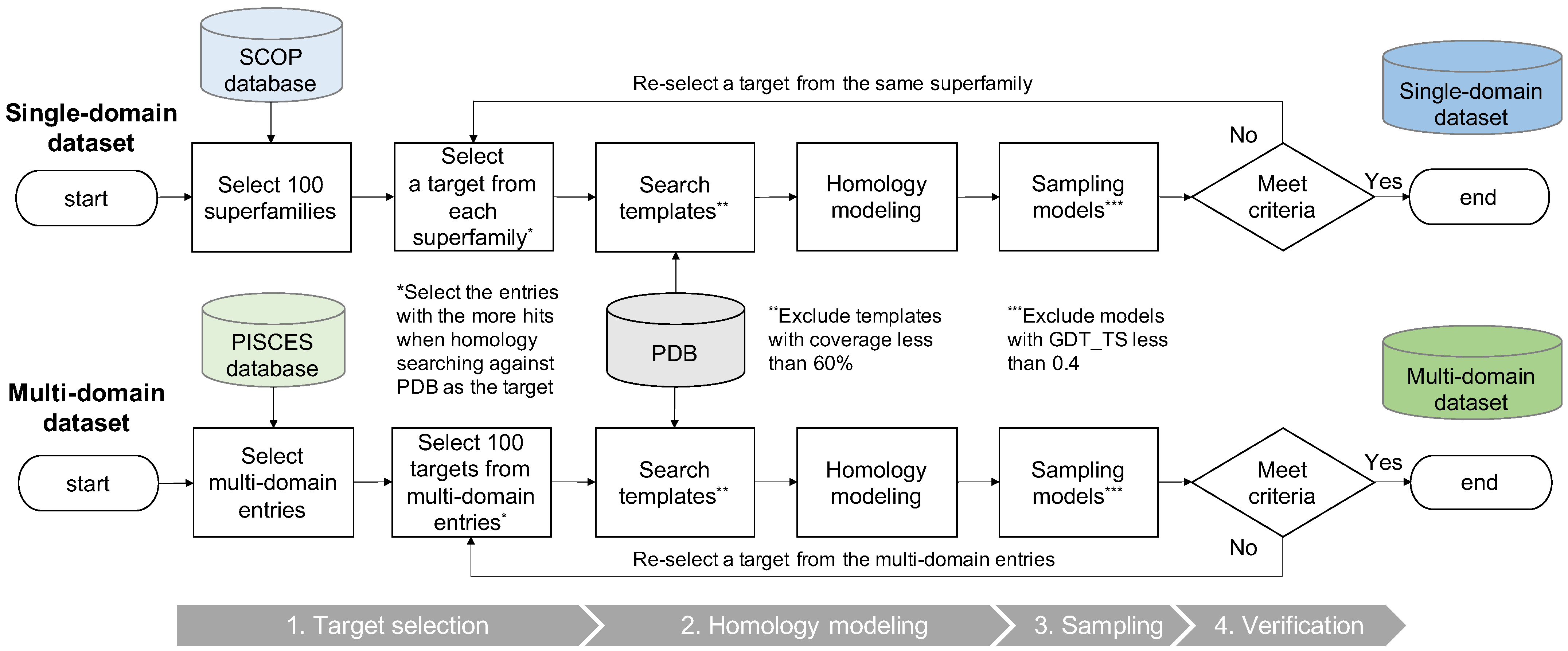
2.1. Dataset Construction
2.1.1. Target Selection
2.1.2. Homology Modeling
2.1.3. Sampling
2.1.4. Verification
2.2. MQA Performance Evaluation for the Constructed Datasets
2.2.1. Evaluation Metrics
2.2.2. Evaluation Methods
3. Results
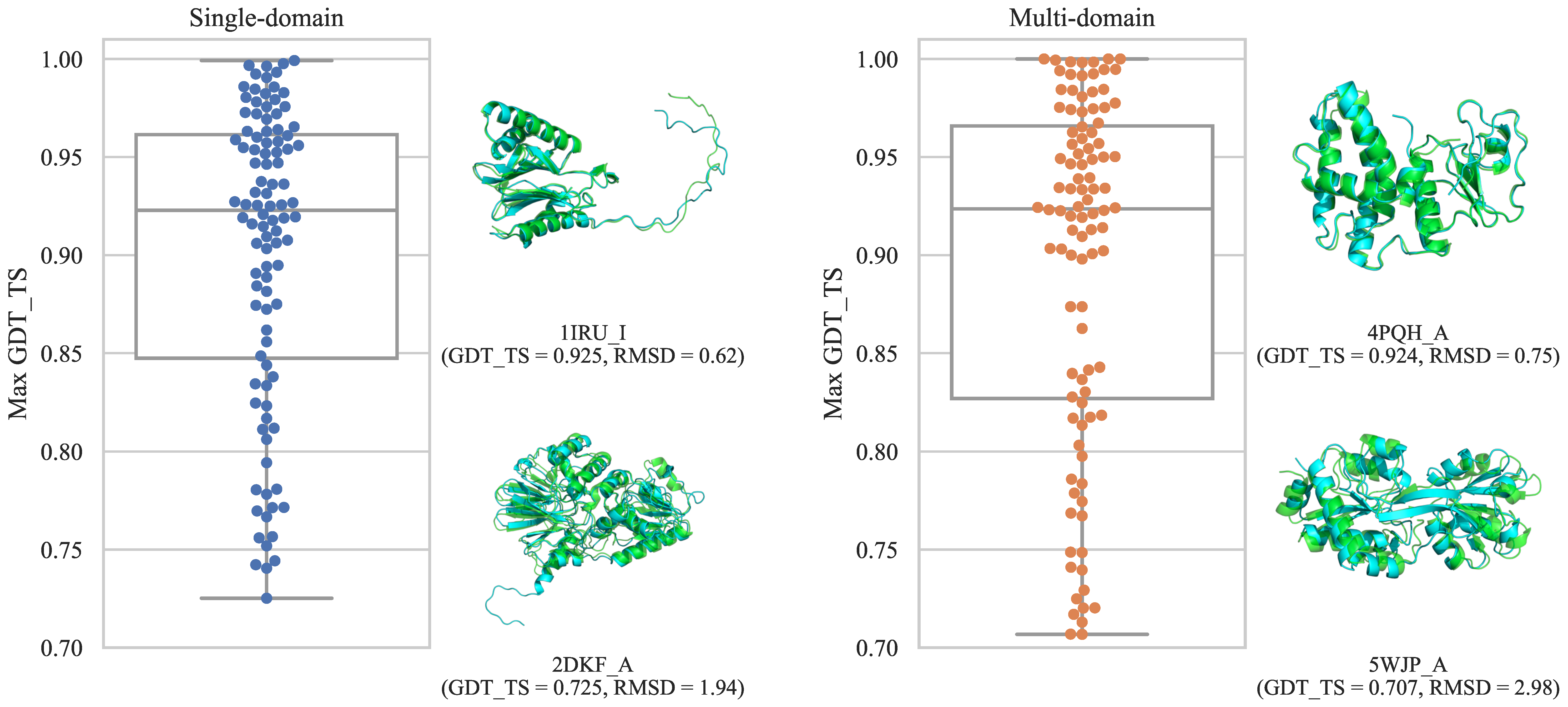
3.1. Constructed Datasets
3.2. Correlation between GDT_TS and the Alignment Quality
3.3. MQA Performance Evaluation for the Constructed Datasets
4. Discussion
4.1. Differences in the Quality of Models with the Same Template
4.2. Situation-Specific MQA Performance Analysis
- Single top: —
- Multi top: — and not single top
- No identical top: —
- High:
- Mid-high:
- Mid-low:
- Low:
5. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MQA | Model Quality Assessment |
| GDT_TS | Global Distance Test Total Score |
| HMDM | Homology Models Dataset for Model quality assessment |
References
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Baek, M.; DiMaio, F.; Anishchenko, I.; Dauparas, J.; Ovchinnikov, S.; Lee, G.R.; Wang, J.; Cong, Q.; Kinch, L.N.; Schaeffer, R.D.; et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021, 373, 871–876. [Google Scholar] [CrossRef] [PubMed]
- Hillisch, A.; Pineda, L.F.; Hilgenfeld, R. Utility of homology models in the drug discovery process. Drug Discov. Today 2004, 9, 659–669. [Google Scholar] [CrossRef]
- Werner, T.; Morris, M.B.; Dastmalchi, S.; Church, W.B. Structural modelling and dynamics of proteins for insights into drug interactions. Adv. Drug Deliv. Rev. 2012, 64, 323–343. [Google Scholar] [CrossRef] [PubMed]
- Cavasotto, C.N.; Phatak, S.S. Homology modeling in drug discovery: Current trends and applications. Drug Discov. Today 2009, 14, 676–683. [Google Scholar] [CrossRef] [PubMed]
- Balmith, M.; Faya, M.; Soliman, M.E.S. Ebola virus: A gap in drug design and discovery - experimental and computational perspective. Chem. Biol. Drug Des. 2017, 89, 297–308. [Google Scholar] [CrossRef]
- Muhammed, M.T.; Aki-Yalcin, E. Homology modeling in drug discovery: Overview, current applications, and future perspectives. Chem. Biol. Drug Des. 2019, 93, 12–20. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, K.; Yazdanpanah, N.; Saghazadeh, A.; Rezaei, N. Computational drug discovery and repurposing for the treatment of COVID-19: A systematic review. Bioorganic Chem. 2021, 106, 104490. [Google Scholar] [CrossRef]
- Igashov, I.; Olechnovic, K.; Kadukova, M.; Venclovas, Č.; Grudinin, S. VoroCNN: Deep convolutional neural network built on 3D Voronoi tessellation of protein structures. bioRxiv 2020. [Google Scholar] [CrossRef]
- Baldassarre, F.; Menéndez Hurtado, D.; Elofsson, A.; Azizpour, H. GraphQA: Protein model quality assessment using graph convolutional networks. Bioinformatics 2020, 37, 360–366. [Google Scholar] [CrossRef] [PubMed]
- Shuvo, M.H.; Bhattacharya, S.; Bhattacharya, D. QDeep: Distance-based protein model quality estimation by residue-level ensemble error classifications using stacked deep residual neural networks. Bioinformatics 2020, 36, i285–i291. [Google Scholar] [CrossRef] [PubMed]
- Haas, J.; Roth, S.; Arnold, K.; Kiefer, F.; Schmidt, T.; Bordoli, L.; Schwede, T. The Protein Model Portal—A comprehensive resource for protein structure and model information. Database 2013, 2013, bat031. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Jia, Y.; Zhang, Y. 3DRobot: Automated generation of diverse and well-packed protein structure decoys. Bioinformatics 2015, 32, 378–387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, D.; Zhang, Y. Improving the Physical Realism and Structural Accuracy of Protein Models by a Two-Step Atomic-Level Energy Minimization. Biophys. J. 2011, 101, 2525–2534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, D.; Zhang, Y. Ab initio protein structure assembly using continuous structure fragments and optimized knowledge-based force field. Proteins Struct. Funct. Bioinform. 2012, 80, 1715–1735. [Google Scholar] [CrossRef] [Green Version]
- Kryshtafovych, A.; Schwede, T.; Topf, M.; Fidelis, K.; Moult, J. Critical assessment of methods of protein structure prediction (CASP)—Round XIII. Proteins Struct. Funct. Bioinform. 2019, 87, 1011–1020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moult, J.; Fidelis, K.; Kryshtafovych, A.; Schwede, T.; Tramontano, A. Critical assessment of methods of protein structure prediction: Progress and new directions in round XI. Proteins Struct. Funct. Bioinform. 2016, 84, 4–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moult, J.; Fidelis, K.; Kryshtafovych, A.; Schwede, T.; Tramontano, A.; Topf, M.; Fidelis, K.; Moult, J.; Fidelis, K.; Kryshtafovych, A.; et al. Critical assessment of methods of protein structure prediction (CASP)—Round XII. Proteins Struct. Funct. Bioinform. 2018, 86, 7–15. [Google Scholar] [CrossRef]
- Zemla, A. LGA: A method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003, 31, 3370–3374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leaver-Fay, A.; Tyka, M.; Lewis, S.M.; Lange, O.F.; Thompson, J.; Jacak, R.; Kaufman, K.; Renfrew, P.D.; Smith, C.A.; Sheffler, W.; et al. Rosetta3: An object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol. 2011, 487, 545–574. [Google Scholar] [CrossRef] [Green Version]
- Kufareva, I.; Rueda, M.; Katritch, V.; Stevens, R.; Abagyan, R. Status of GPCR Modeling and Docking as Reflected by Community-wide GPCR Dock 2010 Assessment. Structure 2011, 19, 1108–1126. [Google Scholar] [CrossRef] [Green Version]
- Vyas, V.K.; Ghate, M.; Patel, K.; Qureshi, G.; Shah, S. Homology modeling, binding site identification and docking study of human angiotensin II type I (Ang II-AT1) receptor. Biomed. Pharmacother. 2015, 74, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Ramharack, P.; Soliman, M.E. Zika virus NS5 protein potential inhibitors: An enhanced in silico approach in drug discovery. J. Biomol. Struct. Dyn. 2018, 36, 1118–1133. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, M.; Yu, J.; Shang, Y.; Jiang, K.; Jia, Y.; Wang, J.; Yang, K. Investigating the binding mechanism of sphingosine kinase 1/2 inhibitors: Insights into subtype selectivity by homology modeling, molecular dynamics simulation and free energy calculation studies. J. Mol. Struct. 2020, 1208, 127900. [Google Scholar] [CrossRef]
- Ekins, S.; Mottin, M.; Ramos, P.R.; Sousa, B.K.; Neves, B.J.; Foil, D.H.; Zorn, K.M.; Braga, R.C.; Coffee, M.; Southan, C.; et al. Déjà vu: Stimulating open drug discovery for SARS-CoV-2. Drug Discov. Today 2020, 25, 928–941. [Google Scholar] [CrossRef] [PubMed]
- Eramian, D.; Shen, M.Y.; Devos, D.; Melo, F.; Sali, A.; Marti-Renom, M.A. A composite score for predicting errors in protein structure models. Protein Sci. 2006, 15, 1653–1666. [Google Scholar] [CrossRef] [Green Version]
- Sadowski, M.I.; Jones, D.T. Benchmarking template selection and model quality assessment for high-resolution comparative modeling. Proteins Struct. Funct. Bioinform. 2007, 69, 476–485. [Google Scholar] [CrossRef]
- Eramian, D.; Eswar, N.; Shen, M.Y.; Sali, A. How well can the accuracy of comparative protein structure models be predicted? Protein Sci. 2008, 17, 1881–1893. [Google Scholar] [CrossRef] [Green Version]
- Mariani, V.; Biasini, M.; Barbato, A.; Schwede, T. IDDT: A local superposition-free score for comparing protein structures and models using distance difference tests. Bioinformatics 2013, 29, 2722–2728. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andreeva, A.; Kulesha, E.; Gough, J.; Murzin, A.G. The SCOP database in 2020: Expanded classification of representative family and superfamily domains of known protein structures. Nucleic Acids Res. 2019, 48, D376–D382. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Dunbrack, R.L., Jr. PISCES: A protein sequence culling server. Bioinformatics 2003, 19, 1589–1591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altschul, S.F.; Gish, W.; Miller, W.; Myers, E.W.; Lipman, D.J. Basic local alignment search tool. J. Mol. Biol. 1990, 215, 403–410. [Google Scholar] [CrossRef]
- Sillitoe, I.; Bordin, N.; Dawson, N.; Waman, V.P.; Ashford, P.; Scholes, H.M.; Pang, C.S.M.; Woodridge, L.; Rauer, C.; Sen, N.; et al. CATH: Increased structural coverage of functional space. Nucleic Acids Res. 2020, 49, D266–D273. [Google Scholar] [CrossRef]
- Webb, B.; Sali, A. Comparative Protein Structure Modeling Using MODELLER. Curr. Protoc. Bioinform. 2016, 54, 5.6.1–5.6.37. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Godzik, A. Cd-hit: A fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics 2006, 22, 1658–1659. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, L.; Niu, B.; Zhu, Z.; Wu, S.; Li, W. CD-HIT: Accelerated for clustering the next-generation sequencing data. Bioinformatics 2012, 28, 3150–3152. [Google Scholar] [CrossRef]
- Zhang, Y.; Skolnick, J. Scoring function for automated assessment of protein structure template quality. Proteins Struct. Funct. Bioinform. 2004, 57, 702–710. [Google Scholar] [CrossRef]
- Shen, M.Y.; Sali, A. Statistical potential for assessment and prediction of protein structures. Protein Sci. 2006, 15, 2507–2524. [Google Scholar] [CrossRef] [Green Version]
- Dong, G.Q.; Fan, H.; Schneidman-Duhovny, D.; Webb, B.; Sali, A. Optimized atomic statistical potentials: Assessment of protein interfaces and loops. Bioinformatics 2013, 29, 3158–3166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uziela, K.; Hurtado, D.M.; Shu, N.; Wallner, B.; Elofsson, A. ProQ3D: Improved model quality assessments using deep learning. Bioinformatics 2017, 33, 1578–1580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karasikov, M.; Pagès, G.; Grudinin, S. Smooth orientation-dependent scoring function for coarse-grained protein quality assessment. Bioinformatics 2019, 35, 2801–2808. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takei, Y.; Ishida, T. P3CMQA: Single-Model Quality Assessment Using 3DCNN with Profile-Based Features. Bioengineering 2021, 8, 40. [Google Scholar] [CrossRef] [PubMed]
- Hiranuma, N.; Park, H.; Baek, M.; Anishchenko, I.; Dauparas, J.; Baker, D. Improved protein structure refinement guided by deep learning based accuracy estimation. Nat. Commun. 2021, 12, 1340. [Google Scholar] [CrossRef]
- Elnaggar, A.; Heinzinger, M.; Dallago, C.; Rehawi, G.; Yu, W.; Jones, L.; Gibbs, T.; Feher, T.; Angerer, C.; Steinegger, M.; et al. ProtTrans: Towards Cracking the Language of Lifes Code Through Self-Supervised Deep Learning and High Performance Computing. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Cheng, J.; Choe, M.H.; Elofsson, A.; Han, K.S.; Hou, J.; Maghrabi, A.H.; McGuffin, L.J.; Menéndez-Hurtado, D.; Olechnovič, K.; Schwede, T.; et al. Estimation of model accuracy in CASP13. Proteins Struct. Funct. Bioinform. 2019, 87, 1361–1377. [Google Scholar] [CrossRef] [Green Version]
- Kwon, S.; Won, J.; Kryshtafovych, A.; Seok, C. Assessment of protein model structure accuracy estimation in CASP14: Old and new challenges. Proteins Struct. Funct. Bioinform. 2021, 89, 1–9. [Google Scholar] [CrossRef] [PubMed]
- The PyMOL Molecular Graphics System, Version 1.8; Schrödinger, LLC.: New York, NY, USA, 2021.


| Method | Loss | MAE | Pearson | Spearman |
|---|---|---|---|---|
| identity(%) | 4.096 | (0.371) | 0.636 | 0.507 |
| positive(%) | 4.902 | (* 0.215) | * 0.661 | * 0.540 |
| coverage(%) | * 10.068 | (* 0.211) | * 0.438 | * 0.359 |
| DOPE | 4.013 | - | * 0.745 | * 0.675 |
| SOAP | 3.818 | - | 0.642 | * 0.603 |
| ProQ3D | 4.562 | * 0.129 | * 0.725 | * 0.663 |
| SBROD | 5.797 | - | 0.676 | * 0.613 |
| P3CMQA | 3.091 | * 0.096 | * 0.838 | * 0.777 |
| DeepAccNet | 3.288 | * 0.238 | * 0.748 | * 0.675 |
| DeepAccNet-Bert | 3.372 | * 0.173 | * 0.821 | * 0.754 |
| Method | Loss | MAE | Pearson | Spearman |
|---|---|---|---|---|
| identity(%) | 4.885 | (0.318) | 0.787 | 0.551 |
| positive(%) | 4.410 | (* 0.171) | * 0.805 | * 0.577 |
| coverage(%) | * 16.252 | (0.285) | * 0.424 | * 0.387 |
| DOPE | * 2.468 | - | 0.809 | * 0.712 |
| SOAP | * 2.921 | - | * 0.741 | * 0.620 |
| ProQ3D | 3.587 | * 0.095 | 0.817 | * 0.723 |
| SBROD | 3.684 | - | 0.785 | * 0.676 |
| P3CMQA | * 1.884 | * 0.075 | * 0.884 | * 0.802 |
| DeepAccNet | 2.873 | * 0.194 | * 0.858 | * 0.734 |
| DeepAccNet-Bert | * 2.760 | * 0.142 | * 0.882 | * 0.788 |
| Category | Num Targets | Method | Loss | Pearson | Spearman |
|---|---|---|---|---|---|
| Single top | 9 | identity(%) | 1.900 | 0.709 | 0.511 |
| positive(%) | 1.900 | 0.734 | 0.554 | ||
| ProQ3D | 4.348 | 0.877 | 0.744 | ||
| P3CMQA | 3.833 | 0.926 | 0.821 | ||
| DeepAccNet | 3.573 | 0.855 | 0.757 | ||
| DeepAccNet-Bert | 2.539 | 0.914 | 0.808 | ||
| Multi top | 41 | identity(%) | 3.177 | 0.661 | 0.481 |
| positive(%) | 3.659 | 0.693 | 0.533 | ||
| ProQ3D | 4.064 | 0.699 | 0.660 | ||
| P3CMQA | 2.459 | 0.822 | 0.769 | ||
| DeepAccNet | 2.070 | 0.752 | 0.671 | ||
| DeepAccNet-Bert | 3.159 | 0.817 | 0.752 | ||
| No identical top | 50 | identity(%) | 5.244 | 0.602 | 0.528 |
| positive(%) | 6.461 | 0.623 | 0.542 | ||
| ProQ3D | 5.008 | 0.718 | 0.651 | ||
| P3CMQA | 3.475 | 0.836 | 0.775 | ||
| DeepAccNet | 4.237 | 0.725 | 0.664 | ||
| DeepAccNet-Bert | 3.697 | 0.807 | 0.745 |
| Category | Num Targets | Method | Loss | Pearson | Spearman |
|---|---|---|---|---|---|
| High | 24 | identity(%) | 4.357 | 0.726 | 0.581 |
| positive(%) | 4.788 | 0.751 | 0.607 | ||
| ProQ3D | 6.376 | 0.659 | 0.605 | ||
| P3CMQA | 5.377 | 0.814 | 0.731 | ||
| DeepAccNet | 5.014 | 0.732 | 0.636 | ||
| DeepAccNet-Bert | 5.760 | 0.762 | 0.672 | ||
| Mid-high | 23 | identity(%) | 3.544 | 0.652 | 0.498 |
| positive(%) | 4.014 | 0.682 | 0.536 | ||
| ProQ3D | 4.543 | 0.753 | 0.703 | ||
| P3CMQA | 1.981 | 0.866 | 0.814 | ||
| DeepAccNet | 2.336 | 0.776 | 0.712 | ||
| DeepAccNet-Bert | 3.056 | 0.848 | 0.781 | ||
| Mid-low | 39 | identity(%) | 3.969 | 0.623 | 0.504 |
| positive(%) | 4.679 | 0.643 | 0.541 | ||
| ProQ3D | 4.413 | 0.731 | 0.669 | ||
| P3CMQA | 2.695 | 0.825 | 0.772 | ||
| DeepAccNet | 2.758 | 0.731 | 0.659 | ||
| DeepAccNet-Bert | 2.598 | 0.830 | 0.773 | ||
| Low | 14 | identity(%) | 4.908 | 0.491 | 0.402 |
| positive(%) | 7.175 | 0.525 | 0.426 | ||
| ProQ3D | 1.896 | 0.771 | 0.681 | ||
| P3CMQA | 2.096 | 0.870 | 0.808 | ||
| DeepAccNet | 3.373 | 0.776 | 0.725 | ||
| DeepAccNet-Bert | 1.954 | 0.851 | 0.796 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takei, Y.; Ishida, T. A Benchmark Dataset for Evaluating Practical Performance of Model Quality Assessment of Homology Models. Bioengineering 2022, 9, 118. https://doi.org/10.3390/bioengineering9030118
Takei Y, Ishida T. A Benchmark Dataset for Evaluating Practical Performance of Model Quality Assessment of Homology Models. Bioengineering. 2022; 9(3):118. https://doi.org/10.3390/bioengineering9030118
Chicago/Turabian StyleTakei, Yuma, and Takashi Ishida. 2022. "A Benchmark Dataset for Evaluating Practical Performance of Model Quality Assessment of Homology Models" Bioengineering 9, no. 3: 118. https://doi.org/10.3390/bioengineering9030118
APA StyleTakei, Y., & Ishida, T. (2022). A Benchmark Dataset for Evaluating Practical Performance of Model Quality Assessment of Homology Models. Bioengineering, 9(3), 118. https://doi.org/10.3390/bioengineering9030118






