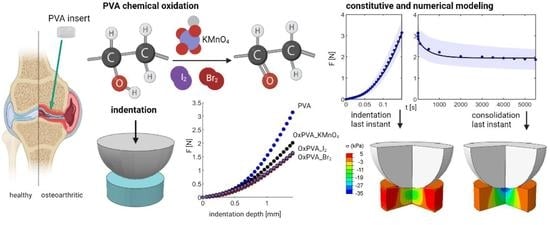
Compressive Mechanical Behavior of Partially Oxidized Polyvinyl Alcohol Hydrogels for Cartilage Tissue Repair
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of PVA and Oxidized PVA Hydrogels
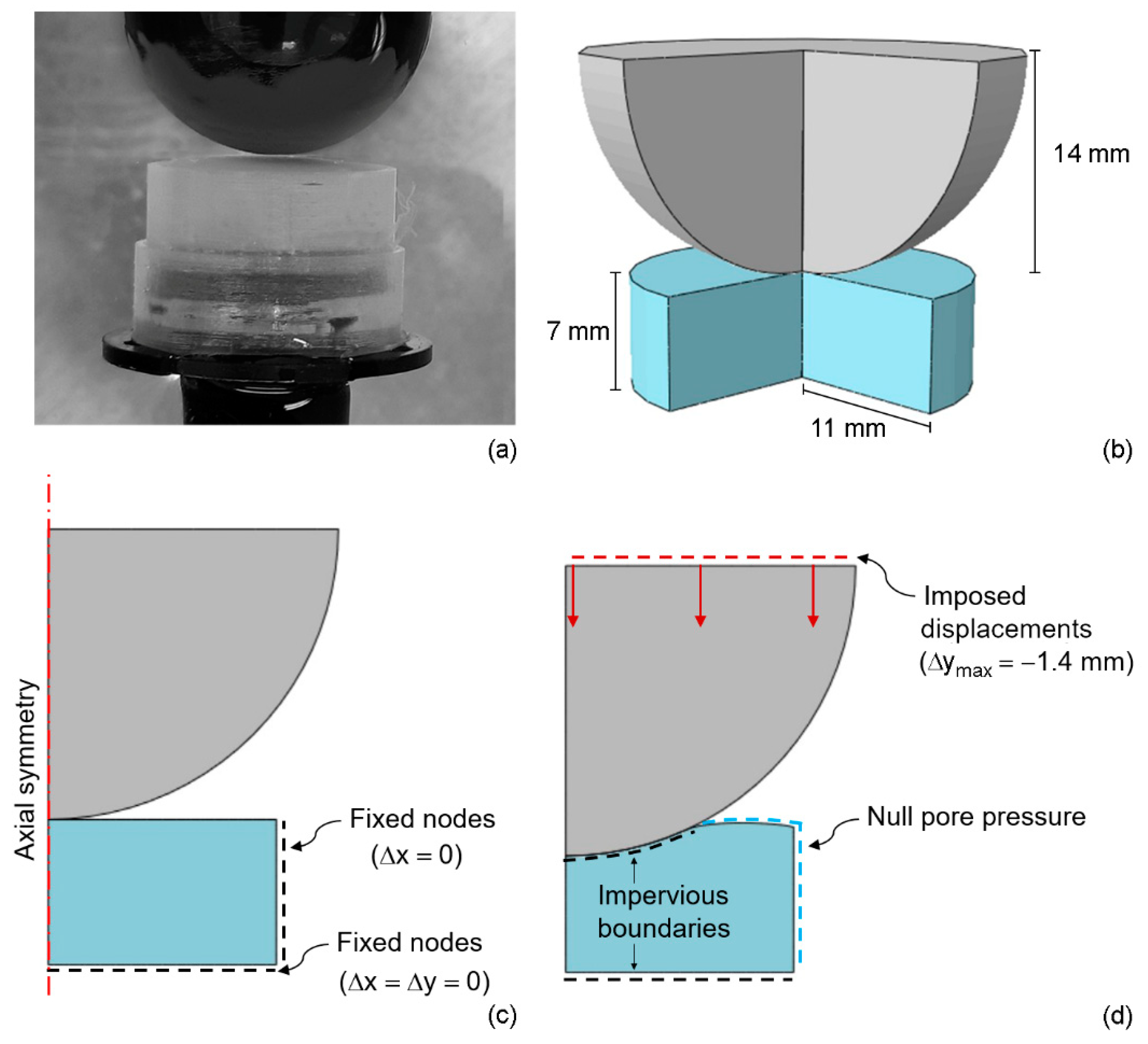
2.2. Mechanical Tests
2.3. Swelling Tests
2.4. Constitutive Models
2.5. Numerical Analyses
2.6. Constitutive Parameters Optimization
2.7. Statistical Analyses
3. Results and Discussion
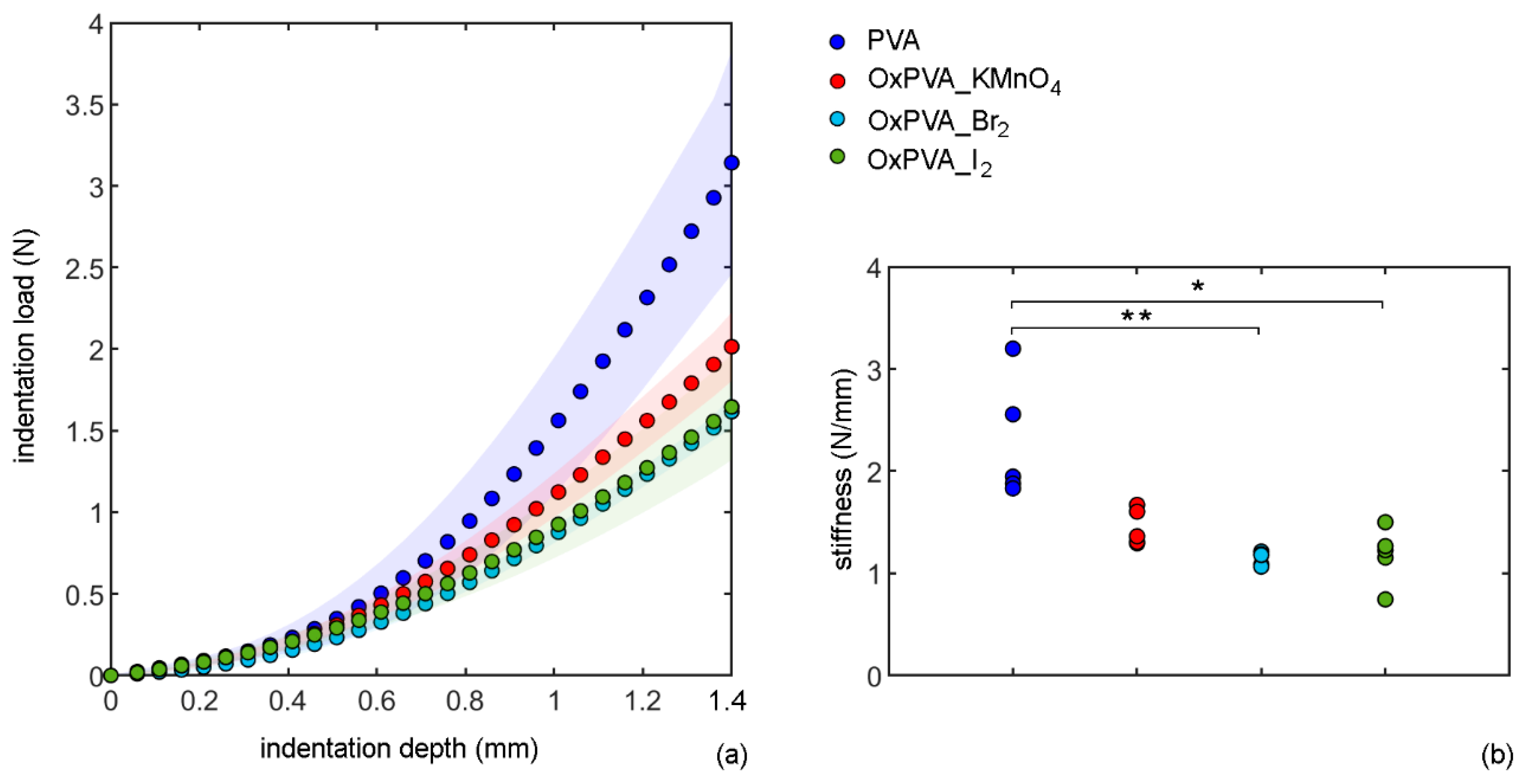
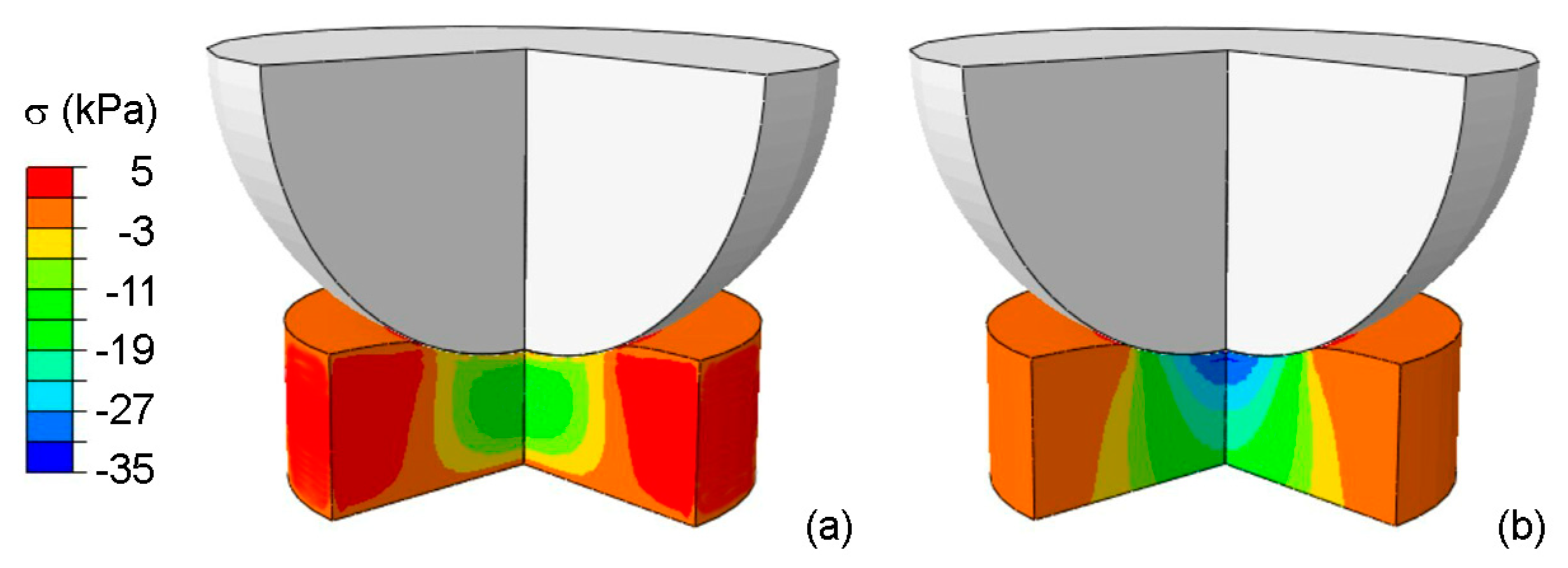
3.1. Indentation Tests
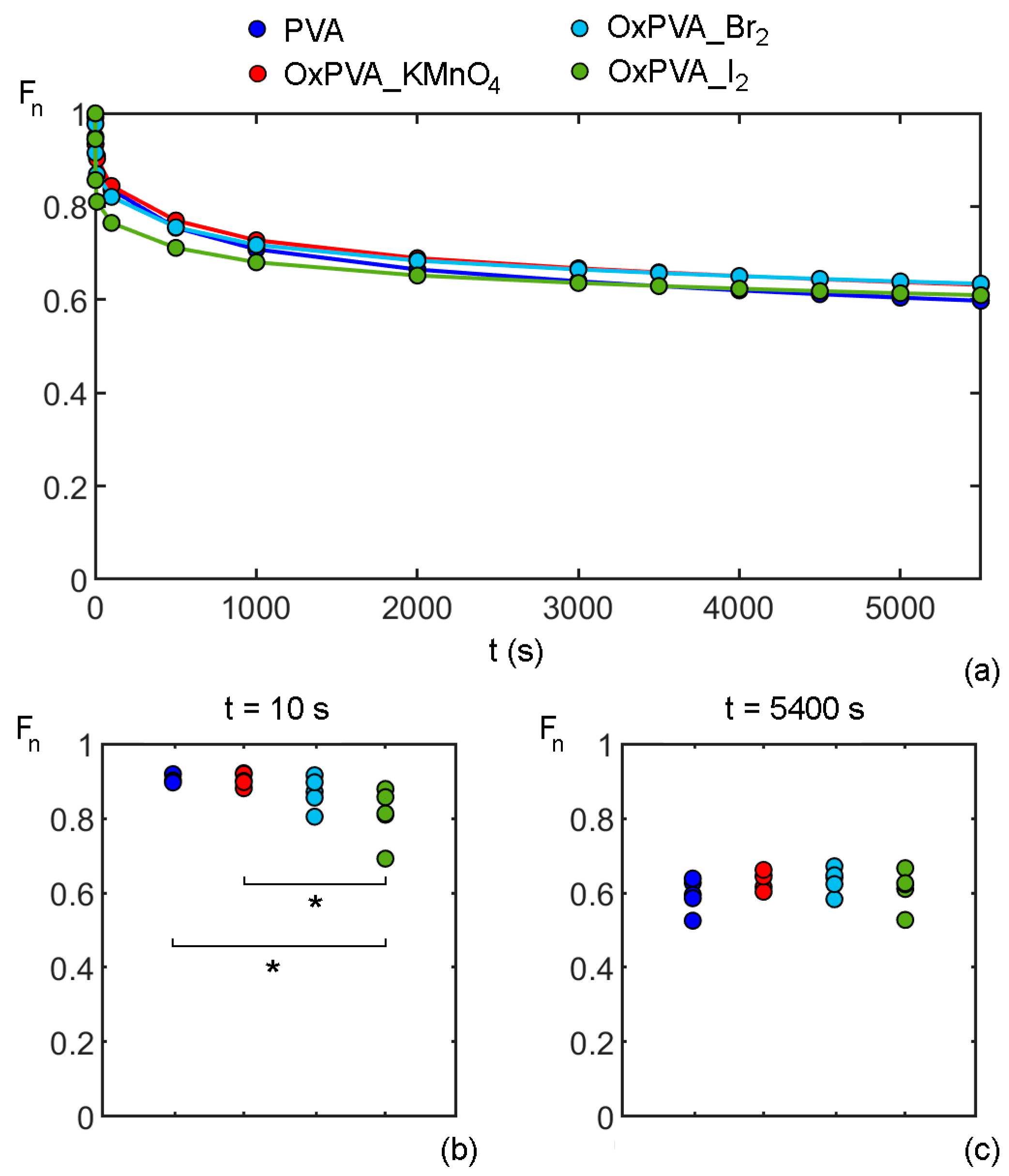
3.2. Consolidation Tests
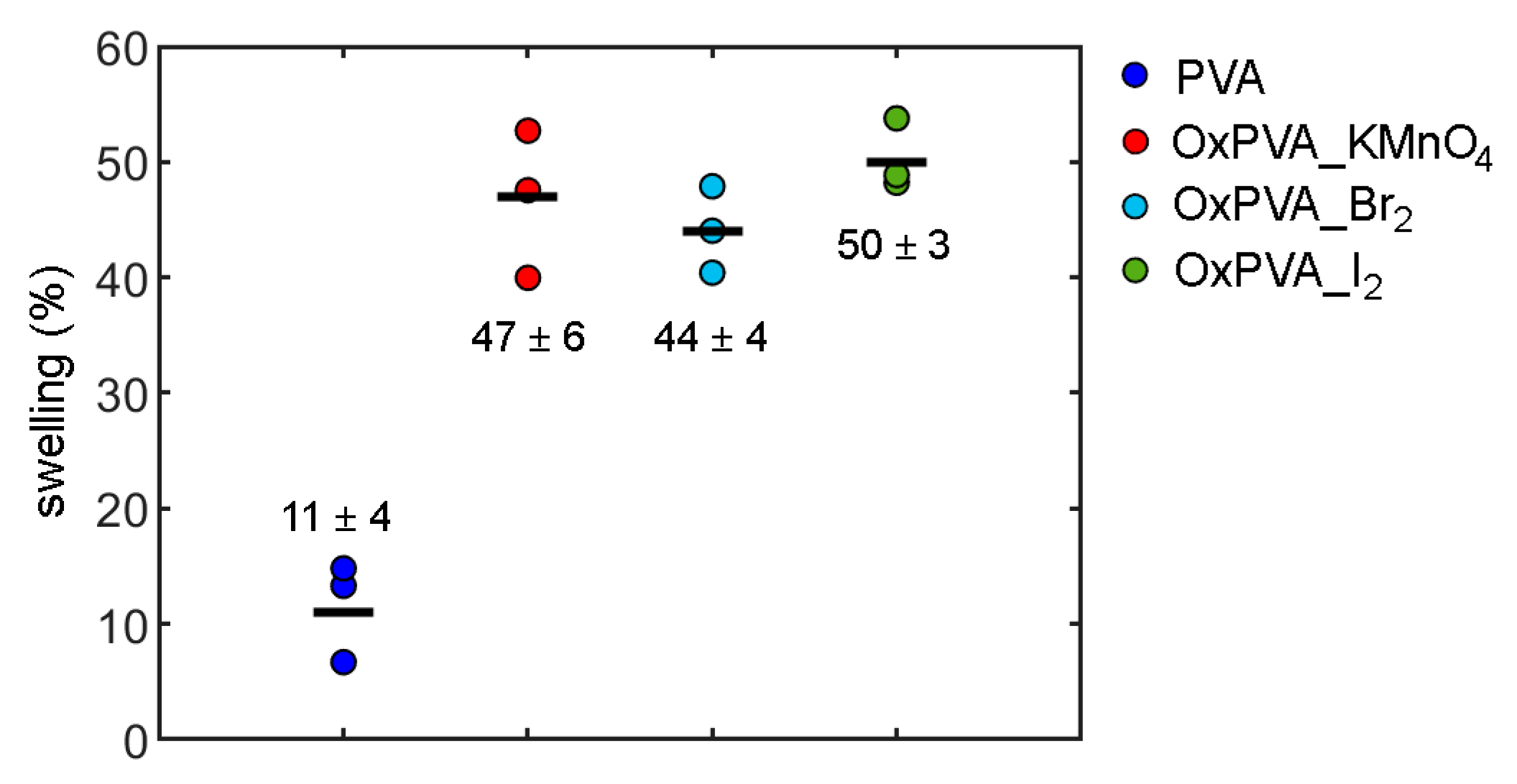
3.3. Swelling Behavior
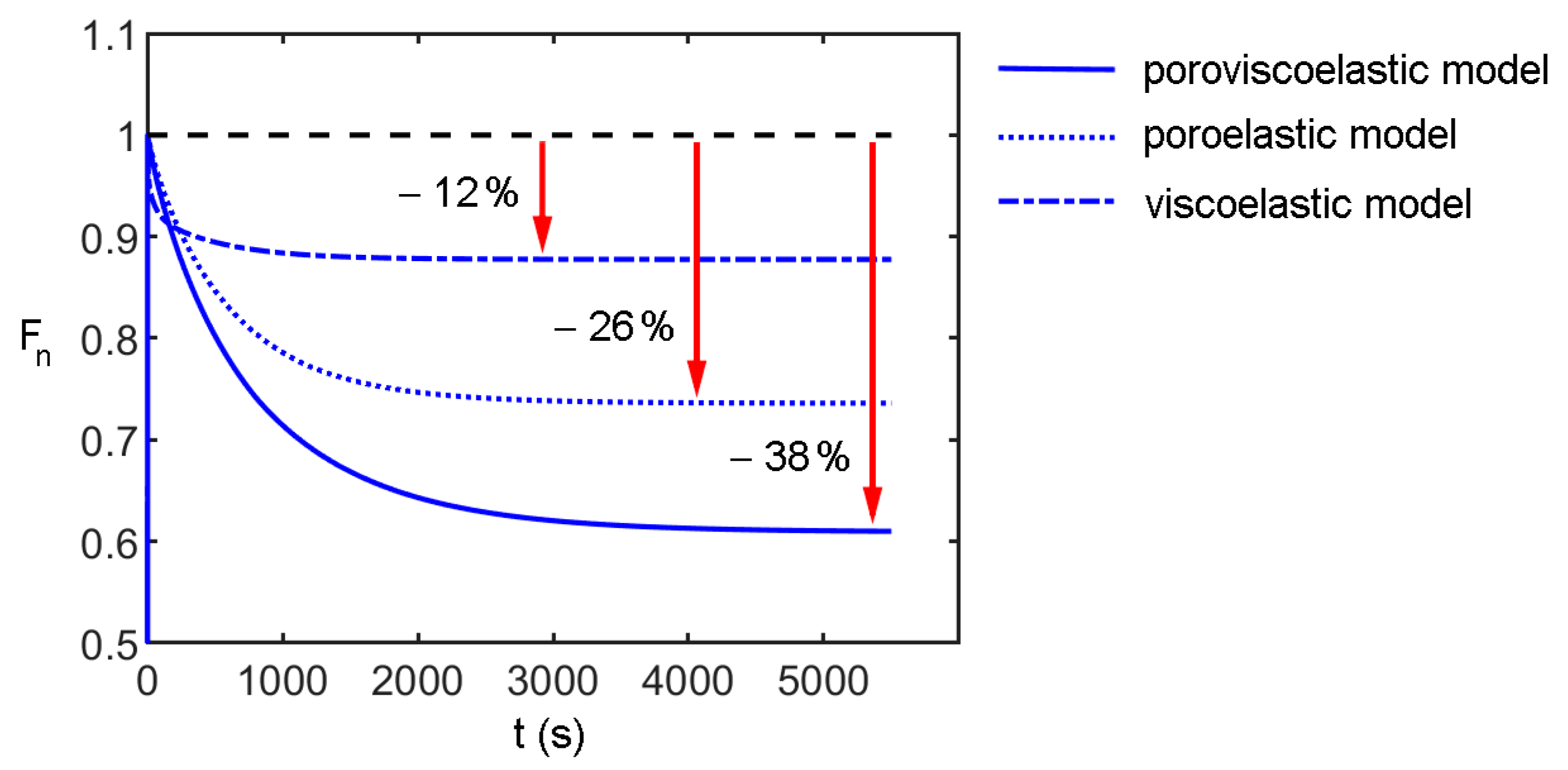
3.4. Constitutive Modeling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TE | Tissue engineering |
| PVA | Polyvinyl alcohol |
| FT | Freeze-thawing |
| MW | Molecular weight |
| OxPVA_KMnO4 | PVA partially oxidized with KMnO4 |
| OxPVA_Br2 | PVA partially oxidized with Br2 |
| OxPVA_I2 | PVA partially oxidized with I2 |
| PBS | Phosphate-buffered saline |
| FE | Finite element |
| MSE | Mean squared error |
| ANOVA | Analysis of variance |
| MSCs | Mesenchymal stem cells |
| Cryo-SEM | Cryogenic Scanning Electron Microscopy |
| NMR | Nuclear magnetic resonance |
References
- Hodge, R.M.; Simon, G.P.; Whittaker, M.R.; Hill, D.J.T.; Whittaker, A.K. Free volume and water uptake in a copolymer hydrogel series. J. Polym. Sci. Part B Polym. Phys. 2015, 36, 463–471. [Google Scholar] [CrossRef]
- Appel, E.A.; Loh, X.J.; Jones, S.T.; Biedermann, F.; Dreiss, C.A.; Scherman, O.A. Ultrahigh-Water-Content Supramolecular Hydrogels Exhibiting Multistimuli Responsiveness. J. Am. Chem. Soc. 2012, 134, 11767–11773. [Google Scholar] [CrossRef] [PubMed]
- Van Vlierberghe, S.; Dubruel, P.; Schacht, E. Biopolymer-Based Hydrogels As Scaffolds for Tissue Engineering Applications: A Review. Biomacromolecules 2011, 12, 1387–1408. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Han, S.S. PVA-based hydrogels for tissue engineering: A review. Int. J. Polym. Mater. Polym. Biomater. 2016, 66, 159–182. [Google Scholar] [CrossRef]
- Hassan, C.M.; Peppas, N.A. Structure and Applications of Poly(vinyl alcohol) Hydrogels Produced by Conventional Crosslinking or by Freezing/Thawing Methods. In Biopolymers PVA Hydrogels, Anionic Polymerisation Nanocomposites; Springer: Berlin/Heidelberg, Germany, 2000; pp. 37–65. [Google Scholar] [CrossRef]
- Baker, M.I.; Walsh, S.P.; Schwartz, Z.; Boyan, B.D. A review of polyvinyl alcohol and its uses in cartilage and orthopedic applications. J. Biomed. Mater. Res. Part B Appl. Biomater. 2012, 100, 1451–1457. [Google Scholar] [CrossRef]
- Barbon, S.; Contran, M.; Stocco, E.; Todros, S.; Macchi, V.; Caro, R.; Porzionato, A. Enhanced Biomechanical Properties of Polyvinyl Alcohol-Based Hybrid Scaffolds for Cartilage Tissue Engineering. Processes 2021, 9, 730. [Google Scholar] [CrossRef]
- Liu, K.; Ovaert, T.C. Poro-viscoelastic constitutive modeling of unconfined creep of hydrogels using finite element analysis with integrated optimization method. J. Mech. Behav. Biomed. Mater. 2011, 4, 440–450. [Google Scholar] [CrossRef]
- Kazimierska-Drobny, K.; El Fray, M.; Kaczmarek, M. Determination of mechanical and hydraulic properties of PVA hydrogels. Mater. Sci. Eng. C 2015, 48, 48–54. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, K.; Bai, Y.; Tang, L.; Jiang, Z.; Liu, Y.; Liu, Z.; Zhou, L.; Zhou, X. Features of the volume change and a new constitutive equation of hydrogels under uniaxial compression. J. Mech. Behav. Biomed. Mater. 2018, 85, 181–187. [Google Scholar] [CrossRef]
- Behravesh, E.; Timmer, M.D.; Lemoine, J.J.; Liebschner, M.A.K.; Mikos, A.G. Evaluation of the in Vitro Degradation of Macroporous Hydrogels Using Gravimetry, Confined Compression Testing, and Microcomputed Tomography. Biomacromolecules 2002, 3, 1263–1270. [Google Scholar] [CrossRef]
- Dastgerdi, J.N.; Koivisto, J.T.; Orell, O.; Rava, P.; Jokinen, J.; Kanerva, M.; Kellomäki, M. Comprehensive characterisation of the compressive behaviour of hydrogels using a new modelling procedure and redefining compression testing. Mater. Today Commun. 2021, 28, 102518. [Google Scholar] [CrossRef]
- McGhee, A.J.; McGhee, E.O.; Famiglietti, J.E.; Schulze, K.D. Dynamic Subsurface Deformation and Strain of Soft Hydrogel Interfaces Using an Embedded Speckle Pattern With 2D Digital Image Correlation. Exp. Mech. 2021, 61, 1017–1027. [Google Scholar] [CrossRef]
- Tan, J.; Chao, Y.; Van Zee, J.; Li, X.; Wang, X.; Yang, M. Assessment of mechanical properties of fluoroelastomer and EPDM in a simulated PEM fuel cell environment by microindentation test. Mater. Sci. Eng. A 2008, 496, 464–470. [Google Scholar] [CrossRef]
- Tan, J.; Chao, Y.; Li, X.; Van Zee, J. Degradation of silicone rubber under compression in a simulated PEM fuel cell environment. J. Power Sources 2007, 172, 782–789. [Google Scholar] [CrossRef]
- Vervoort, S.; Patlazhan, S.; Weyts, J.; Budtova, T. Solvent release from highly swollen gels under compression. Polymer 2005, 46, 121–127. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Tang, L.Q.; Xie, B.X.; Xu, K.J.; Liu, Z.J.; Liu, Y.P.; Jiang, Z.Y.; Dong, S.B. A Variable Mass Meso-Model for the Mechanical and Water-Expelled Behaviors of PVA Hydrogel in Compression. Int. J. Appl. Mech. 2017, 9, 1750044. [Google Scholar] [CrossRef]
- Urayama, K.; Taoka, Y.; Nakamura, K.; Takigawa, T. Markedly compressible behaviors of gellan hydrogels in a constrained geometry at ultraslow strain rates. Polymer 2008, 49, 3295–3300. [Google Scholar] [CrossRef]
- Korchagin, V.; Dolbow, J.; Stepp, D. A theory of amorphous viscoelastic solids undergoing finite deformations with application to hydrogels. Int. J. Solids Struct. 2007, 44, 3973–3997. [Google Scholar] [CrossRef]
- Gabler, S.; Stampfl, J.; Koch, T.; Seidler, S.; Schuller, G.; Redl, H.; Juras, V.; Trattnig, S.; Weidisch, R. Determination of the viscoelastic properties of hydrogels based on polyethylene glycol diacrylate (PEG-DA) and human articular cartilage. Int. J. Mater. Eng. Innov. 2009, 1, 3. [Google Scholar] [CrossRef]
- Lozinsky, V.I.; Solodova, E.V.; Zubov, A.L.; Simenel, I.A. Study of cryostructuration of polymer systems. XI. The formation of PVA cryogels by freezing–thawing the polymer aqueous solutions containing additives of some polyols. J. Appl. Polym. Sci. 1995, 58, 171–177. [Google Scholar] [CrossRef]
- Luo, T.; Tan, B.; Zhu, L.; Wang, Y.; Liao, J. A Review on the Design of Hydrogels With Different Stiffness and Their Effects on Tissue Repair. Front. Bioeng. Biotechnol. 2022, 10, 817391. [Google Scholar] [CrossRef] [PubMed]
- Milcovich, G.; Antunes, F.E.; Farra, R.; Grassi, G.; Grassi, M.; Asaro, F. Modulating carbohydrate-based hydrogels as viscoelastic lubricant substitute for articular cartilages. Int. J. Biol. Macromol. 2017, 102, 796–804. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Wei, Z.; Zhu, W.; Weng, X. Recent Developments and Current Applications of Hydrogels in Osteoarthritis. Bioengineering 2022, 9, 132. [Google Scholar] [CrossRef] [PubMed]
- Ngadimin, K.D.; Stokes, A.; Gentile, P.; Ferreira, A.M. Biomimetic hydrogels designed for cartilage tissue engineering. Biomater. Sci. 2021, 9, 4246–4259. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Hong, Y.; Zhang, X.; Yang, L.; Li, J.; Jiang, D.; Bunpetch, V.; Hu, Y.; Ouyang, H.; Zhang, S. Tough hydrogel with enhanced tissue integration and in situ forming capability for osteochondral defect repair. Appl. Mater. Today 2018, 13, 32–44. [Google Scholar] [CrossRef]
- Tan, G.; Xu, J.; Yu, Q.; Zhang, J.; Hu, X.; Sun, C.; Zhang, H. Photo-Crosslinkable Hydrogels for 3D Bioprinting in the Repair of Osteochondral Defects: A Review of Present Applications and Future Perspectives. Micromachines 2022, 13, 1038. [Google Scholar] [CrossRef]
- Stocco, E.; Barbon, S.; Grandi, F.; Gamba, P.G.; Borgio, L.; Del Gaudio, C.; Dalzoppo, D.; Lora, S.; Rajendran, S.; Porzionato, A.; et al. Partially oxidized polyvinyl alcohol as a promising material for tissue engineering. J. Tissue Eng. Regen. Med. 2015, 11, 2060–2070. [Google Scholar] [CrossRef]
- Porzionato, A.; Barbon, S.; Stocco, E.; Dalzoppo, D.; Contran, M.; De Rose, E.; Parnigotto, P.P.; Macchi, V.; Grandi, C.; De Caro, R. Development of Oxidized Polyvinyl Alcohol-Based Nerve Conduits Coupled with the Ciliary Neurotrophic Factor. Materials 2019, 12, 1996. [Google Scholar] [CrossRef]
- Barbon, S.; Stocco, E.; Dalzoppo, D.; Todros, S.; Canale, A.; Boscolo-Berto, R.; Pavan, P.; Macchi, V.; Grandi, C.; De Caro, R.; et al. Halogen-Mediated Partial Oxidation of Polyvinyl Alcohol for Tissue Engineering Purposes. Int. J. Mol. Sci. 2020, 21, 801. [Google Scholar] [CrossRef]
- Grandi, F.; Stocco, E.; Barbon, S.; Rambaldo, A.; Contran, M.; Leon, F.F.; Gamba, P.; Parnigotto, P.P.; Macchi, V.; De Caro, R.; et al. Composite Scaffolds Based on Intestinal Extracellular Matrices and Oxidized Polyvinyl Alcohol: A Preliminary Study for a New Regenerative Approach in Short Bowel Syndrome. BioMed Res. Int. 2018, 2018, 7824757. [Google Scholar] [CrossRef]
- Todros, S.; Barbon, S.; Stocco, E.; Favaron, M.; Macchi, V.; De Caro, R.; Porzionato, A.; Pavan, P.G. Time-dependent mechanical behavior of partially oxidized polyvinyl alcohol hydrogels for tissue engineering. J. Mech. Behav. Biomed. Mater. 2021, 125, 104966. [Google Scholar] [CrossRef]
- Patel, J.; Wise, B.; Bonnevie, E.D.; Mauck, R.L. A Systematic Review and Guide to Mechanical Testing for Articular Cartilage Tissue Engineering. Tissue Eng. Part C Methods 2019, 25, 593–608. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Chao, Y.J.; Li, X.; Van Zee, J.W. Microindentation Test for Assessing the Mechanical Properties of Silicone Rubber Exposed to a Simulated Polymer Electrolyte Membrane Fuel Cell Environment. J. Fuel Cell Sci. Technol. 2009, 6, 041017. [Google Scholar] [CrossRef]
- Lai, Y.; He, D.; Hu, Y. Indentation adhesion of hydrogels over a wide range of length and time scales. Extrem. Mech. Lett. 2019, 31, 100540. [Google Scholar] [CrossRef]
- Huth, S.; Sindt, S.; Selhuber-Unkel, C. Automated analysis of soft hydrogel microindentation: Impact of various indentation parameters on the measurement of Young’s modulus. PLoS ONE 2019, 14, e0220281. [Google Scholar] [CrossRef]
- Delavoipière, J.; Tran, Y.; Verneuil, E.; Chateauminois, A. Poroelastic indentation of mechanically confined hydrogel layers. Soft Matter. 2016, 12, 8049–8058. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; An, Y.H.; Wu, Y.-D.; Song, Y.C.; Chao, Y.J.; Chien, C.-H. Microindentation test for assessing the mechanical properties of cartilaginous tissues. J. Biomed. Mater. Res. Part B Appl. Biomater. 2006, 80B, 25–31. [Google Scholar] [CrossRef]
- Zevenbergen, L.; Gsell, W.; Cai, L.; Chan, D.; Famaey, N.; Sloten, J.V.; Himmelreich, U.; Neu, C.; Jonkers, I. Cartilage-on-cartilage contact: Effect of compressive loading on tissue deformations and structural integrity of bovine articular cartilage. Osteoarthr. Cartil. 2018, 26, 1699–1709. [Google Scholar] [CrossRef]
- Kabir, W.; Di Bella, C.; Choong, P.F.; O’Connell, C.D. Assessment of Native Human Articular Cartilage: A Biomechanical Protocol. CARTILAGE 2020, 13, 427S–437S. [Google Scholar] [CrossRef]
- Nagarkar, R.; Patel, J. Polyvinyl Alcohol: A Comprehensive Study, Acta sci. Pharm. Sci. 2019, 3, 34–44. [Google Scholar]
- Saxena, R.; Bhatt, S.C. Molecular Association Studies on Polyvinyl Alcohol at Different Concentrations. Adv. Mater. Sci. Eng. 2018, 2018, 1738612. [Google Scholar] [CrossRef]
- Holzapfel, G.A. On large strain viscoelasticity: Continuum formulation and finite element applications to elastomeric structures. Int. J. Numer. Methods Eng. 1996, 39, 3903–3926. [Google Scholar] [CrossRef]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Providence, R.I., Ed.; Dassault Systèmes Simulia Corp: Providence County, RI, USA, 2009. [Google Scholar]
- Urayama, K.; Takigawa, T.; Masuda, T. Poisson ratio of poly(vinylalcohol) gels. Macromolecules 1993, 26, 3092–3096. [Google Scholar] [CrossRef]
- Chen, F.; Kang, D.-J.; Park, J.-H. New measurement method of Poisson’s ratio of PVA hydrogels using an optical flow analysis for a digital imaging system. Meas. Sci. Technol. 2013, 24, 055602. [Google Scholar] [CrossRef]
- Drury, J.L.; Mooney, D.J. Hydrogels for tissue engineering: Scaffold design variables and applications. Biomaterials 2003, 24, 4337–4351. [Google Scholar] [CrossRef]
- Toh, W.S.; Lim, T.C.; Kurisawa, M.; Spector, M. Modulation of mesenchymal stem cell chondrogenesis in a tunable hyaluronic acid hydrogel microenvironment. Biomaterials 2012, 33, 3835–3845. [Google Scholar] [CrossRef]
- Wang, L.-S.; Du, C.; Toh, W.S.; Wan, A.C.; Gao, S.J.; Kurisawa, M. Modulation of chondrocyte functions and stiffness-dependent cartilage repair using an injectable enzymatically crosslinked hydrogel with tunable mechanical properties. Biomaterials 2014, 35, 2207–2217. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Kluge, J.A.; Rosiello, N.C.; Leisk, G.G.; Kaplan, D.L.; Dorfmann, A.L. The consolidation behavior of silk hydrogels. J. Mech. Behav. Biomed. Mater. 2010, 3, 278–289. [Google Scholar] [CrossRef]
- June, R.K.; Ly, S.; Fyhrie, D.P. Cartilage stress-relaxation proceeds slower at higher compressive strains. Arch. Biochem. Biophys. 2009, 483, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Pierce, D.M.; Isaksen, V.; Davies, C.D.L.; Drogset, J.O.; Lilledahl, M.B. Comparison of Compressive Stress-Relaxation Behavior in Osteoarthritic (ICRS Graded) Human Articular Cartilage. Int. J. Mol. Sci. 2018, 19, 413. [Google Scholar] [CrossRef]
- Jamshidi, M.; Falamaki, C. Image analysis method for heterogeneity and porosity characterization of biomimetic hydrogels. F1000Research 2021, 9, 1461. [Google Scholar] [CrossRef] [PubMed]
- Podhorská, B.; Vetrík, M.; Chylíková-Krumbholcová, E.; Kománková, L.; Banafshehvaragh, N.R.; Šlouf, M.; Dušková-Smrčková, M.; Janoušková, O. Revealing the True Morphological Structure of Macroporous Soft Hydrogels for Tissue Engineering. Appl. Sci. 2020, 10, 6672. [Google Scholar] [CrossRef]
- Chui, M.M.; Phillips, R.J.; McCarthy, M.J. Measurement of the Porous Microstructure of Hydrogels by Nuclear Magnetic Resonance. J. Colloid Interface Sci. 1995, 174, 336–344. [Google Scholar] [CrossRef]
- Leal-Egaña, A.; Braumann, U.-D.; Cuenca, A.D.; Nowicki, M.; Bader, A. Determination of pore size distribution at the cell-hydrogel interface. J. Nanobiotechnology 2011, 9, 24. [Google Scholar] [CrossRef] [PubMed]

| γ1 | τ1 (s) | γ2 | τ2 (s) | γ3 | τ3 (s) | γ4 | τ4 (s) | |
|---|---|---|---|---|---|---|---|---|
| PVA | 0.020 | 0.523 | 0.039 | 5.00 | 0.044 | 50.0 | 0.057 | 500.0 |
| OxPVA_KMnO4 | 0.016 | 0.538 | 0.025 | 5.00 | 0.043 | 50.0 | 0.082 | 500.0 |
| OxPVA_Br2 | 0.009 | 0.439 | 0.029 | 4.93 | 0.042 | 50.0 | 0.079 | 499.8 |
| OxPVA_I2 | 0.009 | 0.560 | 0.023 | 4.98 | 0.037 | 50.0 | 0.085 | 500.1 |
| E (KPa) | ν | ks (N/mm) | |
|---|---|---|---|
| PVA | 66 | 0.46 | 5.5 × 10−7 |
| OxPVA_KmnO4 | 42 | 0.47 | 1.0 × 10−6 |
| OxPVA_Br2 | 34 | 0.47 | 1.2 × 10−6 |
| OxPVA_I2 | 35 | 0.46 | 1.4 × 10−6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Todros, S.; Spadoni, S.; Barbon, S.; Stocco, E.; Confalonieri, M.; Porzionato, A.; Pavan, P.G. Compressive Mechanical Behavior of Partially Oxidized Polyvinyl Alcohol Hydrogels for Cartilage Tissue Repair. Bioengineering 2022, 9, 789. https://doi.org/10.3390/bioengineering9120789
Todros S, Spadoni S, Barbon S, Stocco E, Confalonieri M, Porzionato A, Pavan PG. Compressive Mechanical Behavior of Partially Oxidized Polyvinyl Alcohol Hydrogels for Cartilage Tissue Repair. Bioengineering. 2022; 9(12):789. https://doi.org/10.3390/bioengineering9120789
Chicago/Turabian StyleTodros, Silvia, Silvia Spadoni, Silvia Barbon, Elena Stocco, Marta Confalonieri, Andrea Porzionato, and Piero Giovanni Pavan. 2022. "Compressive Mechanical Behavior of Partially Oxidized Polyvinyl Alcohol Hydrogels for Cartilage Tissue Repair" Bioengineering 9, no. 12: 789. https://doi.org/10.3390/bioengineering9120789
APA StyleTodros, S., Spadoni, S., Barbon, S., Stocco, E., Confalonieri, M., Porzionato, A., & Pavan, P. G. (2022). Compressive Mechanical Behavior of Partially Oxidized Polyvinyl Alcohol Hydrogels for Cartilage Tissue Repair. Bioengineering, 9(12), 789. https://doi.org/10.3390/bioengineering9120789