PPG2ABP: Translating Photoplethysmogram (PPG) Signals to Arterial Blood Pressure (ABP) Waveforms
Abstract
1. Introduction
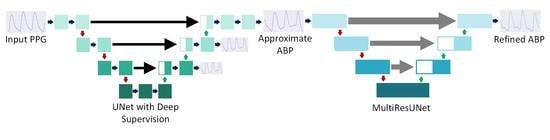
- To overcome the challenges in ABP estimation, we propose PPG2ABP, which is a cascaded approach to divide this challenging task into two stages and reach a robust outcome in the end.
- The Approximation network approximates the ABP waveforms, and the Refinement network refines the outputs of the Approximation network.
- Our proposed PPG2ABP only requires PPG waveforms for ABP estimation, thus mitigating the need for ECG probes in parallel to PPG collection devices. This makes the solution simple, cost-effective, and user-friendly.
- PPG2ABP performs better than most studies in the literature while working on a large dataset.
2. Materials and Methods
2.1. Dataset
2.2. Proposed Methodology
2.2.1. Preprocessing
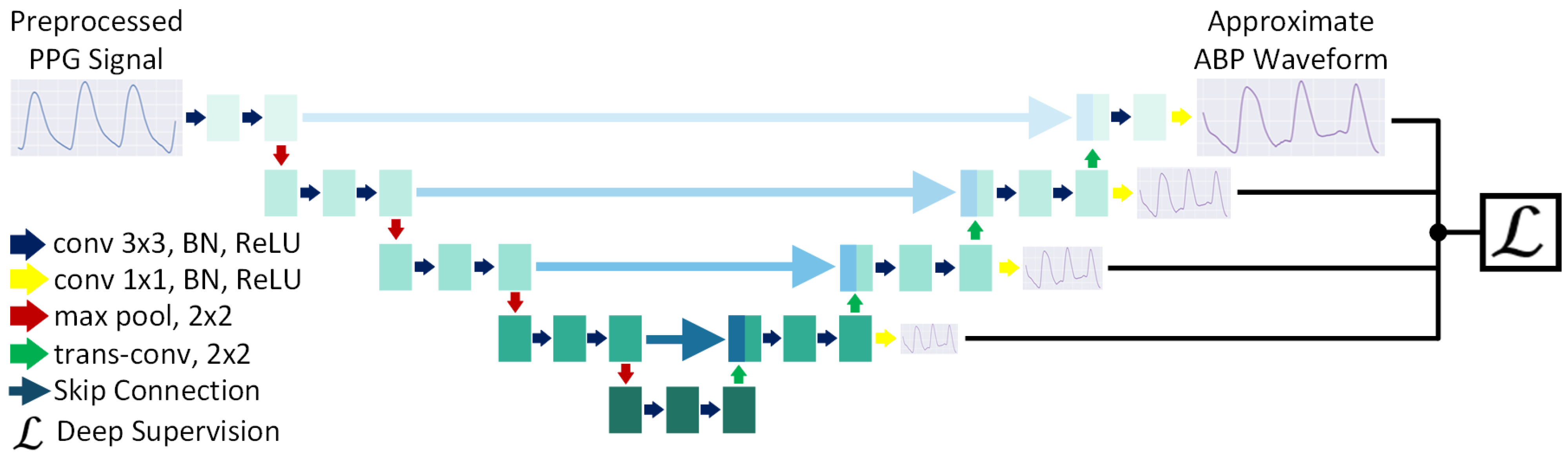
2.2.2. Approximation Network
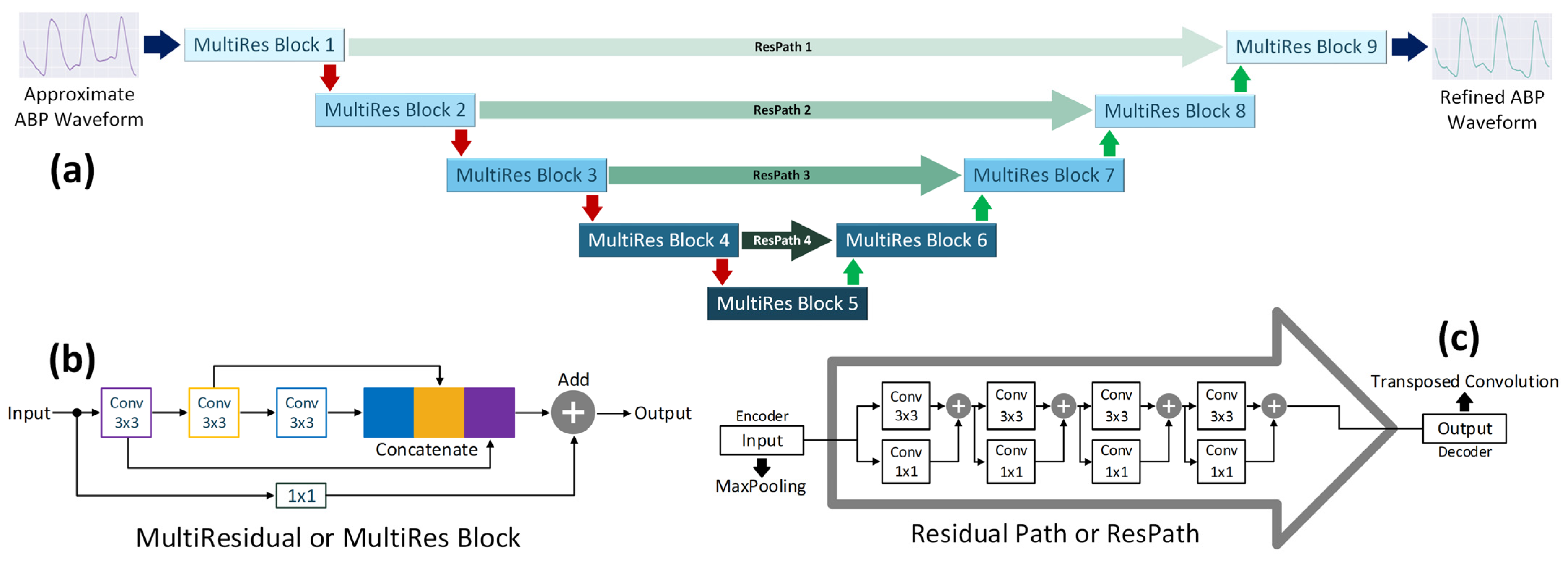
2.2.3. Refinement Network
2.2.4. BP Parameters Calculation
3. Experiments
3.1. Selection of Models
3.2. Selection of Loss Functions
3.3. Effect of Number of Convolutional Filters
3.4. Effect of Deep Supervision
3.5. Training Methodology
3.6. K-Fold Cross Validation
3.7. Evaluation Metrics
4. Results and Discussion
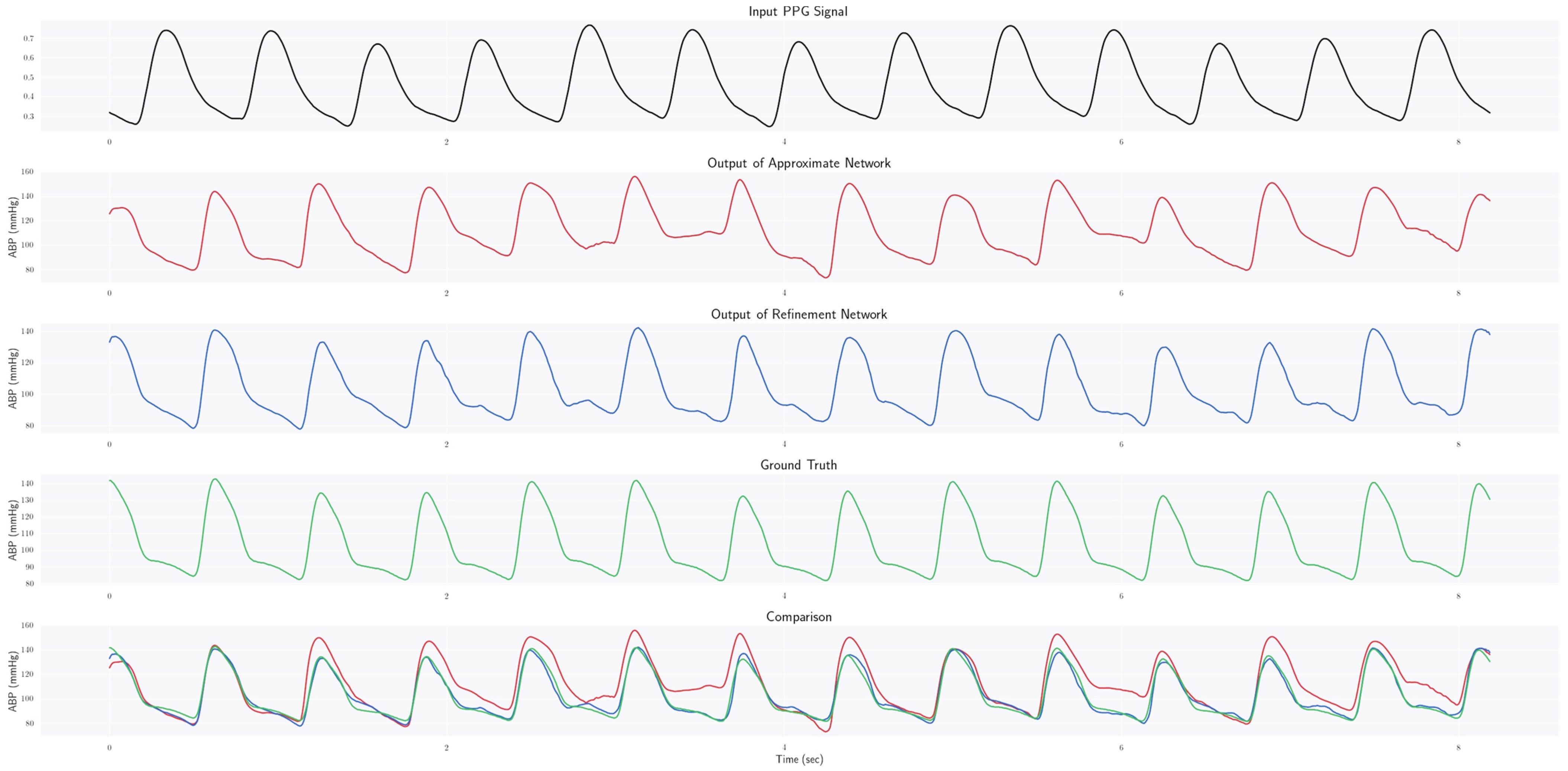
4.1. Estimating ABP Waveform
4.2. BHS Standard
4.3. AAMI Standard
4.4. Statistical Analysis
4.5. Comparison with the Existing Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laflamme, M.A.; Murry, C.E. Heart regeneration. Nature 2011, 473, 326–335. [Google Scholar] [CrossRef] [PubMed]
- Townsend, N.; Wilson, L.; Bhatnagar, P.; Wickramasinghe, K.; Rayner, M.; Nichols, M. Cardiovascular disease in Europe: Epidemiological update 2016. Eur. Heart J. 2016, 37, 3232–3245. [Google Scholar] [CrossRef] [PubMed]
- Vital Signs: Awareness and Treatment of Uncontrolled Hypertension Among Adults—The United States, 2003–2010. Centers for Disease Control and Prevention, 7 September 2012. Available online: https://www.cdc.gov/mmwr/preview/mmwrhtml/mm6135a3.htm (accessed on 22 October 2022).
- A Global Brief on Hypertension: Silent Killer, Global Public Health Crisis: World Health Day 2013. World Health Organization. Available online: https://www.who.int/publications/i/item/a-global-brief-on-hypertension-silent-killer-global-public-health-crisis-world-health-day-2013 (accessed on 22 October 2022).
- Symplicity HTN-1 Investigators. Catheter-based renal sympathetic denervation for resistant hypertension: Durability of blood pressure reduction out to 24 months. Hypertension 2011, 57, 911–917. [Google Scholar] [CrossRef]
- Landry, C.; Peterson, S.D.; Arami, A. A fusion approach to improve accuracy and estimate uncertainty in cuffless blood pressure monitoring. Sci. Rep. 2022, 12, 7948. [Google Scholar] [CrossRef] [PubMed]
- Shaltis, P.A.; Reisner, A.T.; Asada, H.H. Cuffless blood pressure monitoring using hydrostatic pressure changes. IEEE Trans. Biomed. Eng. 2008, 55, 1775–1777. [Google Scholar] [CrossRef] [PubMed]
- Shriram, R.; Wakankar, A.; Daimiwal, N.; Ramdasi, D. Continuous cuffless blood pressure monitoring based on ptt. In 2010 International Conference on Bioinformatics and Biomedical Technology; IEEE: Piscataway, NJ, USA, 2010; pp. 51–55. [Google Scholar]
- Luo, N.; Dai, W.; Li, C.; Zhou, Z.; Lu, L.; Poon, C.C.; Chen, S.-C.; Zhang, Y.; Zhao, N. Flexible piezoresistive sensor patch enabling ultralow power cuffless blood pressure measurement. Adv. Funct. Mater. 2016, 26, 1178–1187. [Google Scholar] [CrossRef]
- Kim, S.-H.; Lilot, M.; Sidhu, K.S.; Rinehart, J.; Yu, Z.; Canales, C.; Cannesson, M. Accuracy and precision of continuous noninvasive arterial pressure monitoring compared with invasive arterial pressure. Anesthesiology 2014, 120, 1080–1097. [Google Scholar] [CrossRef]
- Ilies, C.; Bauer, M.; Berg, P.; Rosenberg, J.; Hedderich, J.; Bein, B.; Hinz, J.; Hanss, R. Investigation of the agreement of a continuous non-invasive arterial pressure device in comparison with invasive radial artery measurement. Br. J. Anaesth. 2012, 108, 202–210. [Google Scholar] [CrossRef]
- Hahn, R.; Rinösl, H.; Neuner, M.; Kettner, S.C. Clinical validation of a continuous non-invasive hemodynamic monitor (CNAP™ 500) during general anesthesia. Br. J. Anaesth. 2012, 108, 581–585. [Google Scholar] [CrossRef]
- Kamboj, N.; Chang, K.; Metcalfe, K.; Chu, C.H.; Conway, A. Accuracy and precision of continuous non-invasive arterial pressure monitoring in critical care: A systematic review and meta-analysis. Intensive Crit. Care Nurs. 2021, 67, 103091. [Google Scholar] [CrossRef]
- Ghamari, M.; Castaneda, D.; Esparza, A.; Soltanpur, C.; Nazeran, H. A review on wearable photoplethysmography sensors and their potential future applications in health care. Int. J. Biosens. Bioelectron. 2018, 4, 195. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Wei, X. Monitoring heart and respiratory rates at radial artery based on ppg. Opt. Int. J. Light Electron Opt. 2013, 124, 3954–3956. [Google Scholar] [CrossRef]
- Sharma, M.; Barbosa, K.; Ho, V.; Griggs, D.; Ghirmai, T.; Krishnan, S.K.; Hsiai, T.K.; Chiao, J.-C.; Cao, H. Cuff-less and continuous blood pressure monitoring: A methodological review. Technologies 2017, 5, 21. [Google Scholar] [CrossRef]
- Kavsaoglu, A.R.; Polat, K.; Hariharan, M. Non-invasive prediction of hemoglobin level using machine learning techniques with the ppg signal’s characteristics features. Appl. Soft Comput. 2015, 37, 983–991. [Google Scholar] [CrossRef]
- Selvaraj, N.; Jaryal, A.K.; Santhosh, J.; Anand, S.; Deepak, K.K. Monitoring of reactive hyperemia using photoplethysmographic pulse amplitude and transit time. J. Clin. Monit. Comput. 2009, 23, 315–322. [Google Scholar] [CrossRef]
- Slapnicar, G.; Mlakar, N.; Luštrek, M. Blood pressure estimation from photoplethysmogram using a spectro-temporal deep neural network. Sensors 2019, 19, 3420. [Google Scholar] [CrossRef]
- Bramwell, J.C.; Hill, A.V. The velocity of the pulse wave in man. Proc. R. Soc. Lond. Ser. B Contain. Pap. Biol. Character 1922, 93, 298–306. [Google Scholar]
- Geddes, L.; Voelz, M.; Babbs, C.; Bourland, J.; Tacker, W. Pulse transit time as an indicator of arterial blood pressure. Psychophysiology 1981, 18, 71–74. [Google Scholar] [CrossRef]
- Wong, M.Y.-M.; Poon, C.C.-Y.; Zhang, Y.-T. An evaluation of the cuffless blood pressure estimation based on pulse transit time technique: A half year study on normotensive subjects. Cardiovasc. Eng. 2009, 9, 32–38. [Google Scholar] [CrossRef]
- Baek, H.J.; Kim, K.K.; Kim, J.S.; Lee, B.; Park, K.S. Enhancing the estimation of blood pressure using pulse arrival time and two confounding factors. Physiol. Meas. 2009, 31, 145. [Google Scholar] [CrossRef]
- Marcinkevics, Z.; Greve, M.; Aivars, J.I.; Erts, R.; Zehtabi, A.H. Relationship between arterial pressure and pulse wave velocity using photoplethysmography during the post-exercise recovery period. Acta Univesitatis Latv. Biol. 2009, 753, 59–68. [Google Scholar]
- Proença, J.; Muehlsteff, J.; Aubert, X.; Carvalho, P. Is pulse transit time a good indicator of blood pressure changes during short physical exercise in a young population? In 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology; IEEE: Piscataway, NJ, USA, 2010; pp. 598–601. [Google Scholar]
- Gesche, H.; Grosskurth, D.; Küchler, G.; Patzak, A. Continuous blood pressure measurement by using the pulse transit time: Comparison to a cuff-based method. Eur. J. Appl. Physiol. 2012, 112, 309–315. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.S.; Firouzmand, M.; Charmi, M.; Hemmati, M.; Moghadam, M.; Ghorbani, Y. Blood pressure estimation from appropriate and inappropriate ppg signals using a whole-based method. Biomed. Signal Process. Control 2019, 47, 196–206. [Google Scholar] [CrossRef]
- Thambiraj, G.; Gandhi, U.; Devanand, V.; Mangalanathan, U. Noninvasive cuffless blood pressure estimation using pulse transit time, Womersley number, and photoplethysmogram intensity ratio. Physiol. Meas. 2019, 40, 075001. [Google Scholar] [CrossRef]
- Thambiraj, G.; Gandhi, U.; Mangalanathan, U.; Jose, V.J.; Anand, M. Investigation on the effect of Womersley number, ECG and PPG features for cuffless blood pressure estimation using machine learning. Biomed. Signal Process. Control 2020, 60, 101942. [Google Scholar] [CrossRef]
- Monte-Moreno, E. Non-invasive estimate of blood glucose and blood pressure from a photoplethysmograph by means of machine learning techniques. Artif. Intell. Med. 2011, 53, 127–138. [Google Scholar] [CrossRef]
- Tazarv, A.; Levorato, M. A deep learning approach to predict blood pressure from ppg signals. In Proceedings of the 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Virtual, 31 October–4 November 2021; pp. 5658–5662. [Google Scholar]
- Fujita, D.; Suzuki, A.; Ryu, K. PPG-based systolic blood pressure estimation method using PLS and level-crossing feature. Appl. Sci. 2019, 9, 304. [Google Scholar] [CrossRef]
- Bose, S.S.N.; Kandaswamy, A. Sparse representation of photoplethysmogram using K-SVD for cuffless estimation of arterial blood pressure. In Proceedings of the 2017 4th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 6–7 January 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Peter, L.; Noury, N.; Cerny, M. A review of methods for non-invasive and continuous blood pressure monitoring: Pulse Transit Time Method is promising? IRBM 2014, 35, 271–282. [Google Scholar] [CrossRef]
- Esmaili, A.; Kachuee, M.; Shabany, M. Nonlinear Cuffless Blood Pressure Estimation of Healthy Subjects Using Pulse Transit Time and Arrival Time. IEEE Trans. Instrum. Meas. 2017, 66, 3299–3308. [Google Scholar] [CrossRef]
- Miao, F.; Liu, Z.-D.; Liu, J.-K.; Wen, B.; He, Q.-Y.; Li, Y. Multi-Sensor Fusion Approach for Cuff-Less Blood Pressure Measurement. IEEE J. Biomed. Health Inform. 2020, 24, 79–91. [Google Scholar] [CrossRef]
- Forouzanfar, M.; Dajani, H.R.; Groza, V.Z.; Bolic, M.; Rajan, S. Feature-Based Neural Network Approach for Oscillometric Blood Pressure Estimation. IEEE Trans. Instrum. Meas. 2011, 60, 2786–2796. [Google Scholar] [CrossRef]
- Hsu, Y.-C.; Li, Y.-H.; Chang, C.-C.; Harfiya, L.N. Generalized deep neural network model for cuffless blood pressure estimation with Photoplethysmogram Signal only. Sensors 2020, 20, 5668. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Ren, J.; Cheng, Y.; Wang, B.; Wei, Z. Health Data Driven on Continuous Blood Pressure Prediction Based on Gradient Boosting Decision Tree Algorithm. IEEE Access 2019, 7, 32423–32433. [Google Scholar] [CrossRef]
- Sasso, A.M.; Datta, S.; Jeitler, M.; Steckhan, N.; Kessler, C.S.; Michalsen, A.; Arnrich, B.; Böttinger, E. HYPE: Predicting blood pressure from photoplethysmograms in a hypertensive population. In Artificial Intelligence in Medicine; Springer: Cham, Switzerland, 2020; pp. 325–335. [Google Scholar]
- Moradi, E.M.H.; Kadkhodamohammadi, A. A multistage deep neural network model for blood pressure estimation using photoplethysmogram signals. Comput. Biol. Med. 2020, 120, 103719. [Google Scholar] [CrossRef]
- Li, Y.H.; Harfiya, L.N.; Purwandari, K.; der Lin, Y. Real-time cuffless continuous blood pressure estimation using deep learning model. Sensors 2020, 20, 5606. [Google Scholar] [CrossRef] [PubMed]
- Miao, F.; Wen, B.; Hu, Z.; Fortino, G.; Wang, X.-P.; Liu, Z.-D.; Tang, M.; Li, Y. Continuous blood pressure measurement from one-channel electrocardiogram signal using deep-learning techniques. Artif. Intell. Med. 2020, 108, 101919. [Google Scholar] [CrossRef]
- Baker, S.; Xiang, W.; Atkinson, I. A hybrid neural network for continuous and non-invasive estimation of blood pressure from raw electrocardiogram and Photoplethysmogram waveforms. Comput. Methods Programs Biomed. 2021, 207, 106191. [Google Scholar] [CrossRef]
- Pradenas, L. A Novel Non-Invasive Estimation of Arterial Blood Pressure from Electrocardiography and Photoplethysmography Signals using Machine Learning. Biomed. J. Sci. Tech. Res. 2020, 30, 106191. [Google Scholar] [CrossRef]
- Hill, B.; Rakocz, N.; Rudas, Á.; Chiang, J.N.; Wang, S.; Hofer, I.; Cannesson, M.; Halperin, E. Imputation of the continuous arterial line blood pressure waveform from non-invasive measurements using deep learning. Sci. Rep. 2021, 11, 15755. [Google Scholar] [CrossRef]
- Li, P.; Laleg-Kirati, T. Central Blood Pressure Estimation from Distal PPG Measurement Using Semiclassical Signal Analysis Features. IEEE Access 2021, 9, 44963–44973. [Google Scholar] [CrossRef]
- Salah, M.; Omer, O.; Hassan, L.; Ragab, M.; Hassan, A.; Abdelreheem, A. Beat-Based PPG-ABP Cleaning Technique for Blood Pressure Estimation. IEEE Access 2022, 10, 55616–55626. [Google Scholar] [CrossRef]
- Rong, M.; Li, K. A multi-type features fusion neural network for blood pressure prediction based on photoplethysmography. Biomed. Signal Process. Control 2021, 68, 102772. [Google Scholar] [CrossRef]
- Mahmud, S.; Ibtehaz, N.; Khandakar, A.; Tahir, A.M.; Rahman, T.; Islam, K.R.; Hossain, M.S.; Rahman, M.S.; Musharavati, F.; Ayari, M.A.; et al. A Shallow U-Net Architecture for Reliably Predicting Blood Pressure (BP) from Photoplethysmogram (PPG) and Electrocardiogram (ECG) Signals. Sensors 2022, 22, 919. [Google Scholar] [CrossRef]
- Athaya, T.; Choi, S. An estimation method of continuous non-invasive arterial blood pressure waveform using photoplethysmography: A u-net architecture-based approach. Sensors 2021, 21, 1867. [Google Scholar] [CrossRef]
- Harfiya, L.N.; Chang, C.C.; Li, Y.H. Continuous blood pressure estimation using exclusively photoplethysmography by lstm-based signal-to-signal translation. Sensors 2021, 21, 2952. [Google Scholar] [CrossRef] [PubMed]
- Mahmud, S.; Ibtehaz, N.; Khandakar, A.; Rahman, M.S.; Gonzales, A.J.R.; Rahman, T.; Hossain, M.S.; Hossain, M.S.A.; Faisal, M.A.A.; Abir, F.F.; et al. NABNet: A nested attention guided BICONVLSTM network for a robust prediction of blood pressure components from reconstructed arterial blood pressure waveforms using PPG and ECG signals. Biomed. Signal Process. Control 2023, 79, 104247. [Google Scholar] [CrossRef]
- Qin, K.; Huang, W.; Zhang, T. Deep generative model with domain adversarial training for predicting arterial blood pressure waveform from photoplethysmogram signal. Biomed. Signal Process. Control 2021, 70, 102972. [Google Scholar] [CrossRef]
- Mehrabadi, M.; Aqajari, S.; Zargari, A.; Dutt, N.; Rahmani, A. Novel Blood Pressure Waveform Reconstruction from Photoplethysmography using Cycle Generative Adversarial Networks. arXiv 2022, arXiv:2201.09976. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. Physiobank, physiotoolkit, and physionet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Saeed, M.; Villarroel, M.; Reisner, A.T.; Clifford, G.; Lehman, L.-W.; Moody, G.; Heldt, T.; Kyaw, T.H.; Moody, B.; Mark, R.G. Multiparameter intelligent monitoring in intensive care ii (mimic-ii): A public-access intensive care unit database. Crit. Care Med. 2011, 39, 952. [Google Scholar] [CrossRef]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuffless high-accuracy calibration-free blood pressure estimation using pulse transit time. In 2015 IEEE International Symposium on Circuits and Systems (ISCAS); IEEE: Piscataway, NJ, USA, 2015; pp. 1006–1009. [Google Scholar]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shaban, M. Cuffless blood pressure estimation algorithms for continuous health-care monitoring. IEEE Trans. Biomed. Eng. 2016, 64, 859–869. [Google Scholar] [CrossRef] [PubMed]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2019. Available online: http://archive.ics.uci.edu/ml (accessed on 13 September 2020).
- Wang, C.; Li, X.; Hu, H.; Zhang, L.; Huang, Z.; Lin, M.; Zhang, Z.; Yin, Z.; Huang, B.; Gong, H.; et al. Monitoring of the central blood pressure waveform via a conformal ultrasonic device. Nat. Biomed. Eng. 2018, 2, 687–695. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. Optimal signal quality index for photoplethysmogram signals. Bioengineering 2016, 3, 21. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.S.; Chowdhury, M.E.; Reaz, M.B.; Ali, S.H.; Bakar, A.A.; Kiranyaz, S.; Khandakar, A.; Alhatou, M.; Habib, R.; Hossain, M.M. Motion artifacts correction from single-channel EEG and fNIRS signals using novel wavelet packet decomposition in combination with canonical correlation analysis. Sensors 2022, 22, 3169. [Google Scholar] [CrossRef]
- Singh, B.N.; Tiwari, A.K. Optimal selection of wavelet basis function applied to ecg signal denoising. Digit. Signal Process. 2006, 16, 275–287. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Lee, C.-Y.; Xie, S.; Gallagher, P.; Zhang, Z.; Tu, Z. Deeply-supervised nets. In Proceedings of the Artificial Intelligence and Statistics, Valencia, Spain, 28–30 March 2015; pp. 562–570. [Google Scholar]
- Ibtehaz, N.; Rahman, M.S. Multiresunet: Rethinking the u-net architecture for multimodal biomedical image segmentation. Neural Netw. 2020, 121, 74–87. [Google Scholar] [CrossRef]
- Ibtehaz, N. GitHub—Nibtehaz/PPG2ABP. GitHub. 2020. Available online: https://github.com/nibtehaz/PPG2ABP (accessed on 13 September 2020).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Xing, X.; Sun, M. Optical blood pressure estimation with photoplethysmography and fft-based neural networks. Biomed. Opt. Express 2016, 7, 3007–3020. [Google Scholar] [CrossRef]
- O’Brien, E.; Petrie, J.; Littler, W.; de Swiet, M.; Padfield, P.L.; Altman, D.; Bland, M.; Coats, A.; Atkins, N. The British hypertension society protocol for the evaluation of blood pressure measuring devices. J. hypertens. 1993, 11 (Suppl. 2), S43–S62. [Google Scholar]
- ANSI/AAMI SP10:2002/(R)2008 and A1:2003/(R)2008 and A2:2006/(R)2008. ANSI Webstore. Available online: https://webstore.ansi.org/Standards/AAMI/ansiaamisp1020022008a12003a2 (accessed on 20 July 2022).
- Giavarina, D. Understanding bland Altman analysis. Biochem. Med. 2015, 25, 141–151. [Google Scholar] [CrossRef]
- Ibtehaz, N.; Mahmud, S.; Chowdhury, M.E.H.; Khandakar, A.; Ayari, M.A.; Tahir, A.; Rahman, M.S. Ppg2abp: Translating photoplethysmogram (ppg) signals to arterial blood pressure (abp) waveforms using fully convolutional neural networks. arXiv 2020, arXiv:2005.01669. [Google Scholar]
- Liang, Y.; Elgendi, M.; Chen, Z.; Ward, R. An optimal filter for short photoplethysmogram signals. Sci. Data 2018, 5, 180076. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, R.; Natarajan, B.; Warren, S. Two-stage approach for detection and reduction of motion artifacts in photoplethysmographic data. IEEE Trans. Biomed. Eng. 2010, 57, 1867–1876. [Google Scholar] [CrossRef]

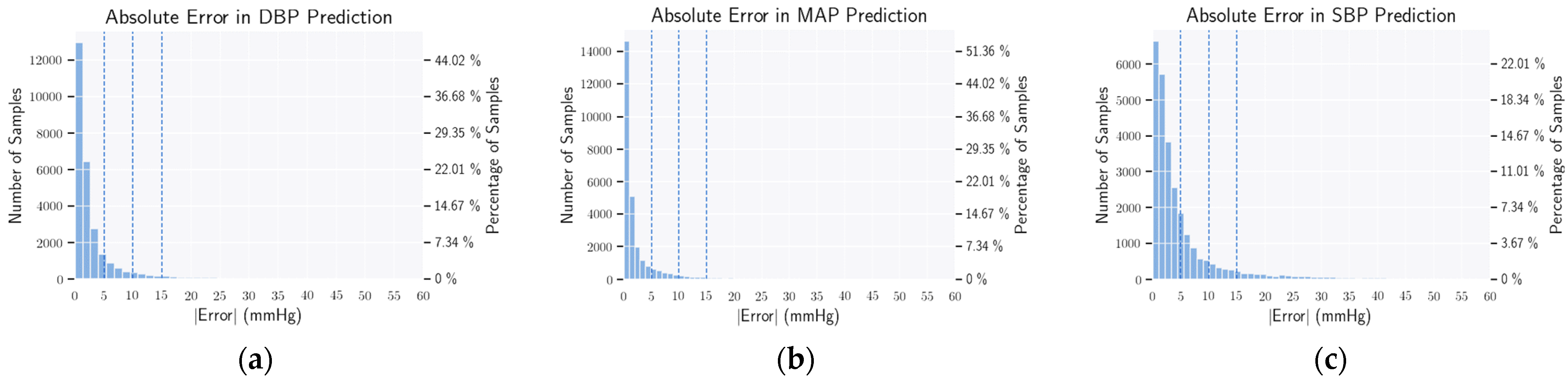
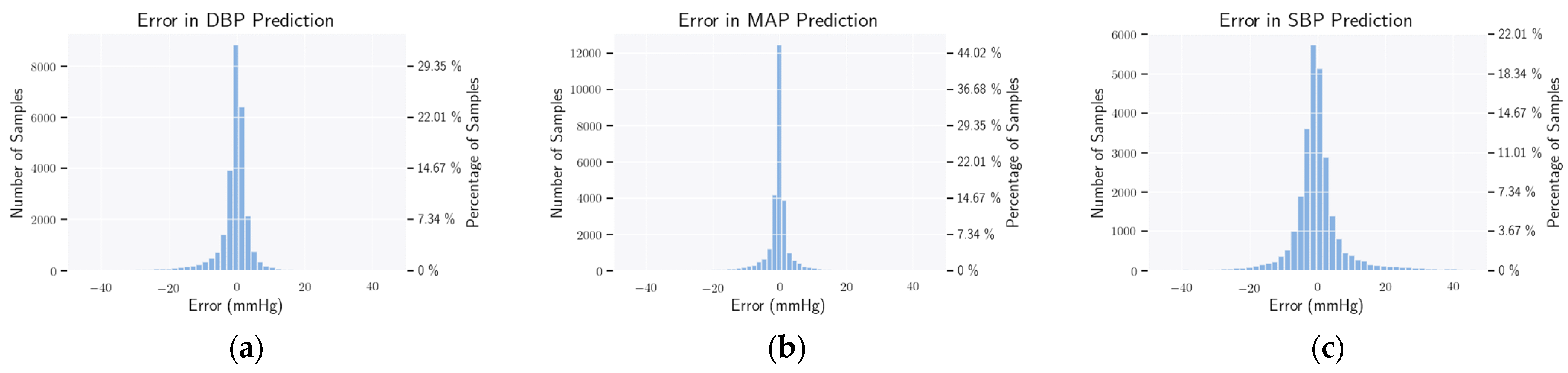
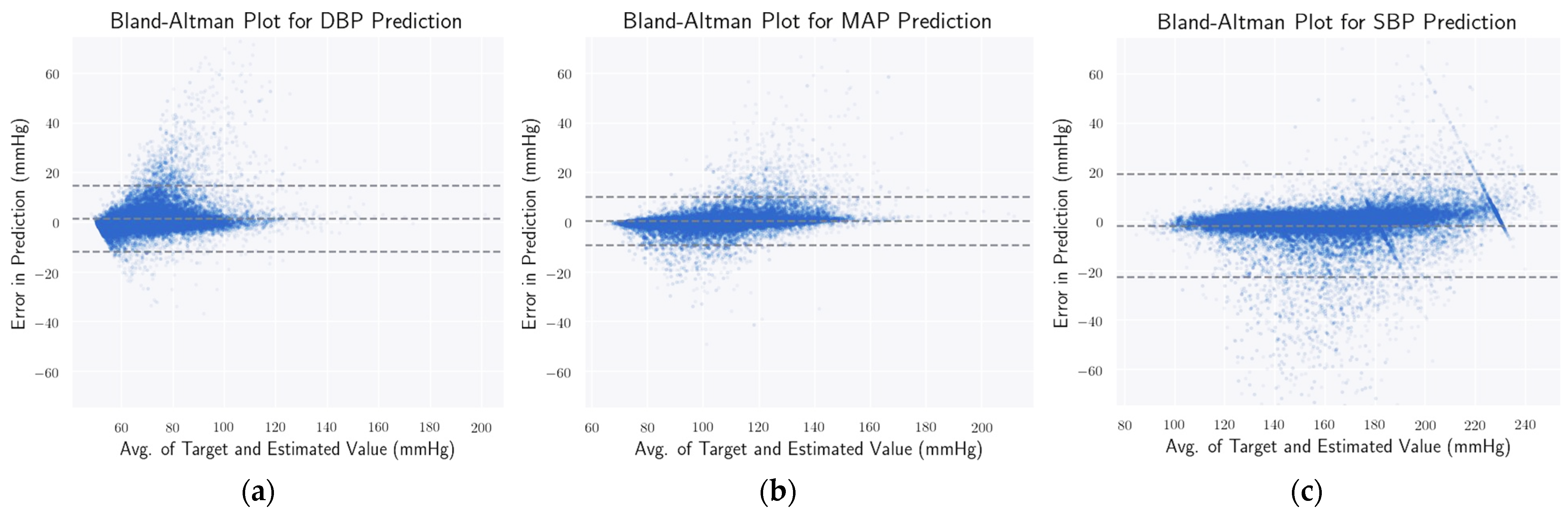
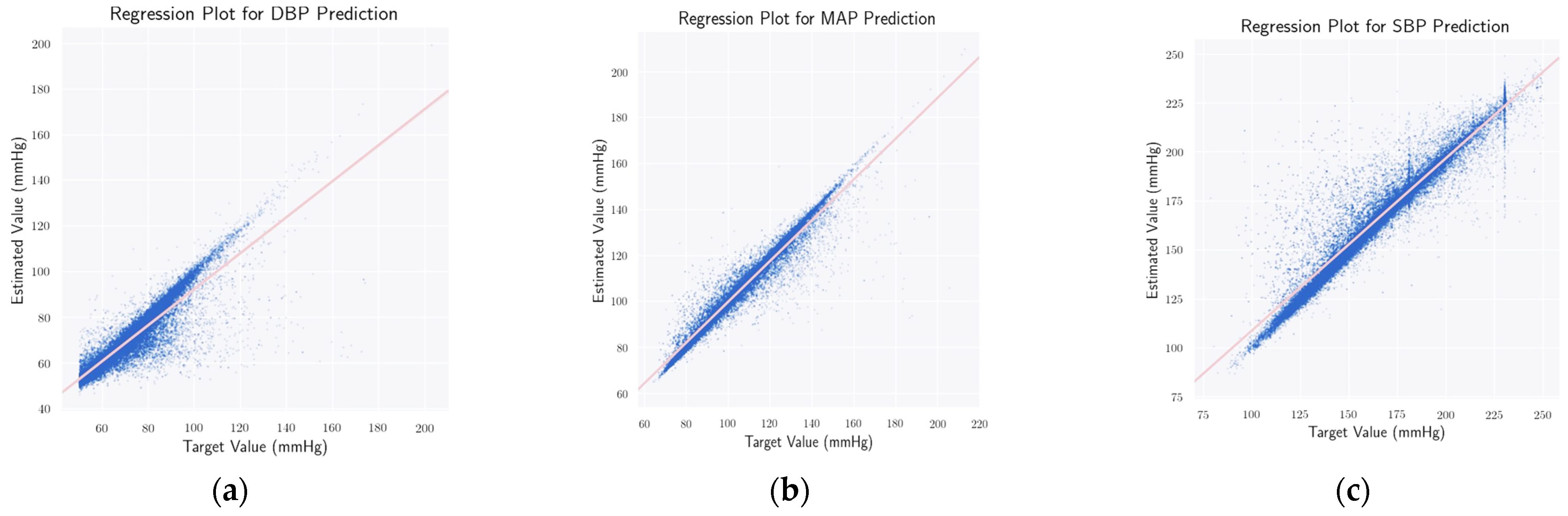
| Min (mmHg) | Max (mmHg) | Mean (mmHg) | Std (mmHg) | |
| DBP | 50 | 165.17 | 66.14 | 11.45 |
| MAP | 59.96 | 176.88 | 90.78 | 14.15 |
| SBP | 71.56 | 199.99 | 134.19 | 22.93 |
| Cumulative Error Percentage | ||||
| ≤5 mmHg | ≤10 mmHg | ≤15 mmHg | ||
| Our Results | DBP | 82.836% | 92.157% | 95.734% |
| MAP | 87.381% | 95.169% | 97.733% | |
| SBP | 70.814% | 85.301% | 90.921% | |
| BHS | Grade A | 60% | 85% | 95% |
| Grade B | 50% | 75% | 90% | |
| Grade C | 40% | 65% | 85% | |
| ME (mmHg) | STD (mmHg) | Number of Subjects | ||
| Our Results | DBP | 1.619 | 6.859 | 942 [59] |
| MAP | 0.631 | 4.962 | ||
| SBP | −1.582 | 10.688 | ||
| AAMI Standard | 5 | 8 | 85 | |
| Study | Appearing Year | Dataset | Input | Results |
| Kachuee et al. [58] | 2015 | MIMIC-III | PPG, ECG | BHS Standard: DBP = Grade B, MAP = Grade C, SBP = Grade D MAE: DBP = 6.34 mmHg, MAP = 7.52 mmHg, SBP = 12.38 mmHg |
| Kachuee et al. [59] | 2016 | MIMIC-III | PPG, ECG | BHS Standard: DBP = Grade B, MAP = Grade C, SBP = Grade D AAMI Standard met for DBP, MAP MAE: DBP = 5.35 mmHg, MAP = 5.92 mmHg, SBP = 11.17 mmHg |
| Mousavi et al. [27] | 2019 | MIMIC-III | PPG | BHS Standard: DBP = Grade A, MAP = Grade B, SBP = Grade D AAMI Standard met for DBP, MAP |
| Slapnivcar et al. [19] | 2019 | MIMIC-III | PPG | MAE: DBP = 9.43 mmHg, SBP = 6.88 mmHg |
| Athaya et al. [51] | 2021 | MIMIC-III | PPG | BHS Standard: DBP = Grade A, MAP = Grade A, SBP = Grade A MAE: DBP = 2.17 mmHg, MAP = 1.97 mmHg, SBP = 3.68 mmHg |
| Harfiya et al. [52] | 2021 | MIMIC-III | PPG | BHS Standard: DBP = Grade A, MAP = Grade A, SBP = Grade A MAE: DBP = 2.41 mmHg, SBP = 4.05 mmHg |
| Qin et al. [54] | 2021 | MIMIC-III | PPG | BHS Standard: DBP = Grade A, MAP = Grade A, SBP = Grade B MAE: DBP = 7.95 mmHg, MAP = 3.83 mmHg, SBP = 4.11 mmHg |
| Mehrabadi et al. [55] | 2022 | MIMIC-III | PPG | BHS Standard: DBP = Grade A, MAP = Grade A, SBP = Grade A MAE: DBP = 1.93 mmHg, SBP = 2.29 mmHg |
| PPG2ABP (Proposed) | 2020 | MIMIC-III | PPG | BHS Standard: DBP = Grade A, MAP = Grade A, SBP = Grade B AAMI Standard met for: DBP, MAP MAE: DBP = 3.45 mmHg, MAP = 2.31 mmHg, SBP = 5.73 mmHg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibtehaz, N.; Mahmud, S.; Chowdhury, M.E.H.; Khandakar, A.; Salman Khan, M.; Ayari, M.A.; Tahir, A.M.; Rahman, M.S. PPG2ABP: Translating Photoplethysmogram (PPG) Signals to Arterial Blood Pressure (ABP) Waveforms. Bioengineering 2022, 9, 692. https://doi.org/10.3390/bioengineering9110692
Ibtehaz N, Mahmud S, Chowdhury MEH, Khandakar A, Salman Khan M, Ayari MA, Tahir AM, Rahman MS. PPG2ABP: Translating Photoplethysmogram (PPG) Signals to Arterial Blood Pressure (ABP) Waveforms. Bioengineering. 2022; 9(11):692. https://doi.org/10.3390/bioengineering9110692
Chicago/Turabian StyleIbtehaz, Nabil, Sakib Mahmud, Muhammad E. H. Chowdhury, Amith Khandakar, Muhammad Salman Khan, Mohamed Arselene Ayari, Anas M. Tahir, and M. Sohel Rahman. 2022. "PPG2ABP: Translating Photoplethysmogram (PPG) Signals to Arterial Blood Pressure (ABP) Waveforms" Bioengineering 9, no. 11: 692. https://doi.org/10.3390/bioengineering9110692
APA StyleIbtehaz, N., Mahmud, S., Chowdhury, M. E. H., Khandakar, A., Salman Khan, M., Ayari, M. A., Tahir, A. M., & Rahman, M. S. (2022). PPG2ABP: Translating Photoplethysmogram (PPG) Signals to Arterial Blood Pressure (ABP) Waveforms. Bioengineering, 9(11), 692. https://doi.org/10.3390/bioengineering9110692