Computational Modeling of Microwave Tumor Ablation
Abstract
1. Introduction
2. Mathematical Models of Tissue and Heat Transport
2.1. Tissue Model
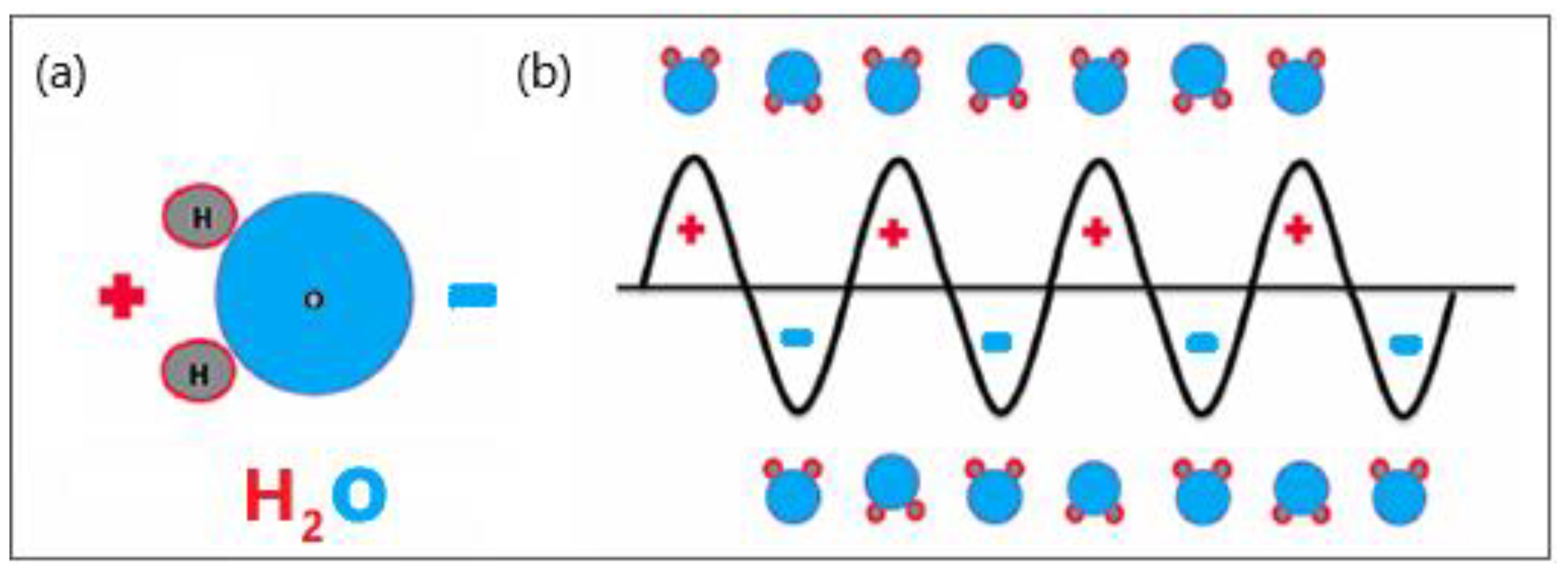
2.1.1. Top-Down Approach
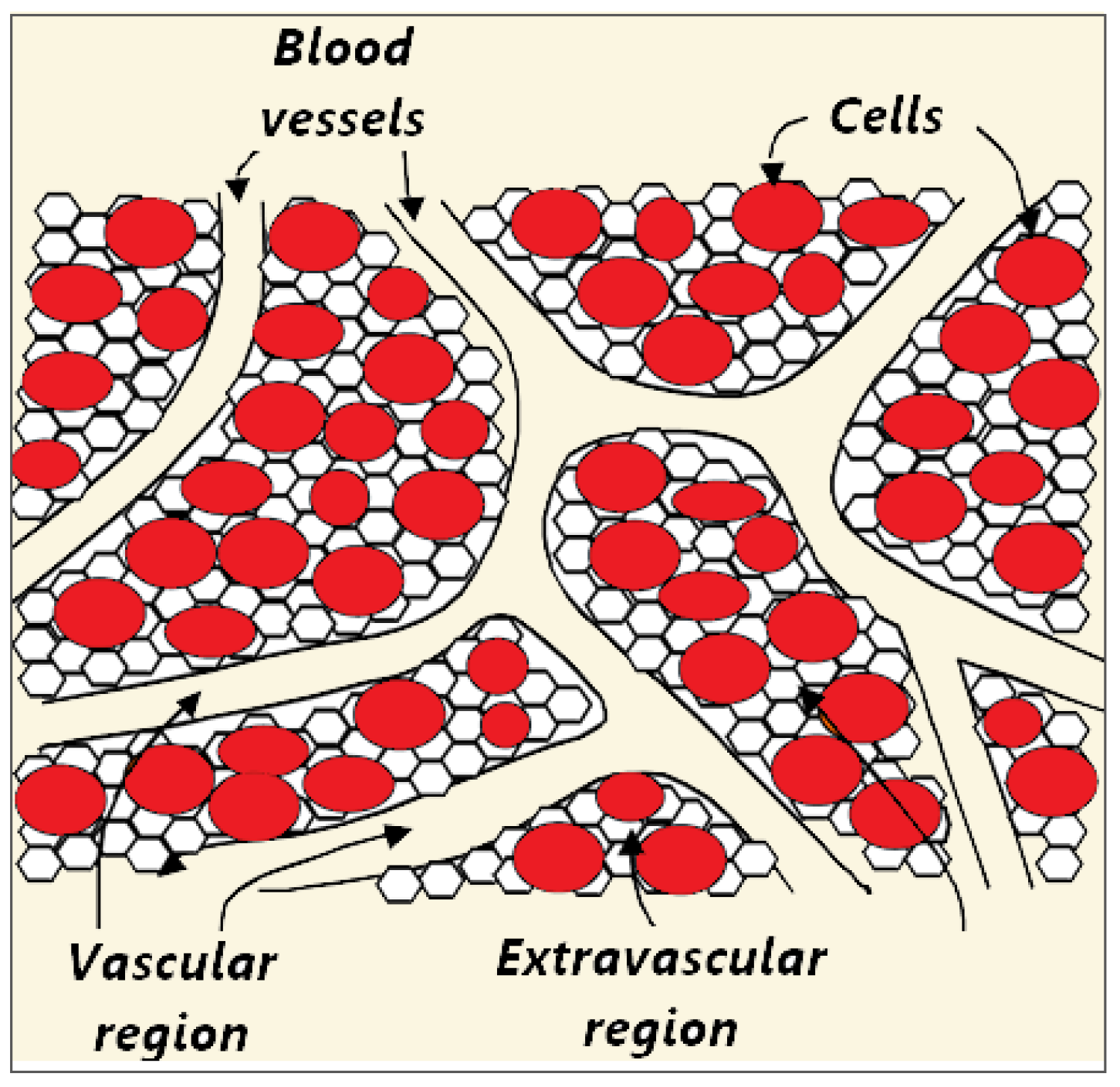
2.1.2. Bottom-Up Approach
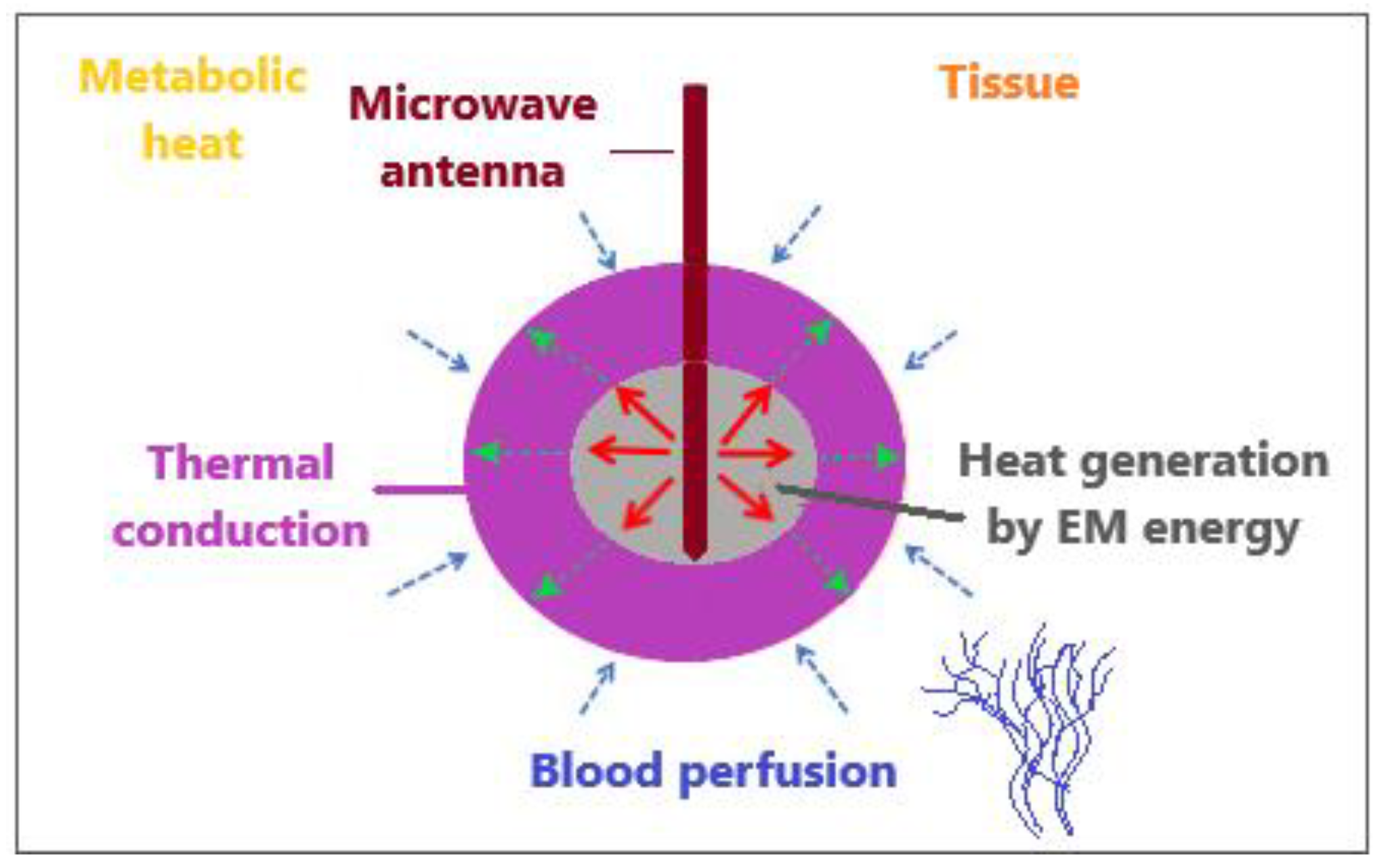
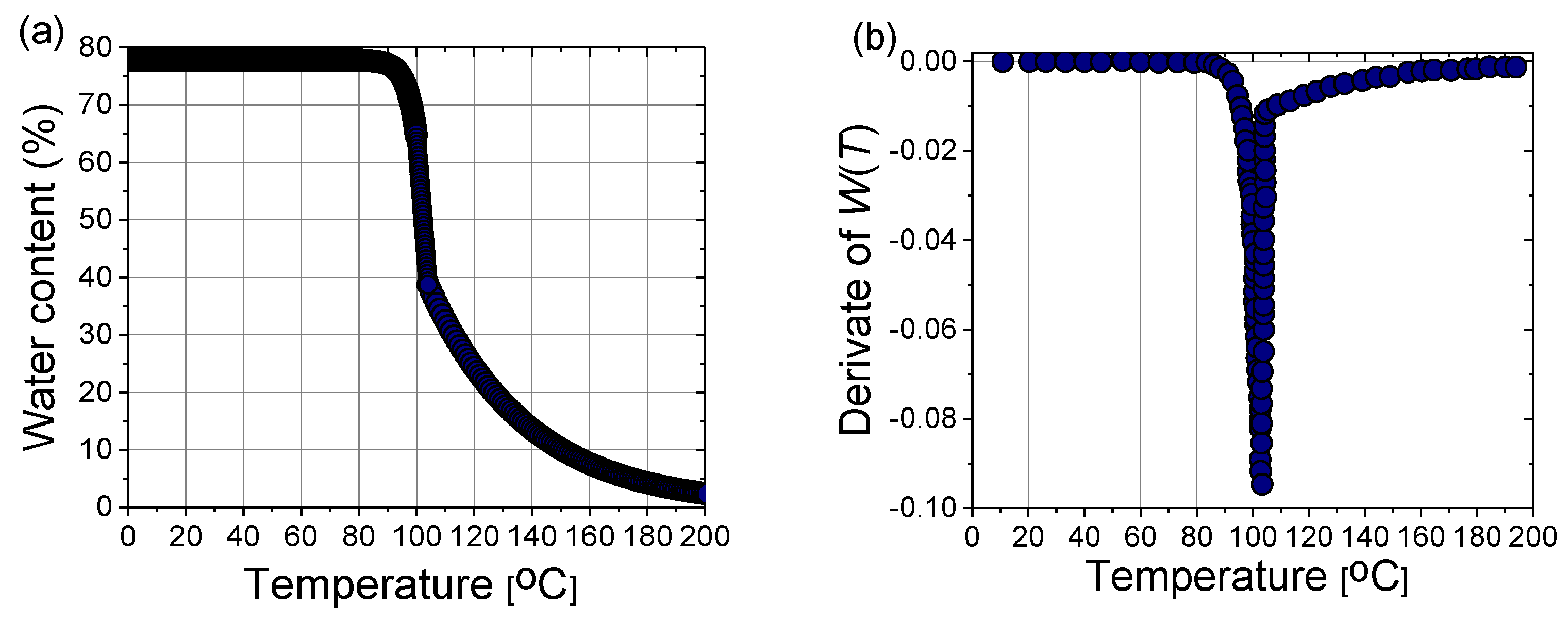
2.2. Heat Transport in Tissues
2.2.1. Pennes Model
2.2.2. Modified Local Thermal Non-Equilibrium (LTNE) Model
2.2.3. Modified Local Thermal Equilibrium (LTE) Model
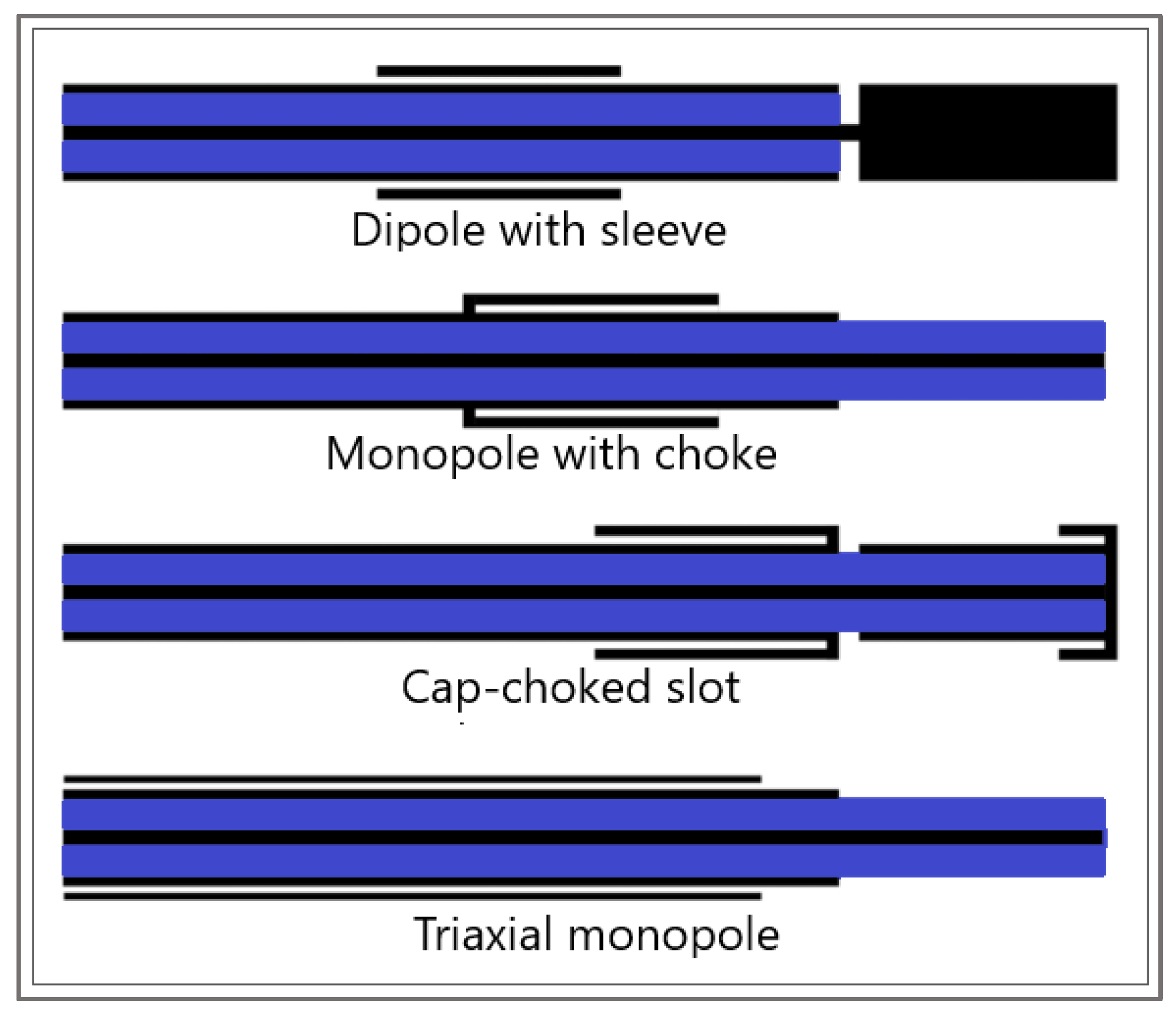
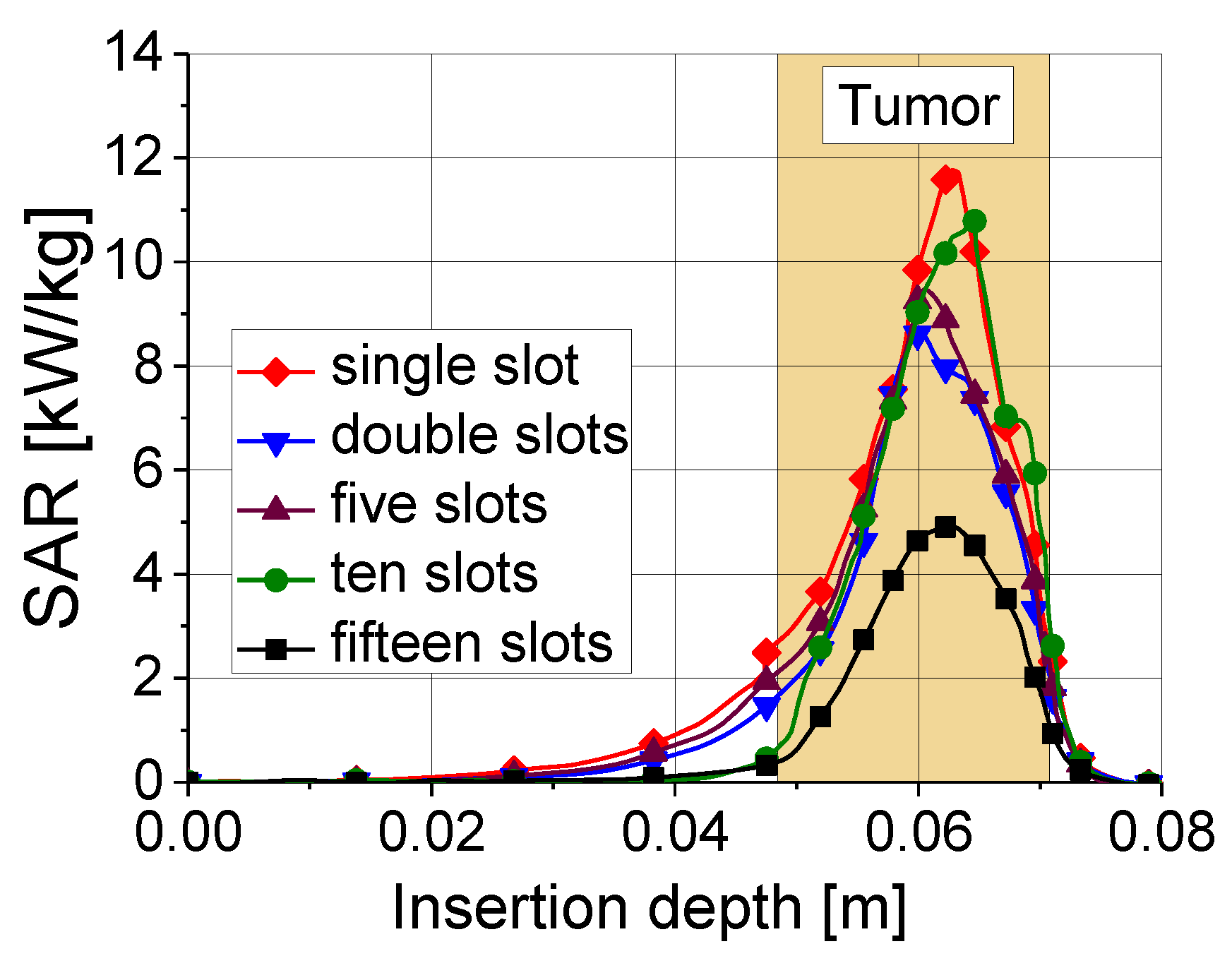
3. Modeling of the Electromagnetic Field Generated by the Antenna
4. Modeling of Microwave Ablation in the Treatment of Hepatocellular Carcinoma
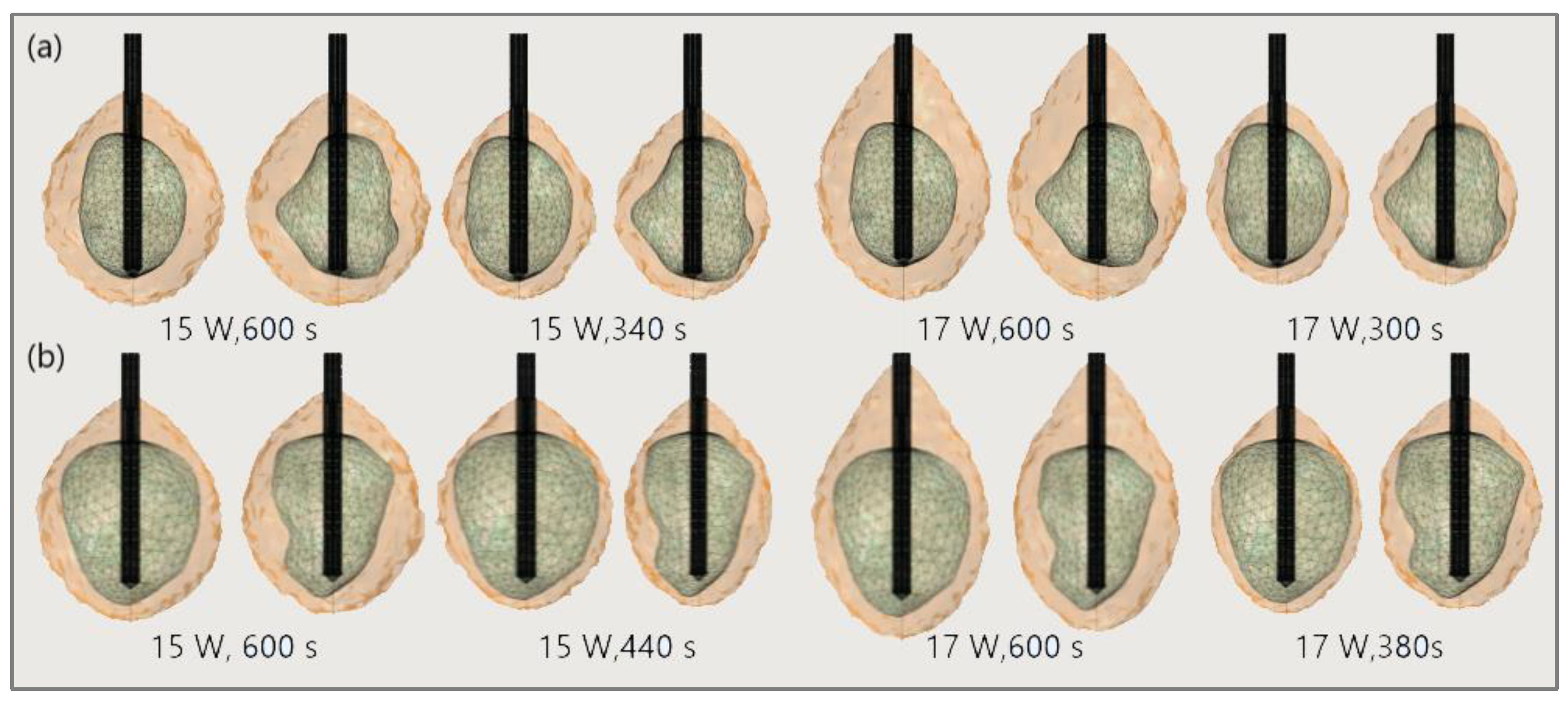
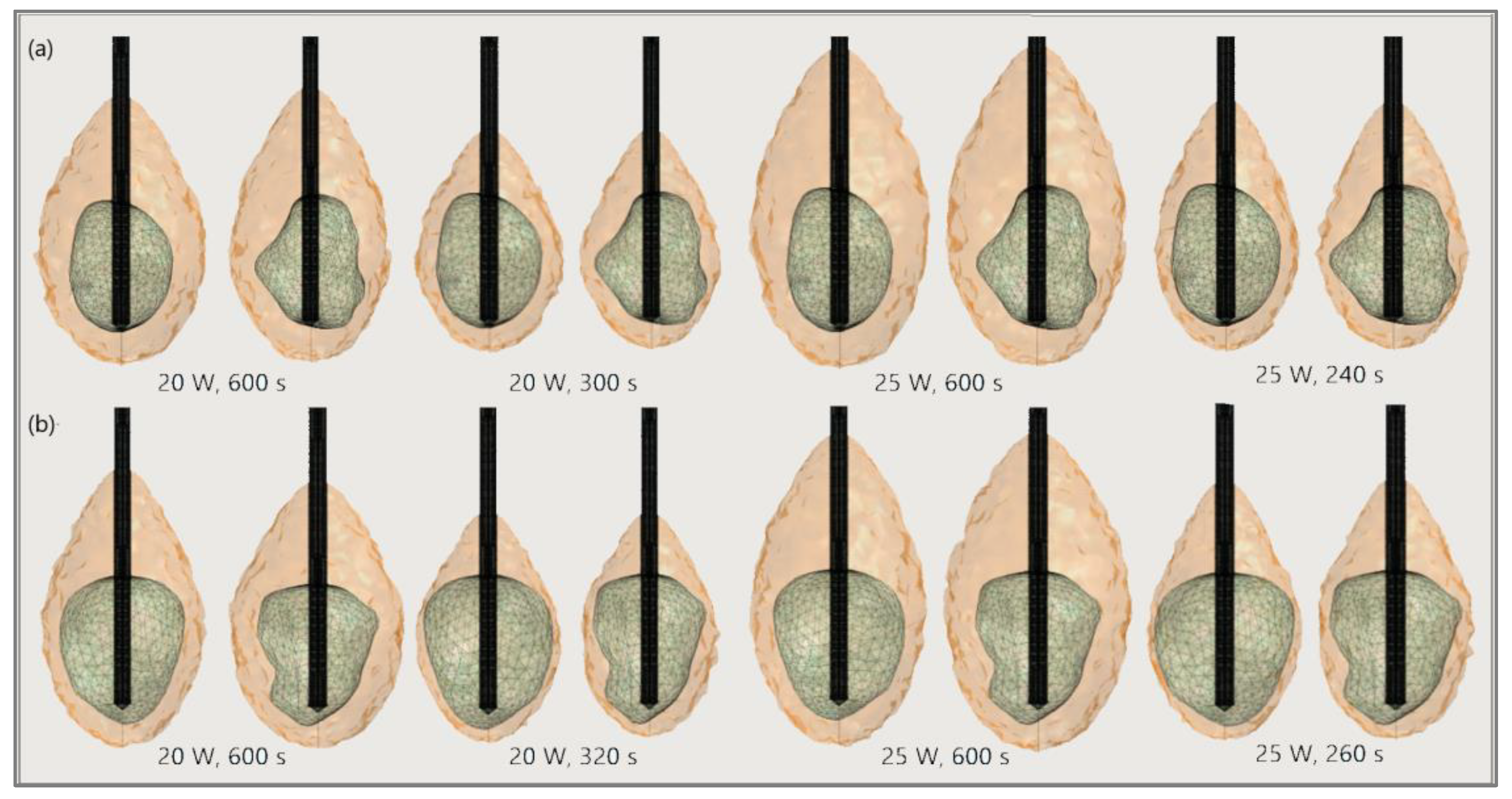
4.1. Results
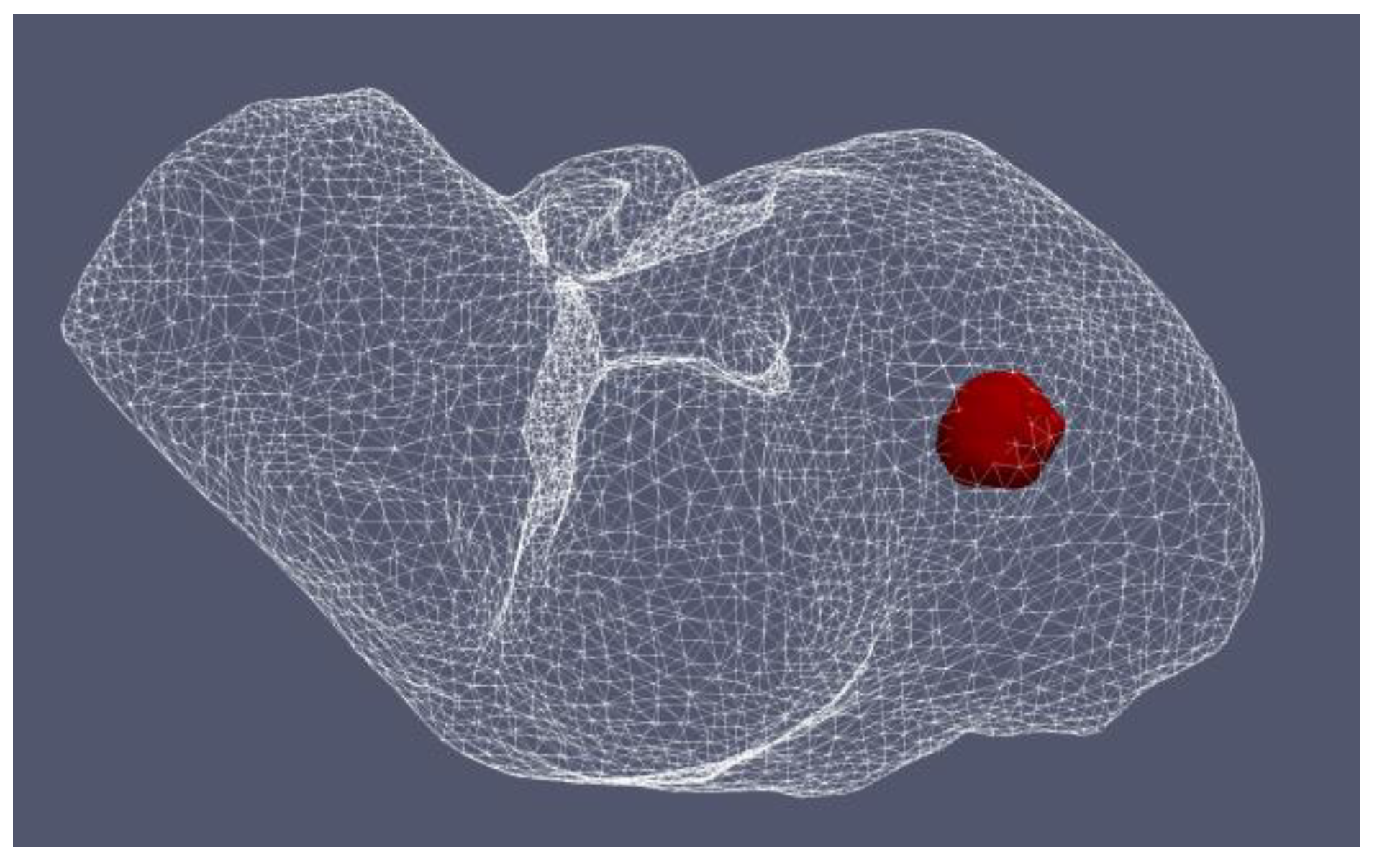
4.1.1. Hepatocellular Carcinoma of Patient 16 in the 3D-IRCADb-01 Database
4.1.2. Hepatocellular Carcinomas of Patient 1 in the 3D-IRCADb-01 Database
5. Discussion
6. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ong, S.L.; Gravante, G.; Metcalfe, M.S.; Strickland, A.D.; Dennison, A.; Lloyd, D.M. Efficacy and safety of microwave ablation for primary and secondary liver malignancies: A systematic review. Eur. J. Gastroenterol. Hepatol. 2009, 21, 599–605. [Google Scholar] [CrossRef] [PubMed]
- Poggi, G.; Tosoratti, N.; Montagna, B.; Picchi, C. Microwave ablation of hepatocellular carcinoma. World J. Hepatol. 2015, 7, 2578–2589. [Google Scholar] [CrossRef] [PubMed]
- Crocetti, L.; Scalise, P.; Bozzi, E.; Campani, D.; Rossi, P.; Cervelli, R.; Bargellini, I.; Ghinolfi, D.; De Simone, P.; Cioni, R. Microwave Ablation of Very-Early- and Early-Stage HCC: Efficacy Evaluation by Correlation with Histology after Liver Transplantation. Cancers 2021, 13, 3420. [Google Scholar] [CrossRef] [PubMed]
- Ausania, F.; Borin, A.; Melendez, R.; del Rio, P.S.; Iglesias, A.; Bodenlle, P.; Paniagua, M.; Arias, M. Microwave ablation of colorectal liver metastases: Impact of a 10-mm safety margin on local recurrence in a tertiary care hospital. Ann. Hepato-Biliary-Pancreatic Surg. 2021, 25, 366–370. [Google Scholar] [CrossRef]
- Lee, S.K.; Chung, D.J.; Cho, S.H. A Real-World Comparative Study of Microwave and Radiofrequency Ablation in Treatment-Naïve and Recurrent Hepatocellular Carcinoma. J. Clin. Med. 2022, 11, 302. [Google Scholar] [CrossRef]
- Facciorusso, A.; Di Maso, M.; Muscatiello, N. Microwave ablation versus radiofrequency ablation for the treatment of hepatocellular carcinoma: A systematic review and meta-analysis. Int. J. Hyperth. 2016, 32, 339–344. [Google Scholar] [CrossRef]
- Violi, N.V.; Duran, R.; Guiu, B.; Cercueil, J.-P.; Aubé, C.; Digklia, A.; Pache, I.; Deltenre, P.; Knebel, J.-F.; Denys, A. Efficacy of microwave ablation versus radiofrequency ablation for the treatment of hepatocellular carcinoma in patients with chronic liver disease: A randomised controlled phase 2 trial. Lancet Gastroenterol. Hepatol. 2018, 3, 317–325. [Google Scholar] [CrossRef]
- Izzo, F.; Granata, V.; Grassi, R.; Fusco, R.; Palaia, R.; Delrio, P.; Carrafiello, G.; Azoulay, D.; Petrillo, A.; A Curley, S. Radiofrequency Ablation and Microwave Ablation in Liver Tumors: An Update. Oncol. 2019, 24, e990–e1005. [Google Scholar] [CrossRef]
- Glassberg, M.B.; Ghosh, S.; Clymer, J.W.; Wright, G.W.J.; Ferko, N.; Amaral, J.F. Microwave ablation compared with hepatic resection for the treatment of hepatocellular carcinoma and liver metastases: A systematic review and meta-analysis. World J. Surg. Oncol. 2019, 17, 98. [Google Scholar] [CrossRef]
- Facciorusso, A.; El Aziz, M.A.A.; Tartaglia, N.; Ramai, D.; Mohan, B.P.; Cotsoglou, C.; Pusceddu, S.; Giacomelli, L.; Ambrosi, A.; Sacco, R. Microwave Ablation Versus Radiofrequency Ablation for Treatment of Hepatocellular Carcinoma: A Meta-Analysis of Randomized Controlled Trials. Cancers 2020, 12, 3796. [Google Scholar] [CrossRef]
- Chong, C.C.; Lee, K.F.; Cheung, S.Y.; Chu, C.C.; Fong, A.K.; Wong, J.; Hui, J.W.; Fung, A.K.; Lok, H.T.; Lo, E.Y.; et al. Prospective double-blinded randomized controlled trial of Microwave versus RadioFrequency Ablation for hepatocellular carcinoma (McRFA trial). HPB 2020, 22, 1121–1127. [Google Scholar] [CrossRef] [PubMed]
- Suwa, K.; Seki, T.; Aoi, K.; Yamashina, M.; Murata, M.; Yamashiki, N.; Nishio, A.; Shimatani, M.; Naganuma, M. Efficacy of microwave ablation versus radiofrequency ablation for hepatocellular carcinoma: A propensity score analysis. Abdom. Radiol. 2021, 46, 3790–3797. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Shi, J.; Ren, C.; Du, Z.; Shu, G.; Wang, Y. Survival analysis following microwave ablation or surgical resection in patients with hepatocellular carcinoma conforming to the Milan criteria. Oncol. Lett. 2020, 19, 4066–4076. [Google Scholar] [CrossRef] [PubMed]
- Andreozzi, A.; Iasiello, M.; Tucci, C. Chapter Six—An overview of mathematical models and modulated-heating protocols for thermal ablation. Adv. Heat Transf. 2020, 52, 489–541. [Google Scholar]
- Lubner, M.G.; Brace, C.L.; Hinshaw, J.L.; Lee, F.T. Microwave Tumor Ablation: Mechanism of Action, Clinical Results, and Devices. J. Vasc. Interv. Radiol. 2010, 21, S192–S203. [Google Scholar] [CrossRef] [PubMed]
- Curto, S.; Taj-Eldin, M.; Fairchild, D.; Prakash, P. Microwave ablation at 915 MHz vs. 2.45 GHz: A theoretical and experimental investigation. Med. Phys. 2015, 42, 6152–6161. [Google Scholar] [CrossRef]
- Simon, C.J.; Dupuy, D.; Mayo-Smith, W.W. Microwave Ablation: Principles and Applications. RadioGraphics 2005, 25, S69–S83. [Google Scholar] [CrossRef]
- Kim, H.J.; Rhim, H.; Lee, M.W.; Jeong, W.K. Measurement of Intrahepatic Pressure during Microwave Ablation in an Ex Vivo Bovine Liver Model. Gut Liver 2015, 9, 784–790. [Google Scholar] [CrossRef]
- Wang, H.; He, Y.; Yang, M.; Yan, Q.; You, F.; Fu, F.; Wang, T.; Huo, X.; Dong, X.; Shi, X. Dielectric properties of human liver from 10Hz to 100MHz: Normal liver, hepatocellular carcinoma, hepatic fibrosis and liver hemangioma. Bio-Medical Mater. Eng. 2014, 24, 2725–2732. [Google Scholar] [CrossRef]
- Zhekov, S.S.; Franek, O.; Pedersen, G.F. Dielectric Properties of Human Hand Tissue for Handheld Devices Testing. IEEE Access 2019, 7, 61949–61959. [Google Scholar] [CrossRef]
- Bottiglieri, A.; Ruvio, G.; O’Halloran, M.; Farina, L. Exploiting Tissue Dielectric Properties to Shape Microwave Thermal Ablation Zones. Sensors 2020, 20, 3960. [Google Scholar] [CrossRef] [PubMed]
- Baker-Jarvis, J.; Kim, S. The Interaction of Radio-Frequency Fields with Dielectric Materials at Macroscopic to Mesoscopic Scales. J. Res. Natl. Inst. Stand. Technol. 2012, 117, 1–60. [Google Scholar] [CrossRef] [PubMed]
- Farsaci, F.; Russo, A.; Ficarra, S.; Tellone, E. Dielectric Properties of Human Normal and Malignant Liver Tissue: A Non-Equilibrium Thermodynamics Approach. Open Access Libr. J. 2015, 2, e1395. [Google Scholar] [CrossRef]
- Fahmy, H.M.; Hamad, A.M.; Sayed, F.A.; Abdelaziz, Y.S.; Abu Serea, E.S.; Mustafa, A.B.E.; Mohammed, M.A.; Saadeldin, A.M. Dielectric spectroscopy signature for cancer diagnosis: A review. Microw. Opt. Technol. Lett. 2020, 62, 3739–3753. [Google Scholar] [CrossRef]
- Stauffer, P.R. Evolving technology for thermal therapy of cancer. Int. J. Hyperth. 2005, 21, 731–744. [Google Scholar] [CrossRef] [PubMed]
- Kuang, M.; Lu, M.D.; Xie, X.Y.; Xu, H.X.; Mo, L.Q.; Liu, G.J.; Xu, Z.F.; Zheng, Y.L.; Liang, J.Y. Liver Cancer: Increased Microwave Delivery to Ablation Zone with Cooled-Shaft Antenna—Experimental and Clinical Studies. Radiology 2007, 242, 914–924. [Google Scholar] [CrossRef]
- Simon, C.J.; Dupuy, D.E.; Iannitti, D.A.; Lu, D.S.K.; Yu, N.C.; Aswad, B.I.; Busuttil, R.W.; Lassman, C. Intraoperative Triple Antenna Hepatic Microwave Ablation. Am. J. Roentgenol. 2006, 187, W333–W340. [Google Scholar] [CrossRef]
- Hojjatollah, F.; Punit, P. Antenna Designs for Microwave Tissue Ablation. Crit. Rev. Biomed. Eng. 2018, 46, 495–521. [Google Scholar]
- Kapoor, H.; Nisiewicz, M.J.; Jayavarapu, R.; Gedaly, R.; Raissi, D. Early Outcomes with Single-antenna High-powered Percutaneous Microwave Ablation for Primary and Secondary Hepatic Malignancies: Safety, Effectiveness, and Predictors of Ablative Failure. J. Clin. Imaging Sci. 2020, 10, 10. [Google Scholar] [CrossRef]
- Hendriks, P.; Berkhout, W.E.M.; Kaanen, C.I.; Sluijter, J.H.; Visser, I.J.; Dobbelsteen, J.J.V.D.; de Geus-Oei, L.F.; Webb, A.G.; Burgmans, M.C. Performance of the Emprint and Amica Microwave Ablation Systems in ex vivo Porcine Livers: Sphericity and Reproducibility Versus Size. Cardiovasc. Interv. Radiol. 2021, 44, 952–958. [Google Scholar] [CrossRef]
- Trujillo-Romero, C.; Leija-Salas, L.; Vera-Hernández, A.; Rico-Martínez, G.; Gutiérrez-Martínez, J. Double Slot Antenna for Microwave Thermal Ablation to Treat Bone Tumors: Modeling and Experimental Evaluation. Electronics 2021, 10, 761. [Google Scholar] [CrossRef]
- Alonzo, M.; Bos, A.; Bennett, S.; Ferral, H. The Emprint™ Ablation System with Thermosphere™ Technology: One of the Newer Next-GenerationMicrowave AblationTechnologies. Semin. Interv. Radiol. 2015, 32, 335–338. [Google Scholar]
- Kuroda, H.; Nagasawa, T.; Fujiwara, Y.; Sato, H.; Abe, T.; Kooka, Y.; Endo, K.; Oikawa, T.; Sawara, K.; Takikawa, Y. Comparing the Safety and Efficacy of Microwave Ablation Using ThermosphereTM Technology versus Radiofrequency Ablation for Hepatocellular Carcinoma: A Propensity Score-Matched Analysis. Cancers 2021, 13, 1295. [Google Scholar] [CrossRef]
- Acikgoz, H.; Turer, I. A Novel Microwave Coaxial Slot Antenna for Liver Tumor Ablation. Adv. Electromagn. 2014, 3, 20–25. [Google Scholar] [CrossRef]
- Towoju, O.; Ishola, F.; Sanni, T.; Olatunji, O. Investigation of Influence of Coaxial Antenna Slot Positioning on Thermal Efficiency in Microwave Ablation using COMSOL. J. Phys. Conf. Ser. 2019, 1378, 32066. [Google Scholar] [CrossRef]
- Liu, D.; Brace, C. Numerical simulation of microwave ablation incorporating tissue contraction based on thermal dose. Phys. Med. Boil. 2017, 62, 2070–2086. [Google Scholar] [CrossRef] [PubMed]
- Rattanadecho, P.; Keangin, P. Numerical study of heat transfer and blood flow in two-layered porous liver tissue during microwave ablation process using single and double slot antenna. Int. J. Heat Mass Transf. 2013, 58, 457–470. [Google Scholar] [CrossRef]
- Maini, S.; Marwaha, A. Modeling and simulation of novel antenna for the treatment of hepatocellular carcinoma using finite element method. Electromagn. Biol. Med. 2013, 32, 373–381. [Google Scholar] [CrossRef]
- Reinhardt, M.; Brandmaier, P.; Seider, D.; Kolesnik, M.; Jenniskens, S.; Sequeiros, R.B.; Eibisberger, M.; Voglreiter, P.; Flanagan, R.; Mariappan, P.; et al. A prospective development study of software-guided radio-frequency ablation of primary and secondary liver tumors: Clinical intervention modelling, planning and proof for ablation cancer treatment (ClinicIMPPACT). Contemp. Clin. Trials Commun. 2017, 8, 25–32. [Google Scholar] [CrossRef]
- Cavagnaro, M.; Pinto, R.; Lopresto, V. Numerical models to evaluate the temperature increase induced by ex vivo microwave thermal ablation. Phys. Med. Biol. 2015, 60, 3287–3311. [Google Scholar] [CrossRef]
- Selmi, M.; Bajahzar, A.; Belmabrouk, H. Effects of target temperature on thermal damage during temperature-controlled MWA of liver tumor. Case Stud. Therm. Eng. 2022, 31, 101821. [Google Scholar] [CrossRef]
- Simanovskii, D.M.; Mackanos, M.A.; Irani, A.R.; O’Connell-Rodwell, C.E.; Contag, C.H.; Schwettman, H.A.; Palanker, D.V. Cellular tolerance to pulsed hyperthermia. Phys. Rev. E 2006, 74, 011915. [Google Scholar] [CrossRef] [PubMed]
- Liljemalm, R.; Nyberg, T. Quantification of a thermal damage threshold for astrocytes using infrared laser generated heat gradients. Ann. Biomed. Eng. 2014, 42, 822–832. [Google Scholar] [CrossRef] [PubMed]
- Chiang, J.; Wang, P.; Brace, C.L. Computational modelling of microwave tumour ablations. Int. J. Hyperth. 2013, 29, 308–317. [Google Scholar] [CrossRef] [PubMed]
- Keangin, P.; Rattanadecho, P. A numerical investigation of microwave ablation on porous liver tissue. Adv. Mech. Eng. 2018, 10, 1–13. [Google Scholar] [CrossRef]
- Radmilović-Radjenović, M.; Radjenović, D. Finite element analysis of the effect of microwave ablation on the liver, lung, kidney, and bone malignant tissues. Eur. Lett. 2021, 136, 28001. [Google Scholar] [CrossRef]
- Chen, C.; Yu, M.-A.; Qiu, L.; Chen, H.-Y.; Zhao, Z.-L.; Wu, J.; Peng, L.-L.; Wang, Z.-L.; Xiao, R.-X. Theoretical Evaluation of Microwave Ablation Applied on Muscle, Fat and Bone: A Numerical Study. Appl. Sci. 2021, 11, 8271. [Google Scholar] [CrossRef]
- Radmilović-Radjenović, M.; Sabo, M.; Prnova, M.; Šoltes, L.; Radjenović, B. Finite Element Analysis of the Microwave Ablation Method for Enhanced Lung Cancer Treatment. Cancers 2021, 13, 3500. [Google Scholar] [CrossRef]
- An, C.; Li, X.; Zhang, M.; Yang, J.; Cheng, Z.; Yu, X.; Han, Z.; Liu, F.; Dong, L.; Yu, J.; et al. 3D visualization ablation planning system assisted microwave ablation for hepatocellular carcinoma (Diameter >3): A precise clinical application. BMC Cancer 2020, 20, 44. [Google Scholar] [CrossRef]
- Radjenović, B.; Sabo, M.; Šoltes, L.; Prnova, M.; Čičak, P.; Radmilović-Radjenović, M. On Efficacy of Microwave Ablation in the Thermal Treatment of an Early-Stage Hepatocellular Carcinoma. Cancers 2021, 13, 5784. [Google Scholar] [CrossRef]
- Loya, R.R.; Jutte, P.C.; Kwee, T.C.; van Ooijen, P.M.A. Computer 3D modeling of radiofrequency ablation of atypical cartilaginous tumours in long bones using finite element methods and real patient anatomy. Eur. Radiol. Exp. 2022, 6, 21. [Google Scholar] [CrossRef]
- Gorman, J.; Tan, W.; Abraham, J. Numerical Simulation of Microwave Ablation in the Human Liver. Processes 2022, 10, 361. [Google Scholar] [CrossRef]
- Radmilović-Radjenović, M.; Bošković, N.; Sabo, M.; Radjenović, B. An Analysis of Microwave Ablation Parameters for Treatment of Liver Tumors from the 3D-IRCADb-01 Database. Biomedicines 2022, 10, 1569. [Google Scholar] [CrossRef] [PubMed]
- Trujillo, M.; Berjano, E. Review of the mathematical functions used to model the temperature dependence of electrical and thermal conductivities of biological tissue in radiofrequency ablation. Int. J. Hyperth. 2013, 29, 590–597. [Google Scholar] [CrossRef] [PubMed]
- Pearce, J.A. Comparative analysis of mathematical models of cell death and thermal damage processes. Int. J. Hyperth. 2013, 29, 262–280. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Modeling Heat Transfer in Tumors: A Review of Thermal Therapies. Ann. Biomed. Eng. 2018, 47, 676–693. [Google Scholar] [CrossRef]
- Tucci, C.; Trujillo, M.; Berjano, E.; Iasiello, M.; Andreozzi, A.; Vanoli, G.P. Mathematical modeling of microwave liver ablation with a variable-porosity medium approach. Comput. Methods Programs Biomed. 2021, 214, 106569. [Google Scholar] [CrossRef]
- Kenyon, D.E. Transient Filtration in a Porous Elastic Cylinder. J. Appl. Mech. 1976, 43, 594–598. [Google Scholar] [CrossRef]
- Mow, V.C.; Lai, W.M. Recent Developments in Synovial Joint Biomechanics. SIAM Rev. 1980, 22, 275–317. [Google Scholar] [CrossRef]
- Mow, V.C.; Kuei, S.C.; Lai, W.M.; Armstrong, C.G. Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments. J. Biomech. Eng. 1980, 102, 73–84. [Google Scholar] [CrossRef]
- Lai, W.M.; Mow, V.C.; Roth, V. Effects of Nonlinear Strain-Dependent Permeability and Rate of Compression on the Stress Behavior of Articular Cartilage. J. Biomech. Eng. 1981, 103, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, C.G.; Lai, W.M.; Mow, V.C. An Analysis of the Unconfined Compression of Articular Cartilage. J. Biomech. Eng. 1984, 106, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Mak, A.F.; Lai, W.M.; Mow, V.C. Biphasic indentation of articular cartilage-I. Theor. Anal. J. Biomech. 1987, 20, 703–714. [Google Scholar] [CrossRef]
- Cowin, S.C. The Specific Growth Rates of Tissues: A Review and a Re-Evaluation. J. Biomech. Eng. 2011, 133, 041001. [Google Scholar] [CrossRef]
- Khaled, A.-R.A.; Vafai, K. The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transf. 2003, 46, 4989–5003. [Google Scholar] [CrossRef]
- Kosari, E.; Vafai, K. Synthesis of Flow and Thermal Transport in Porous Media as Applied to Biological Applications. J. Heat Transf. 2021, 143, 062701. [Google Scholar] [CrossRef]
- Allan, F.; Hamdan, M. Fluid mechanics of the interface region between two porous layers. Appl. Math. Comput. 2002, 128, 37–43. [Google Scholar] [CrossRef]
- Mahjoob, S.; Vafai, K. Analysis of Bioheat Transport Through a Dual Layer Biological Media. J. Heat Transf. 2009, 132, 031101. [Google Scholar] [CrossRef]
- Yang, K.; Huang, W.; Li, X.; Wang, J. Analytical Analysis of Heat Transfer and Entropy Generation in a Tube Filled with Double-Layer Porous Media. Entropy 2020, 22, 1214. [Google Scholar] [CrossRef]
- Li, L.; Liang, M.; Yu, B.; Yang, S. Analysis of thermal conductivity in living biological tissue with vascular network and convection. Int. J. Therm. Sci. 2014, 86, 219–226. [Google Scholar] [CrossRef]
- Li, X.; Qin, Q.-H.; Tian, X. Thermomechanical response of porous biological tissue based on local thermal non-equilibrium. J. Therm. Stress. 2019, 42, 1481–1498. [Google Scholar] [CrossRef]
- Ragab, M.; Abouelregal, A.E.; AlShaibi, H.F.; Mansouri, R.A. Heat Transfer in Biological Spherical Tissues during Hyperthermia of Magnetoma. Biology 2021, 10, 1259. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zheng, L.; Liu, F. Research on macroscopic and microscopic heat transfer mechanisms based on non-Fourier constitutive model. Int. J. Heat Mass Transf. 2018, 127, 165–172. [Google Scholar] [CrossRef]
- Wang, L.Q.; Xu, M.T.; Wei, X.H. Multiscale Theorems. Adv. Chem. Eng. 2008, 34, 175–468. [Google Scholar]
- Miller, C.T.; Gray, W.G.; Schrefler, B.A. A continuum mechanical framework for modeling tumor growth and treatment in two- and three-phase systems. Ingenieur-Archiv 2021, 92, 461–489. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.M.; Feng, Y.; Yankeelov, T.E.; Oden, J.T. A fully coupled space–time multiscale modeling framework for predicting tumor growth. Comput. Methods Appl. Mech. Eng. 2017, 320, 261–286. [Google Scholar] [CrossRef]
- Goyal, H.; Vlachos, D.G. Multiscale modeling of microwave-heated multiphase systems. Chem. Eng. J. 2020, 397, 125262. [Google Scholar] [CrossRef]
- Wang, L.; Fan, J. Modeling Bioheat Transport at Macroscale. J. Heat Transf. 2010, 133, 011010. [Google Scholar] [CrossRef]
- Eringen, A.; Ingram, J.D. A Continuum theory of chemically reacting media—I. Int. J. Eng. Sci. 1965, 3, 197–212. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, J.; Zhang, Y. Dual-phase lag effects on thermal damage to biological tissues caused by laser irradiation. Comput. Biol. Med. 2009, 39, 286–293. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Y.W.; Chen, J.K. An Axisymmetric Dual-PhaseLag Bioheat Model for Laser Heating of Living Tissues. Int. J. Therm. Sci. 2009, 48, 1477–1485. [Google Scholar] [CrossRef]
- Tucci, C.; Trujillo, M.; Berjano, E.; Iasiello, M.; Andreozzi, A.; Vanoli, G.P. Pennes’ bioheat equation vs. porous media approach in computer modeling of radiofrequency tumor ablation. Sci. Rep. 2021, 11, 5272. [Google Scholar] [CrossRef] [PubMed]
- Habibishandiz, M.; Saghir, M. A critical review of heat transfer enhancement methods in the presence of porous media, nanofluids, and microorganisms. Therm. Sci. Eng. Prog. 2022, 30, 101267. [Google Scholar] [CrossRef]
- Nakayama, A.; Kuwahara, F. A general bioheat transfer model based on the theory of porous media. Int. J. Heat Mass Transf. 2008, 51, 3190–3199. [Google Scholar] [CrossRef]
- Prakash, P. Microwave ablation: Physical principles and technology. In Principles and Technologies for Electromagnetic Energy Based Therapies, 1st ed.; Editor Prakash, P., Srimathveeravalli, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 139–167. [Google Scholar]
- Singh, S.; Kumar, S. A Study on the Effect of Metabolic Heat Generation on Biological Tissue Freezing. Sci. World J. 2013, 2013, 398386. [Google Scholar] [CrossRef]
- Kalsi, K.K.; Chiesa, S.T.; Trangmar, S.J.; Ali, L.; Lotlikar, M.D.; González-Alonso, J. Mechanisms for the control of local tissue blood flow during thermal interventions: Influence of temperature-dependent ATP release from human blood and endothelial cells. Exp. Physiol. 2017, 102, 228–244. [Google Scholar] [CrossRef]
- Ingram, J.D.; Eringen, A.C. A continuum theory of chemically reacting media—II Constitutive equations of reacting fluid mixtures. Int. J. Eng. Sci. 1967, 5, 289–322. [Google Scholar] [CrossRef]
- Bedford, A.; Drumheller, D.S. Theories of immiscible and structured mixtures. Int. J. Eng. Sci. 1983, 21, 863–960. [Google Scholar] [CrossRef]
- Lakhssassi, A.; Kengne, E.; Semmaoui, H. Modifed pennes’ equation modelling bio-heat transfer in living tissues: Analytical and numerical analysis. Nat. Sci. 2010, 2, 1375–1385. [Google Scholar] [CrossRef]
- Hristov, J. Bio-Heat Models Revisited: Concepts, Derivations, Nondimensalization and Fractionalization Approaches. Front. Phys. 2019, 7, 189. [Google Scholar] [CrossRef]
- Roetzel, W.; Xuan, Y. Bioheat equation of the human thermal system. Chem. Eng. Technol. 1997, 20, 268–276. [Google Scholar]
- Prakash, P.; Converse, M.C.; Webster, J.G.; Mahvi, D.M. An optimal sliding choke antenna for hepatic microwave ablation. IEEE Trans. Bio-Med. Eng. 2009, 56, 2470–2476. [Google Scholar]
- Cavagnaro, M.; Amabile, C.; Bernardi, P.; Pisa, S.; Tosoratti, N. A Minimally Invasive Antenna for Microwave Ablation Therapies: Design, Performances, and Experimental Assessment. IEEE Trans. Biomed. Eng. 2010, 58, 949–959. [Google Scholar] [CrossRef]
- Yang, D.S.; Bertram, J.M.; Converse, M.C.; O’Rourke, A.P.; Webster, J.G.; Hagness, S.C.; Will, J.A.; Mahvi, D.M. A floating sleeve antenna yields localized hepatic microwave ablation. IEEE Trans. Bio-Med. Eng. 2006, 53, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Maini, S. FEM simulation of tapered cap floating sleeve antenna for hepatocellular carcinoma therapy. Electromagn. Biol. Med. 2015, 35, 152–160. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Cheng, Z.G.; Dong, L.; Zhang, G.M.; Wang, Y.; Liang, P. Comparison of temperature curve and ablation zone between 915-and 2450 MHz cooled-shaft microwave antenna: Results in ex vivo porcine livers. Eur. J. Radiol. 2015, 81, 553–557. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, G.; Qiu, B.S. Theoretical evaluation of the treatment effectiveness of a novel coaxial multi-slot antenna for conformal microwave ablation of tumors. Int. J. Heat Mass Transf. 2015, 90, 81–91. [Google Scholar] [CrossRef]
- Luyen, H.; Hagness, S.C.; Behdad, N. Reduced-diameter designs of coax-fed microwave ablation antennas equipped with baluns IEEE Antennas Wirel. Propag. 2017, 16, 1385–1388. [Google Scholar]
- Ge, M.; Jiang, H.; Huang, X.; Zhou, Y.; Zhi, D.; Zhao, G.; Chen, Y.; Wang, L.; Qiu, B. A multi-slot coaxial microwave antenna for liver tumor ablation. Phys. Med. Biol. 2018, 63, 175011. [Google Scholar] [CrossRef]
- Tehrani, M.H.H.; Soltani, M.; Kashkooli, F.M.; Raahemifar, K. Use of microwave ablation for thermal treatment of solid tumors with different shapes and sizes—A computational approach. PLoS ONE 2020, 15, e0233219. [Google Scholar] [CrossRef] [PubMed]
- Lopresto, V.; Pinto, R.; Lovisolo, G.A.; Cavagnaro, M. Changes in the dielectric properties of ex vivo bovine liver during microwave thermal ablation at 2.45 GHz. Phys. Med. Boil. 2012, 57, 2309–2327. [Google Scholar] [CrossRef] [PubMed]
- Prakash, P. Theoretical Modeling for Hepatic Microwave Ablation. Open Biomed. Eng. J. 2010, 4, 27–38. [Google Scholar] [CrossRef]
- O’Rourke, A.P.; Lazebnik, M.; Bertram, J.M.; Converse, M.C.; Hagness, S.C.; Webster, J.G.; Mahvi, D.M. Dielectric properties of human normal, malignant and cirrhotic liver tissue: In vivo and ex vivo measurements from 0.5 to 20 GHz using a precision open-ended coaxial probe. Phys. Med. Biol. 2007, 52, 4707–4719. [Google Scholar] [CrossRef] [PubMed]
- Rossmanna, C.; Haemmerich, D. Review of Temperature Dependence of Thermal Properties, Dielectric Properties, and Perfusion of Biological Tissues at Hyperthermic and Ablation Temperatures. Crit. Rev. Biomed. Eng. 2014, 42, 467–492. [Google Scholar] [CrossRef] [PubMed]
- Berjano, E.J. Theoretical modeling for radiofrequency ablation: State-of-the-art and challenges for the future. Biomed. Eng. Online 2006, 5, 24. [Google Scholar] [CrossRef] [PubMed]
- Balogh, J.; Victor, D.; Asham, E.H.; Burroughs, S.G.; Boktour, M.; Saharia, A.; Li, X.; Ghobrial, R.M.; Monsour, H.P., Jr. Hepatocellular carcinoma: A review. J. Hepatocell. Carcinoma 2016, 3, 41–53. [Google Scholar] [CrossRef]
- Villanueva, A. Hepatocellular Carcinoma. N. Engl. J. Med. 2019, 380, 1450–1462. [Google Scholar] [CrossRef]
- Llovet, J.M.; Kelley, R.K.; Villanueva, A.; Singal, A.G.; Pikarsky, E.; Roayaie, S.; Lencioni, R.; Koike, K.; Zucman-Rossi, J.; Finn, R.S. Hepatocellular carcinoma. Nat. Rev. Dis. Primers 2021, 7, 6. [Google Scholar] [CrossRef]
- Wang, S.; Yang, D.; Kong, W. Prediction of Overall Survival Rate in Patients With Hepatocellular Carcinoma Using an Integrated Model Based on Autophagy Gene Marker. Front. Genet. 2021, 12, 1–10. [Google Scholar] [CrossRef]
- Chen, Z.H.; Hong, Y.F.; Chen, X.; Chen, J.; Lin, Q.; Lin, J.; Li, X.; Wen, J.Y.; Ruan, D.Y.; Dong, M.; et al. Comparison of five staging systems in predicting the survival rate of patients with hepatocellular carcinoma undergoing trans-arterial chemoembolization therapy. Oncology Letters 2018, 15, 855–862. [Google Scholar] [CrossRef] [PubMed]
- Hui, T.; Kwan, J.; Pua, U. Advanced Techniques in the Percutaneous Ablation of Liver Tumours. Diagnostics 2021, 11, 585. [Google Scholar] [CrossRef] [PubMed]
- Comsol Multiphysics. 1986–2020. Burlington (MA): COMSOL, Inc. Available online: https://www.comsol.com/comsol-multiphysics (accessed on 7 March 2022).
- D-IRCADb. Strasbourg (F): IrcadFrance. Available online: https://www.ircad.fr/research/data-sets/liver-segmentation-3d-ircadb-01 (accessed on 7 March 2022).












| Parameter | Value |
|---|---|
| Healthy liver tissue | |
| Density | 1079 kg/m3 |
| Thermal conductivity | 0.52 W/m °C |
| Specific heat | 3540 J/kg °C |
| Tumoral liver tissue | |
| Density | 1040 kg/m3 |
| Thermal conductivity | 0.57 W/m °C |
| Specific heat | 3960 J/kg °C |
| Blood | |
| Density | 1060 kg/m3 |
| Thermal conductivity | 0.5 W/m °C |
| Specific heat | 3600 J/kg °C |
| Temperature | 37 °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radmilović-Radjenović, M.; Bošković, N.; Radjenović, B. Computational Modeling of Microwave Tumor Ablation. Bioengineering 2022, 9, 656. https://doi.org/10.3390/bioengineering9110656
Radmilović-Radjenović M, Bošković N, Radjenović B. Computational Modeling of Microwave Tumor Ablation. Bioengineering. 2022; 9(11):656. https://doi.org/10.3390/bioengineering9110656
Chicago/Turabian StyleRadmilović-Radjenović, Marija, Nikola Bošković, and Branislav Radjenović. 2022. "Computational Modeling of Microwave Tumor Ablation" Bioengineering 9, no. 11: 656. https://doi.org/10.3390/bioengineering9110656
APA StyleRadmilović-Radjenović, M., Bošković, N., & Radjenović, B. (2022). Computational Modeling of Microwave Tumor Ablation. Bioengineering, 9(11), 656. https://doi.org/10.3390/bioengineering9110656







