A Review on Damage and Rupture Modelling for Soft Tissues
Abstract
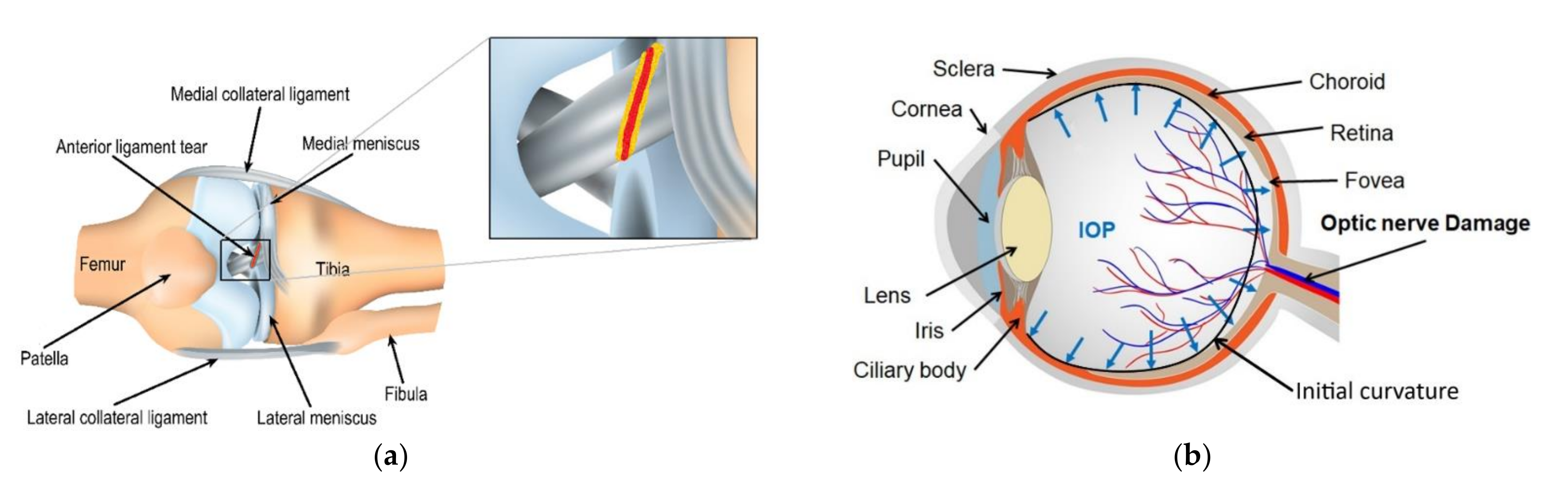
1. Introduction
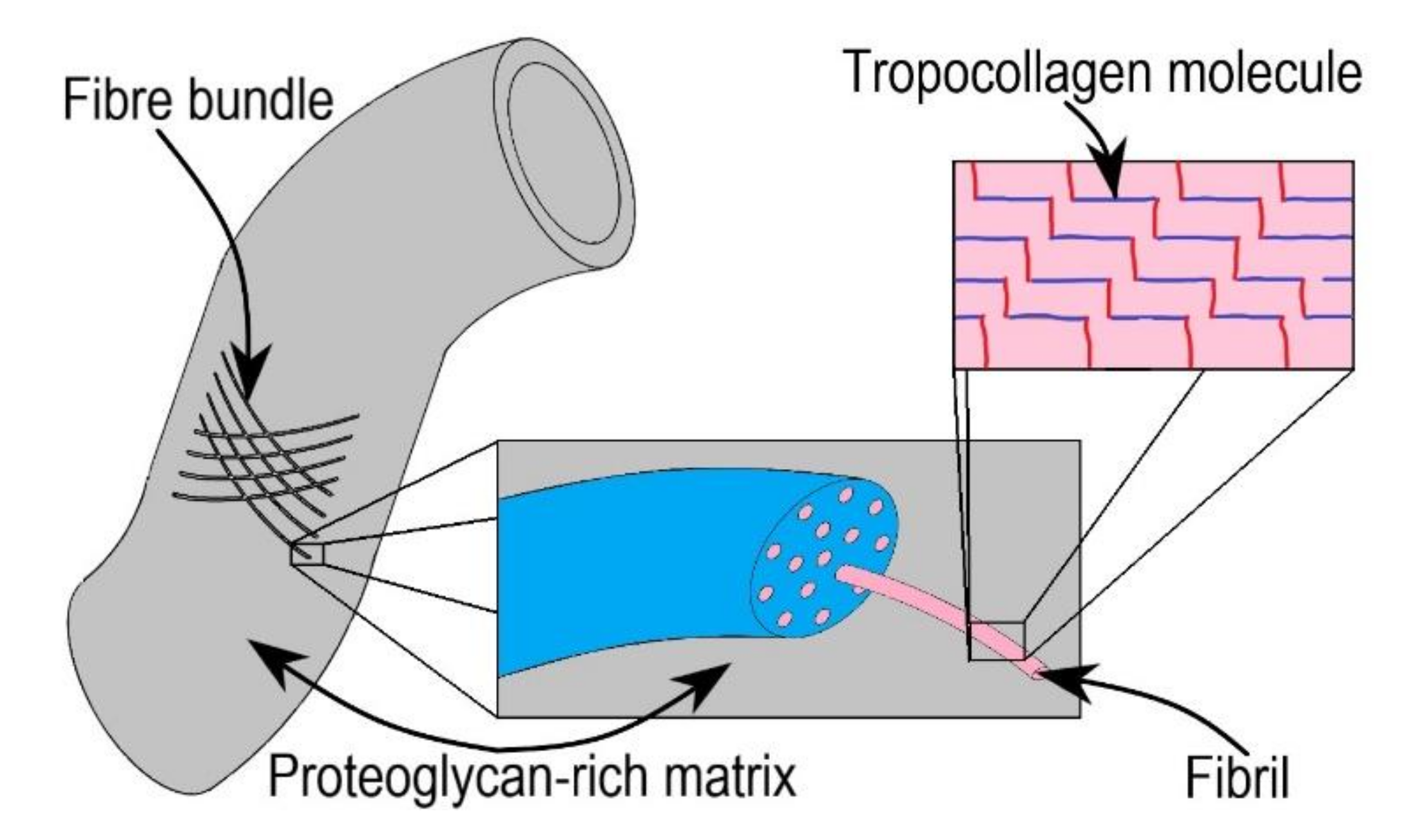
- The initial region of the stress-strain response, i.e., phase-I (toe region). The soft tissue’s mechanical behaviour in this region is similar to a soft isotropic rubber sheet. The collagen fibres are in a relaxed state, and they appear wavy and crimped. Therefore, very low stress is required for attaining large deformation without stretching the collagen fibres. As a result, the mechanical behaviour in phase-I is approximately linear, and the elastic modulus is low (0.1–2 MPa) [25,28].
- In phase-II (heel region), the tissue exhibits a highly non-linear mechanical behaviour [25]. The collagen fibres get uncrimped as they elongate with the increase in the load. The elongated fibres slide into the matrix and align themselves to the direction of load, thereby increasing the load-carrying capacity.
- In Phase-III (linear region), the tissue exhibits stiffer and linear behaviour. Most of the fibres get aligned to the loading direction; hence, no crimp pattern is observed. The aligned and straightened fibres resist the load, making the tissue stiffer and linear in mechanical behaviour [23,28]. Beyond phase III, ultimate tensile strength is reached, resulting in tissue rupture.
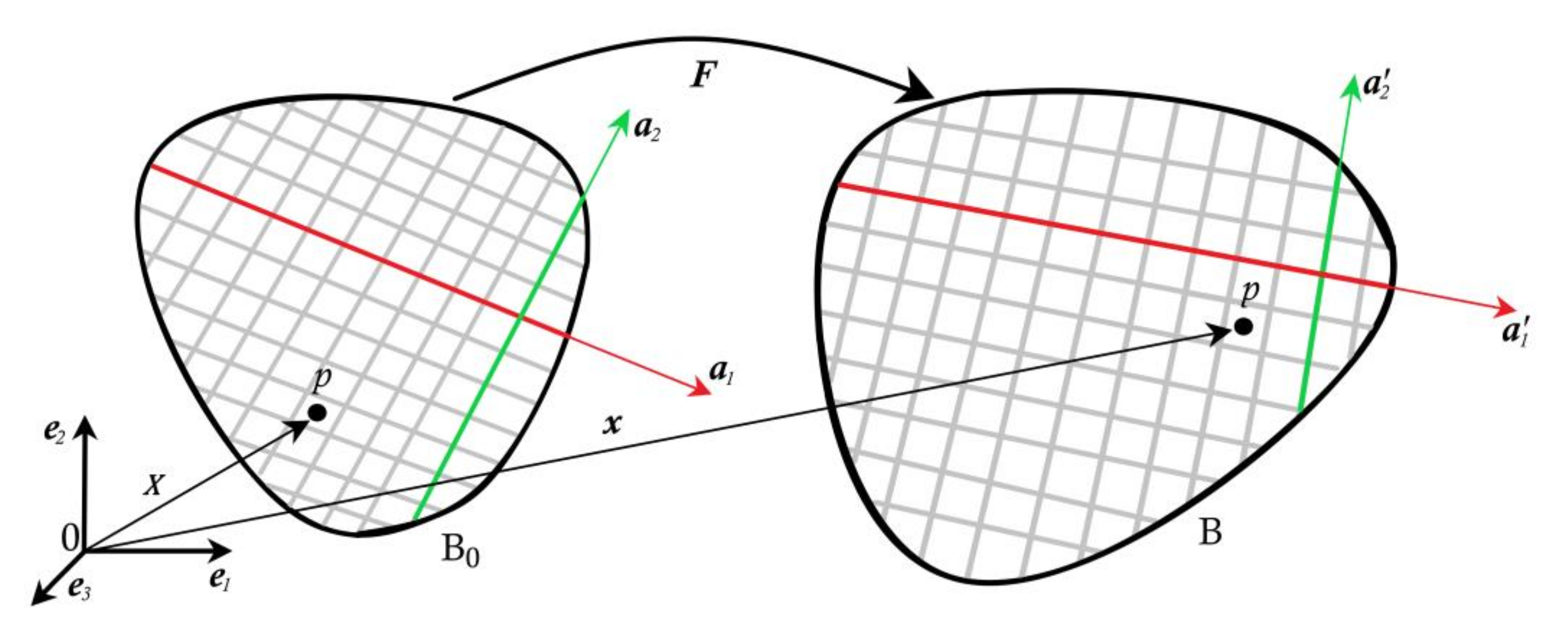
2. Kinematics and Constitutive Model
3. Damage Models
3.1. Continuum Damage Mechanics (CDM)
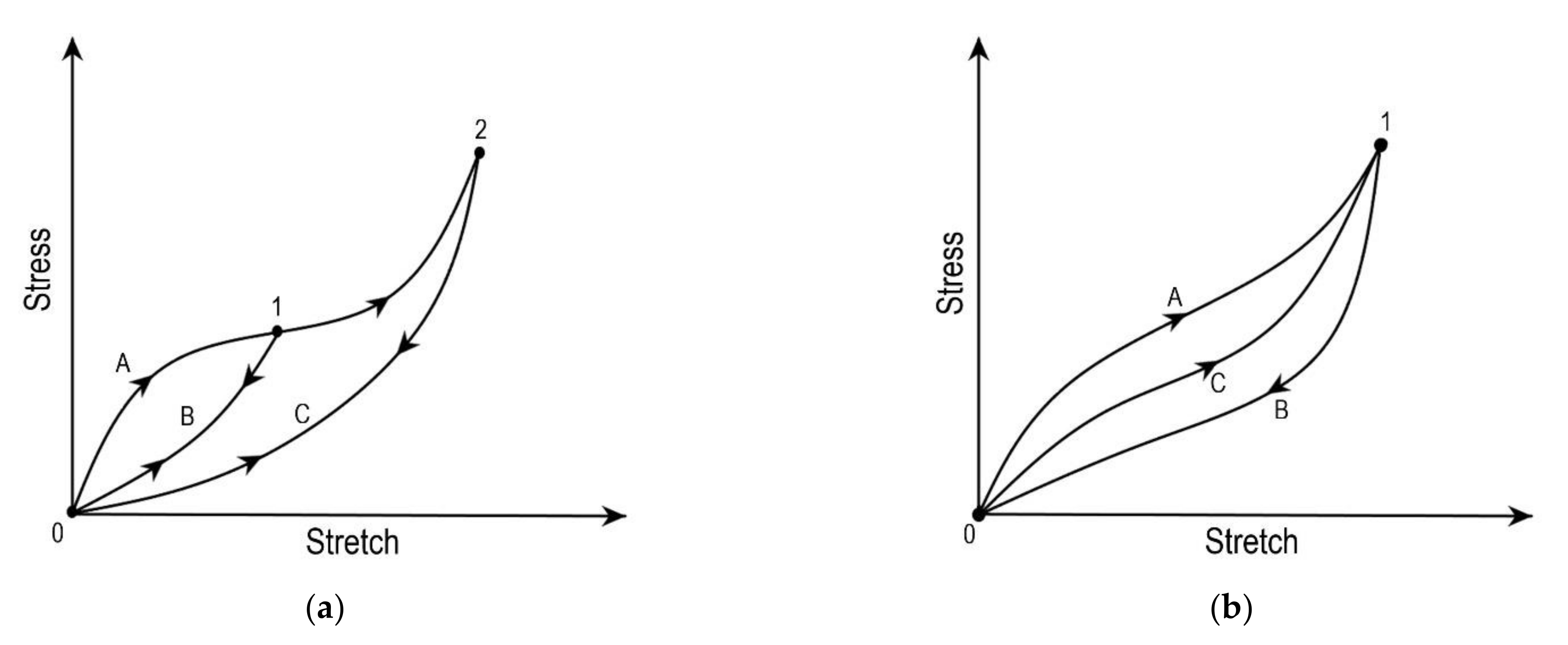
3.2. Pseudo-Elasticity
3.3. Hyperelastic Softening
4. Rupture Modelling
4.1. Extended Finite Element Method (XFEM)
4.1.1. XFEM Using Fracture Mechanics
4.1.2. XFEM Using Cohesive Law
4.2. Cohesive Zone Modelling
4.3. Crack Phase-Field Modelling
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Masri, C.; Chagnon, G.; Favier, D.; Sartelet, H.; Girard, E. Experimental characterization and constitutive modeling of the biomechanical behavior of male human urethral tissues validated by histological observations. Biomech. Model. Mechanobiol. 2018, 17, 939–950. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A. Biomechanics of Soft Tissue. In Handbook of Materials Behavior Models; Elsevier BV: Amsterdam, The Netherlands, 2001; pp. 1057–1071. ISBN 0124433413. [Google Scholar]
- Al-Mayah, A. Biomechanics of Soft Tissues, 1st ed.; CRC Press: Milton, MA, USA, 2018; ISBN 1498766226. [Google Scholar]
- Martini, F. Fundamentals of Anatomy & Physiology, 9th ed.; Nath, J.L., Ed.; Pearson: London, UK, 2012; ISBN 9780321709332. [Google Scholar]
- Spindler, K.P.; Wright, R.W. Anterior Cruciate Ligament Tear. N. Engl. J. Med. 2008, 359, 2135–2142. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Fereidoonnezhad, B. Modeling of Damage in Soft Biological Tissues; Elsevier BV: Amsterdam, The Netherlands, 2017; pp. 101–123. ISBN 9780128040607. [Google Scholar]
- Li, W. Damage Models for Soft Tissues: A Survey. J. Med. Biol. Eng. 2016, 36, 285–307. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wang, Y.; Wei, P.; Jhanji, V. Biomechanics and structure of the cornea: Implications and association with corneal disorders. Surv. Ophthalmol. 2018, 63, 851–861. [Google Scholar] [CrossRef] [PubMed]
- Mantravadi, A.V.; Vadhar, N. Glaucoma. Prim. Care Clin. Off. Pr. 2015, 42, 437–449. [Google Scholar] [CrossRef]
- Vinciguerra, R.; Rehman, S.; Vallabh, N.A.; Batterbury, M.; Czanner, G.; Choudhary, A.; Cheeseman, R.; Elsheikh, A.; Willoughby, C. Corneal biomechanics and biomechanically corrected intraocular pressure in primary open-angle glaucoma, ocular hypertension and controls. Br. J. Ophthalmol. 2020, 104, 121–126. [Google Scholar] [CrossRef]
- Marieswaran, M.; Jain, I.; Garg, B.; Sharma, V.; Kalyanasundaram, D. A Review on Biomechanics of Anterior Cruciate Ligament and Materials for Reconstruction. Appl. Bionics Biomech. 2018, 2018, 4657824. [Google Scholar] [CrossRef]
- Tonsomboon, K.; Koh, C.T.; Oyen, M.L. Time-dependent fracture toughness of cornea. J. Mech. Behav. Biomed. Mater. 2014, 34, 116–123. [Google Scholar] [CrossRef] [PubMed]
- Purslow, P. Measurement of the fracture toughness of extensible connective tissues. J. Mater. Sci. 1983, 18, 3591–3598. [Google Scholar] [CrossRef]
- Lopes, B.T.; Bao, F.; Wang, J.; Liu, X.; Wang, L.; Abass, A.; Eliasy, A.; Elsheikh, A. Review of in-vivo characterisation of corneal biomechanics. Med. Nov. Technol. Devices 2021, 11, 100073. [Google Scholar] [CrossRef]
- Elsheikh, A.; Kassem, W.; Jones, S.W. Strain-rate sensitivity of porcine and ovine corneas. Acta Bioeng. Biomech. 2011, 13, 25–36. [Google Scholar]
- Pissarenko, A.; Yang, W.; Quan, H.; Poyer, B.; Williams, A.; Brown, K.A.; Meyers, M.A. The toughness of porcine skin: Quantitative measurements and microstructural characterization. J. Mech. Behav. Biomed. Mater. 2020, 109, 103848. [Google Scholar] [CrossRef] [PubMed]
- Franceschini, G.; Bigoni, D.; Regitnig, P.; Holzapfel, G. Brain tissue deforms similarly to filled elastomers and follows consolidation theory. J. Mech. Phys. Solids 2006, 54, 2592–2620. [Google Scholar] [CrossRef]
- Leng, X.; Zhou, B.; Deng, X.; Davis, L.; Lessner, S.; Sutton, M.A.; Shazly, T. Experimental and numerical studies of two arterial wall delamination modes. J. Mech. Behav. Biomed. Mater. 2018, 77, 321–330. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liu, X.; Bao, F.; Lopes, B.T.; Wang, L.; Eliasy, A.; Abass, A.; Elsheikh, A. Review of ex-vivo characterisation of corneal biomechanics. Med. Nov. Technol. Devices 2021, 11, 100074. [Google Scholar] [CrossRef]
- Marino, M. Constitutive Modeling of Soft Tissues. In Encyclopedia of Biomedical Engineering; Elsevier BV: Amsterdam, The Netherlands, 2019; pp. 81–110. ISBN 9780128012383. [Google Scholar]
- Chagnon, G.; Ohayon, J.; Martiel, J.-L.; Favier, D. Hyperelasticity Modeling for Incompressible Passive Biological Tissues. In Biomechanics of Living Organs; Elsevier BV: Amsterdam, The Netherlands, 2017; pp. 3–30. ISBN 9780128040607. [Google Scholar]
- Thompson, M.S.; Bajuri, M.N.; Khayyeri, H.; Isaksson, H. Mechanobiological modelling of tendons: Review and future opportunities. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2017, 231, 369–377. [Google Scholar] [CrossRef] [PubMed]
- Haut, R.C. Biomechanics of Soft Tissue. In Accidental Injury; Springer: New York, NY, USA, 2002; pp. 228–253. ISBN 1111111111. [Google Scholar]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Groves, R.B.; Coulman, S.; Birchall, J.; Evans, S.L. An anisotropic, hyperelastic model for skin: Experimental measurements, finite element modelling and identification of parameters for human and murine skin. J. Mech. Behav. Biomed. Mater. 2013, 18, 167–180. [Google Scholar] [CrossRef] [PubMed]
- Fratzl, P. Collagen: Structure and Mechanics, an Introduction. In Collagen: Structure and Mechanics; Fratzl, P., Ed.; Springer: Boston, MA, USA, 2008; pp. 1–13. ISBN 978-0-387-73906-9. [Google Scholar]
- Buehler, M.J.; Wong, S.Y. Entropic Elasticity Controls Nanomechanics of Single Tropocollagen Molecules. Biophys. J. 2007, 93, 37–43. [Google Scholar] [CrossRef]
- Brown, I.A. A scanning electron microscope study of the effects of uniaxial tension on human skin. Br. J. Dermatol. 1973, 89, 383–393. [Google Scholar] [CrossRef]
- Famaey, N.; Kuhl, E.; Holzapfel, G.A.; Sloten, J.V. Cardiovascular Tissue Damage: An Experimental and Computational Framework. In Computer Models in Biomechanics; Holzapfel, G.A., Kuhl, E., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 129–148. ISBN 978-94-007-5463. [Google Scholar]
- Bircher, K.; Zündel, M.; Pensalfini, M.; Ehret, A.E.; Mazza, E. Tear resistance of soft collagenous tissues. Nat. Commun. 2019, 10, 792. [Google Scholar] [CrossRef] [PubMed]
- Bircher, K.; Ehret, A.E.; Spiess, D.; Ehrbar, M.; Simões-Wüst, A.P.; Ochsenbein-Kölble, N.; Zimmermann, R.; Mazza, E. On the defect tolerance of fetal membranes. Interface Focus 2019, 9, 20190010. [Google Scholar] [CrossRef]
- Gasser, T.C. Damage in Vascular Tissues and Its Modeling; Springer: Singapore, 2017; pp. 85–118. ISBN 9783319450711. [Google Scholar]
- Gültekin, O.; Holzapfel, G.A. A Brief Review on Computational Modeling of Rupture in Soft Biological Tissues. Comput. Methods Appl. Sci. 2018, 46, 113–144. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2005, 3, 15–35. [Google Scholar] [CrossRef]
- Ghasemi, M.; Nolan, D.R.; Lally, C. An investigation into the role of different constituents in damage accumulation in arterial tissue and constitutive model development. Biomech. Model. Mechanobiol. 2018, 17, 1757–1769. [Google Scholar] [CrossRef] [PubMed]
- Mullins, L. Effect of Stretching on the Properties of Rubber. Rubber Chem. Technol. 1948, 21, 281–300. [Google Scholar] [CrossRef]
- Balzani, D.; Schröder, J.; Gross, D. Simulation of discontinuous damage incorporating residual stresses in circumferentially overstretched atherosclerotic arteries. Acta Biomater. 2006, 2, 609–618. [Google Scholar] [CrossRef]
- Peña, E.; Peña, J.A.; Doblaré, M. On the Mullins effect and hysteresis of fibered biological materials: A comparison between continuous and discontinuous damage models. Int. J. Solids Struct. 2009, 46, 1727–1735. [Google Scholar] [CrossRef]
- Pena, E.; Martins, P.; Mascarenhas, T.; Jorge, R.N.; Ferreira, A.; Doblaré, M.; Calvo, B. Mechanical characterization of the softening behavior of human vaginal tissue. J. Mech. Behav. Biomed. Mater. 2011, 4, 275–283. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Sommer, G.; Gasser, C.T.; Regitnig, P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am. J. Physiol. Circ. Physiol. 2005, 289, H2048–H2058. [Google Scholar] [CrossRef]
- Weisbecker, H.; Pierce, D.M.; Regitnig, P.; Holzapfel, G.A. Layer-specific damage experiments and modeling of human thoracic and abdominal aortas with non-atherosclerotic intimal thickening. J. Mech. Behav. Biomed. Mater. 2012, 12, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Balzani, D. Damage in Soft Biological Tissues. In Encyclopedia of Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2020; Volume 553, pp. 562–576. [Google Scholar]
- Hoeltzel, D.A.; Altman, P.; Buzard, K.; Choe, K.-I. Strip Extensiometry for Comparison of the Mechanical Response of Bovine, Rabbit, and Human Corneas. J. Biomech. Eng. 1992, 114, 202–215. [Google Scholar] [CrossRef] [PubMed]
- Boyce, B.; Jones, R.; Nguyen, T.; Grazier, J. Stress-controlled viscoelastic tensile response of bovine cornea. J. Biomech. 2007, 40, 2367–2376. [Google Scholar] [CrossRef]
- Maher, E.; Creane, A.; Lally, C.; Kelly, D. An anisotropic inelastic constitutive model to describe stress softening and permanent deformation in arterial tissue. J. Mech. Behav. Biomed. Mater. 2012, 12, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Maher, E.; Creane, A.; Sultan, S.; Hynes, N.; Lally, C.; Kelly, D.J. Inelasticity of Human Carotid Atherosclerotic Plaque. Ann. Biomed. Eng. 2011, 39, 2445–2455. [Google Scholar] [CrossRef]
- Zhang, W.; Sacks, M.S. Modeling the response of exogenously crosslinked tissue to cyclic loading: The effects of permanent set. J. Mech. Behav. Biomed. Mater. 2017, 75, 336–350. [Google Scholar] [CrossRef]
- Gültekin, O.; Hager, S.P.; Dal, H.; Holzapfel, G.A. Computational modeling of progressive damage and rupture in fibrous biological tissues: Application to aortic dissection. Biomech. Model. Mechanobiol. 2019, 18, 1607–1628. [Google Scholar] [CrossRef] [PubMed]
- Noble, C.; Smulders, N.; Lewis, R.; Carré, M.J.; Franklin, S.E.; MacNeil, S.; Taylor, Z.A. Controlled peel testing of a model tissue for diseased aorta. J. Biomech. 2016, 49, 3667–3675. [Google Scholar] [CrossRef][Green Version]
- Su, P.; Lu, D.A.; Deng, S.; Zhang, L.; Hao, Y.; Yang, Y. Three-dimensional biomechanical modeling and simulation of trephine cutting cornea for keratoplasty. Acta Bioeng. Biomech. 2018, 20, 23–33. [Google Scholar]
- Su, P.; Yang, Y.; Zhang, L.; Huang, L. Biomechanical simulation of needle insertion into cornea based on distortion energy failure criterion. Acta Bioeng. Biomech. 2016, 18, 65–75. [Google Scholar] [PubMed]
- Chen, S.; Chen, J.; Li, N. Finite element analysis of microneedle insertion into skin. Micro Nano Lett. 2012, 7, 1206–1209. [Google Scholar] [CrossRef]
- Nilsson, P.; Ståhle, P.; Sundin, K. On the behavior of crack surface ligaments. Nucl. Eng. Des. 1998, 184, 145–153. [Google Scholar] [CrossRef]
- Simo, J.; Ju, J. Strain- and stress-based continuum damage models—I. Formulation. Int. J. Solids Struct. 1987, 23, 821–840. [Google Scholar] [CrossRef]
- Lemaitre, J. Phenomenological Aspects of Damage. In A Course on Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 1–37. [Google Scholar]
- Peña, E. Computational aspects of the numerical modelling of softening, damage and permanent set in soft biological tissues. Comput. Struct. 2014, 130, 57–72. [Google Scholar] [CrossRef]
- Balzani, D.; Brinkhues, S.; Holzapfel, G.A. Constitutive framework for the modeling of damage in collagenous soft tissues with application to arterial walls. Comput. Methods Appl. Mech. Eng. 2012, 213–216, 139–151. [Google Scholar] [CrossRef]
- Fung, Y.C.; Fronek, K.; Patitucci, P. Pseudoelasticity of arteries and the choice of its mathematical expression. Am. J. Physiol. Circ. Physiol. 1979, 237, H620–H631. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. Int. J. Solids Struct. 2004, 41, 1855–1878. [Google Scholar] [CrossRef]
- Ogden, R.; Roxburgh, D.G. A pseudo–elastic model for the Mullins effect in filled rubber. Proc. R. Soc. A Math. Phys. Eng. Sci. 1999, 455, 2861–2877. [Google Scholar] [CrossRef]
- Weisbecker, H.; Pierce, D.D.M.; Holzapfel, G.A.G. Modeling of damage-induced softening for arterial tissues. In Proceedings of the 2011 SCATh Joint Workshop on New Tecnologies for Computer/Robot Assisted Surgery, Graz, Austria, 11–13 July 2011; pp. 1–4. [Google Scholar]
- Volokh, K. Hyperelasticity with softening for modeling materials failure. J. Mech. Phys. Solids 2007, 55, 2237–2264. [Google Scholar] [CrossRef]
- Li, W.; Luo, X.Y. An Invariant-Based Damage Model for Human and Animal Skins. Ann. Biomed. Eng. 2016, 44, 3109–3122. [Google Scholar] [CrossRef]
- Blanco, S.; Polindara, C.A.; Goicolea, J.M. A regularised continuum damage model based on the mesoscopic scale for soft tissue. Int. J. Solids Struct. 2015, 58, 20–33. [Google Scholar] [CrossRef]
- Comellas, E.; Bellomo, F.J.; Oller, S. A generalized finite-strain damage model for quasi-incompressible hyperelasticity using hybrid formulation. Int. J. Numer. Methods Eng. 2016, 105, 781–800. [Google Scholar] [CrossRef]
- Polindara, C.; Waffenschmidt, T.; Menzel, A. Simulation of balloon angioplasty in residually stressed blood vessels—Application of a gradient-enhanced fibre damage model. J. Biomech. 2016, 49, 2341–2348. [Google Scholar] [CrossRef]
- Ferreira, J.P.; Parente, M.; Jorge, R.N. Modeling of soft tissues with damage. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2017, 231, 131–139. [Google Scholar] [CrossRef]
- Rausch, M.K.; Karniadakis, G.E.; Humphrey, J.D. Modeling Soft Tissue Damage and Failure Using a Combined Particle/Continuum Approach. Biomech. Model. Mechanobiol. 2016, 16, 249–261. [Google Scholar] [CrossRef] [PubMed]
- Fathi, F.; Ardakani, S.H.; Dehaghani, P.F.; Mohammadi, S. A finite strain integral-type anisotropic damage model for fiber-reinforced materials: Application in soft biological tissues. Comput. Methods Appl. Mech. Eng. 2017, 322, 262–295. [Google Scholar] [CrossRef]
- Gao, X.; Zhu, Q.; Gu, W. An anisotropic multiphysics damage model with application to annulus fibrosus. J. Biomech. 2017, 61, 88–93. [Google Scholar] [CrossRef]
- Mousavi, S.J.; Farzaneh, S.; Avril, S. Computational predictions of damage propagation preceding dissection of ascending thoracic aortic aneurysms. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2944. [Google Scholar] [CrossRef]
- Martins, P.; Peña, E.; Jorge, R.N.; Santos, A.; Santos, L.; Mascarenhas, T.; Calvo, B. Mechanical characterization and constitutive modelling of the damage process in rectus sheath. J. Mech. Behav. Biomed. Mater. 2012, 8, 111–122. [Google Scholar] [CrossRef]
- Waffenschmidt, T.; Polindara, C.; Menzel, A.; Blanco, S. A gradient-enhanced large-deformation continuum damage model for fibre-reinforced materials. Comput. Methods Appl. Mech. Eng. 2014, 268, 801–842. [Google Scholar] [CrossRef]
- Polindara, C.; Waffenschmidt, T.; Menzel, A. A computational framework for modelling damage-induced softening in fibre-reinforced materials—Application to balloon angioplasty. Int. J. Solids Struct. 2017, 118–119, 235–256. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering Science. Meccanica 2002, 37, 489–490. [Google Scholar] [CrossRef]
- Simo, J.C. On a fully three-dimensional finite-strain viscoelastic damage model: Formulation and computational aspects. Comput. Methods Appl. Mech. Eng. 1987, 60, 153–173. [Google Scholar] [CrossRef]
- Weiss, J.A. A Constitutive Model and Finite Element Representation for Transversely Isotropic Soft Tissues. Ph.D. Thesis, The University of Utah, Salt Lake City, UT, USA, 1994. [Google Scholar]
- Pezowicz, C. Analysis of selected mechanical properties of intervertebral disc annulus fibrosus in macro and microscopic scale. J. Theor. Appl. Mech. 2010, 48, 917–932. [Google Scholar]
- Saez, P.; Alastrué, V.; Pena, E.; Doblaré, M.; Martinez, M.A. Anisotropic microsphere-based approach to damage in soft fibered tissue. Biomech. Model. Mechanobiol. 2011, 11, 595–608. [Google Scholar] [CrossRef]
- Miehe, C. A micro-macro approach to rubber-like materials? Part I: The non-affine micro-sphere model of rubber elasticity. J. Mech. Phys. Solids 2004, 52, 2617–2660. [Google Scholar] [CrossRef]
- Dal, H.; Kaliske, M. A micro-continuum-mechanical material model for failure of rubber-like materials: Application to ageing-induced fracturing. J. Mech. Phys. Solids 2009, 57, 1340–1356. [Google Scholar] [CrossRef]
- Peña, J.A.; Martínez, M.A.; Peña, E. Failure damage mechanical properties of thoracic and abdominal porcine aorta layers and related constitutive modeling: Phenomenological and microstructural approach. Biomech. Model. Mechanobiol. 2019, 18, 1709–1730. [Google Scholar] [CrossRef]
- Peña, E. Damage functions of the internal variables for soft biological fibred tissues. Mech. Res. Commun. 2011, 38, 610–615. [Google Scholar] [CrossRef]
- Pierce, D.M.; Maier, F.; Weisbecker, H.; Viertler, C.; Verbrugghe, P.; Famaey, N.; Fourneau, I.; Herijgers, P.; Holzapfel, G.A. Human thoracic and abdominal aortic aneurysmal tissues: Damage experiments, statistical analysis and constitutive modeling. J. Mech. Behav. Biomed. Mater. 2015, 41, 92–107. [Google Scholar] [CrossRef]
- He, R.; Zhao, L.G.; Silberschmidt, V.V.; Liu, Y.; Vogt, F. Finite element evaluation of artery damage in deployment of polymeric stent with pre- and post-dilation. Biomech. Model. Mechanobiol. 2020, 19, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Ogden, R.W. A damage model for collagen fibres with an application to collagenous soft tissues. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190821. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Ogden, R.W. An arterial constitutive model accounting for collagen content and cross-linking. J. Mech. Phys. Solids 2020, 136, 103682. [Google Scholar] [CrossRef]
- Volokh, K.Y. Constitutive model of human artery adventitia enhanced with a failure description. Mech. Soft Mater. 2019, 1, 8. [Google Scholar] [CrossRef]
- Volokh, K. Prediction of arterial failure based on a microstructural bi-layer fiber–matrix model with softening. J. Biomech. 2008, 41, 447–453. [Google Scholar] [CrossRef]
- Volokh, K. Modeling failure of soft anisotropic materials with application to arteries. J. Mech. Behav. Biomed. Mater. 2011, 4, 1582–1594. [Google Scholar] [CrossRef]
- Chaboche, J. Continuum damage mechanics: Present state and future trends. Nucl. Eng. Des. 1987, 105, 19–33. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Melenk, J.; Babuška, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Yin, G.; Li, Y.; Zhang, J.; Ni, J. Soft Tissue Modeling Using Tetrahedron Finite Element Method in Surgery Simulation. In Proceedings of the 2009 First International Conference on Information Science and Engineering, Nanjing, China, 26–28 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 3705–3708. [Google Scholar]
- Farag, S.; Abdelrahman, W.; Nahavandi, S.; Creighton, D. Physically based simulation of heterogeneous deformable models using XFEM. In Proceedings of the 2011 9th IEEE International Conference on Industrial Informatics, Lisbon, Portugal, 26–29 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 233–237. [Google Scholar]
- Gutiérrez, L.F.; Félix, R. XFEM framework for cutting soft tissues—Including topological changes in a surgery simulation. In Proceedings of the International Conference on Computer Graphics Theory and Applications, Angers, France, 17–21 May 2010; SciTePress—Science and Technology Publications: Setúbal, Portugal, 2010; pp. 275–283. [Google Scholar]
- Rempler, H.-U.; Ehlers, W. Modelling of tear propagation in soft hydrated biological tissue. PAMM 2007, 7, 4030009–4030010. [Google Scholar] [CrossRef]
- Rempler, H.-U.; Ehlers, W. Tear Propagation in Soft Hydrated Biological Tissue. PAMM 2008, 8, 10235–10236. [Google Scholar] [CrossRef]
- Paritala, P.K.; Yarlagadda, P.K.; Wang, J.; Gu, Y.; Li, Z. Numerical investigation of atherosclerotic plaque rupture using optical coherence tomography imaging and XFEM. Eng. Fract. Mech. 2018, 204, 531–541. [Google Scholar] [CrossRef]
- Wang, L.; Hill, N.A.; Roper, S.M.; Luo, X. Modelling peeling- and pressure-driven propagation of arterial dissection. J. Eng. Math. 2018, 109, 227–238. [Google Scholar] [CrossRef]
- Barenblatt, G. The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-symmetric cracks. J. Appl. Math. Mech. 1959, 23, 622–636. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Ferrara, A.; Pandolfi, A. Numerical modelling of fracture in human arteries. Comput. Methods Biomech. Biomed. Eng. 2008, 11, 553–567. [Google Scholar] [CrossRef] [PubMed]
- Ferrara, A.; Pandolfi, A. A numerical study of arterial media dissection processes. Int. J. Fract. 2010, 166, 21–33. [Google Scholar] [CrossRef]
- Ortiz, M.; Pandolfi, A. Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int. J. Numer. Methods Eng. 1999, 44, 1267–1282. [Google Scholar] [CrossRef]
- Gasser, T.C.; Holzapfel, G.A. Modeling the propagation of arterial dissection. Eur. J. Mech.-A/Solids 2006, 25, 617–633. [Google Scholar] [CrossRef]
- Moes, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Gültekin, O.; Dal, H.; Holzapfel, G.A. A phase-field approach to model fracture of arterial walls: Theory and finite element analysis. Comput. Methods Appl. Mech. Eng. 2016, 312, 542–566. [Google Scholar] [CrossRef]
- Gültekin, O.; Dal, H.; Holzapfel, G.A. Numerical aspects of anisotropic failure in soft biological tissues favor energy-based criteria: A rate-dependent anisotropic crack phase-field model. Comput. Methods Appl. Mech. Eng. 2018, 331, 23–52. [Google Scholar] [CrossRef]
- Gueltekin, O. A Phase-Field Approach to the Fracture of Anisotropic Medium. Master’s Thesis, Universitat Stuttgart, Stuttgart, Germany, 2014. [Google Scholar]
- Raina, A.; Miehe, C. A phase-field model for fracture in biological tissues. Biomech. Model. Mechanobiol. 2015, 15, 479–496. [Google Scholar] [CrossRef]
- Wang, L.; Roper, S.; Luo, X.Y.; Hill, N.A. Modelling of tear propagation and arrest in fibre-reinforced soft tissue subject to internal pressure. J. Eng. Math. 2015, 95, 249–265. [Google Scholar] [CrossRef]
- Karimi, A.; Razaghi, R.; Koyama, M. A patient-specific numerical modeling of the spontaneous coronary artery dissection in relation to atherosclerosis. Comput. Methods Programs Biomed. 2019, 182, 105060. [Google Scholar] [CrossRef] [PubMed]
- Lindström, P.; Jonsson, A.; Jernberg, A.; Østby, E. Non-linear fracture mechanics in LS-DYNA and. In Proceedings of the 10th European LS-DYNA conference 2015, Würzburg, Germany, 15–17 June 2015; DYNAmore GmbH.: Würzburg, Germany, 2015. [Google Scholar]
- Jayendiran, R.; Ruimi, A. Numerical Modeling of Crack Propagation in Human Aorta. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017; New York, NY, USA, 2017. Volume 3: Biomedical and Biotechnology Engineering; American Society of Mechanical Engineers. pp. 1–8. [Google Scholar]
- Wang, L.; Roper, S.; Hill, N.A.; Luo, X. Propagation of dissection in a residually-stressed artery model. Biomech. Model. Mechanobiol. 2017, 16, 139–149. [Google Scholar] [CrossRef]
- Badel, P.; Avril, S.; Sutton, M.A.; Lessner, S.M. Numerical simulation of arterial dissection during balloon angioplasty of atherosclerotic coronary arteries. J. Biomech. 2014, 47, 878–889. [Google Scholar] [CrossRef] [PubMed]
- Leng, X.; Davis, L.A.; Deng, X.; Sutton, M.A.; Lessner, S. Numerical modeling of experimental human fibrous cap delamination. J. Mech. Behav. Biomed. Mater. 2016, 59, 322–336. [Google Scholar] [CrossRef]
- Noble, C.; van der Sluis, O.; Voncken, R.M.; Burke, O.; Franklin, S.E.; Lewis, R.; Taylor, Z. Simulation of arterial dissection by a penetrating external body using cohesive zone modelling. J. Mech. Behav. Biomed. Mater. 2017, 71, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Van Den Bosch, M.J.; Schreurs, P.J.G.; Geers, M.G.D. On the development of a 3D cohesive zone element in the presence of large deformations. Comput. Mech. 2008, 42, 171–180. [Google Scholar] [CrossRef]
- Maiti, S.; Geubelle, P.H. A cohesive model for fatigue failure of polymers. Eng. Fract. Mech. 2005, 72, 691–708. [Google Scholar] [CrossRef]
- Fortunato, R.N.; Robertson, A.M.; Sang, C.; Maiti, S. Computational modeling reveals the relationship between intrinsic failure properties and uniaxial biomechanical behavior of arterial tissue. Biomech. Model. Mechanobiol. 2019, 18, 1791–1807. [Google Scholar] [CrossRef] [PubMed]
- Ferrer, G.A.; Fortunato, R.N.; Musahl, V.; Maiti, S.; Debski, R.E. Effect of localized tendon remodeling on supraspinatus tear propagation. J. Biomech. 2020, 108, 109903. [Google Scholar] [CrossRef] [PubMed]
- Hakim, V.; Karma, A. Laws of crack motion and phase-field models of fracture. J. Mech. Phys. Solids 2009, 57, 342–368. [Google Scholar] [CrossRef]
- Sommer, G.; Gasser, T.C.; Regitnig, P.; Auer, M.; Holzapfel, G.A. Dissection Properties of the Human Aortic Media: An Experimental Study. J. Biomech. Eng. 2008, 130, 21007. [Google Scholar] [CrossRef]
- Kachanov, L.M.; Krajcinovic, D. Introduction to Continuum Damage Mechanics. J. Appl. Mech. 1986, 54, 481. [Google Scholar] [CrossRef]
- Camasão, D.B.; Mantovani, D. The mechanical characterization of blood vessels and their substitutes in the continuous quest for physiological-relevant performances. A critical review. Mater. Today Bio 2021, 10, 100106. [Google Scholar] [CrossRef]
- Aranda, C.A.P.; Gamboa, F.; Castillo-Cruz, O.; Cauich-Rodríguez, J.V.; Avilés, F. Design and analysis of a burst strength device for testing vascular grafts. Rev. Sci. Instrum. 2019, 90, 14301. [Google Scholar] [CrossRef] [PubMed]
- Buehler, M.J. Nanomechanics of collagen fibrils under varying cross-link densities: Atomistic and continuum studies. J. Mech. Behav. Biomed. Mater. 2008, 1, 59–67. [Google Scholar] [CrossRef]
- Stemper, B.D.; Yoganandan, N.; Pintar, F.A. Methodology to study intimal failure mechanics in human internal carotid arteries. J. Biomech. 2005, 38, 2491–2496. [Google Scholar] [CrossRef]
- Tong, J.; Sommer, G.; Regitnig, P.; Holzapfel, G.A. Dissection Properties and Mechanical Strength of Tissue Components in Human Carotid Bifurcations. Ann. Biomed. Eng. 2011, 39, 1703–1719. [Google Scholar] [CrossRef] [PubMed]
- Calvo, B.; Peña, E.; Martinez, M.A.; Doblaré, M. An uncoupled directional damage model for fibred biological soft tissues. Formulation and computational aspects. Int. J. Numer. Methods Eng. 2006, 69, 2036–2057. [Google Scholar] [CrossRef]
- Ebara, S.; Iatridis, J.C.; Setton, L.A.; Foster, R.J.; Mow, V.C.; Weidenbaum, M. Tensile Properties of Nondegenerate Human Lumbar Anulus Fibrosus. Spine 1996, 21, 452–461. [Google Scholar] [CrossRef]
- Skaggs, D.L.; Weidenbaum, M.; Latridis, J.C.; Ratcliffe, A.; Mow, V.C. Regional Variation in Tensile Properties and Biochemical Composition of the Human Lumbar Anulus Fibrosus. Spine 1994, 19, 1310–1319. [Google Scholar] [CrossRef]
- Annaidh, A.N.; Ottenio, M.; Bruyère, K.; Destrade, M.; Gilchrist, M.D. Mechanical Properties of Excised Human Skin. In IFMBE Proceedings, Proceedings of the 6th World Congress of Biomechanics (WCB 2010), Singapore, 1–6 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; Volume 31, pp. 1000–1003. [Google Scholar]
- Viano, D.C.; King, A.I.; Melvin, J.W.; Weber, K. Injury biomechanics research: An essential element in the prevention of trauma. J. Biomech. 1989, 22, 403–417. [Google Scholar] [CrossRef]
- Comellas, E.; Gasser, T.C.; Bellomo, F.J.; Oller, S. A homeostatic-driven turnover remodelling constitutive model for healing in soft tissues. J. R. Soc. Interface 2016, 13, 20151081. [Google Scholar] [CrossRef] [PubMed]
- Zuo, D.; He, Y.; Avril, S.; Yang, H.; Hackl, K. A thermodynamic framework for unified continuum models for the healing of damaged soft biological tissue. J. Mech. Phys. Solids 2021, 158, 104662. [Google Scholar] [CrossRef]
- He, Y.; Zuo, D.; Hackl, K.; Yang, H.; Mousavi, S.J.; Avril, S. Gradient-enhanced continuum models of healing in damaged soft tissues. Biomech. Model. Mechanobiol. 2019, 18, 1443–1460. [Google Scholar] [CrossRef] [PubMed]
- Benam, K.H.; Dauth, S.; Hassell, B.; Herland, A.; Jain, A.; Jang, K.-J.; Karalis, K.; Kim, H.J.; MacQueen, L.; Mahmoodian, R.; et al. Engineered In Vitro Disease Models. Annu. Rev. Pathol. Mech. Dis. 2015, 10, 195–262. [Google Scholar] [CrossRef] [PubMed]
- Golubovsky, J.L.; Colbrunn, R.W.; Klatte, R.S.; Nagle, T.F.; Briskin, I.N.; Chakravarthy, V.B.; Gillespie, C.M.; Reith, J.D.; Jasty, N.; Benzel, E.C.; et al. Development of a novel in vitro cadaveric model for analysis of biomechanics and surgical treatment of Bertolotti syndrome. Spine J. 2020, 20, 638–656. [Google Scholar] [CrossRef] [PubMed]


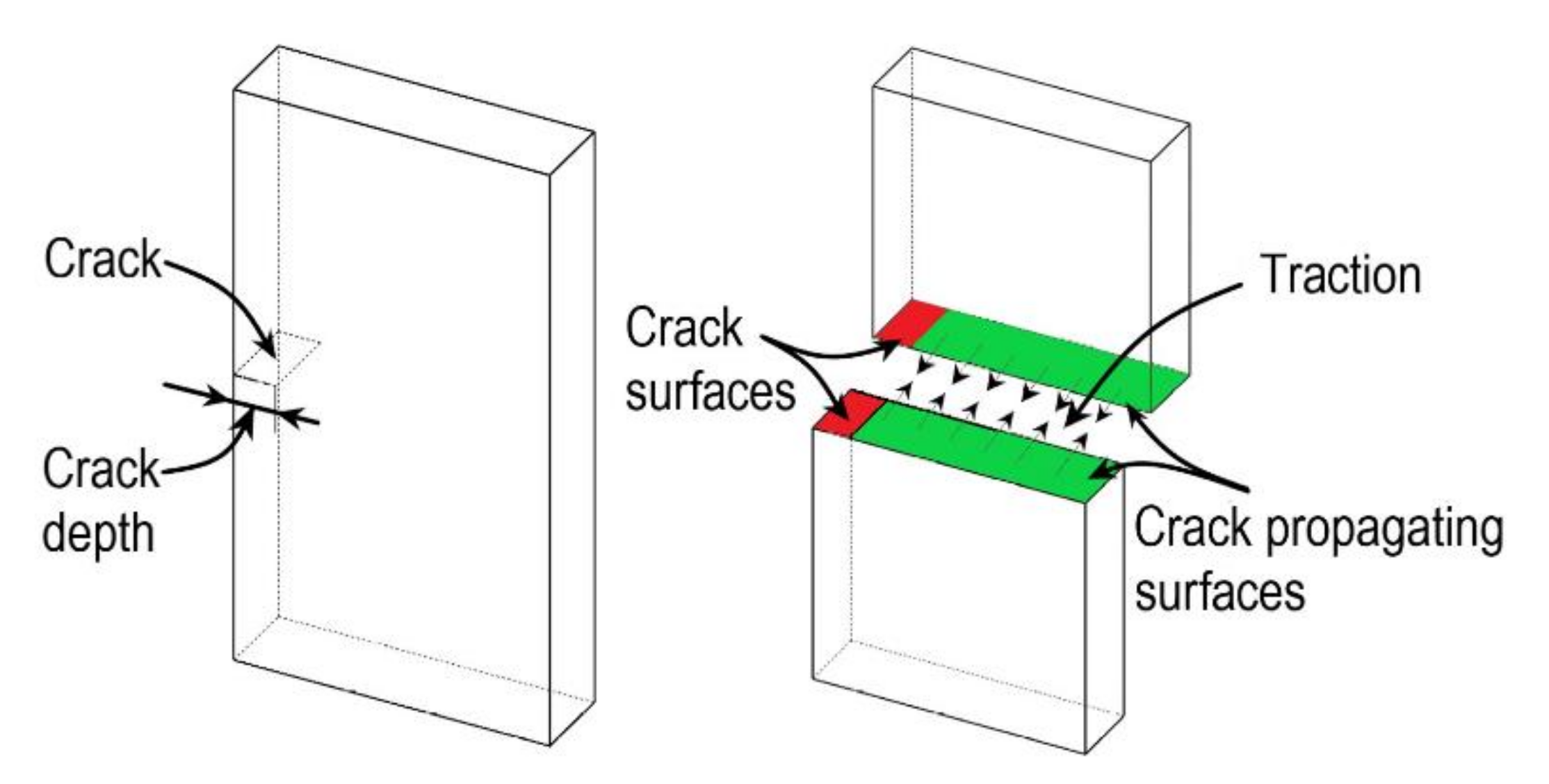
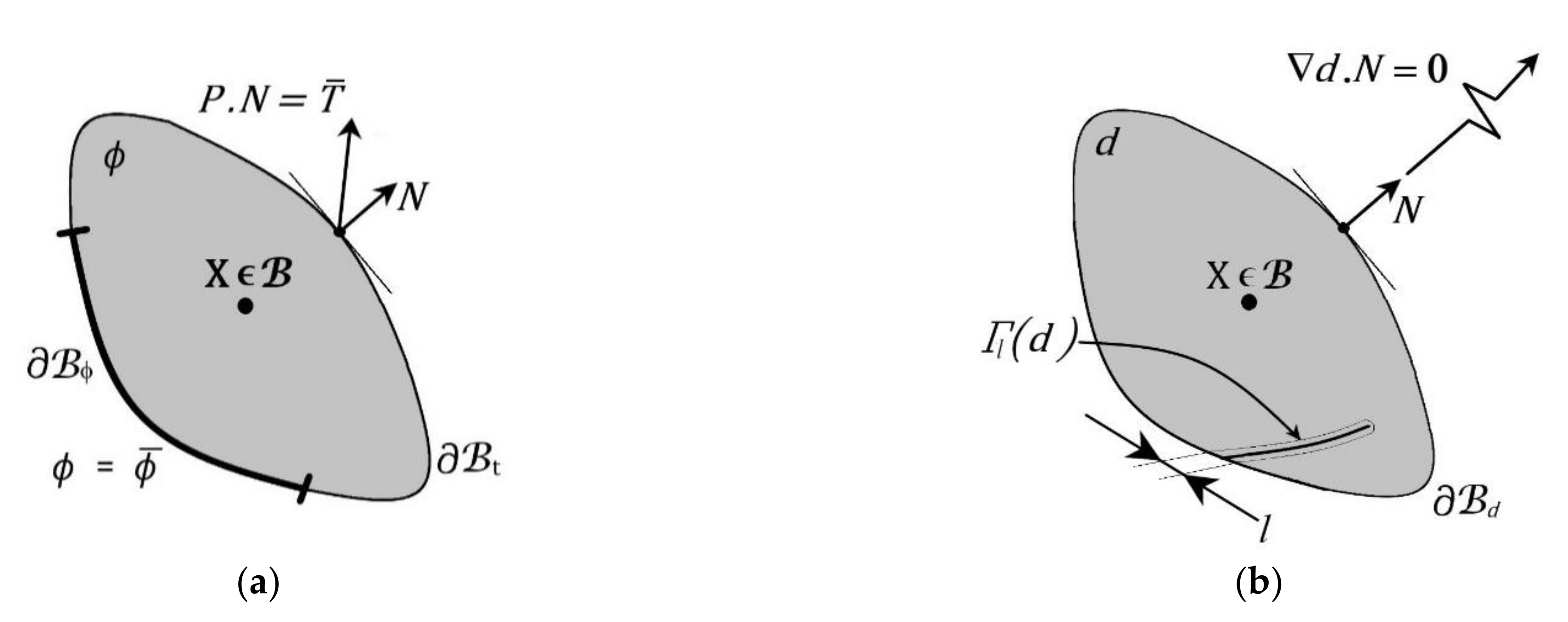
| Modelling Considerations | Continuum Damage Mechanics | Pseudo-Elasticity | Softening Hyperelasticity |
|---|---|---|---|
| Strain energy density | |||
| Damage parameter | –damage variable –damage function | –energy limiter | |
| Damage initiation | –damage threshold at the current time. | Based on the critical stretch in fibres, i.e., | Strain softening incorporated using energy limiters. |
| Damage evolution | Based on the model. Discontinuous damage modelled with the maximum strain in the loading path. Continuous damage is strain-rate-dependent | ||
| Thermodynamic consideration | ), which is maximum strain energy without damage. | evolves, which is consistent with Clausius–Duham inequality. | Energy limiters activate the irreversible damage and dissipation that ensure the thermodynamic stability of the model. |
| References | Tissue | Tissue Structure | Damage | Modelling Features |
|---|---|---|---|---|
| Balanco et al. [64] | Soft tissue with fibres | Isotropic matrix and collagen fibres | Matrix and fibres | (1) Anisotropic, incompressible, (2) HGO strain energy function, (3) three parameters to define the damage, (4) continuum damage based on Simo and Ju [55]. |
| Comellas et al. [65] | Rectus sheath | Isotropic matrix | Matrix | (1) Isotropic, incompressible, (2) strain energy function: neo-Hookean and Ogden, (3) one parameter related to the softening effect. |
| Polindara et al. [66] | Blood vessel | Isotropic matrix and collagen fibres | Fibres | (1) Anisotropic, incompressible, (2) HGO strain energy function, (3) two parameters to define the damage, (4) continuum damage based on Simo and Ju [55]. |
| Ferreira et al. [67] | Arteries | Isotropic matrix and collagen fibres | Matrix and fibres | (1) Anisotropic, incompressible, (2) HGO strain energy function, (3) seven parameters to define the damage, (4) continuum damage based on Simo [68]. |
| Rausch et al. [68] | Soft tissue with fibres | Isotropic matrix and collagen fibres | Matrix and fibres | (1) Anisotropic, incompressible, (2) HGO strain energy function, (3) two parameters to define the damage, (4) continuum damage based on Simo [68]. |
| Fathi et al. [69] | Soft tissue with fibres | Isotropic matrix and collagen fibres | Matrix and fibres | (1) Anisotropic, incompressible, (2) HGO strain energy function, (3) six parameters to define the damage, (4) continuum damage based on Simo and Ju [55]. |
| Gao et al. [70] | Annulus fibrosus | Isotropic matrix and collagen fibres | Matrix and fibres | (1) Anisotropic, incompressible, (2) HGO strain energy function, (3) four parameters to define the damage, (4) damage model is based on [38]. |
| Mousavi et al. [71] | Ascending thoracic aortic aneurysms | Smooth muscle cells and collagen fibres distributed in the elastin matrix | Elastin matrix and collagen fibres | (1) Anisotropic, incompressible, (2) HGO strain energy function for fibres, (3) three parameters to define the damage, (4) damage model is based on linear softening by [66] |
| Ghasemi et al. [35] | Arteries | Elastin and collagen fibres in an isotropic matrix | Elastin fibres and collagen fibres | (1) Anisotropic, incompressible, (2) HGO strain energy function, (3) four parameters to define the damage, (4) continuum damage based on [58]. |
| Damage Approach | Capabilities | Tissues | Benefits |
|---|---|---|---|
| CDM | Mullins effect Hysteresis Permanent set | Artery, Rectus sheath, ligament, annulus fibrosus, ascending aortic aneurysm, thoracic aneurysm. |
|
| Pseudo-elasticity | Mullins effect Hysteresis Permanent set | Aortic aneurysms, brain tissue |
|
| Softening hyperelasticity | Permanent set | Skin, artery |
|
| Reference | Tissue | Mechanism | Validation |
|---|---|---|---|
| Blanco et al. [64] | Soft tissue | Mullins effect | Numerical simulation of tropocollagen failure by Buehler et al. [132] |
| Comellas et al. [65] | Rectus sheath | Mullins effect | Based on the uniaxial tension experiments of Martins et al. [72] |
| Polindara et al. [66] | Blood Vessel | Permanent set | Wedge geometry simulation for balloon angioplasty was validated with analytical of neo-Hookean tube tests [75]. |
| Ferreira et al. [67] | Arteries | Mullins effect | The damage model is not validated. |
| Rausch et al. [68] | Arteries | Permanent set Rupture | Damage model with results of Stepmer et al. [133] and tear simulations with Tong et al. [134] and Sommer et al. [128] |
| Fathi et al. [69] | Rectus sheath Ligament | Mullins effect Rupture | Uniaxial tension experiments of Martins et al., [72] and numerical results of Waffenschmidt et al. [73] for rectus sheath. For ligament, the model is validated with experimental results of Weiss [77] and numerical results of Calvo et al. [135] |
| Gao et al. [72] | Annulus fibrosus | Permanent set | Simulation results validated with the experimental results of Ebara et al. [136] and Skaggs et al. [137] |
| Mousavi et al. [71] | Ascending thoracic aortic aneurysms | Permanent set | Buldge inflation test with graft size of 45 × 45 mm2 and inflation of circular area of diameter 30 mm. |
| Ghasemi et al. [35] | Arteries | Mullins effect Hysteresis Permanent set | Experiments of uniaxial tension tests and cyclic loading in uniaxial tension. |
| Pierce et al. [84] | Thoracic aortic tissues Abdominal aortic tissues | Permanent set Mullins effect | Experimental results from tissues under uniaxial tension and cyclic loading. |
| Holzapfel and Ogden [86] | Soft tissue | Mullins effect | A reduced model with uniaxial fibres is validated with the rat tail tendon experiment results of Pins and Silver. |
| Li and Luo [63] | Skin | Permanent set | Experimental results of Annaidh et al. [138] for human skin under uniaxial tension. Additionally, validate with porcine skin. |
| Volokh [88] | Artery adventitia | Permanent set | Uniaxial tension tests of artery adventitia in longitudinal and circumferential directions. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chittajallu, S.N.S.H.; Richhariya, A.; Tse, K.M.; Chinthapenta, V. A Review on Damage and Rupture Modelling for Soft Tissues. Bioengineering 2022, 9, 26. https://doi.org/10.3390/bioengineering9010026
Chittajallu SNSH, Richhariya A, Tse KM, Chinthapenta V. A Review on Damage and Rupture Modelling for Soft Tissues. Bioengineering. 2022; 9(1):26. https://doi.org/10.3390/bioengineering9010026
Chicago/Turabian StyleChittajallu, Sai Naga Sri Harsha, Ashutosh Richhariya, Kwong Ming Tse, and Viswanath Chinthapenta. 2022. "A Review on Damage and Rupture Modelling for Soft Tissues" Bioengineering 9, no. 1: 26. https://doi.org/10.3390/bioengineering9010026
APA StyleChittajallu, S. N. S. H., Richhariya, A., Tse, K. M., & Chinthapenta, V. (2022). A Review on Damage and Rupture Modelling for Soft Tissues. Bioengineering, 9(1), 26. https://doi.org/10.3390/bioengineering9010026







