Predicting Corrosion Delamination Failure in Active Implantable Medical Devices: Analytical Model and Validation Strategy
Abstract
1. Introduction
2. Materials and Methods
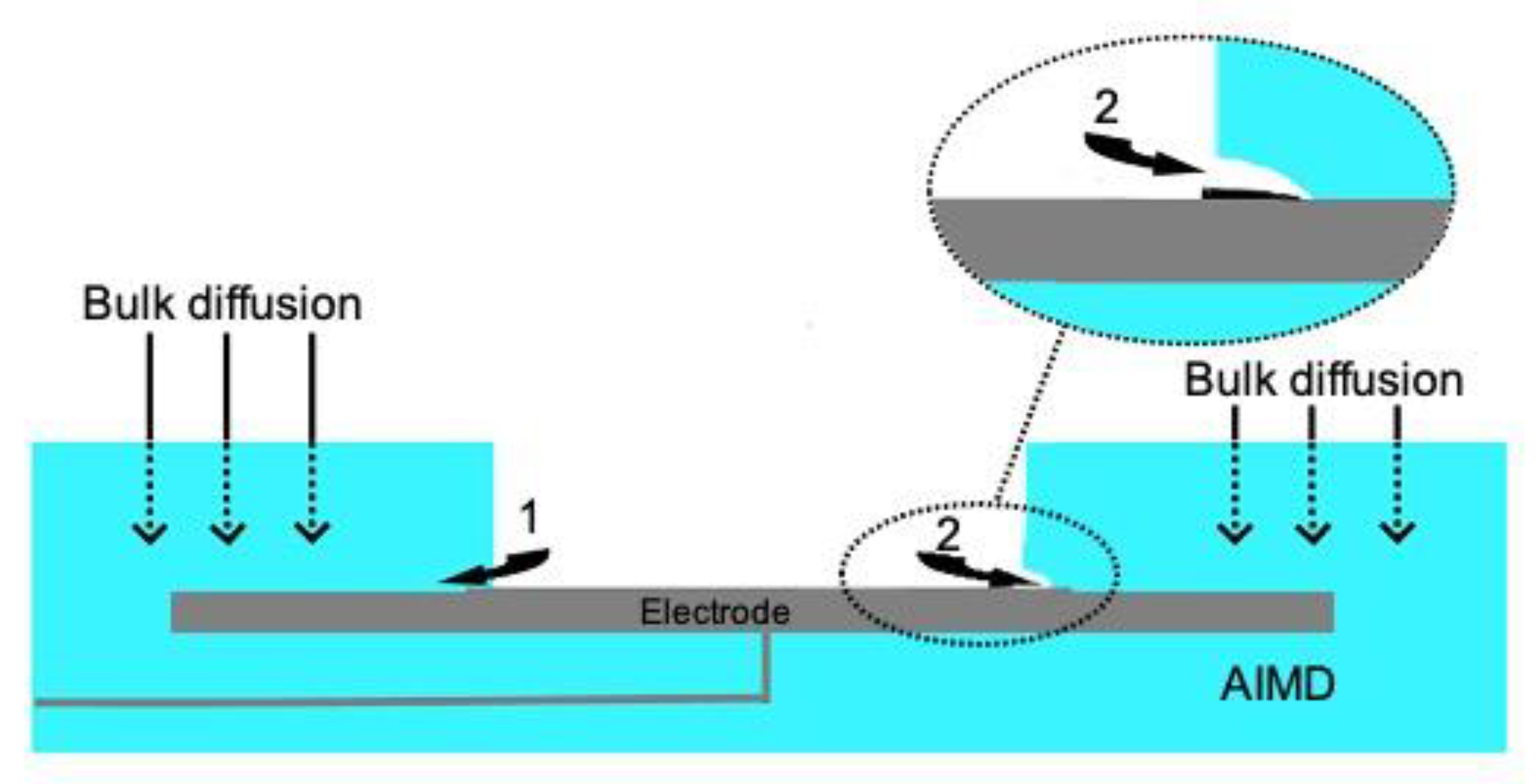
2.1. Rationale of the Study
2.2. PDMS
2.3. Metal
2.4. Corroding Agent
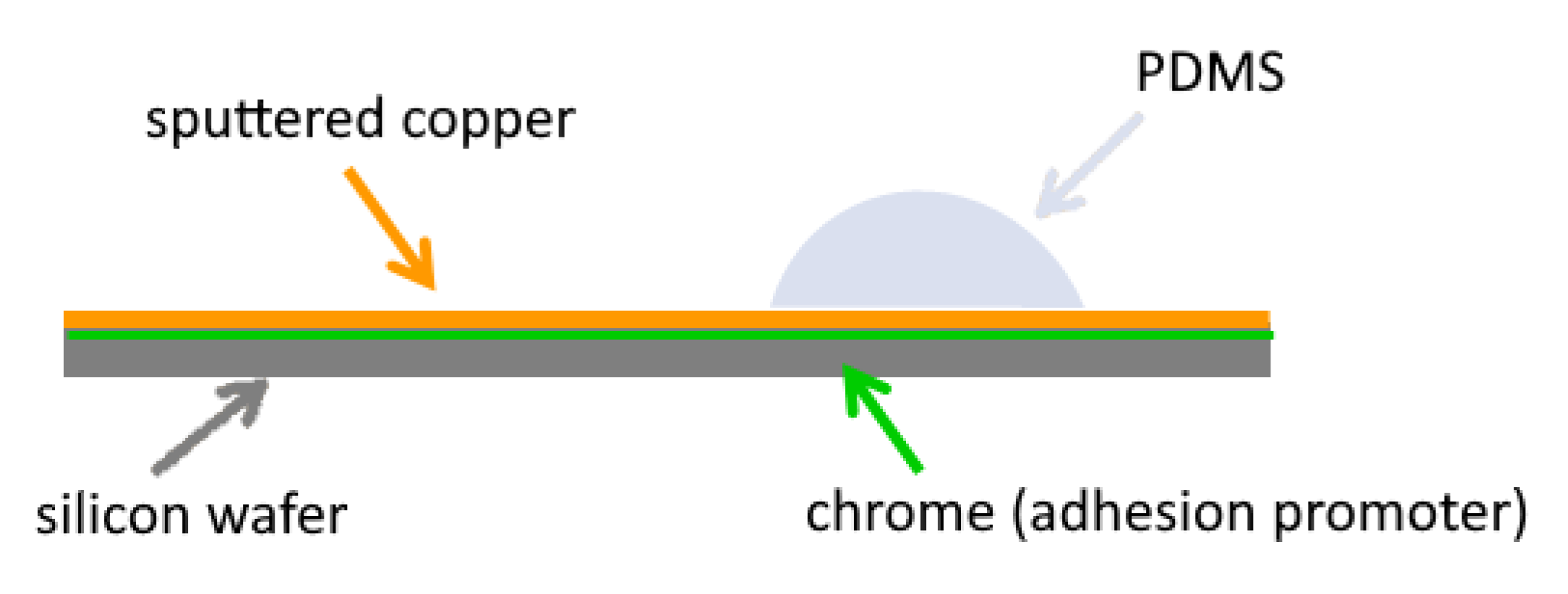
2.5. Specimen for Interface Diffusion
2.6. Specimen for Volume Diffusion
3. Results
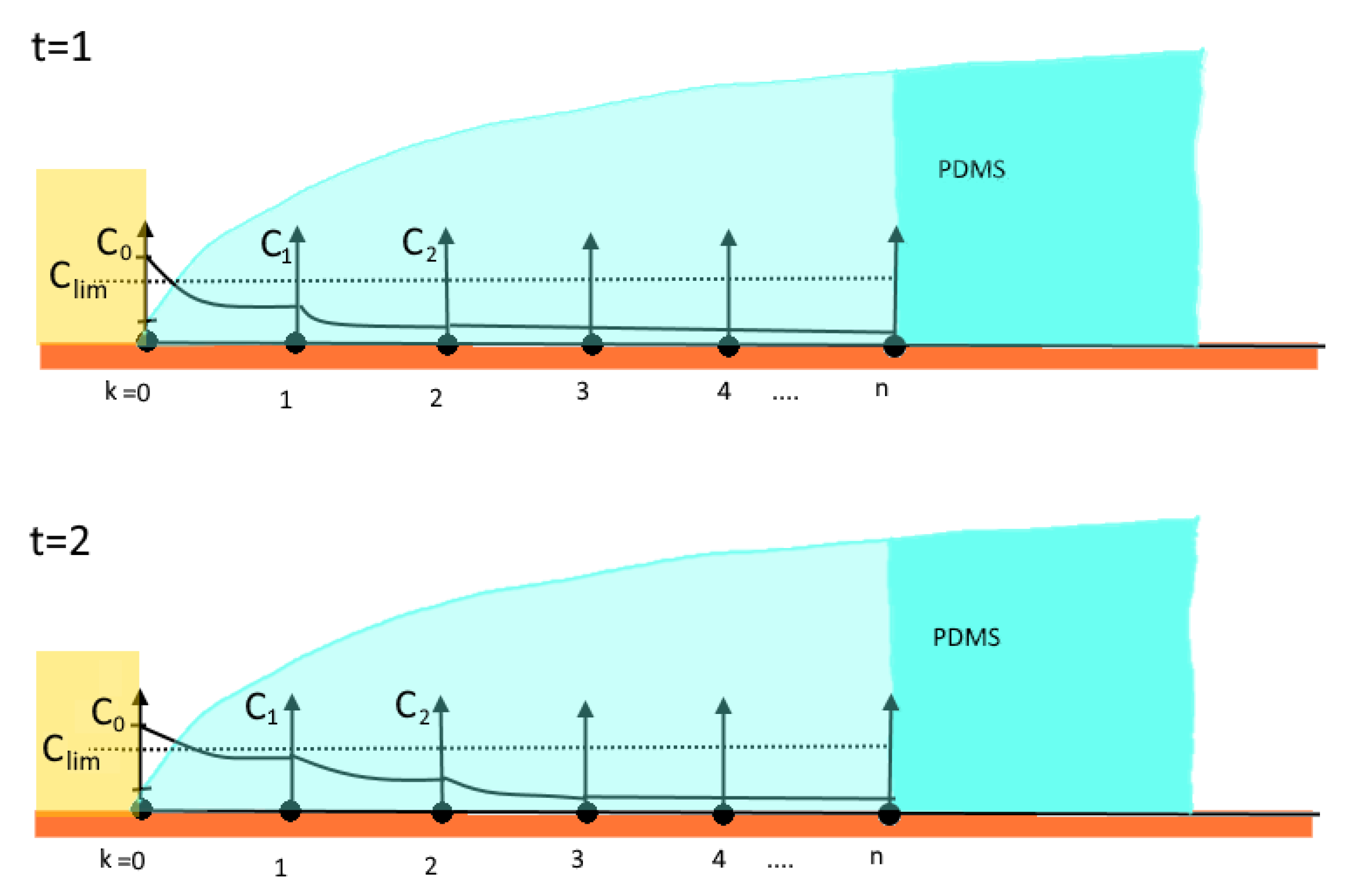
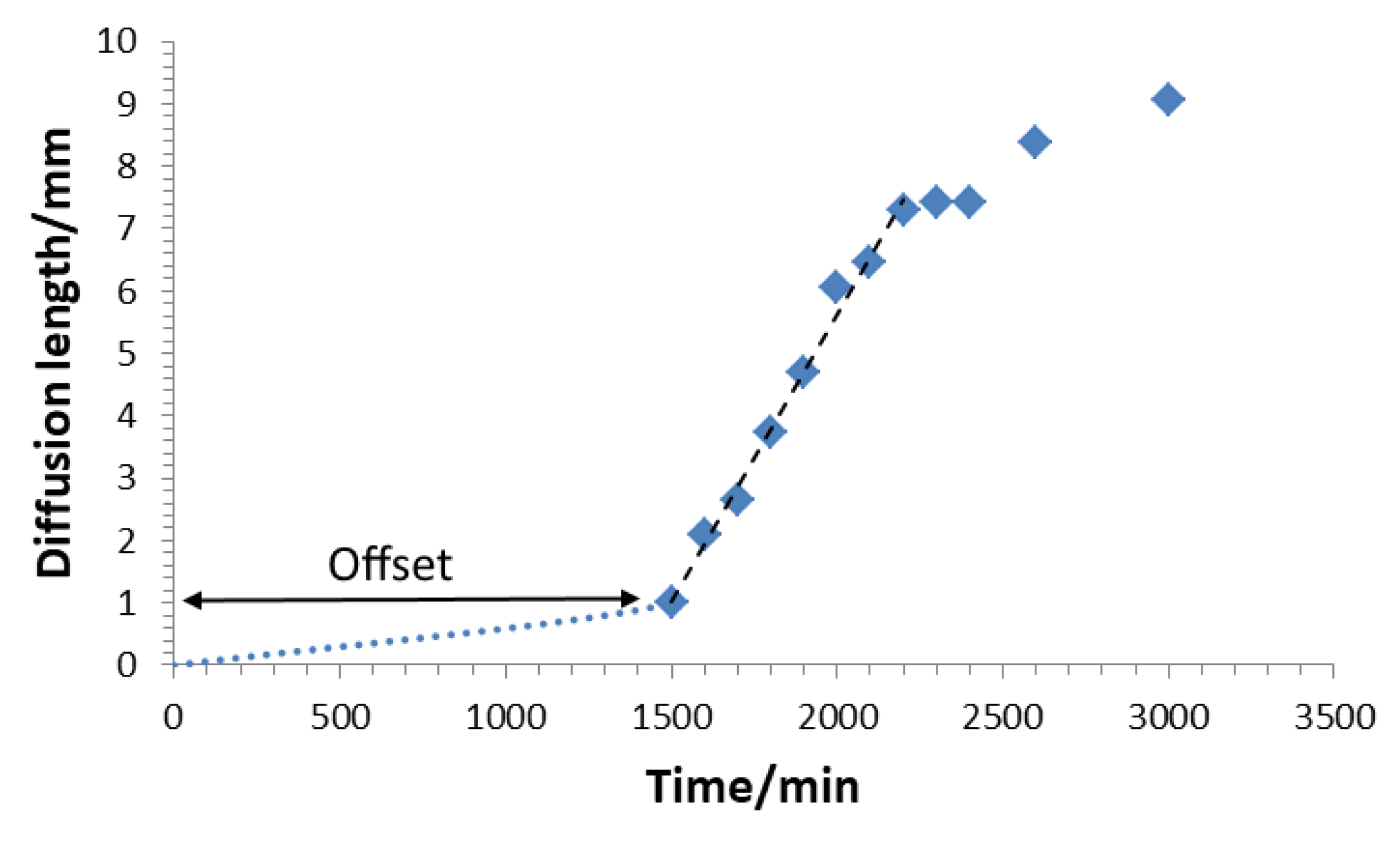
3.1. Phase I
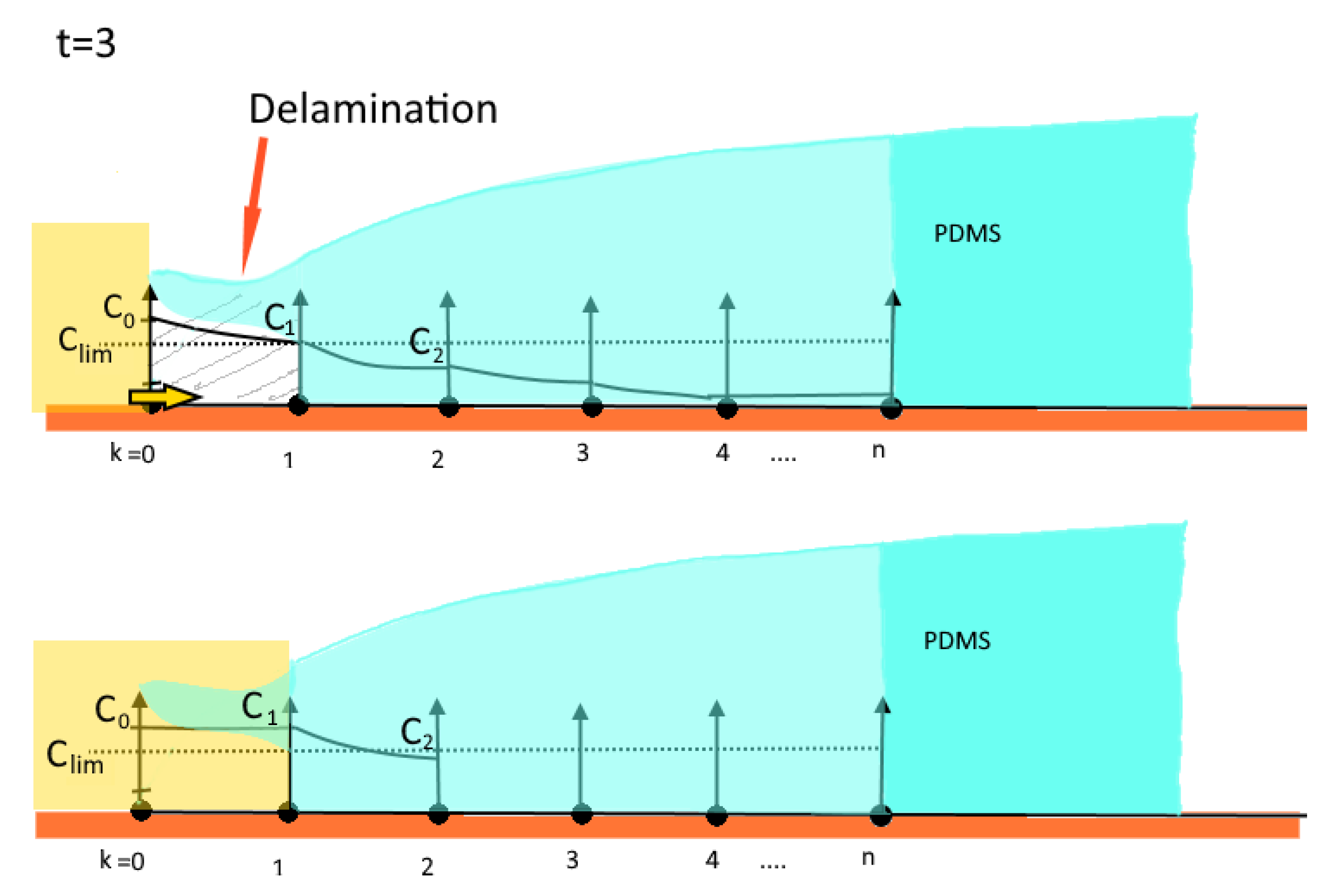
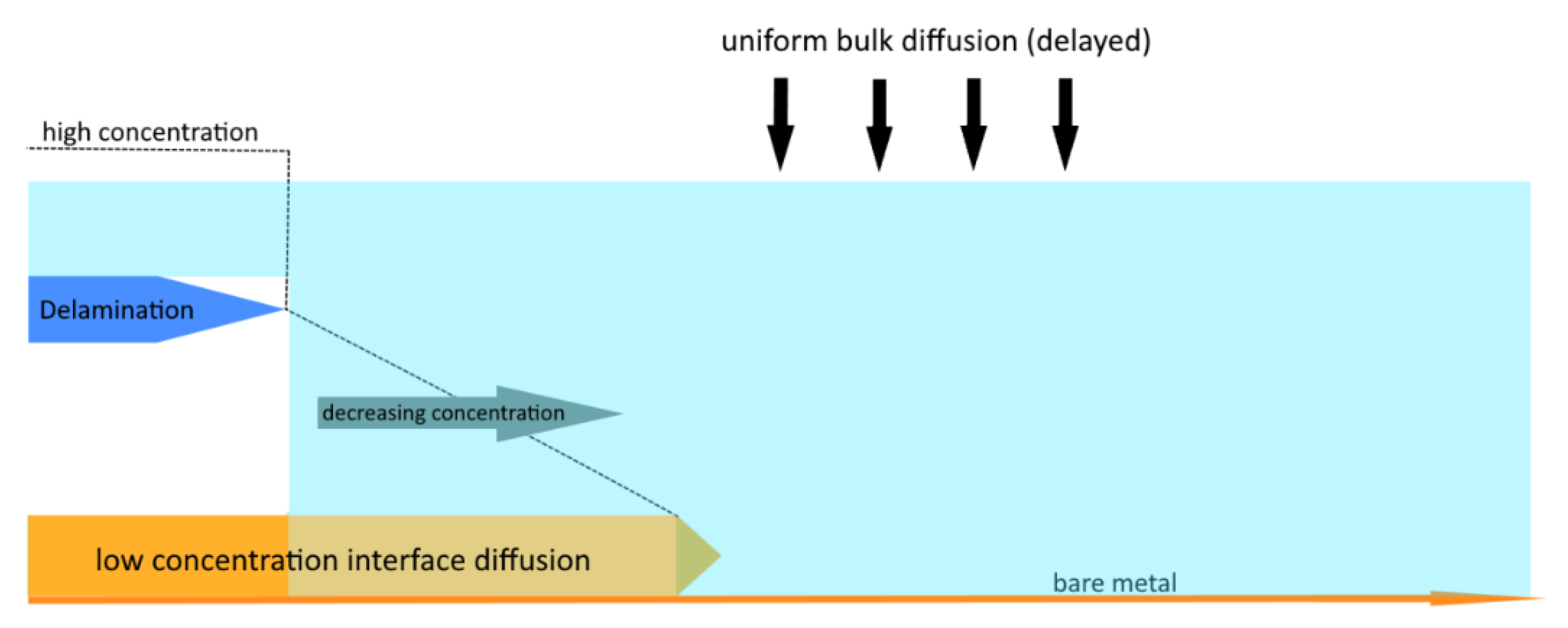
3.2. Phase II
3.3. Phase III
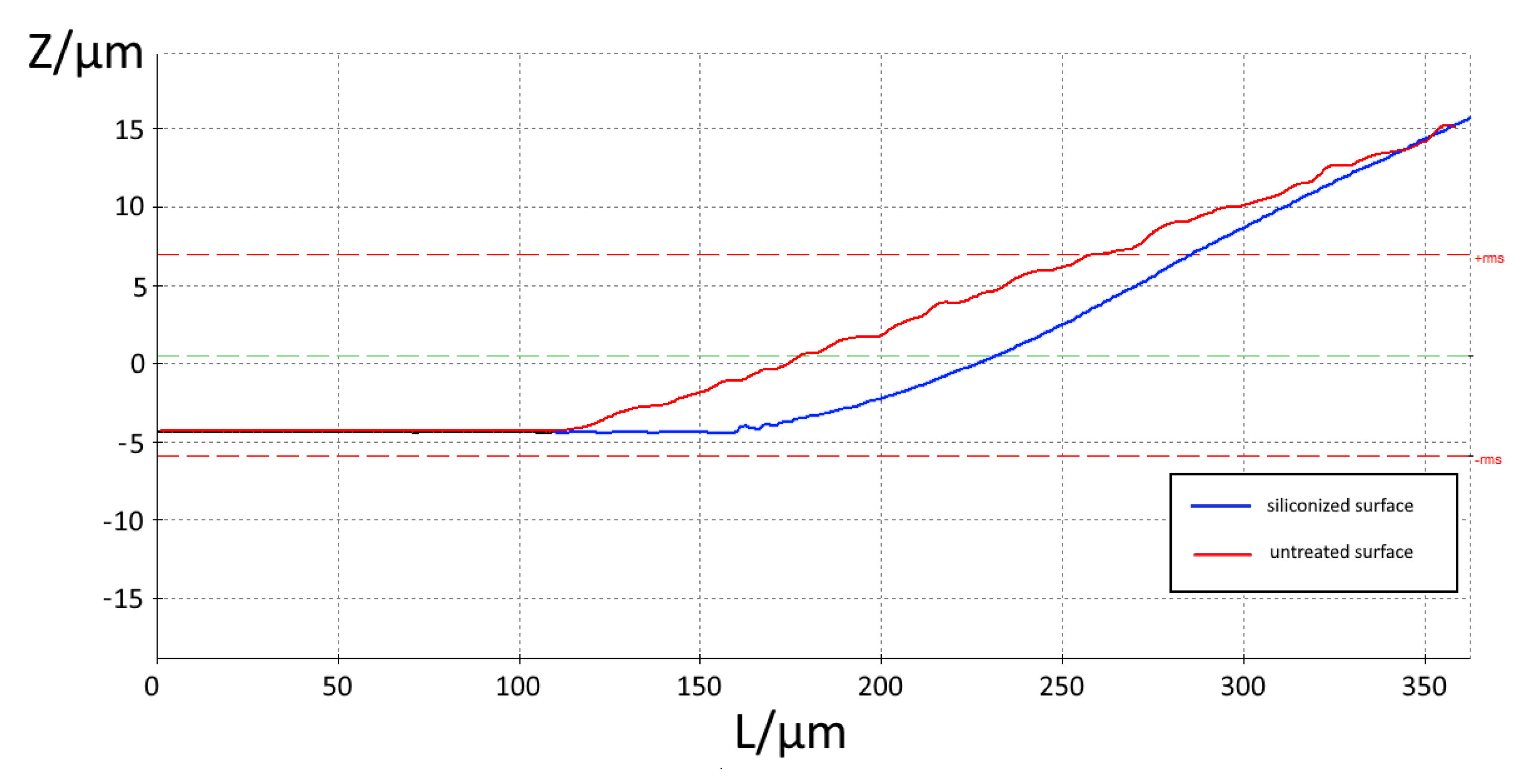
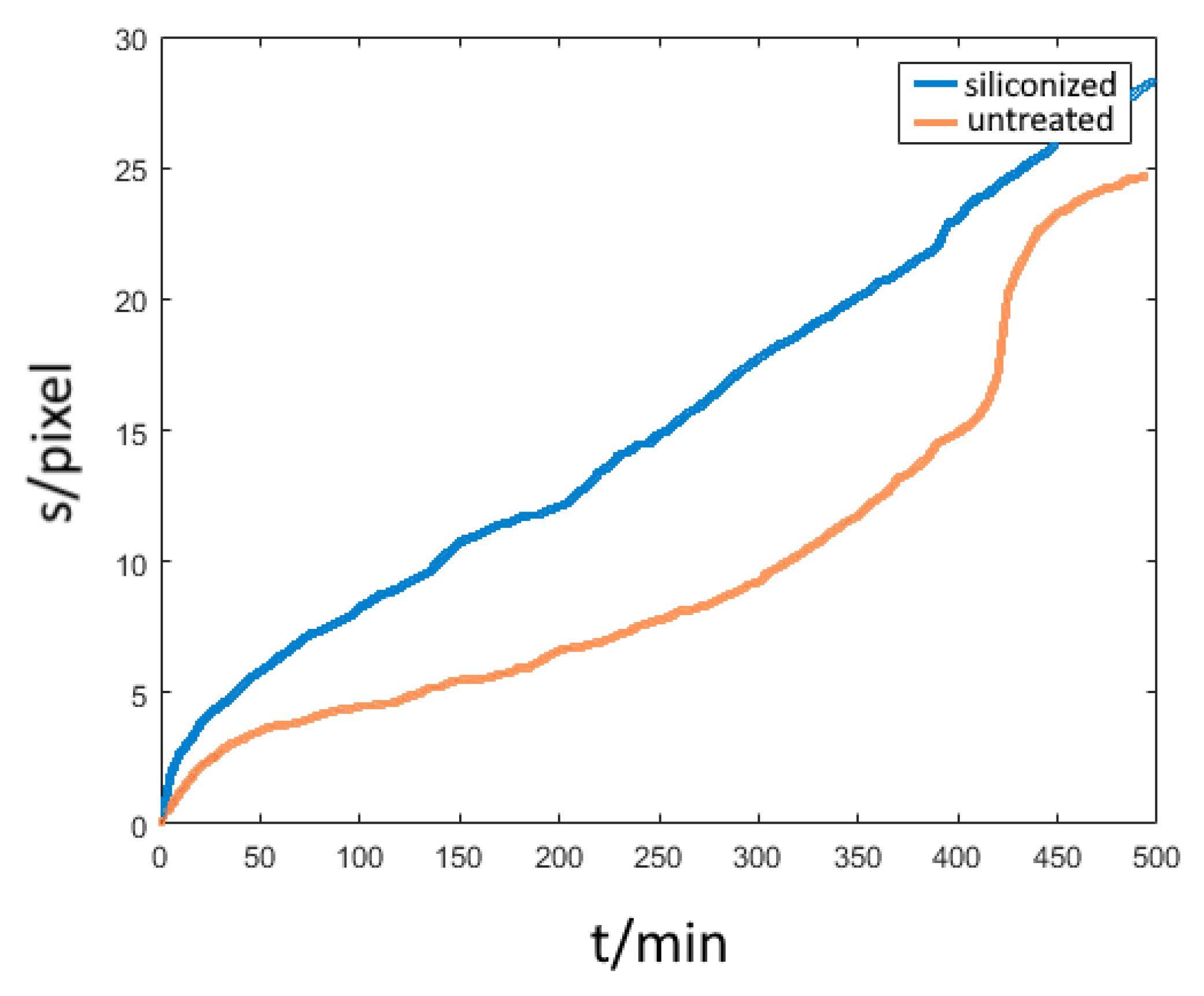
3.4. Influence of Surface Modification
4. Discussion
4.1. Phase I
4.2. Phase II
4.3. Phase III
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Medical Device Regulation. MDR–Article 2–Definitions–Medical Device Regulation. 2019. Available online: https://www.medical-device-regulation.eu/2019/07/10/mdr-article-2-definitions/ (accessed on 2 November 2021).
- Nag, S.; Thakor, N.V. Implantable neurotechnologies: Electrical stimulation and applications. Med. Biol. Eng. Comput. 2016, 54, 63–76. [Google Scholar] [CrossRef] [PubMed]
- Stieglitz, T. Neuroprothetik und Neuromodulation. Bundesgesundheitsbl 2010, 53, 783–790. [Google Scholar] [CrossRef]
- NIDCD. Cochlear Implants. 2021. Available online: https://www.nidcd.nih.gov/health/cochlear-implants (accessed on 2 November 2021).
- Pachler, H.; Hawle, L.; Schwarz, M.; Neuhold, H. Wissenswertes über ein Cochlea-Implantat (CI) für Betroffene und Angehörige. Einklang 2001. [Google Scholar]
- Kempe, M.D. Control of moisture ingress into photovoltaic modules. In Proceedings of the Conference Record of the Thirty-First IEEE Photovoltaic Specialists Conference, Lake Buena Vista, FL, USA, 3–7 January 2005; p. 503. [Google Scholar]
- Sia, S.K.; Whitesides, G.M. Microfluidic devices fabricated in Poly(dimethylsiloxane) for biological studies. Electrophoresis 2003, 24, 3563–3576. [Google Scholar] [CrossRef] [PubMed]
- Vullev, V.I.; Wan, J.; Heinrich, V.; Landsman, P.; Bower, P.E.; Xia, B.; Millare, B.; Jones, G. Nonlithographic Fabrication of Microfluidic Devices. J. Am. Chem. Soc. 2006, 128, 16062–16072. [Google Scholar] [CrossRef] [PubMed]
- Barrie, J.A.; Machin, D. The sorption and diffusion of water in silicone rubbers: Part I. Unfilled rubbers. J. Macromol. Sci. Part B 1969, 3, 645–672. [Google Scholar] [CrossRef]
- Harley, S.J.; Glascoe, E.A.; Maxwell, R.S. Thermodynamic Study on Dynamic Water Vapor Sorption in Sylgard-184. J. Phys. Chem. B 2012, 116, 14183–14190. [Google Scholar] [CrossRef] [PubMed]
- Park, G.S. Transport Principles: Solution, Diffusion and Permeation in Polymer Membranes; Kluwer: Dordrecht, The Netherlands, 1986; Volume 181, pp. 1–20. [Google Scholar]
- Watson, J.M.; Baron, M.G. The behaviour of water in poly(dimethylsiloxane). J. Membr. Sci. 1996, 110, 47–57. [Google Scholar] [CrossRef]
- Walter, H.; Bauer, J.; Keller, J.; Hölck, O.; Becker, K.-F.; Wunderle, B.T. Grenzflächendiffusion und Adhäsionsverhalten nanostrukturierter Epoxidharzverbunde in Sensorapplikationen. Beiträge des 3. In Proceedings of the GMM-Workshops, Stuttgart, Germany, 3–4 March 2011; GMM-Fachbericht 68, CD-ROM. VDE-Verl: Berlin, Germany, 2011. [Google Scholar]
- Maile, F.J.; Schauer, T.; Eisenbach, C.D. Evaluation of the delamination of coatings with scanning reference electrode technique. Prog. Org. Coat. 2000, 38, 117–120. [Google Scholar] [CrossRef]
- Battmer, R.-D.; Linz, B.; Lenarz, T. A review of device failure in more than 23 years of clinical experience of a cochlear implant program with more than 3400 implantees. Otol. Neurotol. 2009, 30, 455–463. [Google Scholar] [CrossRef]
- Ordonez, J.; Schuettler, M.; Boehler, C.; Boretius, T.; Stieglitz, T. Thin films and microelectrode arrays for neuroprosthetics. MRS Bull. 2012, 37, 590–598. [Google Scholar] [CrossRef]
- Pröbster, M. Elastisch Kleben. Aus der Praxis Für Die Praxis; Springer Fachmedien Wiesbaden GmbH: Wiesbaden, Germany, 2013. [Google Scholar]
- Gleich, H.; Lohse, H. Alterungseffekte im Zeitraffertest. Adhaes Kleb. Dicht. 2017, 61, 36–41. [Google Scholar] [CrossRef]
- Hörmann, M. Nichtlineare Versagensanalyse von Faserverbundstrukturen. Ph.D. Dissertation, Stuttgart University, Stuttgart, Germany, 2002. [Google Scholar]
- Normausschuss Mater. im DIN Deutschen Institut für Normung e.V. Bezeichnung der Wichtigsten Bruchbilder DIN EN ISO 10365:1995-08. 1995. Available online: https://www.beuth.de/de/norm/din-en-iso-10365/2602068 (accessed on 1 December 2021).
- Mao, Y.; Pechenizkiy, I.; Stieglitz, T.; Doll, T. Numerical Evaluation on Residual Thermal Stress-Induced Delamination at PDMS–Metal Interface of Neural Prostheses. Micromachines 2021, 12, 669. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, P.A.; Dam-Johansen, K.; Weinell, C.E.; Kiil, S. Cathodic delamination: Quantification of ionic transport rates along coating–steel interfaces. Prog. Org. Coat. 2010, 68, 70–78. [Google Scholar] [CrossRef]
- Akgun, O.C.; Nanbakhsh, K.; Giagka, V.; Serdijn, W.A. A Chip Integrity Monitor for Evaluating Moisture/Ion Ingress in mm-Sized Single-Chip Implants. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 658–670. [Google Scholar] [CrossRef] [PubMed]
- Moustaka, M.E.; Norton, M.M.; Blanc, B.; Horvath, V.; Aghvami, S.A.; Fraden, S. Partition, Reaction, and Diffusion Coefficients of Bromine in Elastomeric Polydimethylsiloxane. J. Phys. Chem. B 2021, 125, 5937–5951. [Google Scholar] [CrossRef]
- Stefan, J. Ueber die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere. Ann. Phys. 1891, 278, 269–286. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford Univeristy Press: Oxford, UK; New York, NY, USA, 1979; pp. 49–51. [Google Scholar]
- Goodman, T.R. The Heat Balance Integral and its Application to Problems Involving Change of Phase. Trans. ASME J. Heat Transf. 1958, 80, 335. [Google Scholar]
- Lu, C.; Sun, Y.; Harley, S.J.; Glascoe, E.A. Modeling Gas Transport and Reactions in Polydimethysiloxane. In Proceedings of the TOUGH Symposium 2012 LBNL, Livermore, CA, USA, 17–19 September 2012. [Google Scholar]
- Nacer, S.; El-Khider, S.-A.; Pierre, C.; Jack, L. On the goodman heat-balance integral method for Stefan like-problems: Further considerations and refinements. Therm. Sci. 2009, 13, 81–96. [Google Scholar] [CrossRef]
- Leung, C.H.; Staggs, J.E.J.; Brindley, J.; Mcintosh, A.C. Modelling of Polymer Ablation Including A Substrate Base. Combust. Sci. Technol. 1997, 126, 53–70. [Google Scholar] [CrossRef]
- Lee, S.W.; Seo, J.-M.; Ha, S.; Kim, E.T.; Chung, H.; Kim, S.J. Development of microelectrode arrays for artificial retinal implants using liquid crystal polymers. Investig. Ophthalmol. Vis. Sci. 2009, 50, 5859–5866. [Google Scholar] [CrossRef] [PubMed]
- Tolstosheeva, E.; Biefeld, V.; Lang, W. Accelerated soak performance of BPDA-PPD polyimide for implantable MEAs. Procedia Eng. 2015, 120, 36–40. [Google Scholar] [CrossRef][Green Version]
- Crank, J.; Gupta, R.S. A Moving Boundary Problem Arising from the Diffusion of Oxygen in Absorbing Tissue. IMA J. Appl. Math. 1972, 10, 19–33. [Google Scholar] [CrossRef]








| Gas | Sylgard-184 |
|---|---|
| cm2/s | |
| cm2/s | |
| cm2/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onken, A.; Schütte, H.; Wulff, A.; Lenz-Strauch, H.; Kreienmeyer, M.; Hild, S.; Stieglitz, T.; Gassmann, S.; Lenarz, T.; Doll, T. Predicting Corrosion Delamination Failure in Active Implantable Medical Devices: Analytical Model and Validation Strategy. Bioengineering 2022, 9, 10. https://doi.org/10.3390/bioengineering9010010
Onken A, Schütte H, Wulff A, Lenz-Strauch H, Kreienmeyer M, Hild S, Stieglitz T, Gassmann S, Lenarz T, Doll T. Predicting Corrosion Delamination Failure in Active Implantable Medical Devices: Analytical Model and Validation Strategy. Bioengineering. 2022; 9(1):10. https://doi.org/10.3390/bioengineering9010010
Chicago/Turabian StyleOnken, Adrian, Helmut Schütte, Anika Wulff, Heidi Lenz-Strauch, Michaela Kreienmeyer, Sabine Hild, Thomas Stieglitz, Stefan Gassmann, Thomas Lenarz, and Theodor Doll. 2022. "Predicting Corrosion Delamination Failure in Active Implantable Medical Devices: Analytical Model and Validation Strategy" Bioengineering 9, no. 1: 10. https://doi.org/10.3390/bioengineering9010010
APA StyleOnken, A., Schütte, H., Wulff, A., Lenz-Strauch, H., Kreienmeyer, M., Hild, S., Stieglitz, T., Gassmann, S., Lenarz, T., & Doll, T. (2022). Predicting Corrosion Delamination Failure in Active Implantable Medical Devices: Analytical Model and Validation Strategy. Bioengineering, 9(1), 10. https://doi.org/10.3390/bioengineering9010010








