Machine Learning Prediction Models for Mitral Valve Repairability and Mitral Regurgitation Recurrence in Patients Undergoing Surgical Mitral Valve Repair
Abstract
1. Introduction
- (1)
- Developing a feature selection technique using features importance ranking of non-linear methods to detect the most relevant predictors from input data.
- (2)
- Evaluating different resampling techniques in order to balance the class distribution, which reflects the real world distribution of MVP.
- (3)
- Performing an experimental analysis testing many well-known ML classification algorithms.
- (4)
- Assessing an additive feature attribution method to improve interpretability of the ML outcomes and to provide a better understanding of data.
2. Materials and Methods
2.1. Study Population
2.2. Echocardiographic Measures
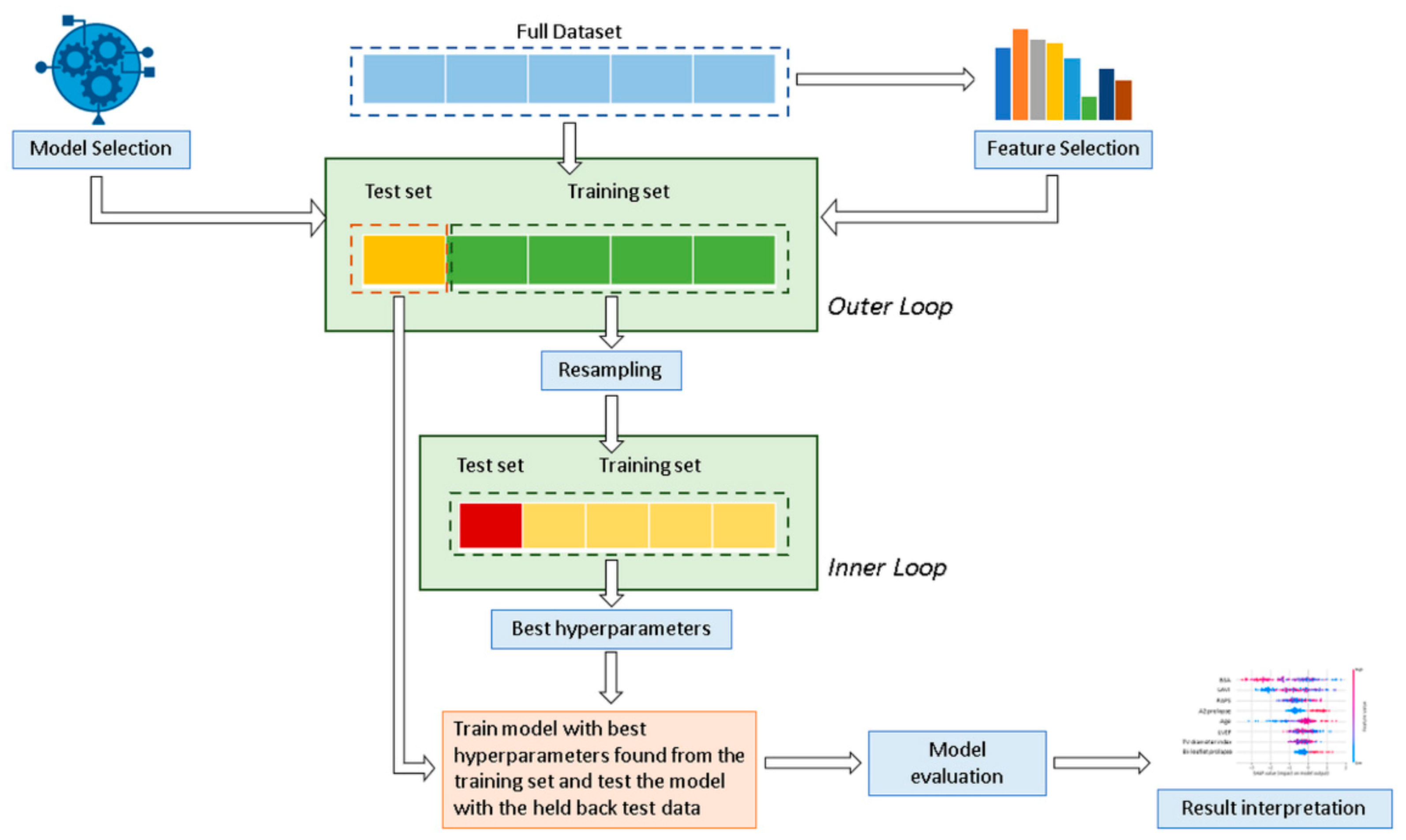
2.3. Study Design
2.4. Pre-Processing
2.5. Clinical Assessment and Statistical Analysis
3. Results
3.1. Cohort Characteristics
3.2. Selected Features
3.3. Model Performance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nkomo, V.T.; Gardin, J.M.; Skelton, T.N.; Gottdiener, J.S.; Scott, C.G.; Enriquez-Sarano, M. Burden of valvular heart diseases: A population based study. Lancet 2006, 368, 1005–1011. [Google Scholar] [CrossRef]
- Dziadzko, V.; Dziadzko, M.; Medina-Inojosa, J.R.; Benfari, G.; Michelena, H.I.; Crestanello, J.A.; Maalouf, J.; Thapa, P.; Enriquez-Sarano, M. Causes and mechanisms of isolated mitral regurgitation in the community: Clinical context and outcome. Eur. Heart J. 2019, 40, 2194–2202. [Google Scholar] [CrossRef] [PubMed]
- Freed, L.A.; Levy, D.; Levine, R.A.; Larson, M.G.; Evans, J.C.; Fuller, D.L.; Lehman, B.; Benjamin, E.J. Prevalence and clinical outcome of mitral-valve prolapse. N. Engl. J. Med. 1999, 341, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Apostolidou, E.; Maslow, A.D.; Poppas, A. Primary mitral valve regurgitation: Update and review. Glob. Cardiol. Sci. Pract. 2017, 2017, e201703. [Google Scholar] [CrossRef]
- Madesis, A.; Tsakiridis, K.; Zarogoulidis, P.; Katsikogiannis, N.; Machairiotis, N.; Kougioumtzi, I.; Kesisis, G.; Tsiouda, T.; Beleveslis, T.; Koletas, A.; et al. Review of mitral valve insufficiency: Repair or replacement. J. Thorac. Dis. 2014, 6, S39–S51. [Google Scholar] [CrossRef]
- Gillinov, A.M.; Blackstone, E.H.; Nowicki, E.R.; Slisatkorn, W.; Al-Dossari, G.; Johnston, D.R.; George, K.M.; Houghtaling, P.L.; Griffin, B.; Sabik, J.F., 3rd; et al. Valve repair versus valve replacement for degenerative mitral valve disease. J. Thorac. Cardiovasc. Surg. 2008, 135, 885–893. [Google Scholar] [CrossRef]
- Gogbashian, A.; Sepic, J.; Soltesz, E.G.; Nascimben, L.; Cohn, L.H. Operative and long-term survival of elderly is significantly improved by mitral valve repair. Am. Heart J. 2006, 151, 1325–1333. [Google Scholar] [CrossRef]
- Nishimura, R.A.; Otto, C.M.; Bonow, R.O.; Carabello, B.A.; Erwin, J.P.; Fleisher, L.A.; Jneid, H.; Mack, M.J.; McLeod, C.J.; O’Gara, P.T.; et al. 2017 AHA/ACC Focused Update of the 2014 AHA/ACC Guideline for the Management of Patients with Valvular Heart Disease: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Circulation 2017, 135, e1159–e1195. [Google Scholar] [CrossRef]
- Gaur, P.; Kaneko, T.; McGurk, S.; Rawn, J.D.; Maloney, A.; Cohn, L.H. Mitral valve repair versus replacement in the elderly: Short-term and long-term outcomes. J. Thorac. Cardiovasc. Surg. 2014, 148, 1400–1406. [Google Scholar] [CrossRef]
- Chan, V.; Elmistekawy, E.; Ruel, M.; Hynes, M.; Mesana, T.G. How Does Mitral Valve Repair Fail in Patients with Prolapse?—Insights From Longitudinal Echocardiographic Follow-Up. Ann. Thorac. Surg. 2016, 102, 1459–1465. [Google Scholar] [CrossRef]
- Flameng, W.J.; Meuris, B.; Herijgers, P.; Herregods, M.C. Durability of mitral valve repair in Barlow disease versus fibroelastic deficiency. J. Thorac. Cardiovasc. Surg. 2008, 135, 274–282. [Google Scholar] [CrossRef]
- Tamborini, G.; Mantegazza, V.; Penso, M.; Muratori, M.; Fusini, L.; Ghulam Ali, S.; Cefalù, C.; Italiano, G.; Volpato, V.; Gripari, P.; et al. Predictive Value of Pre-Operative 2D and 3D Transthoracic Echocardiography in Patients Undergoing Mitral Valve Repair: Long Term Follow Up of Mitral Valve Regurgitation Recurrence and Heart Chamber Remodeling. J. Cardiovasc. Dev. Dis. 2020, 7, 46. [Google Scholar] [CrossRef]
- Suri, R.M.; Clavel, M.A.; Schaff, H.V.; Michelena, H.I.; Huebner, M.; Nishimura, R.A.; Enriquez-Sarano, M. Effect of Recurrent Mitral Regurgitation Following Degenerative Mitral Valve Repair. J. Am. Coll. Cardiol. 2016, 67, 488–498. [Google Scholar] [CrossRef]
- Nishida, H.; Fukui, T.; Kasegawa, H.; Kin, H.; Yamazaki, M.; Takanashi, S. Causes of repair failure for degenerative mitral valve disease and reoperation outcomes. Eur. J. Cardiothorac. Surg. 2018, 53, 1244–1250. [Google Scholar] [CrossRef]
- Gardner, M.A.; Hossack, K.F.; Smith, I.R. Long-Term Results Following Repair for Degenerative Mitral Regurgitation—Analysis of Factors Influencing Durability. Heart Lung Circ. 2019, 28, 1852–1865. [Google Scholar] [CrossRef] [PubMed]
- Chan, V.; Ruel, M.; Hynes, M.; Chaudry, S.; Mesana, T.G. Impact of mitral annular calcification on early and late outcomes following mitral valve repair of myxomatous degeneration. Interact. Cardiovasc. Thorac. Surg. 2013, 17, 120–125. [Google Scholar] [CrossRef]
- Baberg, H.T.; Dirlich, M.; Laczkovics, A.; Grewe, P.; Bojara, W.; de Zeeuw, J.; Bauer, T.T.; Kugler, J.; Mügge, A. Determinants of health-related quality of life after aortic valve replacement in six-month survivors of intervention. J. Heart Valve Dis. 2004, 13, 914–920. [Google Scholar] [PubMed]
- Reed, D.; Abbott, R.D.; Smucker, M.L.; Kaul, S. Prediction of outcome after mitral valve replacement in patients with symptomatic chronic mitral regurgitation. The importance of left atrial size. Circulation 1991, 84, 23–34. [Google Scholar] [CrossRef]
- Gasser, S.; von Stumm, M.; Sinning, C.; Schaefer, U.; Reichenspurner, H.; Girdauskas, E. Can We Predict Failure of Mitral Valve Repair? J. Clin. Med. 2019, 8, 526. [Google Scholar] [CrossRef]
- Johnson, K.W.; Torres Soto, J.; Glicksberg, B.S.; Shameer, K.; Miotto, R.; Ali, M.; Ashley, E.; Dudley, J.T. Artificial intelligence in cardiology. J. Am. Coll. Cardiol. 2018, 71, 2668–2679. [Google Scholar] [CrossRef]
- Krittanawong, C.; Zhang, H.; Wang, Z.; Aydar, M.; Kitai, T. Artificial intelligence in precision cardiovascular medicine. J. Am. Coll. Cardiol. 2017, 69, 2657–2664. [Google Scholar] [CrossRef]
- Sahni, N.; Simon, G.; Arora, R. Development and Validation of Machine Learning Models for Prediction of 1-Year Mortality Utilizing Electronic Medical Record Data Available at the End of Hospitalization in Multicondition Patients: A Proof-of-Concept Study. J. Gen. Intern. Med. 2018, 33, 921–928. [Google Scholar] [CrossRef]
- Weng, S.F.; Reps, J.; Kai, J.; Garibaldi, J.M.; Qureshi, N. Can machine-learning improve cardiovascular risk prediction using routine clinical data? PLoS ONE 2017, 12, e0174944. [Google Scholar] [CrossRef]
- Parikh, R.B.; Manz, C.; Chivers, C.; Regli, S.H.; Braun, J.; Draugelis, M.E.; Schuchter, L.M.; Shulman, L.N.; Navathe, A.S.; Patel, M.S.; et al. Machine Learning Approaches to Predict 6-Month Mortality Among Patients with Cancer. JAMA Netw. Open 2019, 2, e1915997. [Google Scholar] [CrossRef]
- Ambale-Venkatesh, B.; Yang, X.; Wu, C.O.; Liu, K.; Hundley, W.G.; McClelland, R.; Gomes, A.S.; Folsom, A.R.; Shea, S.; Guallar, E.; et al. Cardiovascular Event Prediction by Machine Learning: The Multi-Ethnic Study of Atherosclerosis. Circ. Res. 2017, 121, 1092–1101. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Preininger, A. AI in Health: State of the Art, Challenges, and Future Directions. Yearb. Med. Inform. 2019, 28, 16–26. [Google Scholar] [CrossRef] [PubMed]
- Zoghbi, W.A.; Adams, D.; Bonow, R.O.; Enriquez-Sarano, M.; Foster, E.; Grayburn, P.A.; Hahn, R.T.; Han, Y.; Hung, J.; Lang, R.M.; et al. Recommendations for Noninvasive Evaluation of Native Valvular Regurgitation: A Report from the American Society of Echocardiography Developed in Collaboration with the Society for Cardiovascular Magnetic Resonance. J. Am. Soc. Echocardiogr. 2017, 30, 303–371. [Google Scholar] [CrossRef] [PubMed]
- Pepi, M.; Tamborini, G.; Galli, C.; Barbier, P.; Doria, E.; Berti, M.; Guazzi, M.; Fiorentini, C. A new formula for echo-Doppler estimation of right ventricular systolic pressure. J. Am. Soc. Echocardiogr. 1994, 7, 20–26. [Google Scholar] [CrossRef]
- Enriquez-Sarano, M.; Akins, C.W.; Vahanian, A. Mitral regurgitation. Lancet 2009, 373, 1382–1394. [Google Scholar] [CrossRef]
- Javadikasgari, H.; Mihaljevic, T.; Suri, R.M.; Svensson, L.G.; Navia, J.L.; Wang, R.Z.; Tappuni, B.; Lowry, A.M.; McCurry, K.R.; Blackstone, E.H.; et al. Simple versus complex degenerative mitral valve disease. J. Thorac. Cardiovasc. Surg. 2018, 156, 122–129. [Google Scholar] [CrossRef]
- Chikwe, J.; Adams, D.H.; Su, K.N.; Anyanwu, A.C.; Lin, H.M.; Goldstone, A.B.; Lang, R.M.; Fischer, G.W. Can three-dimensional echocardiography accurately predict complexity of mitral valve repair? Eur. J. Cardiothorac. Surg. 2012, 41, 518–524. [Google Scholar] [CrossRef]
- Chang, B.C.; Youn, Y.N.; Ha, J.W.; Lim, S.H.; Hong, Y.S.; Chung, N. Long-term clinical results of mitral valvuloplasty using flexible and rigid rings: A prospective and randomized study. J. Thorac. Cardiovasc. Surg. 2007, 133, 995–1003. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Picard, R.R.; Cook, R.D. Cross-validation of regression models. J. Am. Stat. Assoc. 1993, 79, 575–583. [Google Scholar] [CrossRef]
- Xu, Q.S.; Liang, Y.Z. Monte Carlo cross validation. Chemom. Intell. Lab. Syst. 2001, 56, 1–11. [Google Scholar] [CrossRef]
- Smyth, P. Clustering Using Monte Carlo Cross-Validation. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 1, pp. 126–133. [Google Scholar]
- Chawla, N.; Bowyer, K.; Hall, L.; Kegelmeyer, P. Smote: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Nguyen, H.M.; Cooper, E.W.; Kamei, K. Borderline over-sampling for imbalanced data classification. Int. J. Knowl. Eng Soft Data Parad. 2011, 3, 4–21. [Google Scholar] [CrossRef]
- Han, H.; Wen-Yuan, H.; Bing-Huan, M. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. Adv. Intell. Comput. 2005, 3644, 878–887. [Google Scholar]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Tomek, I. An experiment with the edited nearest-neighbor rule. IEEE Trans. Syst. Man. Cybern. 1976, 6, 448–452. [Google Scholar]
- Batista, G.E.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. J. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Proc. Adv. Neural Inf. Process. Syst. 2017, 4765–4774. Available online: https://proceedings.neurips.cc/paper/2017/file/8a20a8621978632d76c43dfd28b67767-Paper.pdf (accessed on 23 August 2021).
- Penso, M.; Pepi, M.; Fusini, L.; Muratori, M.; Cefalù, C.; Mantegazza, V.; Gripari, P.; Ghulam Ali, S.; Fabbiocchi, F.; Bartorelli, A.L. Predicting Long-Term Mortality in TAVI Patients Using Machine Learning Techniques. J. Cardiovasc. Dev. Dis. 2021, 8, 44. [Google Scholar] [CrossRef]
- Pepi, M.; Tamborini, G.; Maltagliati, A.; Galli, C.A.; Sisillo, E.; Salvi, L.; Naliato, M.; Porqueddu, M.; Parolari, A.; Zanobini, M.; et al. Head-to-head comparison of two- and three-dimensional transthoracic and transesophageal echocardiography in the localization of mitral valve prolapse. J. Am. Coll. Cardiol. 2006, 48, 2524–2530. [Google Scholar] [CrossRef]
- Ciarka, A.; Braun, J.; Delgado, V.; Versteegh, M.; Boersma, E.; Klautz, R.; Dion, R.; Bax, J.J.; Van de Veire, N. Predictors of mitral regurgitation recurrence in patients with heart failure undergoing mitral valve annuloplasty. Am. J. Cardiol. 2010, 106, 395–401. [Google Scholar] [CrossRef]
- Baumgartner, H.; Falk, V.; Bax, J.J.; De Bonis, M.; Hamm, C.; Holm, P.J.; Iung, B.; Lancellotti, P.; Lansac, E.; Rodriguez Muñoz, D.; et al. 2017 ESC/EACTS Guidelines for the management of valvular heart disease. Eur. Heart J. 2017, 38, 2739–2791. [Google Scholar] [CrossRef] [PubMed]
- Gillinov, A.M.; Cosgrove, D.M.; Blackstone, E.H.; Diaz, R.; Arnold, J.H.; Lytle, B.W.; Smedira, N.G.; Sabik, J.F.; McCarthy, P.M.; Loop, F.D. Durability of mitral valve repair for degenerative disease. J. Thorac. Cardiovasc. Surg. 1998, 116, 734–743. [Google Scholar] [CrossRef]
- Flameng, W.; Herijgers, P.; Bogaerts, K. Recurrence of mitral valve regurgitation after mitral valve repair in degenerative valve disease. Circulation 2003, 107, 1609–1613. [Google Scholar] [CrossRef] [PubMed]
- Kaneyuki, D.; Nakajima, H.; Asakura, T.; Yoshitake, A.; Tokunaga, C.; Tochii, M.; Hayashi, J.; Takazawa, A.; Izumida, H.; Iguchi, A. Recurrent mitral regurgitation after mitral valve repair for bileaflet lesions in the modern era. J. Cardiothorac. Surg. 2019, 14, 205. [Google Scholar] [CrossRef] [PubMed]
- Meyer, M.A.; von Segesser, L.K.; Hurni, M.; Stumpe, F.; Eisa, K.; Ruchat, P. Long-term outcome after mitral valve repair: A risk factor analysis. Eur. J. Cardiothorac. Surg. 2007, 32, 301–307. [Google Scholar] [CrossRef]


| Resampling Algorithms | ||
|---|---|---|
| Name | Strategy | Briefly Description |
| SMOTE [36] | Oversampling | Creates synthetic elements for the minority class, based on those that already exist, using a k-nearest neighbour algorithm. |
| SVMSMOTE [37] | Oversampling | Variant of SMOTE algorithm which uses an SVM algorithm to detect sample to use for generating new synthetic samples |
| BorderlineSMOTE 1 and 2 [38] | Oversampling | Creates synthetic samples from the minority class along the decision boundary between the two classes. |
| ADASYN [39] | Oversampling | Creates synthetic elements according to the data density. |
| ENN [40] | Undersampling | Remove samples close to the decision boundary using the edited nearest neighbour algorithm. |
| TomekLinks [40] | Undersampling | Removes overlap between classes. |
| SMOTEENN [41] | Hybrid | Combines SMOTE and ENN algorithms. |
| SMOTETomek [41] | Hybrid | Apply SMOTE and TomekLinks algorithms. |
| Characteristics | Dataset 1 | Dataset 2 | ||||
|---|---|---|---|---|---|---|
| Group 1 | Group 2 | p-Value | Group 3 | Group 4 | p-Value | |
| (n = 757) | (n = 60) | (n = 268) | (n = 27) | |||
| Age, years | 61.1 ± 12.2 | 67.7 ± 11.6 | <0.001 | 59.8 ± 12.5 | 63.3 ± 15.3 | 0.183 |
| Female, n(%) | 89(11.8%) | 12(20%) | 0.062 | 88(32.8%) | 10(37.0%) | 0.668 |
| Body surface area, m2 | 1.84 ± 0.19 | 1.72 ± 0.18 | <0.001 | 1.82 ± 0.19 | 1.81 ± 0.22 | 0.805 |
| MVP etiology | 0.206 | 0.154 | ||||
| FED | 219(28.9%) | 22(36.7%) | 68(25.4%) | 3(11.1%) | ||
| Barlow | 538(71.1%) | 38(63.3%) | 200(74.6%) | 24(88.9%) | ||
| Atrial fibrillation | 89(11.8%) | 12(20.0%) | 0.062 | 21(7.8%) | 3(11.1%) | 0.472 |
| Complex MV prolapse | 392(51.8%) | 45(75%) | 0.001 | 130(48.5%) | 17(63.0%) | 0.157 |
| Complex surgical procedure | 286(37.8%) | 25(41.7%) | 0.620 | 83(31.0%) | 16(59.3%) | 0.003 |
| Antero-posterior mitral annulus diameter (mm) | 36.65 ± 5.20 | 36.10 ± 5.20 | 0.429 | 37.05 ± 5.26 | 36.15 ± 5.09 | 0.394 |
| Medio-lateral mitral annulus diameter (mm) | 39.78 ± 5.00 | 38.83 ± 4.98 | 0.155 | 39.77 ± 4.91 | 38.56 ± 4.36 | 0.217 |
| Prolapse | ||||||
| P1 | 84(11.1%) | 6(10.0%) | 0.794 | 20(7.5%) | 3(11.1%) | 0.455 |
| P2 | 652(86.1%) | 41(68.3%) | <0.001 | 237(88.4%) | 18(66.7%) | 0.001 |
| P3 | 174(23.0%) | 18(30.0%) | 0.217 | 60(22.4%) | 6(22.2%) | 0.976 |
| A1 | 44(5.8%) | 10(16.7%) | 0.001 | 16(6.0%) | 2(7.4%) | 0.675 |
| A2 | 204(26.9%) | 29(48.3%) | <0.001 | 74(27.6%) | 9(33.3%) | 0.537 |
| A3 | 154(20.3%) | 16(26.7%) | 0.315 | 52(19.4%) | 6(22.2%) | 0.733 |
| Bi-leaflet prolapse | 178(23.5%) | 20(33.3%) | 0.088 | 67(25.0%) | 6(22.2%) | 0.742 |
| Commissure | ||||||
| Anterolateral | 13(1.7%) | 1(1.7%) | 1.000 | 2(0.7%) | 1(3.7%) | 0.252 |
| Posteromedial | 105(13.9%) | 12(20.0%) | 0.192 | 34(12.7%) | 5(18.5%) | 0.377 |
| Calcification | 152(20.1%) | 19(31.7%) | 0.034 | 52(19.4%) | 7(25.9%) | 0.425 |
| Cleft | 75(9.9%) | 6(10.0%) | 0.982 | 27(10.1%) | 4(14.8%) | 0.506 |
| Ruptured chordae | 567(74.9%) | 34(56.7%) | 0.002 | 201(75.0%) | 24(88.9%) | 0.152 |
| LVEDV index (mL/m2) | 77.2 ± 18.9 | 73.0 ± 16.5 | 0.090 | 77.0 ± 19.1 | 80.7 ± 20.9 | 0.342 |
| LVESV index (mL/m2) | 27.5 ± 9.1 | 26.6 ± 7.5 | 0.477 | 26.8 ± 9.4 | 29.1 ± 10.7 | 0.239 |
| LVSV index (mL/m2) | 49.8 ± 12.7 | 46.4 ± 11.8 | 0.048 | 50.2 ± 12.8 | 51.6 ± 12.9 | 0.582 |
| LVEF (%) | 64.5 ± 6.7 | 63.4 ± 6.4 | 0.219 | 65.3 ± 6.8 | 64.6 ± 7.1 | 0.606 |
| LA area (cm2) | 29.6 ± 7.4 | 30.3 ± 7.8 | 0.510 | 29.9 ± 7.4 | 32.3 ± 7.6 | 0.115 |
| LA volume index (mL/m2) | 57.6 ± 22.1 | 59.4 ± 22.1 | 0.540 | 64.3 ± 24.4 | 66.7 ± 27.2 | 0.628 |
| PAPS (mmHg) | 36 ± 10 | 40 ± 13 | 0.002 | 35 ± 10 | 46 ± 18 | 0.006 |
| Tricuspid valve diameter index (mm/m2) | 19.5 ± 2.7 | 20.6 ± 3.4 | 0.004 | 19.6 ± 2.8 | 20.9 ± 4.9 | 0.187 |
| Tricuspid regurgitation > 2 | 40(5.3%) | 9(15.0%) | 0.002 | 18(6.7%) | 4(14.8%) | 0.130 |
| Mitral regurgitation > 3 | 709(93.7%) | 51(85.0%) | 0.011 | 249(92.9%) | 24(88.9%) | 0.424 |
| Tricuspid valvuloplasty | 103(13.6%) | 11(18.3%) | 0.309 | 44(16.4%) | 8(29.6%) | 0.088 |
| Aortic valve | 0.653 | 0.531 | ||||
| Repair | 16(2.1%) | 2(3.3%) | 6(2.3%) | 0(0%) | ||
| Replacement | 6(0.8%) | 0(0%) | 6(2.3%) | 0(0%) | ||
| Ascending aorta | 6(0.8%) | 0(0%) | 1.000 | 3(1.1%) | 0(0%) | 1.000 |
| CABG | 45(5.9%) | 1(1.7%) | 0.244 | 28(10.4%) | 3(11.1%) | 1.000 |
| PFO closure | 7(0.9%) | 1(1.7%) | 0.458 | 6(2.3%) | 1(3.7%) | 0.494 |
| Left atrial appendage closure | 20(2.6%) | 1(1.7%) | 1.000 | 16(6.0%) | 1(3.7%) | 1.000 |
| Atrial fibrillation ablation | 27(3.6%) | 0(0%) | 0.253 | 21(7.8%) | 2(7.4%) | 1.000 |
| LVEDV index 6M (mL/m2) | 57.0 ± 14.8 * | 61.6 ± 16.5 * | 0.124 | |||
| LVESV index 6M (mL/m2) | 24.4 ± 10.7 * | 26.4 ± 10.6 * | 0.360 | |||
| LVSV index 6M (mL/m2) | 32.5 ± 7.6 * | 35.2 ± 9.4 * | 0.087 | |||
| LVEF 6M (%) | 58.0 ± 7.9 * | 57.9 ± 9.6 | 0.953 | |||
| LA area 6M (cm2) | 22.6 ± 5.6 * | 25.9 ± 5.3 * | 0.003 | |||
| LA volume index 6M (mL/m2) | 44.3 ± 17.5 * | 53.4 ± 18.5 * | 0.011 | |||
| PAPS 6M (mmHg) | 28 ± 6 * | 31 ± 8 | 0.025 | |||
| Mitral regurgitation 6M ≥ 2 | 10(3.7%) | 19(70.4%) | <0.001 | |||
| Dataset 1 | ||
| Multivariate | ||
| OR (95% CI) | p-value | |
| Age, years | 1.051 (1.023–1.080) | <0.001 |
| Body surface area | 0.080 (0.018–0.361) | 0.001 |
| A2 prolapse | 2.757 (1.582–4.805) | <0.001 |
| Left atrial area | 1.033 (1.021–1.067) | 0.047 |
| Dataset 2 | ||
| Multivariate | ||
| OR (95% CI) | p-value | |
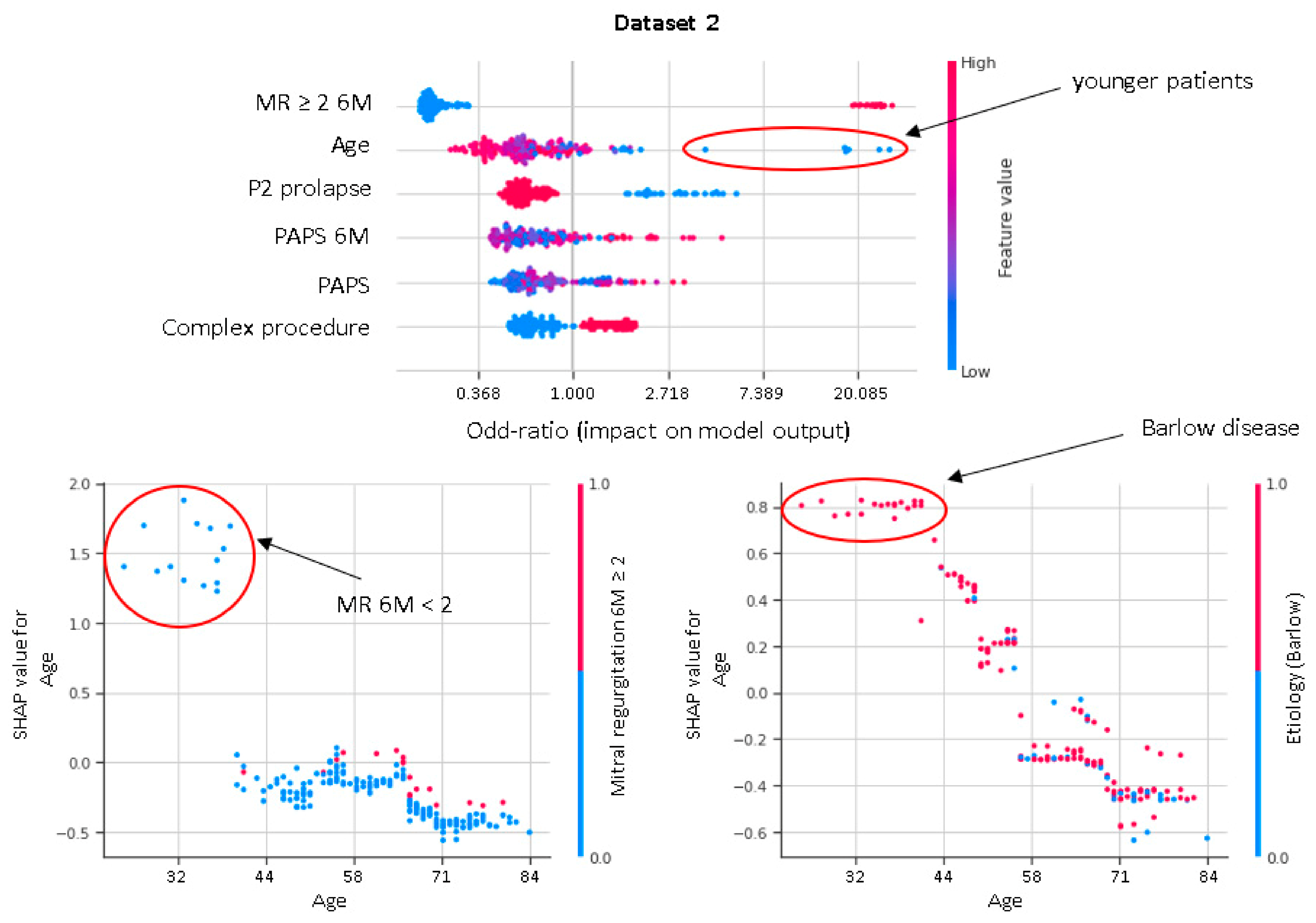
| P2 prolapse | 0.190 (0.055–0.654) | <0.001 |
| Systolic pulmonary artery pressure | 1.053 (1.010–1.099) | 0.001 |
| Mitral regurgitation 6M ≥2 | 53.761 (16.666–173.421) | <0.001 |
| Dataset 1 | |||||
| Algorithm | PPV | NPV | AUC | Resampling | Feature selection |
| DT | 0.16 | 0.95 | 0.61 | BorderlineSMOTE 1 | Random Forest |
| RF | 0.24 | 0.95 | 0.69 | BorderlineSMOTE 1 | Random Forest |
| SVM | 0.18 | 0.95 | 0.64 | SVMSMOTE | eXtreme Gradient boosted |
| NB | 0.16 | 0.96 | 0.71 | SMOTEENN | eXtreme Gradient boosted |
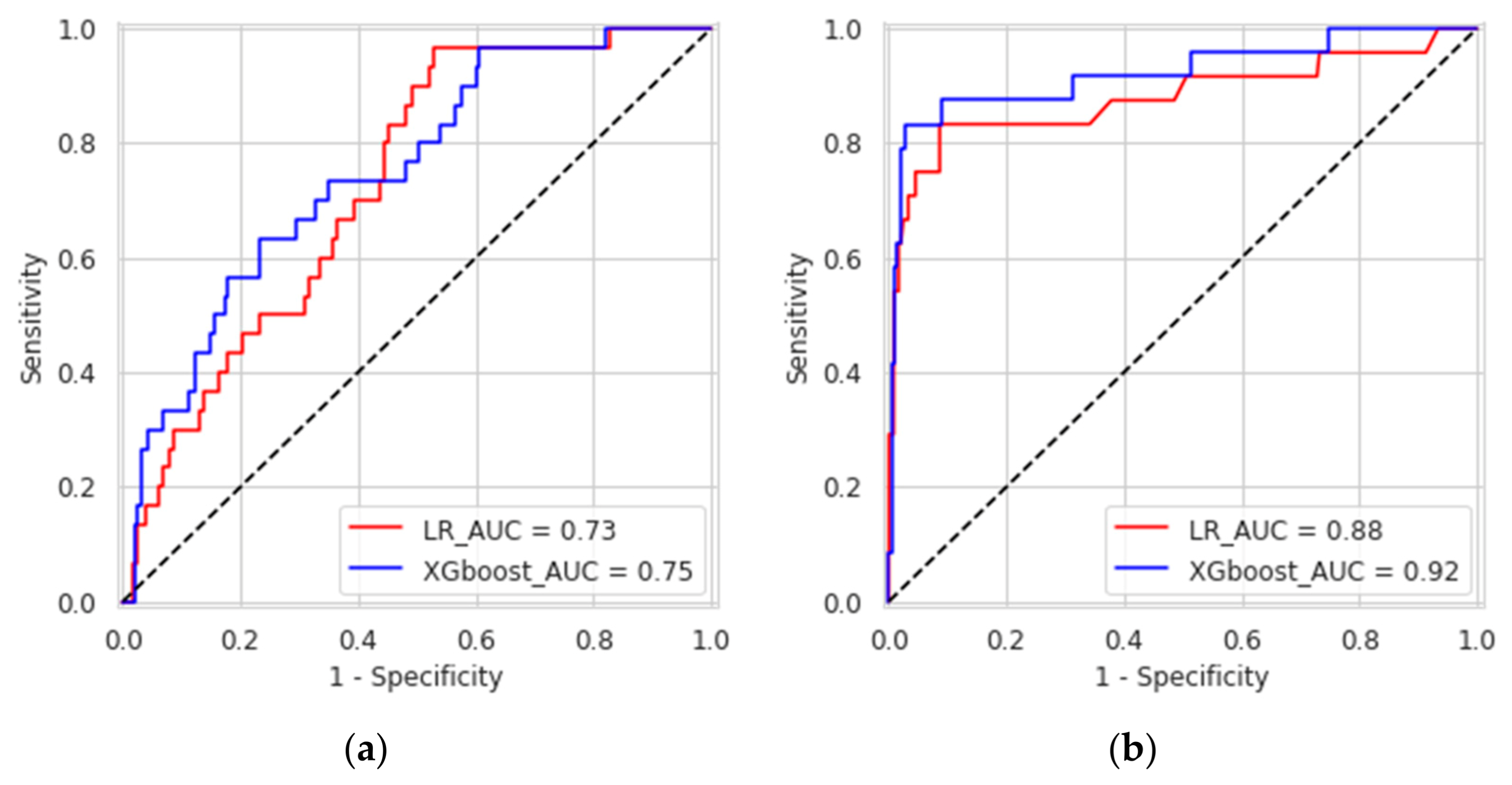
| XGboost | 0.29 | 0.96 | 0.75 | SVMSMOTE | eXtreme Gradient boosted |
| MLP | 0.19 | 0.96 | 0.65 | BorderlineSMOTE 1 | eXtreme Gradient boosted |
| LR | 0.29 | 0.95 | 0.73 | / | Multivariate logistic regression |
| Dataset 2 | |||||
| Algorithm | PPV | NPV | AUC | Resampling | Feature selection |
| DT | 0.41 | 0.96 | 0.78 | BorderlineSMOTE 1 | Random Forest |
| RF | 0.64 | 0.97 | 0.88 | BorderlineSMOTE 1 | Random Forest |
| SVM | 0.45 | 0.96 | 0.80 | SVMSMOTE | eXtreme Gradient boosted |
| NB | 0.65 | 0.97 | 0.89 | SVMSMOTE | eXtreme Gradient boosted |
| XGboost | 0.77 | 0.97 | 0.92 | BorderlineSMOTE 1 | eXtreme Gradient boosted |
| MLP | 0.64 | 0.96 | 0.83 | BorderlineSMOTE 1 | eXtreme Gradient boosted |
| LR | 0.70 | 0.97 | 0.88 | / | Multivariate logistic regression |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penso, M.; Pepi, M.; Mantegazza, V.; Cefalù, C.; Muratori, M.; Fusini, L.; Gripari, P.; Ghulam Ali, S.; Caiani, E.G.; Tamborini, G. Machine Learning Prediction Models for Mitral Valve Repairability and Mitral Regurgitation Recurrence in Patients Undergoing Surgical Mitral Valve Repair. Bioengineering 2021, 8, 117. https://doi.org/10.3390/bioengineering8090117
Penso M, Pepi M, Mantegazza V, Cefalù C, Muratori M, Fusini L, Gripari P, Ghulam Ali S, Caiani EG, Tamborini G. Machine Learning Prediction Models for Mitral Valve Repairability and Mitral Regurgitation Recurrence in Patients Undergoing Surgical Mitral Valve Repair. Bioengineering. 2021; 8(9):117. https://doi.org/10.3390/bioengineering8090117
Chicago/Turabian StylePenso, Marco, Mauro Pepi, Valentina Mantegazza, Claudia Cefalù, Manuela Muratori, Laura Fusini, Paola Gripari, Sarah Ghulam Ali, Enrico G. Caiani, and Gloria Tamborini. 2021. "Machine Learning Prediction Models for Mitral Valve Repairability and Mitral Regurgitation Recurrence in Patients Undergoing Surgical Mitral Valve Repair" Bioengineering 8, no. 9: 117. https://doi.org/10.3390/bioengineering8090117
APA StylePenso, M., Pepi, M., Mantegazza, V., Cefalù, C., Muratori, M., Fusini, L., Gripari, P., Ghulam Ali, S., Caiani, E. G., & Tamborini, G. (2021). Machine Learning Prediction Models for Mitral Valve Repairability and Mitral Regurgitation Recurrence in Patients Undergoing Surgical Mitral Valve Repair. Bioengineering, 8(9), 117. https://doi.org/10.3390/bioengineering8090117









