Evolution of Meniscal Biomechanical Properties with Growth: An Experimental and Numerical Study
Abstract
1. Introduction
2. Materials and Methods
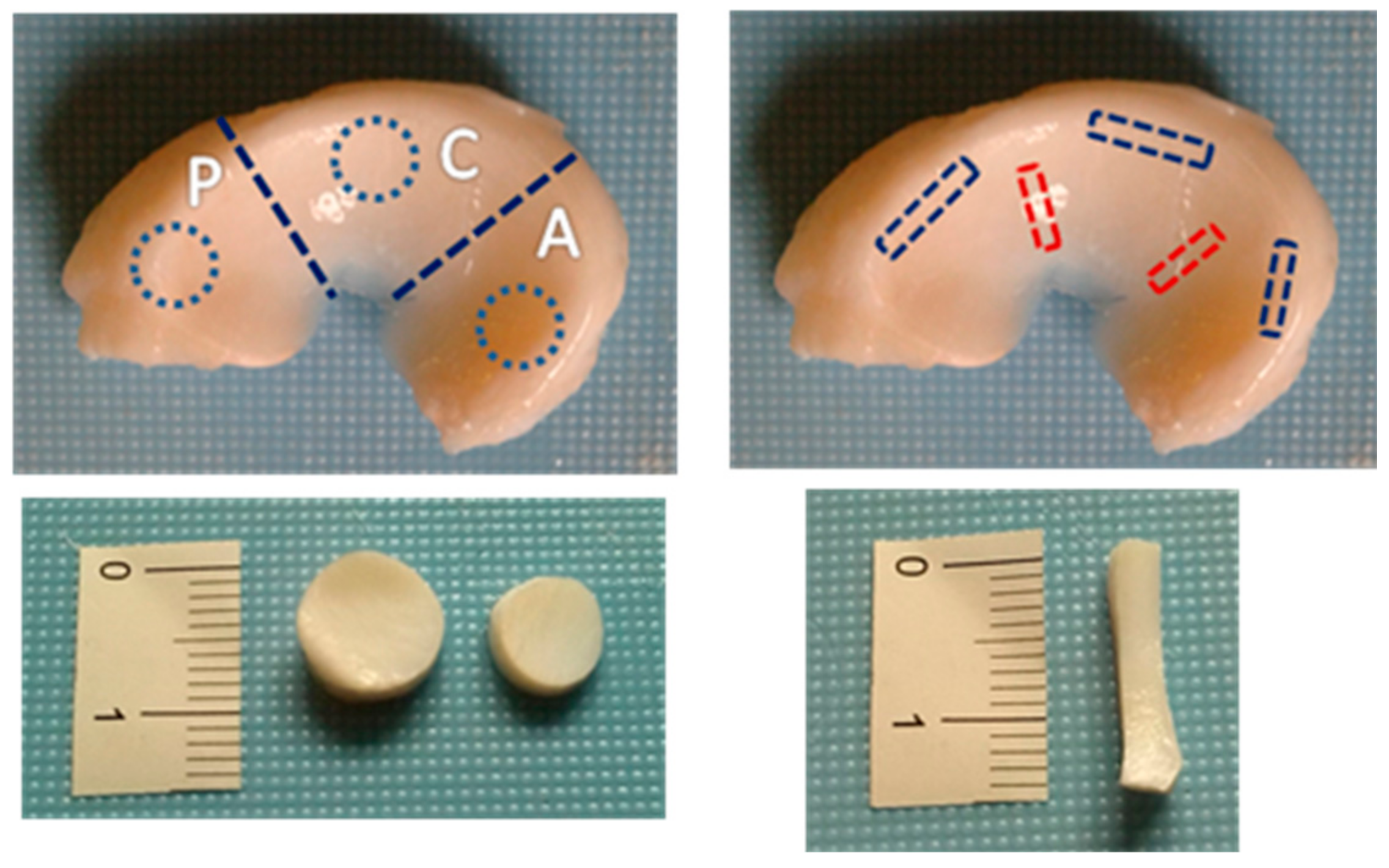
2.1. Sample Collection and Preparation
2.2. Biochemical Analyses
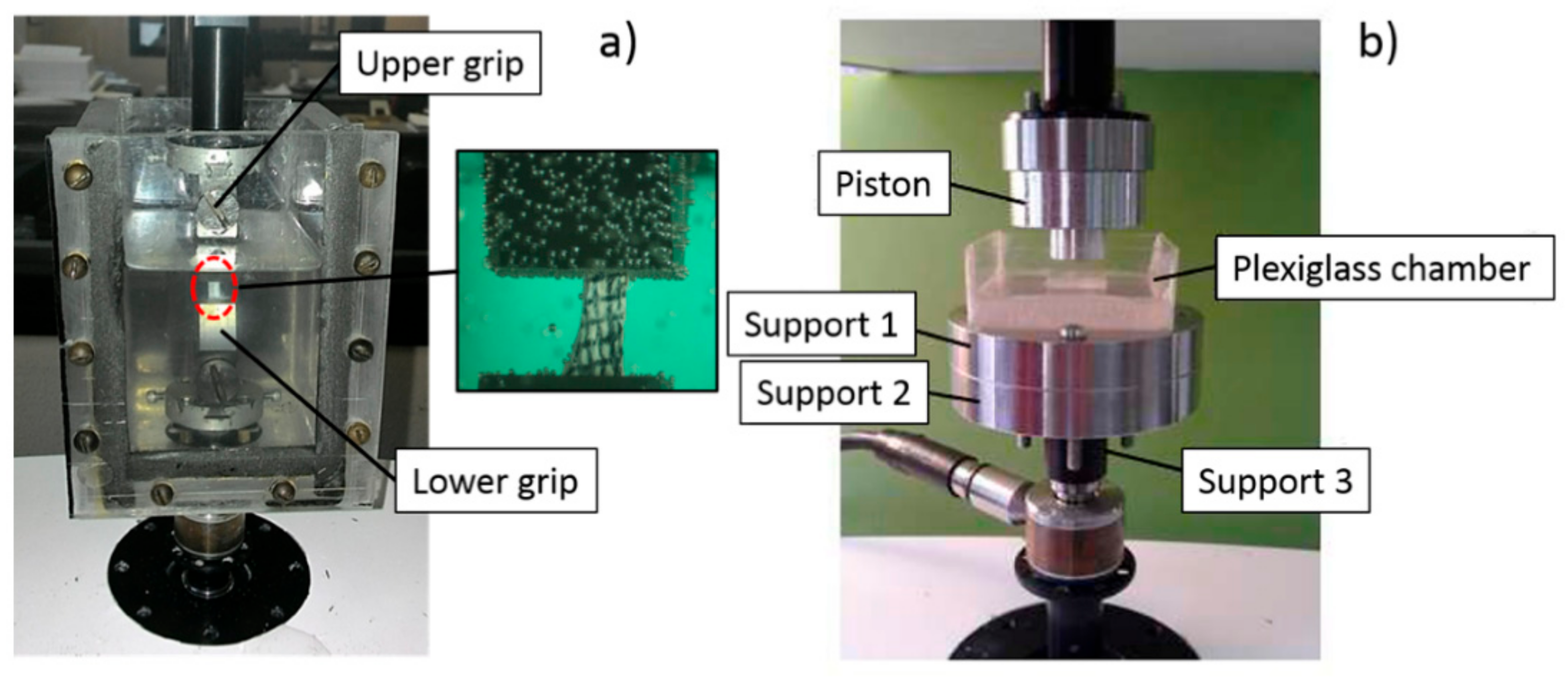
2.3. Uniaxial Tension Test
2.4. Unconfined Compression Test
2.5. Statistical Analyses
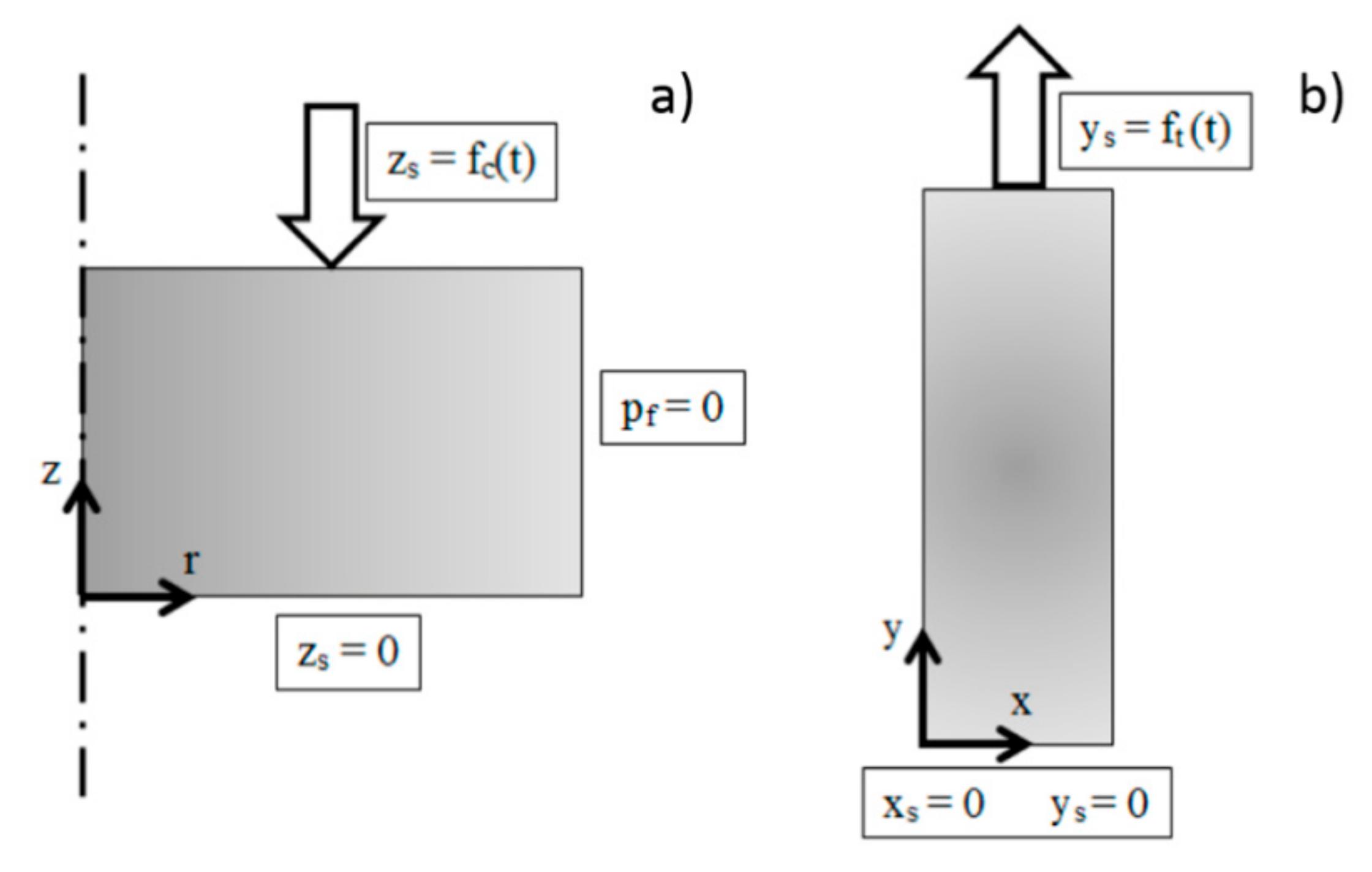
2.6. Numerical Model
3. Results
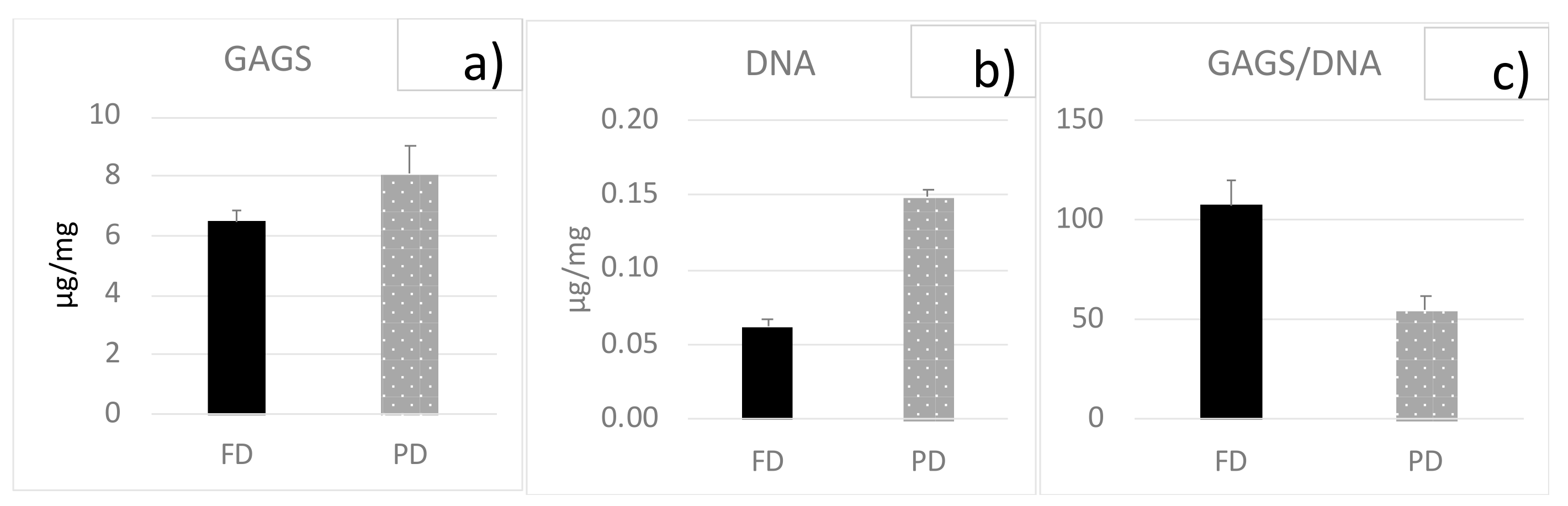
3.1. Biochemical Analyses
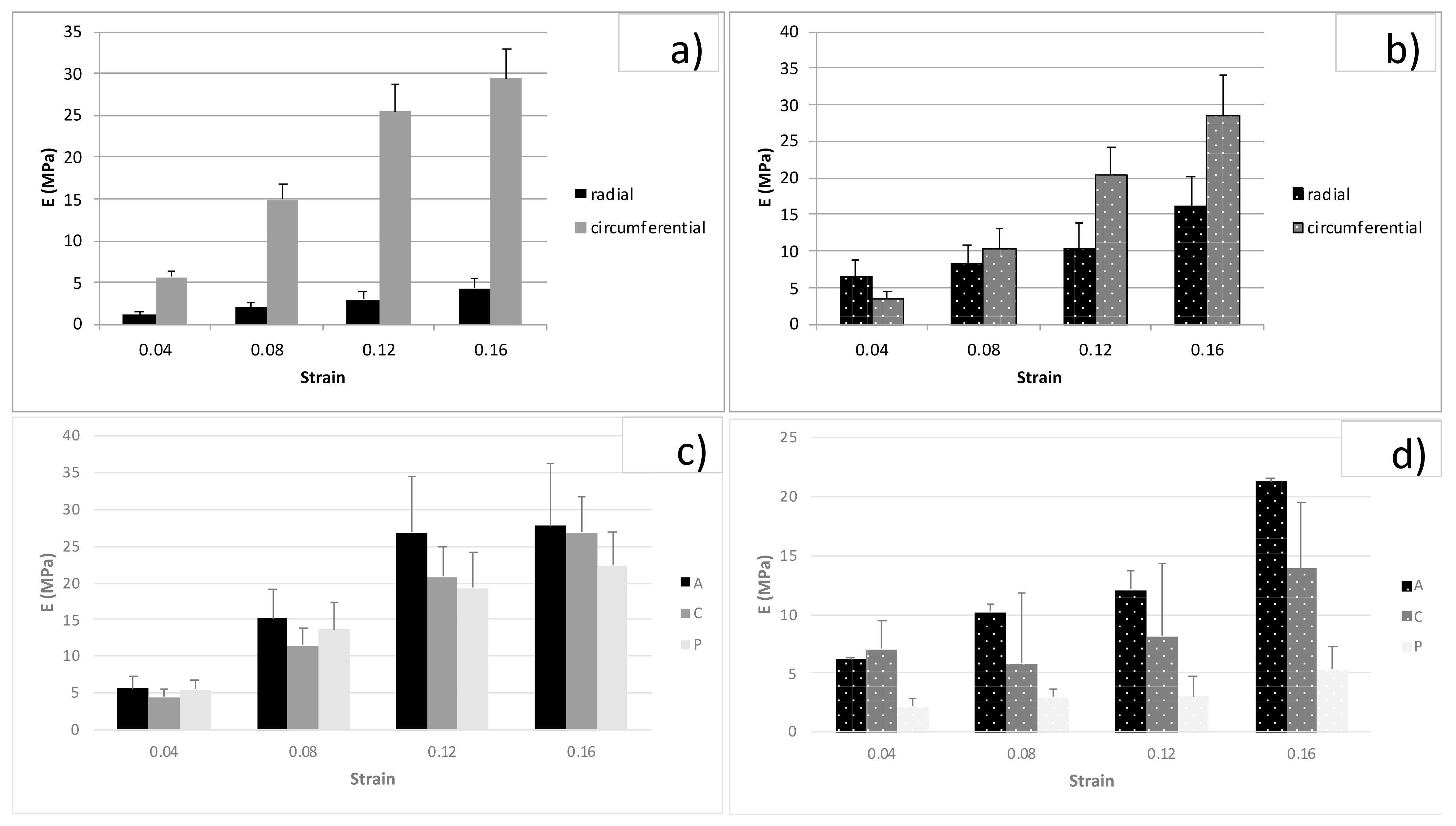
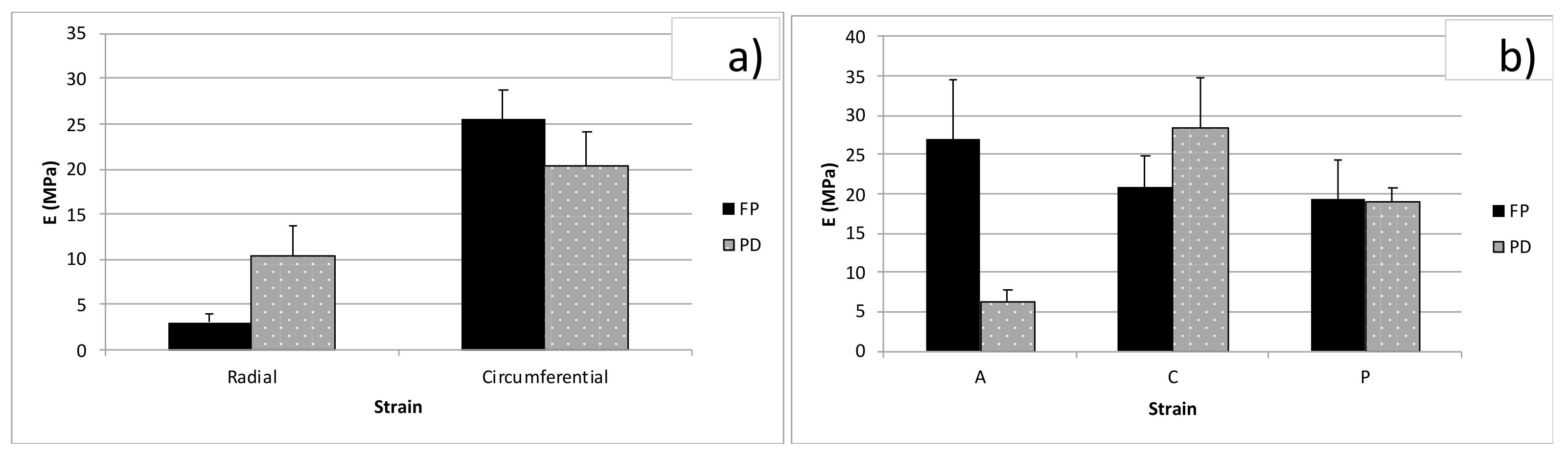
3.2. Tension Tests
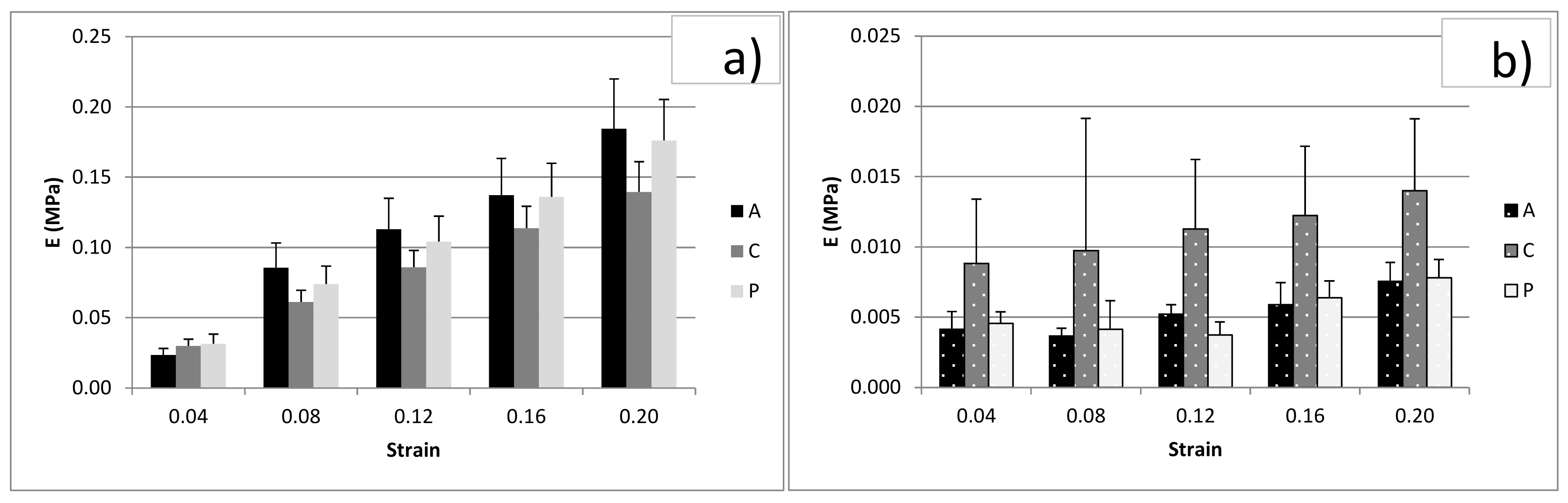
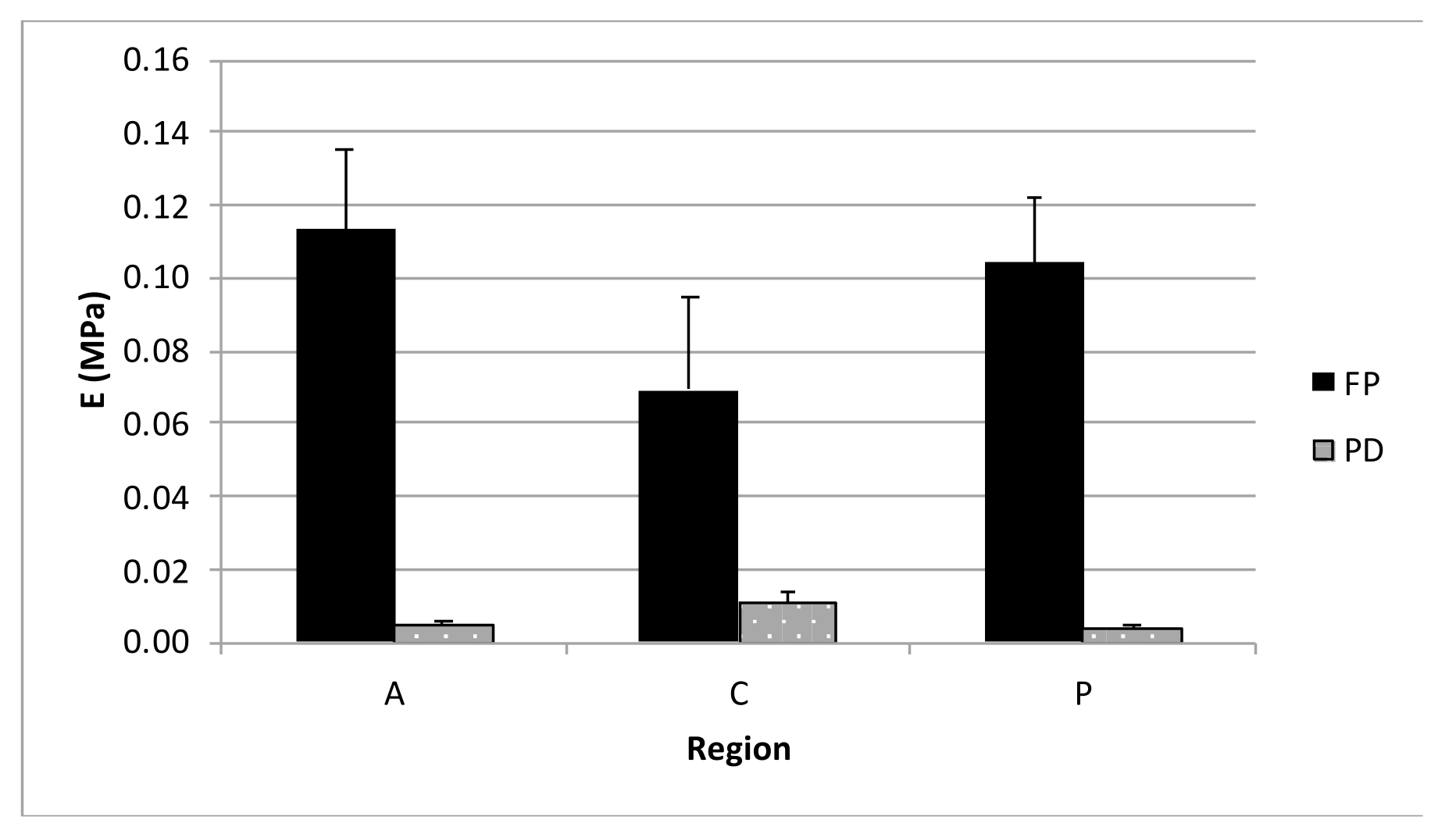
3.3. Unconfined Compression
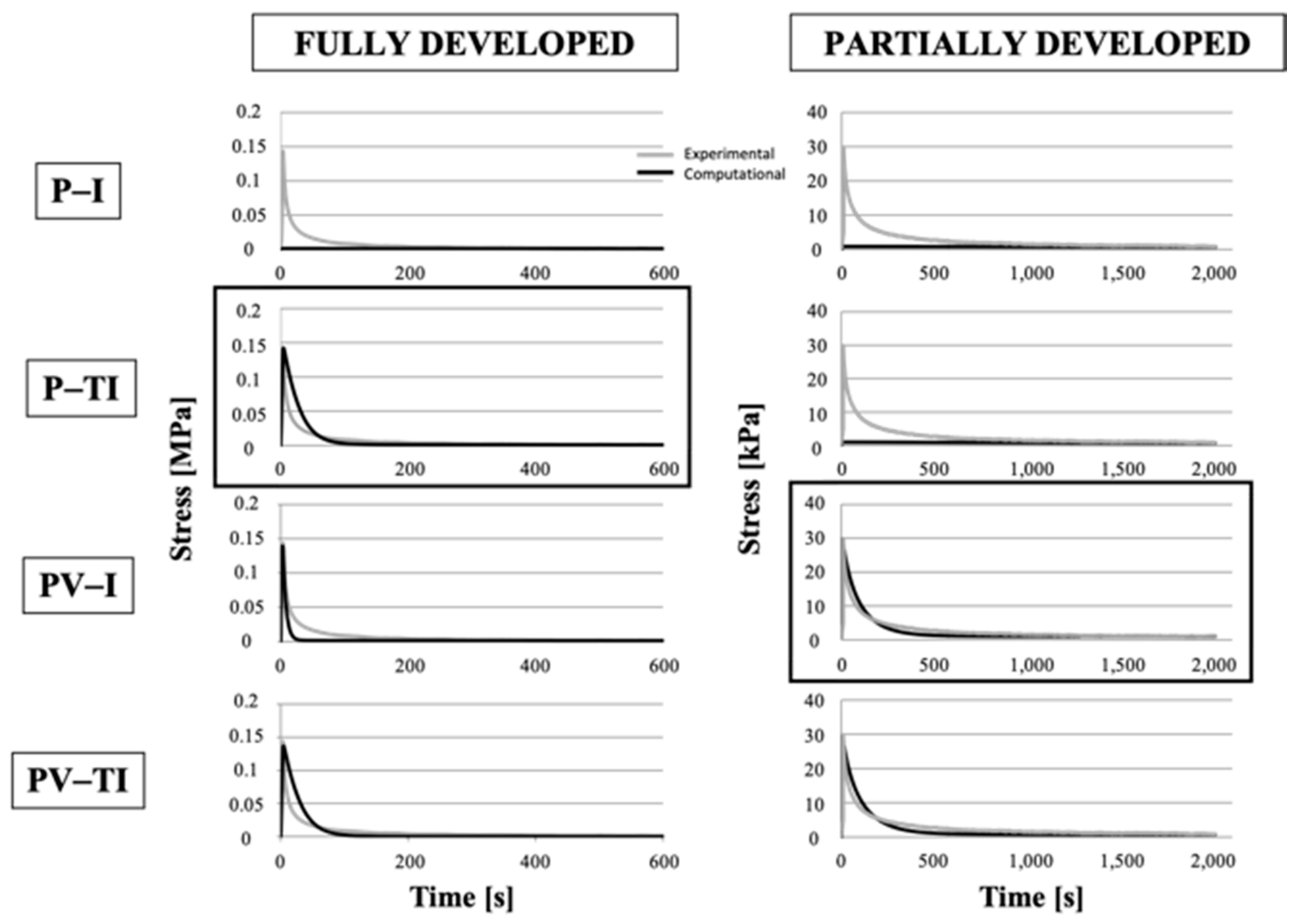
3.4. Numerical Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ahmed, A.M.; Burke, D.L.; Yu, A. In-Vitro Measurement of Static Pressure Distribution in Synovial Joints—Part II: Retropatellar Surface. J. Biomech. Eng. 1983, 105, 226–236. [Google Scholar] [CrossRef] [PubMed]
- King, D. The healing of semilunar cartilages. 1936. Clin. Orthop. Relat. Res. 1990, 252, 4–7. [Google Scholar]
- Krause, W.; Pope, M.; Johnson, R.; Wilder, D. Mechanical changes in the knee after meniscectomy. J. Bone Jt. Surg. Am. Vol. 1976, 58, 599–604. [Google Scholar] [CrossRef]
- Seedhom, B.B. Transmission of the Load in the Knee Joint with Special Reference to the Role of the Menisci. Eng. Med. 1979, 8, 207–219. [Google Scholar] [CrossRef]
- Levy, I.M.; A Torzilli, P.; Gould, J.D.; Warren, R.F. The effect of lateral meniscectomy on motion of the knee. J. Bone Jt. Surg. Am. Vol. 1989, 71, 401–406. [Google Scholar] [CrossRef]
- McDevitt, C.A.; Webber, R.J. The ultrastructure and biochemistry of meniscal cartilage. Clin. Orthop. Relat. Res. 1990, 252, 8–18. [Google Scholar] [CrossRef]
- Adams, M.E.; Hukins, D.W.L. The extracellular matrix of the meniscus. Knee Meniscus Basic Clin. Found. 1992, 15–28. [Google Scholar]
- DI Giancamillo, A.; Deponti, D.; Addis, A.; Domeneghini, C.; Peretti, G.M. Meniscus maturation in the swine model: Changes occurring along with anterior to posterior and medial to lateral aspect during growth. J. Cell. Mol. Med. 2014, 18, 1964–1974. [Google Scholar] [CrossRef] [PubMed]
- Shrive, N.G.; O’Connor, J.J.; Goodfellow, J.W. Load-Bearing in the Knee Joint. Clin. Orthop. Relat. Res. 1978, 279–287. [Google Scholar] [CrossRef]
- Arnoczky, S.P.; Warren, R.F. The microvasculature of the meniscus and its response to injury. Am. J. Sports Med. 1983, 11, 131–141. [Google Scholar] [CrossRef]
- Ding, Z.; Huang, H. Mesenchymal stem cells in rabbit meniscus and bone marrow exhibit a similar feature but a heterogeneous multi-differentiation potential: Superiority of meniscus as a cell source for meniscus repair. BMC Musculoskelet. Disord. 2015, 16, 1–14. [Google Scholar] [CrossRef]
- Ionescu, L.C.; Lee, G.C.; Huang, K.L.; Mauck, R.L. Growth factor supplementation improves native and engineered meniscus repair in vitro. Acta Biomater. 2012, 8, 3687–3694. [Google Scholar] [CrossRef]
- Osawa, A.; Harner, C.D.; Gharaibeh, B.; Matsumoto, T.; Mifune, Y.; Kopf, S.; Ingham, S.J.M.; Schreiber, V.; Usas, A.; Huard, J. The Use of Blood Vessel–Derived Stem Cells for Meniscal Regeneration and Repair. Med. Sci. Sports Exerc. 2013, 45, 813–823. [Google Scholar] [CrossRef]
- Proctor, C.S.; Schmidt, M.B.; Whipple, R.R.; Kelly, M.A.; Mow, V.C. Material properties of the normal medial bovine meniscus. J. Orthop. Res. 1989, 7, 771–782. [Google Scholar] [CrossRef]
- Chia, H.N.; Hull, M.L. Compressive moduli of the human medial meniscus in the axial and radial directions at equilibrium and at a physiological strain rate. J. Orthop. Res. 2008, 26, 951–956. [Google Scholar] [CrossRef]
- Danso, E.; Mäkelä, J.; Tanska, P.; Mononen, M.; Honkanen, J.; Jurvelin, J.; Töyräs, J.; Julkunen, P.; Korhonen, R. Characterization of site-specific biomechanical properties of human meniscus—Importance of collagen and fluid on mechanical nonlinearities. J. Biomech. 2015, 48, 1499–1507. [Google Scholar] [CrossRef]
- Danso, E.K.; Oinas, J.M.; Saarakkala, S.; Mikkonen, S.; Töyräs, J.; Korhonen, R.K. Structure-function relationships of human meniscus. J. Mech. Behav. Biomed. Mater. 2017, 67, 51–60. [Google Scholar] [CrossRef]
- Peretti, G.M.; Polito, U.; Di Giancamillo, M.; Andreis, M.E.; Boschetti, F.; Di Giancamillo, A. Swine Meniscus: Are Femoral-Tibial Surfaces Properly Tuned to Bear the Forces Exerted on the Tissue? Tissue Eng. Part A 2019, 25, 978–989. [Google Scholar] [CrossRef]
- Lechner, K.; Hull, M.L.; Howell, S.M. Is the circumferential tensile modulus within a human medial meniscus affected by the test sample location and cross-sectional area? J. Orthop. Res. 2000, 18, 945–951. [Google Scholar] [CrossRef]
- Peloquin, J.M.; Santare, M.H.; Elliott, D.M. Advances in Quantification of Meniscus Tensile Mechanics Including Nonlinearity, Yield, and Failure. J. Biomech. Eng. 2016, 138, 021002–02100213. [Google Scholar] [CrossRef]
- Bansal, S.; Peloquin, J.M.; Keah, N.M.; O’Reilly, O.C.; Elliott, D.M.; Mauck, R.L.; Zgonis, M.H. Structure, function, and defect tolerance with maturation of the radial tie fiber network in the knee meniscus. J. Orthop. Res. 2020, 38, 2709–2720. [Google Scholar] [CrossRef] [PubMed]
- Norberg, C.; Filippone, G.; Andreopoulos, F.; Best, T.M.; Baraga, M.; Jackson, A.R.; Travascio, F. Viscoelastic and equilibrium shear properties of human meniscus: Relationships with tissue structure and composition. J. Biomech. 2021, 120, 110343. [Google Scholar] [CrossRef]
- Tsujii, A.; Nakamura, N.; Horibe, S. Age-related changes in the knee meniscus. Knee 2017, 24, 1262–1270. [Google Scholar] [CrossRef] [PubMed]
- Kwok, J.; Grogan, S.; Meckes, B.; Arce, F.; Lal, R.; D’Lima, D. Atomic force microscopy reveals age-dependent changes in nanomechanical properties of the extracellular matrix of native human menisci: Implications for joint degeneration and osteoarthritis. Nanomed. Nanotechnol. Biol. Med. 2014, 10, 1777–1785. [Google Scholar] [CrossRef] [PubMed]
- Nesbitt, D.Q.; Siegel, D.N.; Nelson, S.J.; Lujan, T.J. Effect of age on the failure properties of human meniscus: High-speed strain mapping of tissue tears. J. Biomech. 2021, 115, 110126. [Google Scholar] [CrossRef] [PubMed]
- Leroux, M.A.; Setton, L.A. Experimental and Biphasic FEM Determinations of the Material Properties and Hydraulic Permeability of the Meniscus in Tension1. J. Biomech. Eng. 2002, 124, 315–321. [Google Scholar] [CrossRef] [PubMed]
- Bendjaballah, M.; Shirazi-Adl, A.; Zukor, D. Biomechanics of the human knee joint in compression: Reconstruction, mesh generation and finite element analysis. Knee 1995, 2, 69–79. [Google Scholar] [CrossRef]
- Meakin, J.R.; Shrive, N.G.; Frank, C.B.; Hart, D.A. Finite element analysis of the meniscus: The influence of geometry and material properties on its behaviour. Knee 2003, 10, 33–41. [Google Scholar] [CrossRef]
- Hennerbichler, A.; Moutos, F.T.; Hennerbichler, D.; Weinberg, J.B.; Guilak, F. Repair Response of the Inner and Outer Regions of the Porcine Meniscus in Vitro. Am. J. Sports Med. 2007, 35, 754–762. [Google Scholar] [CrossRef]
- Deponti, D.; Di Giancamillo, A.; Scotti, C.; Peretti, G.M.; Martin, I. Animal models for meniscus repair and regeneration. J. Tissue Eng. Regen. Med. 2013, 9, 512–527. [Google Scholar] [CrossRef]
- Proffen, B.L.; McElfresh, M.; Fleming, B.C.; Murray, M.M. A comparative anatomical study of the human knee and six animal species. Knee 2012, 19, 493–499. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Aoyama, T.; Ito, A.; Tajino, J.; Nagai, M.; Yamaguchi, S.; Iijima, H.; Kuroki, H. Regional comparisons of porcine menisci. J. Orthop. Res. 2014, 32, 1602–1611. [Google Scholar] [CrossRef] [PubMed]
- Biot, M.A. Mechanics of Deformation and Acoustic Propagation in Porous Media. J. Appl. Phys. 1962, 33, 1482–1498. [Google Scholar] [CrossRef]
- Chen, T. Determining Viscoelastic Strain Data a Prony Material Series for a from Time Varying; NASA Langley Research Center: Hampton, VA, USA, 2000. [Google Scholar]
- Taylor, V.; Hicks, J.; Ferguson, C.; Willey, J.; Danelson, K. Effects of tissue culture on the biomechanical properties of porcine meniscus explants. Clin. Biomech. 2019, 69, 120–126. [Google Scholar] [CrossRef]
- Danso, E.; Julkunen, P.; Korhonen, R. Poisson’s ratio of bovine meniscus determined combining unconfined and confined compression. J. Biomech. 2018, 77, 233–237. [Google Scholar] [CrossRef]
- Chahine, N.; Wang, C.C.-B.; Hung, C.T.; A Ateshian, G. Anisotropic strain-dependent material properties of bovine articular cartilage in the transitional range from tension to compression. J. Biomech. 2004, 37, 1251–1261. [Google Scholar] [CrossRef]
- A Sweigart, M.; A Athanasiou, K. Biomechanical characteristics of the normal medial and lateral porcine knee menisci. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2005, 219, 53–62. [Google Scholar] [CrossRef]

| Directions | ||
|---|---|---|
| Analysis Performed | Radial | Circumferential |
| Biomechanical tensile test (FD) | 6 (5 anterior and 1 central) | 34 (11 anterior, 14 central, and 9 posterior) |
| Biomechanical tensile test (PD) | 11 (3 anterior, 5 central, and 3 posterior) | 9 (3 anterior, 3 central, and 3 posterior) |
| Total samples | 48 | |
| Portions | |||
|---|---|---|---|
| Analysis Performed | Anterior Horn | Central Body | Posterior Horn |
| Biomechanical UC (FD) | 22 | 22 | 22 |
| Biomechanical UC (PD) | 6 | 7 | 5 |
| Total samples | 84 | ||
| Parameter | Value | Description |
|---|---|---|
| velload | 1%∙L mm/s | Velocity of loading, referred to the reference dimension (L), i.e., thickness for compression or length for tension |
| trelax | 600/1200/2000 s | Relaxation time for compression and tension tests for FD and PD menisci |
| ν | 0.05/0.49 | Poisson’s coefficient for compression and tensile tests |
| ρmatrix | 1050 kg/m3 | Drained density of solid component |
| εp | 0.675 | Averaged porosity |
| αB | 1 | Biot–Willis coefficient |
| ρ | 1000 kg/m3 | Fluid density |
| µ | 0.001 Pa∙s | Fluid dynamic viscosity |
| χf | 10−19 1/Pa | Fluid compressibility |
| FULLY DEVELOPED | PARTIALLY DEVELOPED | ||||
|---|---|---|---|---|---|
| Parameter | Value | Parameter | Value | ||
| UC: P-TI model | UC: PV-I model | K | 6.26 × 10−15 m2 | ||
| Ez | 4.51 kPa | ||||
| K | 7.67 × 10−18 m2 | G1 | 136 kPa | ||
| Er | 15.3 MPa | G2 | 0.901 kPa | ||
| Eϕ | 15.3 MPa | G3 | 0.04 kPa | ||
| Ez | 0.142 MPa | τ1 | 103 s | ||
| τ 2 | 3114 s | ||||
| τ 3 | 9321 s | ||||
| TENSILE: V-I model | Ez | 7.12 MPa | TENSILE: V-I model | Ez | 17.8 MPa |
| G1 | 3.43 MPa | G1 | 2.33 MPa | ||
| G2 | 3.43 MPa | G2 | 2.33 MPa | ||
| G3 | 3.43 MPa | G3 | 2.33 MPa | ||
| τ1 | 10 s | τ1 | 5.9 s | ||
| τ 2 | 173.3 s | τ 2 | 31.9 s | ||
| τ 3 | 4200 s | τ 3 | 1088 s | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferroni, M.; Belgio, B.; Peretti, G.M.; Di Giancamillo, A.; Boschetti, F. Evolution of Meniscal Biomechanical Properties with Growth: An Experimental and Numerical Study. Bioengineering 2021, 8, 70. https://doi.org/10.3390/bioengineering8050070
Ferroni M, Belgio B, Peretti GM, Di Giancamillo A, Boschetti F. Evolution of Meniscal Biomechanical Properties with Growth: An Experimental and Numerical Study. Bioengineering. 2021; 8(5):70. https://doi.org/10.3390/bioengineering8050070
Chicago/Turabian StyleFerroni, Marco, Beatrice Belgio, Giuseppe M. Peretti, Alessia Di Giancamillo, and Federica Boschetti. 2021. "Evolution of Meniscal Biomechanical Properties with Growth: An Experimental and Numerical Study" Bioengineering 8, no. 5: 70. https://doi.org/10.3390/bioengineering8050070
APA StyleFerroni, M., Belgio, B., Peretti, G. M., Di Giancamillo, A., & Boschetti, F. (2021). Evolution of Meniscal Biomechanical Properties with Growth: An Experimental and Numerical Study. Bioengineering, 8(5), 70. https://doi.org/10.3390/bioengineering8050070