Viscoelastic Characterization of Parasagittal Bridging Veins and Implications for Traumatic Brain Injury: A Pilot Study
Abstract
:1. Introduction
2. Data and Methods
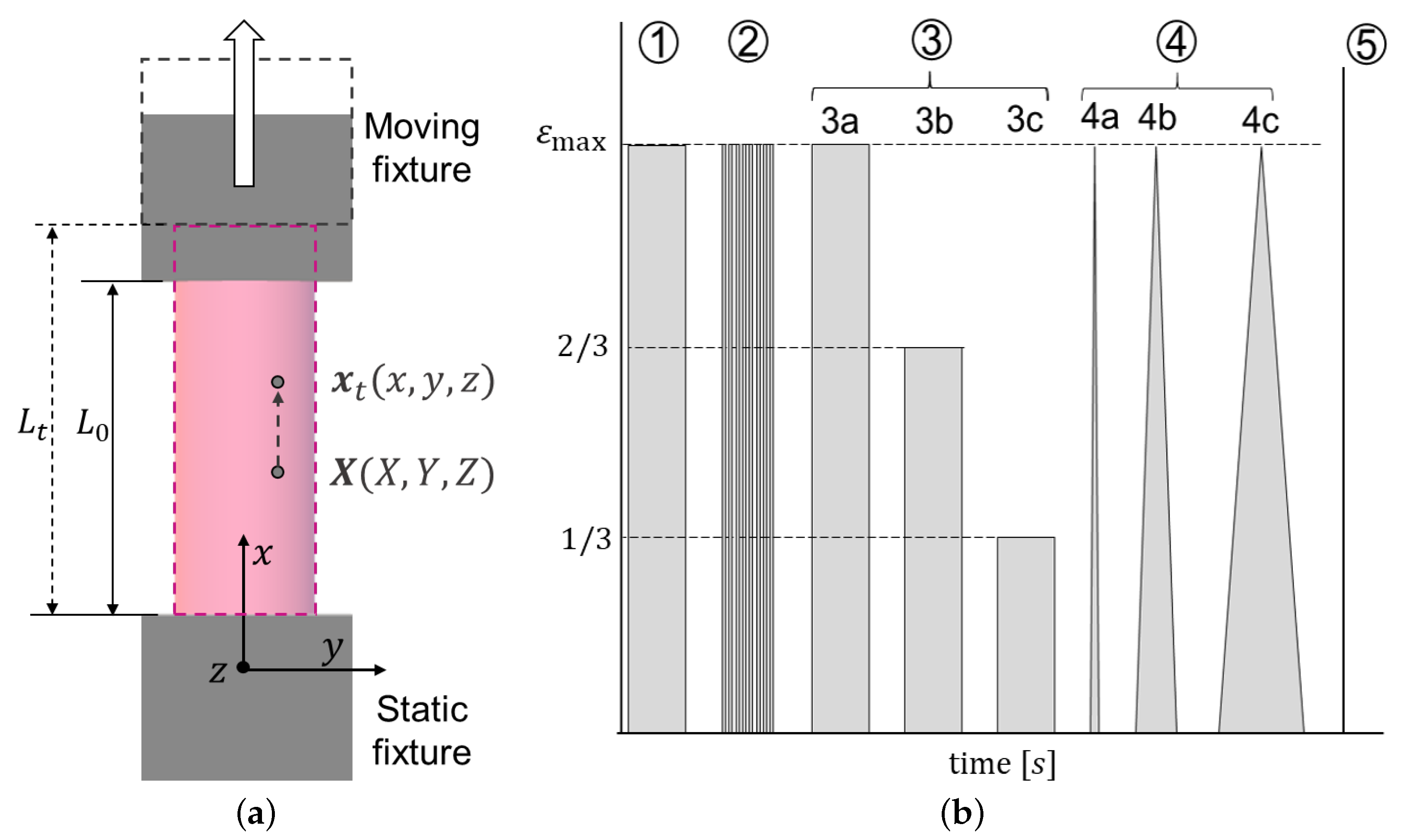
2.1. Material and Specimen Preparation
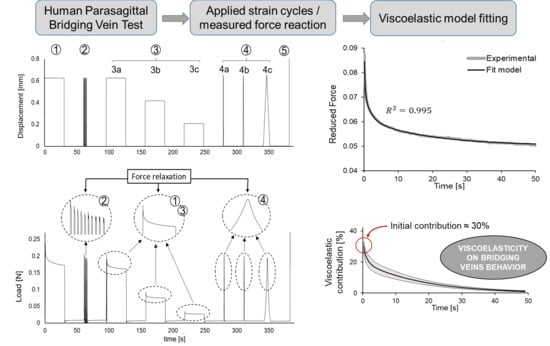
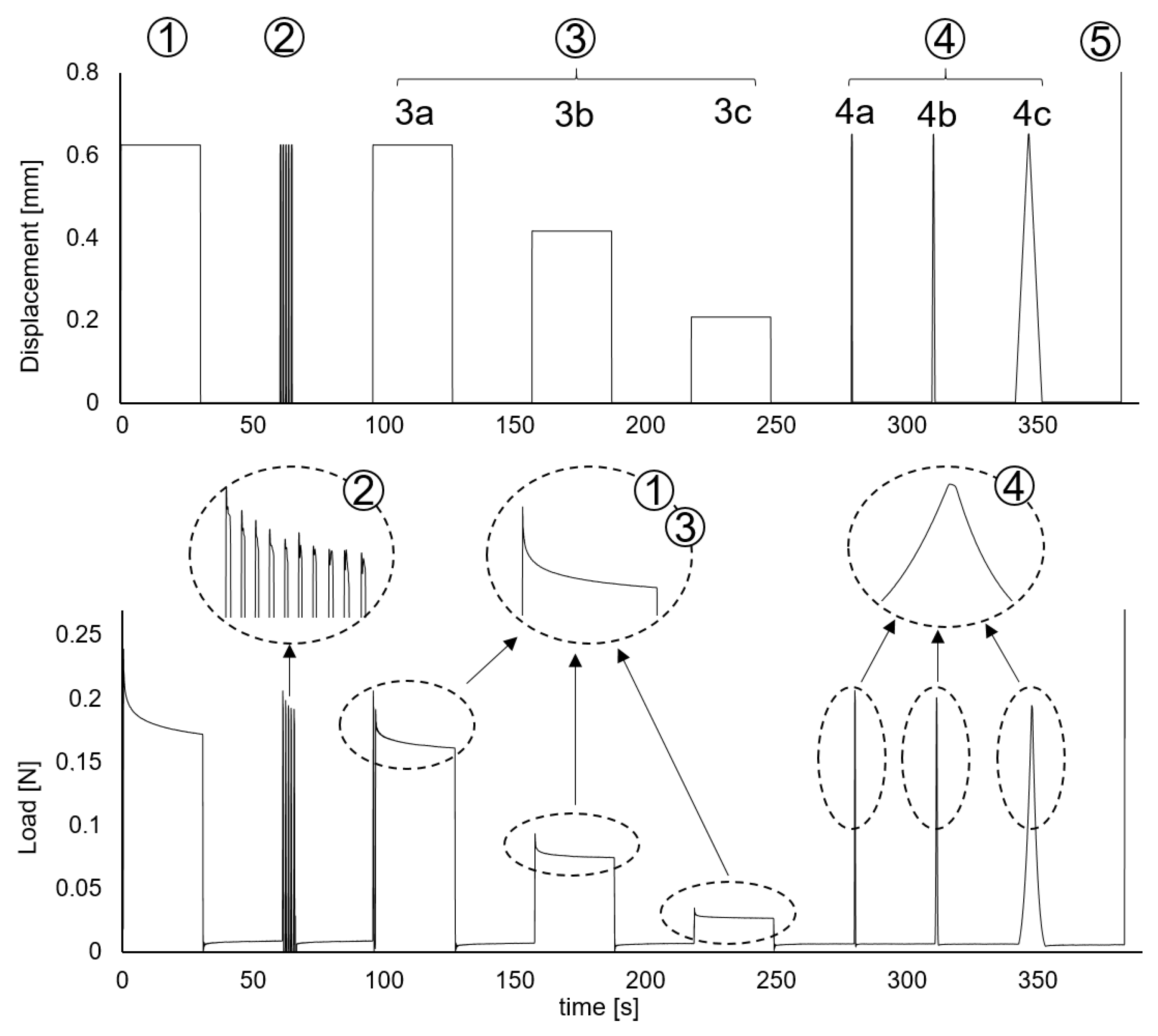
2.2. Cyclic and Relaxation Tests
2.3. Quasi-Linear Viscoelastic Model
3. Results
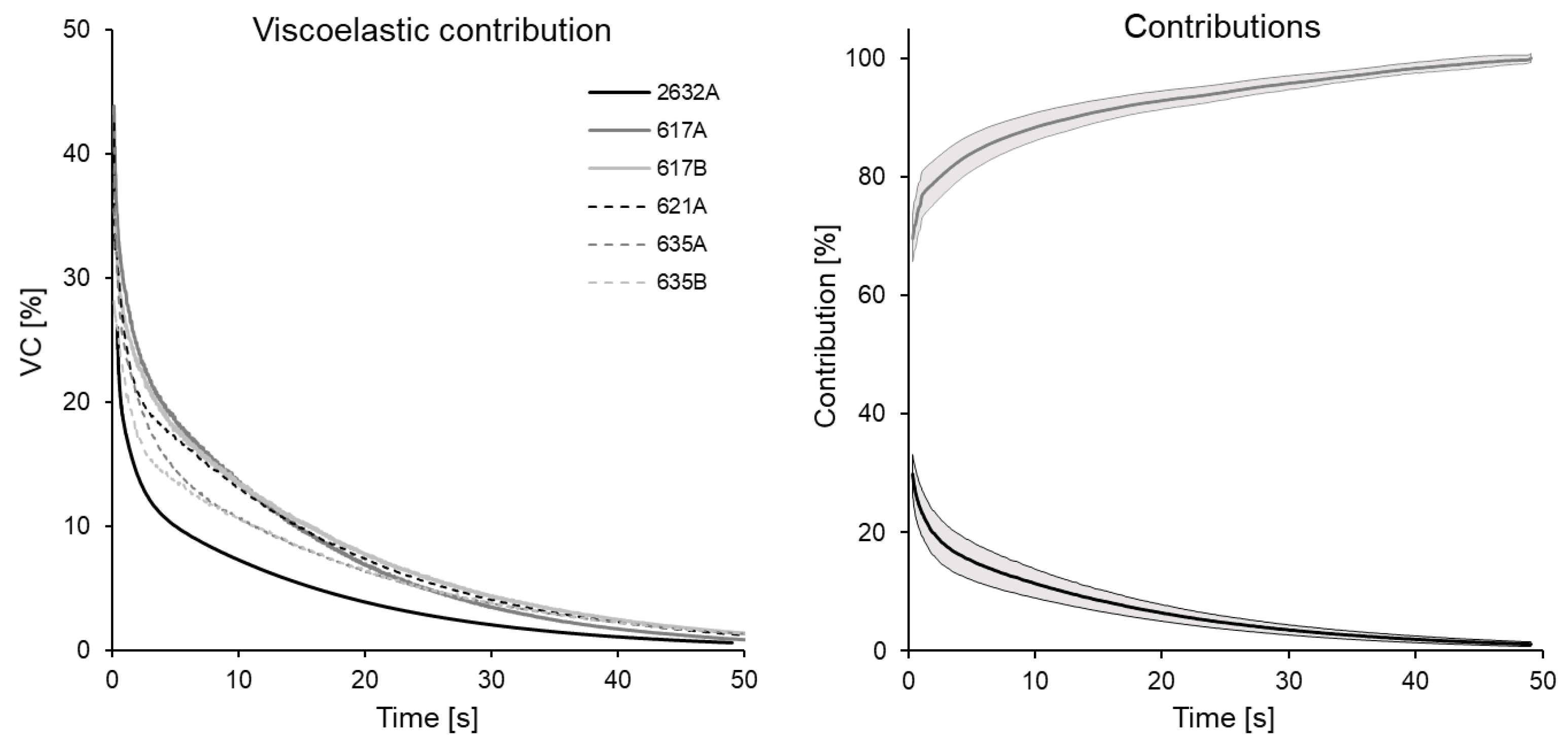
3.1. Relaxation Tests
- Notice that, although for the coefficient is quantitatively adequate, qualitatively it is observed that the fit does not adequately represent the vertical asymptote of force drop, nor the curve in general.
- With there is a marked improvement in the fit ().
- Finally, for (), both the asymptote and the curve are adequately represented by the viscoelastic model.
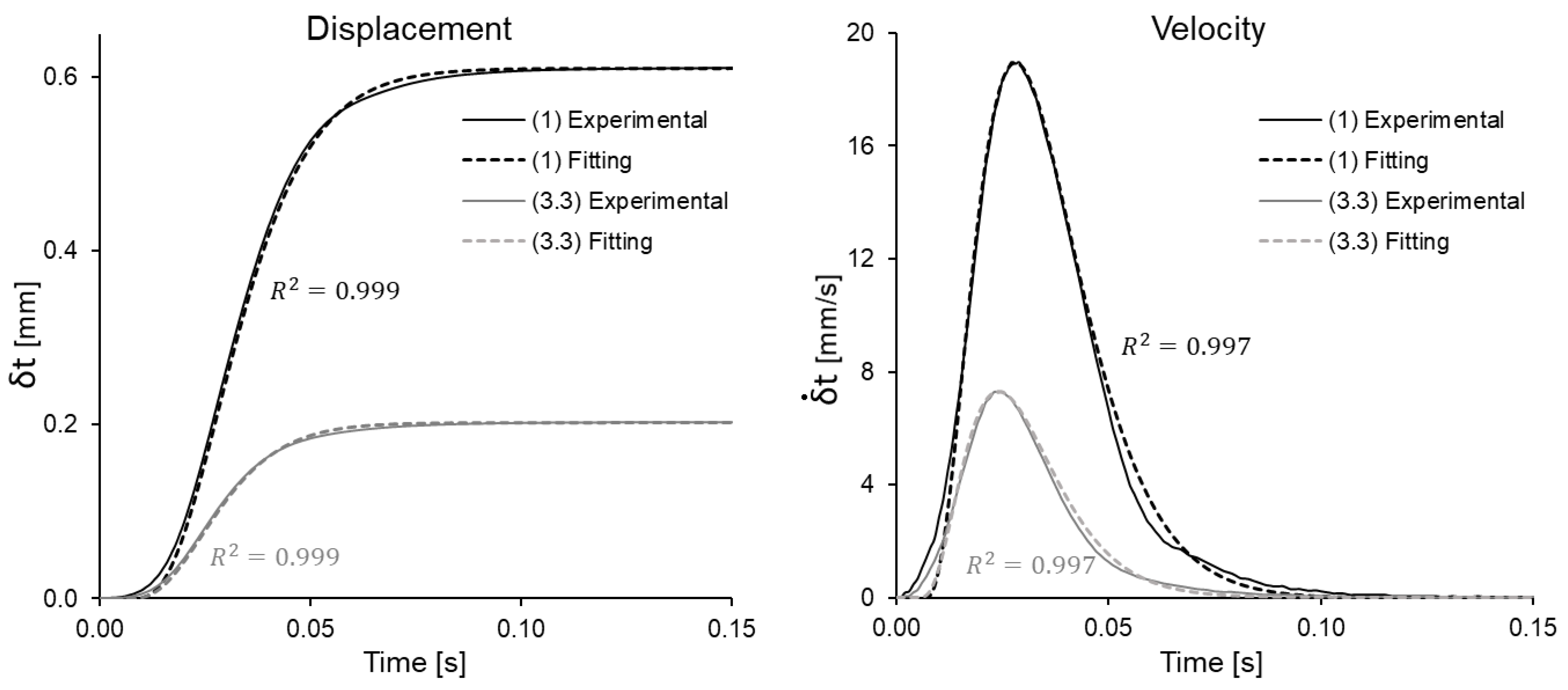
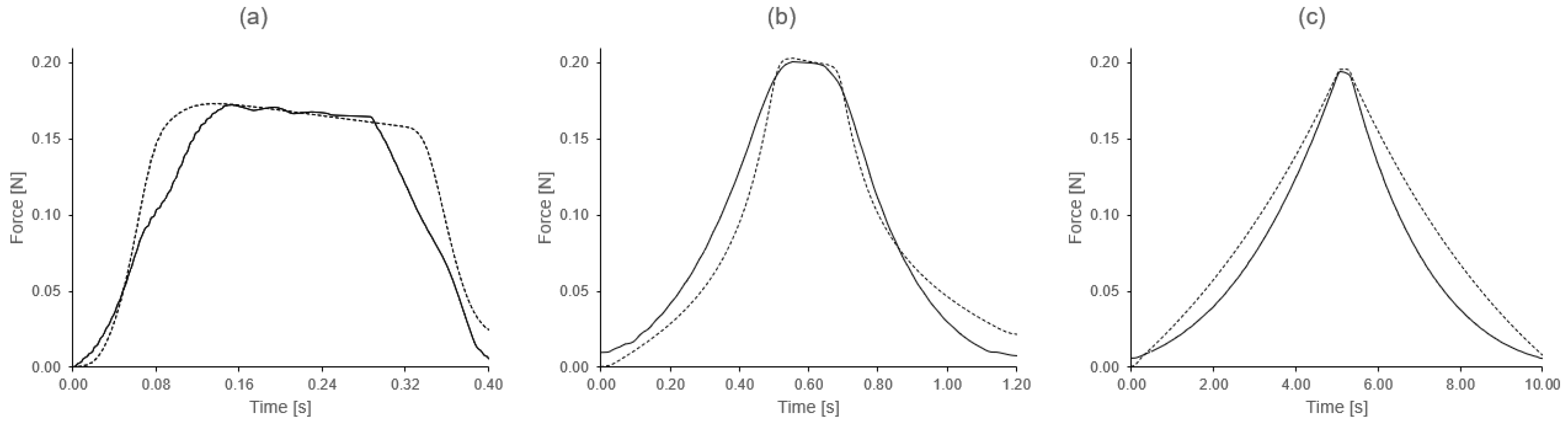
3.2. Fast Loading/Unloading Cycle Tests
3.3. Load-Unload Tests
4. Discussion
- Clinicians are charged with the significant task of distinguishing between accidental and inflicted head trauma. Some times this distinction is straightforward, but in many cases the probabilities of injuries from accidental scenarios are unknown, making the differential diagnosis difficult [31]. A refinement of the knowledge of the tolerance ranges against rupture of PSBVs may provide greater accuracy in the reconstruction of injury mechanisms.
- Computational biomechanics can simulate many potentially traumatic situations, so that models already allow detailed reconstructions of the sequence of events leading to a severe SDH. Accurate knowledge of the material behavior can improve FEHMs, as their inaccuracy is often not so much a computational problem, but a poor characterization of the biomechanical behavior of brain structures. For example, a good number of FEHMs use a stress-strain response for PSBVs that does not reflect the measured nonlinear behavior [3], e.g., the UDS FEHM (Université de Strasbourg) [32], the KTH FEHM (KTH Royal Institute of Technology) [33], UCDBTM (University College Dublin) [34,35], WSUBIM (Wayne State University) [36] or G/LHM [37] also model PSBVs as elastic beams with a linear stress-strain response [9]. The recognition of the importance of the nonlinear behavior and viscoelasticity of brain structures has been explicitly pointed out by the developers of YEAHM (University of Aveiro) [38] and interestingly, some FEHMs model PSBVs as nonlinear elastic materials [39]. In particular, Equation (4), together with the averages obtained from Table 2, allow us to compute an estimation of the viscoelastic effect, independent of the starting elastic model for the PSBVs, which is being used in the FEHM.
- The improvement of injury metrics used to assess restraint systems in vehicles or the design of other preventive elements against head trauma. Currently, the estimation is often done by the injury metric called “relative motion damage measure” (RMDM) [40,41], used to predict the probability of a SDH due to the failure of PSBVs [42,43]. However, that metric was developed based on obsolete data [26], and the data from this study can be used to update that injury metric.
- The sample used is consistent but small. So, the effects of age, gender, or other anthropometric characteristics on the viscoelastic mechanical properties could not be determined.
- In addition, a QLVE model has been used in which the relaxation function is separable, in the sense of [13]. Given the low strain levels used for the tests (since care was taken not to cause irreversible damage to the specimen from one test stage to the next), no effects of non-separability were found. However, further work could build a somewhat more general model on that basis. In any case, the proposed model is a first approximation that even explains the data that were not used for the fits (see Section 3.3).
- Moreover, a further extension of this work would be to examine whether the relaxation curves could be modeled, using the Prony series of stretched exponential relaxation [44]. This could lead to series with fewer and/or more accurate terms, although it is not clear if this is the case. Further work is needed in order to determine whether the use of stretched exponentials or a more general non-separable viscoelastic model would provide better models.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PSBV(s) | Parasagittal Bridging Vein(s) |
| FEHM | Finite Element Head Model |
| QLVE | Quasi-Linear Viscoelastic |
| SDH | Subdural Hematoma |
| TBI | Traumatic Brain Injury |
| VC | Viscoelastic Contribution |
Appendix A. Prediction of the USF
References
- Dewan, M.C.; Rattani, A.; Gupta, S.; Baticulon, R.E.; Hung, Y.C.; Punchak, M.; Agrawal, A.; Adeleye, A.O.; Shrime, M.G.; Rubiano, A.M.; et al. Estimating the global incidence of traumatic brain injury. J. Neurosurg. 2018, 130, 1080–1097. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.C.; Haut, R.C. Insensitivity of tensile failure properties of human bridging veins to strain rate: Implications in biomechanics of subdural hematoma. J. Biomech. 1989, 22, 537–542. [Google Scholar] [CrossRef]
- Sánchez-Molina, D.; García-Vilana, S.; Llumà, J.; Galtés, I.; Velázquez-Ameijide, J.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Mechanical behaviour of blood vessels during a Traumatic Brain Injury: Elastic and viscoelastic contributions. Biology 2021, 10, 831. [Google Scholar] [CrossRef]
- Delye, H.; Goffin, J.; Verschueren, P.; Vander Sloten, J.; Van der Perre, G.; Alaerts, H.; Verpoest, I.; Berckmans, D. Biomechanical properties of the superior sagittal sinus-bridging vein complex (No. 2006-22-0024). Sae Tech. Pap. 2006, 50, 1–12. [Google Scholar]
- Monson, K.L.; Converse, M.I.; Manley, G.T. Cerebral blood vessel damage in traumatic brain injury. Clin. Biomech. 2019, 64, 98–113. [Google Scholar] [CrossRef]
- Monson, K.L.; Goldsmith, W.; Barbaro, N.M.; Manley, G.T. Axial mechanical properties of fresh human cerebral blood vessels. J. Biomech. Eng. 2003, 125, 288–294. [Google Scholar] [CrossRef] [PubMed]
- Monea, A.G.; Baeck, K.; Verbeken, E.; Verpoest, I.; Vander Sloten, J.; Goffin, J.; Depreitere, B. The biomechanical behaviour of the bridging vein–superior sagittal sinus complex with implications for the mechanopathology of acute subdural haematoma. J. Mech. Behav. Biomed. Mater. 2014, 32, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.C.; Haut, R.C. Strain rate effects on tensile failure properties of the common carotid artery and jugular veins of ferrets. J. Biomech. 1992, 25, 925–927. [Google Scholar] [CrossRef]
- Famaey, N.; Cui, Z.Y.; Musigazi, G.U.; Ivens, J.; Depreitere, B.; Verbeken, E.; Vander Sloten, J. Structural and mechanical characterisation of bridging veins: A review. J. Mech. Behav. Biomed. Mater. 2015, 41, 222–240. [Google Scholar] [CrossRef] [PubMed]
- Pasquesi, S.A.; Margulies, S.S. Failure and fatigue properties of immature human and porcine parasagittal bridging veins. Ann. Biomed. Eng. 2017, 45, 1877–1889. [Google Scholar] [CrossRef]
- Wang, Z.; Golob, M.J.; Chesler, N.C. Viscoelastic properties of cardiovascular tissues. Viscoelastic Viscoplastic Mater. 2016, 2, 64. [Google Scholar]
- Funk, J.R.; Hall, G.W.; Crandall, J.R.; Pilkey, W.D. Linear and quasi-linear viscoelastic characterization of ankle ligaments. J. Biomech. Eng. 2000, 122, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Davis, F.M.; De Vita, R. A nonlinear constitutive model for stress relaxation in ligaments and tendons. Ann. Biomed. Eng. 2012, 40, 2541–2550. [Google Scholar] [CrossRef] [PubMed]
- Pascoletti, G.; Di Nardo, M.; Fragomeni, G.; Barbato, V.; Capriglione, T.; Gualtieri, R.; Talevi, R.; Catapano, G.; Zanetti, E.M. Dynamic characterization of the biomechanical behaviour of bovine ovarian cortical tissue and its short-term effect on ovarian tissue and follicles. Materials 2020, 13, 3759. [Google Scholar] [CrossRef]
- Miller, J.D.; Nader, R. Acute subdural hematoma from bridging vein rupture: A potential mechanism for growth. J. Neurosurg. 2014, 120, 1378–1384. [Google Scholar] [CrossRef]
- Costa, J.M.; Fernandes, F.A.; de Sousa, R.J.A. Prediction of subdural haematoma based on a detailed numerical model of the cerebral bridging veins. J. Mech. Behav. Biomed. Mater. 2020, 111, 103976. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics Mechanical Properties of Living Tissues; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Jin, Z.H. Some notes on the linear viscoelasticity of functionally graded materials. Math. Mech. Solids 2006, 11, 216–224. [Google Scholar] [CrossRef]
- Soussou, J.E.; Moavenzadeh, F.; Gradowczyk, M.H. Application of Prony series to linear viscoelasticity. Trans. Soc. Rheol. 1970, 14, 573–584. [Google Scholar] [CrossRef]
- Tzikang, C. Determining a Prony Series for a Viscoelastic Material from Time Varying Strain Data; NASA Center for Aero Space Information (CASI): Hampton, VA, USA, 2000.
- Tapia-Romero, M.A.; Dehonor-Gómez, M.; Lugo-Uribe, L.E. Prony series calculation for viscoelastic behavior modeling of structural adhesives from DMA data. Ing. Investig. Tecnol. 2020, 21, 1–10. [Google Scholar] [CrossRef]
- Sun, Z.; Gepner, B.D.; Lee, S.H.; Rigby, J.; Cottler, P.S.; Hallman, J.J.; Kerrigan, J.R. Multidirectional mechanical properties and constitutive modeling of human adipose tissue under dynamic loading. Acta Biomater. 2021, 129, 188–198. [Google Scholar] [CrossRef]
- Braess, D. Finite Elements: Theory, Fast Solvers, and Applications in Solid Mechanics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Iriarte, Y.A.; Varela, H.; Gómez, H.J.; Gómez, H.W. A Gamma-Type distribution with applications. Symmetry 2020, 12, 870. [Google Scholar] [CrossRef]
- Al-A’asam, J.A. Deriving the composite Simpson rule by using Bernstein polynomials for solving Volterra integral equations. Baghdad Sci. J. 2014, 11, 1274–1282. [Google Scholar]
- Löwenhielm, P. Dynamic properties of the parasagittal bridging beins. Z. FüR Rechtsmed. 1974, 74, 55–62. [Google Scholar] [CrossRef]
- Sánchez-Molina, D.; García-Vilana, S.; Velázquez-Ameijide, J.; Arregui-Dalmases, C. Probabilistic assessment for clavicle fracture under compression loading: Rate-dependent behavior. Biomed. Eng. Appl. Basis Commun. 2020, 32, 2050040. [Google Scholar] [CrossRef]
- Gefen, A.; Margulies, S.S. Are in vivo and in situ brain tissues mechanically similar? J. Biomech. 2004, 37, 1339–1352. [Google Scholar] [CrossRef]
- Komatsu, K.; Sanctuary, C.; Shibata, T.; Shimada, A.; Botsis, J. Stress-relaxation and microscopic dynamics of rabbit periodontal ligament. J. Biomech. 2007, 40, 634–644. [Google Scholar] [CrossRef]
- Zhang, K.; Siegmund, T.; Chan, R.W. Modeling of the transient responses of the vocal fold lamina propria. J. Mech. Behav. Biomed. Mater. 2009, 2, 93–104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coats, B.; Eucker, S.A.; Sullivan, S.; Margulies, S.S. Finite element model predictions of intracranial hemorrhage from non-impact, rapid head rotations in the piglet. Int. J. Dev. Neurosci. 2012, 30, 191–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raul, J.S.; Roth, S.; Ludes, B.; Willinger, R. Influence of the benign enlargement of the subarachnoid space on the bridging veins strain during a shaking event: A finite element study. Int. J. Leg. Med. 2008, 122, 337–340. [Google Scholar] [CrossRef]
- Kleiven, S. Predictors for traumatic brain injuries evaluated through accident reconstructions (No. 2007-22-0003). SAE Tech. Pap. 2007, 51, 1–35. [Google Scholar]
- Doorly, M.C. Investigations into Head Injury Criteria Using Numerical Reconstruction of Real Life Accident Cases. Ph.D. Thesis, University College Dublin, Dublin, Ireland, 2007. [Google Scholar]
- Yan, W.; Pangestu, O.D. A modified human head model for the study of impact head injury. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 1049–1057. [Google Scholar] [CrossRef] [PubMed]
- Viano, D.C.; Casson, I.R.; Pellman, E.J.; Zhang, L.; King, A.I.; Yang, K.H. Concussion in professional football: Brain responses by finite element analysis: Part 9. Neurosurgery 2005, 57, 891–916. [Google Scholar] [CrossRef]
- Zoghi-Moghadam, M.; Sadegh, A.M. Global/local head models to analyse cerebral blood vessel rupture leading to ASDH and SAH. Comput. Methods Biomech. Biomed. Eng. 2009, 12, 1–12. [Google Scholar] [CrossRef]
- Fernandes, F.A.; Tchepel, D.; de Sousa, R.J.A.; Ptak, M. Development and validation of a new finite element human head model: Yet another head model (YEAHM). Eng. Comput. 2018, 35, 477–496. [Google Scholar] [CrossRef]
- Mao, H.; Zhang, L.; Jiang, B.; Genthikatti, V.V.; Jin, X.; Zhu, F.; Yang, K.H. Development of a finite element human head model partially validated with thirty five experimental cases. J. Biomech. Eng. 2013, 135, 111002. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Molina, D.; Velazquez-Ameijide, J.; Arregui-Dalmases, C.; Crandall, J.R.; Untaroiu, C.D. Minimization of analytical injury metrics for head impact injuries. Traffic Inj. Prev. 2012, 13, 278–285. [Google Scholar] [CrossRef]
- Sánchez-Molina, D.; Arregui-Dalmases, C.; Velázquez-Ameijide, J.; Angelini, M.; Kerrigan, J.; Crandall, J. Traumatic brain injury in pedestrian–vehicle collisions: Convexity and suitability of some functionals used as injury metrics. Comput. Methods Programs Biomed. 2016, 136, 55–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takhounts, E.G.; Ridella, S.A.; Hasija, V.; Tannous, R.E.; Campbell, J.Q.; Malone, D.; Duma, S. Investigation of traumatic brain injuries using the next generation of simulated injury monitor (SIMon) finite element head model (No. 2008-22-0001). SAE Tech. Pap. 2008, 52, 1. [Google Scholar]
- Fernandes, F.A.; Sousa, R.J.A.D. Head injury predictors in sports trauma—A state-of-the-art review. Proc. Inst. Mech. Eng. Part J. Eng. Med. 2015, 229, 592–608. [Google Scholar] [CrossRef]
- Mauro, J.C.; Mauro, Y.Z. On the Prony series representation of stretched exponential relaxation. Phys. Stat. Mech. Appl. 2018, 506, 75–87. [Google Scholar] [CrossRef] [Green Version]


| N | [–] | [–] | [–] | [s] | [s] | [s] |
|---|---|---|---|---|---|---|
| 0.360 | — | — | 10.756 | — | — | |
| 0.243 | 0.393 | — | 13.397 | 0.799 | — | |
| 0.215 | 0.221 | 0.398 | 18.162 | 1.885 | 0.211 |
| Specimen | [–] | [–] | [–] | [s] | [s] | [s] |
|---|---|---|---|---|---|---|
| 2632A | 0.10 ± 0.05 | 0.13 ± 0.04 | 1.70 ± 0.29 | 10.96 ± 2.64 | 0.88 ± 0.19 | 0.07 ± 0.01 |
| 617A | 0.21 ± 0.10 | 0.32 ± 0.16 | 0.34 ± 0.06 | 15.38 ± 4.90 | 1.99 ± 2.62 | 0.17 ± 0.19 |
| 617B | 0.24 ± 0.07 | 0.13 ± 0.08 | 0.30 ± 0.23 | 13.78 ± 9.15 | 0.96 ± 0.70 | 0.09 ± 0.08 |
| 621A | 0.20 ± 0.07 | 0.18 ± 0.10 | 0.48 ± 0.42 | 17.08 ± 16.11 | 1.20 ± 1.23 | 0.09 ± 0.10 |
| 635A | 0.12 ± 0.07 | 0.13 ± 0.07 | 0.84 ± 1.13 | 20.73 ± 13.34 | 2.16 ± 1.46 | 0.20 ± 0.10 |
| 635B | 0.14 ± 0.06 | 0.16 ± 0.08 | 1.60 ± 1.62 | 25.41 ± 8.22 | 1.76 ± 1.93 | 0.17 ± 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Vilana, S.; Sánchez-Molina, D.; Llumà, J.; Galtés, I.; Velázquez-Ameijide, J.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Viscoelastic Characterization of Parasagittal Bridging Veins and Implications for Traumatic Brain Injury: A Pilot Study. Bioengineering 2021, 8, 145. https://doi.org/10.3390/bioengineering8100145
García-Vilana S, Sánchez-Molina D, Llumà J, Galtés I, Velázquez-Ameijide J, Rebollo-Soria MC, Arregui-Dalmases C. Viscoelastic Characterization of Parasagittal Bridging Veins and Implications for Traumatic Brain Injury: A Pilot Study. Bioengineering. 2021; 8(10):145. https://doi.org/10.3390/bioengineering8100145
Chicago/Turabian StyleGarcía-Vilana, Silvia, David Sánchez-Molina, Jordi Llumà, Ignasi Galtés, Juan Velázquez-Ameijide, M. Carmen Rebollo-Soria, and Carlos Arregui-Dalmases. 2021. "Viscoelastic Characterization of Parasagittal Bridging Veins and Implications for Traumatic Brain Injury: A Pilot Study" Bioengineering 8, no. 10: 145. https://doi.org/10.3390/bioengineering8100145
APA StyleGarcía-Vilana, S., Sánchez-Molina, D., Llumà, J., Galtés, I., Velázquez-Ameijide, J., Rebollo-Soria, M. C., & Arregui-Dalmases, C. (2021). Viscoelastic Characterization of Parasagittal Bridging Veins and Implications for Traumatic Brain Injury: A Pilot Study. Bioengineering, 8(10), 145. https://doi.org/10.3390/bioengineering8100145