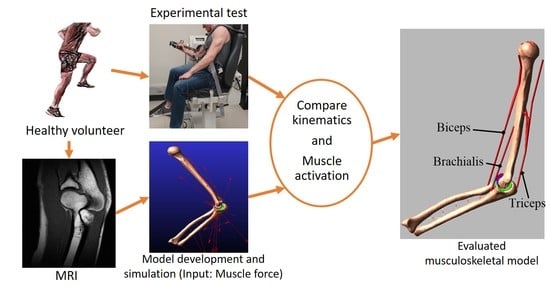
Musculoskeletal Model Development of the Elbow Joint with an Experimental Evaluation
Abstract
1. Introduction
2. Materials and Methods
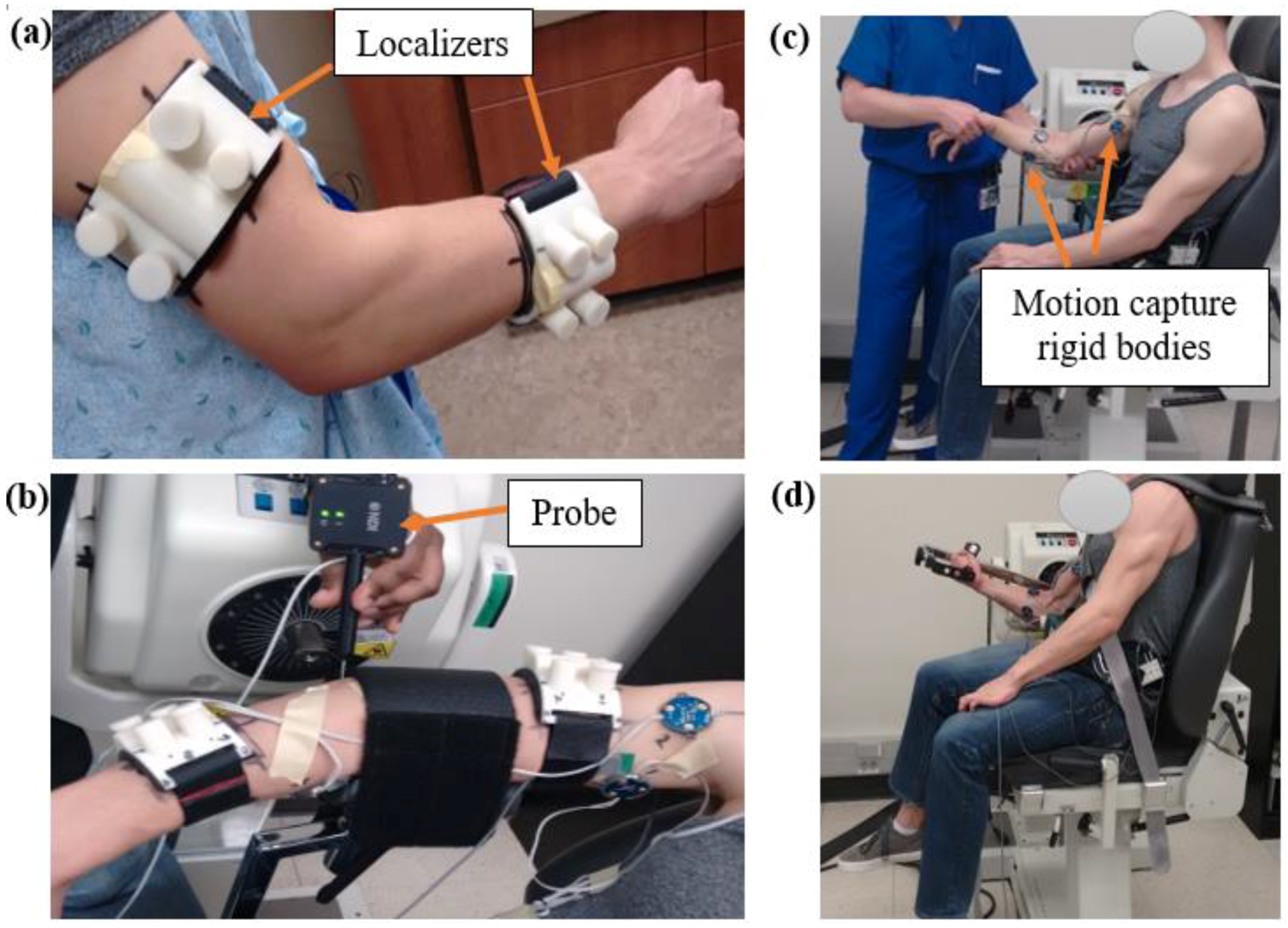
2.1. Experimental Measures
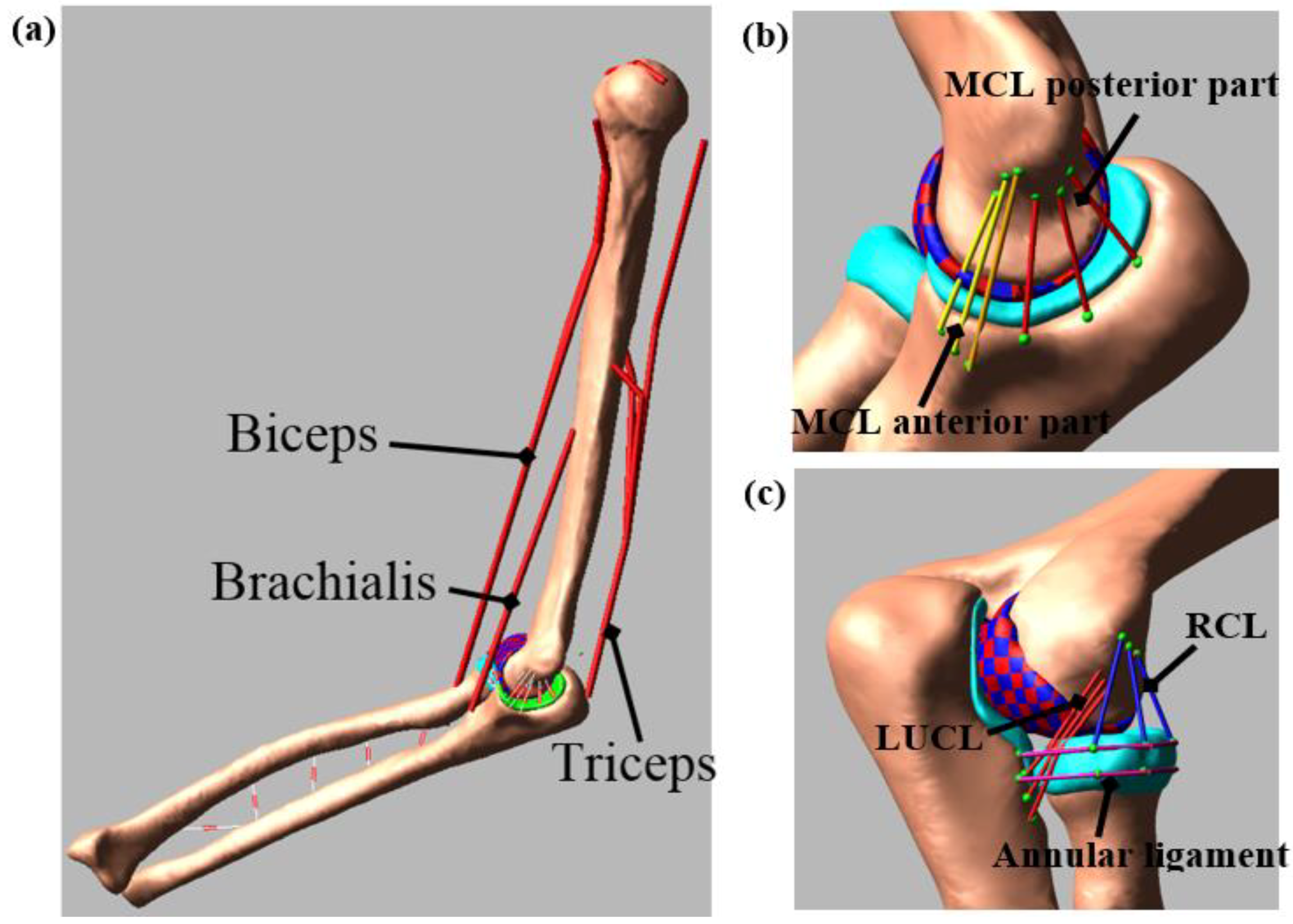
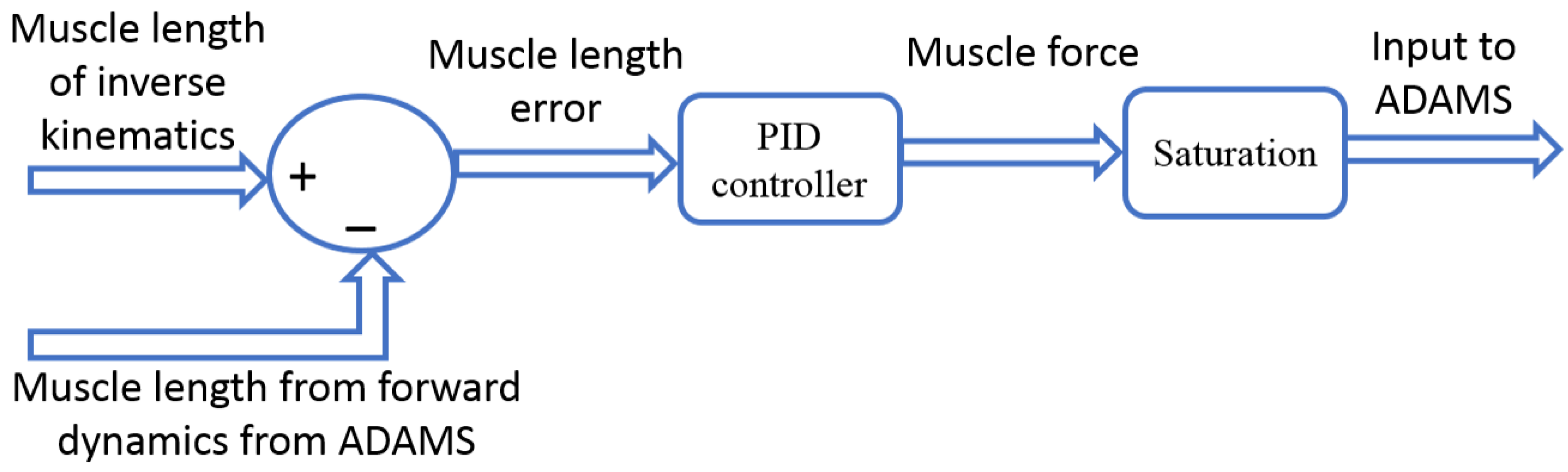
2.2. Computational Model
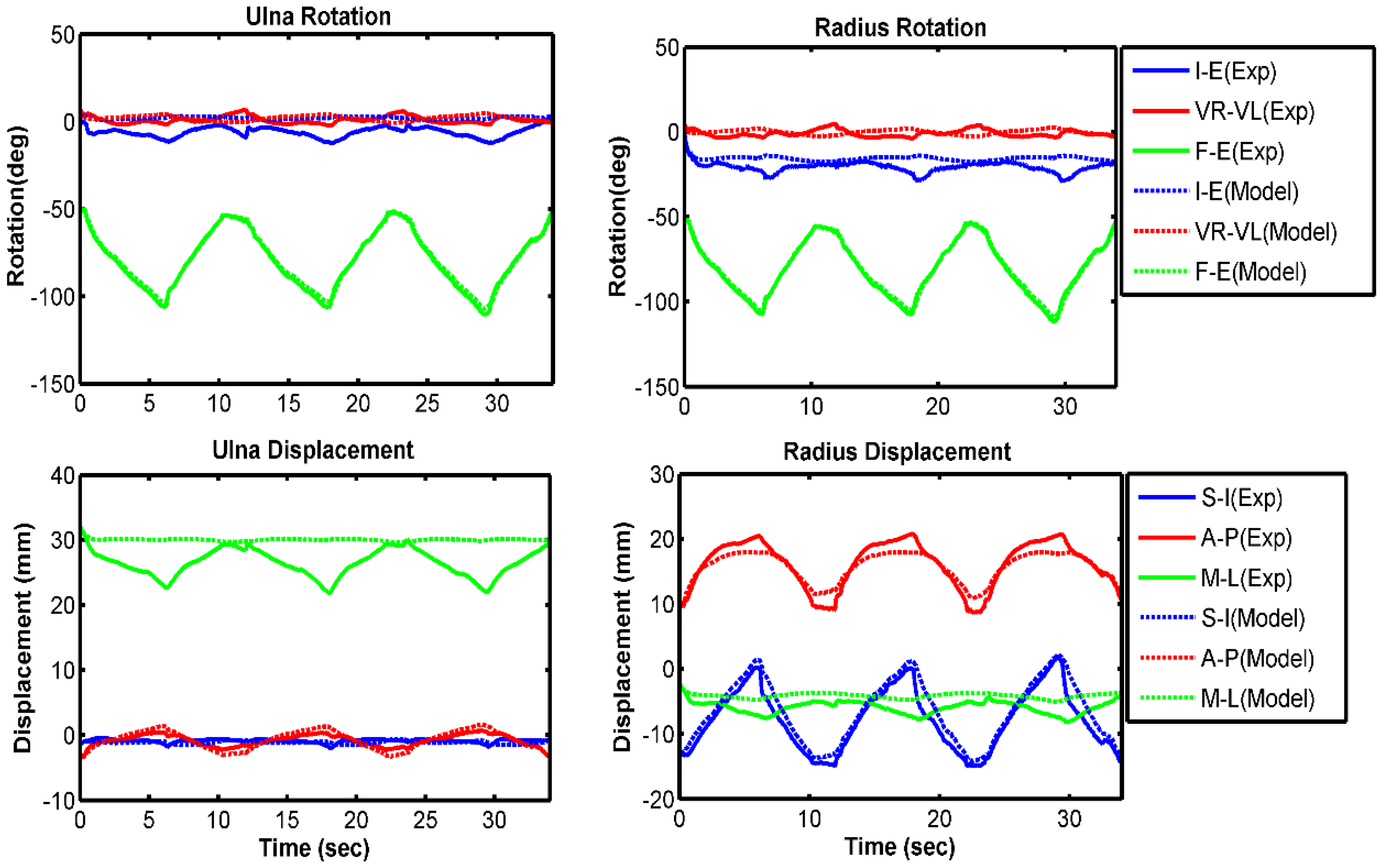
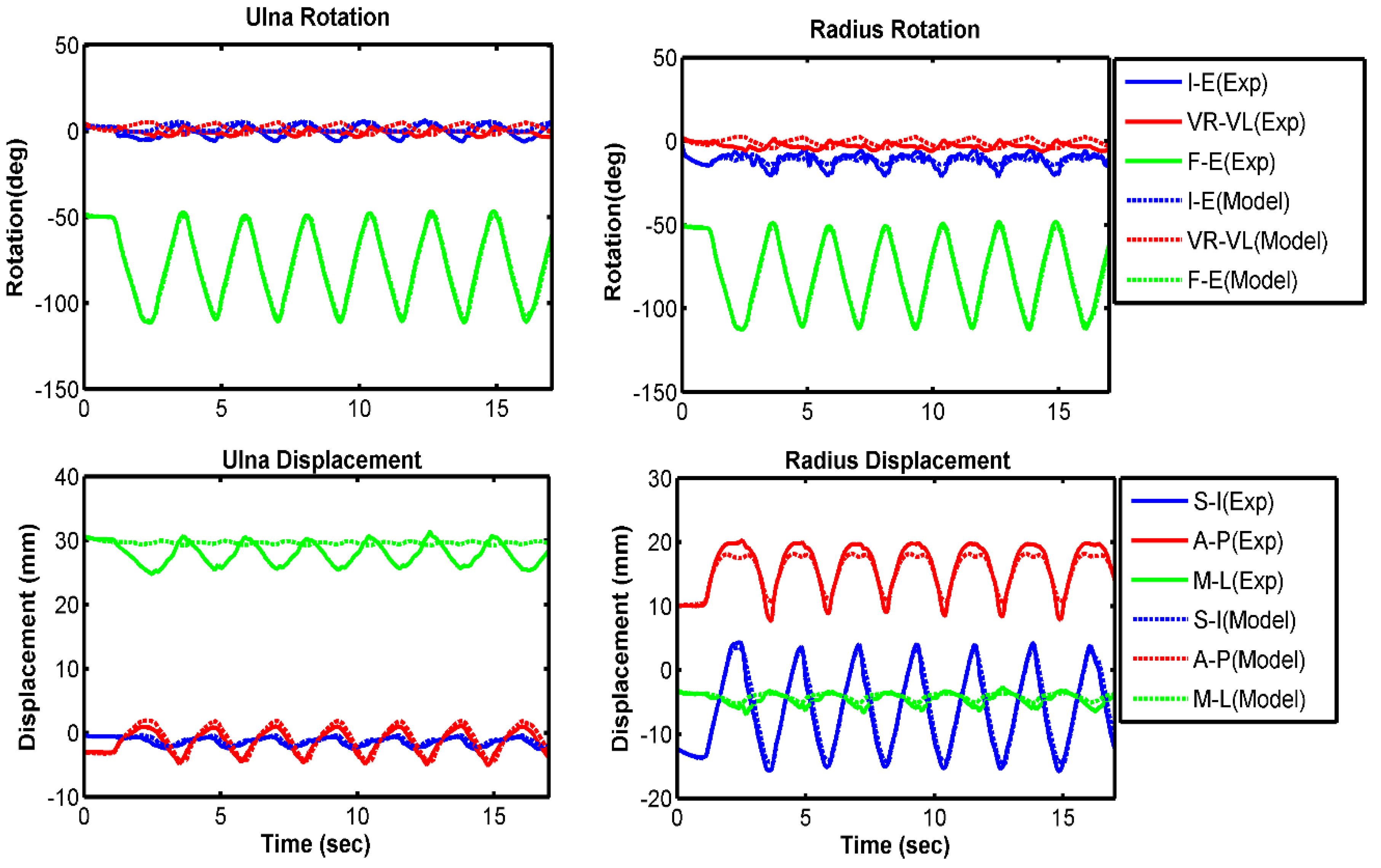
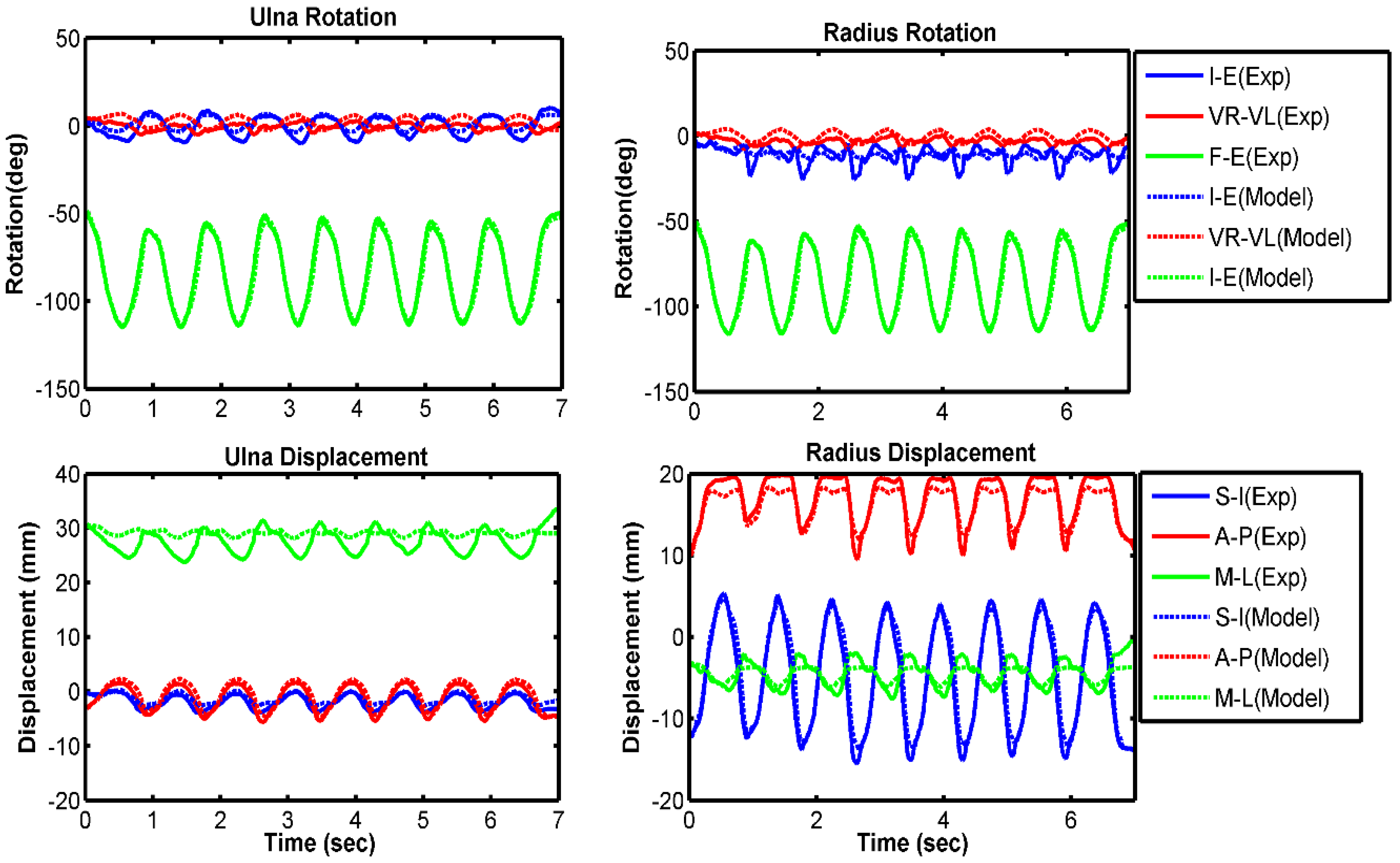
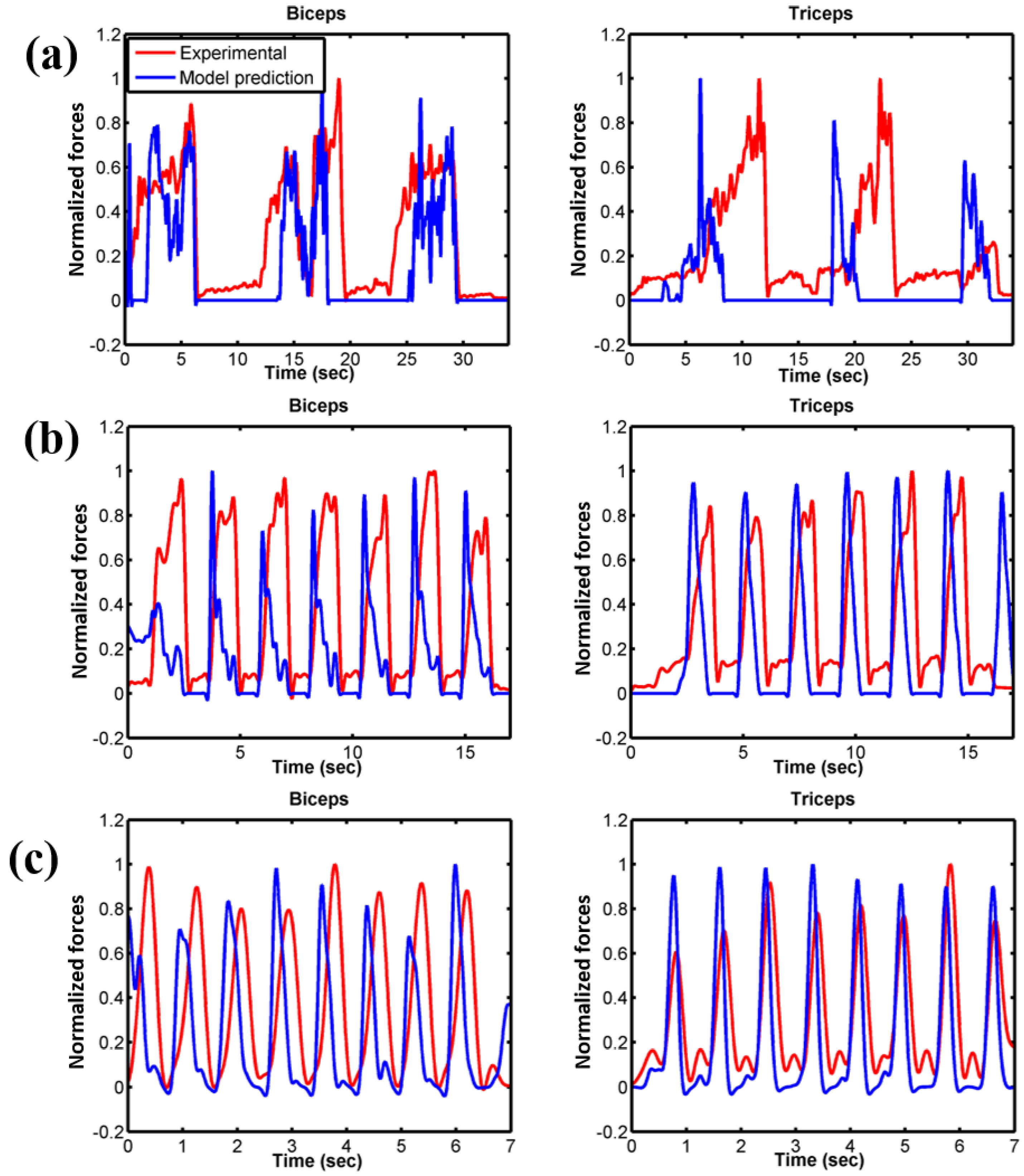
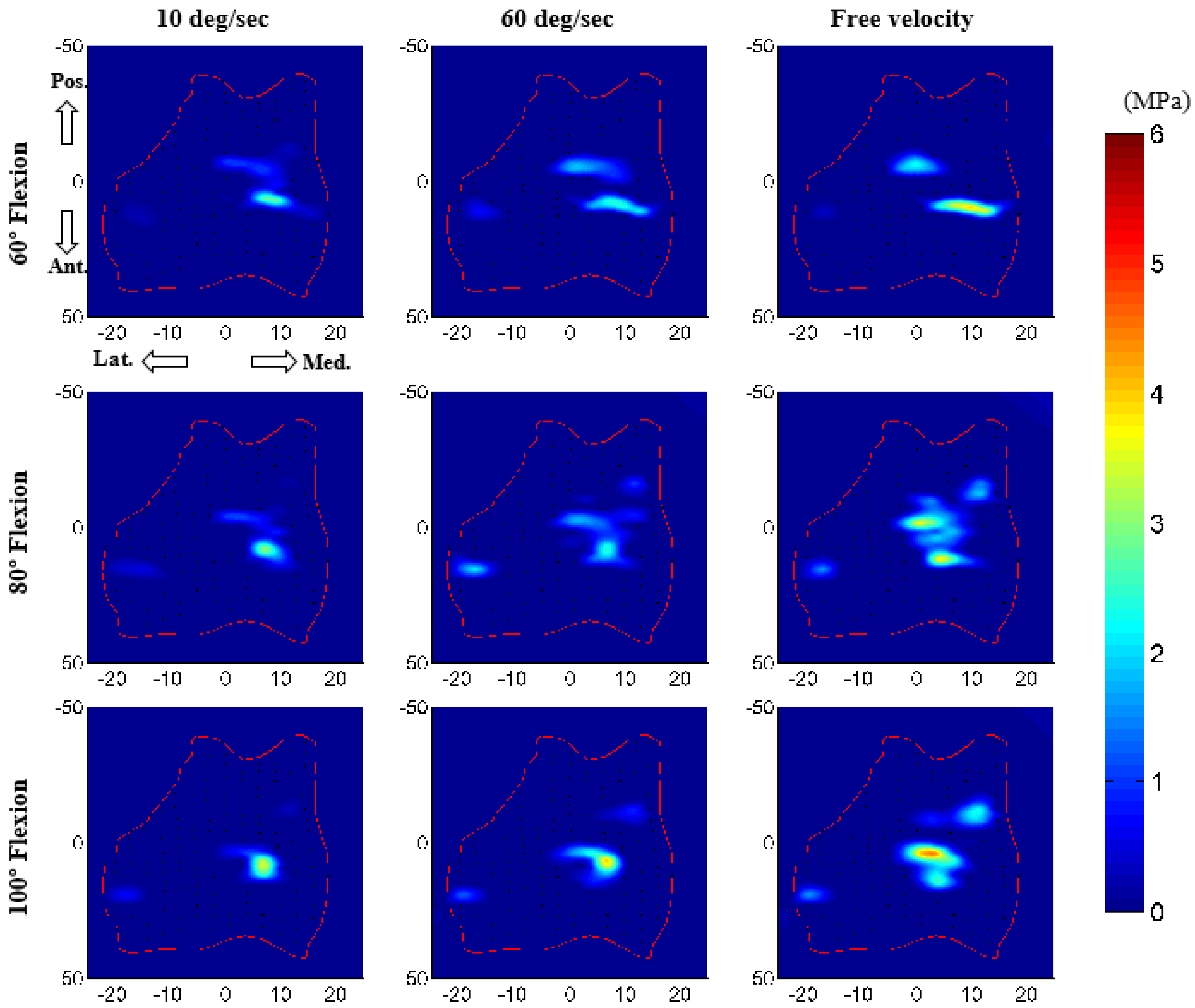
3. Results
3.1. Model Evaluation
3.2. Force Prediction
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Morrey, B.F. The Elbow and Its Disorders; W.B. Saunders: Philadelphia, PA, USA, 2000. [Google Scholar]
- Garner, B.A.; Pandy, M.G. Musculoskeletal model of the upper limb based on the visible human male dataset. Comput. Methods Biomech. Biomed. Eng. 2001, 4, 93–126. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.V.; Hutchins, E.L.; Barr, R.E.; Abraham, L.D. Development and evaluation of a musculoskeletal model of the elbow joint complex. J. Biomech. Eng. 1996, 118, 32–40. [Google Scholar] [CrossRef] [PubMed]
- Holzbaur, K.R.; Murray, W.M.; Delp, S.L. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Ann. Biomed. Eng. 2005, 33, 829–840. [Google Scholar] [CrossRef] [PubMed]
- Willing, R.T.; Nishiwaki, M.; Johnson, J.A.; King, G.J.; Athwal, G.S. Evaluation of a computational model to predict elbow range of motion. Comput. Aided Surg. 2014, 19, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Benham, M.P.; Wright, D.K.; Bibb, R. Modelling soft tissue for kinematic analysis of multi-segment human body models. Biomed. Sci. Instrum. 2001, 37, 111–116. [Google Scholar] [PubMed]
- Tanaka, S.; An, K.-N.; Morrey, B.F. Kinematics and laxity of ulnohumeral joint under valgus-varus stress. J. Musculoskelet. Res. 1998, 2, 45–54. [Google Scholar] [CrossRef]
- Fisk, J.P.; Wayne, J.S. Development and validation of a computational musculoskeletal model of the elbow and forearm. Ann. Biomed. Eng. 2009, 37, 803–812. [Google Scholar] [CrossRef] [PubMed]
- Asraf Ali, M.; Sundaraj, K.; Badlishah Ahmad, R.; Ahamed, N.U.; Islam, A. Recent observations in surface electromyography recording of triceps brachii muscle in patients and athletes. Appl. Bionics Biomech. 2014, 11, 105–118. [Google Scholar] [CrossRef][Green Version]
- Van Woensel, W.; Arwert, H. Effects of external load and abduction angle on emg level of shoulder muscles during isometric action. Electromyogr. Clin. Neurophysiol. 1993, 33, 185–191. [Google Scholar] [PubMed]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. Meshlab: An open-source mesh processing tool. In Proceedings of the Sixth Eurographics Italian Chapter Conference, Salerno, Italy, 2–4 July 2008; pp. 129–136. [Google Scholar]
- Donahue, T.L.; Hull, M.L.; Rashid, M.M.; Jacobs, C.R. A finite element model of the human knee joint for the study of tibio-femoral contact. J. Biomech. Eng. 2002, 124, 273–280. [Google Scholar] [PubMed]
- Zielinska, B.; Donahue, T.L. 3D finite element model of meniscectomy: Changes in joint contact behavior. J. Biomech. Eng. 2006, 128, 115–123. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.; Cil, A.; Johnson, M.; Lu, Y.; Guess, T.M. Development and validation of a computational multibody model of the elbow joint. Adv. Biomech. Appl. 2014, 1, 169–185. [Google Scholar] [CrossRef]
- Rahman, M.; Cil, A.; Bogener, J.W.; Stylianou, A.P. Lateral collateral ligament deficiency of the elbow joint: A modeling approach. J. Orthop. Res. 2016, 34, 1645–1655. [Google Scholar] [CrossRef] [PubMed]
- Miyake, J.; Moritomo, H.; Masatomi, T.; Kataoka, T.; Murase, T.; Yoshikawa, H.; Sugamoto, K. In vivo and 3-dimensional functional anatomy of the anterior bundle of the medial collateral ligament of the elbow. J. Shoulder Elb. Surg. 2012, 21, 1006–1012. [Google Scholar] [CrossRef] [PubMed]
- Morrey, B.F.; An, K.N. Functional anatomy of the ligaments of the elbow. Clin. Orthop. Relat. Res. 1985, 84–90. [Google Scholar] [CrossRef]
- Blankevoort, L.; Huiskes, R. Ligament-bone interaction in a three-dimensional model of the knee. J. Biomech. Eng. 1991, 113, 263–269. [Google Scholar] [CrossRef] [PubMed]
- Wismans, J.; Veldpaus, F.; Janssen, J.; Huson, A.; Struben, P. A three-dimensional mathematical model of the knee-joint. J. Biomech. 1980, 13, 677–685. [Google Scholar] [CrossRef]
- Li, G.; Gil, J.; Kanamori, A.; Woo, S.L. A validated three-dimensional computational model of a human knee joint. J. Biomech. Eng. 1999, 121, 657–662. [Google Scholar] [CrossRef] [PubMed]
- Blankevoort, L.; Kuiper, J.H.; Huiskes, R.; Grootenboer, H.J. Articular contact in a three-dimensional model of the knee. J. Biomech. 1991, 24, 1019–1031. [Google Scholar] [CrossRef]
- Regan, W.D.; Korinek, S.L.; Morrey, B.F.; An, K.N. Biomechanical study of ligaments around the elbow joint. Clin. Orthop. Relat. Res. 1991, 170–179. [Google Scholar] [CrossRef]
- Bloemker, K.H.; Guess, T.M.; Maletsky, L.; Dodd, K. Computational knee ligament modeling using experimentally determined zero-load lengths. Open Biomed. Eng. J. 2012, 6, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.; Cil, A.; Stylianou, A.P. Prediction of elbow joint contact mechanics in the multibody framework. Med. Eng. Phys. 2016, 38, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Guess, T.M.; Stylianou, A.P.; Kia, M. Concurrent prediction of muscle and tibiofemoral contact forces during treadmill gait. J. Biomech. Eng. 2014, 136, 021032. [Google Scholar] [CrossRef] [PubMed]
- Kia, M.; Stylianou, A.P.; Guess, T.M. Evaluation of a musculoskeletal model with prosthetic knee through six experimental gait trials. Med. Eng. Phys. 2014, 36, 335–344. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Renani, M.S.; Rahman, M.; Cil, A.; Stylianou, A.P. Calibrating multibody ulno-humeral joint cartilage using a validated finite element model. Multibody Syst. Dyn. 2018. [Google Scholar] [CrossRef]
- Stylianou, A.P.; Guess, T.M.; Cook, J.L. Development and validation of a multi-body model of the canine stifle joint. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 370–377. [Google Scholar] [CrossRef] [PubMed]
- Stylianou, A.P.; Guess, T.M.; Kia, M. Multibody muscle driven model of an instrumented prosthetic knee during squat and toe rise motions. J. Biomech. Eng. 2013, 135, 041008. [Google Scholar] [CrossRef] [PubMed]
- Renani, M.S.; Rahman, M.; Cil, A.; Stylianou, A.P. Ulna-humerus contact mechanics: Finite element analysis and experimental measurements using a tactile pressure sensor. Med. Eng. Phys. 2017, 50, 22–28. [Google Scholar] [CrossRef] [PubMed]
- Carmichael, M.G.; Liu, D. Upper limb strength estimation of physically impaired persons using a musculoskeletal model: A sensitivity analysis. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2015, 2015, 2438–2441. [Google Scholar] [PubMed]
- Gonzalez, R.V.; Abraham, L.D.; Barr, R.E.; Buchanan, T.S. Muscle activity in rapid multi-degree-of-freedom elbow movements: Solutions from a musculoskeletal model. Biol. Cybern. 1999, 80, 357–367. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.V.; Andritsos, M.J.; Barr, R.E.; Abraham, L.D. Comparison of experimental and predicted muscle activation patterns in ballistic elbow joint movements. Biomed. Sci. Instrum. 1993, 29, 9–16. [Google Scholar] [PubMed]
- O’Driscoll, S.W.; An, K.N.; Korinek, S.; Morrey, B.F. Kinematics of semi-constrained total elbow arthroplasty. J. Bone Jt. Surg. Br. 1992, 74, 297–299. [Google Scholar] [CrossRef]
- Morrey, B.F.; An, K.N. Articular and ligamentous contributions to the stability of the elbow joint. Am. J. Sports Med. 1983, 11, 315–319. [Google Scholar] [CrossRef] [PubMed]
- Pigeon, P.; Yahia, L.; Feldman, A.G. Moment arms and lengths of human upper limb muscles as functions of joint angles. J. Biomech. 1996, 29, 1365–1370. [Google Scholar] [CrossRef]
- Eckstein, F.; Merz, B.; Muller-Gerbl, M.; Holzknecht, N.; Pleier, M.; Putz, R. Morphomechanics of the humero-ulnar joint: II. Concave incongruity determines the distribution of load and subchondral mineralization. Anat. Rec. 1995, 243, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Brand, R.A. Joint contact stress: A reasonable surrogate for biological processes? Iowa Orthop. J. 2005, 25, 82–94. [Google Scholar] [PubMed]
| Parameters | Values |
|---|---|
| Contact type | Impact (deformable) |
| Contact element size | 3 mm × 3 mm |
| Friction | No |
| Stiffness (kc) | 40 N/mm |
| Damping coefficient (Bc(δ)) | 5 Ns/mm |
| Exponent (n) | 3.05 |
| Interpenetration of the geometries (δ) | 0.1 mm |
| Kinematics Description | 10 deg/s | 60 deg/s | Free Velocity | |||
|---|---|---|---|---|---|---|
| RMS Error | Correlation Coefficient | RMS Error | Correlation Coefficient | RMS Error | Correlation Coefficient | |
| Ulna I–E rotation | 7.4 | 0.48 | 2.9 | 0.86 | 4.0 | 0.92 |
| Ulna VR–VL rotation | 2.8 | −0.63 | 2.9 | −0.13 | 2.7 | 0.57 |
| Ulna F–E rotation | 1.3 | 0.99 | 1.2 | 0.99 | 2.7 | 0.99 |
| Radius I–E rotation | 5.5 | 0.44 | 2.3 | 0.55 | 3.6 | 0.08 |
| Radius VR–VL rotation | 2.6 | −0.60 | 2.8 | −0.15 | 2.6 | 0.61 |
| Radius F–E rotation | 1.1 | 0.99 | 1.1 | 0.99 | 2.7 | 0.99 |
| Ulna S–I displacement | 0.4 | 0.07 | 0.2 | 0.90 | 0.4 | 0.97 |
| Ulna A–P displacement | 0.4 | 0.98 | 0.4 | 0.99 | 0.6 | 0.98 |
| Ulna M–L displacement | 3.4 | −0.45 | 2.0 | −0.62 | 2.3 | −0.14 |
| Radius S–I displacement | 1.3 | 0.99 | 0.6 | 0.99 | 1.3 | 0.99 |
| Radius A–P displacement | 1.0 | 0.98 | 0.8 | 0.99 | 0.8 | 0.97 |
| Radius M–L displacement | 1.5 | 0.86 | 0.6 | 0.91 | 0.9 | 0.91 |
| Ligament | Bundles | Peak Ligament Load (N) | ||
|---|---|---|---|---|
| 10 deg/s | 60 deg/s | Free Velocity | ||
| MCL anterior part | Anterior | 23 | 37 | 101 |
| Central | 45 | 61 | 123 | |
| Posterior | 61 | 76 | 112 | |
| MCL posterior part | Anterior | 35 | 40 | 55 |
| Central | 30 | 44 | 87 | |
| Posterior | 24 | 47 | 125 | |
| LUCL | Anterior | 43 | 58 | 80 |
| Central | 23 | 33 | 44 | |
| Posterior | 26 | 25 | 50 | |
| RCL | Anterior | 21 | 44 | 131 |
| Central | 18 | 26 | 55 | |
| Posterior | 12 | 31 | 88 | |
| Annular ligament | Proximal | 46 | 51 | 52 |
| Distal | 36 | 41 | 41 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.; Sharifi Renani, M.; Cil, A.; Stylianou, A.P. Musculoskeletal Model Development of the Elbow Joint with an Experimental Evaluation. Bioengineering 2018, 5, 31. https://doi.org/10.3390/bioengineering5020031
Rahman M, Sharifi Renani M, Cil A, Stylianou AP. Musculoskeletal Model Development of the Elbow Joint with an Experimental Evaluation. Bioengineering. 2018; 5(2):31. https://doi.org/10.3390/bioengineering5020031
Chicago/Turabian StyleRahman, Munsur, Mohsen Sharifi Renani, Akin Cil, and Antonis P. Stylianou. 2018. "Musculoskeletal Model Development of the Elbow Joint with an Experimental Evaluation" Bioengineering 5, no. 2: 31. https://doi.org/10.3390/bioengineering5020031
APA StyleRahman, M., Sharifi Renani, M., Cil, A., & Stylianou, A. P. (2018). Musculoskeletal Model Development of the Elbow Joint with an Experimental Evaluation. Bioengineering, 5(2), 31. https://doi.org/10.3390/bioengineering5020031