Nonstandard Finite Difference Method Applied to a Linear Pharmacokinetics Model
Abstract
:1. Introduction
2. Methods
2.1. Finite Difference Method
2.2. Nonstandard Finite Difference Method
NSFD Modeling Fundamental Principles
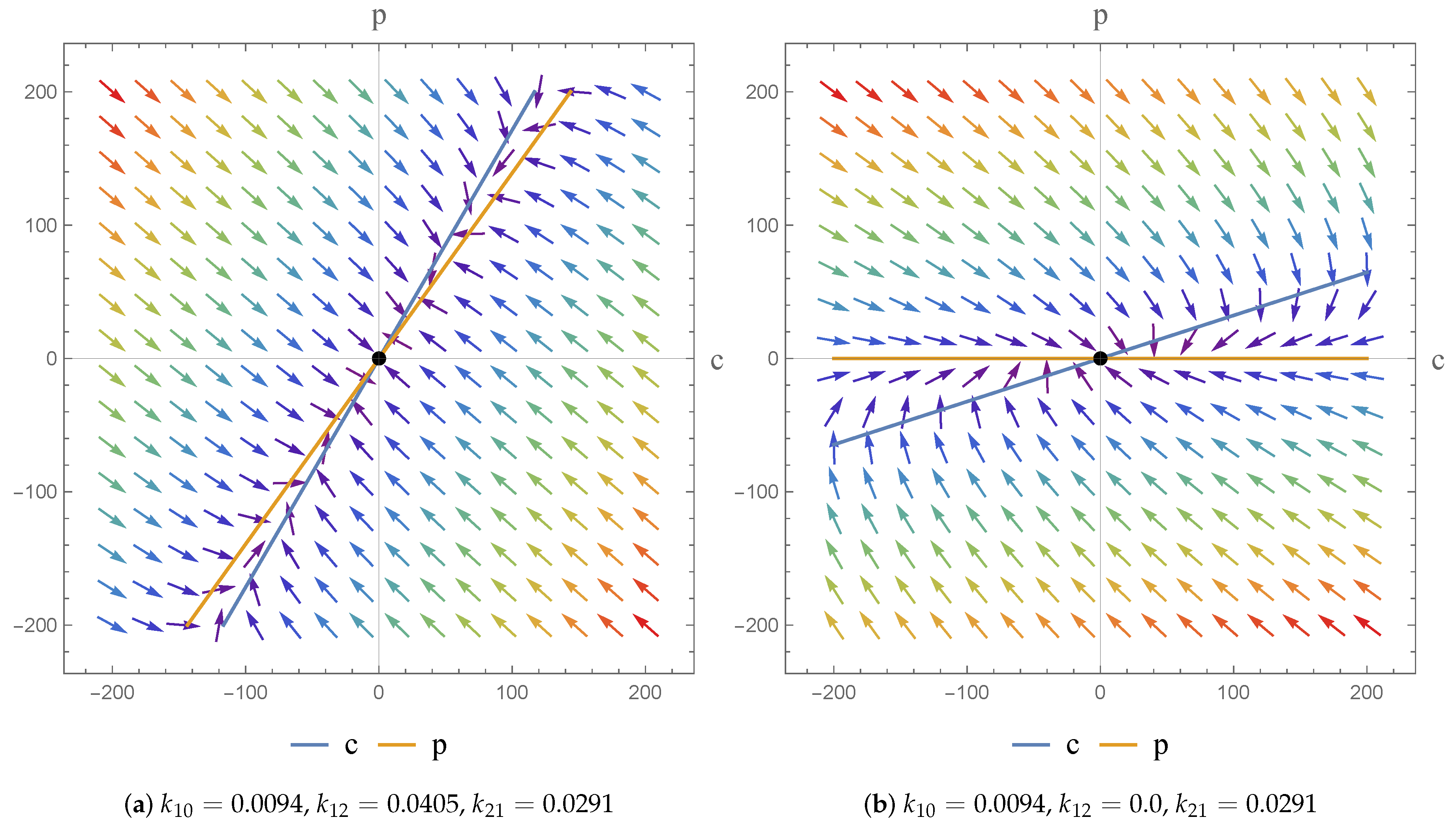
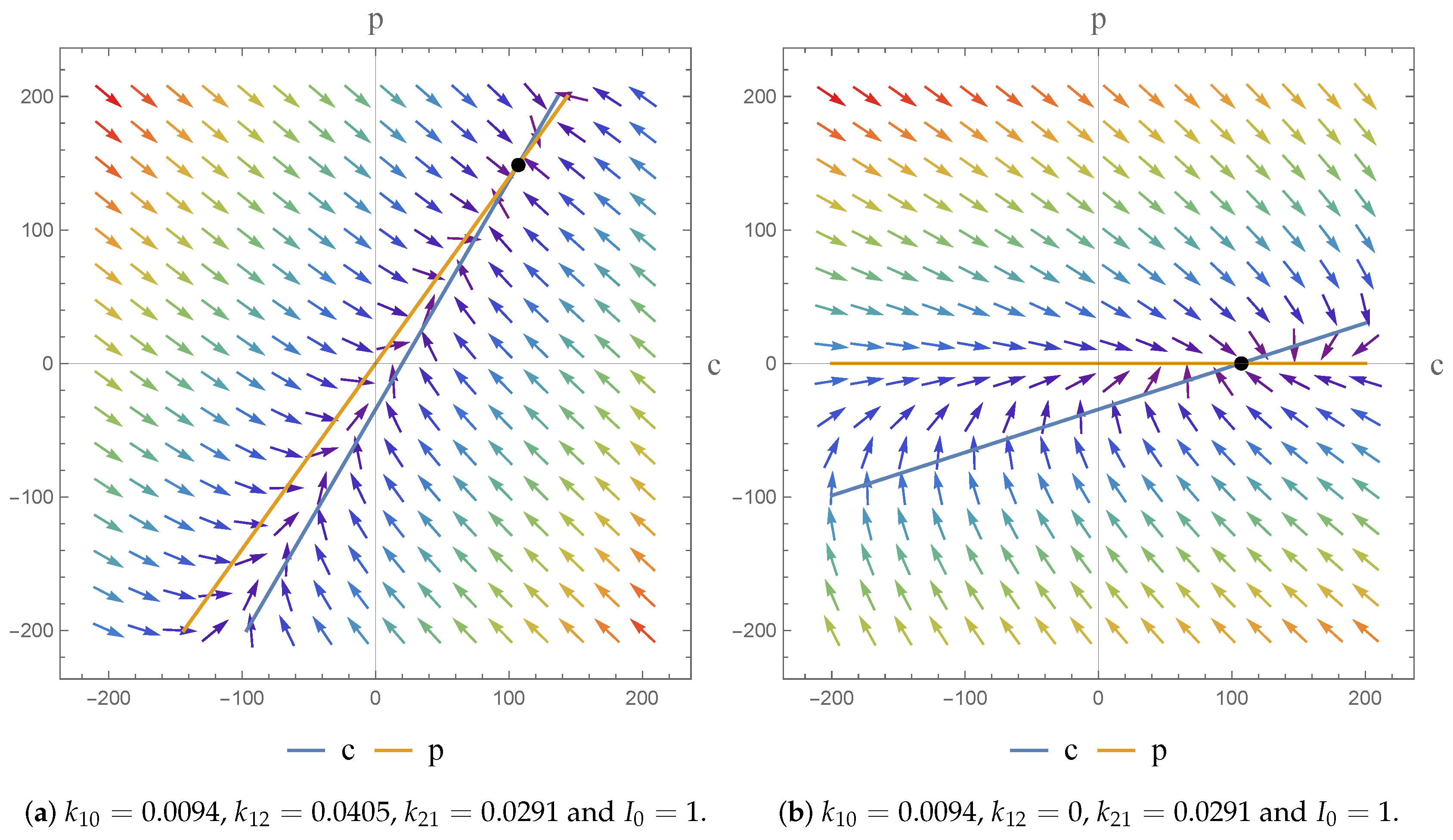
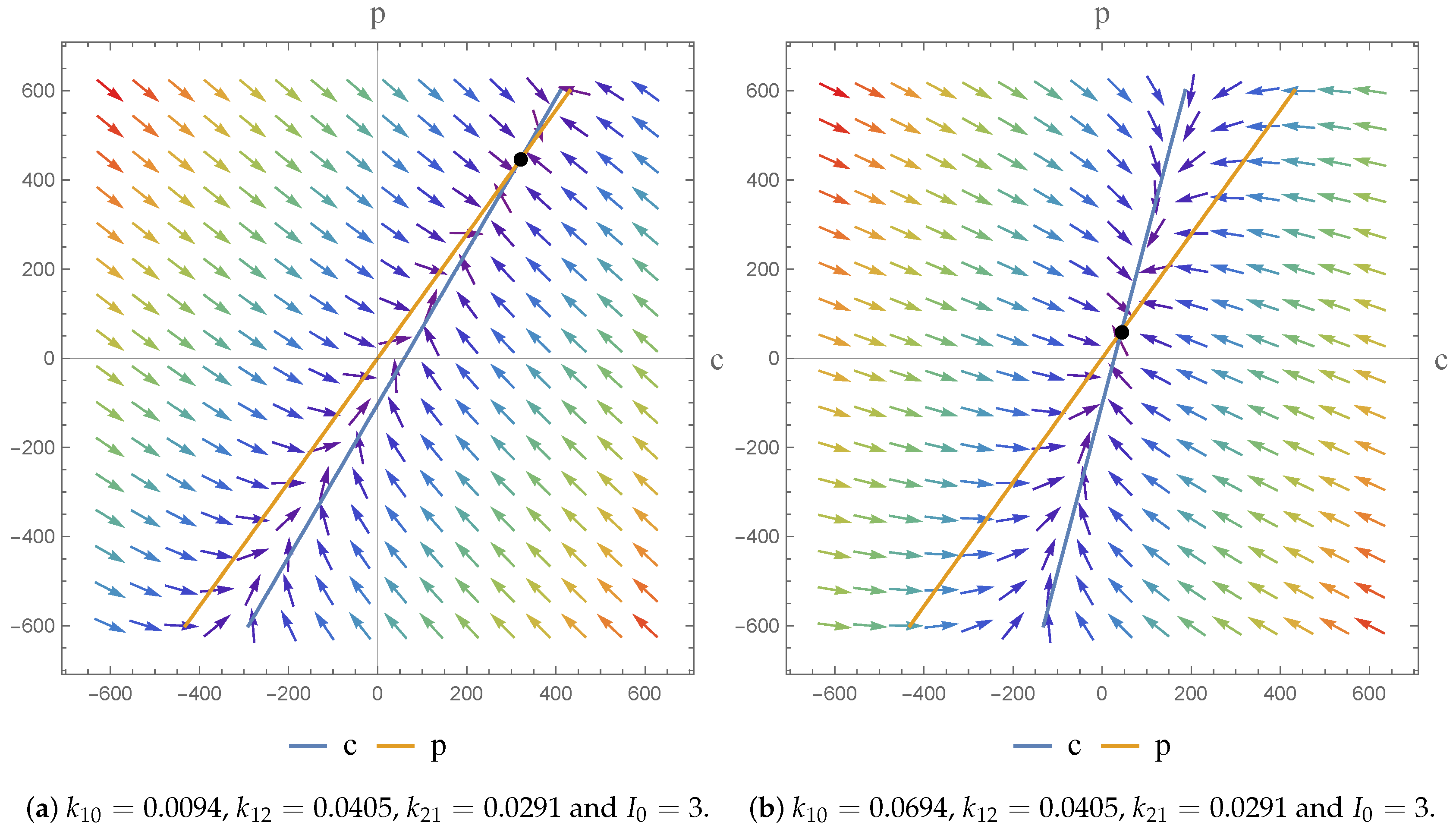
2.3. Phase Plane Analysis
3. Results
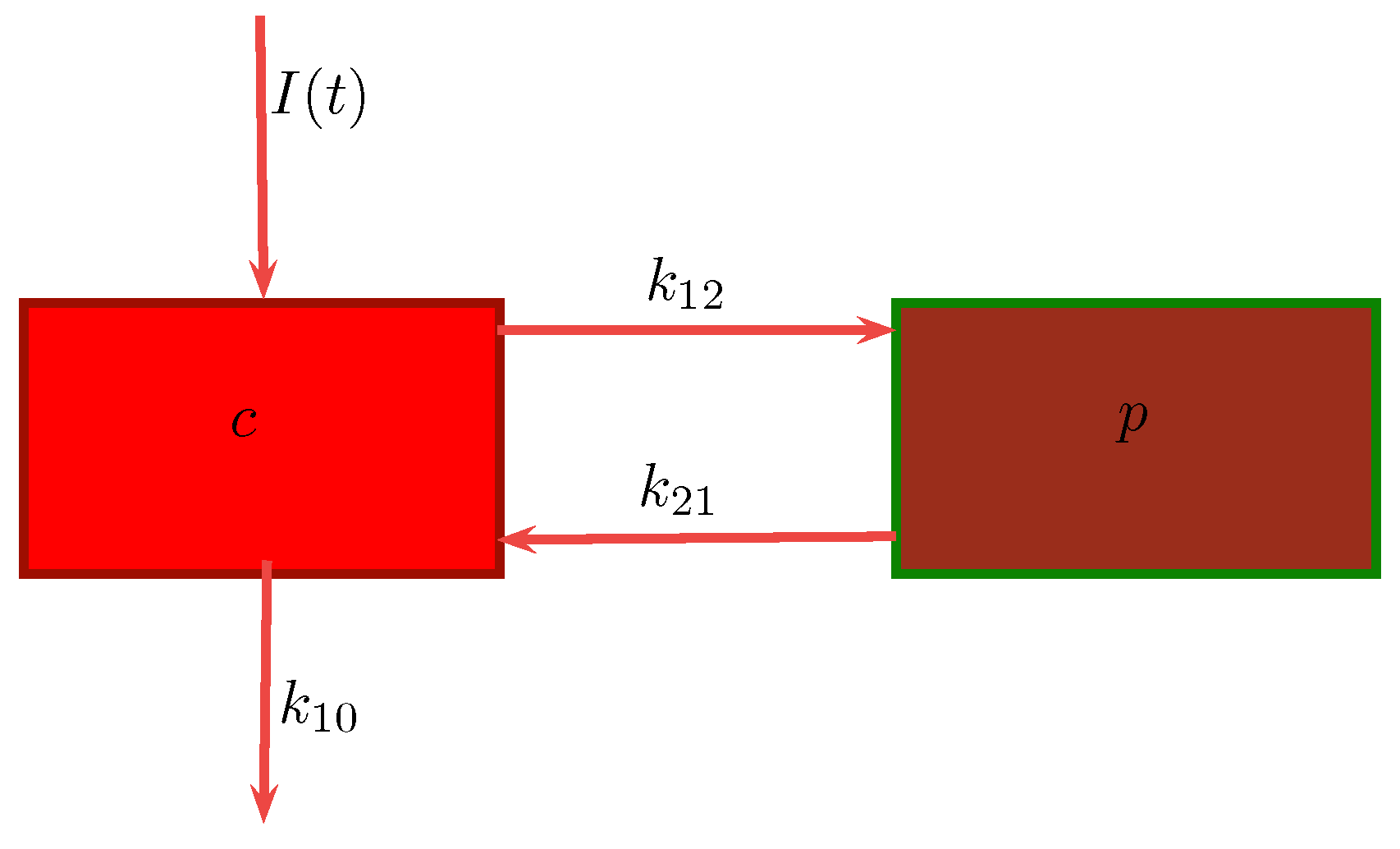
3.1. Compartmental Models for Pharmacokinetics
- c : Concentration of drug in central compartment.
- p : Concentration of drug in peripheral compartment.
- : Transfer rate of drug from central to peripheral compartment.
- : Degradation rate of drug in peripheral compartment.
- : Clearance rate of drug leaving the central compartment.
Case 1:
Case 2:
3.2. Analytical Solution
3.2.1. Case 1
3.2.2. Case 2
3.2.3. Remarks
3.3. Nonstandard Finite Difference Scheme
3.3.1. Case 1
3.3.2. Case 2:
4. Discussion
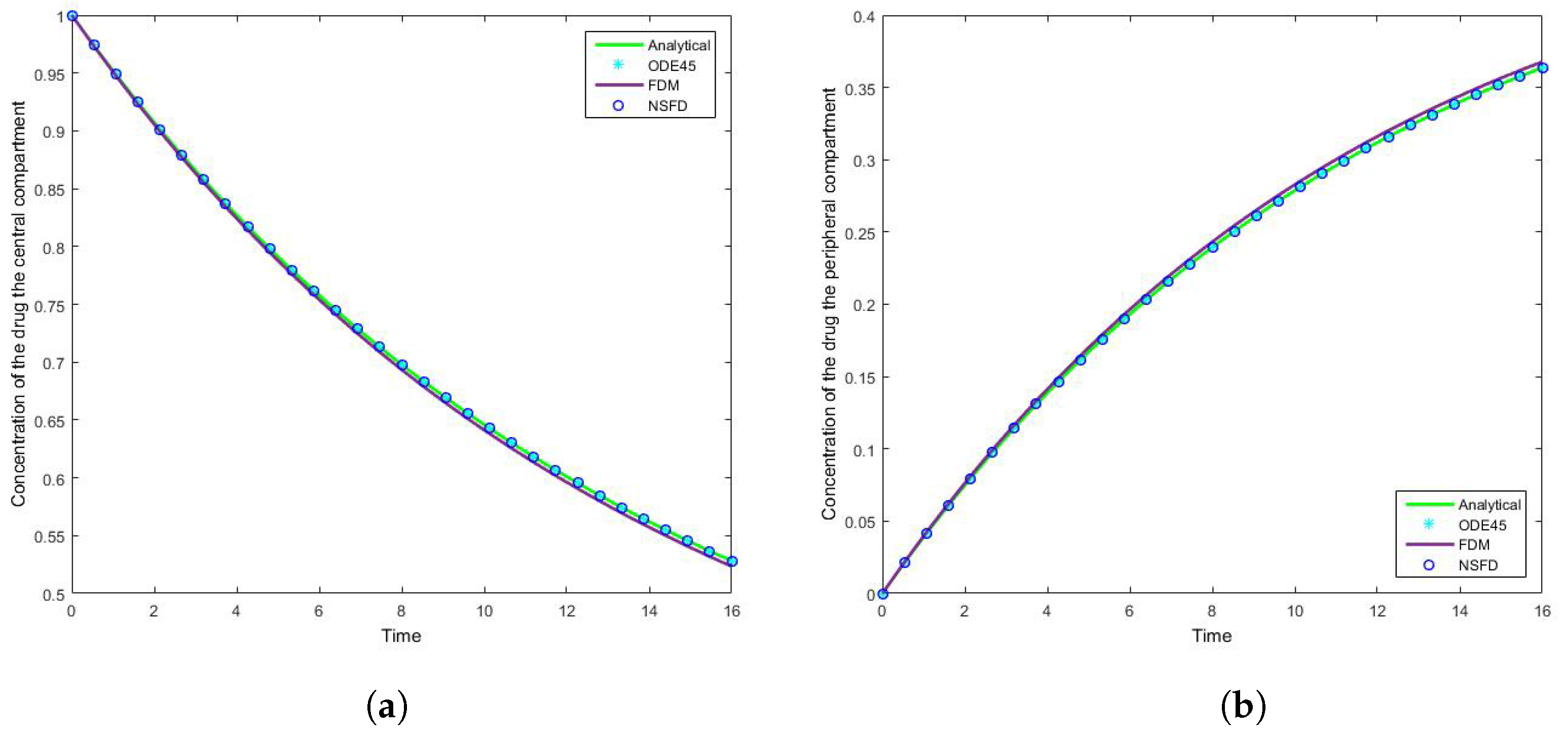
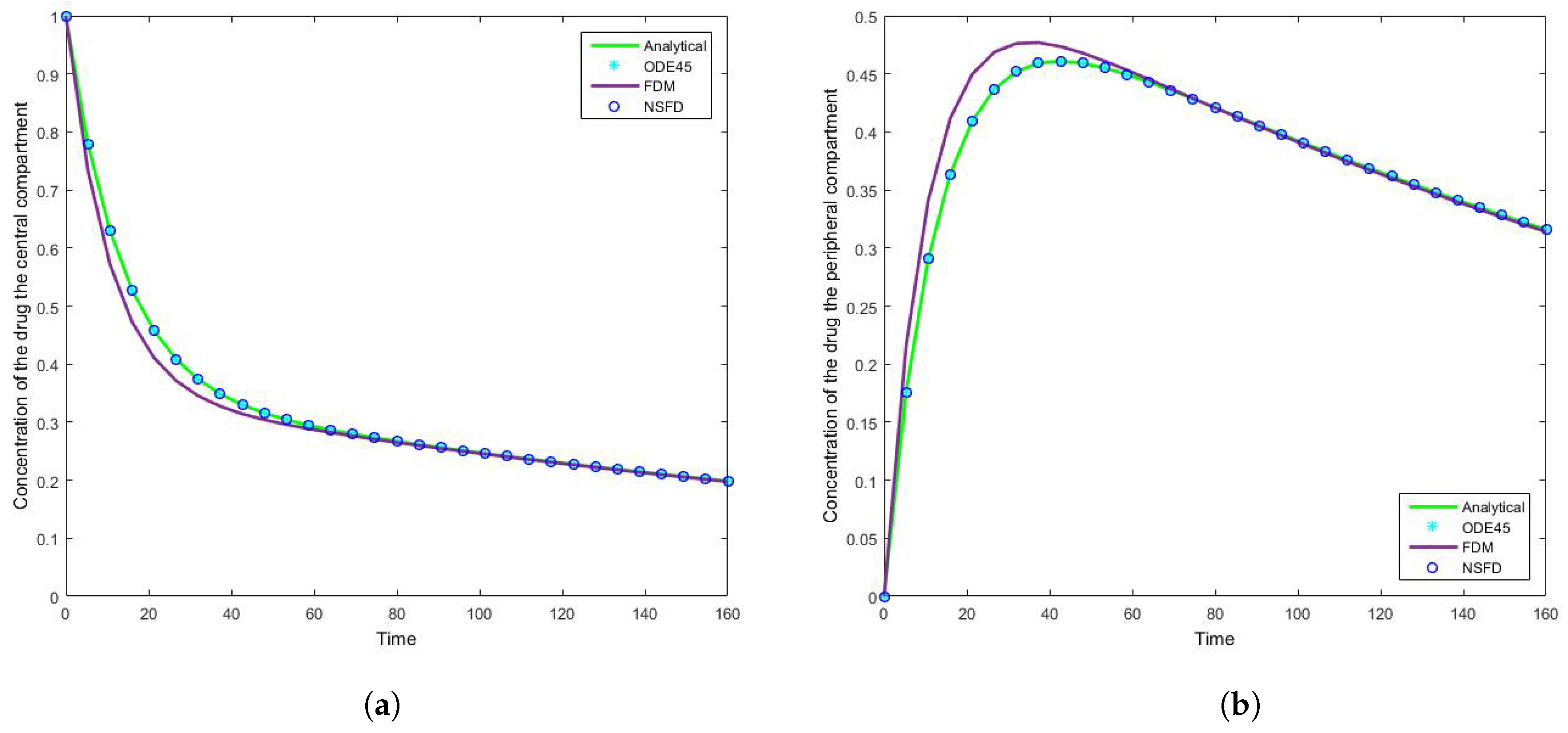
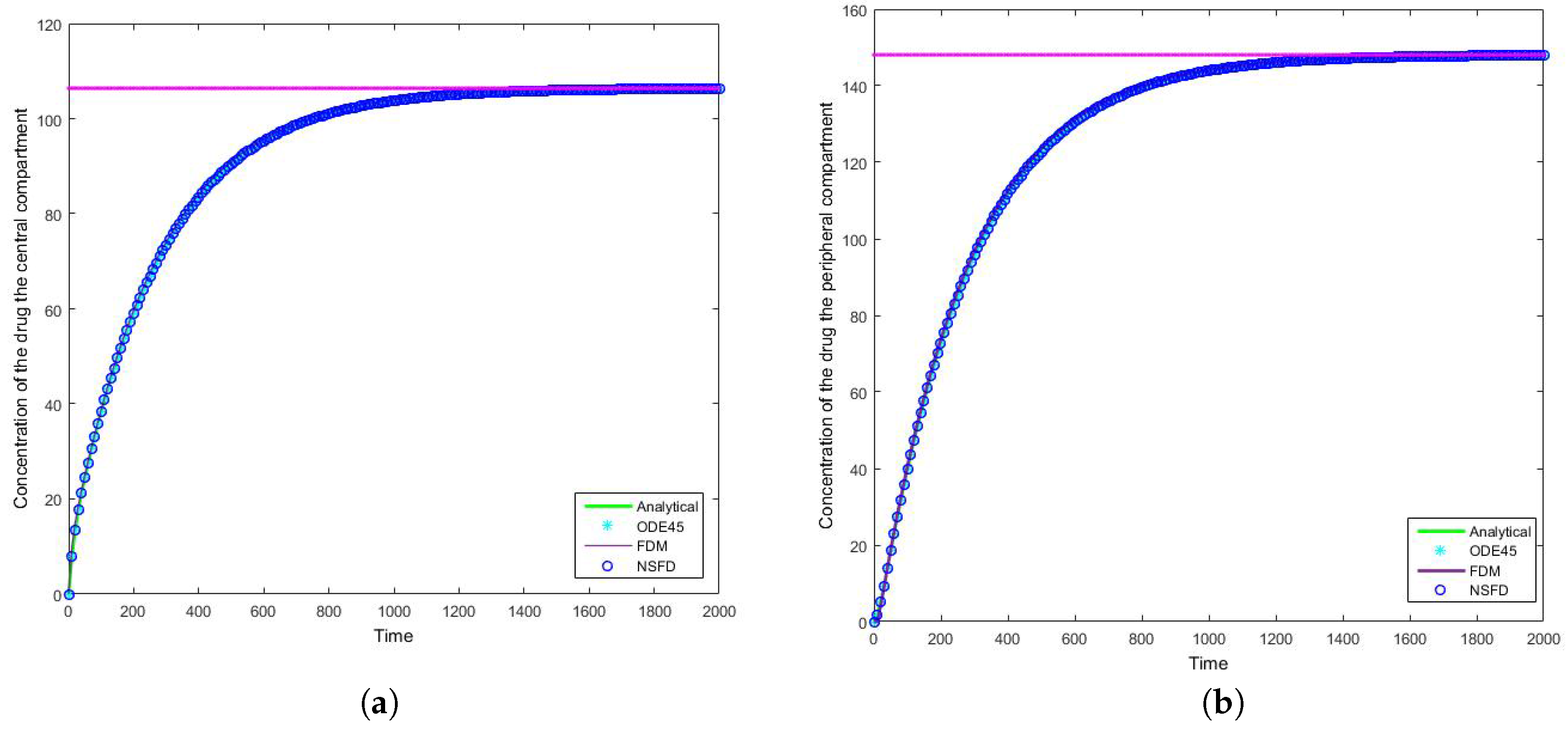
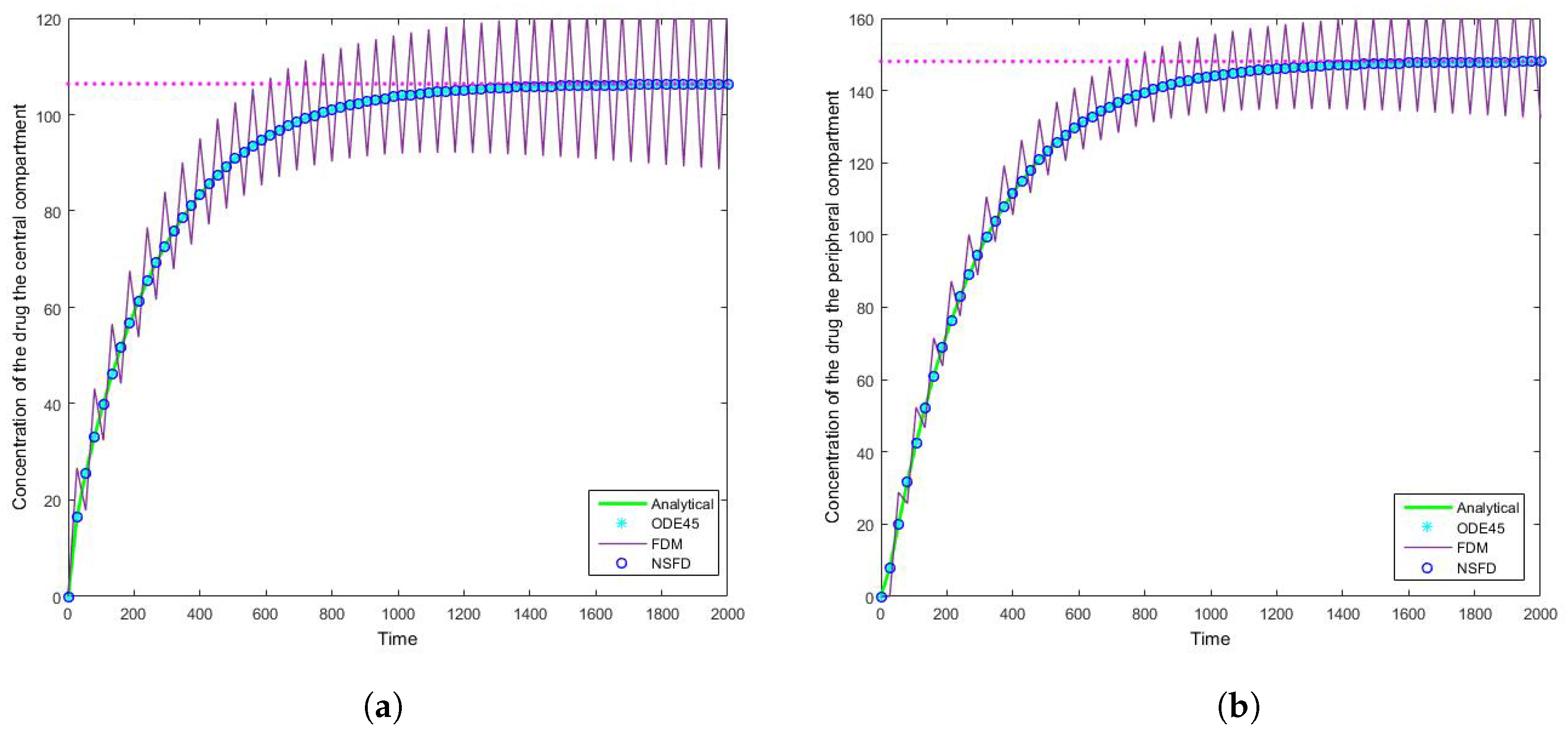
4.1. Case 1: Simulation Results
4.2. Case 2: Simulation Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PK | pharmacokinetic |
| PD | pharmacodynamic |
| I.V. | intravenous |
| NSFD | nonstandard finite difference |
| SFD | standard finite difference |
References
- Buchanan, A. Physiologic effects of the inhalation of ether. Lond. Med. Gaz. 1847, 39, 715–717. [Google Scholar]
- Michealis, L.; Menten, M.L. Die Kinetik der Invertinwirking. Biochem. Z. 1913, 49, 333–369. [Google Scholar]
- Widmark, E.; Tandberg, J. Uber die bedingungen f’tir die Akkumulation Indifferenter Narkoliken Theoretische Bereckerunger. Biochem. Z. 1924, 147, 358–369. [Google Scholar]
- Teorell, T. Kinetics of distribution of substances administered to the body. I. The extravascular modes of administration. Arch. Int. Pharmacodyn. Ther. 1937, 57, 205–225. [Google Scholar]
- Holford, N.H.G.; Sheiner, L.B. Kinetics of pharmacologic response. Pharmacol. Ther. 1982, 16, 143–166. [Google Scholar] [CrossRef]
- Huang, S.-M.; Abernethy, D.R.; Wang, Y.; Zhao, P.; Zineh, I. The utility of modelling and simulation in drug development and regulatory review. J. Pharm. Sci. 2013, 102, 2912–2923. [Google Scholar] [CrossRef] [PubMed]
- Bonate, P.L. Pharmacokinetic-Pharmacodynamic Modelling and Simulation; Springer: New York, NY, USA, 2011; p. 2. [Google Scholar]
- Shargel, L.; Yu, A.; Wu-Pong, S. Introduction to Biopharmaceutics and Pharmacokinetics. In Applied Biopharmaceutics & Pharmacokinetics, 6th ed.; McGraw-Hill: New York, NY, USA, 2012; Chapter 1; pp. 1–17. [Google Scholar]
- Shargel, L.; Yu, A.; Wu-Pong, S. Multicompartment Models: Intravenous Bolus Administration. In Applied Biopharmaceutics & Pharmacokinetics, 6th ed.; McGraw-Hill: New York, NY, USA, 2012; Chapter 4; pp. 58–79. [Google Scholar]
- Shargel, L.; Yu, A.; Wu-Pong, S. Physiologic Pharmacokinetic Models, Mean Residence Time, and Statistical Moment Theory. In Applied Biopharmaceutics & Pharmacokinetics, 6th ed.; McGraw-Hill: New York, NY, USA, 2012; Chapter 22; pp. 658–690. [Google Scholar]
- Beňová, M.; Gombárska, D.; Dobrcký, B. Using Euler’s and Taylor’s expansion method for solution of non-linear differential equation system in pharmacokinetics. Electr. Rev. 2013, 89, 259–261. [Google Scholar]
- Mickens, R.E. Dynamic consistency: A fundamental principle for constructing nonstandard finite difference schemes for differential equations. J. Differ. Equ. Appl. 2005, 11, 645–653. [Google Scholar] [CrossRef]
- Mickens, R.E. Application of Nonstandard Finite Difference Schemes, 1st ed.; World Scientific: Singapore, 2000. [Google Scholar]
- Mickens, R.E. Nonstandard finite difference schemes for differential equations. J. Differ. Equ. Appl. 2002, 8, 823–847. [Google Scholar] [CrossRef]
- Mickens, R.E. A nonstandard finite difference scheme for the diffusionless Burgers equation with logistic reaction. Math. Comput. Simul. 2003, 62, 117–124. [Google Scholar] [CrossRef]
- Mickens, R.E. A numerical integration technique for conservative oscillators combining nonstandard finite-difference methods with a Hamilton’s principle. J. Sound Vib. 2005, 285, 477–482. [Google Scholar] [CrossRef]
- Liao, C.; Ding, X. Nonstandard finite difference variational integrators for nonlinear Schrödinger equation with variable coefficients. Adv. Differ. Equ. 2013, 2013, 1–22. [Google Scholar] [CrossRef]
- Arenas, A.J.; González-Parra, G.; Chen-Charpentier, B.M. A nonstandard numerical scheme of predictor-corrector type for epidemic models. Comput. Math. Appl. 2010, 59, 3740–3749. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenas, A.J.; Chen-Charpentier, B.M. Combination of nonstandard schemes and Richardson’s extrapolation to improve the numerical solution of population models. Math. Comput. Model. 2010, 52, 1030–1036. [Google Scholar] [CrossRef]
- Jordan, P.M. A nonstandard finite difference scheme for nonlinear heat transfer in a thin finite rod. J. Differ. Equ. Appl. 2003, 9, 1015–1021. [Google Scholar] [CrossRef]
- Malek, A. Applications of nonstandard finite difference methods to nonlinear heat transfer problems. In Heat Transfer—Mathematical Modelling, Numerical Methods and Information Technology; InTech: Rijeka, Croatia, 2011. [Google Scholar] [CrossRef]
- Introduction to Non-Standard Finite-Difference Modelling. Available online: https://www.crewes.org/ForOurSponsors/ResearchReports/2006/2006-46.pdf (accessed on 1 January 2016).
- Mickens, R.E. Lie methods in mathematical modelling: Difference equation models of differential equation. Math. Comput. Model. 1988, 11, 528–530. [Google Scholar] [CrossRef]
- Mickens, R.E. Exact solutions to a finite-difference model of a nonlinear reaction-advection equation: Implications for numerical analysis. J. Differ. Equ. Appl. 2003, 9, 995–1006. [Google Scholar] [CrossRef]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Anguelov, R.; Lubuma, J.M.-S. Nonstandard finite difference method by nonlocal approximation. Math. Comput. Simul. 2003, 61, 465–475. [Google Scholar] [CrossRef]
- Gurski, K.F. A simple construction of nonstandard finite-difference schemes for small nonlinear systems applied to SIR models. Comput. Math. Appl. 2013, 66, 2165–2177. [Google Scholar] [CrossRef]
- Péchère, J.-C.; Péchère, M.-M.; Dugal, R. Clinical Pharmacokinetics of Sisomicin: Two-Compartment Model Analysis of Serum Data after I.V. and I.M. Administration. Eur. J. Clin. Pharmacol. 1976, 10, 251–256. [Google Scholar] [CrossRef]
- Widder, D.V. The Laplace Transform; Princeton University Press: Princeton, NJ, USA, 1966. [Google Scholar]
- Koch, G. Modeling of Pharmacokinetics and Pharmacodynamics with Application to Cancer and Arthritis. Ph.D. Thesis, University of Konstanz, Konstanz, Germany, 2012. [Google Scholar]
- Foster, D.M. Noncompartmental versus Compartmental Approaches to Pharmacokinetic Analysis. In Principles of Clinical Pharmacology, 2nd ed.; Atkinson, A.J., Abernethy, D.R., Daniels, C.E., Dedrick, R.L., Markey, S.P., Eds.; Academic Press: New York, NY, USA, 2014; pp. 89–105. [Google Scholar]
- Wang, Z.; Kim, S.; Quinney, S.K.; Zhou, J.; Li, L. Non-compartment model to compartment model pharmacokinetics transformation meta-analysis–a multivariate nonlinear mixed model. BMC Syst. Biol. 2010, 4, S8. [Google Scholar] [CrossRef] [PubMed]
- Jang, G.R.; Harris, R.Z.; Lau, D.T. Pharmacokinetics and its role in small molecule drug discovery research. Med. Res. Rev. 2001, 21, 382–396. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Unit | Value: Subject 1 | Value: Subject 2 | Value: Subject 3 | Value: Subject 4 |
|---|---|---|---|---|---|
| 0.00940 | 0.01110 | 0.01030 | 0.01520 | ||
| 0.04050 | 0.02504 | 0.02750 | 0.04120 | ||
| 0.02910 | 0.02230 | 0.02830 | 0.02410 | ||
| D | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| Absolute Error for | ||||
|---|---|---|---|---|
| N | h | Error in SFD | Error in ODE45 | Error in NSFD |
| 2 | 10.00000 | 0.144913386 | 0.000000010 | 0.000000000 |
| 4 | 5.00000 | 0.053199386 | 0.000000010 | 0.000000000 |
| 8 | 2.50000 | 0.024396686 | 0.000000010 | 0.000000000 |
| 16 | 1.25000 | 0.011669111 | 0.000000022 | 0.000000000 |
| 32 | 0.62500 | 0.005719559 | 0.000000028 | 0.000000000 |
| 64 | 0.31250 | 0.002831162 | 0.000000028 | 0.000000000 |
| 128 | 0.15625 | 0.001408639 | 0.000000028 | 0.000000000 |
| 256 | 0.07812 | 0.000702591 | 0.000000028 | 0.000000000 |
| 512 | 0.03906 | 0.000350865 | 0.000000028 | 0.000000000 |
| 1024 | 0.01953 | 0.000175326 | 0.000000029 | 0.000000000 |
| Absolute Error for | ||||
|---|---|---|---|---|
| N | h | Error in SFD | Error in ODE45 | Error in NSFD |
| 2 | 10.00000 | 0.126270717 | 0.000000009 | 0.000000000 |
| 4 | 5.00000 | 0.046283217 | 0.000000009 | 0.000000000 |
| 8 | 2.50000 | 0.021180830 | 0.000000009 | 0.000000000 |
| 16 | 1.25000 | 0.010127446 | 0.000000019 | 0.000000000 |
| 32 | 0.62500 | 0.004961080 | 0.000000025 | 0.000000000 |
| 64 | 0.31250 | 0.002455508 | 0.000000025 | 0.000000000 |
| 128 | 0.15625 | 0.001221609 | 0.000000025 | 0.000000000 |
| 256 | 0.07812 | 0.000609284 | 0.000000025 | 0.000000000 |
| 512 | 0.03906 | 0.000304265 | 0.000000025 | 0.000000000 |
| 1024 | 0.01953 | 0.000152038 | 0.000000026 | 0.000000000 |
| Absolute Error for | ||||
|---|---|---|---|---|
| N | h | Error in SFD | Error in ODE45 | Error in NSFD |
| 2 | 10.00000 | 1.98326261 | 0.00000008 | 0.00000000 |
| 4 | 5.00000 | 0.73839463 | 0.00000010 | 0.00000000 |
| 8 | 2.50000 | 0.34211236 | 0.00000012 | 0.00000000 |
| 16 | 1.25000 | 0.16473051 | 0.00000018 | 0.00000000 |
| 32 | 0.62500 | 0.08083009 | 0.00000021 | 0.00000000 |
| 64 | 0.31250 | 0.04005593 | 0.00000019 | 0.00000000 |
| 128 | 0.15625 | 0.01993844 | 0.00000022 | 0.00000000 |
| 256 | 0.07812 | 0.00994725 | 0.00000023 | 0.00000000 |
| 512 | 0.03906 | 0.00496814 | 0.00000022 | 0.00000000 |
| 1024 | 0.01953 | 0.00248270 | 0.00000023 | 0.00000000 |
| Absolute Error for | ||||
|---|---|---|---|---|
| N | h | Error in SFD | Error in ODE45 | Error in NSFD |
| 2 | 10.00000 | 1.57898904 | 0.00000007 | 0.00000000 |
| 4 | 5.00000 | 0.56648904 | 0.00000009 | 0.00000000 |
| 8 | 2.50000 | 0.25172781 | 0.00000011 | 0.00000000 |
| 16 | 1.25000 | 0.12005326 | 0.00000016 | 0.00000000 |
| 32 | 0.62500 | 0.05860324 | 0.00000018 | 0.00000000 |
| 64 | 0.31250 | 0.02895478 | 0.00000017 | 0.00000000 |
| 128 | 0.15625 | 0.01439233 | 0.00000020 | 0.00000000 |
| 256 | 0.07812 | 0.00717515 | 0.00000021 | 0.00000000 |
| 512 | 0.03906 | 0.00358234 | 0.00000019 | 0.00000000 |
| 1024 | 0.01953 | 0.00178986 | 0.00000020 | 0.00000000 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egbelowo, O.; Harley, C.; Jacobs, B. Nonstandard Finite Difference Method Applied to a Linear Pharmacokinetics Model. Bioengineering 2017, 4, 40. https://doi.org/10.3390/bioengineering4020040
Egbelowo O, Harley C, Jacobs B. Nonstandard Finite Difference Method Applied to a Linear Pharmacokinetics Model. Bioengineering. 2017; 4(2):40. https://doi.org/10.3390/bioengineering4020040
Chicago/Turabian StyleEgbelowo, Oluwaseun, Charis Harley, and Byron Jacobs. 2017. "Nonstandard Finite Difference Method Applied to a Linear Pharmacokinetics Model" Bioengineering 4, no. 2: 40. https://doi.org/10.3390/bioengineering4020040
APA StyleEgbelowo, O., Harley, C., & Jacobs, B. (2017). Nonstandard Finite Difference Method Applied to a Linear Pharmacokinetics Model. Bioengineering, 4(2), 40. https://doi.org/10.3390/bioengineering4020040







