HHV Predicting Correlations for Torrefied Biomass Using Proximate and Ultimate Analyses
Abstract
:1. Introduction
2. Materials and Methods
Estimation Errors
3. Results and Discussion
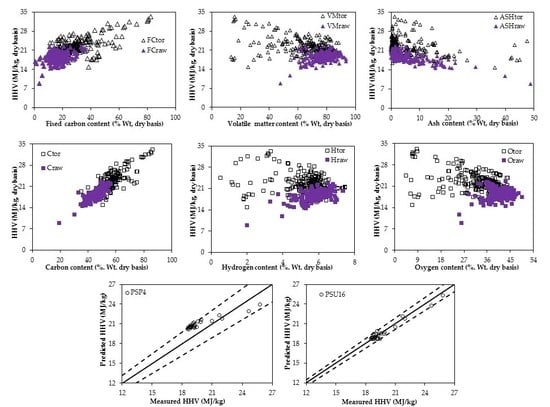
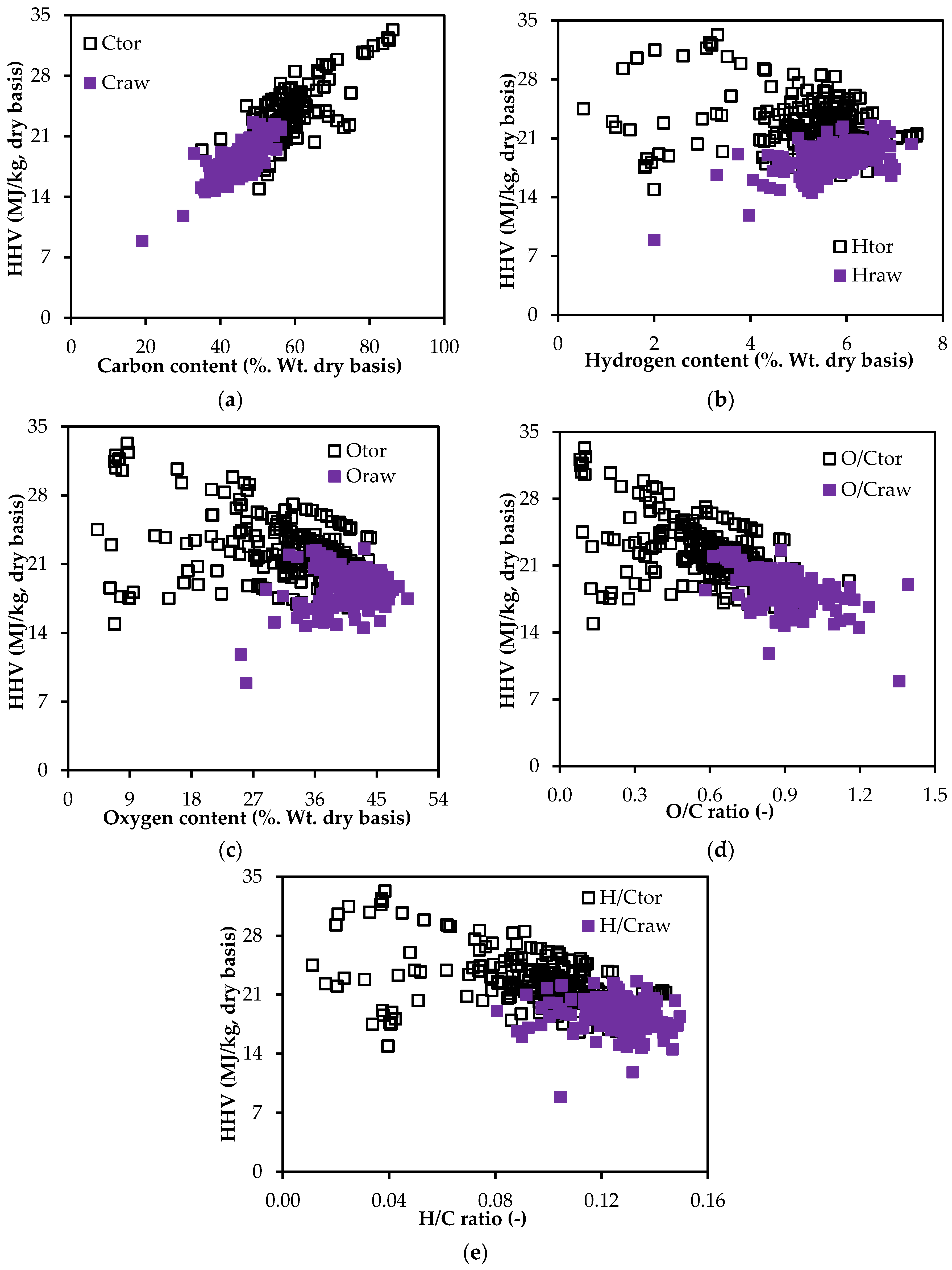
3.1. Scatter Distribution of Data
3.2. Validation of Existing Correlations Using Data from Torrefied Biomass
3.3. New HHV Predicting Correlations
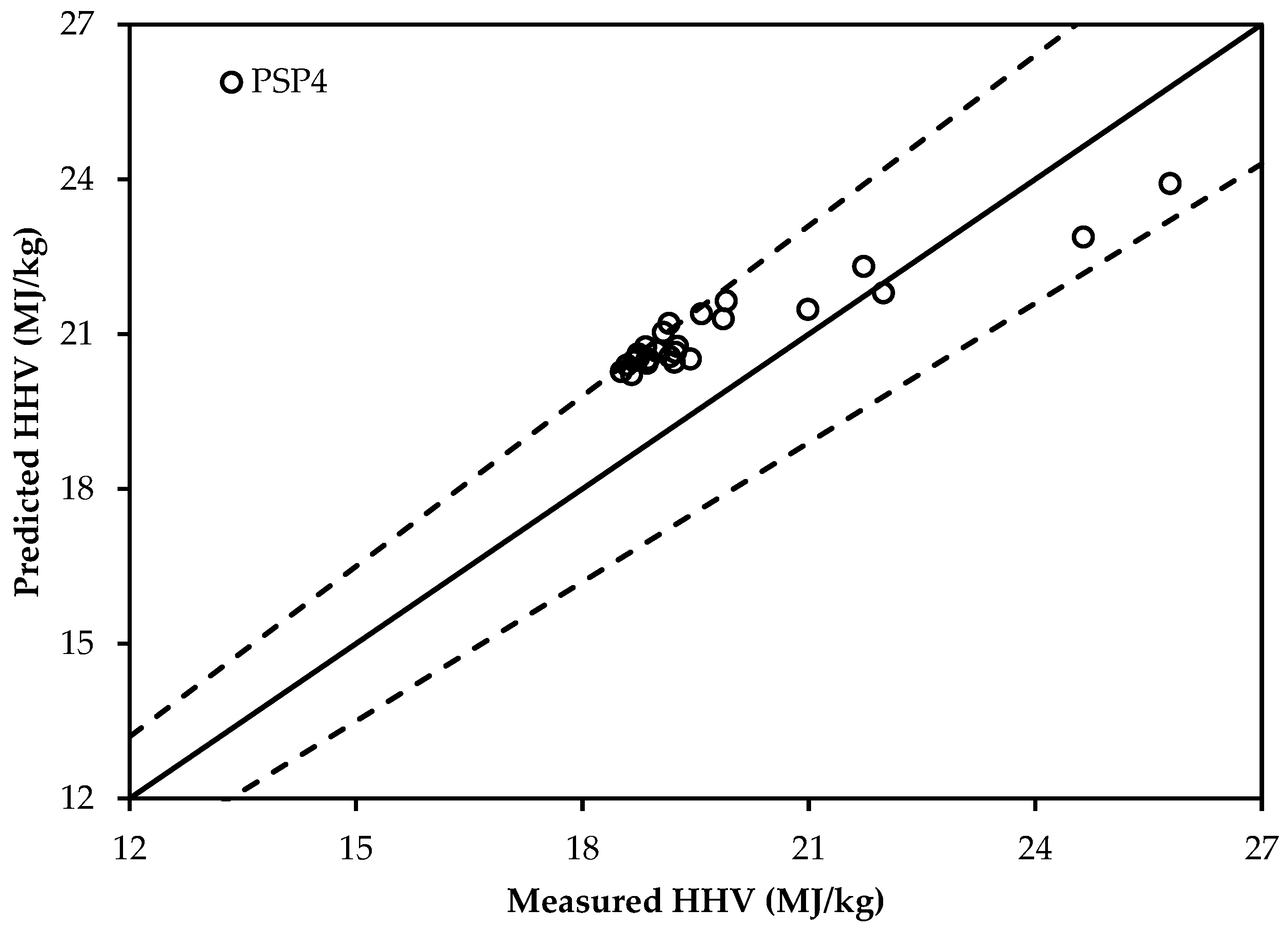
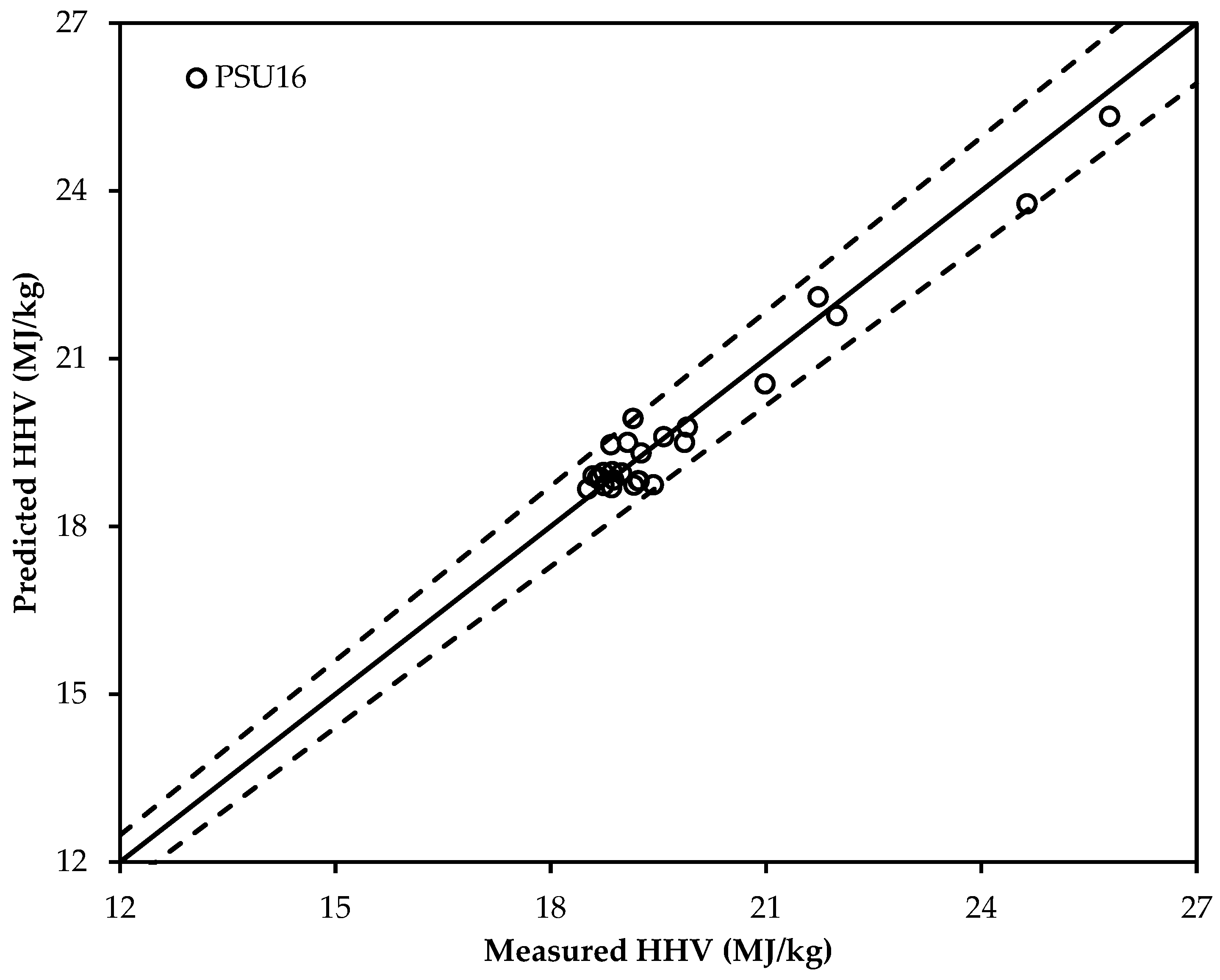
3.4. Validation of the Selected New Correlations
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nhuchhen, D.R.; Salam, P.A. Estimation of higher heating value of biomass from proximate analysis: A new approach. Fuel 2012, 99, 55–63. [Google Scholar] [CrossRef]
- Channiwala, S.A.; Parikh, P.P. A unified correlation for estimating HHV of solid, liquid and gaseous fuels. Fuel 2002, 81, 1051–1063. [Google Scholar] [CrossRef]
- Moreno, J.M.V.; Ferre, A.J.C.; Alonso, J.P.; Marti, B.V. A review of the mathematical models for predicting the heating value of biomass materials. Renew. Sustain. Energy Rev. 2012, 16, 3065–3083. [Google Scholar] [CrossRef]
- Demirbas, A. Calculation of higher heating values of biomass fuels. Fuel 1997, 76, 431–434. [Google Scholar] [CrossRef]
- Jimennez, L.; Gonzales, F. Study of the physical and chemical properties of lignocellulosic residues with a view to the production of fuels. Fuel 1991, 70, 947–950. [Google Scholar] [CrossRef]
- Cordero, T.; Marquez, F.; Mirasol, J.R.; Rodriguez, J.J. Predicting heating values of lignocellulosics and carbonaceous materials from proximate analysis. Fuel 2001, 80, 1567–1571. [Google Scholar] [CrossRef]
- Parikh, J.; Channiwala, S.A.; Ghosal, G.K. A correlation for calculating HHV from proximate analysis of solid fuels. Fuel 2005, 84, 487–494. [Google Scholar] [CrossRef]
- Sheng, C.; Azevedo, J.L.T. Estimating the higher heating value of biomass fuels from basic analysis data. Biomass Bioenergy 2005, 28, 499–507. [Google Scholar] [CrossRef]
- Yin, C.Y. Prediction of higher heating values of biomass from proximate and ultimate analyses. Fuel 2011, 90, 1128–1132. [Google Scholar] [CrossRef]
- Akkaya, A.V. Proximate analysis based multiple regression models for higher heating value estimation of low rank coals. Fuel Process. Technol. 2009, 90, 165–170. [Google Scholar] [CrossRef]
- Elneel, R.; Anwar, S.; Ariwahjoedi, B. Prediction of heating values of oil palm fronds from ultimate analysis. J. Appl. Sci. 2013, 13, 491–496. [Google Scholar] [CrossRef]
- Soponpongpipat, N.; Sittikul, D.; Sae-Ueng, U. Higher heating value prediction of torrefaction char produced from non-woody biomass. Front. Energy 2015, 9, 461–471. [Google Scholar] [CrossRef]
- Nhuchhen, D.R.; Basu, P.; Acharya, B. A comprehensive review on biomass torrefaction. Int. J. Renew. Energy Biofuels 2014, 2014, 56. [Google Scholar] [CrossRef]
- Tumuluru, J.S.; Wright, C.T.; Hess, J.R.; Kenney, K.L. A review of biomass densification systems to develop uniform feedstock commodities for bioenergy application. Biofuels Bioprod. Biorefin. 2011, 5, 683–707. [Google Scholar] [CrossRef]
- Chen, W.H.; Peng, J.; Bi, X.T. A state-of-the-art of biomass torrefaction, densification and applications. Renew. Sustain. Energy Rev. 2015, 44, 847–866. [Google Scholar] [CrossRef]
- van der Stelt, M.J.C.; Gerhauser, H.; Kiel, J.H.A.; Ptasinski, K.J. Biomass upgrading by torrefaction for the production of biofuels: A review. Biomass Bioenergy 2011, 35, 3748–3762. [Google Scholar] [CrossRef]
- Acharya, B.; Sule, I.; Dutta, A. A review on advances of torrefaction technologies for biomass processing. Biomass Convers. Biorefin. 2012, 2, 349–369. [Google Scholar] [CrossRef]
- McNamee, P.; Darvell, L.I.; Jones, J.M.; Williams, A. The combustion characteristics of high-heating-rate chars from untreated and torrefied biomass fuels. Biomass Bioenergy 2015, 82, 63–72. [Google Scholar] [CrossRef]
- Pohlmann, J.G.; Osorio, E.; Vilela, A.C.F.; Diez, M.A.; Borrego, A.G. Integrating physicochemical information to follow the transformation of biomass upon torrefaction and low temperature carbonization. Fuel 2014, 131, 17–27. [Google Scholar] [CrossRef]
- Thanh, K.L.; Commandre, J.M.; Valette, J.; Volle, G.; Meyer, M. Detailed identification and quantification of the condensable species released during torrefaction of lignocellulosic biomasses. Fuel Process. Technol. 2015, 139, 226–235. [Google Scholar] [CrossRef]
- Bach, Q.V.; Tran, K.Q.; Skreiberg, O.; Trinh, T.T. Effects of wet torrefaction on pyrolysis of woody biomass fuels. Energy 2015, 88, 443–456. [Google Scholar] [CrossRef]
- Bach, Q.V.; Tran, K.Q.; Skreiberg, O. Accelerating wet torrefaction rate and ash removal by carbon dioxide addition. Fuel Process. Technol. 2015, 140, 297–303. [Google Scholar] [CrossRef]
- Cao, L.; Yuan, X.; Li, H.; Li, C.; Xiao, Z.; Jiang, L.; Huang, B.; Xiao, Z.; Chen, X.; Wang, H.; Zeng, G. Complementary effects of torrefaction and co-pelletization: Energy consumption and characteristics of pellets. Bioresour. Technol. 2015, 185, 254–262. [Google Scholar] [CrossRef] [PubMed]
- Nam, H.; Capareda, S. Experimental investigation of torrefaction of two agricultural wastes of different composition using RSM (response surface methodology). Energy 2015, 91, 507–516. [Google Scholar] [CrossRef]
- Chen, D.; Zheng, Z.; Fu, K.; Zeng, Z.; Wang, J.; Lu, M. Torrefaction of biomass stalk and its effect on the yield and quality of pyrolysis products. Fuel 2015, 159, 27–32. [Google Scholar] [CrossRef]
- Yang, H.; Liu, B.; Chen, Y.; Chen, W.; Yang, Q.; Chen, H. Application of biomass pyrolytic polygeneration technology using retort reactors. Bioresour. Technol. 2016, 200, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, R.H.H.; Darvell, L.I.; Jones, J.M.; Williams, A. Physicochemical characterization of torrefied biomass. J. Anal. Appl. Pyrolysis 2013, 103, 21–30. [Google Scholar] [CrossRef]
- Lu, K.M.; Lee, W.J.; Chen, W.H.; Liu, S.H.; Lin, T.C. Torrefaction and low temperature carbonization of oil palm fiber and eucalyptus in nitrogen and air atmospheres. Bioresour. Technol. 2012, 123, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Arias, B.; Pevida, C.; Fermoso, J.; Plaza, M.G.; Rubiera, F.; Pis, J.J. Influence of torrefaction on the grindability and reactivity of woody biomass. Fuel Process. Technol. 2008, 89, 169–175. [Google Scholar] [CrossRef]
- Pala, M.; Kantarli, I.C.; Buyukisik, H.B.; Yanik, J. Hydrothermal carbonization and torrefaction of grape pomace: A comparative evaluation. Bioresource Technology 2014, 161, 255–262. [Google Scholar] [CrossRef] [PubMed]
- Eseltine, D.; Thanapal, S.S.; Annamalai, K.; Ranjan, D. Torrefaction of woody biomass (Juniper and Mesquite) using inert and non-inert gases. Fuel 2013, 113, 379–388. [Google Scholar] [CrossRef]
- Wannapeera, J.; Worasuwannarak, N. Upgrading of woody biomass by torrefaction under pressure. J. Anal. Appl. Pyrolysis 2012, 96, 173–180. [Google Scholar] [CrossRef]
- Wannapeera, J.; Fungtammasan, B.; Worasuwannarak, N. Effects of temperature and holding time during torrefaction on the pyrolysis behaviors of woody biomass. J. Anal. Appl. Pyrolysis 2011, 92, 99–105. [Google Scholar] [CrossRef]
- Park, J.; Meng, J.; Lim, K.H.; Rojas, O.J.; Park, S. Transformation of lignocellulosic biomass during torrefaction. J. Anal. Appl. Pyrolysis 2013, 100, 199–206. [Google Scholar] [CrossRef]
- Kambo, H.S.; Dutta, A. Comparative evaluation of torrefaction and hydrothermal carbonization of lignocellulosic biomass for the production of solid biofuel. Energy Convers. Manag. 2015, 105, 746–755. [Google Scholar] [CrossRef]
- Bridgeman, T.G.; Jones, J.M.; Williams, A.; Waldron, D.J. An investigation of the grindability of two torrefied energy crops. Fuel 2010, 89, 3911–3918. [Google Scholar] [CrossRef]
- Xue, G.; Kwapinska, M.; Kwapinski, W.; Czajka, K.M.; Kennedy, J.; Leahy, J.J. Impact of torrefaction on properties of Miscanthus × giganteus relevant to gasification. Fuel 2014, 121, 189–197. [Google Scholar] [CrossRef]
- Costa, F.F.; Costa, M. Evaluation of particle fragmentation of raw and torrefied biomass in a drop tube furnace. Energy Procedia 2015, 66, 277–280. [Google Scholar] [CrossRef]
- Barontini, F.; Biagini, E.; Bonini, F.; Tognotti, L. An experimental investigation on the devolatilization behavior of raw and torrefied lignocellulosic biofuels. Chem. Eng. Trans. 2015, 43, 481–486. [Google Scholar]
- Li, J.; Zhang, X.; Pawlak-Kruczek, H.; Yang, W.; Kruczek, P.; Blasiak, W. Process simulation of co-firing torrefied biomass in a 220MWe coal-fired power plant. Energy Convers. Manag. 2014, 84, 503–511. [Google Scholar] [CrossRef]
- Park, S.W.; Jang, C.H.; Baek, K.R.; Yang, J.K. Torrefaction and low-temperature carbonization of woody biomass: Evaluation of fuel characteristics of the products. Energy 2012, 45, 676–685. [Google Scholar] [CrossRef]
- Berrueco, C.; Recari, J.; Guell, B.M.; Alamo, G.D. Pressurized gasification of torrefied woody biomass in a lab scale fluidized bed. Energy 2014, 70, 68–78. [Google Scholar] [CrossRef]
- Chen, D.; Zhou, J.; Zhang, Q.; Zhu, X.; Lu, Q. Upgrading of rice husk by torrefaction and its influence on the fuel properties. Bioresources 2014, 9, 5893–5905. [Google Scholar] [CrossRef]
- Zhang, S.; Dong, Q.; Zhang, L.; Xiong, Y.; Liu, X.; Zhu, S. Effects of water washing and torrefaction pretreatments on rice husk pyrolysis by microwave heating. Bioresour. Technol. 2015, 193, 442–448. [Google Scholar] [CrossRef] [PubMed]
- Bach, Q.V.; Tran, K.Q. Dry and wet torrefaction of woody biomass—A comparative study on combustion kinetics. Energy Procedia 2015, 75, 150–155. [Google Scholar] [CrossRef]
- Strandberg, M.; Olofsson, I.; Pommer, L.; Wiklund-Lindstrom, S.; Aberg, K.; Nordin, A. Effects of temperature and residence time on continuous torrefaction of spruce wood. Fuel Process. Technol. 2015, 134, 387–398. [Google Scholar] [CrossRef]
- Yang, Z.; Sarkar, M.; Kumar, A.; Tumuluru, J.S.; Huhnke, R.L. Effects of torrefaction and densification on switchgrass pyrolysis products. Bioresour. Technol. 2014, 174, 266–273. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.H.; Cheng, W.Y.; Lu, K.M.; Huang, Y.P. An evaluation on improvement of pulverized biomass property for solid fuel through torrefaction. Appl. Energy 2011, 88, 3636–3644. [Google Scholar] [CrossRef]
- Rousset, P.; Aguiar, C.; Labbe, N.; Commandre, J.M. Enhancing the combustible properties of bamboo by torrefaction. Bioresour. Technol. 2011, 102, 8225–8231. [Google Scholar] [CrossRef] [PubMed]
- Phichai, K.; Pragrobpondee, P.; Khumpart, T.; Hirunpraditkoon, S. Prediction heating values of lignocellulosics from biomass characteristics. Int. J. Chem. Mol. Nucl. Mater. Metall. Eng. 2013, 7, 214–217. [Google Scholar]
- Bach, Q.V.; Tran, K.Q.; Khalil, R.A.; Skreiberg, O. Comparative assessment of wet torrefaction. Energy Fuels 2013, 27, 6743–6753. [Google Scholar] [CrossRef]
- Ren, S.; Lei, H.; Wang, L.; Bu, Q.; Wei, Y.; Liang, J.; Liu, Y.; Julson, J.; Chen, S.; Wu, J.; et al. Microwave torrefaction of douglass fir sawdust pellets. Energy Fuels 2012, 26, 5936–5943. [Google Scholar] [CrossRef]
- Mafu, L.D.; Neomagus, H.W.; Everson, R.C.; Carrier, M.; Strydom, C.A.; Bunt, J.R. Structural and chemical modifications of typical South African biomasses during torrefaction. Bioresour. Technol. 2016, 202, 192–197. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.H.; Hsu, H.C.; Lu, K.M.; Lee, W.J.; Lin, T.C. Thermal pretreatment of wood (Luan) block by torrefaction and its influence on the properties of the biomass. Energy 2011, 36, 3012–3021. [Google Scholar] [CrossRef]
- Huang, Y.F.; Chen, W.R.; Chiueh, P.T.; Kuan, W.H.; Lo, S.L. Micorwave torrefaction of rice straw and pennistum. Bioresour. Technol. 2012, 123, 1–7. [Google Scholar] [CrossRef] [PubMed]
- PhanPhanich, M.; Mani, S. Impact of torrefaction on the grindability and fuel characteristics of forest biomass. Bioresour. Technol. 2011, 102, 1246–1253. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Wang, G.J.; Kuang, J.H.; Zhang, Y.L.; Luo, Y.H. Pretreatment of agricultural residues for co-gasification via torrefaction. J. Anal. Appl. Pyrolysis 2009, 86, 331–337. [Google Scholar] [CrossRef]
- Acquah, G.E.; Krigstin, S.; Wetzel, S.; Cooper, P.; Cormier, D. Heterogeneity of forest harvest residue from Eastern Ontario Biomass Harvests. For. Prod. J. 2015, 66, 164–175. [Google Scholar] [CrossRef]
- Wang, M.J.; Huang, Y.F.; Chiueh, P.T.; Kuan, W.H.; Lo, S.L. Microwave-induced torrefaction of rice husk and sugarcane residues. Energy 2012, 37, 177–184. [Google Scholar] [CrossRef]
- Xiao, R.; Chen, X.; Wang, F.; Yu, G. Pyrolysis pretreatment of biomass for entrained-flow gasification. Appl. Energy 2010, 87, 149–155. [Google Scholar] [CrossRef]
- Ebeling, J.M.; Jenkins, B.M. Physical and chemical properties of biomass fuels. Trans. ASAE 1985, 28, 898–902. [Google Scholar] [CrossRef]
- Kathiravale, S.; Yunus, M.N.M.; Sopian, K.; Samsuddin, A.H.; Rahman, R.A. Modeling the heating value of municipal solid waste. Fuel 2003, 82, 1119–1125. [Google Scholar] [CrossRef]
- Demirbas, A. Sustainable cofiring of biomass with coal. Energy Conversat. Manag. 2003, 44, 1465–1479. [Google Scholar] [CrossRef]
- Demirbas, A. Prediction of higher heating values for vegetable oils and animal fats from proximate analysis data. Energy Source A 2009, 31, 1264–1270. [Google Scholar] [CrossRef]
- Callejon-Ferre, A.J.; Velazquez-Marti, B.; Lopez-Martinez, J.A.; Manzano-Agugliaro, F. Greenhouse crop residues: Energy potential and models for the prediction of their higher heating value. Renew. Sustain. Energy Rev. 2011, 15, 948–955. [Google Scholar] [CrossRef]
- Huang, C.J.; Han, L.J.; Liu, X.; Yang, Z. Models predicting calorific value of straw from the ash content. Int. J. Green Energy 2008, 5, 533–539. [Google Scholar] [CrossRef]
- Tillman, D.A. Wood as an Energy Source; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Friedl, A.; Padouvas, E.; Rotter, H.; Varmuza, K. Prediction of heating values of biomass fuel from elemental composition. Anal. Chem. Acta 2005, 544, 191–198. [Google Scholar] [CrossRef]
- Tumuluru, J.S.; Wright, C.T.; Boardman, R.D.; Kremer, T. Proximate and ultimate compositional changes in Corn Stover during torrefaction using thermogravimetric analyzer and microwaves. In Proceedings of the 2012 ASABE Annual International Meeting, Dallas, TX, USA, 29 July–1 August 2012.
- Sanchez, F.; Miguel, G.S. Improved fuel properties of whole table olive stones via pyrolytic processing. Biomass Bioenergy 2016, 92, 1–11. [Google Scholar] [CrossRef]
- Barta-Rajnai, E.; Jakab, E.; Sebestyen, Z.; May, Z.; Barta, Z.; Wang, L.; Skreiberg, O.; Gronli, M.; Bozi, J.; Czegeny, Z. Comprehensive compositional study of torrefied wood and herbaceous materials by chemical analysis and thermoanalytical methods. Energy Fuels 2016, 30, 8019–8030. [Google Scholar] [CrossRef]

| Representation | New Forms of Correlations |
|---|---|
| Proximate analysis | |
| PSP1 | |
| PSP2 | |
| PSP3 | |
| PSP4 | |
| PSP5 | |
| PSP6 | |
| PSP7 | |
| PSP8 | |
| PSP9 | |
| PSP10 | |
| PSP11 | |
| PSP12 | |
| Ultimate analysis | |
| PSU1 | |
| PSU2 | |
| PSU3 | |
| PSU4 | |
| PSU5 | |
| PSU6 | |
| PSU7 | |
| PSU8 | |
| PSU9 | |
| PSU10 | |
| PSU11 | |
| PSU12 | |
| PSU13 | |
| PSU14 | |
| PSU15 | |
| PSU16 |
| Equation (P) | Existing Proximate Analysis-Based Correlations | MAE | AAE | ABE | Ref. |
|---|---|---|---|---|---|
| 1 | HHV = 20.067 − 0.234ASH | 3.67 | 15.48 | −15.14 | [61] |
| 2 | HHV = 26.601 − 0.304ASH − 0.082VM | 2.89 | 12.26 | −11.80 | [61] |
| 3 | HHV = −10.81408 + 0.3133(FC + VM) | 3.70 | 15.81 | −15.29 | [5] |
| 4 | HHV = 0.196FC + 14.119 | 3.03 | 13.37 | −10.43 | [4] |
| 5 | HHV = 0.312FC + 0.1534VM | 3.33 | 14.43 | −13.94 | [4] |
| 6 | HHV = 0.3543FC + 0.1708VM | 1.58 | 6.88 | −3.29 | [6] |
| 7 | HHV = 0.356248VM − 6.998497 | 6.85 | 28.94 | −25.56 | [62] |
| 8 | HHV = −0.0066FC2 + 0.5866FC + 8.752 | 3.66 | 15.50 | −13.28 | [63] |
| 9 | HHV = −0.0066VM2 + 0.7371VM + 1.2305 | 3.62 | 15.26 | −12.08 | [63] |
| 10 | HHV = 19.914 − 0.2324ASH | 3.80 | 16.08 | −15.79 | [8] |
| 11 | HHV = −3.036 + 0.2218VM + 0.2601FC | 3.39 | 14.36 | −14.06 | [8] |
| 12 | HHV = 0.3536FC + 0.1559VM − 0.0078ASH | 2.25 | 9.82 | −8.04 | [7] |
| 13 | HHV = −0.1882VM + 32.94 | 3.24 | 14.68 | −6.23 | [64] |
| 14 | HHV = 0.1905VM + 0.2521FC | 2.69 | 10.61 | −10.61 | [9] |
| 15 | HHV = 20.86 − 0.261ASH | 3.14 | 13.19 | −12.28 | [65] |
| 16 | HHV = −13.173 + 0.416VM | 8.75 | 37.27 | −35.84 | [65] |
| 17 | HHV = −2.057 − 0.092ASH + 0.279VM | 6.99 | 29.71 | −28.66 | [65] |
| 18 | HHV = 35.4879 − 0.3023ASH − 0.1905VM | 1.73 | 7.58 | −3.68 | [12] |
| 19 | HHV = 19.2880 − 0.2135VM/FC − 1.9584ASH/VM + 0.0234FC/ASH | 3.40 | 14.19 | −12.82 | [1] |
| 20 | HHV = 18.96016 − 0.22527ASH | 4.69 | 20.06 | −19.94 | [66] |
| Equation (U) | Existing Ultimate Analysis-Based Correlations | MAE | AAE | ABE | Ref. |
|---|---|---|---|---|---|
| 1 | HHV = −3.147 + 0.468C | 1.49 | 6.66 | 3.26 | [65] |
| 2 | HHV = −1.642 − 0.024ASH + 0.475(C + N) − 0.376(H + N) | 1.58 | 7.00 | 2.52 | [65] |
| 3 | HHV = 23.668 − 7.032H − 0.002A2 + 0.005C2 + 0.771H2 + 0.019N2 | 2.95 | 12.93 | 11.11 | [65] |
| 4 | HHV = −0.763 + 0.301C + 0.525H + 0.064O | 1.73 | 7.24 | −5.78 | [61] |
| 5 | HHV = −1.3675 + 0.3137C + 0.7009H + 0.0318O | 1.71 | 7.20 | −5.96 | [8] |
| 6 | HHV = 0.335C + 1.423H − 0.154O − 0.145N | 1.59 | 6.99 | 5.35 | [4] |
| 7 | HHV = 0.3259C + 3.4597 | 1.37 | 5.96 | −2.37 | [8] |
| 8 | HHV = 0.4373C − 1.6701 | 1.37 | 6.13 | 2.27 | [67] |
| 9 | HHV = (3.55C2 − 232C − 2230H + 51.2CH + 131N + 20600)×10−3 | 1.09 | 4.81 | −0.52 | [68] |
| 10 | HHV = 0.879C + 0.3214H + 0.056O − 24.826 | 5.51 | 25.43 | 23.88 | [11] |
| 11 | HHV = 0.924C − 22.403 | 7.14 | 31.10 | 30.19 | [11] |
| Equation (P) | Developed Proximate Analysis-Based Correlations and Estimation Errors | MAE | AAE | ABE | Ref. |
|---|---|---|---|---|---|
| 1 | HHV = 22.9976 − 0.1135ASH | 2.14 | 9.37 | 1.53 | PSP1 |
| 2 | HHV = 18.1418 + 0.1438FC | 1.78 | 8.17 | 1.14 | PSP2 |
| 3 | HHV = 26.2841 − 0.0604VM | 2.11 | 9.59 | 1.61 | PSP3 |
| 4 | HHV = 0.1846VM + 0.3525FC | 1.38 | 6.17 | 0.60 | PSP4 |
| 5 | HHV = 0.6663FC − 0.0575ASH | 6.60 | 29.64 | −15.56 | PSP5 |
| 6 | HHV = 0.3545ASH + 0.2960VM | 4.39 | 18.73 | −1.88 | PSP6 |
| 7 | HHV = 2.4830 + 0.1602VM + 0.3225FC | 1.40 | 6.25 | 0.75 | PSP7 |
| 8 | HHV = 21.1811 + 1.8812FC/VM | 1.96 | 9.00 | 1.44 | PSP8 |
| 9 | HHV = 20.4755 + 0.0007FC + 0.0018FC2 | 1.73 | 7.97 | 1.12 | PSP9 |
| 10 | HHV = 3.7950 − 0.2177VM − 0.4096FC + 0.0011VM2 − 0.0004FC2 | 1.39 | 6.24 | 0.73 | PSP10 |
| 11 | HHV = 36.4042 − 0.2177VM − 0.4096ASH + 0.0005VM2 + 0.0023ASH2 | 1.38 | 6.21 | 0.72 | PSP11 |
| 12 | HHV = 19.5785 + 0.1111FC − 0.2602ASH + 0.0007FC2 + 0.0030ASH2 | 1.37 | 6.17 | 0.72 | PSP12 |
| Equation (U) | Developed Ultimate Analysis-based Correlations and Estimation Errors | MAE | AAE | ABE | Ref. |
|---|---|---|---|---|---|
| 1 | HHV = 4.4804 + 0.3194C | 1.25 | 5.66 | 0.64 | PSU1 |
| 2 | HHV = 24.7975 − 0.4680H | 2.23 | 10.01 | 1.72 | PSU2 |
| 3 | HHV = 26.5113 − 0.1278O | 2.08 | 9.44 | 1.57 | PSU3 |
| 4 | HHV = 1.4036 + 0.3409C + 0.3586H | 1.21 | 5.43 | 0.59 | PSU4 |
| 5 | HHV = 2.4544 + 0.3381C + 0.0300O | 1.23 | 5.52 | 0.62 | PSU5 |
| 6 | HHV = 25.0602 + 0.9092H − 0.2290O | 2.03 | 9.22 | 1.49 | PSU6 |
| 7 | HHV = 3.6165 + 0.3181C + 0.6107H − 0.4380N − 0.0613O | 1.21 | 5.44 | 0.58 | PSU7 |
| 8 | HHV = 27.0624 − 7.8378O/C | 1.88 | 8.54 | 1.35 | PSU8 |
| 9 | HHV = 28.1442 − 50.0874H/C | 2.04 | 9.24 | 1.46 | PSU9 |
| 10 | HHV = 26.8463 − 8.8867O/C + 8.8489H/C | 1.87 | 8.52 | 1.35 | PSU10 |
| 11 | HHV = 5.1906 + 0.2957C − 0.0002C2 | 1.25 | 5.66 | 0.64 | PSU11 |
| 12 | HHV = 7.8546 + 0.1255C + 0.1563H + 0.0018C2 − 0.0320H2 | 1.21 | 5.44 | 0.59 | PSU12 |
| 13 | HHV = 3.3965 + 00.3359C − 0.0666O + 0.0001C2 + 0.0019O2 | 1.23 | 5.54 | 0.62 | PSU13 |
| 14 | HHV = 27.2908 − 8.8671O/C + 0.9733(O/C)2 | 1.88 | 8.55 | 1.36 | PSU14 |
| 15 | HHV = 25.5411 − 186247O/C + 103.1710H/C + 8.0136(O/C)2 − 515.0026(H/C)2 | 1.85 | 8.45 | 1.32 | PSU15 |
| 16 | HHV = 32.7934 + 0.0053C2 − 0.5321C − 2.8769H + 0.0608CH − 0.2401N | 1.13 | 5.01 | 0.49 | PSU16 |
| Material | MJ/kg | Proximate Analysis (%) | Ultimate Analysis (%) | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HHV | VM | FC | ASH | C | H | N | O | S | ||
| Corn stover | 18.59 | 75.38 | 18.39 | 6.23 | 45.88 | 5.90 | 0.50 | 41.52 | 0.05 | [69] |
| 18.69 | 74.87 | 18.89 | 6.24 | 45.76 | 5.90 | 0.46 | 41.67 | 0.04 | ||
| 18.88 | 75.50 | 18.64 | 5.85 | 45.65 | 5.86 | 0.52 | 42.23 | 0.05 | ||
| 18.74 | 75.57 | 18.90 | 5.54 | 46.03 | 5.92 | 0.44 | 42.13 | 0.04 | ||
| 18.86 | 76.24 | 18.04 | 5.73 | 46.09 | 5.88 | 0.47 | 41.91 | 0.06 | ||
| 18.75 | 75.10 | 18.94 | 5.96 | 45.26 | 5.78 | 0.50 | 42.53 | 0.04 | ||
| 18.99 | 75.12 | 19.29 | 5.61 | 46.02 | 5.85 | 0.48 | 42.11 | 0.06 | ||
| 18.65 | 74.78 | 18.18 | 7.04 | 45.72 | 5.80 | 0.51 | 40.96 | 0.05 | ||
| 18.85 | 74.20 | 19.25 | 6.53 | 45.19 | 5.71 | 0.60 | 42.07 | 0.04 | ||
| 18.52 | 74.76 | 18.36 | 6.87 | 45.10 | 5.66 | 0.62 | 41.84 | 0.05 | ||
| 19.22 | 73.17 | 19.71 | 7.11 | 45.60 | 5.64 | 0.61 | 41.22 | 0.05 | ||
| 19.16 | 74.27 | 19.43 | 6.30 | 45.31 | 5.70 | 0.57 | 42.26 | 0.04 | ||
| 19.23 | 73.14 | 20.27 | 6.59 | 45.54 | 5.63 | 0.56 | 41.89 | 0.05 | ||
| 19.43 | 72.84 | 20.06 | 7.09 | 45.31 | 5.60 | 0.58 | 41.63 | 0.04 | ||
| 19.26 | 70.38 | 22.03 | 7.58 | 47.35 | 5.27 | 0.76 | 39.13 | 0.06 | ||
| 19.07 | 70.54 | 22.72 | 6.73 | 47.92 | 5.37 | 0.68 | 39.36 | 0.04 | ||
| 19.87 | 68.28 | 24.65 | 7.07 | 48.01 | 5.07 | 0.74 | 39.14 | 0.05 | ||
| 19.58 | 68.48 | 24.82 | 6.70 | 48.36 | 5.14 | 0.75 | 39.13 | 0.05 | ||
| 19.91 | 65.03 | 27.34 | 7.63 | 48.94 | 4.99 | 0.69 | 37.82 | 0.05 | ||
| Olive stones | 20.99 | 77.40 | 20.40 | 2.20 | 50.30 | 6.50 | 0.30 | 40.10 | 0.00 | [70] |
| 21.99 | 75.50 | 22.30 | 2.20 | 53.30 | 6.40 | 0.20 | 37.90 | 0.00 | ||
| 24.64 | 67.80 | 29.40 | 2.80 | 58.30 | 6.10 | 0.40 | 32.40 | 0.00 | ||
| 25.79 | 61.20 | 35.80 | 2.90 | 62.10 | 5.80 | 0.30 | 28.80 | 0.00 | ||
| Rape straw | 18.84 | 72.33 | 20.99 | 6.67 | 47.23 | 5.22 | 0.00 | 41.19 | 0.00 | [71] |
| Wheat straw | 19.15 | 68.59 | 24.24 | 7.17 | 48.49 | 6.62 | 0.00 | 38.11 | 0.00 | |
| 21.73 | 56.85 | 33.52 | 9.62 | 56.12 | 4.63 | 0.00 | 29.97 | 0.00 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nhuchhen, D.R.; Afzal, M.T. HHV Predicting Correlations for Torrefied Biomass Using Proximate and Ultimate Analyses. Bioengineering 2017, 4, 7. https://doi.org/10.3390/bioengineering4010007
Nhuchhen DR, Afzal MT. HHV Predicting Correlations for Torrefied Biomass Using Proximate and Ultimate Analyses. Bioengineering. 2017; 4(1):7. https://doi.org/10.3390/bioengineering4010007
Chicago/Turabian StyleNhuchhen, Daya Ram, and Muhammad T. Afzal. 2017. "HHV Predicting Correlations for Torrefied Biomass Using Proximate and Ultimate Analyses" Bioengineering 4, no. 1: 7. https://doi.org/10.3390/bioengineering4010007
APA StyleNhuchhen, D. R., & Afzal, M. T. (2017). HHV Predicting Correlations for Torrefied Biomass Using Proximate and Ultimate Analyses. Bioengineering, 4(1), 7. https://doi.org/10.3390/bioengineering4010007