Purification of Monoclonal Antibodies Using a Fiber Based Cation-Exchange Stationary Phase: Parameter Determination and Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Chemicals
2.1.2. Stationary Phase and Column Packing
2.2. Methods
2.2.1. Gradient Elution Experiments
2.2.2. Inverse Size Exclusion Chromatography
2.2.3. Isocratic Retention Experiments
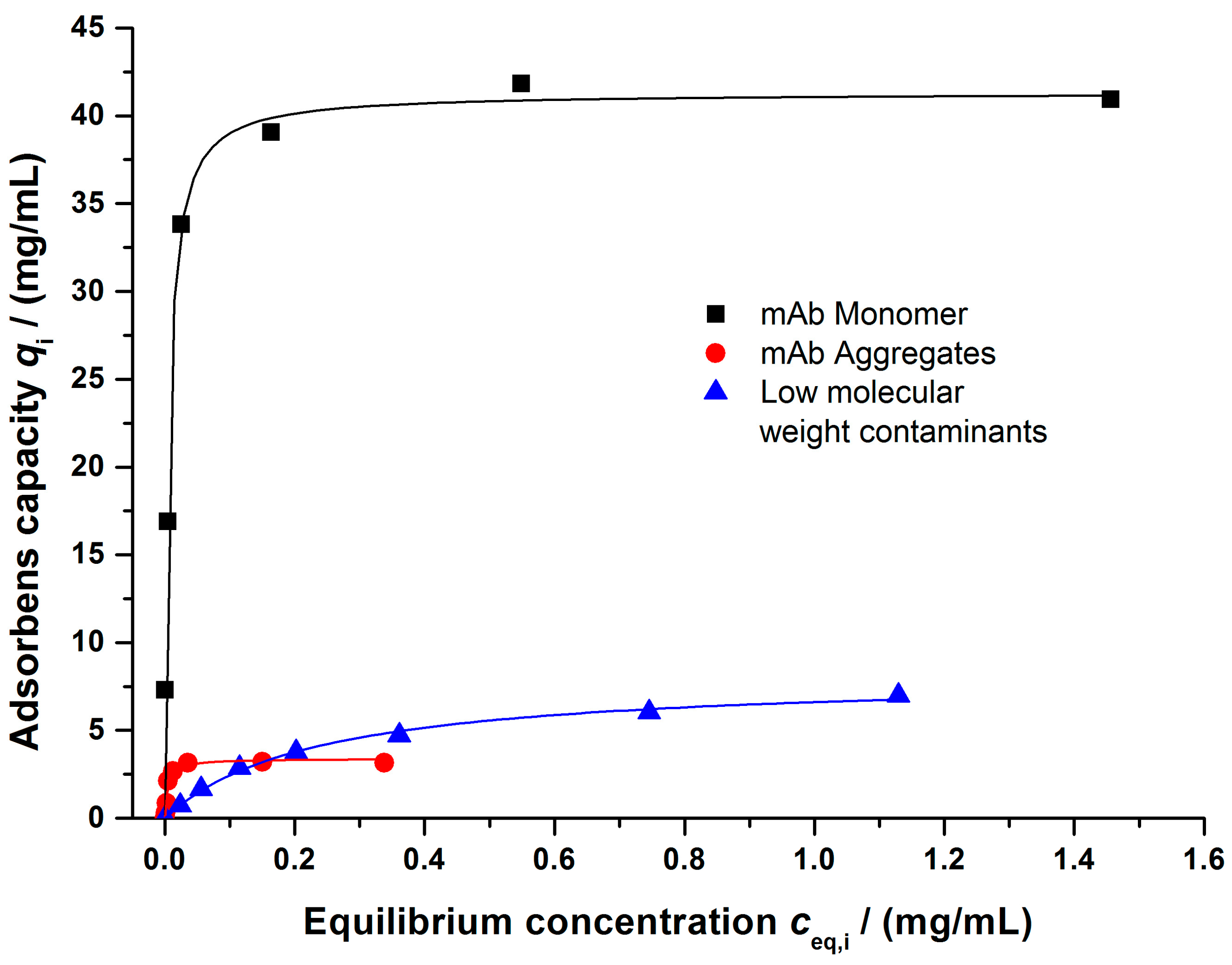
2.2.4. Batch Adsorption Experiments
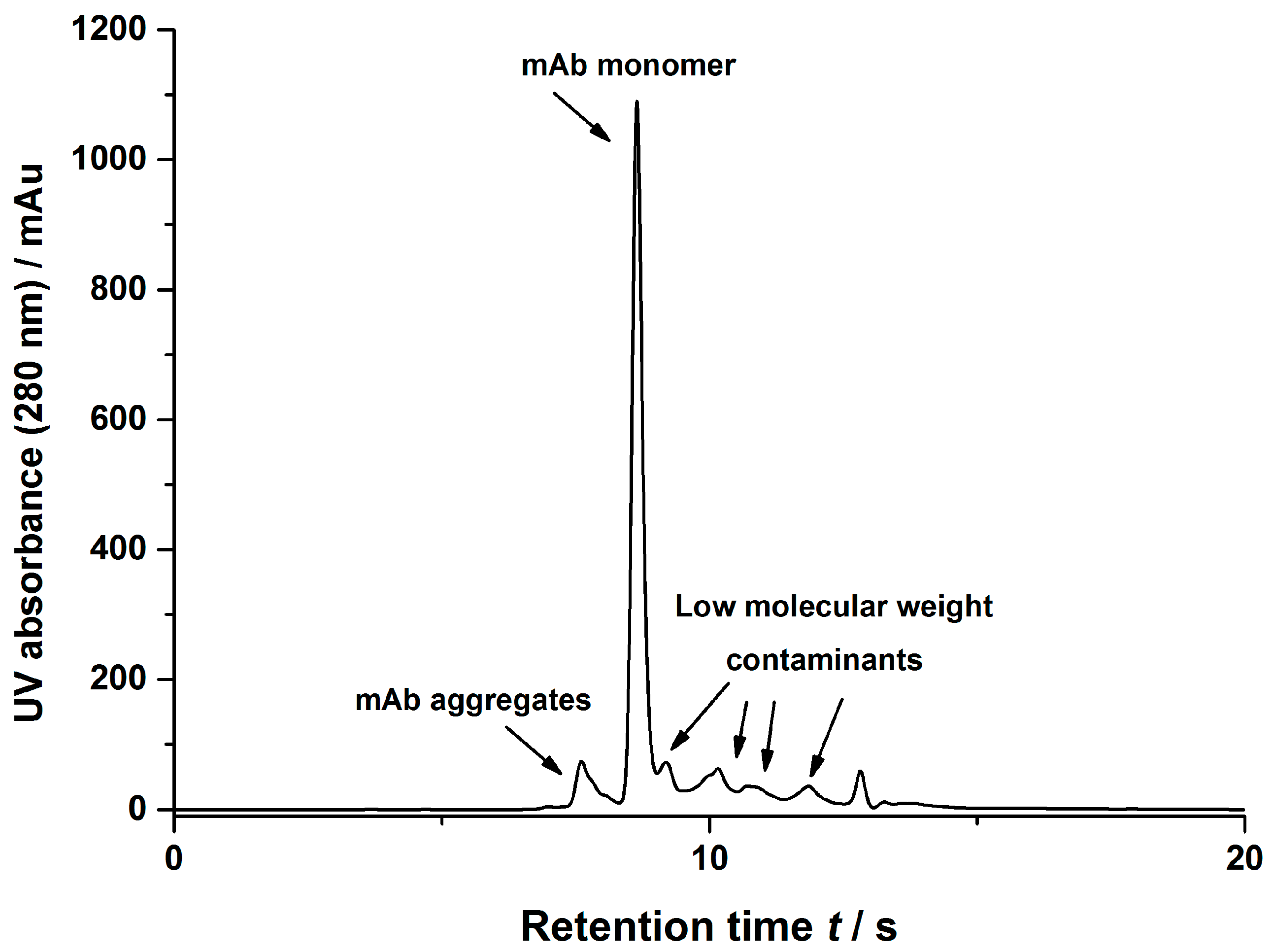
2.2.5. Size Exclusion Chromatography
2.2.6. Protein A Chromatography
2.2.7. Scanning Electron Microscopy
3. Theoretical
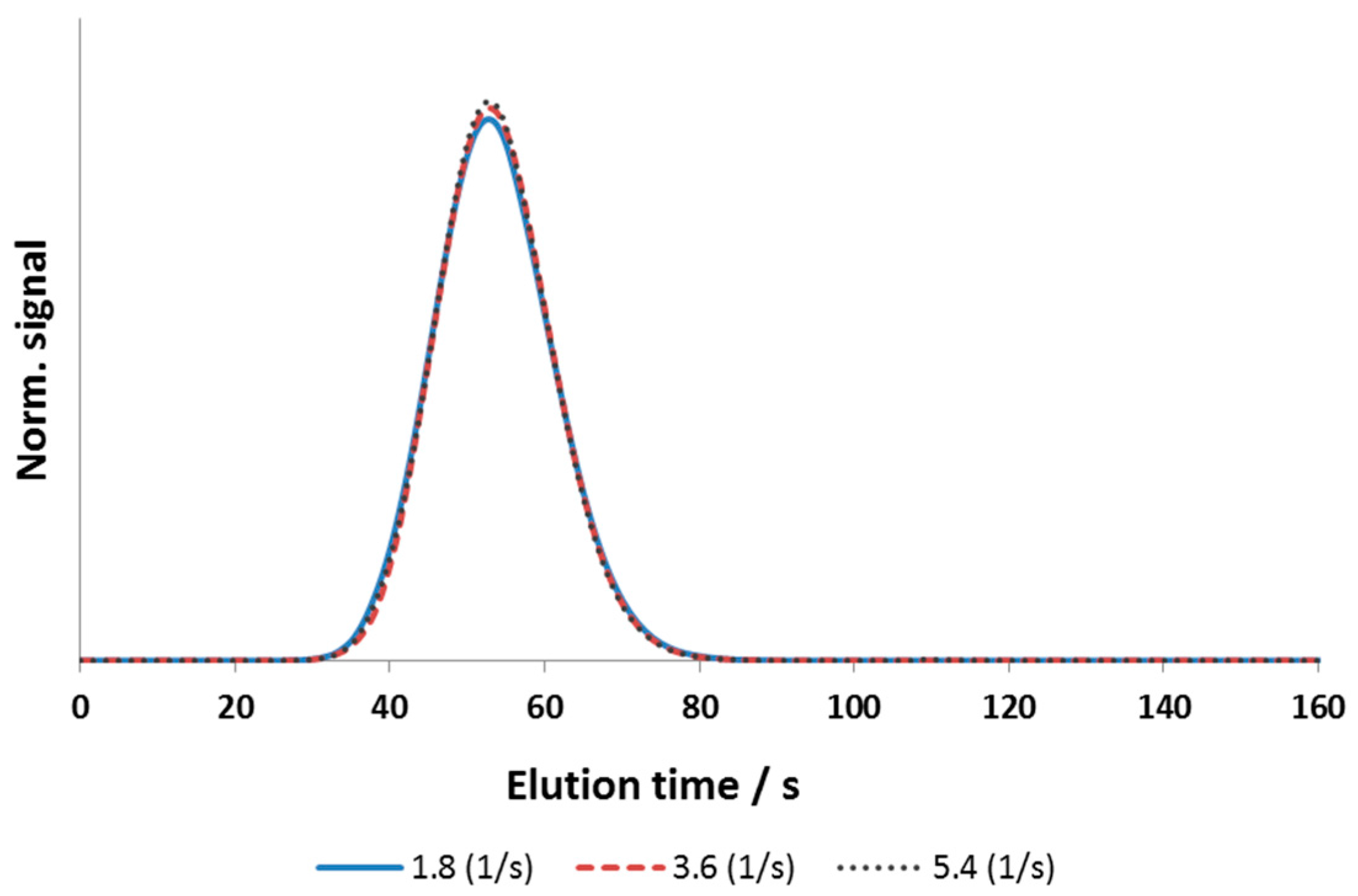
3.1. Column Model and System Dispersion
3.2. Parameter Determination
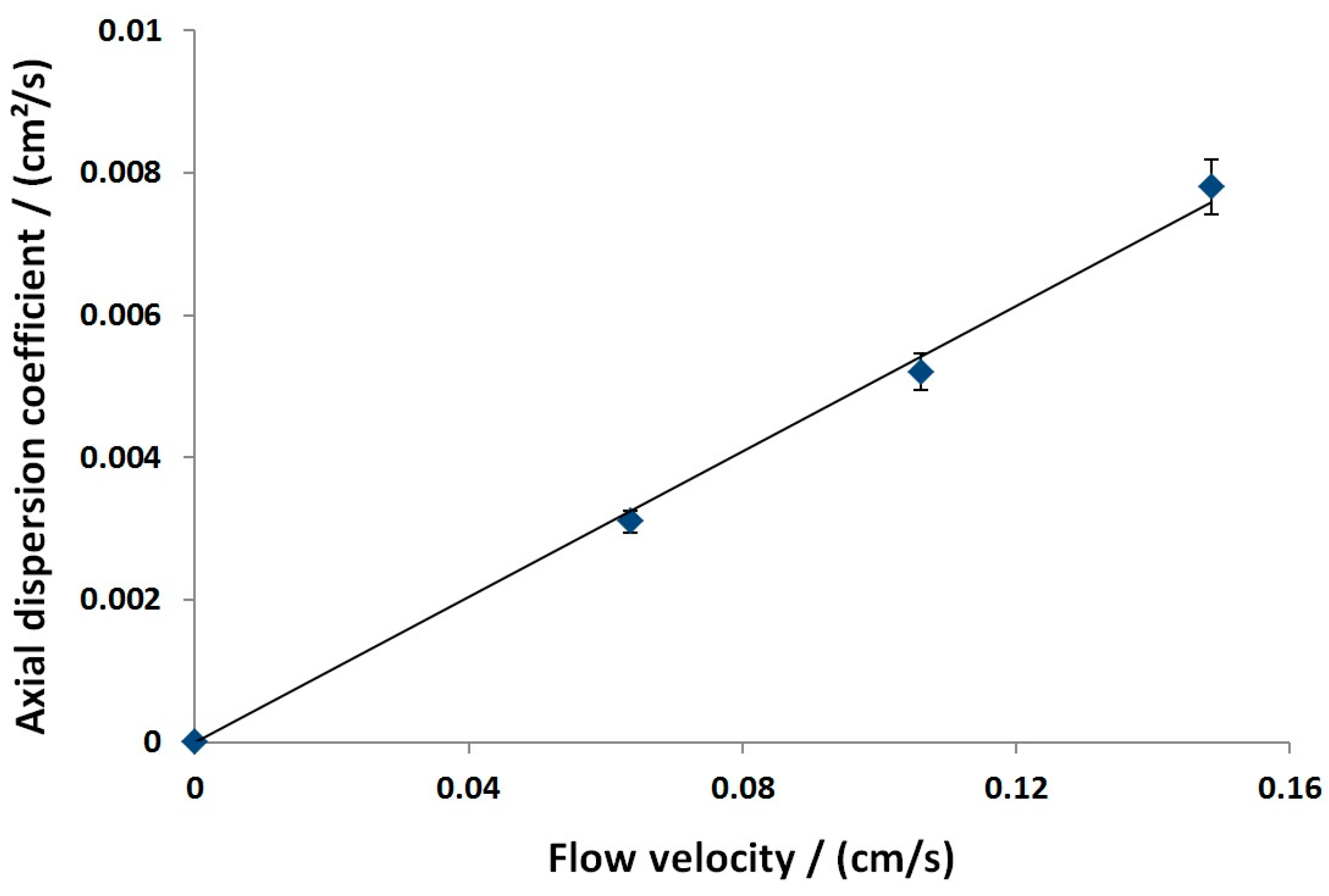
3.2.1. Axial Dispersion and Voidage of the Fiber Bed Column
3.2.2. Effective Mass-Transfer Coefficient and Exchange Area
3.2.3. Salt-Dependent Binding Behavior
4. Results and Discussion
4.1. Parameter Determination
4.1.1. Column Model
4.1.2. Salt-Dependent Binding Behavior
4.2. Model Validation
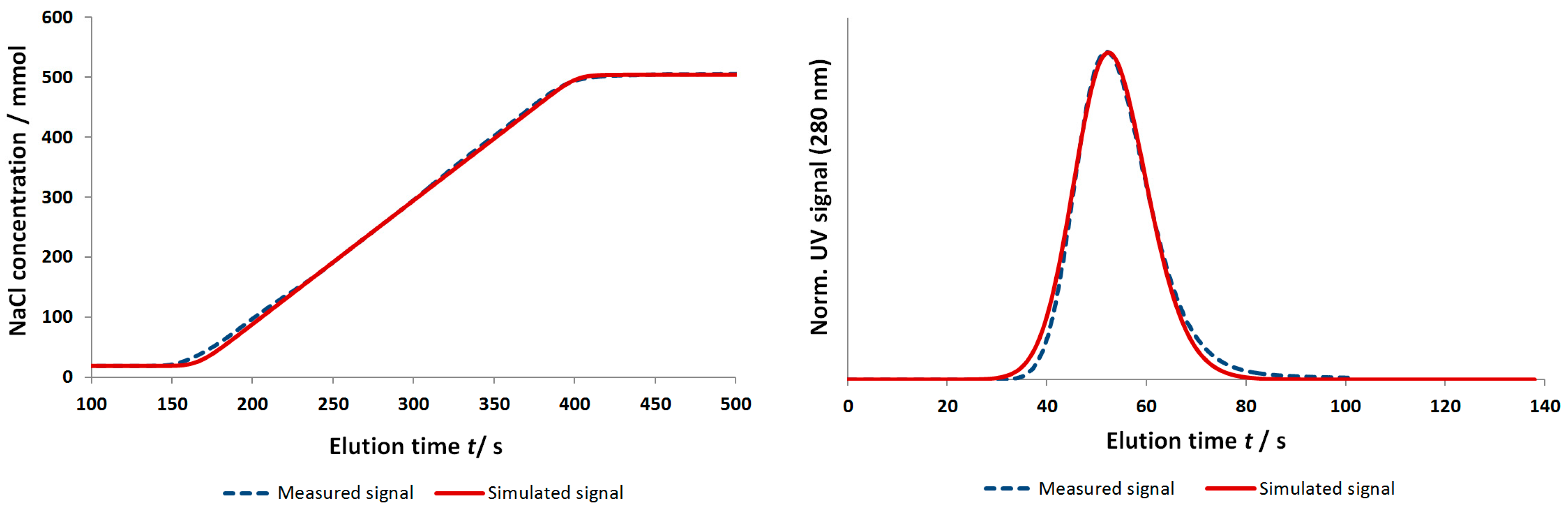
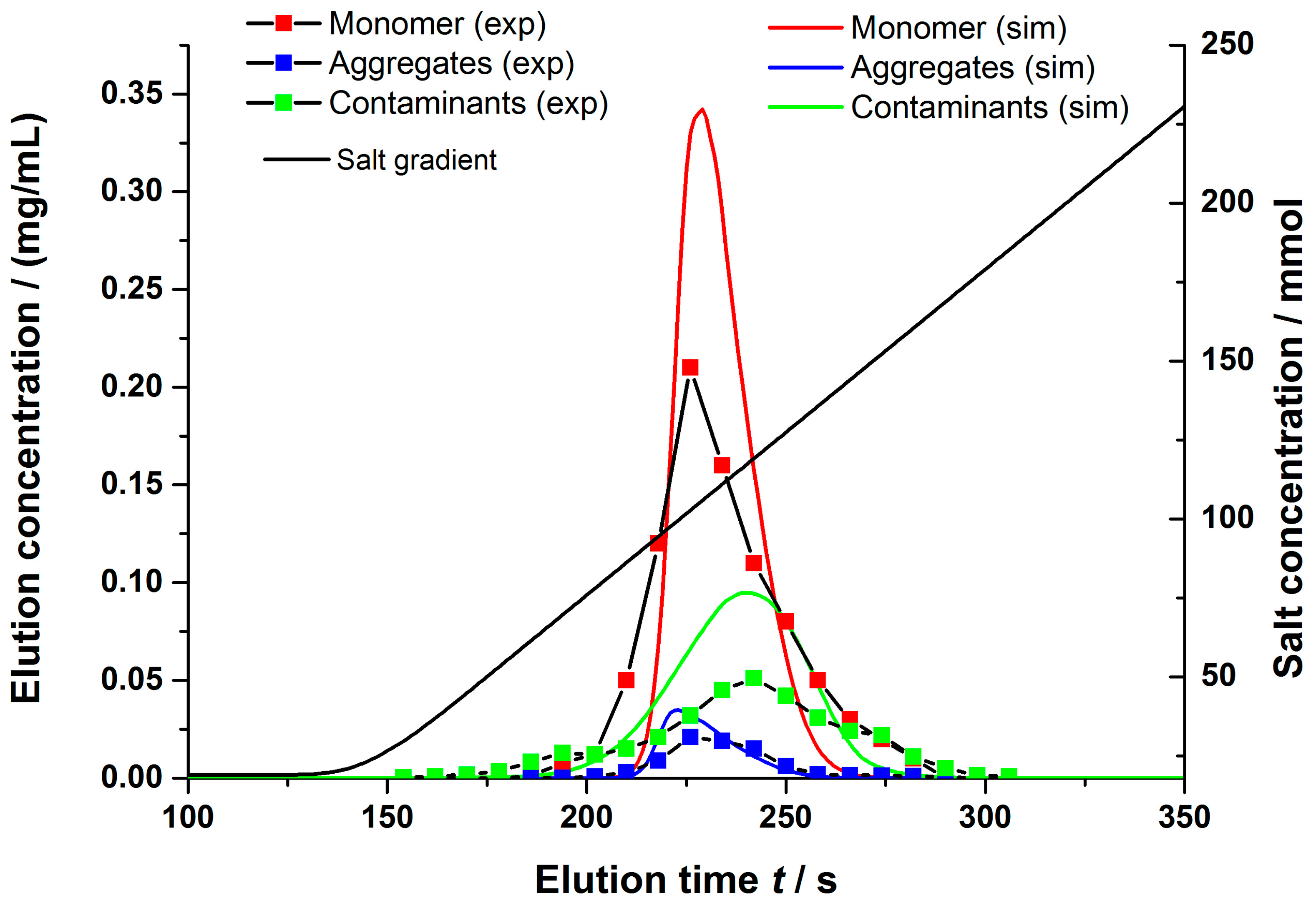
4.2.1. Gradient Elution Experiments
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sommerfeld, S.; Strube, J. Challenges in biotechnology production—Generic processes and process optimization for monoclonal antibodies. Chem. Eng. Process. Process Intensif. 2005, 44, 1123–1137. [Google Scholar] [CrossRef]
- Gronemeyer, P.; Ditz, R.; Strube, J. Trends in Upstream and Downstream Process Development for Antibody Manufacturing. Bioengineering 2014, 1, 188–212. [Google Scholar] [CrossRef]
- Saraswat, M.; Musante, L.; Ravidá, A.; Shortt, B.; Byrne, B.; Holthofer, H. Preparative Purification of Recombinant Proteins: Current Status and Future Trends. BioMed Res. Int. 2013, 2013, 312709. [Google Scholar] [CrossRef] [PubMed]
- Freitag, R. Chromatographic Techniques in the Downstream Processing of Proteins in Biotechnology. In Animal Cell Biotechnology SE—25; Pörtner, R., Ed.; Methods in Molecular Biology; Humana Press: New York, NY, USA, 2014; Volume 1104, pp. 419–458. [Google Scholar]
- Ghosh, R. Protein separation using membrane chromatography: Opportunities and challenges. J. Chromatogr. A 2002, 952, 13–27. [Google Scholar] [CrossRef]
- Charcosset, C. Review Purification of Proteins by Membrane Chromatography. J. Chem. Technol. Biotechnol. 1998, 71, 95–110. [Google Scholar] [CrossRef]
- Hahn, R.; Panzer, M.; Hansen, E.; Mollerup, J.; Jungbauer, A. Mass transfer properties of monoliths. Sep. Sci. Technol. 2002, 37, 1545–1565. [Google Scholar] [CrossRef]
- Jungbauer, A. Chromatographic media for bioseparation. J. Chromatogr. A 2005, 1065, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Burton, S.J.; Carbonell, R.G.; Gurgel, P.V.; Zheng, Y. High-Surface Area Fibers and Nonwoven Membranes for Use in Bioseparations. Patent WO 2012068442 A1, 24 May 2012. [Google Scholar]
- Schwellenbach, J.; Taft, F.; Villain, L.; Strube, J. Preparation and characterization of high capacity, strong cation-exchange fiber based adsorbents. J. Chromatogr. A 2016, 1447, 92–106. [Google Scholar] [CrossRef] [PubMed]
- Randunu, K.M.; Marcus, R.K. Microbore polypropylene capillary channeled polymer (C-CP) fiber columns for rapid reversed-phase HPLC of proteins. Anal. Bioanal. Chem. 2012, 404, 721–729. [Google Scholar] [CrossRef] [PubMed]
- Marcus, R.K. Use of polymer fiber stationary phases for liquid chromatography separations: Part II—Applications. J. Sep. Sci. 2009, 32, 695–705. [Google Scholar] [CrossRef] [PubMed]
- Yavorsky, D.; Amara, J.; Umana, J.; Cataldo, W.; Kozlov, M.; Stone, M. Chromatography Media and Method. Patent WO 2012015908 A2, 2 February 2012. [Google Scholar]
- Borrmann, C.; Helling, C.; Lohrmann, M.; Sommerfeld, S.; Strube, J. Phenomena and Modeling of Hydrophobic Interaction Chromatography. Sep. Sci. Technol. 2011, 46, 1289–1305. [Google Scholar] [CrossRef]
- Ndocko Ndocko, E.; Ditz, R.; Josch, J.-P.; Strube, J. New Material Design Strategy for Chromatographic Separation Steps in Bio-Recovery and Downstream Processing. Chem. Ing. Tech. 2011, 83, 113–129. [Google Scholar] [CrossRef]
- Shekhawat, L.K.; Manvar, A.P.; Rathore, A.S. Enablers for QbD implementation: Mechanistic modeling for ion-exchange membrane chromatography. J. Membr. Sci. 2016, 500, 86–98. [Google Scholar] [CrossRef]
- Zobel, S.; Helling, C.; Ditz, R.; Strube, J. Design and Operation of Continuous Countercurrent Chromatography in Biotechnological Production. Ind. Eng. Chem. Res. 2014, 53, 9169–9185. [Google Scholar] [CrossRef]
- Kaczmarski, K.; Antos, D.; Sajonz, H.; Sajonz, P.; Guiochon, G. Comparative modeling of breakthrough curves of bovine serum albumin in anion-exchange chromatography. J. Chromatogr. A 2001, 925, 1–17. [Google Scholar] [CrossRef]
- Gu, T.; Mehay, A. A General Rate Model of Ion-Exchange Chromatography for Investigating Ion-Exchange Behavior and Scale-up. J. Microb. Biochem. Technol. 2014, 6, 216–222. [Google Scholar]
- Guelat, B.; Khalaf, R.; Lattuada, M.; Costioli, M.; Morbidelli, M. Protein adsorption on ion exchange resins and monoclonal antibody charge variant modulation. J. Chromatogr. A 2016, 1447, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Steinebach, F.; Angarita, M.; Karst, D.J.; Müller-Späth, T.; Morbidelli, M. Model based adaptive control of a continuous capture process for monoclonal antibodies production. J. Chromatogr. A 2016, 1444, 50–56. [Google Scholar] [CrossRef] [PubMed]
- Jungbauer, A. Insights into the chromatography of proteins provided by mathematical modeling. Curr. Opin. Biotechnol. 1996, 7, 210–218. [Google Scholar] [CrossRef]
- Dimartino, S.; Boi, C.; Sarti, G.C. A validated model for the simulation of protein purification through affinity membrane chromatography. J. Chromatogr. A 2011, 1218, 1677–1690. [Google Scholar] [CrossRef] [PubMed]
- Boi, C.; Dimartino, S.; Sarti, G.C. Modelling and simulation of affinity membrane adsorption. J. Chromatogr. A 2007, 1162, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Boi, C.; Dimartino, S.; Sarti, G.C. Experimental and simulation analysis of membrane adsorbers used for the primary capture step in antibody manufacturing. In Proceedings of the 1/st intern. Conference on industrial biotechnology (Chemical Engineering Transactions), Napoli, Italy, 8–11 June 2008; pp. 91–96.
- Ladd Effio, C.; Hahn, T.; Seiler, J.; Oelmeier, S.A.; Asen, I.; Silberer, C.; Villain, L.; Hubbuch, J. Modeling and simulation of anion-exchange membrane chromatography for purification of Sf9 insect cell-derived virus-like particles. J. Chromatogr. A 2016, 1429, 142–154. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Yuan, Q.; Zhao, J.; Li, Y. Comparison of general rate model with a new model—Artificial neural network model in describing chromatographic kinetics of solanesol adsorption in packed column by macroporous resins. J. Chromatogr. A 2007, 1145, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Francis, P.; von Lieres, E.; Haynes, C. Zonal rate model for stacked membrane chromatography. I: Characterizing solute dispersion under flow-through conditions. J. Chromatogr. A 2011, 1218, 5071–5078. [Google Scholar] [CrossRef] [PubMed]
- Franke, A.; Forrer, N.; Butté, A.; Cvijetić, B.; Morbidelli, M.; Jöhnck, M.; Schulte, M. Role of the ligand density in cation exchange materials for the purification of proteins. J. Chromatogr. A 2010, 1217, 2216–2225. [Google Scholar] [CrossRef] [PubMed]
- Tejeda-Mansir, A.; Montesinos, R.M.; Guzmán, R. Mathematical analysis of frontal affinity chromatography in particle and membrane configurations. J. Biochem. Biophys. Methods 2001, 49, 1–28. [Google Scholar] [CrossRef]
- Yang, H.; Etzel, M.R. Evaluation of Three Kinetic Equations in Models of Protein Purification Using Ion-Exchange Membranes. Ind. Eng. Chem. Res. 2003, 42, 890–896. [Google Scholar] [CrossRef]
- Tatárová, I.; Dreveňák, P.; Kosior, A.; Polakovič, M. Equilibrium and kinetics of protein binding on ion-exchange cellulose membranes with grafted polymer layer. Chem. Pap. 2013, 67, 1527–1536. [Google Scholar] [CrossRef]
- Morbidelli, M.; Servida, A.; Storti, G.; Carra, S. Simulation of Multicomponent Adsorption Beds. Model Analysis and Numerical Solution. Ind. Eng. Chem. Fundam. 1982, 21, 123–131. [Google Scholar] [CrossRef]
- Tatárová, I.; Fáber, R.; Denoyel, R.; Polakovič, M. Characterization of pore structure of a strong anion-exchange membrane adsorbent under different buffer and salt concentration conditions. J. Chromatogr. A 2009, 1216, 941–947. [Google Scholar] [CrossRef] [PubMed]
- DePhillips, P.; Lenhoff, A.M. Pore size distributions of cation-exchange adsorbents determined by inverse size-exclusion chromatography. J. Chromatogr. A 2000, 883, 39–54. [Google Scholar] [CrossRef]
- Al-Bokari, M.; Cherrak, D.; Guiochon, G. Determination of the porosities of monolithic columns by inverse size-exclusion chromatography. J. Chromatogr. A 2002, 975, 275–284. [Google Scholar] [CrossRef]
- Desta, M.B. Batch Sorption Experiments: Langmuir and Freundlich Isotherm Studies for the Adsorption of Textile Metal Ions onto Teff Straw (Eragrostis tef) Agricultural Waste. J. Thermodyn. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Camperi, S.A.; Navarro, A.; Wolman, F.J.; Smolko, E.E.; Cascone, O.; Grasselli, M. Protein Adsorption onto Tentacle Cation-Exchange Hollow-Fiber Membranes. Biotechnol. Progress 1999, 15, 500–505. [Google Scholar] [CrossRef] [PubMed]
- Lan, Q.; Bassi, A.S.; Zhu, J.X.; Margaritis, A. A modified Langmuir model for the prediction of the effects of ionic strength on the equilibrium characteristics of protein adsorption onto ion exchange/affinity adsorbents. Chem. Eng. J. 2001, 81, 179–186. [Google Scholar] [CrossRef]
- Liu, H.-C.; Fried, J.R. Breakthrough of lysozyme through an affinity membrane of cellulose-cibacron blue. AIChE J. 1994, 40, 40–49. [Google Scholar] [CrossRef]
- Liapis, A.I.; Rippin, D.W.T. The simulation of binary adsorption in continuous countercurrent operation and a comparison with other operating modes. AIChE J. 1979, 25, 455–460. [Google Scholar] [CrossRef]
- Forrer, N. Antibody Purification: Ion-Exchange Chromatography; ETH Zuerich: Zuerich, Switzerland, 2008. [Google Scholar]
- Yamamoto, S.; Nakanishi, K.; Matsuno, R.; Kamikubo, T. Ion exchange chromatography of proteins-prediction of elution curves and operating conditions. I. Theoretical considerations. Biotechnol. Bioeng. 1983, 25, 1465–1483. [Google Scholar] [CrossRef] [PubMed]
- Haynes, H.W. A Model for the Application of Gas Chromatography to measurements of Diffusion in Bidisperse Structured Catalysts. AIChE J. 1973, 19, 1043–1046. [Google Scholar] [CrossRef]
- Thomas, H.; de Neuville, B.C.; Storti, G.; Morbidelli, M.; Joehnck, M.; Schulte, M. Role of tentacles and protein loading on pore accessibility and mass transfer in cation exchange materials for proteins. J. Chromatogr. A 2013, 1285, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Goto, M.; McCoy, B.J. Inverse size-exclusion chromatography for distributed pore and solute sizes. Chem. Eng. Sci. 2000, 55, 723–732. [Google Scholar] [CrossRef]
- Wilson, E.J.; Geankoplis, C.J. Liquid Mass Transfer at Very Low Reynolds Numbers in Packed Beds. Ind. Eng. Chem. Fundam. 1966, 5, 9–14. [Google Scholar] [CrossRef]
- Glueckauf, E. Theory of chromatography. Part 10.—Formulae for diffusion into spheres and their application to chromatography. Trans. Faraday Soc. 1955, 51, 1540–1551. [Google Scholar] [CrossRef]
- Guiochon, G. Preparative liquid chromatography. J. Chromatogr. A 2002, 965, 129–161. [Google Scholar] [CrossRef]
- Carta, G.; Cincotti, A. Film model approximation for non-linear adsorption and diffusion in spherical particles. Chem. Eng. Sci. 1998, 53, 3483–3488. [Google Scholar] [CrossRef]
- Wrzosek, K.; Ačai, P.; Gramblička, M.; Polakovič, M. Modeling of equilibrium and kinetics of human polyclonal immunoglobulin G adsorption on a tentacle cation exchanger. Chem. Pap. 2013, 67, 1537–1547. [Google Scholar] [CrossRef]
- Langmuir, I. The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]

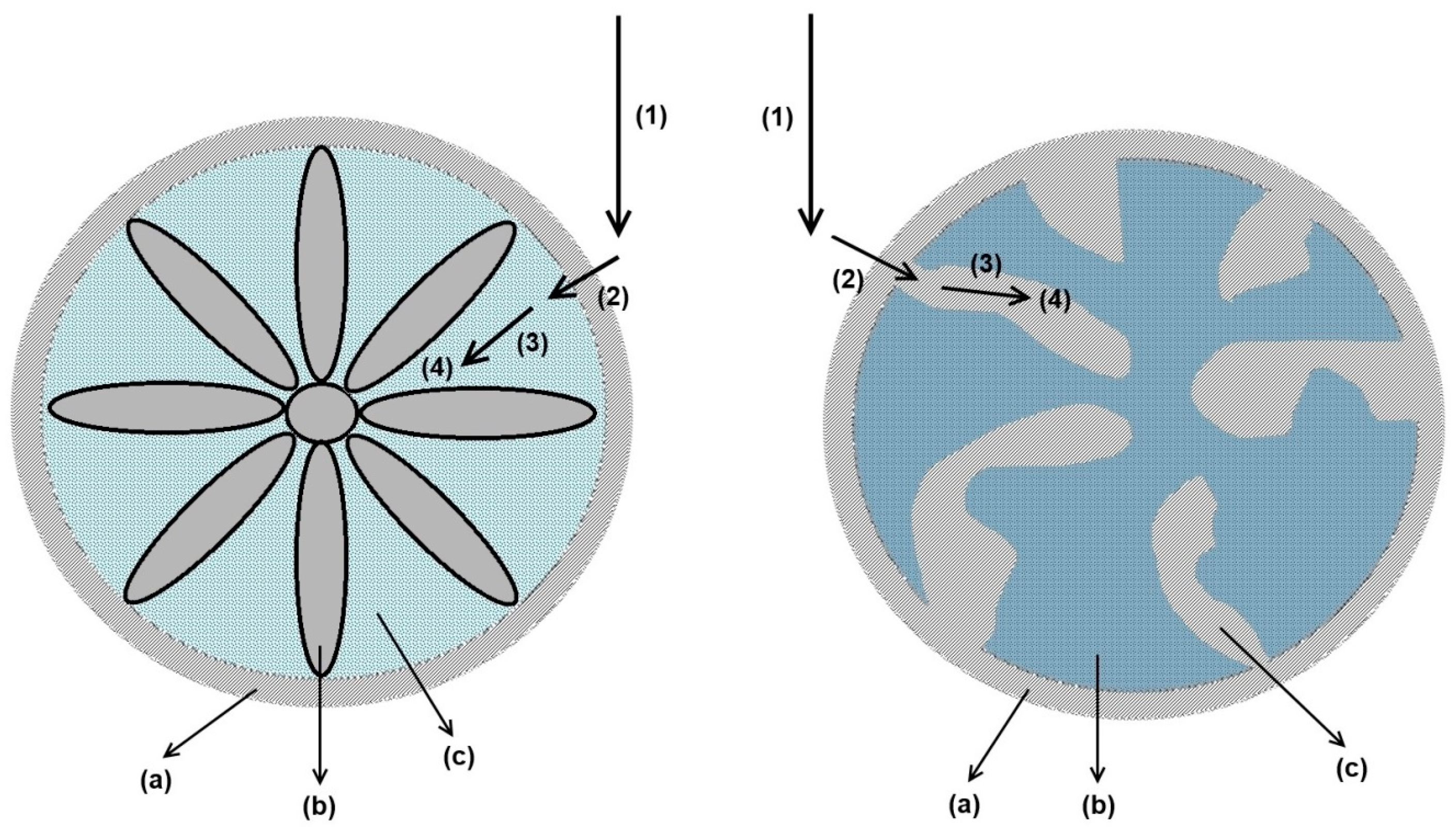




| Model Equations | Description |
|---|---|
| |
| |
| |
|
| Parameter | Value | Method of Determination | |
|---|---|---|---|
| 0.76 | Inverse size exclusion chromatography | ||
| 0.54 | |||
| 0.48 | |||
| /cm | 0.051 | Moment analysis | |
| Molecular Diffusion Coefficient/(m2/s) | (1/s) | Correlation/Geometrical consideration (Section 3.2.2) | |
| NaCl | 1.99 × 10−9 | 6.44 | |
| Acetone | 1.14 × 10−9 | 3.67 | |
| mAb | 4.00 × 10−11 | 0.129 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwellenbach, J.; Zobel, S.; Taft, F.; Villain, L.; Strube, J. Purification of Monoclonal Antibodies Using a Fiber Based Cation-Exchange Stationary Phase: Parameter Determination and Modeling. Bioengineering 2016, 3, 24. https://doi.org/10.3390/bioengineering3040024
Schwellenbach J, Zobel S, Taft F, Villain L, Strube J. Purification of Monoclonal Antibodies Using a Fiber Based Cation-Exchange Stationary Phase: Parameter Determination and Modeling. Bioengineering. 2016; 3(4):24. https://doi.org/10.3390/bioengineering3040024
Chicago/Turabian StyleSchwellenbach, Jan, Steffen Zobel, Florian Taft, Louis Villain, and Jochen Strube. 2016. "Purification of Monoclonal Antibodies Using a Fiber Based Cation-Exchange Stationary Phase: Parameter Determination and Modeling" Bioengineering 3, no. 4: 24. https://doi.org/10.3390/bioengineering3040024
APA StyleSchwellenbach, J., Zobel, S., Taft, F., Villain, L., & Strube, J. (2016). Purification of Monoclonal Antibodies Using a Fiber Based Cation-Exchange Stationary Phase: Parameter Determination and Modeling. Bioengineering, 3(4), 24. https://doi.org/10.3390/bioengineering3040024







