Transient Mechanical Response of Lung Airway Tissue during Mechanical Ventilation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Airway Tissue Model
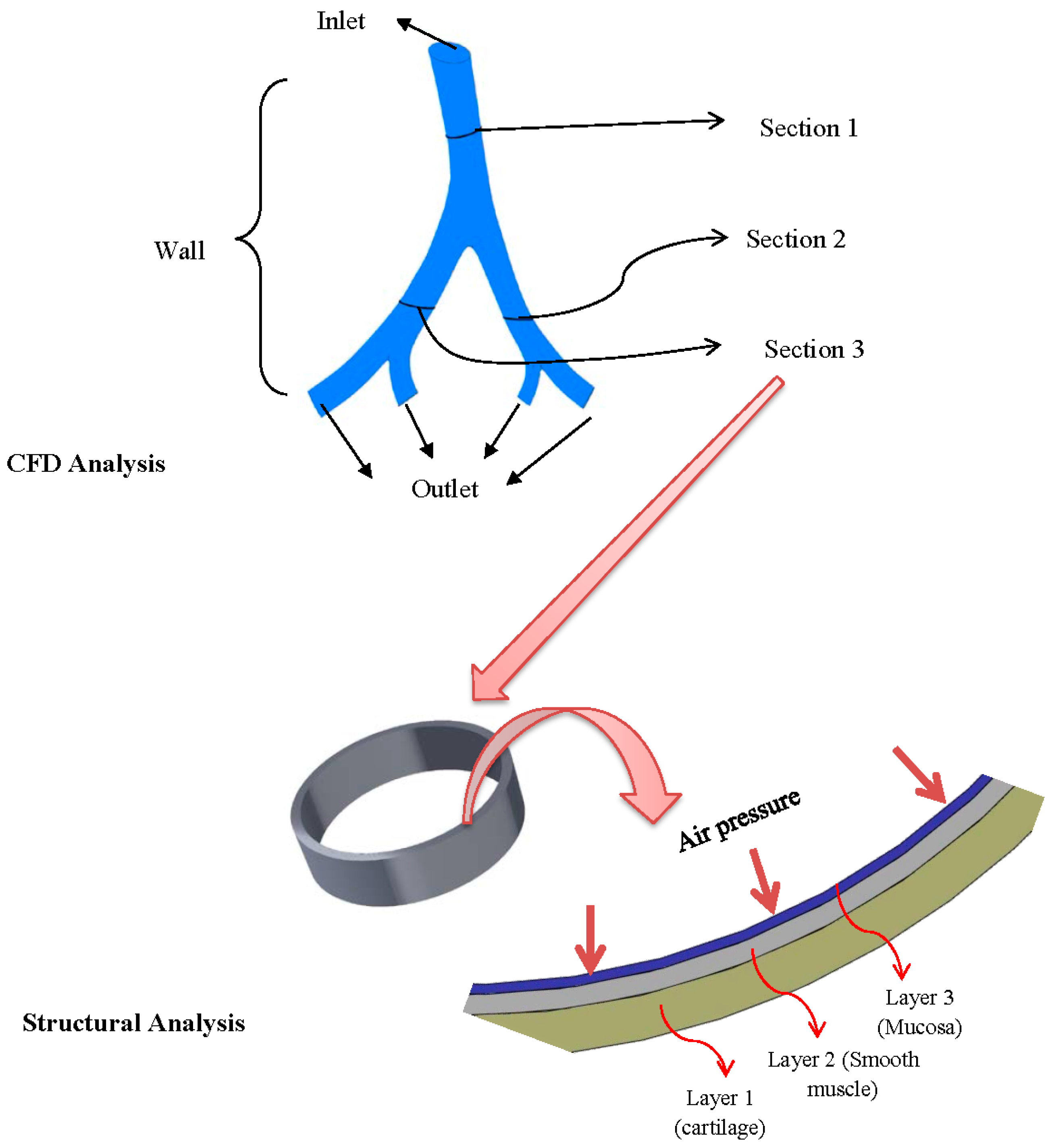
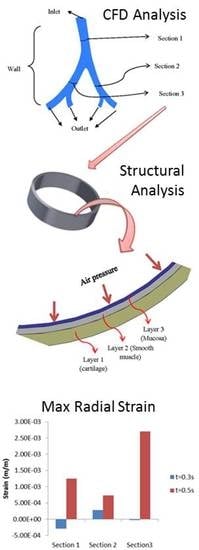
2.2. Computational Models and Boundary Conditions
2.2.1. Airflow Model
2.2.2. Airway Deformation
| Layer Name | Layer Number | Thickness at Each Section | ||
|---|---|---|---|---|
| Section 1 | Section 2 | Section 3 | ||
| Mucosa | Layer 1 | 66.56 µm | 49.59 µm | 38.61 µm |
| Smooth Muscle | Layer 2 | 31.95 µm | 22.17 µm | 18.53 µm |
| Cartilage | Layer 3 | 15.29 µm | 11.37 µm | 8.86 µm |
2.2.3. Numerical Solution to the Models
3. Results and Discussion
3.1. Airflow Simulation
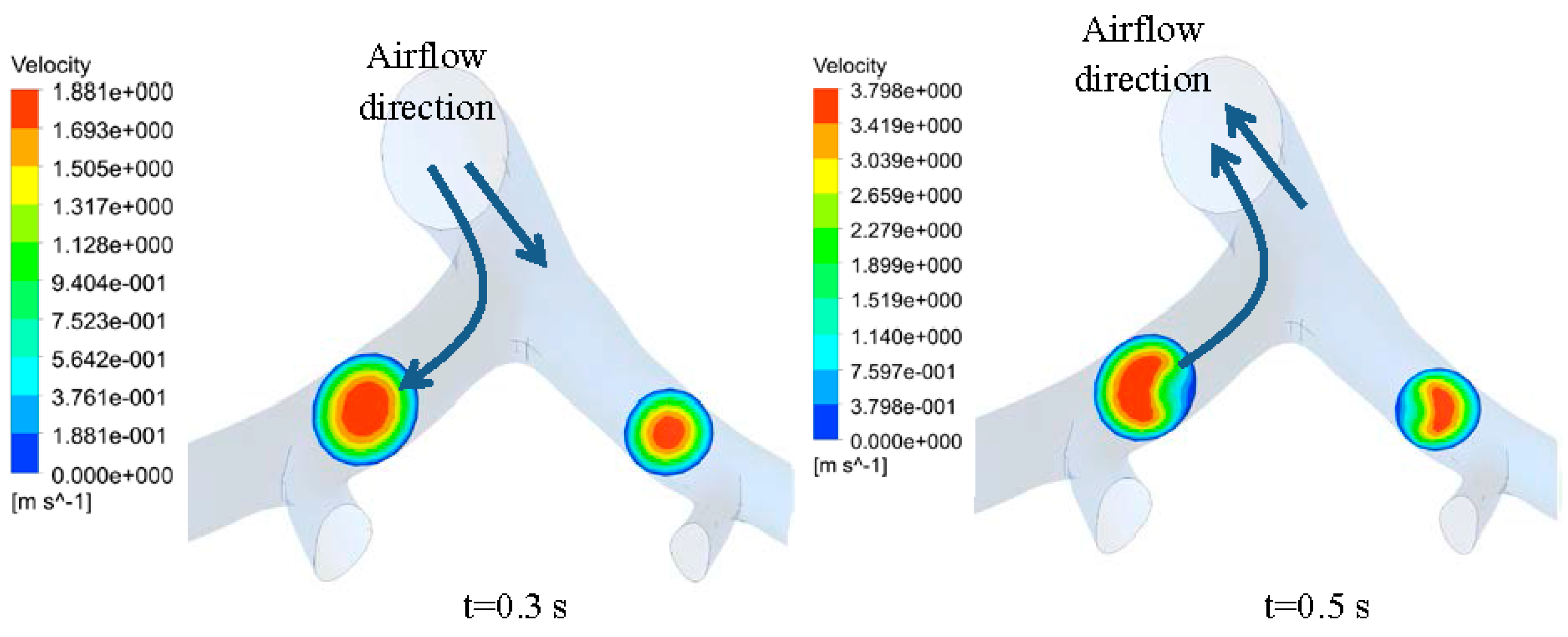
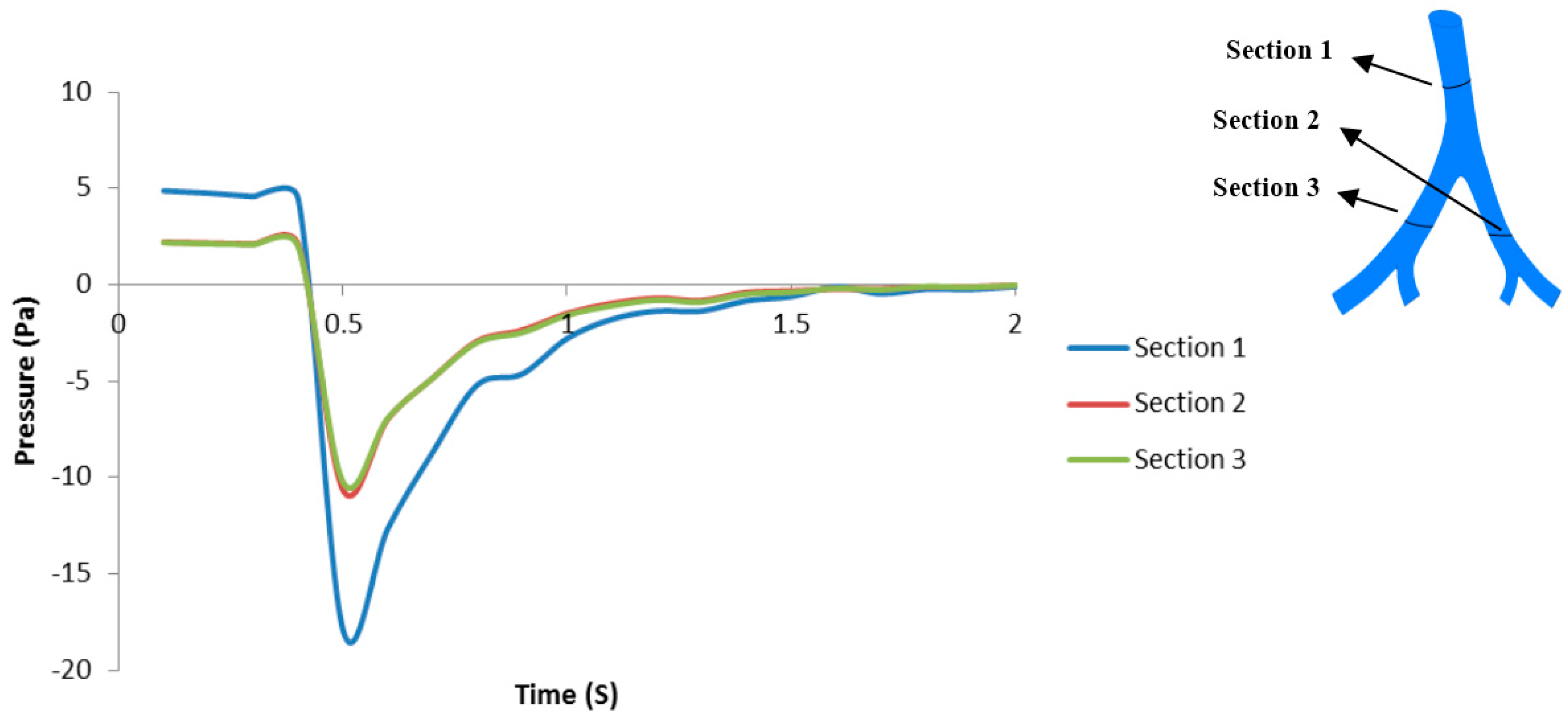
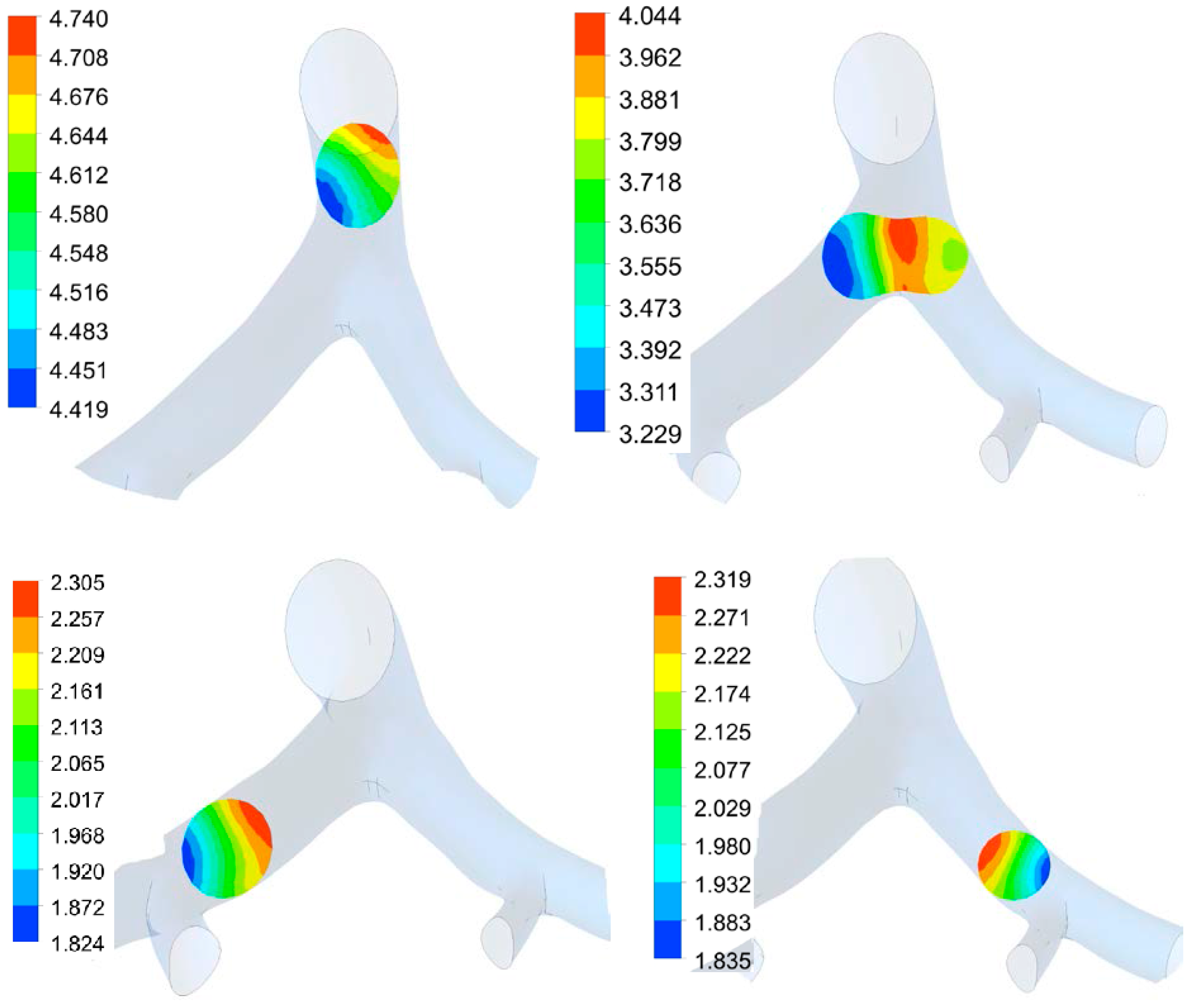
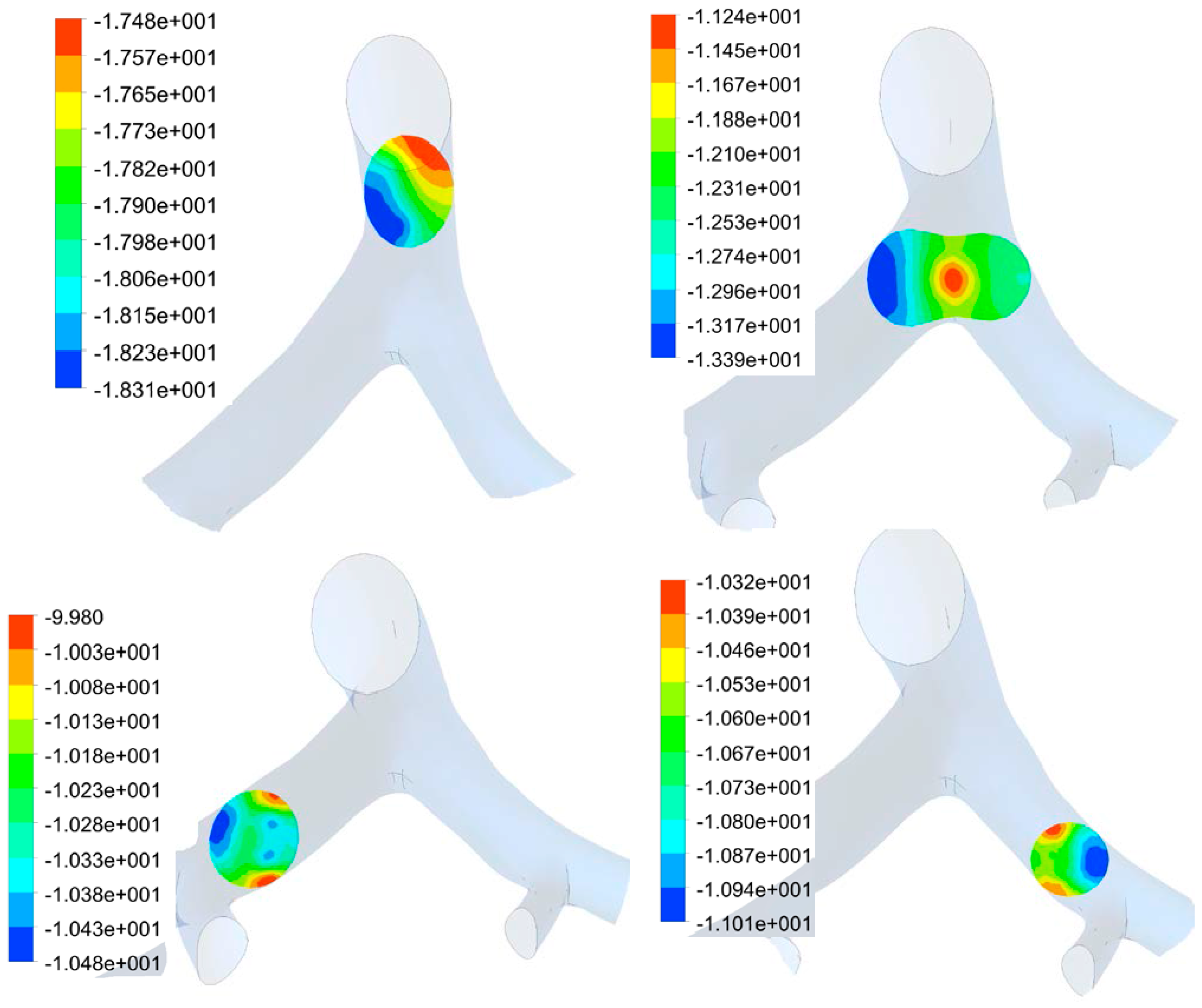
3.2. Transient Mechanical Response
3.2.1. Mesh Convergence Study
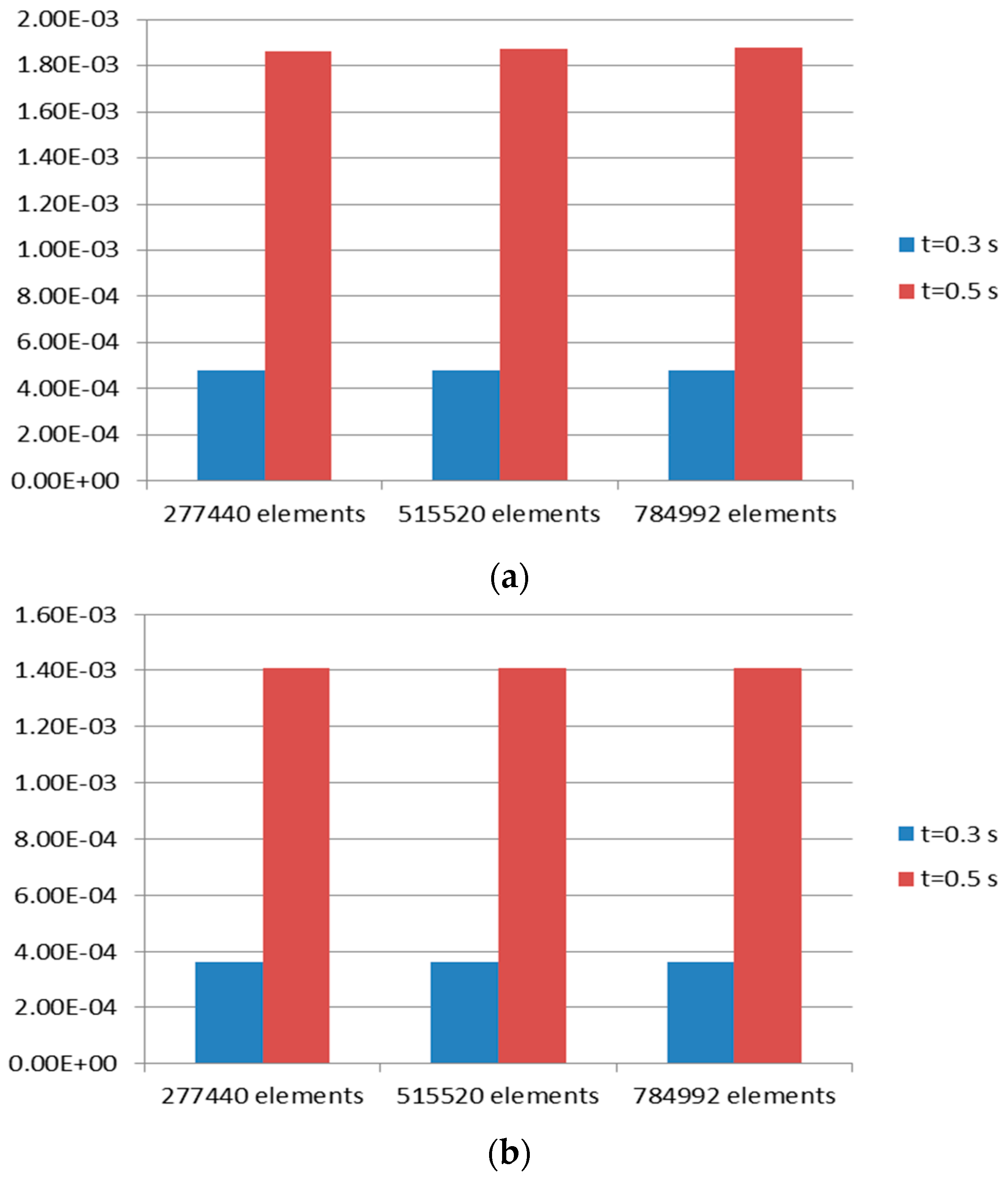
| Case Name | Number of Elements | t = 0.3 s | t = 0.5 s |
|---|---|---|---|
| Case 1 | 277,440 | 3.45 × 10−0.06 | 1.40 × 10−0.05 |
| Case 2 | 515,520 | 1.24 × 10−0.06 | 5.00 × 10−0.06 |
| Case 3 | 784,992 |
| Case Name | Number of Elements | t = 0.3 s | t = 0.5 s |
|---|---|---|---|
| Case 1 | 277,440 | −1.00 × 10−0.08 | −1.00 × 10−0.07 |
| Case 2 | 515,520 | 0.00 | 0.00 |
| Case 3 | 784,992 |
3.2.2. Airway Strains
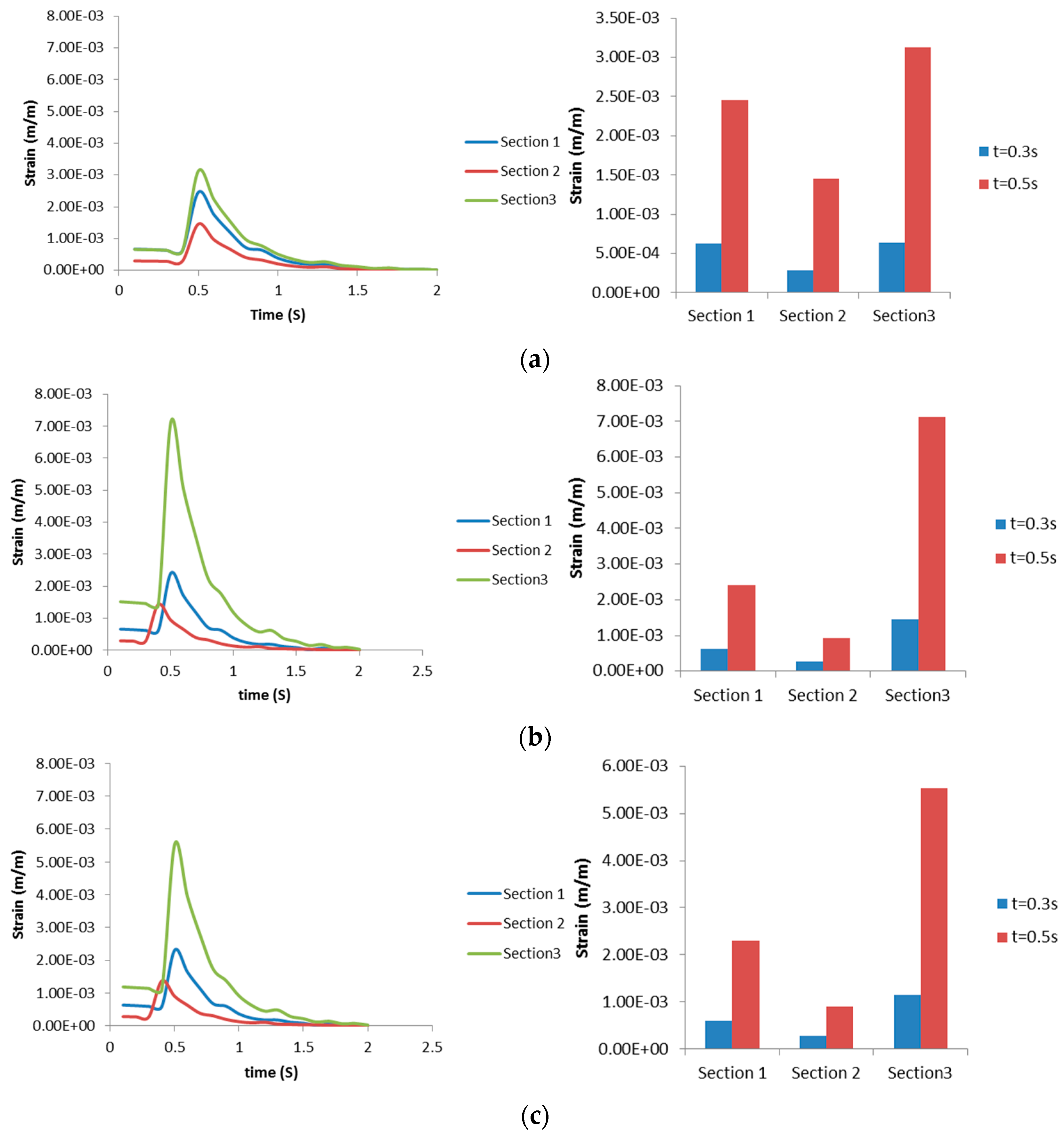
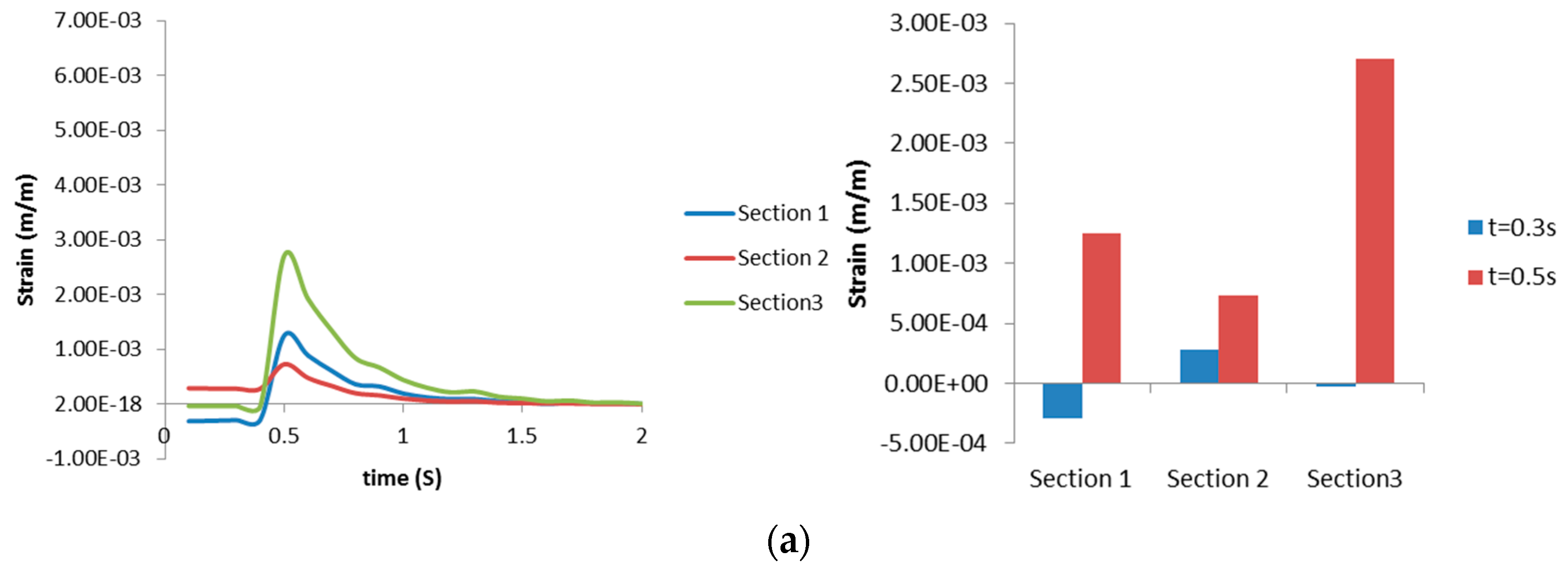
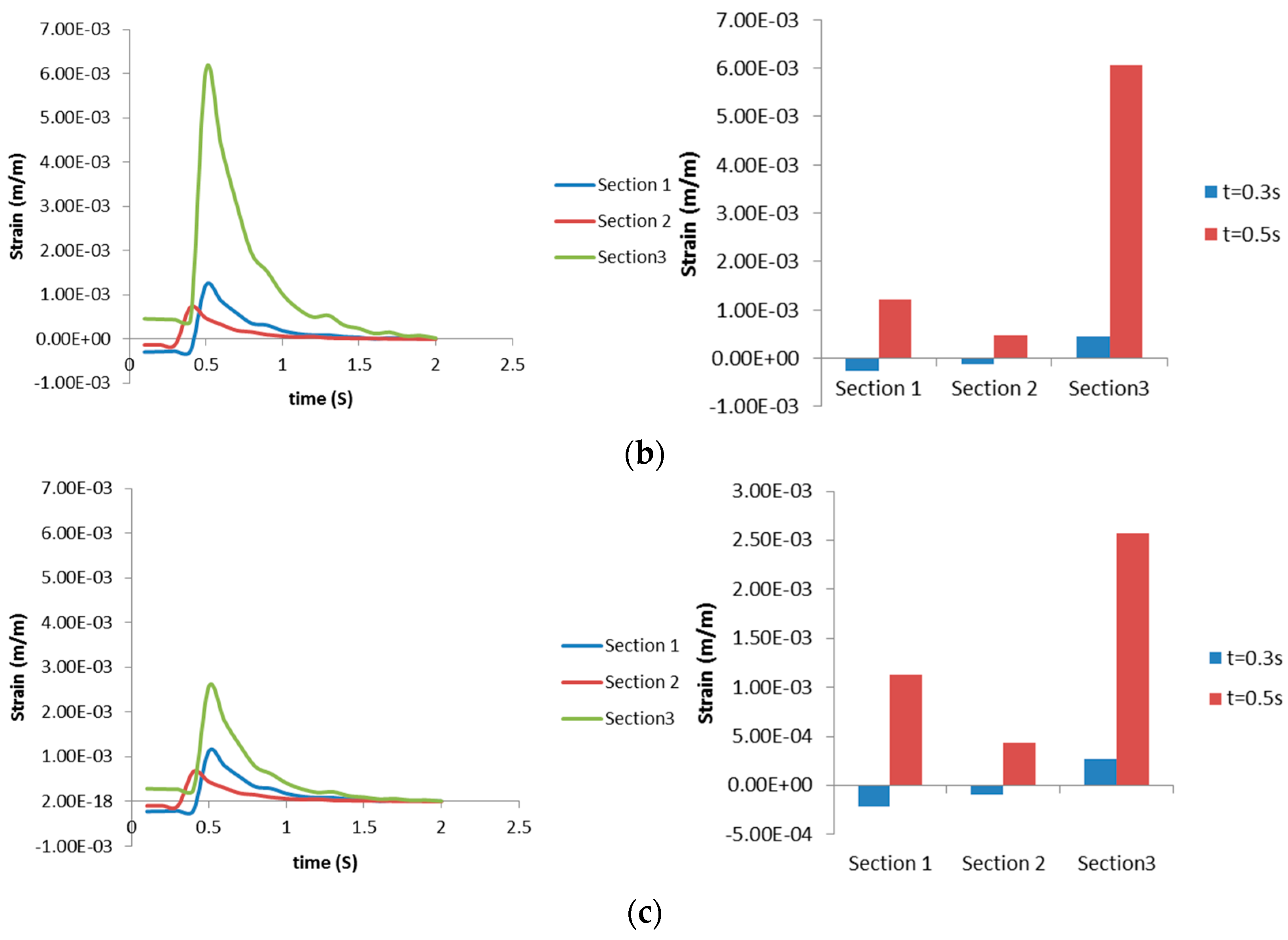
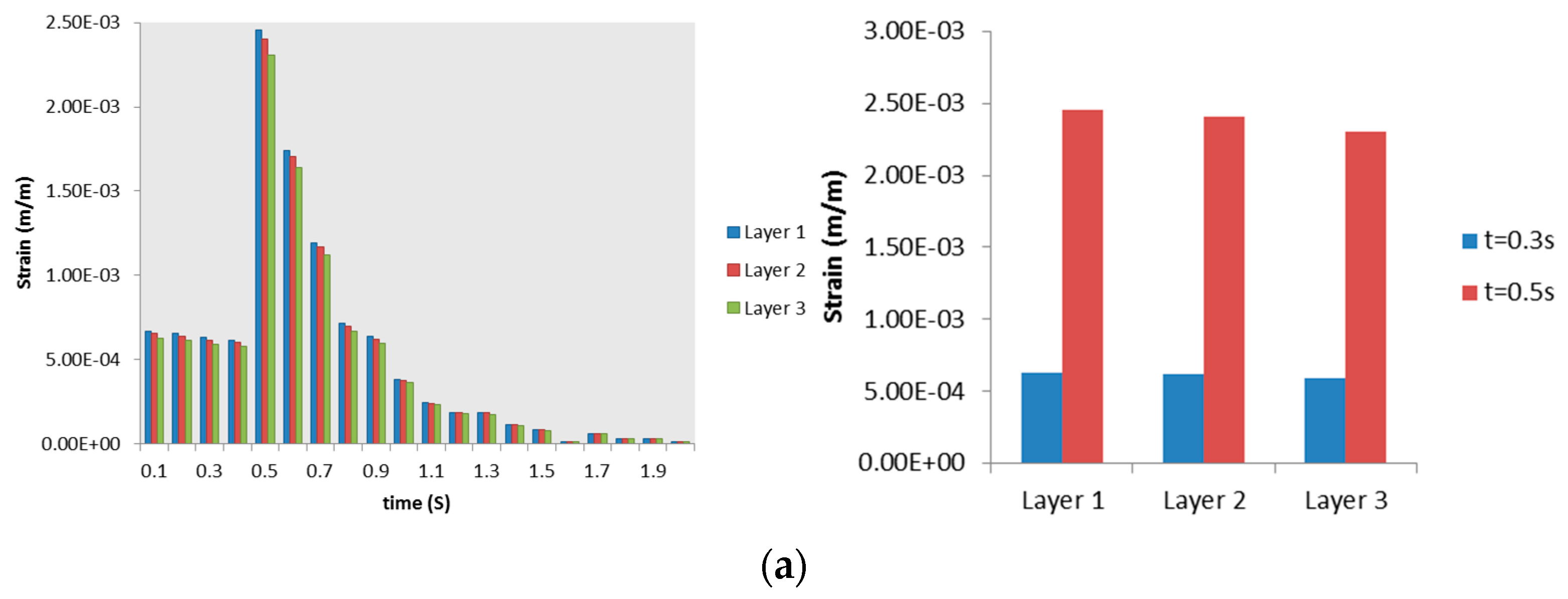
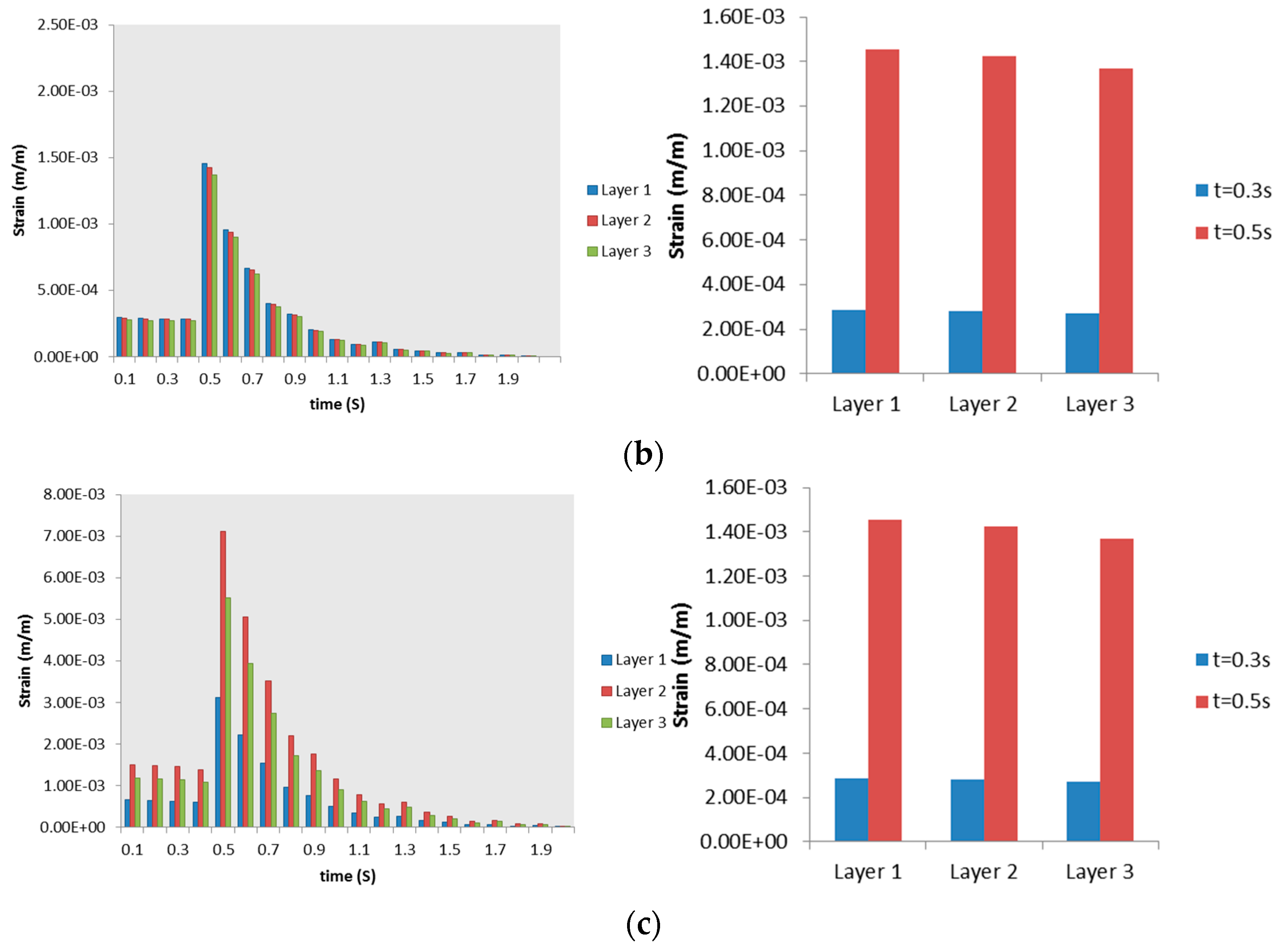
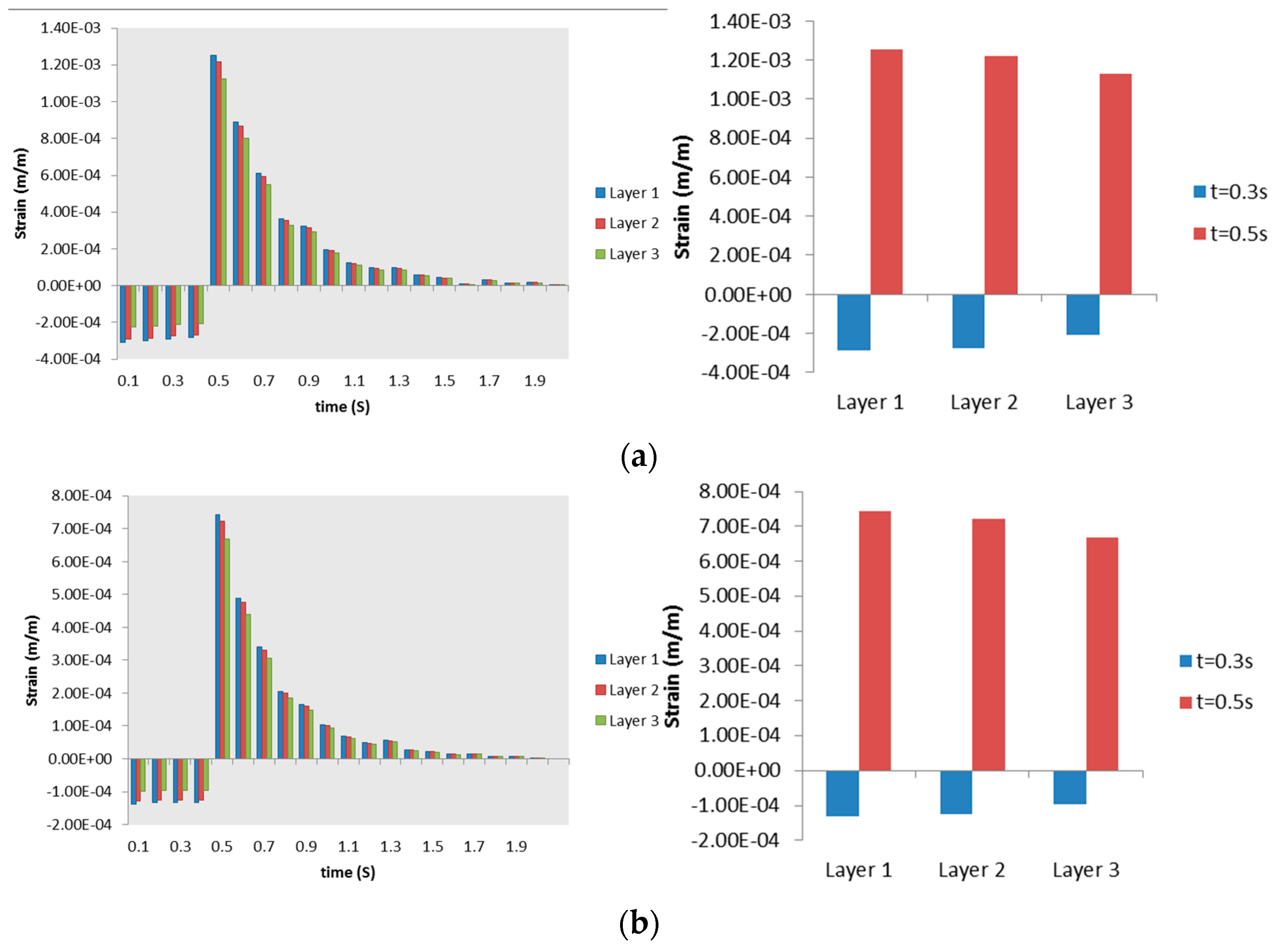
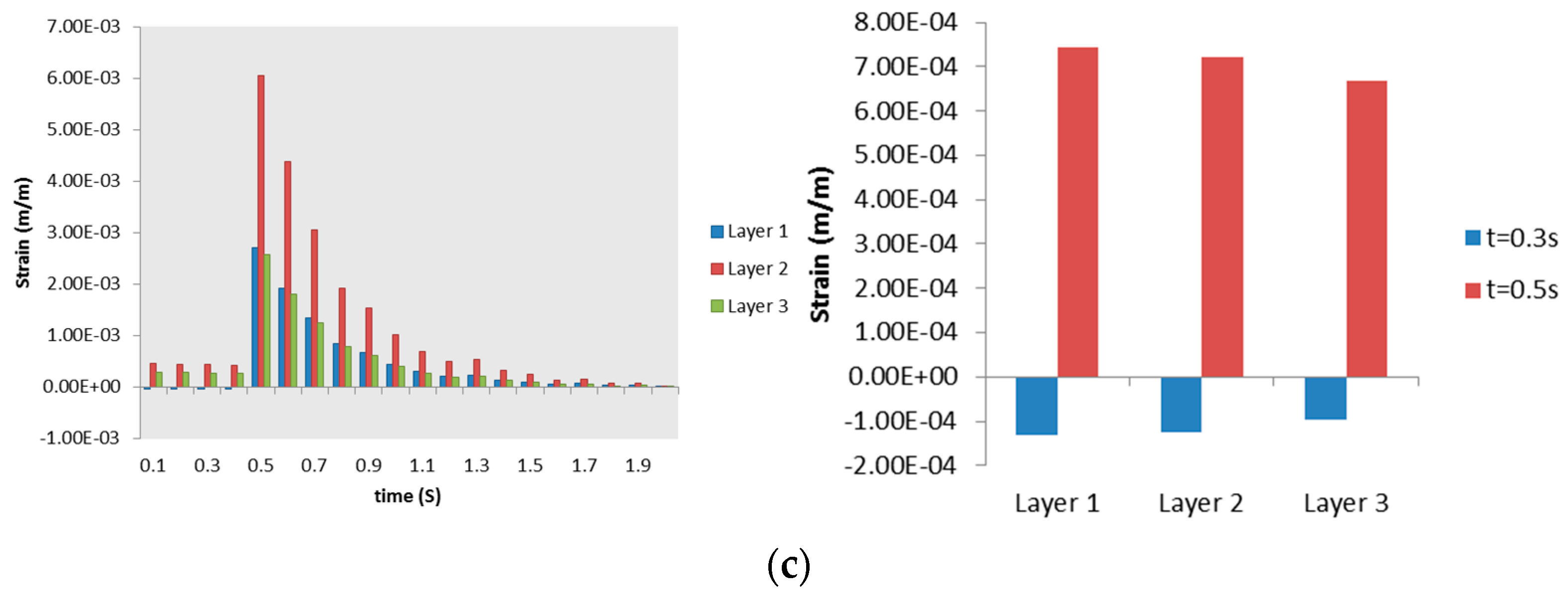

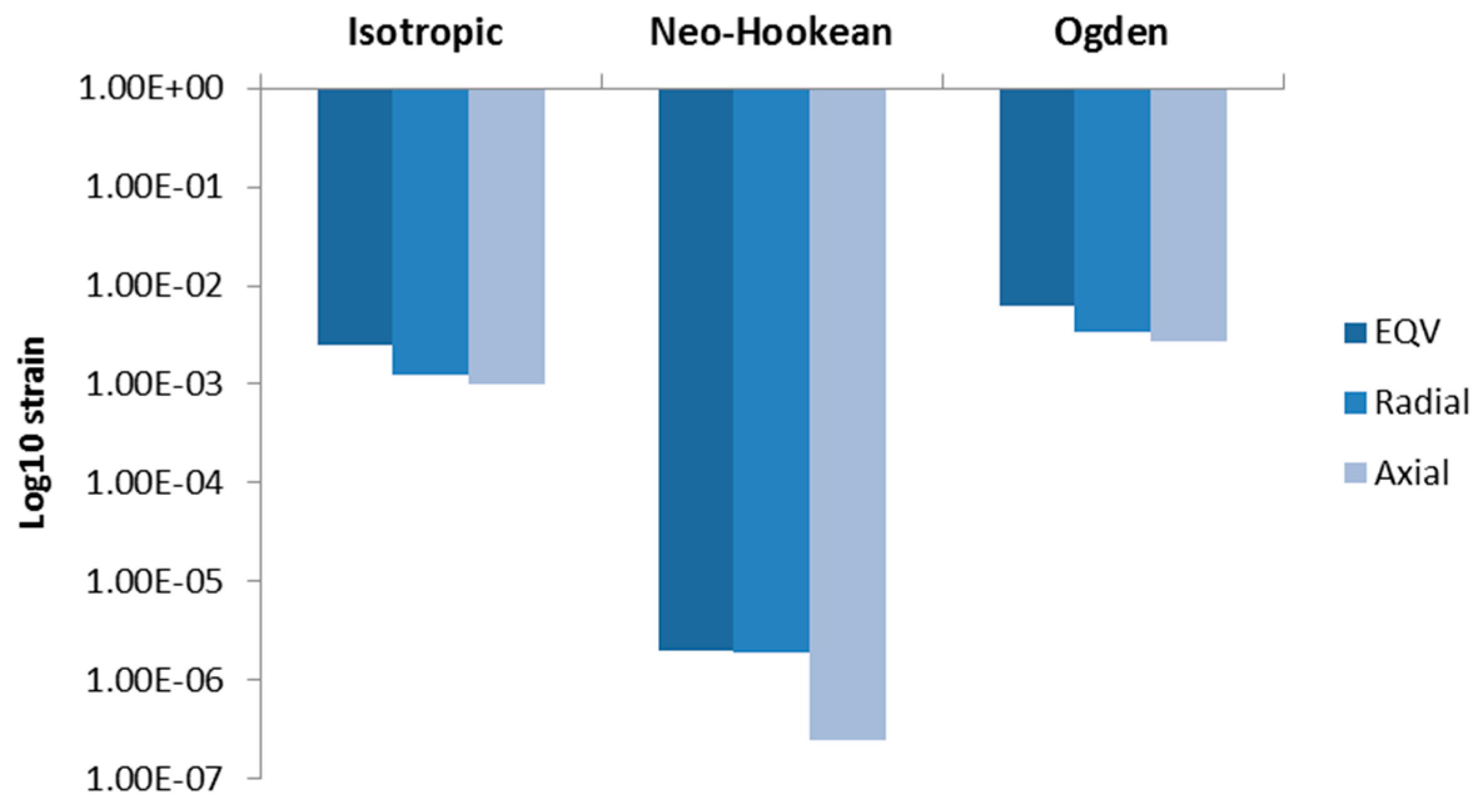
3.3. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ricard, J.D.; Dreyfuss, D.; Saumon, G. Ventilator-induced lung injury. Eur. Respir. J. Suppl. 2003, 42, S2–S9. [Google Scholar] [CrossRef]
- Pinhu, L.; Whitehead, T.; Evans, T.; Griffiths, M. Ventilator-associated lung injury. Lancet 2003, 3613, 32–40. [Google Scholar] [CrossRef]
- Parker, J.C.; Townsley, M.I.; Rippe, B.; Taylor, A.E.; Thigpen, J. Increased microvascular permeability in dog lungs due to high peak airway pressures. J. Appl. Physiol. 1984, 571, 1809–1816. [Google Scholar]
- Dreyfuss, D.; Saumon, G. Role of tidal volume, FRC, and end-inspiratory volume in the development of pulmonary edema following mechanical ventilation. Am. Rev. Respir. Dis. 1993, 1481, 1194–1203. [Google Scholar] [CrossRef] [PubMed]
- Hernandez, L.A.; Peevy, K.J.; Moise, A.A.; Parker, J.C. Chest wall restriction limits high airway pressure-induced lung injury in young rabbits. J. Appl. Physiol. 1989, 662, 2364–2368. [Google Scholar]
- Dos Santos, C.C.; Slutsky, A.S. The contribution of biophysical lung injury to the development of biotrauma. Annu. Rev. Physiol. 2006, 68, 585–618. [Google Scholar] [CrossRef] [PubMed]
- Ning, Q.; Wang, X. Activations of mitogen-activated protein kinase and nuclear factor-kappaB by mechanical stretch result in ventilation-induced lung injury. Med. Hypotheses 2007, 683, 56–60. [Google Scholar] [CrossRef]
- Matsuoka, T.; Kawano, T.; Miyasaka, K. Role of high-frequency ventilation in surfactant-depleted lung injury as measured by granulocytes. J. Appl. Physiol. 1994, 765, 539–544. [Google Scholar]
- Sugiura, M.; McCulloch, P.R.; Wren, S.; Dawson, R.H.; Froese, A.B. Ventilator pattern influences neutrophil influx and activation in atelectasis-prone rabbit lung. J. Appl. Physiol. 1994, 771, 1355–1365. [Google Scholar]
- Guan, X.; Segal, R.A.; Shearer, M.; Martonen, T.B. Mathematical Model of Airflow in the Lungs of Children II: Effects of Ventilatory Parameters. J. Theor. Med. 2000, 3, 51–62. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Zhang, Z. Targeted drug aerosol deposition analysis for a four-generation lung airway model with hemispherical tumors. J. Biomech. Eng. 2003, 125, 197–206. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.L.; Liu, Y.; Luo, H.Y. Respiratory flow in obstructed airways. J. Biomech. 2006, 39, 2743–2751. [Google Scholar] [CrossRef] [PubMed]
- Brouns, M.; Jayaraju, S.T.; Lacor, C.; de Mey, J.; Noppen, M.; Vincken, W.; Verbanck, S. Tracheal stenosis: A flow dynamics study. J. Appl. Physiol. 2007, 102, 1178–1184. [Google Scholar] [CrossRef] [PubMed]
- Koombua, K.; Pidaparti, R.M. Inhalation Induced Stresses and Flow Characteristics in Human Airways through Fluid-Structure Interaction Analysis. Model. Simul. Eng. 2008. Available online: http://www.hindawi.com/journals/mse/2008/358748/ (accessed on 28 September 2015). [Google Scholar] [CrossRef]
- Rolle, T.; Pidaparti, R.M. Tissue strains induced in airways due to mechanical ventilation. In Proceedings of the ASME Early Career Technical Conference, Atlanta, Georgia, USA, 4–5 November 2011.
- Pidaparti, R.M.; Koombua, K. Tissue strains induced in airways due to mechanical ventilation. Mol. Cell Biomech. 2011, 81, 149–168. [Google Scholar]
- Koombua, K.; Pidaparti, R.M.; Longest, P.W.; Ward, K.R. Biomechanical Aspects of Compliant Airways due to Mechanical Ventilation. Mol. Cell Biomech. 2009, 6, 203–216. [Google Scholar] [PubMed]
- Kamm, R.D. Airway wall mechanics. Annu. Rev. Biomed. Eng. 1999, 1, 47–72. [Google Scholar] [CrossRef] [PubMed]
- Bai, A.; Eidelman, D.H.; Hogg, J.C.; James, A.L.; Lambert, R.K.; Ludwig, M.S.; Martin, J.; McDonald, D.M.; Mitzner, W.A.; et al. Proposed nomenclature for quantifying subdivisions of the bronchial wall. J. Appl. Physiol. 1994, 72, 1011–1014. [Google Scholar]
- Arambakam, R.; Pidaparti, R.; Reynolds, R.M.; Heise, A. Computational Fluid Dynamics Anslysis of Typical Lower Lung Bifurcations under Mechanical Ventilation and Normal Breathing. In Proceedings of the Fourteenth Annual Early Career Technical Conference, Birmingham, UK, 1–2 November 2014.
- Weed, B.; Patnaik, S.; Rougeau-Browning, M.; Brazile, B.; Liao, J.; Prabhu, R.; Williams, L. Experimental Evidence of Mechanical Isotropy in Porcine Lung Parenchyma. Materials 2015, 82, 2454–2466. [Google Scholar] [CrossRef]
- Xia, G.; Tawhai, M.H.; Hoffman, E.A.; Lin, C.L. Airway wall stiffening increases peak wall shear stress: A fluid-structure interaction study in rigid and compliant airways. Ann. Biomed. Eng. 2010, 38, 1836–1853. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.J.; Yager, D.; Fung, Y.C. Measurement of the Mechanical Properties of the Human Lung Tissue. J. Biomech. Eng. 1987, 109, 169–174. [Google Scholar] [CrossRef] [PubMed]
- Sul, B.; Wallqvist, A.; Morris, M.J.; Reifman, J.; Rakesh, V. A computational study of the respiratory airflow characteristics in normal and obstructed human airways. Comput. Biol. Med. 2014, 52, 130–143. [Google Scholar] [CrossRef] [PubMed]
- Isabey, D.; Chang, H.K. A model study of flow dynamics in human central airways. Part II: Secondary flow velocities. Respir. Physiol. 1982, 499, 97–113. [Google Scholar] [CrossRef]
- Shah, M.R.; Wedgwood, S.; Czech, L.; Kim, G.A.; Lakshminrusimha, S.; Schumacker, P.T.; Steinhorn, R.H.; Farrow, K.N. Cyclic stretch induces inducible nitric oxide synthase and soluble guanylate cyclase in pulmonary artery smooth muscle cells. Int. J. Mol. Sci. 2013, 144, 4334–4348. [Google Scholar] [CrossRef] [PubMed]
- Tepper, R.S.; Ramchandani, R.; Argay, E.; Zhang, L.; Xue, Z.; Liu, Y.; Gunst, S.J. Chronic strain alters the passive and contractile properties of rabbit airways. J. Appl. Physiol. 2005, 98, 1949–1954. [Google Scholar] [CrossRef] [PubMed]
- Chapman, K.E.; Sinclair, S.E.; Zhuang, D.; Hassid, A.; Desai, L.P.; Waters, C.M. Cyclic mechanical strain increases reactive oxygen species production in pulmonary epithelial cells. Am. J. Physiol. Lung Cell Mol. Physiol. 2005, 289, L834–L841. [Google Scholar] [CrossRef] [PubMed]
- Chandel, N.S.; Sznajder, J.I. Stretching the lung and programmed cell death. Am. J. Physiol. Lung Cell Mol. Physiol. 2000, 279, L1003–L1004. Available online: http://ajplung.physiology.org/content/279/6/L1003.abstract (accessed on 15 March 2015). [Google Scholar]
- Copland, I.B.; Post, M. Stretch-activated signaling pathways responsible for early response gene expression in fetal lung epithelial cells. J. Cell. Physiol. 2007, 210, 133–143. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, A.; Koombua, K.; Pidaparti, R.M.; Ward, K.R. Cellular Automata Modeling of Pulmonary Inflammation. Mol. Cell Biomech. 2012, 91, 141–156. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, I.B.M.; Aghasafari, P.; Pidaparti, R.M. Transient Mechanical Response of Lung Airway Tissue during Mechanical Ventilation. Bioengineering 2016, 3, 4. https://doi.org/10.3390/bioengineering3010004
Ibrahim IBM, Aghasafari P, Pidaparti RM. Transient Mechanical Response of Lung Airway Tissue during Mechanical Ventilation. Bioengineering. 2016; 3(1):4. https://doi.org/10.3390/bioengineering3010004
Chicago/Turabian StyleIbrahim, Israr Bin Muhammad, Parya Aghasafari, and Ramana M. Pidaparti. 2016. "Transient Mechanical Response of Lung Airway Tissue during Mechanical Ventilation" Bioengineering 3, no. 1: 4. https://doi.org/10.3390/bioengineering3010004
APA StyleIbrahim, I. B. M., Aghasafari, P., & Pidaparti, R. M. (2016). Transient Mechanical Response of Lung Airway Tissue during Mechanical Ventilation. Bioengineering, 3(1), 4. https://doi.org/10.3390/bioengineering3010004