Dementia and Heart Failure Classification Using Optimized Weighted Objective Distance and Blood Biomarker-Based Features
Abstract
1. Introduction
2. Literature Review
2.1. Feature Studies of Dementia and Heart Failure
2.2. ML-Based Classifications for Dementia and Heart Failure
2.3. Classification with Distance Measurements
2.4. The Proposed Study
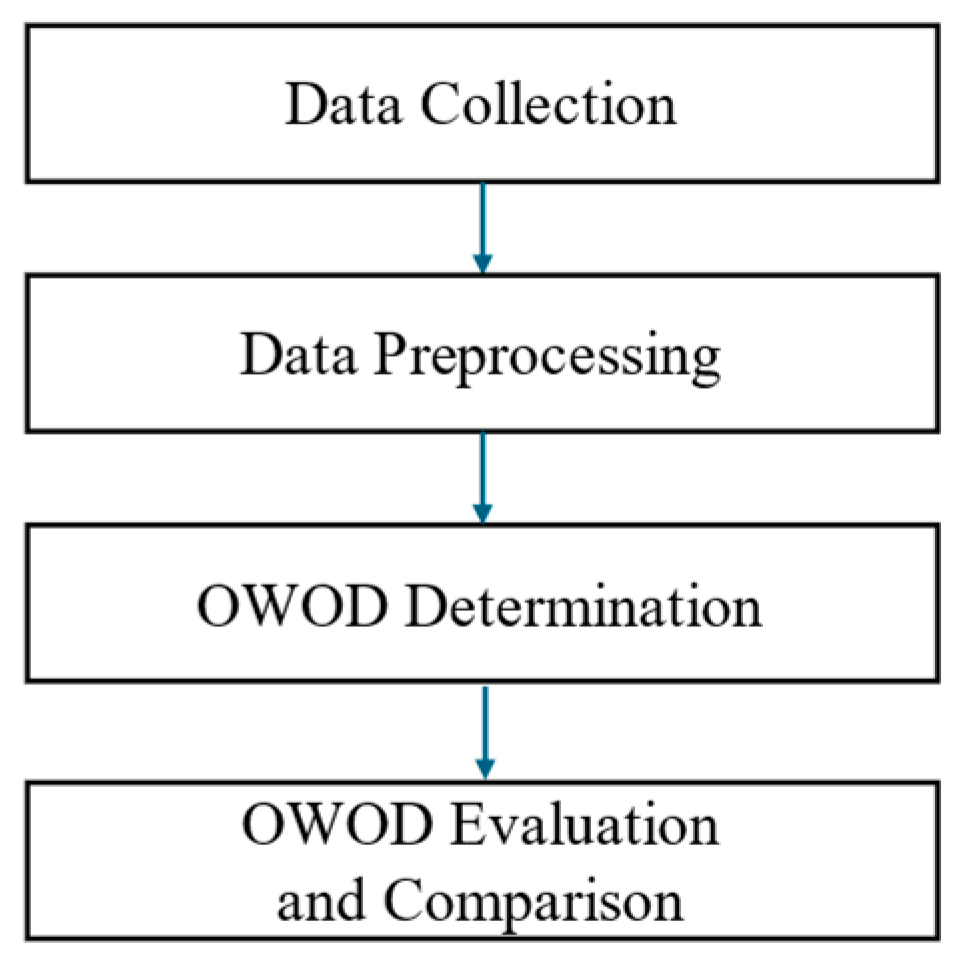
3. Research Methodology
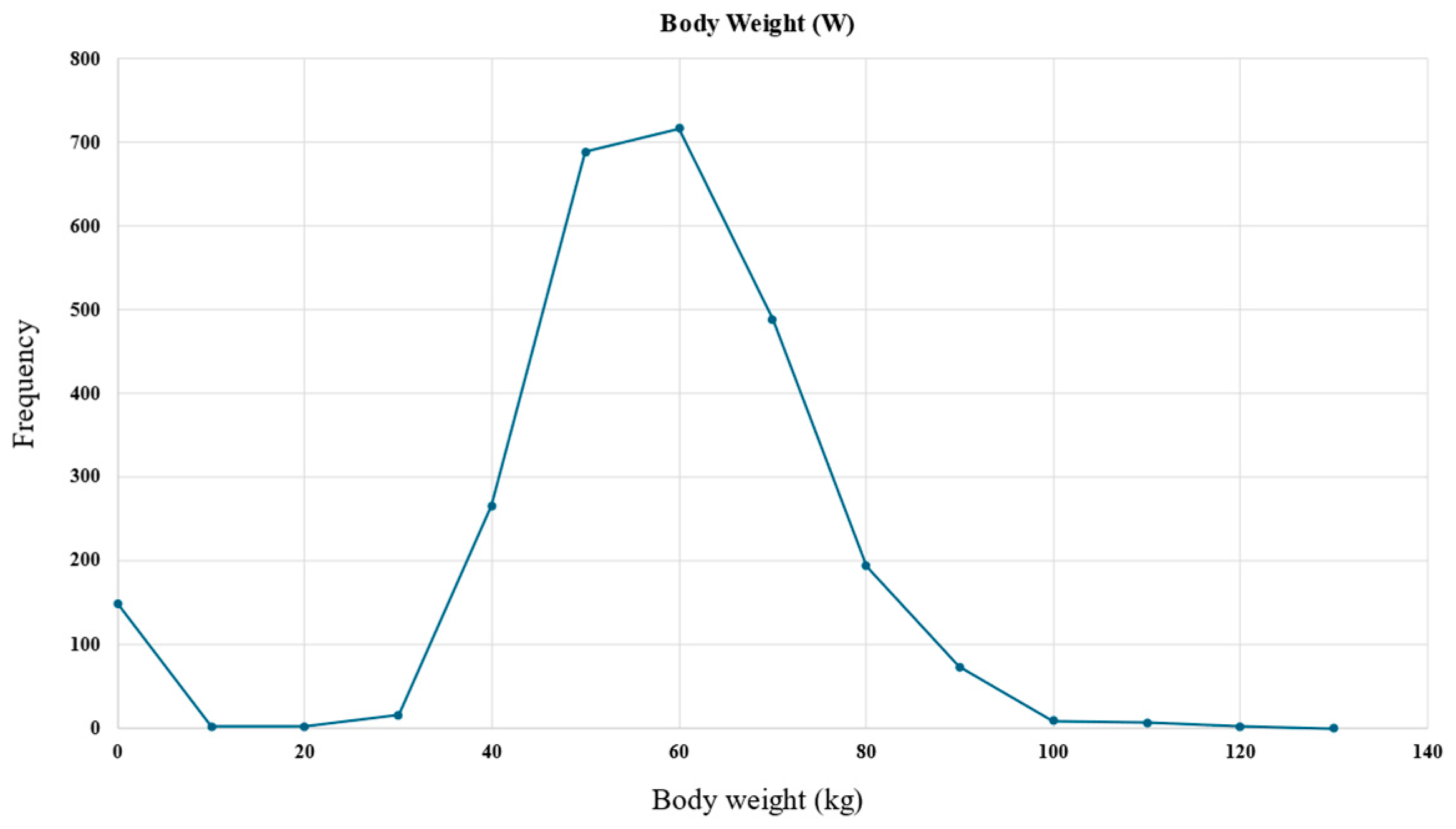
3.1. Data Collection
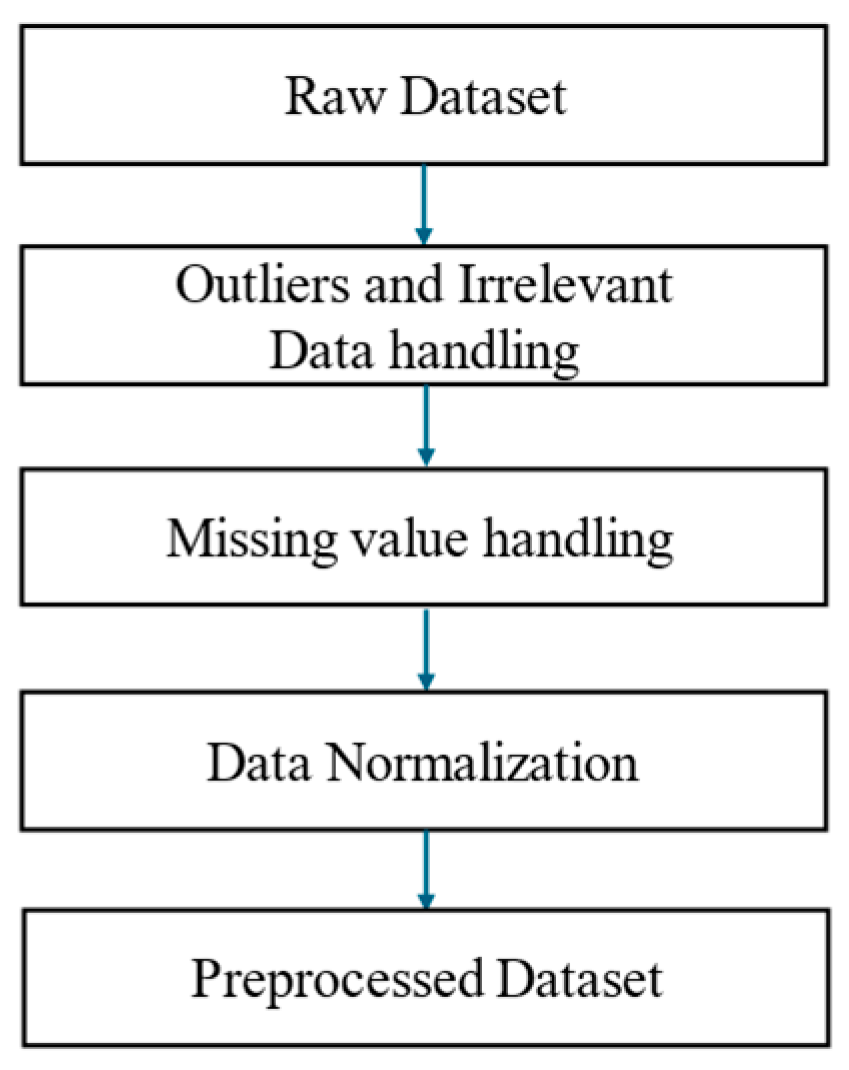
3.2. Data Preprocessing
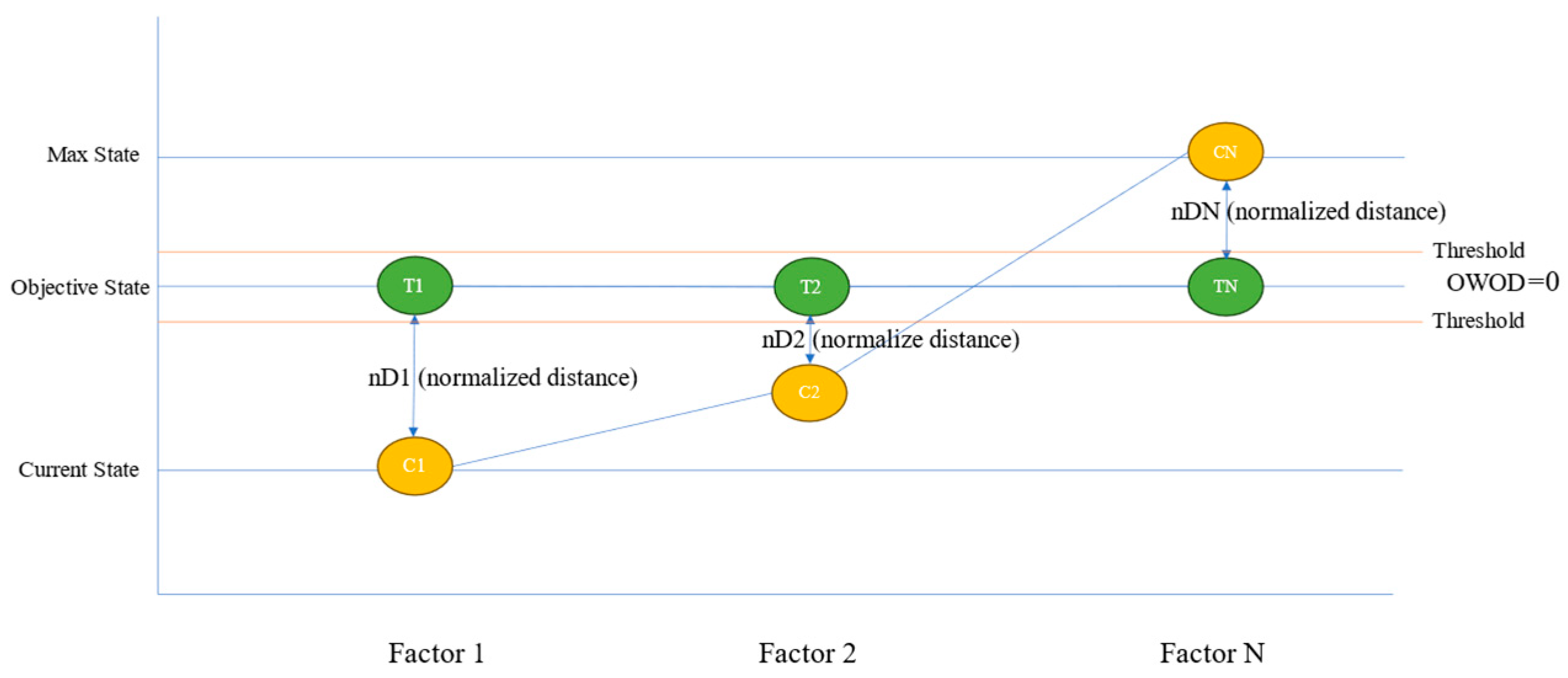
3.3. The OWOD Concept
3.4. OWOD Determination
3.4.1. Feature Selection
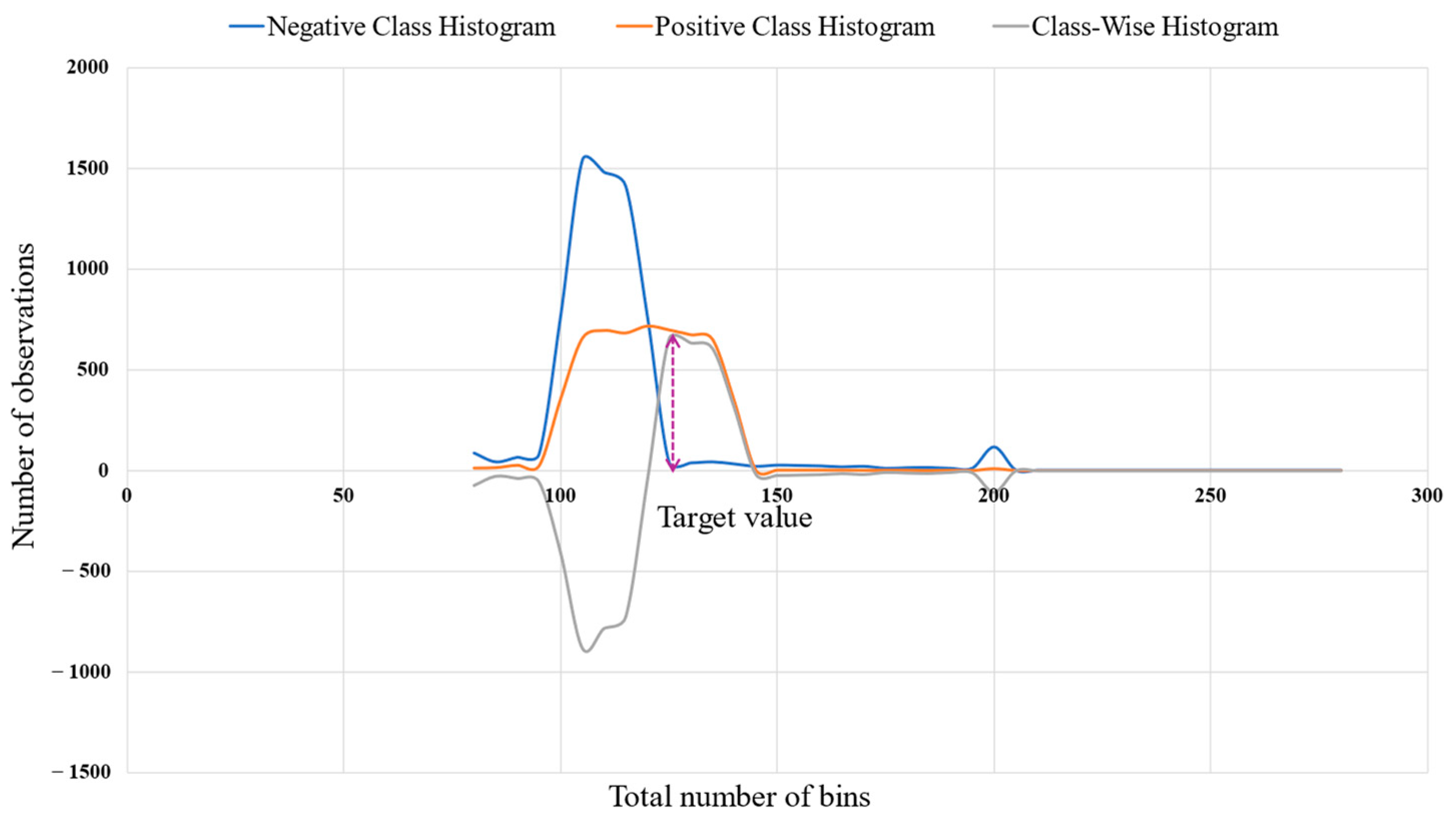
3.4.2. Objective Class Determination
3.4.3. Distance Normalization
3.4.4. Weight Determination
- Entropy.
- Information Gain.
3.4.5. OWOD Calculation
3.4.6. OWOD Algorithm
| Algorithm 1: OWOD calculation |
| Input: List of selected features (F) Output: Table of computed OWOD values 1: Initialize storage results 2: For each sample S in the dataset do 3: For each feature F do 4: Retrieve C (current level), T (target level), A (acceptable level) 5: Compute Euclidean distances: dTC ← √((T − C)2) dTA ← √((T − A)2) 6: Compute Normalized distances: ndTC ← dTC/A ndTA ← dTA/A 7: Compute Normalized distance ratios: rTC ← ndTC/(ndTC + ndTA) rTA ← ndTA/(ndTC + ndTA) 8: Compute Entropy, information gain, and gain score: EP ← calculate entropy (rTC, rTA) IG ← calculate information gain (EP) G ← calculate gain (IG) 9: Compute Entropy–gain ratio and weight: rEG ← EP/G SrEG ← sum (rEG) W ← rEG/SrEG 10: Compute Distance difference, weight*distance and normalize: DF ← |ndTC − ndTA| WD ← W × DF MxWD ← max (WD), MnWD ← min (WD) nWD ← (WD − MnWD)/(MxWD − MnWD) 11: Compute OWOD: OWOD ← average (nWD) 12: Store S, F, and OWOD values 13: End for 14: End for 15: Return OWOD result table |
3.4.7. Sample Calculation
3.4.8. OWOD Evaluation and Comparison
4. Results and Discussion
4.1. Optimal Feature Dimension Results
4.2. OWOD Classification Results
Confusion Matrix Evaluation
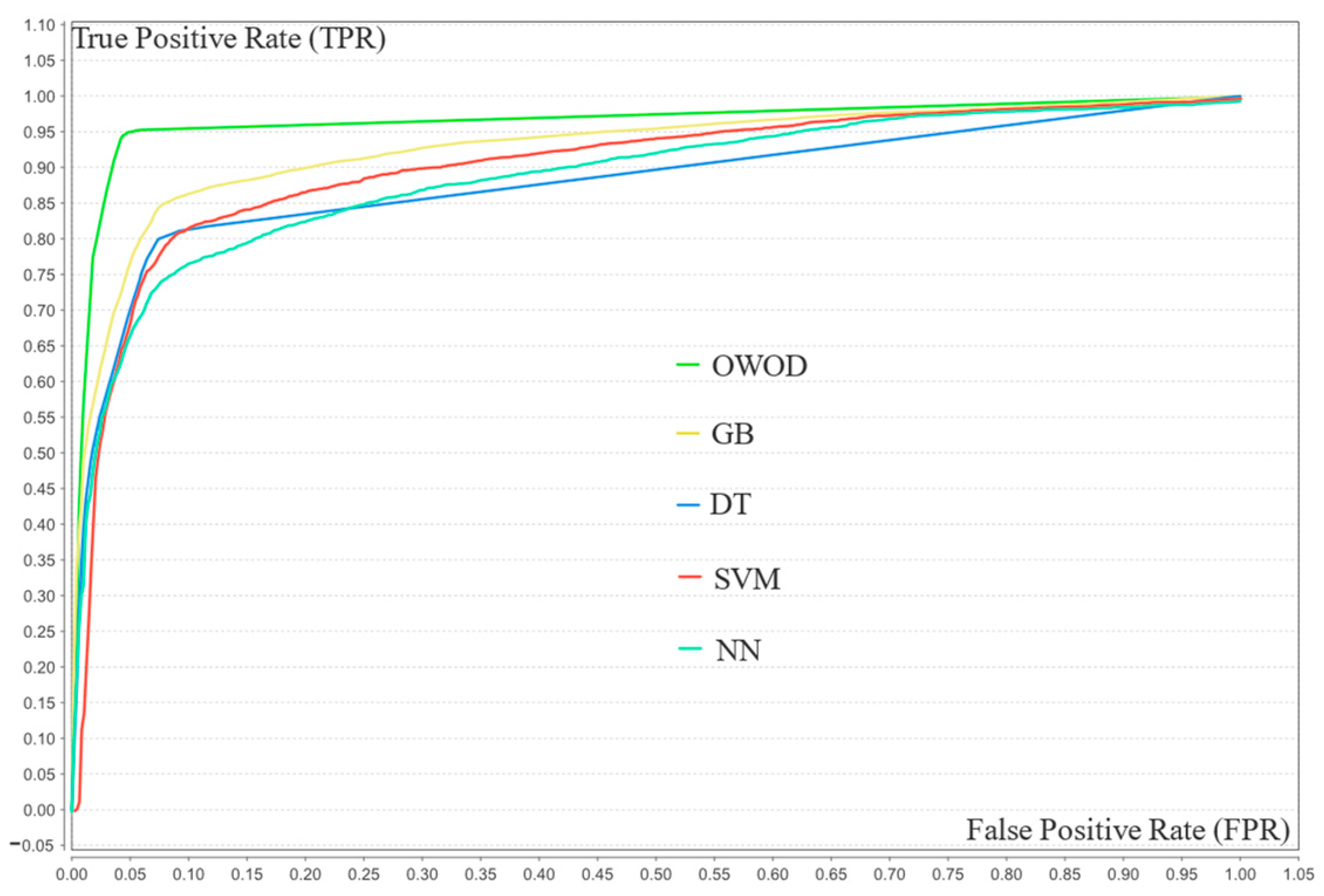
4.3. Model Validation Results
4.4. Statistical Significance Comparison
4.5. Model Comparison and Discussion
| Classification Method | No. of Features | Accuracy % | Precision % | Recall % | F1-Score % | AUC-ROC % |
|---|---|---|---|---|---|---|
| OWOD | 20 | 95.45 | 96.14 | 94.70 | 95.42 | 97.10 |
| Gradient boosting (GB) | 20 | 88.20 | 90.90 | 84.90 | 87.80 | 92.40 |
| Decision tree (DT) | 20 | 86.20 | 91.04 | 80.30 | 85.33 | 87.30 |
| Support vector machine (SVM) | 20 | 84.40 | 84.89 | 83.70 | 84.29 | 90.10 |
| Neural network (NN) | 20 | 83.75 | 88.14 | 78.00 | 82.76 | 88.80 |
Evaluation of Model Performances
4.6. Suggestions and Future Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Livingston, G.; Huntley, J.; Liu, K.Y.; Costafreda, S.G.; Selbæk, G.; Alladi, S.; Ames, D.; Banerjee, S.; Burns, A.; Brayne, C.; et al. Dementia prevention, intervention, and care: 2024 report of the Lancet standing commission. Lancet 2024, 404, 572–628. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Gao, D.; Liang, J.; Ji, M.; Zhang, W.; Pan, Y.; Zheng, F.; Xie, W. The role of life’s crucial 9 in cardiovascular disease incidence and dynamic transitions to dementia. Commun. Med. 2025, 5, 223. [Google Scholar] [CrossRef] [PubMed]
- Ye, S.; Huynh, Q.; Potter, E.L. Cognitive dysfunction in heart failure: Pathophysiology and implications for patient management. Comorbidities 2022, 19, 303–315. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, G.; Liang, Y.; He, S.; Lyu, M.; Zhu, Y. Heart–brain interaction in cardiogenic dementia: Pathophysiology and therapeutic potential. Front. Cardiovasc. Med. 2024, 11, 1304864. [Google Scholar] [CrossRef]
- Khan, S.S.; Matsushita, K.; Sang, Y.; Ballew, S.H.; Grams, M.E.; Surapaneni, A.; Blaha, M.J. Development and validation of the American Heart Association’s PREVENT equations. Circulation 2024, 149, 430–449. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Dementia. WHO Fact Sheets. 31 March 2025. Available online: https://www.who.int/news-room/fact-sheets/detail/dementia (accessed on 8 September 2025).
- GBD 2019 Dementia Forecasting Collaborators. Estimation of the global prevalence of dementia in 2019 and forecasted prevalence in 2050: An analysis for the Global Burden of Disease Study 2019. Lancet Public Health 2022, 7, e105–e125. [Google Scholar] [CrossRef]
- Sohn, M.; Yang, J.; Sohn, J.; Lee, J. Digital healthcare for dementia and cognitive impairment: A scoping review. Int. J. Nurs. Stud. 2023, 140, 104413. [Google Scholar] [CrossRef]
- Stoppa, E.; Di Donato, G.W.; Parde, N.; Santambrogio, M.D. Computer-aided dementia detection: How informative are your features? In Proceedings of the IEEE 7th Forum on Research and Technologies for Society and Industry Innovation (RTSI), Paris, France, 24–26 August 2022. [Google Scholar] [CrossRef]
- Chaiyo, Y.; Temdee, P. A comparison of machine learning methods with feature extraction for classification of patients with dementia risk. In Proceedings of the Joint International Conference on Digital Arts, Media and Technology with ECTI Northern Section Conference on Electrical, Electronics, Computer and Telecommunications Engineering (ECTI DAMT & NCON), Chiang Rai, Thailand, 26–28 January 2022. [Google Scholar] [CrossRef]
- Hu, S.; Yang, C.; Luo, H. Current trends in blood biomarker detection and imaging for Alzheimer’s disease. Biosens. Bioelectron. 2022, 210, 114278. [Google Scholar] [CrossRef]
- Savarese, G.; Becher, P.M.; Lund, L.H.; Seferovic, P.; Rosano, G.M.C.; Coats, A.J.S. Global burden of heart failure: A comprehensive and updated review of epidemiology. Cardiovasc. Res. 2022, 118, 3272–3287. [Google Scholar] [CrossRef]
- Li, R.; Wang, X.; Lawler, K.; Garg, S.; Bai, Q.; Alty, J. Applications of artificial intelligence to aid early detection of dementia: A scoping review on current capabilities and future directions. J. Biomed. Inform. 2022, 127, 104030. [Google Scholar] [CrossRef] [PubMed]
- Mahendran, N.; Durai Raj Vincent, P.M. A deep learning framework with an embedded-based feature selection approach for the early detection of Alzheimer’s disease. Comput. Biol. Med. 2022, 141, 105056. [Google Scholar] [CrossRef]
- Ahmed, H.; Soliman, H.; Elmogy, M. Early detection of Alzheimer’s disease using single nucleotide polymorphisms analysis based on gradient boosting tree. Comput. Biol. Med. 2022, 146, 105622. [Google Scholar] [CrossRef]
- Park, J.E.; Kim, H.J.; Kim, Y.E.; Jang, H.; Cho, S.H.; Kim, S.J.; Na, D.L.; Won, H.; Ki, C.; Seo, S.W. Analysis of dementia-related gene variants in APOE ε4 noncarrying Korean patients with early-onset Alzheimer’s disease. Neurobiol. Aging 2020, 85, 155.e5–155.e8. [Google Scholar] [CrossRef]
- El-Sappagh, S.; Ali, F.; Abuhmed, T.; Singh, J.; Alonso, J.M. Automatic detection of Alzheimer’s disease progression: An efficient information fusion approach with heterogeneous ensemble classifiers. Neurocomputing 2022, 512, 203–224. [Google Scholar] [CrossRef]
- Shanmugam, J.V.; Duraisamy, B.; Simon, B.C.; Bhaskaran, P. Alzheimer’s disease classification using pre-trained deep networks. Biomed. Signal Process. Control 2022, 71, 103217. [Google Scholar] [CrossRef]
- Di Benedetto, M.; Carrara, F.; Tafuri, B.; Nigro, S.; De Blasi, R.; Falchi, F.; Gennaro, C.; Gigli, G.; Logroscino, G.; Amato, G. Deep networks for behavioral variant frontotemporal dementia identification from multiple acquisition sources. Comput. Biol. Med. 2022, 148, 105937. [Google Scholar] [CrossRef] [PubMed]
- Rallabandi, V.P.S.; Seetharaman, K. Deep learning-based classification of healthy aging controls, mild cognitive impairment and Alzheimer’s disease using fusion of MRI-PET imaging. Biomed. Signal Process. Control 2023, 80, 104312. [Google Scholar] [CrossRef]
- Li, J.P.; Haq, A.U.; Din, S.U.; Khan, J.; Khan, A.; Saboor, A. heart disease identification method using machine learning classification in e-healthcare. IEEE Access 2020, 8, 107562–107582. [Google Scholar] [CrossRef]
- Ahmad, A.A.; Polat, H. Prediction of heart disease based on machine learning using jellyfish optimization algorithm. Diagnostics 2023, 13, 2392. [Google Scholar] [CrossRef] [PubMed]
- Aslam, M.U.; Xu, S.; Hussain, S.; Waqas, M.; Abiodun, N.L. Machine learning based classification of valvular heart disease using cardiovascular risk factors. Sci. Rep. 2024, 14, 24396. [Google Scholar] [CrossRef] [PubMed]
- Chulde-Fernández, B.; Enríquez-Ortega, D.; Tirado-Espín, A.; Vizcaíno-Imacaña, P.; Guevara, C.; Navas, P.; Villalba-Meneses, F.; Cadena-Morejon, C.; Almeida-Galarraga, D.; Acosta-Vargas, P. Classification of heart failure using machine learning: A comparative study. Life 2025, 15, 496. [Google Scholar] [CrossRef]
- Yongcharoenchaiyasit, K.; Arwatchananukul, S.; Temdee, P.; Prasad, R. Gradient boosting-based model for elderly heart failure, aortic stenosis, and dementia classification. IEEE Access 2023, 11, 48677–48696. [Google Scholar] [CrossRef]
- Yongcharoenchaiyasit, K.; Arwatchananukul, S.; Hristov, G.; Temdee, P. Enhanced multi-model machine learning-based dementia detection using a data enrichment framework: Leveraging the blessing of dimensionality. Bioengineering 2025, 12, 592. [Google Scholar] [CrossRef]
- Chaising, S.; Temdee, P.; Prasad, R. Weighted objective distance for the classification of elderly people with hypertension. Knowl.-Based Syst. 2020, 210, 106441. [Google Scholar] [CrossRef]
- Nuankaew, P.; Chaising, S.; Temdee, P. Average weighted objective distance-based method for type 2 diabetes prediction. IEEE Access 2021, 9, 49018–49031. [Google Scholar] [CrossRef]
- Daugherty, A.M. Hypertension-related risk for dementia: A summary review with future directions. Semin. Cell Dev. Biol. 2021, 116, 82–89. [Google Scholar] [CrossRef]
- Brown, J.; Xiong, X.; Wu, J.; Li, M.; Lu, Z.K. CO76 Hypertension and the risk of dementia among medicare beneficiaries in the U.S. Value Health 2022, 25, S318. [Google Scholar] [CrossRef]
- Campbell, G.; Jha, A. Dementia risk and hypertension: A literature review. J. Neurol. Sci. 2019, 405, 146. [Google Scholar] [CrossRef]
- Park, K.; Nam, G.; Han, K.; Hwang, H. Body weight variability and the risk of dementia in patients with type 2 diabetes mellitus: A nationwide cohort study in Korea. Diabetes Res. Clin. Pract. 2022, 190, 110015. [Google Scholar] [CrossRef] [PubMed]
- Iwagami, M.; Qizilbash, N.; Gregson, J.; Douglas, I.; Johnson, M.; Pearce, N.; Evans, S.; Pocock, S. Blood cholesterol and risk of dementia in more than 1.8 million people over two decades: A retrospective cohort study. Lancet Healthy Longev. 2021, 2, e498–e506. [Google Scholar] [CrossRef] [PubMed]
- Gong, J.; Harris, K.; Peters, S.A.E.; Woodward, M. Serum lipid traits and the risk of dementia: A cohort study of 254,575 women and 214,891 men in the UK Biobank. Lancet 2022, 54, 101695. [Google Scholar] [CrossRef]
- Bertini, F.; Allevi, D.; Lutero, G.; Calzà, L.; Montesi, D. An automatic Alzheimer’s disease classifier based on spontaneous spoken English. Comput. Speech Lang. 2022, 72, 101298. [Google Scholar] [CrossRef]
- Milana, S. Dementia classification using attention mechanism on audio data. In Proceedings of the 2023 IEEE 21st World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 19–21 January 2023. [Google Scholar] [CrossRef]
- Meng, X.; Fang, S.; Zhang, S.; Li, H.; Ma, D.; Ye, Y.; Su, J.; Sun, J. Multidomain lifestyle interventions for cognition and the risk of dementia: A systematic review and meta-analysis. Int. J. Nurs. Stud. 2022, 130, 104236. [Google Scholar] [CrossRef] [PubMed]
- Cilia, N.D.; De Gregorio, G.; De Stefano, C.; Fontanella, F.; Marcelli, A.; Parziale, A. Diagnosing Alzheimer’s disease from on-line handwriting: A novel dataset and performance benchmarking. Eng. Appl. Artif. Intell. 2022, 111, 104822. [Google Scholar] [CrossRef]
- Masuo, A.; Ito, Y.; Kanaiwa, T.; Naito, K.; Sakuma, T.; Kato, S. Dementia screening based on SVM using qualitative drawing error of clock drawing test. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, UK, 11–15 July 2022. [Google Scholar] [CrossRef]
- Wong, R.; Lovier, M.A. Sleep disturbances and dementia risk in older adults: Findings from 10 years of national U.S. prospective data. Am. J. Prev. Med. 2023, 64, 781–787. [Google Scholar] [CrossRef] [PubMed]
- Khosroazad, S.; Abedi, A.; Hayes, M.J. Sleep signal analysis for early detection of Alzheimer’s disease and related dementia (ADRD). IEEE J. Biomed. Health Inform. 2023, 27, 3235391. [Google Scholar] [CrossRef]
- Chiu, S.Y.; Wyman-Chick, K.A.; Ferman, T.J.; Bayram, E.; Holden, S.K.; Choudhury, P.; Armstrong, M.J. Sex differences in dementia with Lewy bodies: Focused review of available evidence and future directions. Park. Relat. Disord. 2023, 107, 105285. [Google Scholar] [CrossRef]
- Alvi, A.M.; Siuly, S.; Wang, H.; Wang, K.; Whittaker, F. A deep learning based framework for diagnosis of mild cognitive impairment. Knowl.-Based Syst. 2022, 248, 108815. [Google Scholar] [CrossRef]
- Lin, H.; Tsuji, T.; Kondo, K.; Imanaka, Y. Development of a risk score for the prediction of incident dementia in older adults using a frailty index and health checkup data: The JAGES longitudinal study. Prev. Med. 2018, 112, 88–96. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, W.; Zhang, W.; Wang, H.; Ou, Y.; Qu, Y.; Shen, X.; Chen, S.; Wu, K.; Zhao, Q.; et al. Modifiable risk factors for incident dementia and cognitive impairment: An umbrella review of evidence. J. Affect. Disord. 2022, 314, 160–167. [Google Scholar] [CrossRef]
- Sigala, E.G.; Vaina, S.; Chrysohoou, C.; Dri, E.; Damigou, E.; Tatakis, F.P.; Sakalidis, A.; Barkas, F.; Liberopoulos, E.; Sfikakis, P.P.; et al. Sex-related differences in the 20-year incidence of CVD and its risk factors: The ATTICA study (2002–2022). Am. J. Prev. Cardiol. 2024, 19, 100709. [Google Scholar] [CrossRef] [PubMed]
- Goldsborough III, E.; Osuji, N.; Blaha, M.J. Assessment of cardiovascular disease risk: A 2022 update. Endocrinol. Metab. Clin. N. Am. 2022, 51, 483–509. [Google Scholar] [CrossRef]
- Young, K.A.; Scott, C.G.; Rodeheffer, R.J.; Chen, H.H. Incidence of preclinical heart failure in a community population. J. Am. Heart Assoc. 2022, 11, e025519. [Google Scholar] [CrossRef] [PubMed]
- Sevilla-Salcedo, C.; Imani, V.; Olmos, P.M.; Gómez-Verdejo, V.; Tohka, J. Multi-task longitudinal forecasting with missing values on Alzheimer’s disease. Comput. Methods Programs Biomed. 2022, 226, 107056. [Google Scholar] [CrossRef]
- Kherchouche, A.; Ben-Ahmed, O.; Guillevin, C.; Tremblais, B.; Julian, A.; Fernandez-Maloigne, C.; Guillevin, R. Attention-guided neural network for early dementia detection using MRS data. Comput. Med. Imag. Graph. 2022, 99, 102074. [Google Scholar] [CrossRef]
- Ahmad, M.; Ahmed, A.; Hashim, H.; Farsi, M.; Mahmoud, N. Enhancing heart disease diagnosis using ECG signal reconstruction and deep transfer learning classification with optional SVM integration. Diagnostics 2025, 15, 1501. [Google Scholar] [CrossRef]
- Menagadevi, M.; Mangai, S.; Madian, N.; Thiyagarajan, D. Automated prediction system for Alzheimer detection based on deep residual autoencoder and support vector machine. Optik 2023, 272, 170212. [Google Scholar] [CrossRef]
- Darmawahyuni, A.; Firdaus, S.N.; Tutuko, B.; Yuwandini, M.; Rachmatullah, M.N. Congestive heart failure waveform classification based on short time-step analysis with recurrent network. Informat. Med. Unlocked 2020, 21, 100441. [Google Scholar] [CrossRef]
- Chaiyo, Y.; Rueangsirarak, W.; Hristov, G.; Temdee, P. Improving early detection of dementia: Extra trees-based classification model using inter-relation-based features and K-means synthetic minority oversampling technique. Big Data Cogn. Comput. 2025, 9, 148. [Google Scholar] [CrossRef]
- Phanbua, P.; Arwatchananukul, S.; Temdee, P. Classification model of dementia and heart failure in older adults using extra trees and oversampling-based technique. In Proceedings of the 2025 Joint International Conference on Digital Arts, Media and Technology with ECTI Northern Section Conference on Electrical, Electronics, Computer and Telecommunications Engineering (ECTI DAMT & NCON), Nan, Thailand, 29 January–1 February 2025. [Google Scholar] [CrossRef]
- Dhar, A.; Dash, N.; Roy, K. Classification of text documents through distance measurement: An experiment with multi-domain Bangla text documents. In Proceedings of the 2017 3rd International Conference on Advances in Computing, Communication & Automation (ICACCA) (Fall), Dehradun, India, 15–16 September 2017. [Google Scholar] [CrossRef]
- Greche, L.; Jazouli, M.; Es-Sbai, N.; Majda, A.; Zarghili, A. Comparison between Euclidean and Manhattan distance measure for facial expressions classification. In Proceedings of the 2017 International Conference on Wireless Technologies, Embedded and Intelligent Systems (WITS), Fez, Morocco, 19–20 April 2017. [Google Scholar] [CrossRef]
- Han, J.; Park, D.C.; Woo, D.M.; Min, S.Y. Comparison of distance measures on Fuzzyc-means algorithm for image classification problem. AASRI Procedia 2013, 4, 50–56. [Google Scholar] [CrossRef]
- Chaichumpa, S.; Temdee, P. Assessment of student competency for personalised online learning using objective distance. Int. J. Innov. Technol. Explor. Eng. 2018, 23, 19–36. [Google Scholar] [CrossRef]
- Chaising, S.; Temdee, P. Determining recommendations for preventing elderly people from cardiovascular disease complication using objective distance. In Proceedings of the 2018 Global Wireless Summit (GWS), Chiang Rai, Thailand, 25–28 November 2018. [Google Scholar] [CrossRef]
- Chaising, S.; Prasad, R.; Temdee, P. Personalized recommendation method for preventing elderly people from cardiovascular disease complication using integrated objective distance. Wirel. Pers. Commun. 2019, 117, 215–233. [Google Scholar] [CrossRef]
- Alhaj, T.A.; Siraj, M.M.; Zainal, A.; Elshoush, H.T.; Elhaj, F. Feature selection using information gain for improved structural-based alert correlation. PLoS ONE 2016, 11, e0166017. [Google Scholar] [CrossRef] [PubMed]
- Pereira, R.B.; Carvalho, A.P.D.; Zadrozny, B.; Merschmann, L.H.D.C. Information gain feature selection for multi-label classification. J. Inf. Data Manag. 2015, 6, 48–58. [Google Scholar]
- Azhagusundari, B.; Thanamani, A.S. Feature selection based on information gain. Int. J. Innov. Technol. Explor. Eng. 2013, 2, 18–21. [Google Scholar]
- Patil, L.H.; Atique, M. A novel feature selection based on information gain using WordNet. In Proceedings of the 2013 International Conference on Information and Network Security (ICINS 2013), London, UK, 7–9 October 2013. [Google Scholar]
- Baobao, B.; Jinsheng, M.; Minru, S. An enhancement of K-Nearest Neighbor algorithm using information gain and extension relativity. In Proceedings of the 2008 International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008. [Google Scholar] [CrossRef]
- Gupta, M. Dynamic k-NN with attribute weighting for automatic web page classification (Dk-NNwAW). Int. J. Comput. Appl. 2012, 58, 34–40. [Google Scholar] [CrossRef]





| Dementia | Heart Failure |
|---|---|
| Body weight [32] | Being overweight/obese [46] |
| Blood cholesterol [33] | Hypercholesterolemia [46] |
| Hypertension [29,30,31] | Hypertension [12,46] |
| Serum lipids [34] | Lipid biomarkers [47] |
| Diabetes [1] | Diabetes mellitus [46] |
| Sex [42] | Sex [12,46,47] |
| ApoE4 gene [16] | Age [12,46,47] |
| Air pollution (NO2, PM2.5) [1] | |
| Sleep disturbances [40] |
| Features | Acronym | Data Range | Group |
|---|---|---|---|
| Body weight (kg) | W | 40.1–116.3 | R |
| Height (cm) | H | 150.1–185.0 | P |
| Body mass index (kg/m2) | BMI | 11.76–39.57 | R |
| Systolic blood pressure (mmHg) | SBP | 76–199 | R |
| Diastolic blood pressure (mmHg) | DBP | 61–126 | R |
| Fasting blood sugar (mg/dL) | FBS | 62–495 | R |
| Triglycerides (mg/dL) | TGS | 51–199 | R |
| Total cholesterol (mg/dL) | TC | 101–429 | R |
| High-density lipoprotein cholesterol (mg/dL) | HDL | 31–93 | R |
| Low-density lipoprotein cholesterol (mg/dL) | LDL | 51–196 | R |
| Hemoglobin (g/dL) | HB | 10.10–20.10 | P |
| White blood cell (count/μL) | WBC | 3100–19,900 | P |
| Polymorphonuclear neutrophils (percentage) | NEUT | 30.20–89.90 | P |
| Thrombocytes (count/μL) | PLAT | 101,000–585,000 | P |
| Lymphocyte cells (percentage) | LYMP | 10.10–59.00 | P |
| Creatinine (mg/dL) | CREA | 0.35–2.99 | P |
| Blood urea nitrogen (mg/dL) | BUN | 4–49 | P |
| Thyroid stimulating hormone (mIU/L) | TSH | 0.01–5.97 | P |
| Potassium (mEq/L) | K | 1.40–7.80 | P |
| Sodium (mEq/L) | NA | 109–167 | P |
| Carbon dioxide (mEq/L) | CO2 | 11–45 | P |
| Feature () | Target Level () | Acceptable Level () |
|---|---|---|
| W | 55 kg | 90 kg |
| SBP | 150 mg/dL | 190 mg/dL |
| DBP | 85 mg/dL | 110 mg/dL |
| FBS | 130 mg/dL | 280 mg/dL |
| TGS | 140 mg/dL | 160 mg/dL |
| TC | 200 mg/dL | 260 mg/dL |
| HDL | 55 mg/dL | 70 mg/dL |
| LDL | 135 mg/dL | 165 mg/dL |
| No. | W | SBP | DBP | FBS | TGS | TC | HDL | LDL |
|---|---|---|---|---|---|---|---|---|
| 1 | 65 | 130 | 75 | 120 | 115 | 175 | 35 | 105 |
| 2 | 70 | 140 | 80 | 105 | 95 | 165 | 50 | 120 |
| 3 | 55 | 155 | 90 | 110 | 110 | 195 | 60 | 140 |
| 4 | 65 | 135 | 75 | 100 | 100 | 185 | 40 | 120 |
| 5 | 50 | 150 | 75 | 115 | 155 | 205 | 50 | 135 |
| 6 | 60 | 135 | 85 | 115 | 100 | 185 | 60 | 145 |
| 7 | 92 | 155 | 85 | 120 | 125 | 220 | 50 | 140 |
| 8 | 77 | 160 | 80 | 115 | 100 | 210 | 50 | 135 |
| 9 | 47 | 121 | 82 | 130 | 85 | 215 | 55 | 130 |
| 10 | 45 | 162 | 77 | 115 | 120 | 205 | 60 | 125 |
| … | … | … | … | … | … | … | … | … |
| 8000 | 65 | 135 | 75 | 100 | 100 | 185 | 40 | 120 |
| No. of Features | Accuracy % | Precision % | Recall % | F1-Score % | AUC-ROC % |
|---|---|---|---|---|---|
| 8 | 56.38 ± 1.94 | 85.05 ± 3.04 | 15.68 ± 5.13 | 26.44 ± 0.97 | 56.40 ± 0.02 |
| 12 | 61.26 ± 1.52 | 89.26 ± 1.84 | 25.62 ± 3.48 | 39.81 ± 0.76 | 61.40 ± 0.016 |
| 16 | 70.43 ± 0.28 | 86.61 ± 0.86 | 48.34 ± 0.86 | 62.05 ± 0.14 | 71.30 ± 0.003 |
| 20 | 94.95 ± 0.96 | 95.64 ± 0.95 | 94.20 ± 1.11 | 94.91 ± 0.48 | 96.60 ± 0.013 |
| No. | Results | Matching Result | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weight | OWOD | Classification | Actual | |||||||||
| SBP | DBP | W | FBS | TGS | TC | HDL | LDL | Result | Result | Result | Correct /Incorrect | |
| 1 | 0.0003 | 0.0003 | 0.1404 | 0.0531 | 0.2095 | 0.1010 | 0.2582 | 0.2371 | 0.4051 | Dementia | Dementia | Correct |
| 2 | 0.1034 | 0.0003 | 0.1117 | 0.1216 | 0.1484 | 0.1484 | 0.1995 | 0.1667 | 0.4258 | Dementia | Dementia | Correct |
| 3 | 0.2727 | 0.0004 | 0.0004 | 0.0611 | 0.2484 | 0.0004 | 0.2409 | 0.1757 | 0.4057 | Dementia | Dementia | Correct |
| 4 | 0.1920 | 0.2168 | 0.0003 | 0.0467 | 0.2251 | 0.0003 | 0.1843 | 0.1344 | 0.5858 | Dementia | Heart failure | Incorrect |
| 5 | 0.2555 | 0.0005 | 0.2705 | 0.1849 | 0.0005 | 0.2872 | 0.0005 | 0.0005 | 0.3583 | Dementia | Dementia | Correct |
| 6 | 0.1356 | 0.0960 | 0.1301 | 0.0815 | 0.1149 | 0.1476 | 0.1475 | 0.1468 | 0.4822 | Heart failure | Heart failure | Correct |
| 7 | 0.1364 | 0.1225 | 0.0772 | 0.1281 | 0.1417 | 0.1378 | 0.1152 | 0.1411 | 0.4411 | Heart failure | Heart failure | Correct |
| 8 | 0.1465 | 0.1284 | 0.1137 | 0.0654 | 0.1207 | 0.1366 | 0.1444 | 0.1444 | 0.8029 | Heart failure | Heart failure | Correct |
| 9 | 0.1231 | 0.1257 | 0.1283 | 0.0862 | 0.1181 | 0.1337 | 0.1435 | 0.1414 | 0.6858 | Heart failure | Heart failure | Correct |
| 10 | 0.1456 | 0.1446 | 0.1158 | 0.0511 | 0.1192 | 0.1229 | 0.1515 | 0.1493 | 0.5363 | Heart failure | Heart failure | Correct |
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| 8000 | 0.1265 | 0.1292 | 0.1144 | 0.0973 | 0.1374 | 0.1081 | 0.1497 | 0.1374 | 0.4680 | Heart failure | Dementia | Incorrect |
| Dementia | Heart Failure | Class Precision | |
|---|---|---|---|
| Predict—Dementia | 3768 (TP) | 172 (FP) | 95.63% |
| Predict—Heart failure | 232 (FN) | 3828 (TN) | 94.29% |
| Class recall | 94.20% | 95.70% |
| Classification Method | No. of Features | Accuracy % | Precision % | Recall % | F1-Score % | AUC-ROC % |
|---|---|---|---|---|---|---|
| OWOD | 20 | 94.95 ± 0.96 | 95.64 ± 0.95 | 94.20 ± 1.11 | 94.91 ± 0.48 | 96.60 ± 0.013 |
| Gradient boosting (GB) | 20 | 88.58 ± 0.77 | 91.34 ± 1.16 | 85.26 ± 1.38 | 88.19 ± 0.39 | 92.90 ± 0.006 |
| Decision tree (DT) | 20 | 86.75 ± 0.72 | 91.83 ± 1.51 | 80.72 ± 1.59 | 85.90 ± 0.36 | 88.10 ± 0.005 |
| Support vector machine (SVM) | 20 | 84.96 ± 1.03 | 85.81 ± 1.03 | 83.78 ± 1.91 | 84.78 ± 0.52 | 90.70 ± 0.007 |
| Neural network (NN) | 20 | 83.34 ± 0.87 | 88.19 ± 2.41 | 77.08 ± 1.59 | 82.23 ± 0.44 | 89.30 ± 0.006 |
| Method | Hyperparameters |
|---|---|
| Gradient boosting | Number of trees = 50; maximal depth = 5; min rows = 10.0; number of bins = 20; learning rate = 0.01; sample rate = 1.0; cross-validation folds = 5 |
| Decision tree | Criterion = gain ratio; maximal depth = 10; confidence = 0.1; minimal gain = 0.01; minimal leaf size = 2; cross-validation folds = 5 |
| Support vector machine | Kernel type = dot; kernel cache = 200; C = 0.0; convergence epsilon = 0.001; max iterations = 100,000; cross-validation folds = 5 |
| Neural network | Hidden layer = 2; training cycle = 200; learning rate = 0.01; momentum = 0.9; cross-validation folds = 5 |
| OWOD | Cross-validation folds = 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noonpan, V.; Chaising, S.; Hristov, G.; Temdee, P. Dementia and Heart Failure Classification Using Optimized Weighted Objective Distance and Blood Biomarker-Based Features. Bioengineering 2025, 12, 980. https://doi.org/10.3390/bioengineering12090980
Noonpan V, Chaising S, Hristov G, Temdee P. Dementia and Heart Failure Classification Using Optimized Weighted Objective Distance and Blood Biomarker-Based Features. Bioengineering. 2025; 12(9):980. https://doi.org/10.3390/bioengineering12090980
Chicago/Turabian StyleNoonpan, Veerasak, Supansa Chaising, Georgi Hristov, and Punnarumol Temdee. 2025. "Dementia and Heart Failure Classification Using Optimized Weighted Objective Distance and Blood Biomarker-Based Features" Bioengineering 12, no. 9: 980. https://doi.org/10.3390/bioengineering12090980
APA StyleNoonpan, V., Chaising, S., Hristov, G., & Temdee, P. (2025). Dementia and Heart Failure Classification Using Optimized Weighted Objective Distance and Blood Biomarker-Based Features. Bioengineering, 12(9), 980. https://doi.org/10.3390/bioengineering12090980







