Modeling and Dynamic Parameterized Predictive Control of Dissolved Oxygen in Dual−Tank Bioreactor Systems
Abstract
1. Introduction
2. Theoretical Model Development
2.1. Dual−Tank Recirculating System in Cell Culture
2.2. Mathematical Modeling of DO in the Cell Growth Zone
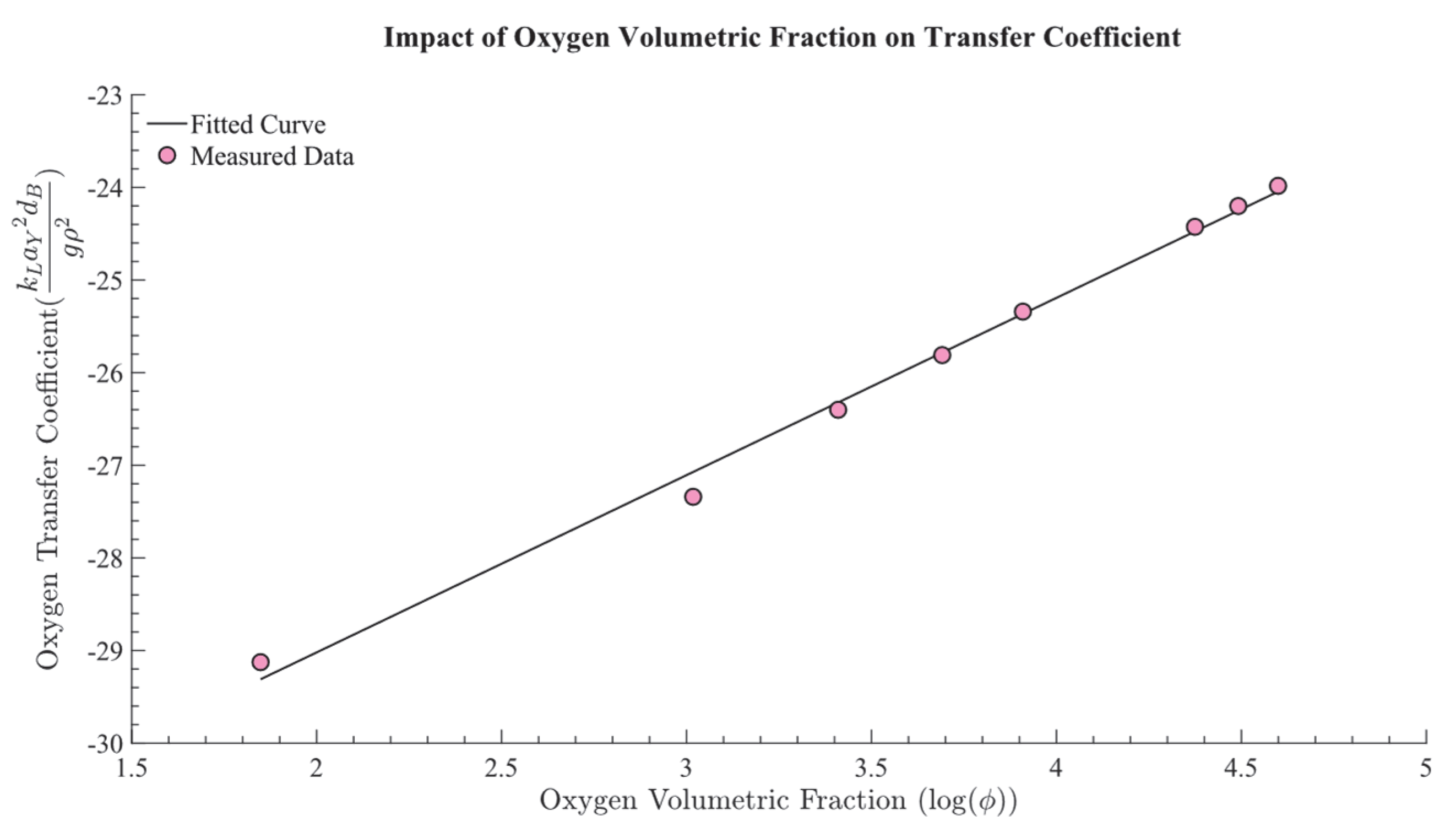
2.2.1. Calculating the Oxygen Transfer Coefficient,
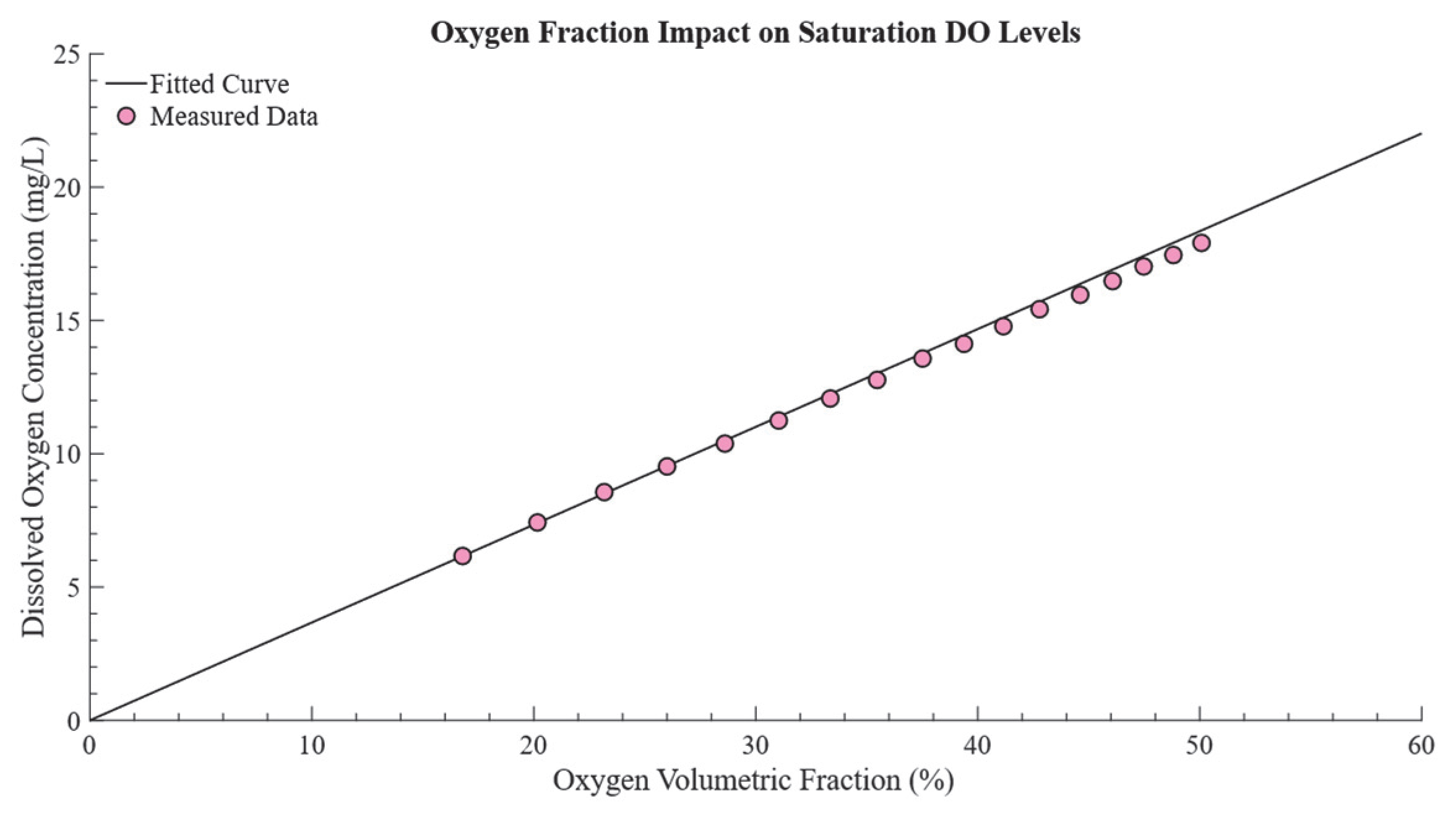
2.2.2. Determining the Saturated DO,
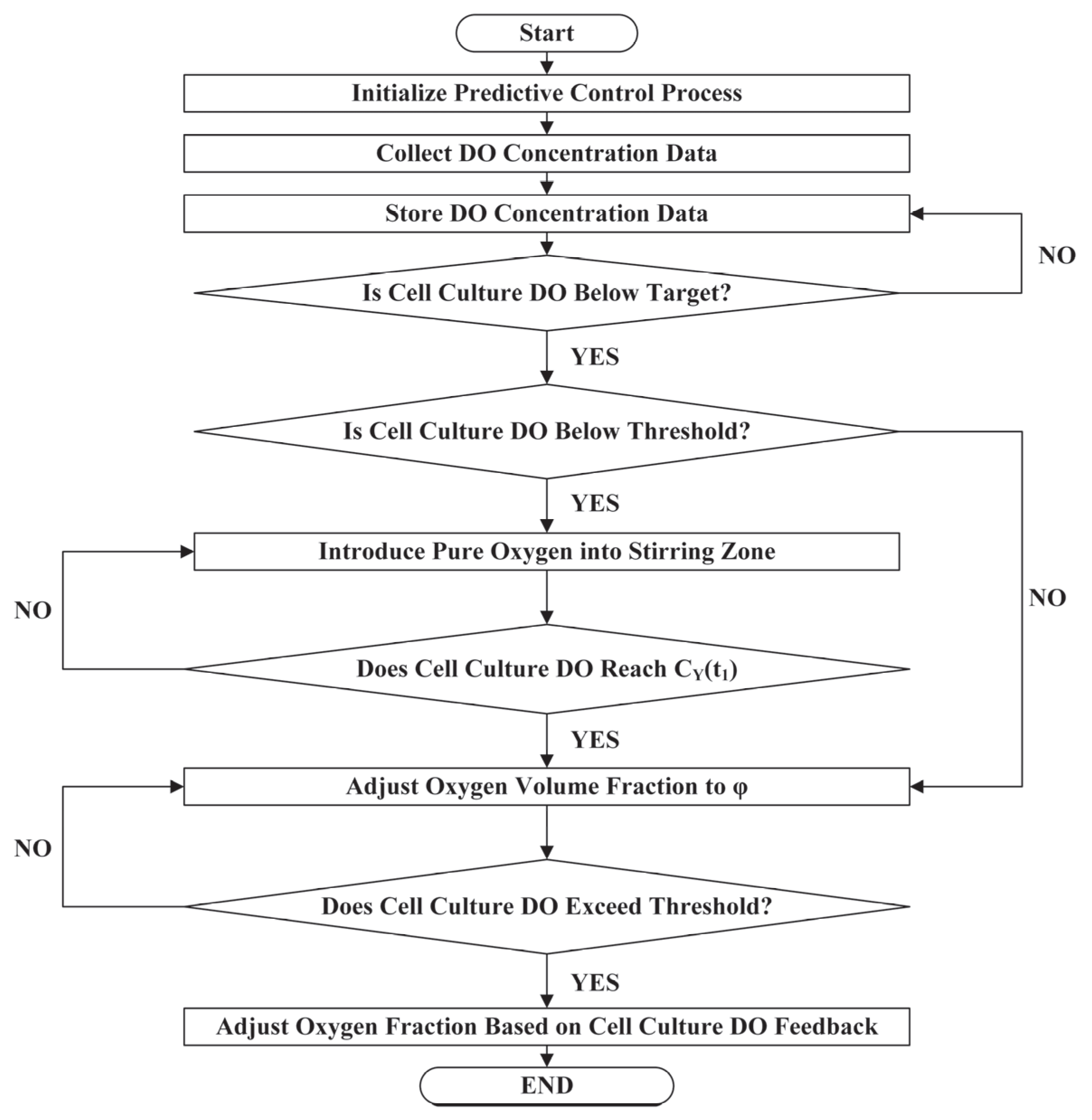
2.3. Dynamic Parameterized Predictive Control (DPPC) Method for DO
3. Experimentally Determined Model Parameterization
3.1. Determination of the Relationship Between and
3.2. Determination of the Relationship Between and
3.3. Coefficient Determination for the Mathematical Model of the Recirculating Culture System
4. Control Performance Assessment of DDPC
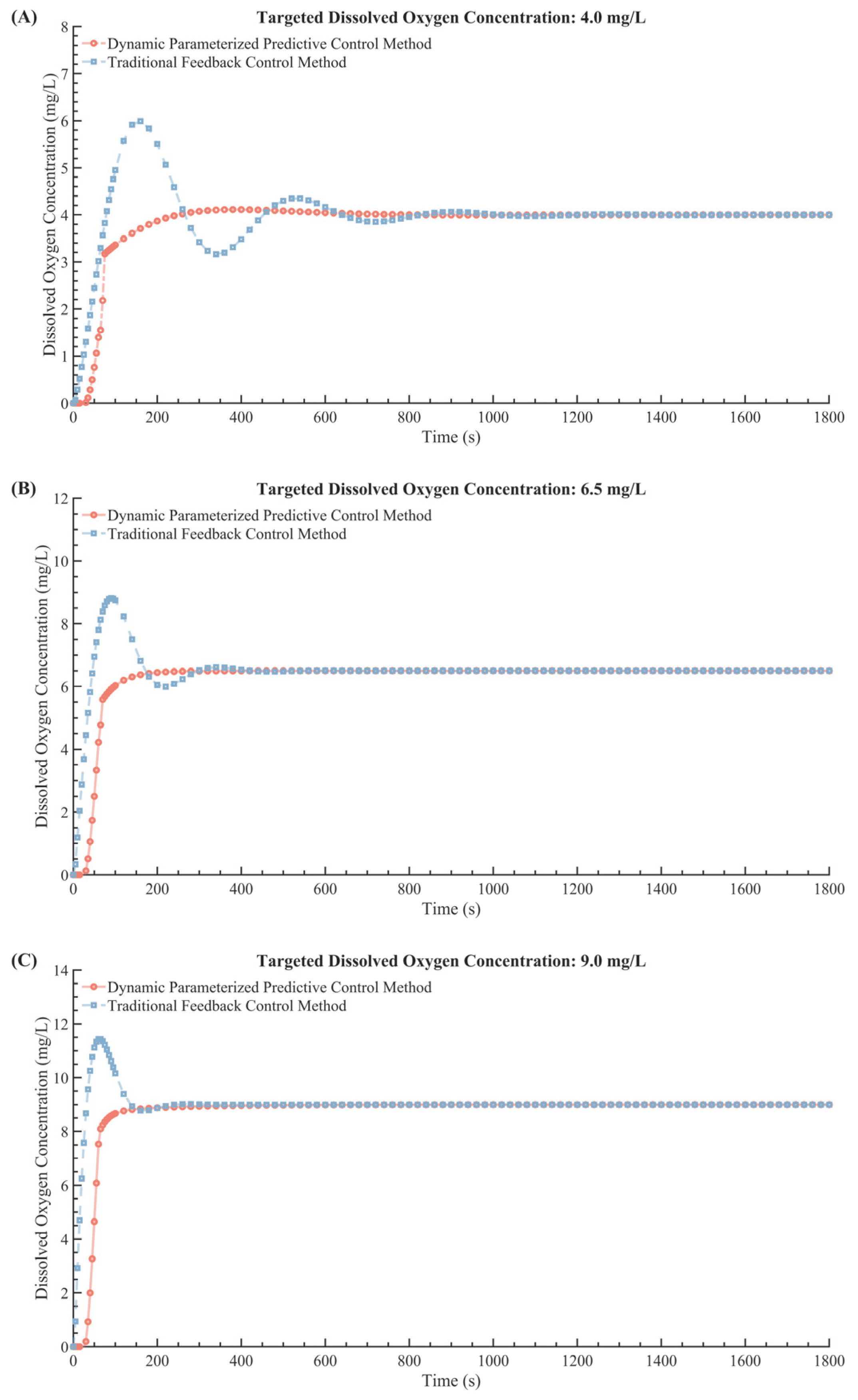
4.1. Simulation−Based Experimental Verification
4.2. Experimentally−Based System Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scibona, E.; Morbidelli, M. Expansion processes for cell−based therapies. Biotechnol. Adv. 2019, 37, 107455. [Google Scholar] [CrossRef] [PubMed]
- Egger, D.; Lavrentieva, A.; Kugelmeier, P.; Kasper, C. Physiologic isolation and expansion of human mesenchymal stem/stromal cells for manufacturing of cell-based therapy products. Eng. Life Sci. 2021, 22, 361–372. [Google Scholar] [CrossRef]
- Bashor, C.J.; Hilton, I.B.; Bandukwala, H.; Smith, D.M.; Veiseh, O. Engineering the next generation of cell−based therapeutics. Nat. Rev. Drug Discov. 2022, 21, 655–675. [Google Scholar] [CrossRef] [PubMed]
- Bahsoun, S.; Coopman, K.; Forsyth, N.R.; Akam, E.C. The Role of Dissolved Oxygen Levels on Human Mesenchymal Stem Cell Culture Success, Regulatory Compliance, and Therapeutic Potential. Stem Cells Dev. 2018, 27, 1303–1321. [Google Scholar] [CrossRef]
- Tse, H.M.; Gardner, G.; Dominguez−Bendala, J.; Fraker, C.A. The Importance of Proper Oxygenation in 3D Culture. Front. Bioeng. Biotechnol. 2021, 9, 634403. [Google Scholar] [CrossRef] [PubMed]
- Schottlender, N.; Gottfried, I.; Ashery, U. Hyperbaric Oxygen Treatment: Effects on Mitochondrial Function and Oxidative Stress. Biomolecules 2021, 11, 1827. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, T.; Huang, X.; He, Y.; Zhou, Y.; Wu, L.; Wu, K.; Fan, M.; Zhu, L. Dissolved oxygen concentration in the medium during cell culture: Defects and improvements. Cell Biol. Int. 2015, 40, 354–360. [Google Scholar] [CrossRef]
- Lüchtefeld, I. The Role of Cell & Membrane Mechanics in Cellular Mechanosensitivity. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2021. [Google Scholar]
- Xu, H. −Q.; Liu, J.−C.; Zhang, Z.−Y.; Xu, C.−X. A review on cell damage, viability, and functionality during 3D bioprinting. Mil. Med. Res. 2022, 9, 70. [Google Scholar] [CrossRef]
- Butkus, M.; Levišauskas, D.; Galvanauskas, V. Simple Gain−Scheduled Control System for Dissolved Oxygen Control in Bioreactors. Processes 2021, 9, 1493. [Google Scholar] [CrossRef]
- Wang, S.; Li, T.; Cheng, X.; Zhu, R.; Xu, Y. Regulating the concentration of dissolved oxygen to achieve the directional transformation of reactive oxygen species: A controllable oxidation process for ciprofloxacin degradation by calcined CuCoFe−LDH. Water Res. 2023, 233, 119744. [Google Scholar] [CrossRef]
- Li, D.; Zou, M.; Jiang, L. Dissolved oxygen control strategies for water treatment: A review. Water Sci. Technol. 2022, 86, 1444–1466. [Google Scholar] [CrossRef] [PubMed]
- Olsson, G.; Åmand, L.; Rieger, L.; Carlsson, B. Aeration control–implementation. In Aeration, Mixing, and Energy: Bubbles and Sparks; IWA Publishing: London, UK, 2018; pp. 143–178. [Google Scholar]
- Stebel, K.; Pospiech, J.; Nocon, W.; Czeczot, J.; Skupin, P. Boundary−Based Predictive Controller and Its Application to Control of Dissolved Oxygen Concentration in Activated Sludge Bioreactor. IEEE Trans. Ind. Electron. 2021, 69, 10541–10551. [Google Scholar] [CrossRef]
- Simon, L.; Karim, M.N. Identification and Control of Dissolved Oxygen in Hybridoma Cell Culture in a Shear Sensitive Environment. Biotechnol. Prog. 2001, 17, 634–642. [Google Scholar] [CrossRef] [PubMed]
- Kuprijanov, A.; Gnoth, S.; Simutis, R.; Lübbert, A. Advanced control of dissolved oxygen concentration in fed batch cultures during recombinant protein production. Appl. Microbiol. Biotechnol. 2009, 82, 221–229. [Google Scholar] [CrossRef]
- Lee, B.; Jung, S.; Hashimura, Y.; Lee, M.; Borys, B.S.; Dang, T.; Kallos, M.S.; Rodrigues, C.A.V.; Silva, T.P.; Cabral, J.M.S. Cell Culture Process Scale−Up Challenges for Commercial−Scale Manufacturing of Allogeneic Pluripotent Stem Cell Products. Bioengineering 2022, 9, 92. [Google Scholar] [CrossRef]
- Lee, J.−S.; Kim, G.−H.; Kim, J.; Lim, T.−H.; Yoon, Y.; Yoon, S.−S. Large−Scale Production of Cronobacter sakazakii Bacteriophage Φ CS01 in Bioreactors via a Two−Stage Self−Cycling Process. J. Microbiol. Biotechnol. 2021, 31, 1430–1437. [Google Scholar] [CrossRef]
- Klöckner, W.; Gacem, R.; Anderlei, T.; Raven, N.; Schillberg, S.; Lattermann, C.; Büchs, J.J.J.o.b.e. Correlation between mass transfer coefficient kLa and relevant operating parameters in cylindrical disposable shaken bioreactors on a bench−to−pilot scale. J. Biol. Eng. 2013, 7, 1–14. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Zheng, J.; Mao, S. A thermodynamic model for the solubility of N2, O2 and Ar in pure water and aqueous electrolyte solutions and its applications. Appl. Geochem. 2019, 107, 58–79. [Google Scholar] [CrossRef]
- Duan, Z.; Møller, N.; Greenberg, J.; Weare, J.H. The prediction of methane solubility in natural waters to high ionic strength from 0 to 250 °C and from 0 to 1600 bar. Geochim. Cosmochim. Acta 1992, 56, 1451–1460. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Peiper, J.C.; Busey, R.H. Thermodynamic Properties of Aqueous Sodium Chloride Solutions. J. Phys. Chem. Ref. Data 1984, 13, 1–102. [Google Scholar] [CrossRef]
- Malpas, P.; Symonds, E. Arterial and venous pressures in the human umbilical cord. Am. J. Obstet. Gynecol. 1967, 98, 261–265. [Google Scholar] [CrossRef]
- Chiu, K.−C.; Du, D. A neural ordinary differential equation model for predicting the growth of Chinese Hamster Ovary cell in a bioreactor system. Biotechnol. Bioprocess Eng. 2024, 100–115. [Google Scholar] [CrossRef]
- Lu, T.; Jin, M.; Yang, M.; Huang, D. Deep Learning−Based Prediction of Critical Parameters in CHO Cell Culture Process and Its Application in Monoclonal Antibody Production. Int. J. Adv. Appl. Sci. Res. 2024, 3, 108–123. [Google Scholar]
- Zhou, X.; Wang, J.; Huang, L.; Li, D.; Duan, Q. Modelling and controlling dissolved oxygen in recirculating aquaculture systems based on mechanism analysis and an adaptive PID controller. Comput. Electron. Agric. 2022, 192, 106583. [Google Scholar] [CrossRef]
- Deasy, B.M.; Jankowski, R.J.; Payne, T.R.; Cao, B.; Goff, J.P.; Greenberger, J.S.; Huard, J. Modeling Stem Cell Population Growth: Incorporating Terms for Proliferative Heterogeneity. Stem Cells 2003, 21, 536–545. [Google Scholar] [CrossRef] [PubMed]
- Bartolini, E.; Manoli, H.; Costamagna, E.; Jeyaseelan, H.A.; Hamad, M.; Irhimeh, M.R.; Khademhosseini, A.; Abbas, A. Population balance modelling of stem cell culture in 3D suspension bioreactors. Chem. Eng. Res. Des. 2015, 101, 125–134. [Google Scholar] [CrossRef]
- Yao, X.; Zhang, G.; Yang, S.; Chen, Y. Adaptive Anti−Disturbance Control of Dissolved Oxygen in Circulating Water Culture Systems. Symmetry 2023, 15, 2015. [Google Scholar] [CrossRef]
- Tiwari, A.; Wong, C.S.; Nekkanti, L.P.; Deane, J.A.; McDonald, C.; Jenkin, G.; Kirkland, M.A. Impact of Oxygen Levels on Human Hematopoietic Stem and Progenitor Cell Expansion. Stem Cells Dev. 2016, 25, 1604–1613. [Google Scholar] [CrossRef]
- Lavrentieva, A.; Majore, I.; Kasper, C.; Hass, R. Effects of hypoxic culture conditions on umbilical cord−derived human mesenchymal stem cells. Cell Commun. Signal. 2010, 8, 18. [Google Scholar] [CrossRef]
- Serra, M.; Brito, C.; Sousa, M.F.; Jensen, J.; Tostões, R.; Clemente, J.; Strehl, R.; Hyllner, J.; Carrondo, M.J.; Alves, P.M. Improving expansion of pluripotent human embryonic stem cells in perfused bioreactors through oxygen control. J. Biotechnol. 2010, 148, 208–215. [Google Scholar] [CrossRef] [PubMed]






| Target DO Range (mg/L) | Critical DO Difference (mg/L) | Regional Error (Maximum) |
|---|---|---|
| 0–5.42 | 0.60 | 4.58% |
| 5.42–12.64 | 1.00 | 4.86% |
| 12.64–18.05 | 1.50 | 4.07% |
| 18.05–25.27 | 2.00 | 4.71% |
| 25.27–32.49 | 2.50 | 4.32% |
| 32.49–36.11 | 3.00 | 4.80% |
| Variable | Description | Setting or Range | Unit |
|---|---|---|---|
| Shaker Speed | Ensures complete suspension of cell–microcarrier complexes. | 150 | rpm |
| Culture Medium Volume | Supports sufficient nutrient supply and waste dilution. | 1 | Liters |
| Simulated Arterial Pressure | Mimics arterial pressure in human umbilical cord. | 80 ± 5 | mmHg |
| Nitrogen Volume Fraction | Adjusted to maintain optimal pH in the culture area. | Adjusted as needed | Percentage |
| Carbon Dioxide Volume Fraction | Adjusted to maintain optimal pH in the culture area. | Adjusted as needed | Percentage |
| Oxygen Volume Fraction | Studies the relationship between oxygen transfer rates and volume fraction. | 0%, 10%, 20%, 30%, 40%, 50% | Percentage |
| pH | Maintains cellular activity and experimental accuracy. | 7.2 ± 0.1 | pH Units |
| Temperature | Consistency with cell growth experiments. | 37 ± 0.1 | °C |
| Reactor Inner Wall Diameter | Specifies the physical dimension of the bioreactor. | 0.128 | Meters |
| Gravity Acceleration | Affects the sedimentation and distribution of cells and particles. | 9.0866 | m/s2 |
| Liquid Density | Impacts fluid dynamics and cell settling. | 1250 | kg/m3 |
| DO Target (mg/L) | RMSE | R2 |
|---|---|---|
| 4.0 | 0.0472 | 0.9986 |
| 6.5 | 0.0465 | 0.9929 |
| 9.0 | 0.0415 | 0.9959 |
| DO Change Program (mg/L) | Dynamic Parameterized Predictive Control Method Overshoot | Traditional Feedback Control Method Overshoot | Percentage Reduction |
|---|---|---|---|
| 0.0–4.0 | 5.62% | 51.73% | 89.13% |
| 4.0–6.5 | 2.80% | 21.79% | 87.15% |
| 6.5–9.0 | 0.00% | 7.23% | 100% |
| 9.0–6.5 | 0.72% | 9.14% | 92.12% |
| 6.5–4.0 | 20.73% | 33.35% | 37.84% |
| Model | Targeted DO (mg/L) | Settling Time (s) | Overshoot |
|---|---|---|---|
| Dynamic Parameterized Predictive Control Method | 4.0 | 139 | 2.80% |
| 6.5 | 108 | 0.00% | |
| 9.0 | 92 | 0.00% | |
| Traditional Feedback Control Method | 4.0 | 412 | 49.94% |
| 6.5 | 243 | 35.7% | |
| 9.0 | 198 | 27.15% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Tang, R.; Li, Y.; Cui, J. Modeling and Dynamic Parameterized Predictive Control of Dissolved Oxygen in Dual−Tank Bioreactor Systems. Bioengineering 2025, 12, 690. https://doi.org/10.3390/bioengineering12070690
Li M, Tang R, Li Y, Cui J. Modeling and Dynamic Parameterized Predictive Control of Dissolved Oxygen in Dual−Tank Bioreactor Systems. Bioengineering. 2025; 12(7):690. https://doi.org/10.3390/bioengineering12070690
Chicago/Turabian StyleLi, Muhang, Ran Tang, Yifei Li, and Junning Cui. 2025. "Modeling and Dynamic Parameterized Predictive Control of Dissolved Oxygen in Dual−Tank Bioreactor Systems" Bioengineering 12, no. 7: 690. https://doi.org/10.3390/bioengineering12070690
APA StyleLi, M., Tang, R., Li, Y., & Cui, J. (2025). Modeling and Dynamic Parameterized Predictive Control of Dissolved Oxygen in Dual−Tank Bioreactor Systems. Bioengineering, 12(7), 690. https://doi.org/10.3390/bioengineering12070690







