AI-Assisted Image Recognition of Cervical Spine Vertebrae in Dynamic X-Ray Recordings
Abstract
1. Introduction
2. Materials and Methods
2.1. Population
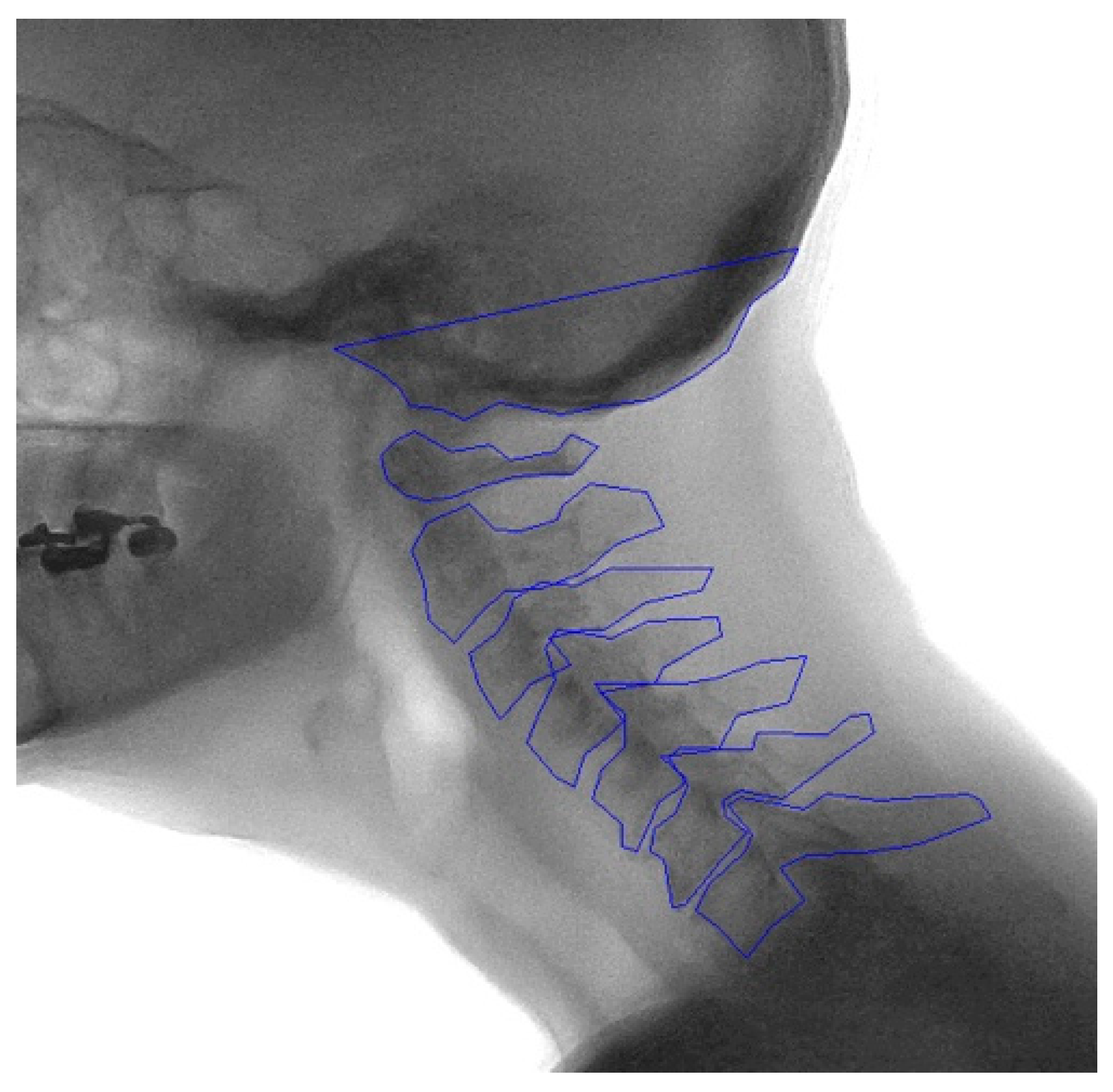
2.2. Manual Annotation
2.3. Development of the Model
2.4. Dataset
2.5. Generation of Mean Shape
2.6. Outcome Measures
3. Results
3.1. Ablation Study 2D+T
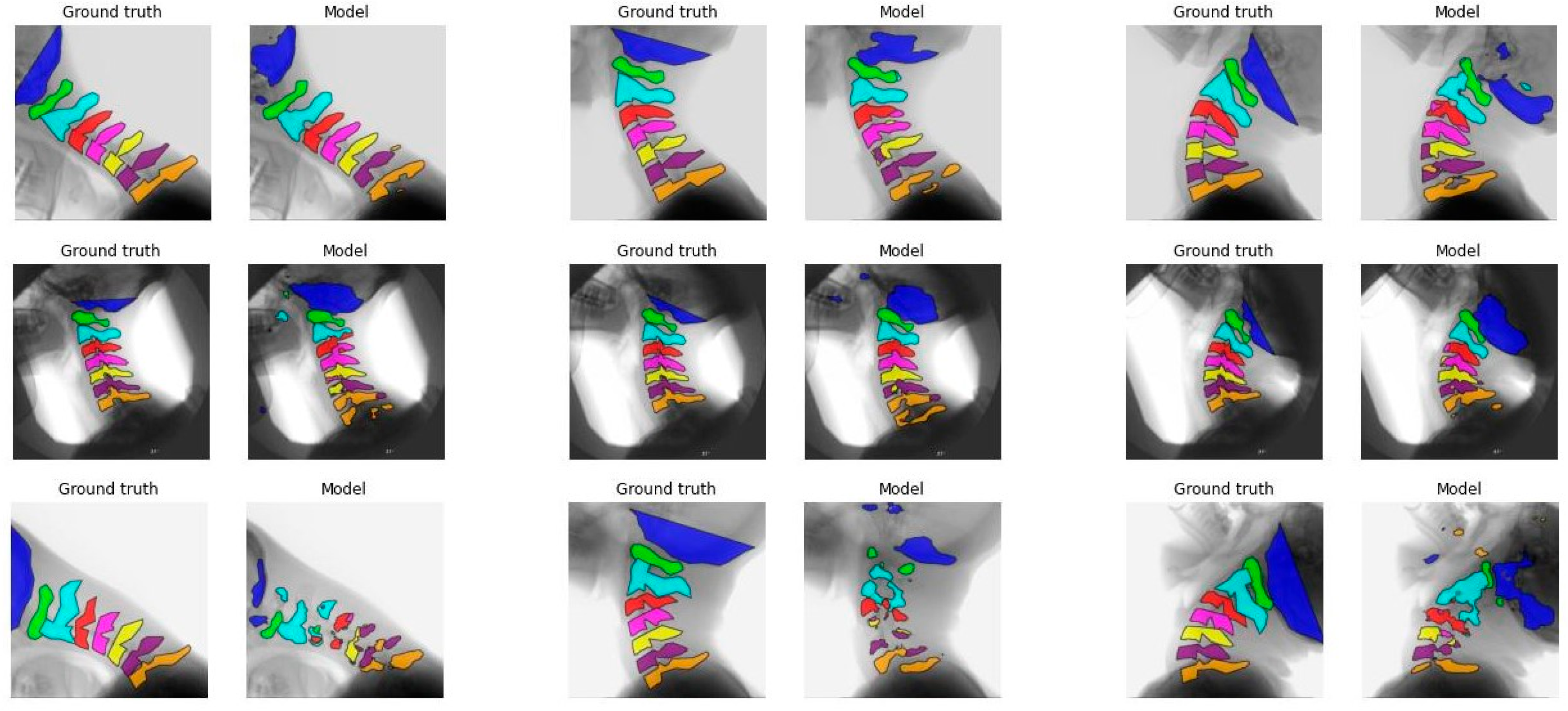
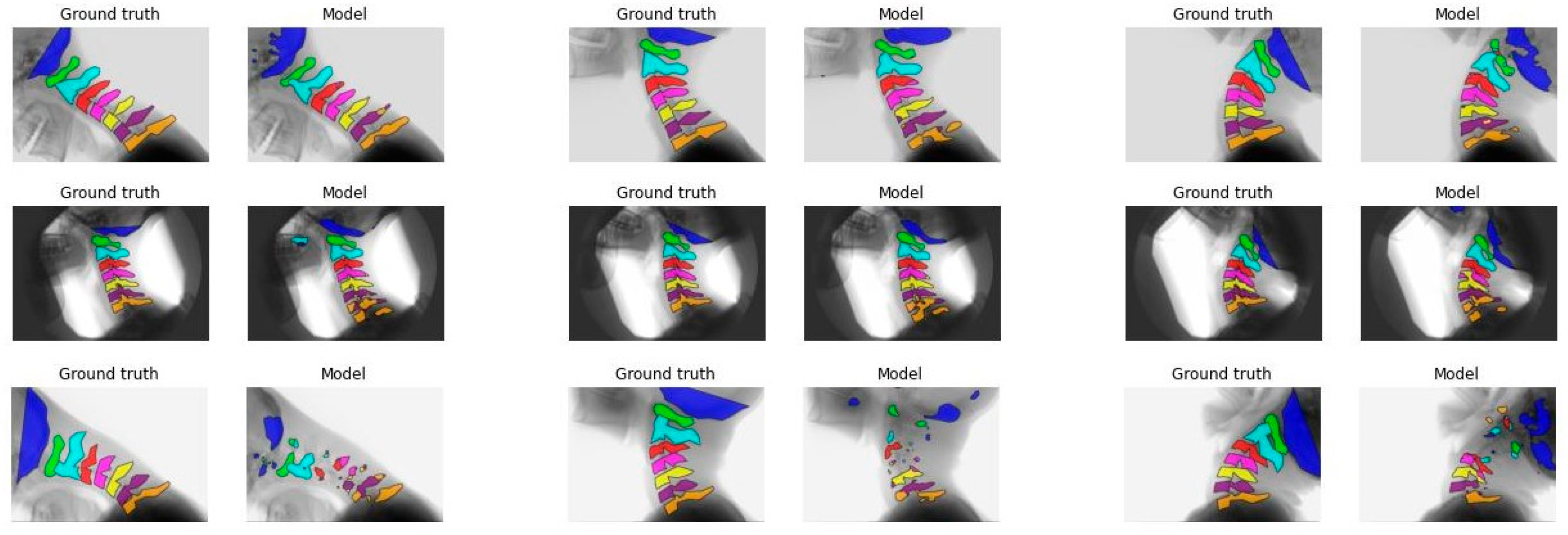
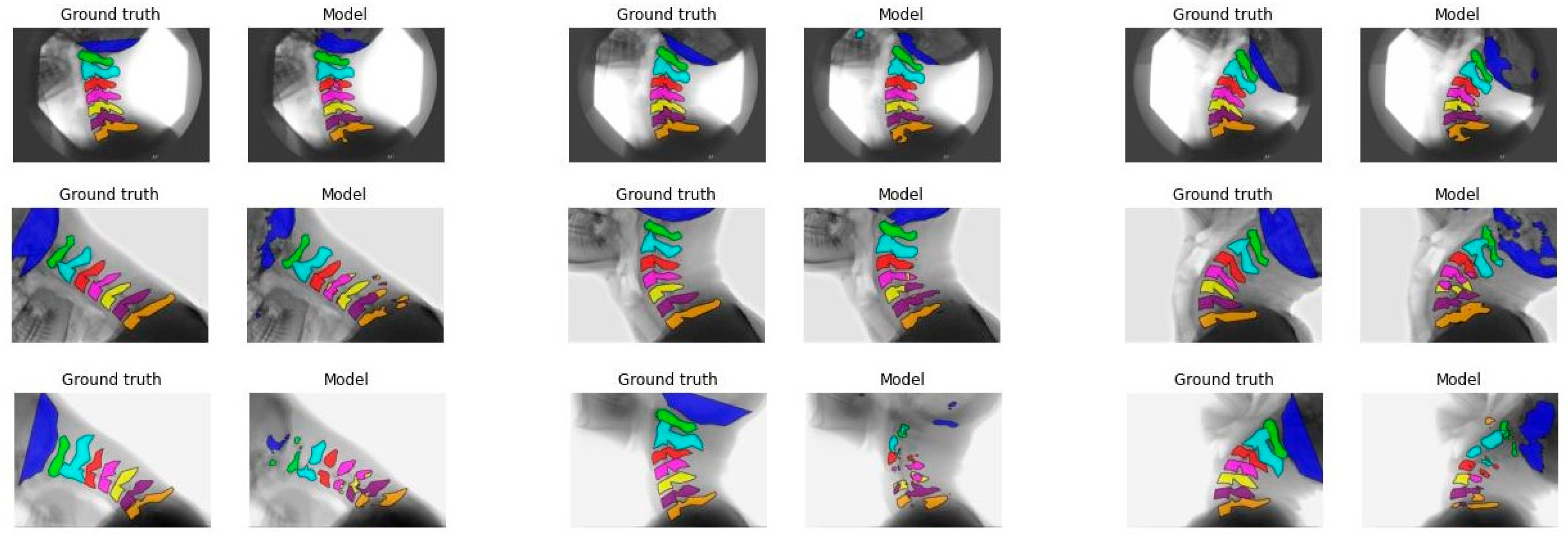
3.2. Model Performance
3.3. Mean Shape
3.4. ICC of Relative Rotation of Individual Vertebrae
3.5. ICC of Relative Rotation of Vertebral Segments
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two dimensional |
| 2D+t | Two dimensional + time |
| AI | Artificial intelligence |
| DSC | Dice similarity coefficient |
| ICC | Intraclass Correlation Coefficient |
| IoU | Intersection over Union |
| ROM | Range of motion |
| sROM | Segmental range of motion |
| SSC | Sequence of segmental contribution |
Appendix A

| Channel | A | B | C | D |
|---|---|---|---|---|
| C0 | 0.7 | 0.8 | 0.9 | 0.4 |
| C1 | 0.1 | 0.1 | 0.1 | 0.6 |
| C2 | 0.9 | 0.9 | 0.5 | 0.9 |
| C3 | 0.1 | 0.1 | 0.7 | 0.7 |
| C4 | 0.1 | 0.1 | 0.3 | 0.1 |
| C5 | 0.1 | 0.1 | 0.1 | 0.1 |
| C6 | 0.1 | 0.1 | 0.1 | 0.1 |
| C7 | 0.1 | 0.1 | 0.1 | 0.1 |
| Background | 0.1 | 0.9 | 0.1 | 0.1 |
| IoU | DSC | |||||||
|---|---|---|---|---|---|---|---|---|
| Frames | 3 | 5 | 7 | 9 | 3 | 5 | 7 | 9 |
| C0 | 0.45 | 0.50 * | 0.45 | 0.44 | 0.61 | 0.65 * | 0.61 | 0.61 |
| C1 | 0.68 | 0.69 | 0.72 * | 0.69 | 0.79 | 0.8 | 0.82 * | 0.8 |
| C2 | 0.49 | 0.72 | 0.72 | 0.73 * | 0.65 | 0.82 | 0.82 | 0.82 * |
| C3 | 0.72 | 0.73 | 0.74 * | 0.7 | 0.82 | 0.82 | 0.83 | 0.8 |
| C4 | 0.59 | 0.62 | 0.63 | 0.6 | 0.72 | 0.74 | 0.74 | 0.71 |
| C5 | 0.47 | 0.5 | 0.52 * | 0.49 | 0.61 | 0.64 | 0.64 * | 0.62 |
| C6 | 0.5 | 0.52 | 0.57 * | 0.54 | 0.63 | 0.65 | 0.7 * | 0.67 |
| C7 | 0.49 | 0.5 | 0.55 * | 0.51 | 0.64 | 0.64 | 0.68 * | 0.65 |
| IoU | DSC | |||||||
|---|---|---|---|---|---|---|---|---|
| Frames | 3 | 5 | 7 | 9 | 3 | 5 | 7 | 9 |
| C0 | 0.48 | 0.48 | 0.49 | 0.46 | 0.63 | 0.63 | 0.64 | 0.62 |
| C1 | 0.68 | 0.71 * | 0.7 | 0.69 | 0.78 | 0.81 | 0.81 | 0.79 |
| C2 | 0.71 | 0.71 | 0.72 | 0.72 * | 0.81 | 0.81 | 0.82 | 0.82 * |
| C3 | 0.71 | 0.69 | 0.72 * | 0.69 | 0.81 | 0.8 | 0.82 * | 0.8 |
| C4 | 0.62 | 0.57 | 0.63 | 0.6 | 0.74 | 0.71 | 0.75 | 0.72 |
| C5 | 0.57 | 0.49 | 0.58 | 0.5 | 0.7 | 0.64 | 0.71 * | 0.64 |
| C6 | 0.59 | 0.52 | 0.59 | 0.53 | 0.72 | 0.66 | 0.73 | 0.66 |
| C7 | 0.55 * | 0.52 | 0.54 | 0.46 | 0.68 * | 0.66 | 0.67 | 0.6 |

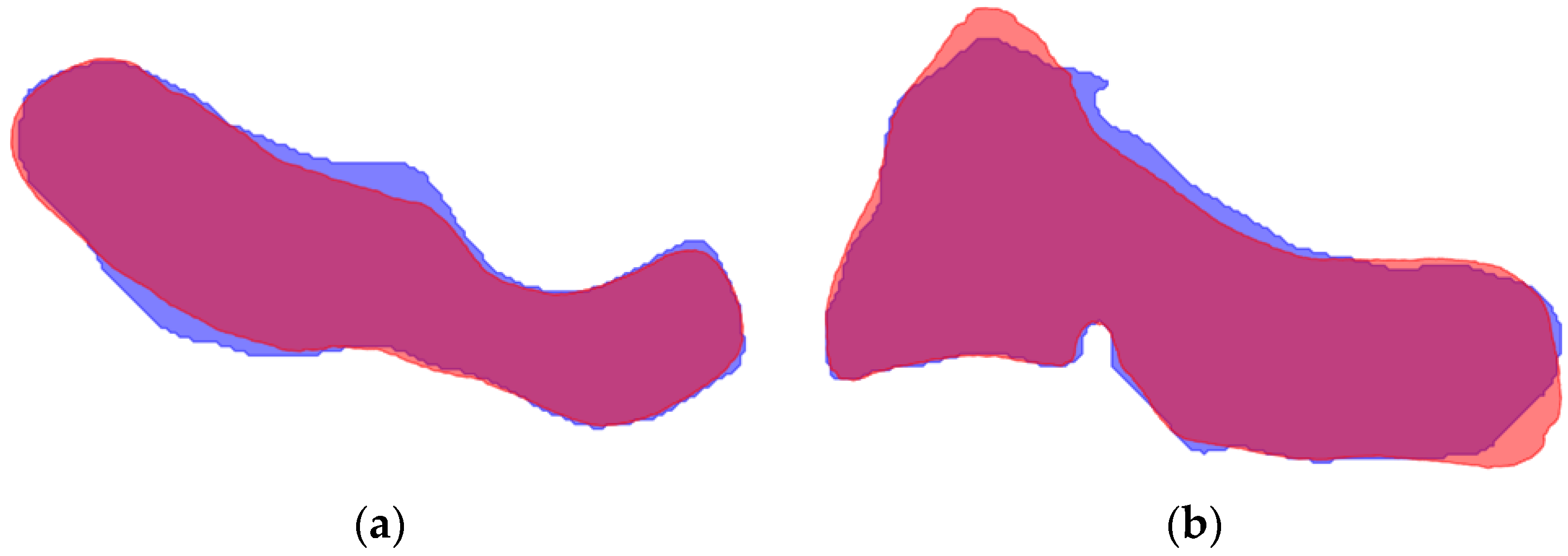
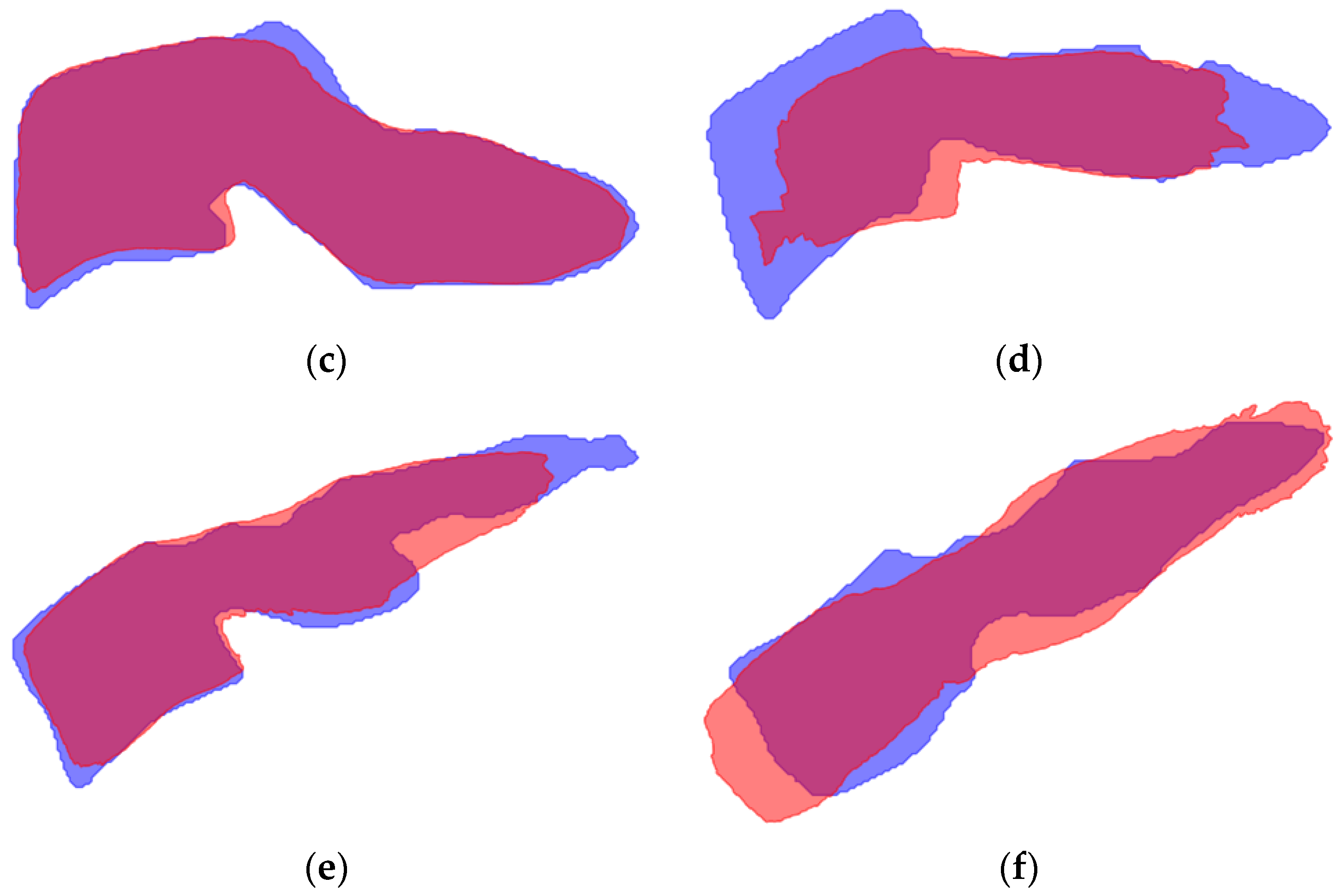
| Model A | Model B | Model C | Model D | |||||
|---|---|---|---|---|---|---|---|---|
| Segment | ICC [min–max] | n | ICC [min–max] | n | ICC [min–max] | n | ICC [min–max] | n |
| C1–C2 | 0.143 [0.056–0.218] | 4 | 0.146 [0.081–0.251] | 3 | 0.205 [0.106–0.346] | 3 | 0.082 [0.052–0.112] | 2 |
| C2–C3 | 0.258 [0.139–0.325] | 3 | 0.238 [0.221–0.254] | 2 | 0.178 [0.063–0.344] | 3 | 0.078 [0.022–0.133] | 2 |
| C3–C4 | 0.017 [n/a] | 1 | 0.112 [0.028–0.245] | 3 | 0.018 [0.007–0.063] | 2 | [n/a] | 0 |
| C4–C5 | [n/a] | 0 | [n/a] | 0 | [n/a] | 0 | 0.1 [0.031–0.069] | 2 |
| C5–C6 | [n/a] | 0 | 0.003 [n/a] | 1 | [n/a] | 0 | 0.041 [n/a] | 1 |
| C6–C7 | [n/a] | 0 | [n/a] | 0 | [n/a] | 0 | 0.043 [0.0–0.086] | 2 |
References
- Bogduk, N.; Mercer, S. Biomechanics of the cervical spine. I: Normal kinematics. Clin. Biomech. 2000, 15, 633–648. [Google Scholar] [CrossRef] [PubMed]
- van Mameren, H. Motion Patterns in the Cervical Spine. Ph.D. Thesis, Maastricht University, Maastricht, The Netherlands, 1988. [Google Scholar]
- Van Mameren, H.; Drukker, J.; Sanches, H.; Beursgens, J. Cervical spine motion in the sagittal plane (I) range of motion of actually performed movements, an X-ray cinematographic study. Eur. J. Morphol. 1990, 28, 47–68. [Google Scholar] [PubMed]
- Boselie, T.F.M.; van Santbrink, H.; de Bie, R.A.; van Mameren, H. Pilot Study of Sequence of Segmental Contributions in the Lower Cervical Spine During Active Extension and Flexion: Healthy Controls Versus Cervical Degenerative Disc Disease Patients. Spine 2017, 42, E642–E647. [Google Scholar] [CrossRef]
- Schuermans, V.N.E.; Breen, A.; Branney, J.; Smeets, A.; van Santbrink, H.; Boselie, T.F.M. Cross-Validation of two independent methods to analyze the sequence of segmental contributions in the cervical spine in extension cineradiographic recordings. In Outcomes of Anterior Cervical Spine Surgery; Maastricht University: Maastricht, The Netherlands, 2024. [Google Scholar]
- Boselie, T.F.; van Mameren, H.; de Bie, R.A.; van Santbrink, H. Cervical spine kinematics after anterior cervical discectomy with or without implantation of a mobile cervical disc prosthesis; an RCT. BMC Musculoskelet. Disord. 2015, 16, 34. [Google Scholar] [CrossRef] [PubMed]
- Schuermans, V.N.E.; Smeets, A.; Curfs, I.; van Santbrink, H.; Boselie, T.F.M. A randomized controlled trial with extended long-term follow-up: Quality of cervical spine motion after anterior cervical discectomy (ACD) or anterior cervical discectomy with arthroplasty (ACDA). Brain Spine 2024, 4, 102726. [Google Scholar] [CrossRef]
- Schuermans, V.N.E.; Smeets, A.; Breen, A.; Branney, J.; Curfs, I.; van Santbrink, H.; Boselie, T.F.M. An observational study of quality of motion in the aging cervical spine: Sequence of segmental contributions in dynamic fluoroscopy recordings. BMC Musculoskelet. Disord. 2024, 25, 330. [Google Scholar] [CrossRef]
- Al Arif, S.; Knapp, K.; Slabaugh, G. Fully automatic cervical vertebrae segmentation framework for X-ray images. Comput. Methods Programs Biomed. 2018, 157, 95–111. [Google Scholar] [CrossRef]
- Shim, J.H.; Kim, W.S.; Kim, K.G.; Yee, G.T.; Kim, Y.J.; Jeong, T.S. Evaluation of U-Net models in automated cervical spine and cranial bone segmentation using X-ray images for traumatic atlanto-occipital dislocation diagnosis. Sci. Rep. 2022, 12, 21438. [Google Scholar] [CrossRef]
- Fujita, K.; Matsuo, K.; Koyama, T.; Utagawa, K.; Morishita, S.; Sugiura, Y. Development and testing of a new application for measuring motion at the cervical spine. BMC Med. Imaging 2022, 22, 193. [Google Scholar] [CrossRef]
- Avesta, A.; Hossain, S.; Lin, M.; Aboian, M.; Krumholz, H.M.; Aneja, S. Comparing 3D, 2.5D, and 2D Approaches to Brain Image Auto-Segmentation. Bioengineering 2023, 10, 181. [Google Scholar] [CrossRef]
- Vu, M.H.; Grimbergen, G.; Nyholm, T.; Lofstedt, T. Evaluation of multislice inputs to convolutional neural networks for medical image segmentation. Med. Phys. 2020, 47, 6216–6231. [Google Scholar] [CrossRef]
- Branney, J. An Observational Study of Changes in Cervical Inter-Vertebral Motion and the Relationship with Patient-Reported Outcomes in Patients Undergoing Spinal Manipulative Therapy for Neck Pain. Ph.D. Thesis, Bournemouth University, Poole, UK, 2014. [Google Scholar]
- Branney, J.; Breen, A.C. Does inter-vertebral range of motion increase after spinal manipulation? A prospective cohort study. Chiropr. Man. Therap. 2014, 22, 24. [Google Scholar] [CrossRef]
- Reinartz, R.; Platel, B.; Boselie, T.; van Mameren, H.; van Santbrink, H.; Romeny, B. Cervical vertebrae tracking in video-fluoroscopy using the normalized gradient field. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2009: 12th International Conference, London, UK, 20–24 September 2009; Volume 12, pp. 524–531. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Siddique, N.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V. U-Net and Its Variants for Medical Image Segmentation: A Review of Theory and Applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Zou, K.H.; Warfield, S.K.; Bharatha, A.; Tempany, C.M.; Kaus, M.R.; Haker, S.J.; Wells, W.M., 3rd; Jolesz, F.A.; Kikinis, R. Statistical validation of image segmentation quality based on a spatial overlap index. Acad. Radiol. 2004, 11, 178–189. [Google Scholar] [CrossRef]
- Kittipongdaja, P.; Siriborvornratanakul, T. Automatic kidney segmentation using 2.5D ResUNet and 2.5D DenseUNet for malignant potential analysis in complex renal cyst based on CT images. EURASIP J. Image Video Process. 2022, 2022, 5. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liao, G.; Sun, W.; Sun, J.; Sheng, T.; Zhu, K.; von Deneen, K.M.; Zhang, Y. A 2.5D semantic segmentation of the pancreas using attention guided dual context embedded U-Net. Neurocomputing 2022, 480, 14–26. [Google Scholar] [CrossRef]
- Gilad, I.; Nissan, M. A study of vertebra and disc geometric relations of the human cervical and lumbar spine. Spine 1986, 11, 154–157. [Google Scholar] [CrossRef]
- Choukali, M.A.; Valizadeh, M.; Amirani, M.C.; Mirbolouk, S. A desired histogram estimation accompanied with an exact histogram matching method for image contrast enhancement. Multimed. Tools Appl. 2023, 82, 28345–28365. [Google Scholar] [CrossRef]
- Salvi, M.; Acharya, U.R.; Molinari, F.; Meiburger, K.M. The impact of pre- and post-image processing techniques on deep learning frameworks: A comprehensive review for digital pathology image analysis. Comput. Biol. Med. 2021, 128, 104129. [Google Scholar] [CrossRef]
- Vogt, S.; Scholl, C.; Grover, P.; Marks, J.; Dreischarf, M.; Braumann, U.D.; Strube, P.; Holzl, A.; Bohle, S. Novel AI-Based Algorithm for the Automated Measurement of Cervical Sagittal Balance Parameters. A Validation Study on Pre- and Postoperative Radiographs of 129 Patients. Glob. Spine J. 2024, 15, 1155–1165. [Google Scholar] [CrossRef] [PubMed]

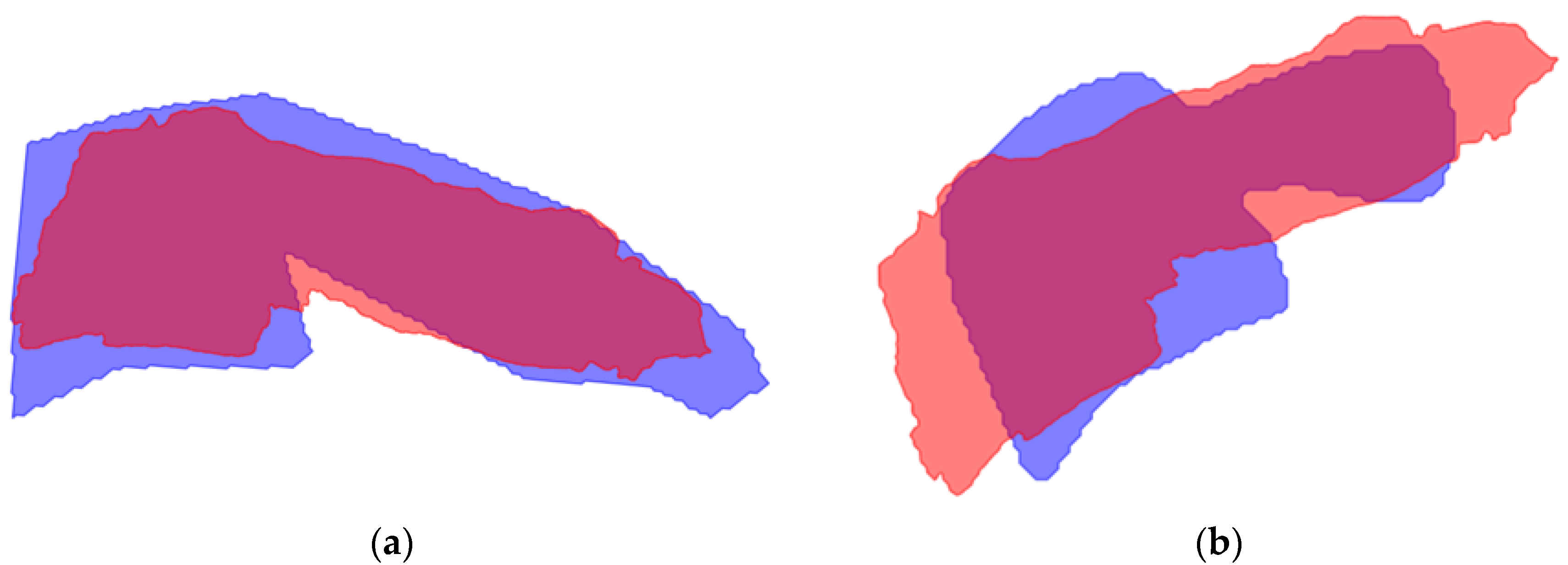

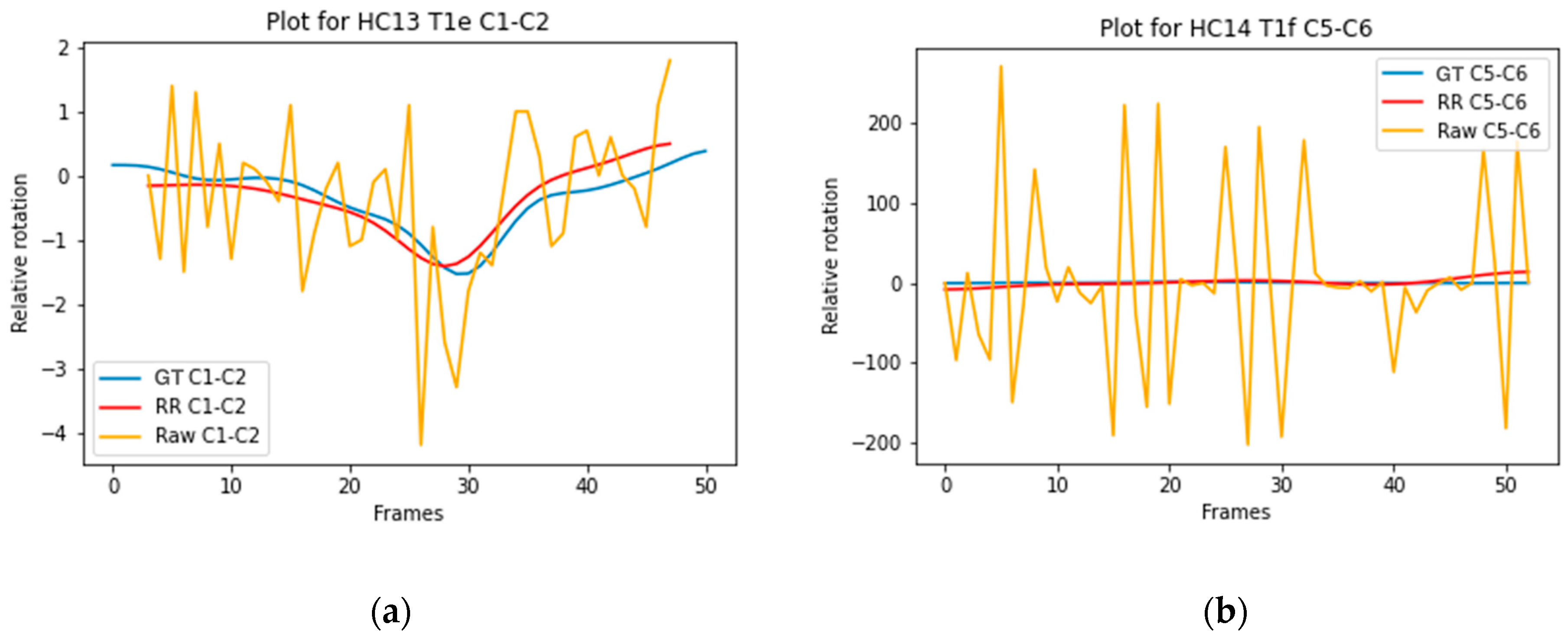
| Model | Dimension | |
|---|---|---|
| A | 640 × 640 | 2D |
| B | 832 × 576 | 2D |
| C | 640 × 640 | 2D + time |
| D | 832 × 576 | 2D + time |
| Data Subset | Individuals (n =) | Recordings (n =) |
|---|---|---|
| Training (55%) | 21 | 52 |
| Validation (20%) | 8 | 18 |
| Testing (25%) | 10 | 19 |
| IoU | DSC | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | A | B | C | D | A | B | C | D |
| C0 | 0.37 | 0.51 * | 0.45 | 0.49 | 0.53 | 0.66 * | 0.61 | 0.64 |
| C1 | 0.71 | 0.72 * | 0.72 | 0.7 | 0.81 | 0.82 * | 0.82 | 0.81 |
| C2 | 0.72 | 0.71 | 0.72 | 0.72 | 0.82 | 0.81 | 0.82 | 0.82 * |
| C3 | 0.7 | 0.72 | 0.74 * | 0.72 | 0.8 | 0.82 | 0.83 * | 0.82 |
| C4 | 0.6 | 0.64 * | 0.63 | 0.63 | 0.72 | 0.76 * | 0.74 | 0.75 |
| C5 | 0.51 | 0.56 | 0.52 | 0.58 * | 0.64 | 0.69 | 0.64 | 0.71 * |
| C6 | 0.51 | 0.55 | 0.57 | 0.59 * | 0.65 | 0.69 | 0.7 | 0.73 * |
| C7 | 0.51 | 0.52 | 0.55 * | 0.54 | 0.65 | 0.66 | 0.68 * | 0.67 |
| A | B | C | D | |
|---|---|---|---|---|
| C1 | 0.76 | 0.76 | 0.78 | 0.75 |
| C2 | 0.80 | 0.79 | 0.78 | 0.76 |
| C3 | 0.79 | 0.84 | 0.84 | 0.84 |
| C4 | 0.69 | 0.81 | 0.78 | 0.75 |
| C5 | 0.56 | 0.62 | 0.61 | 0.61 |
| C6 | 0.60 | 0.56 | 0.63 | 0.66 |
| C7 | 0.63 | 0.63 | 0.62 | 0.56 |
| Model A | Model B | Model C | Model D | |||||
|---|---|---|---|---|---|---|---|---|
| Vertebra | ICC [min–max] | n | ICC [min–max] | n | ICC [min–max] | n | ICC [min–max] | n |
| C1 | 0.962 [0.916–0.993] | 7 | 0.948 [0.834–0.996] | 13 | 0.888 [0.471–0.997] | 12 | 0.843 [0.479–0.982] | 12 |
| C2 | 0.904 [0.699–0.996] | 10 | 0.882 [0.449–0.978] | 12 | 0.868 [0.413–0.988] | 12 | 0.796 [0.400–0.985] | 12 |
| C3 | 0.871 [0.422–0.993] | 7 | 0.917 [0.826–0.976] | 9 | 0.741 [0.132–0.979] | 7 | 0.620 [0.298–0.909] | 6 |
| C4 | 0.880 [0.814–0.960] | 3 | 0.812 [0.601–0.927] | 7 | 0.907 [0.899–0.923] | 3 | 0.636 [0.343–0.820] | 3 |
| C5 | 0.904 [n/a] | 1 | 0.798 [0.650–0.945] | 2 | 0.683 [0.658–0.680] | 2 | 0.775 [0.707–0.864] | 3 |
| C6 | 0.982 [n/a] | 1 | 0.830 [0.665–0.995] | 2 | 0.769 [0.471–0.979] | 4 | 0.878 [0.639–0.966] | 8 |
| C7 | 0.819 [0.732–0.905] | 2 | 0.869 [0.650–0.954] | 5 | 0.879 [0.785–0.974] | 5 | 0.863 [0.697–0.942] | 4 |
| Model A | Model B | Model C | Model D | |||||
|---|---|---|---|---|---|---|---|---|
| Segment | ICC [min–max] | n | ICC [min–max] | n | ICC [min–max] | n | ICC [min–max] | n |
| C1–C2 | 0.685 [0.481–0.988] | 5 | 0.627 [0.136–0.938] | 5 | 0.713 [0.283–0.937] | 7 | 0.724 [0.559–0.890] | 4 |
| C2–C3 | 0.512 [0.181–0.934] | 4 | 0.408 [0.025–0.661] | 4 | 0.500 [0.321–0.615] | 6 | 0.340 [0.006–0.647] | 4 |
| C3–C4 | 0.511 [n/a] | 1 | 0.412 [0.025–0.831] | 5 | 0.382 [0.355–0.409] | 2 | 0.645 [n/a] | 1 |
| C4–C5 | [n/a] | 0 | 0.489 [0.464–0.514] | 2 | 0.578 [0.492–0.663] | 2 | 0.281 [n/a] | 1 |
| C5–C6 | [n/a] | 0 | 0.605 [0.505–0.705] | 2 | 0.535 [n/a] | 1 | 0.542 [0.314–0.772] | 3 |
| C6–C7 | 0.674 [n/a] | 1 | [n/a] | 0 | 0.770 [n/a] | 1 | 0.685 [n/a] | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Santbrink, E.; Schuermans, V.; Cerfonteijn, E.; Breeuwer, M.; Smeets, A.; van Santbrink, H.; Boselie, T. AI-Assisted Image Recognition of Cervical Spine Vertebrae in Dynamic X-Ray Recordings. Bioengineering 2025, 12, 679. https://doi.org/10.3390/bioengineering12070679
van Santbrink E, Schuermans V, Cerfonteijn E, Breeuwer M, Smeets A, van Santbrink H, Boselie T. AI-Assisted Image Recognition of Cervical Spine Vertebrae in Dynamic X-Ray Recordings. Bioengineering. 2025; 12(7):679. https://doi.org/10.3390/bioengineering12070679
Chicago/Turabian Stylevan Santbrink, Esther, Valérie Schuermans, Esmée Cerfonteijn, Marcel Breeuwer, Anouk Smeets, Henk van Santbrink, and Toon Boselie. 2025. "AI-Assisted Image Recognition of Cervical Spine Vertebrae in Dynamic X-Ray Recordings" Bioengineering 12, no. 7: 679. https://doi.org/10.3390/bioengineering12070679
APA Stylevan Santbrink, E., Schuermans, V., Cerfonteijn, E., Breeuwer, M., Smeets, A., van Santbrink, H., & Boselie, T. (2025). AI-Assisted Image Recognition of Cervical Spine Vertebrae in Dynamic X-Ray Recordings. Bioengineering, 12(7), 679. https://doi.org/10.3390/bioengineering12070679






