AI-Powered Spectral Imaging for Virtual Pathology Staining
Abstract
1. Introduction
2. Methodology
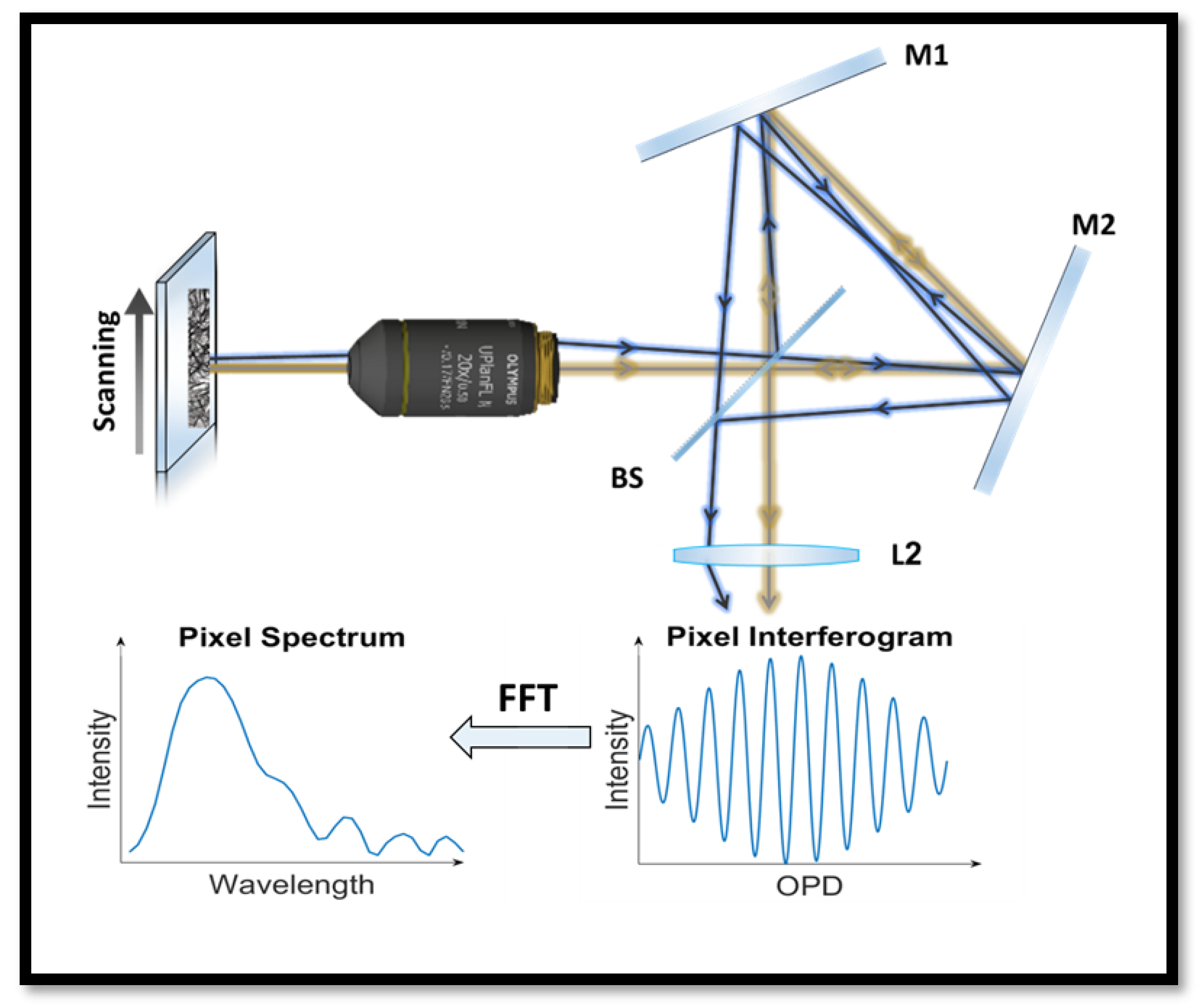
2.1. Spectral Imaging System
2.2. Sample Preparation
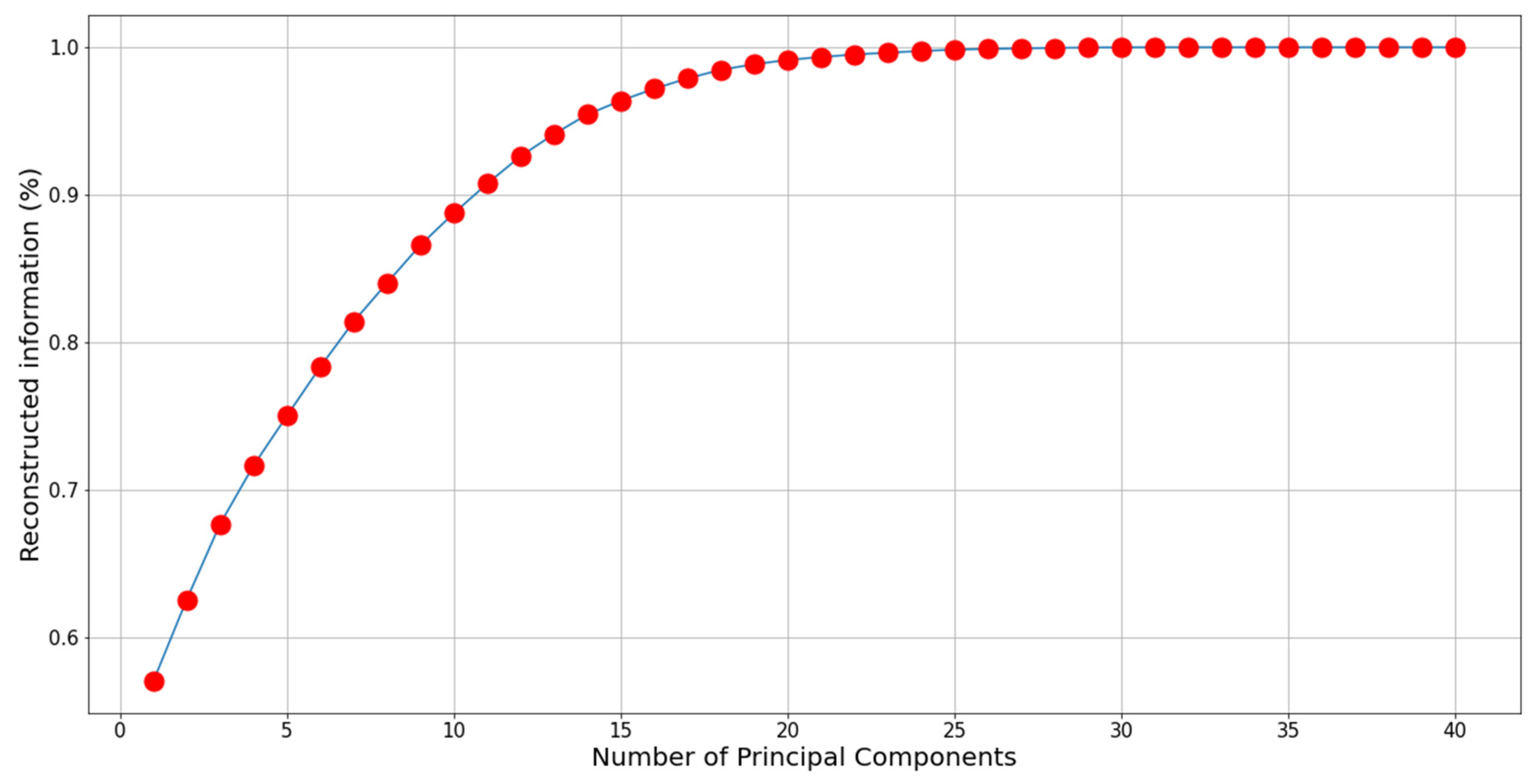
2.3. Principal Component Analysis
2.4. Network Architecture
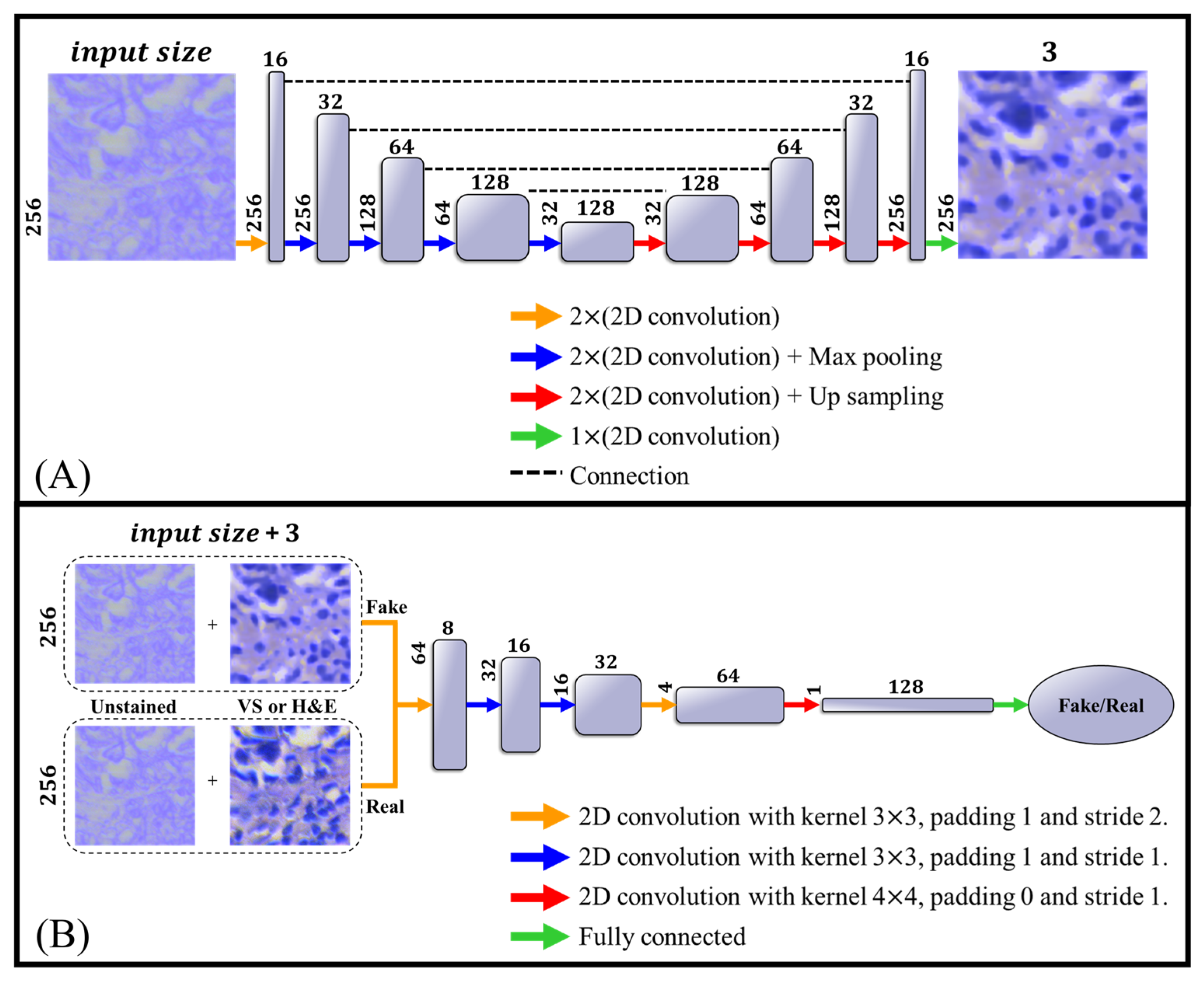
3. Results
Model Training
4. Discussion
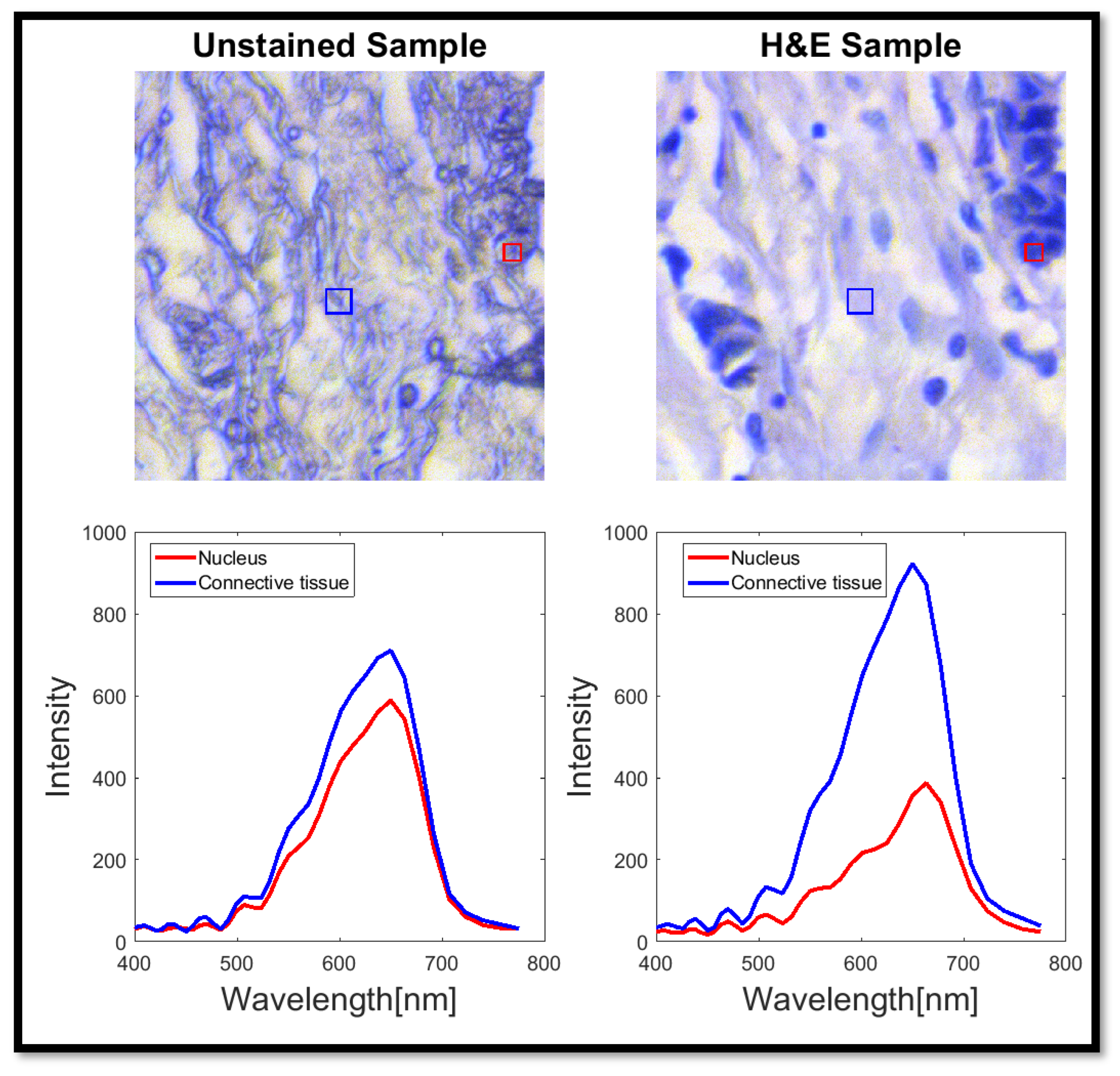
- There is a difference in the morphology of unstained and stained tissue irrespective of ‘fake’ or true H&E staining. This is most obvious for areas without cells that are found throughout tissue (see Figure 7); such areas became smaller and changed their shapes after H&E staining. Considering this observation, other morphologies must change as well but are not as obvious to the eye. Such changes after H&E staining are not currently known in the field. Thus, further studies will need to be performed to define the staining-induced differences in morphology and to determine whether they matter in clinical diagnosis.
- While the concordance between real H&E and ‘fake’ H&E is high (Table 1), ‘fake’ H&E appears to sometimes add ‘stained’ structures (looking like cells) or fails to identify some cells that were stained by H&E. Further studies need to investigate the reason for this difference.
- It is expected that these minor differences between ‘fake’ H&E and true H&E staining should not impact the diagnostic value of the ‘fake’ H&E. It is important to perform a blind study that will compare a series of patient samples examined after fake H&E and true H&E staining. If the examination of such samples by a pathologist leads to identical results in diagnosis, the minor differences reported in this study should not matter for clinical evaluation.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- El Alaoui, Y.; Elomri, A.; Qaraqe, M.; Padmanabhan, R.; Yasin Taha, R.; El Omri, H.; EL Omri, A.; Aboumarzouk, O. A Review of Artificial Intelligence Applications in Hematology Management: Current Practices and Future Prospects. J. Med. Internet Res. 2022, 24, e36490. [Google Scholar] [CrossRef]
- Serajian, M.; Testagrose, C.; Prosperi, M.; Boucher, C. A Comparative Study of Antibiotic Resistance Patterns in Mycobacterium Tuberculosis. Sci. Rep. 2025, 15, 5104. [Google Scholar] [CrossRef] [PubMed]
- Irani, H.; Metsis, V. Enhancing Time-Series Prediction with Temporal Context Modeling: A Bayesian and Deep Learning Synergy. Int. FLAIRS Conf. Proc. 2024, 37. [Google Scholar] [CrossRef]
- Shamai, G.; Livne, A.; Polónia, A.; Sabo, E.; Cretu, A.; Bar-Sela, G.; Kimmel, R. Deep Learning-Based Image Analysis Predicts PD-L1 Status from H&E-Stained Histopathology Images in Breast Cancer. Nat. Commun. 2022, 13, 6753. [Google Scholar] [CrossRef]
- De Haan, K.; Zhang, Y.; Zuckerman, J.E.; Liu, T.; Sisk, A.E.; Diaz, M.F.P.; Jen, K.-Y.; Nobori, A.; Liou, S.; Zhang, S.; et al. Deep Learning-Based Transformation of H&E Stained Tissues into Special Stains. Nat. Commun. 2021, 12, 4884. [Google Scholar] [CrossRef]
- Yoon, C.; Park, E.; Misra, S.; Kim, J.Y.; Baik, J.W.; Kim, K.G.; Jung, C.K.; Kim, C. Deep Learning-Based Virtual Staining, Segmentation, and Classification in Label-Free Photoacoustic Histology of Human Specimens. Light. Sci. Appl. 2024, 13, 226. [Google Scholar] [CrossRef] [PubMed]
- Kleppe, A.; Skrede, O.-J.; De Raedt, S.; Liestøl, K.; Kerr, D.J.; Danielsen, H.E. Designing Deep Learning Studies in Cancer Diagnostics. Nat. Rev. Cancer 2021, 21, 199–211. [Google Scholar] [CrossRef] [PubMed]
- Khare, S.K.; Blanes-Vidal, V.; Booth, B.B.; Petersen, L.K.; Nadimi, E.S. A Systematic Review and Research Recommendations on Artificial Intelligence for Automated Cervical Cancer Detection. WIREs Data Min. Knowl. Discov. 2024, 14, e1550. [Google Scholar] [CrossRef]
- Soker, A.; Brozgol, E.; Barshack, I.; Garini, Y. Advancing Automated Digital Pathology by Rapid Spectral Imaging and AI for Nuclear Segmentation. Opt. Laser Technol. 2025, 181, 111988. [Google Scholar] [CrossRef]
- Wahid, A.; Mahmood, T.; Hong, J.S.; Kim, S.G.; Ullah, N.; Akram, R.; Park, K.R. Multi-Path Residual Attention Network for Cancer Diagnosis Robust to a Small Number of Training Data of Microscopic Hyperspectral Pathological Images. Eng. Appl. Artif. Intell. 2024, 133, 108288. [Google Scholar] [CrossRef]
- Gao, H.; Wang, H.; Chen, L.; Cao, X.; Zhu, M.; Xu, P. Semi-Supervised Segmentation of Hyperspectral Pathological Imagery Based on Shape Priors and Contrastive Learning. Biomed. Signal Process. Control 2024, 91, 105881. [Google Scholar] [CrossRef]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral Super-Resolution by Coupled Spectral Unmixing. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3586–3594. [Google Scholar]
- Garini, Y.; Tauber, E. Spectral Imaging: Methods, Design, and Applications. In Biomedical Optical Imaging Technologies: Design and Applications; Liang, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 111–161. ISBN 978-3-642-28391-8. [Google Scholar]
- Lindner, M.; Shotan, Z.; Garini, Y. Rapid Microscopy Measurement of Very Large Spectral Images. Opt. Express 2016, 24, 9511. [Google Scholar] [CrossRef]
- Bai, B.; Yang, X.; Li, Y.; Zhang, Y.; Pillar, N.; Ozcan, A. Deep Learning-Enabled Virtual Histological Staining of Biological Samples. Light. Sci. Appl. 2023, 12, 57. [Google Scholar] [CrossRef]
- Li, J.; Garfinkel, J.; Zhang, X.; Wu, D.; Zhang, Y.; De Haan, K.; Wang, H.; Liu, T.; Bai, B.; Rivenson, Y.; et al. Biopsy-Free in Vivo Virtual Histology of Skin Using Deep Learning. Light. Sci. Appl. 2021, 10, 233. [Google Scholar] [CrossRef]
- Fairman, H.S.; Brill, M.H.; Hemmendinger, H. How the CIE 1931 Color-Matching Functions Were Derived from Wright-Guild Data. Color. Res. Appl. 1997, 22, 11–23. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal Components Analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- McNeil, C.; Wong, P.F.; Sridhar, N.; Wang, Y.; Santori, C.; Wu, C.-H.; Homyk, A.; Gutierrez, M.; Behrooz, A.; Tiniakos, D.; et al. An End-to-End Platform for Digital Pathology Using Hyperspectral Autofluorescence Microscopy and Deep Learning-Based Virtual Histology. Mod. Pathol. 2024, 37, 100377. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-Mean-Square Error (RMSE) or Mean Absolute Error (MAE): When to Use Them or Not. Geosci. Model. Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Korhonen, J.; You, J. Peak Signal-to-Noise Ratio Revisited: Is Simple Beautiful? In Proceedings of the 2012 Fourth International Workshop on Quality of Multimedia Experience, Melbourne, Australia, 5–7 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 37–38. [Google Scholar]
- Hassan, M.; Bhagvati, C. Structural Similarity Measure for Color Images. Int. J. Comput. Appl. 2012, 43, 7–12. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, W.; Deng, Y. Frechet Inception Distance (FID) for Evaluating GANs; China University of Mining and Technology Beijing Graduate School: Beijing, China, 2021. [Google Scholar]
- Bińkowski, M.; Sutherland, D.J.; Arbel, M.; Gretton, A. Demystifying MMD GANs. arXiv 2021, arXiv:1801.01401. [Google Scholar]
- Brozgol, E.; Kumar, P.; Necula, D.; Bronshtein-Berger, I.; Lindner, M.; Medalion, S.; Twito, L.; Shapira, Y.; Gondra, H.; Barshack, I.; et al. Cancer Detection from Stained Biopsies Using High-Speed Spectral Imaging. Biomed. Opt. Express 2022, 13, 2503. [Google Scholar] [CrossRef] [PubMed]
- Garini, Y.; Macville, M.; Du Manoir, S.; Buckwald, R.A.; Lavi, M.; Katzir, N.; Wine, D.; Bar-Am, I.; Schröck, E.; Cabib, D.; et al. Spectral Karyotyping. Bioimaging 1996, 4, 65–72. [Google Scholar] [CrossRef]
- Garini, Y.; Young, I.T.; McNamara, G. Spectral Imaging: Principles and Applications. Cytom. Part. J. Int. Soc. Anal. Cytol. 2006, 69, 735–747. [Google Scholar] [CrossRef]
- Farris, A.B.; Cohen, C.; Rogers, T.E.; Smith, G.H. Whole Slide Imaging for Analytical Anatomic Pathology and Telepathology: Practical Applications Today, Promises, and Perils. Arch. Pathol. Lab. Med. 2017, 141, 542–550. [Google Scholar] [CrossRef] [PubMed]
- Bell, R. Introductory Fourier Transform Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Boyat, A.K.; Joshi, B.K. A Review Paper: Noise Models in Digital Image Processing. Signal Image Process. Int. J. 2015, 6, 63–75. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Chan, T.; Esedoglu, S.; Park, F.; Yip, A. Total Variation Image Restoration: Overview and Recent Developments. In Handbook of Mathematical Models in Computer Vision; Paragios, N., Chen, Y., Faugeras, O., Eds.; Springer US: Boston, MA, USA, 2006; pp. 17–31. ISBN 978-0-387-28831-4. [Google Scholar]
- Xu, J.; Li, Z.; Du, B.; Zhang, M.; Liu, J. Reluplex Made More Practical: Leaky ReLU. In Proceedings of the 2020 IEEE Symposium on Computers and Communications (ISCC), Rennes, France, 7–10 July 2020; pp. 1–7. [Google Scholar]
- Huang, L.; Qin, J.; Zhou, Y.; Zhu, F.; Liu, L.; Shao, L. Normalization Techniques in Training DNNs: Methodology, Analysis and Application. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10173–10196. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. ICLR 2015, 3, 7–9. [Google Scholar]
- Stelzer. Contrast, Resolution, Pixelation, Dynamic Range and Signal-to-noise Ratio: Fundamental Limits to Resolution in Fluorescence Light Microscopy. J. Microsc. 1998, 189, 15–24. [Google Scholar] [CrossRef]
- Young, I.T. Quantitative Microscopy. IEEE Eng. Med. Biol. Mag. 1996, 15, 59–66. [Google Scholar] [CrossRef]
- Liu, K.; Lin, S.; Zhu, S.; Chen, Y.; Yin, H.; Li, Z.; Chen, Z. Hyperspectral Microscopy Combined with DAPI Staining for the Identification of Hepatic Carcinoma Cells. Biomed. Opt. Express 2021, 12, 173. [Google Scholar] [CrossRef]
- Ortega, S.; Halicek, M.; Fabelo, H.; Camacho, R.; Plaza, M.D.L.L.; Godtliebsen, F.; Callicó, G.M.; Fei, B. Hyperspectral Imaging for the Detection of Glioblastoma Tumor Cells in H&E Slides Using Convolutional Neural Networks. Sensors 2020, 20, 1911. [Google Scholar] [CrossRef] [PubMed]
- Souza, M.M.; Carvalho, F.A.; Sverzut, E.F.V.; Requena, M.B.; Garcia, M.R.; Pratavieira, S. Hyperspectral Imaging System for Tissue Classification in H&E-Stained Histological Slides. In Proceedings of the 2021 SBFoton International Optics and Photonics Conference (SBFoton IOPC), Sao Carlos, Brazil, 31 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–4. [Google Scholar]
- Bayramoglu, N.; Kaakinen, M.; Eklund, L.; Heikkila, J. Towards Virtual H&E Staining of Hyperspectral Lung Histology Images Using Conditional Generative Adversarial Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 64–71. [Google Scholar]
- Zhu, R.; He, H.; Chen, Y.; Yi, M.; Ran, S.; Wang, C.; Wang, Y. Deep Learning for Rapid Virtual H&E Staining of Label-Free Glioma Tissue from Hyperspectral Images. Comput. Biol. Med. 2024, 180, 108958. [Google Scholar] [CrossRef]

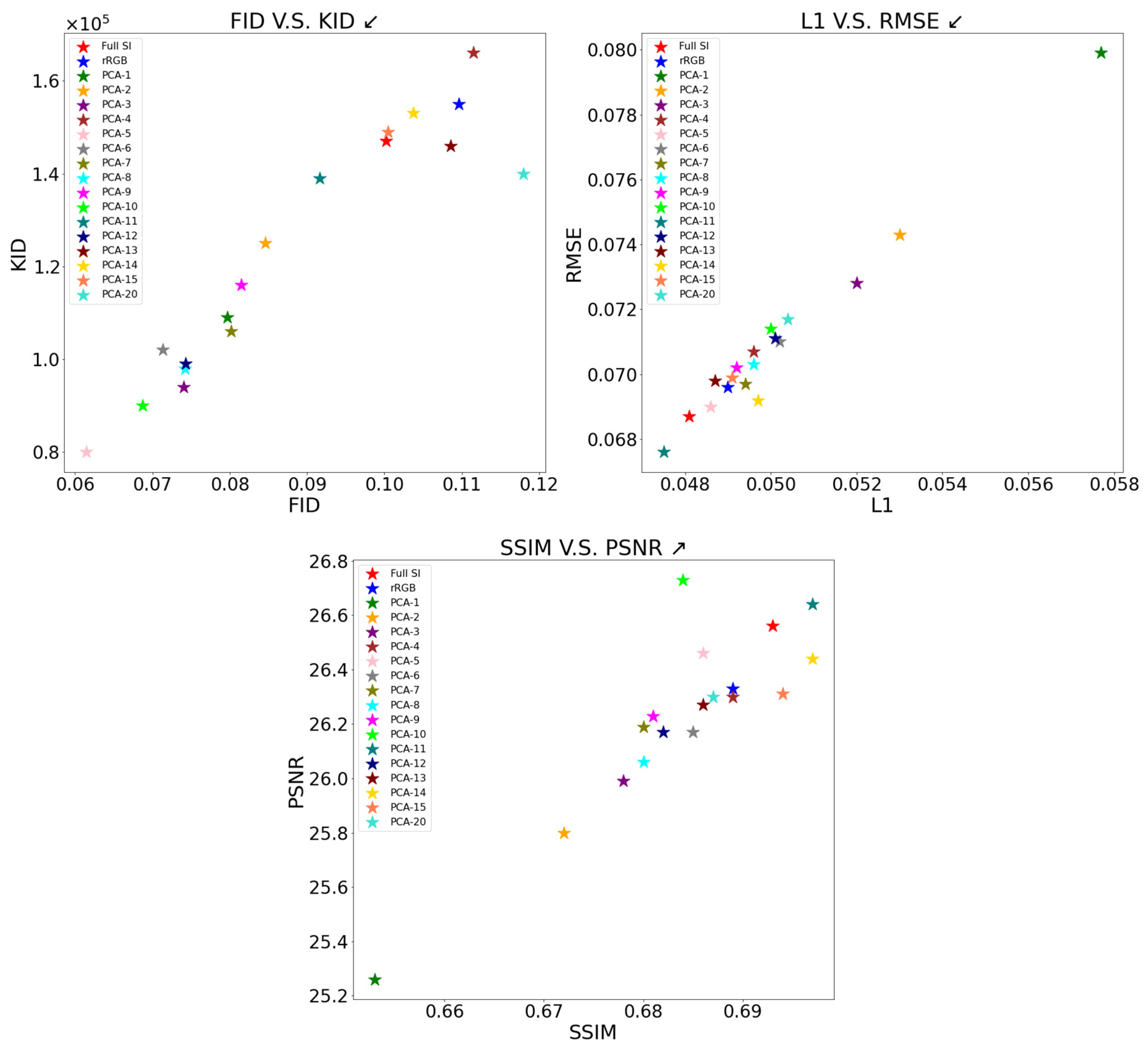

| Dataset | FID↓ | KID↓ | L1↓ | RMSE↓ | SSIM↑ | PSNR↑ |
|---|---|---|---|---|---|---|
| Full SI | ||||||
| rRGB | ||||||
| PCA-5 | ||||||
| PCA-10 | 0.0500 | |||||
| PCA-15 | ||||||
| PCA-20 | 0.1180 | 0.0504 | 0.0717 | 0.687 | 26.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soker, A.; Almagor, M.; Mai, S.; Garini, Y. AI-Powered Spectral Imaging for Virtual Pathology Staining. Bioengineering 2025, 12, 655. https://doi.org/10.3390/bioengineering12060655
Soker A, Almagor M, Mai S, Garini Y. AI-Powered Spectral Imaging for Virtual Pathology Staining. Bioengineering. 2025; 12(6):655. https://doi.org/10.3390/bioengineering12060655
Chicago/Turabian StyleSoker, Adam, Maya Almagor, Sabine Mai, and Yuval Garini. 2025. "AI-Powered Spectral Imaging for Virtual Pathology Staining" Bioengineering 12, no. 6: 655. https://doi.org/10.3390/bioengineering12060655
APA StyleSoker, A., Almagor, M., Mai, S., & Garini, Y. (2025). AI-Powered Spectral Imaging for Virtual Pathology Staining. Bioengineering, 12(6), 655. https://doi.org/10.3390/bioengineering12060655







