Optimizing Input Feature Sets Using Catch-22 and Personalization for an Accurate and Reliable Estimation of Continuous, Cuffless Blood Pressure
Abstract
1. Introduction
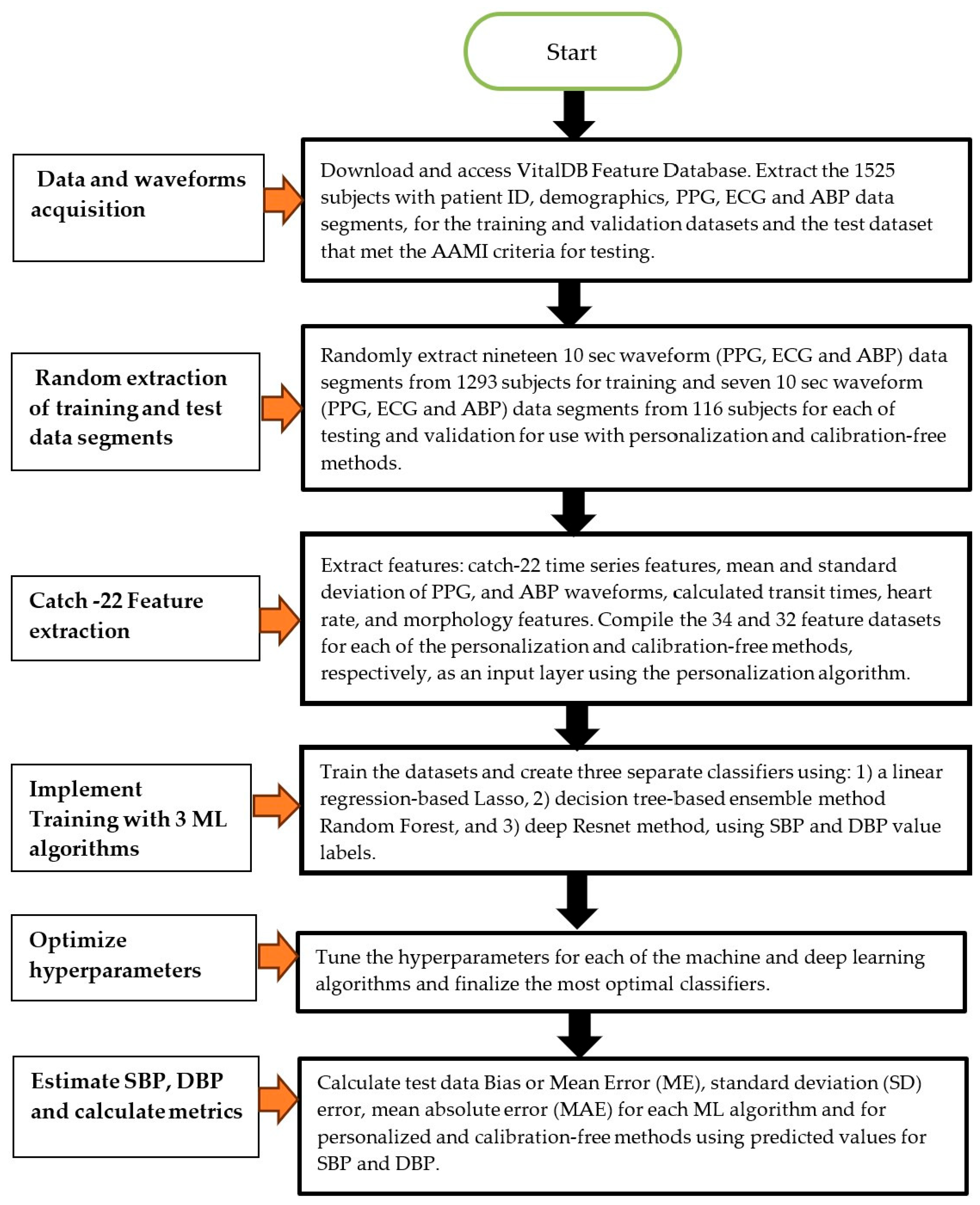
2. Methods
2.1. Human Data Ethical Statement
2.2. Patient Data
2.3. Feature Extraction
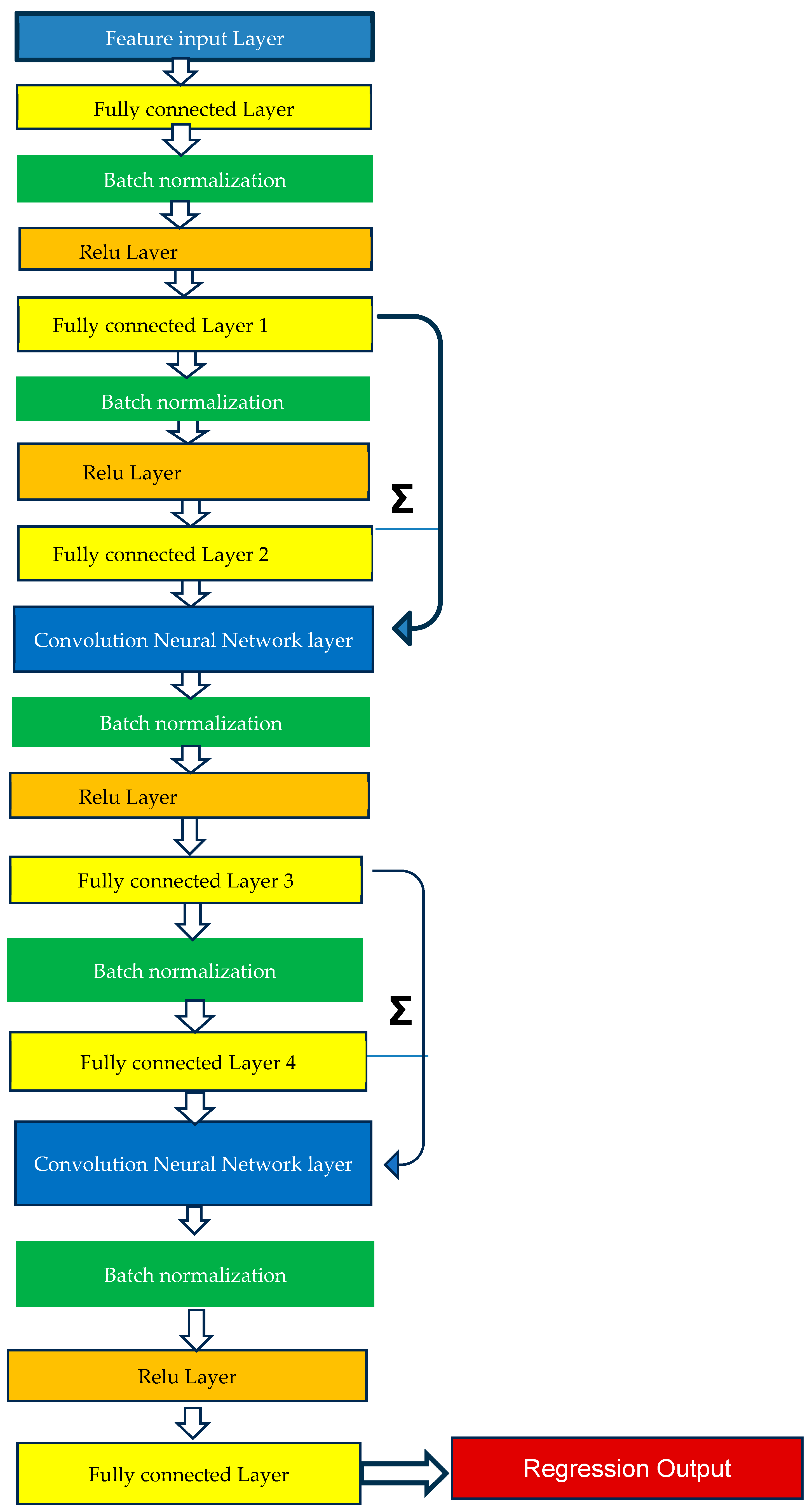
2.4. Method of Analysis—Machine Learning Model Training
2.5. Method of Analysis—Personalized and Calibration-Free Model Testing
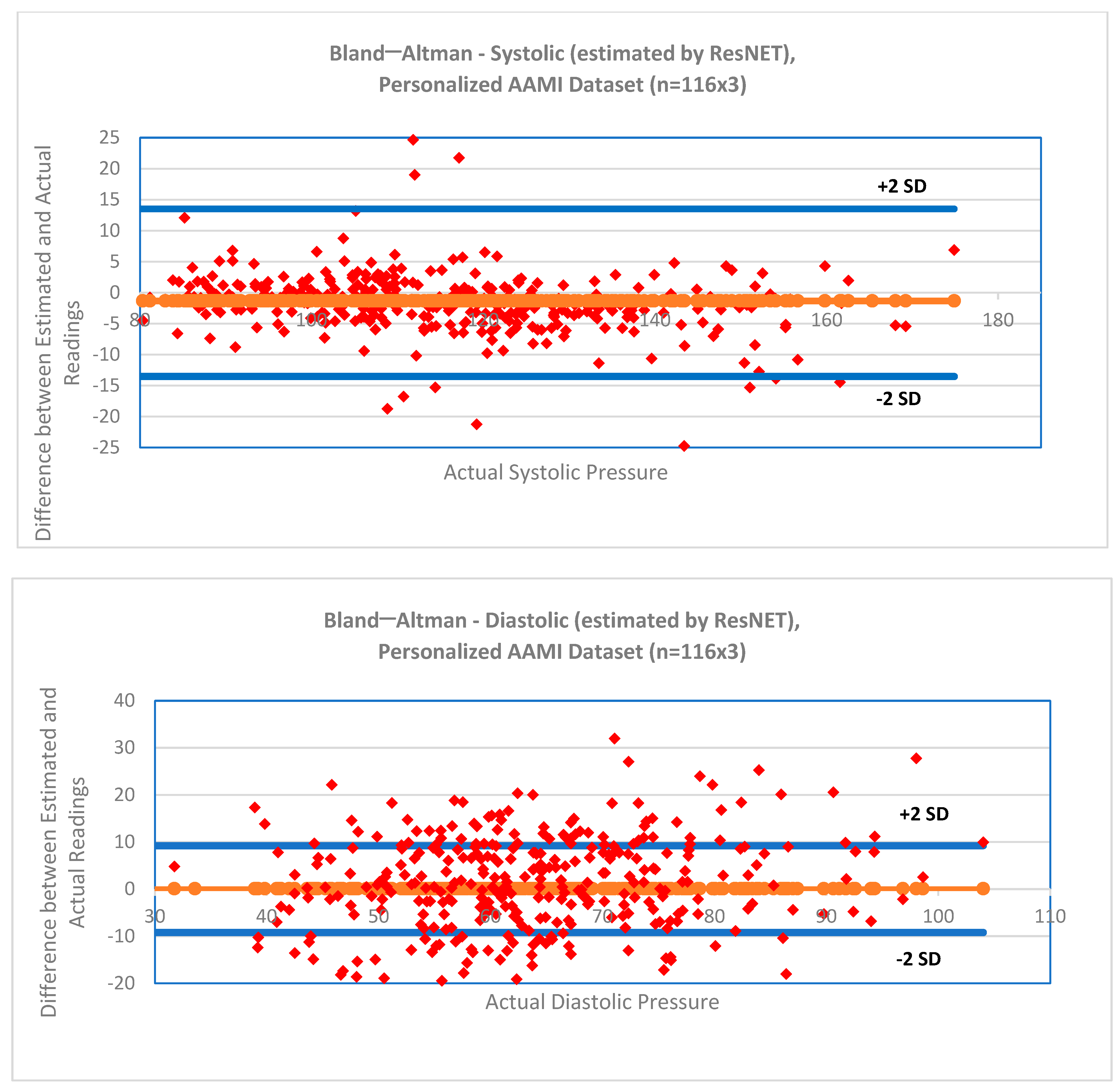
2.6. Statistical Analysis
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Catch-22 Detailed Description
| # | Feature Name | Description |
|---|---|---|
| I. | Distribution-related features | |
| 1 | DN_HistogramMode_5 | Mode of z-scored distribution (5-bin histogram) |
| 2 | DN_HistogramMode_10 | Mode of z-scored distribution (10-bin histogram) |
| II. | Simple temporal statistics | |
| 3 | SB_BinaryStats_mean_longstretch1 | Longest period of consecutive values above the mean |
| 4 | DN_OutlierInclude_p_001_mdrmd | Time intervals between successive extreme events above the mean |
| 5 | DN_OutlierInclude_n_001_mdrmd | Time intervals between successive extreme events below the mean |
| III. | Linear autocorrelation | |
| 6 | CO_flecac | First 1/e crossing of autocorrelation function |
| 7 | CO_FirstMin_ac | First minimum of autocorrelation function |
| 8 | SP_Summaries_welch_rect_area_5_1 | Total power in lowest fifth of frequencies in the Fourier power spectrum |
| 9 | SP_Summaries_welch_rect_centroid | Centroid of the Fourier power spectrum |
| 10 | FC_LocalSimple_mean3_stderr | Mean error from a rolling 3-sample mean forecasting |
| IV. | Non-linear autocorrelation | |
| 11 | CO_trev_1_num | Time reversibility statistic |
| 12 | CO_HistogramAMI_even_2_5 | Automutual information, m = 2, r = 5 |
| 13 | IN_AutoMutualInfoStats_40_gaussian_fnni | First minimum of the automutual information function |
| V. | Successive differences | |
| 14 | MD_hrv_classic_pnn40 | Proportion of successive differences exceeding 0.04σ |
| 15 | SB_BinaryStats_mean_longstretch0 | Longest period of successive incremental decreases |
| 16 | SB_MotifThree_quantile_hh | Shannon entropy of two successive letters in equiprobable 3-letter symbolization |
| 17 | FC_LocalSimple_mean3_stderr | Change in correlation length after iterative differencing |
| 18 | CO_embed2_Dist_tau_d_expfit_meandiff | Exponential fit to successive distances in 2-d embedding space |
| VI. | Fluctuation analysis | |
| 19 | SC_FlucAnal_2_dfa_50_1_2_logi_prop_r1 | Proportion of slower timescale fluctuations that scale with DFA (50% sampling) |
| 20 | SC_FlucAnal_2_rsrangefit_50_1_logi_prop_r1 | Proportion of slower timescale fluctuations that scale with linearly rescaled range fits |
| V | Others | |
| 21 | SB_TransitionMatrix_3ac_sumdiagcov | Trace of covariance of transition matrix between symbols in 3-letter alphabet |
| 22 | PD_PeriodicityWang_th0_01 | Periodicity measure |
References
- Zhao, L.; Liang, C.; Huang, Y.; Zhou, G.; Xiao, Y.; Ji, N.; Zhang, Y.T.; Zhao, N. Emerging sensing and modeling technologies for wearable and cuffless blood pressure monitoring. NPJ Digit. Med. 2023, 6, 93. [Google Scholar] [CrossRef] [PubMed]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1–R39. [Google Scholar] [CrossRef] [PubMed]
- Kario, K.; Hoshide, S.; Mizuno, H.; Kabutoya, T.; Nishizawa, M.; Yoshida, T.; Abe, H.; Katsuya, T.; Fujita, Y.; Okazaki, O.; et al. Nighttime blood pressure phenotype and cardiovascular prognosis: Practitioner-based nationwide JAMP study. Circulation 2020, 142, 1810–1820. [Google Scholar] [CrossRef] [PubMed]
- Parati, G. Nocturnal Hypertension and associated mechanisms. In Proceedings of the 32nd European Meeting on Hypertension and Cardiovascular Protection, Milan, Italy, 23–26 June 2023. [Google Scholar]
- Mukkamalla, S.K.R.; Kashyap, S.; Recio-Boiles, A.; Babiker, H.M. Gallbladder Carcinoma. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2023. [Google Scholar]
- Sola, A.M.; David, A.P.; Rosbe, K.W.; Baba, A.; Ramirez-Avila, L.; Chan, D.K. Prevalence of SARS-CoV-2 infection in children without symptoms of coronavirus disease 2019. JAMA Pediatr. 2021, 175, 198–201. [Google Scholar] [CrossRef]
- Stergiou, G.S.; Mukkamala, R.; Avolio, A.; Kyriakoulis, K.G.; Mieke, S.; Murray, A.; Parati, G.; Schutte, A.E.; Sharman, J.E.; Asmar, R.; et al. Cuffless blood pressure measuring devices: Review and statement by the European Society of Hypertension working group on blood pressure monitoring and cardiovascular variability. J. Hypertens. 2022, 40, 1449–1460. [Google Scholar] [CrossRef]
- The Aurora-BP Study and Dataset. Available online: https://github.com/microsoft/aurorabp-sample-data/ (accessed on 2 November 2022).
- Stergiou, G.S.; Avolio, A.P.; Palatini, P.; Kyriakoulis, K.G.; Schutte, A.E.; Mieke, S.; Kollias, A.; Parati, G.; Asmar, R.; Pantazis, N.; et al. European Society of Hypertension recommendations for the validation of cuffless blood pressure measuring devices. J. Hypertens. 2023, 12, 10–97. [Google Scholar]
- Tanveer, M.S.; Hasan, M.K. Cuffless blood pressure estimation from electrocardiogram and photoplethysmogram using waveform-based ANN-LSTM network. Biomed. Signal Process. Control 2019, 51, 382–392. [Google Scholar] [CrossRef]
- Eom, H.; Lee, D.; Han, S.; Hariyani, Y.S.; Lim, Y.; Sohn, I.; Park, K.; Park, C. End-To-End Deep Learning Architecture for Continuous Blood Pressure Estimation Using Attention Mechanism. Sensors 2020, 20, 2338. [Google Scholar] [CrossRef]
- Sadrawi, M.; Lin, Y.-T.; Lin, C.-H.; Mathunjwa, B.; Fan, S.-Z.; Abbod, M.F.; Shieh, J.-S. Genetic Deep Convolutional Autoencoder Applied for Generative Continuous Arterial Blood Pressure via Photoplethysmography. Sensors 2020, 20, 3829. [Google Scholar] [CrossRef]
- Athaya, T.; Choi, S. An Estimation Method of Continuous Non-Invasive Arterial Blood Pressure Waveform Using Photoplethysmography: A U-Net Architecture-Based Approach. Sensors 2021, 21, 1867. [Google Scholar] [CrossRef]
- Jeong, D.U.; Lim, K.M. Combined deep CNN-LSTM network-based multitasking learning architecture for noninvasive continuous blood pressure estimation using difference in ECG-PPG features. Sci. Rep. 2021, 11, 13539. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Wang, H.; Zhao, Y.; Li, Y.; Tsui, K.L. An Adaptive Weight Learning-Based Multitask Deep Network for Continuous Blood Pressure Estimation Using Electrocardiogram Signals. Sensors 2021, 21, 1595. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Wang, D.; Yang, C. PPG-based blood pressure estimation can benefit from scalable multi-scale fusion neural networks and multi-task learning. Biomed. Signal Process. Control 2022, 78, 103891. [Google Scholar] [CrossRef]
- Ibtehaz, N.; Mahmud, S.; Chowdhury, M.E.H.; Khandakar, A.; Khan, M.S.; Ayari, M.A.; Tahir, A.M.; Rahman, M.S. PPG2ABP: Translating Photoplethysmogram (PPG) Signals to Arterial Blood Pressure (ABP) Waveforms. Bioengineering 2022, 9, 692. [Google Scholar] [CrossRef]
- Jiang, H.; Zou, L.; Huang, D.; Feng, Q. Continuous Blood Pressure Estimation Based on Multi-Scale Feature Extraction by the Neural Network with Multi-Task Learning. Front. Neurosci. 2022, 16, 883693. [Google Scholar] [CrossRef]
- Mahmud, S.; Ibtehaz, N.; Khandakar, A.; Tahir, A.M.; Rahman, T.; Islam, K.R.; Hossain, M.S.; Rahman, M.S.; Musharavati, F.; Ayari, M.A.; et al. A Shallow U-Net Architecture for Reliably Predicting Blood Pressure (BP) from Photoplethysmogram (PPG) and Electrocardiogram (ECG) Signals. Sensors 2022, 22, 919. [Google Scholar] [CrossRef]
- Seok, W.; Lee, K.J.; Cho, D.; Roh, J.; Kim, S. Blood Pressure Monitoring System Using a Two-Channel Ballistocardiogram and Convolutional Neural Networks. Sensors 2021, 21, 2303. [Google Scholar] [CrossRef]
- Treebupachatsakul, T.; Boosamalee, A.; Shinnakerdchoke, S.; Pechprasarn, S.; Thongpance, N. Cuff-Less Blood Pressure Prediction from ECG and PPG Signals Using Fourier Transformation and Amplitude Randomization Preprocessing for Context Aggregation Network Training. Biosensors 2022, 12, 159. [Google Scholar] [CrossRef]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuff-less high-accuracy calibration-free blood pressure estimation using pulse transit time. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 1006–1009. [Google Scholar]
- Mahardika, T.N.Q.; Fuadah, Y.N.; Jeong, D.U.; Lim, K.M. PPG Signals-Based Blood-Pressure Estimation Using Grid Search in Hyperparameter Optimization of CNN–LSTM. Diagnostics 2023, 13, 2566. [Google Scholar] [CrossRef]
- van Vliet, M.; Monnink, S.H.; Kuiper, M.J.; Constandse, J.C.; Hoftijzer, D.; Ronner, E. Evaluation of a novel cuffless photoplethysmography-based wristband for measuring blood pressure according to the regulatory standards. Eur. Heart J.—Digit. Health 2024, 5, 335–343. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, L.; Li, C.; Peng, J.; Hu, Q.; Sun, Y.; Ren, H.; Lyu, W.; Jin, W.; Tian, J.; et al. AI-driven system for non-contact continuous nocturnal blood pressure monitoring using fiber optic ballistocardiography. Commun. Eng. 2024, 3, 183. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.-H.; Sun, Y.; Wu, B.-Y.; Chen, W.; Zhu, X. Using machine learning models for cuffless blood pressure estimation with ballistocardiogram and impedance plethysmogram. Front. Digit. Health 2025, 7, 1511667. [Google Scholar] [CrossRef] [PubMed]
- Kasbekar, R.S.; Ji, S.; Clancy, E.A.; Goel, A. Optimizing the input feature sets and machine learning algorithms for reliable and accurate estimation of continuous, cuffless blood pressure. Sci. Rep. 2023, 13, 7750. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. Optimal signal quality index for photoplethysmogram signals. Bioengineering 2016, 3, 21. [Google Scholar] [CrossRef]
- Kasbekar, R.S.; Mendelson, Y. Evaluation of key design parameters for mitigating motion artefact in the mobile reflectance PPG signal to improve estimation of arterial oxygenation. Physiol. Meas. 2018, 39, 075008. [Google Scholar] [CrossRef]
- Wang, W.; Mohseni, P.; Kilgore, K.L.; Najafizadeh, L. PulseDB: A large, cleaned dataset based on MIMIC-III and VitalDB for benchmarking cuff-less blood pressure estimation methods. Front. Digit. Health 2023, 4, 1090854. [Google Scholar] [CrossRef]
- Lee, H.-C.; Park, Y.; Yoon, S.B.; Yang, S.M.; Park, D.; Jung, C.-W. VitalDB, a high-fidelity multi-parameter vital signs database in surgical patients. Sci. Data 2022, 9, 1–9. [Google Scholar] [CrossRef]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef]
- Elgendi, M.; Norton, I.; Brearley, M.; Abbott, D.; Schuurmans, D. Systolic peak detection in acceleration photoplethysmograms measured from emergency responders in tropical conditions. PLoS ONE 2013, 8, e76585. [Google Scholar] [CrossRef]
- IEC/AAMI 80601-2-30:2018; Medical Electrical Equipment—Part 2–30: Requirements for Basic Safety and Essential Performance of Automated Non-Invasive Sphygmomanometers. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2018.
- Lubba, C.H.; Sethi, S.S.; Knaute, P.; Schultz, S.R.; Fulcher, B.D.; Jones, N.S. catch22: CAnonical Time-series CHaracteristics: Selected through highly comparative time-series analysis. Data Min. Knowl. Discov. 2019, 33, 1821–1852. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- O’Brien, E.; Petrie, J.; Littler, W.; de Swiet, M.; Padfield, P.L.; Altman, D.G.; Bland, M.; Coats, A.; Atkins, N. An outline of the revised British Hypertension Society protocol for the evaluation of blood pressure measuring devices. J. Hypertens. 1993, 11, 677–679. [Google Scholar] [CrossRef] [PubMed]
- Schrumpf, F.; Frenzel, P.; Aust, C.; Osterhoff, G.; Fuchs, M. Assessment of Non-Invasive Blood Pressure Prediction from PPG and rPPG Signals Using Deep Learning. Sensors 2021, 21, 6022. [Google Scholar] [CrossRef] [PubMed]
- Leitner, J.J.; Chiang, P.-H.; Dey, S. Personalized blood pressure estimation using photoplethysmography: A transfer learning approach. IEEE J. Biomed. Health Inform. 2022, 26, 218–228. [Google Scholar] [CrossRef]
- Bresch, E.; Derkx, R.; Paulussen, I.; Noordergraaf, G.J.; Schmitt, L.; Muehlsteff, J. Personalization of pulse arrival time-based blood pressure surrogates through single spot check measurements. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Guadalajara, Mexico, 1–5 November 2021; pp. 5437–5440. [Google Scholar]
- Samartkit, P.; Pullteap, S.; Bernal, O. A non-invasive heart rate and blood pressure monitoring system using piezoelectric and photoplethysmographic sensors. Measurement 2022, 196, 111211. [Google Scholar] [CrossRef]
- Lin, Q.; Huang, J.; Yang, J.; Huang, Y.; Zhang, Y.; Wang, Y.; Zhang, J.; Wang, Y.; Yuan, L.; Cai, M.; et al. Highly sensitive flexible iontronic pressure sensor for fingertip pulse monitoring. Adv. Healthc. Mater. 2020, 9, 2001023. [Google Scholar] [CrossRef]
- Nichols, W.W. Clinical measurement of arterial stiffness obtained from noninvasive pressure waveforms. Am. J. Hypertens. 2005, 18, 3S–10S. [Google Scholar] [CrossRef]
| Authors | Year | Sensor Signal | Method Used | Sample Size | Data Source | Study Duration | Mean ± SD Errors (mm Hg) |
|---|---|---|---|---|---|---|---|
| Tanveer et al. | [10]/2019 | ECG, PPG | Artificial neural network-long short-term memory network | 39 (hemodynamically compromised) | Prospective | Short term (40 s) | SBP: 1.10 (MAE) DBP: 0.58 (MAE) |
| Eom et al. | [11]/2020 | PPG | Convolution neural network and bi-directional gated recurrent network | 15 (healthy) | Prospective | Short term (<1 h) | SBP: −0.20 ± 5.83 DBP: −0.02 ± 4.91 |
| Sadrawi et al. | [12]/2020 | PPG | Genetic deep convolution autoencoder | 18 (healthy, hemodynamically compromised) | Prospective | Short term (<6 h) | SBP: −1.66 ± 7.496 DBP: 0.66 ± 3.31 |
| Athaya et al. | [13]/2021 | PPG | U-net deep learning architecture | 100 (hemodynamically compromised) | MIMIC, MIMIC III | Short term (3.4 h) | SBP: 3.68 ± 4.42 DBP: 1.97 ± 2.92 MAP: 2.17 ± 3.06 |
| Jeong et al. | [14]/2021 | ECG, PPG | Convolution neural network-long short-term memory combination | 48 (healthy) | Prospective | Short Term (<800 s) | SBP: 0.2 ± 1.3 DBP: 0.0 ± 1.6 |
| Fan et al. | [15]/2021 | ECG | Bi-layer long short-term memory network | 942 (hemodynamically compromised) | MIMIC II | Short Term (~230 s) | SBP: 7.69 ±10.83 DBP: 4.36 ± 5.90 MAP: 4.76 ± 6.47 |
| Hu Q et al. | [16]/2022 | PPG | Convolution neural network with attention mechanism, multi-task learning | 1825 (hemodynamically compromised) | UC, Irvine database | Short Term (<20 min) | SBP: 0.97 ± 8.87 DBP: 0.55 ± 4.23 |
| Ibtehaz et al. | [17]/2022 | PPG | Two-stage cascaded convolution neural network | 942 (healthy and hemodynamically compromised) | MIMIC III | Short Term (<30 min) | SBP: 5.7 ± 9.2 DBP: 3.4 ± 6.1 MAP: 2.3 ± 4.4 |
| Jiang et al. | [18]/2022 | ECG, PPG | Neural network with multi-task learning | 3000 (hemodynamically compromised) | MIMIC-II | Short Term (60 h) | SBP: 4.04 ± 5.8 DBP: 2.29 ± 3.55 MAP: 2.46 ± 3.58 |
| Mahmud et al. | [19]/2022 | ECG, PPG | Shallow one-dimensional auto-encoder (U-net architecture) | 942 (hemodynamically compromised) | MIMIC II | Short Term (<21 min) | SBP: 2.73 (MAE) DBP: 1.17 (MAE) |
| Seok et al. | [20]/2021 | BCG | Convolution neural network | 30 (healthy) | Prospective | Short Term (<10 s) | SBP: 0.93 ± 6.24 DBP: 0.21 ± 5.42 |
| Treebupachatsakul et al. | [21]/2022 | ECG, PPG | Fourier transformation followed by deep learning | >2500 (healthy and hemodynamically compromised) | Kachuee et al., 2015 [22] | Short Term (<30 min) | SBP: 7 DBP: 6 |
| Mahardika et al. | [23]/2023 | PPG, ABP | Convolution neural network, long short-term memory network | 55 | MIMIC-III | Short Term (<5 min) | SBP: 0.13 ± 7.04 DBP: 0.48 ± 3.79 |
| Vliet et al. | [24]/2024 | PPG | Machine learning algorithm—exact method not disclosed | 124 | Prospective | Short Term (<30 s) | SBP: ±3.7 ± 4.4 DBP: ±2.5 ± 3.7 |
| Huang et al. | [25]/2024 | BCG | Deep learning UUNet | 40 (nighttime) | Kansas dataset | Short term (<30 min) | SBP: −0.19 ± 8.31 DBP: −0.04 ± 4.48 |
| Liu et al. | [26]/2025 | BCG, IPG | Random forest, XGBoost | 17 | Prospective (healthy) | Short term (<18 min) | SBP, MAD: 3.54 DBP, MAD: 2.57 |
| Lasso | Random Forest | ResNET | |
|---|---|---|---|
| Type | Machine Learning | Machine Learning | Deep Learning |
| Principle | Based on least square multiple regression adjusted for overfitting | Based on an ensemble of decision trees based on bagging or boosting these trees | Based on multiple layers (18) of convolution neural networks with batch normalization and ReLU activation function |
| Cross-validation | Yes—10-fold | Yes—10-fold | Yes—5-fold |
| Complexity | Low | Medium | High |
| Hyperparameter | Alpha—Lasso to ridge ratio | Learning rate, leaf size, learning cycles, splits and features to sample | Number of epochs, learning rate |
| Computation time | Low | High | High |
| Input feature type | Binary, numerical | Binary, numerical | Binary, numerical, and categorical |
| Fit parameters | 100 | 492 | 840 |
| Data amount (>10 times fit parameter) | Can work with relatively less data | Needs more data for effective performance | Needs large amounts of data |
| Descriptor | Training Subjects | Validation Subjects | Test Subjects |
|---|---|---|---|
| Male | 751 (58%) | 69 (59%) | 69 (59%) |
| Female | 542 (42%) | 47 (41%) | 47 (41%) |
| Age (>40 years) | 1137 (88%) | 103 (89%) | 103 (89%) |
| Total | 1293 | 116 | 116 |
| (a) | ||||||
| Lasso | Random Forest | ResNET | ||||
| μ ± SD | (MAE) | μ ± SD | (MAE) | μ ± SD | (MAE) | |
| SBP | −2.11 ± 18.78 | 14.25 | −1.08 ± 18.76 | 14.20 | −1.86 ± 19.55 | 14.69 |
| DBP | −0.68 ± 11.77 | 9.18 | −0.24 ± 11.06 | 8.56 | 0.11 ± 11.55 | 9.06 |
| (b) | ||||||
| Lasso | Random Forest | ResNET | ||||
| μ ± SD | (MAE) | μ ± SD | (MAE) | μ ± SD | (MAE) | |
| SBP * | −1.51 ± 8.04 | 4.88 | −1.32 ± 7.97 | 4.95 | −1.31 ± 7.91 | 4.83 |
| DBP * | −0.52 ± 4.69 | 2.62 | −0.43 ± 4.62 | 2.60 | 0.10 ± 4.59 | 2.65 |
| (c) | ||||||
| Absolute Difference | ||||||
| ≤5 mm Hg | ≤10 mm Hg | ≤15 mm Hg | Grade | |||
| BHS Standard | SBP, DBP | 60% | 85% | 95% | A | |
| 50% | 75% | 90% | B | |||
| 40% | 65% | 80% | C | |||
| Worse than C | D | |||||
| Proposed Model: Personalized, ResNET | SBP | 65.8% | 91.7% | 95% | A | |
| DBP | 85.9% | 96.8% | 98.6% | A | ||
| Method | SBP | DBP |
|---|---|---|
| F-Statistic, p-Value | F-Statistic, p-Value | |
| Machine Learning Algorithm | F(1) = 0.00, 0.99 | F(1) = 0.19, 0.82 |
| Method (Calibration-free vs. Personalized) | F(2) = 45.9, 0.00 | F(2) = 46.9, 0.00 |
| Method | Systolic BP Estimation Errors | Diastolic BP Estimation Errors | ||||
|---|---|---|---|---|---|---|
| Bias | SD | MAE | Bias | SD | MAE | |
| Estimated by algorithm (in mm Hg) | −1.31 | 7.91 | 4.83 | 0.10 | 4.59 | 2.65 |
| Estimated using ”ground truth” (in mm Hg) | −1.21 | 19.46 | 14.75 | −0.40 | 13.68 | 9.87 |
| p-values and F-statistic, bias (ANOVA) | F = 1.28, p = 0.26 | F = 2.06, p = 0.15 | ||||
| p-values and F-statistic, variance (Levene’s test) | F = 91.42, p = 0.00 | F = 99.04, p = 0.00 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasbekar, R.S.; Radhakrishnan, S.; Ji, S.; Goel, A.; Clancy, E.A. Optimizing Input Feature Sets Using Catch-22 and Personalization for an Accurate and Reliable Estimation of Continuous, Cuffless Blood Pressure. Bioengineering 2025, 12, 493. https://doi.org/10.3390/bioengineering12050493
Kasbekar RS, Radhakrishnan S, Ji S, Goel A, Clancy EA. Optimizing Input Feature Sets Using Catch-22 and Personalization for an Accurate and Reliable Estimation of Continuous, Cuffless Blood Pressure. Bioengineering. 2025; 12(5):493. https://doi.org/10.3390/bioengineering12050493
Chicago/Turabian StyleKasbekar, Rajesh S., Srinivasan Radhakrishnan, Songbai Ji, Anita Goel, and Edward A. Clancy. 2025. "Optimizing Input Feature Sets Using Catch-22 and Personalization for an Accurate and Reliable Estimation of Continuous, Cuffless Blood Pressure" Bioengineering 12, no. 5: 493. https://doi.org/10.3390/bioengineering12050493
APA StyleKasbekar, R. S., Radhakrishnan, S., Ji, S., Goel, A., & Clancy, E. A. (2025). Optimizing Input Feature Sets Using Catch-22 and Personalization for an Accurate and Reliable Estimation of Continuous, Cuffless Blood Pressure. Bioengineering, 12(5), 493. https://doi.org/10.3390/bioengineering12050493







